在小样本数据处理方法上,游文杰等[2]利用非参数检验和偏最小二乘回归理论建立了小样本的预测模型,并通过算例证明了该方法对小样本数据的可行性;罗为和刘鲁[3]利用优化的最小二乘方法建立了小样本的预测模型,实现了无人机研制费用的预测。除对小样本数据建立模型进行预测分析外,还可用Bootstrap重抽样方法对小样本进行扩充,变成易于分析的大样本数据。张守玉和封伟书[4]在分析了3种基于Bootstrap的抽样样本产生法的优劣的基础上,优选出了与正态分布拟合程度高,具有实际应用价值的Bootstrap样本产生法。文献[5-6]则指出用Bootstrap方法产生的随机样本是有偏差的,在小样本情况下要慎用Bootstrap进行仿真。针对上述问题,文献[7]利用验前信息弥补了现场试验信息的不足,在将验前信息与试验数据相融合的基础上,再借助Bootstrap方法进行小样本数据的处理,提高了试验评估的精度。
根据小样本少数据、贫信息的特点,还可采用邓聚龙[8]教授提出的灰色系统理论进行研究。曾波和刘思峰[9]提出了一种基于灰色关联度的小样本预测模型,用灰色关联理论成功实现了小样本的数据处理问题。刘义等[10]在灰色系统理论的基础上,提出了灰色距离测度的概念,并基于此设计了小样本数据的区间估计方法,给出了满
足一定灰色置信度的灰色置信区间的计算方法。利用该方法可量化系统的评估结果,对工程中的小样本数据评估问题具有重要意义。文献[11]将小样本数据的3种灰色区间估计方法进行了对比,分析了各方法的性能及相互之间的关系。
在以上研究的基础上,重新定义了灰色距离及灰色置信度的概念,并给出了灰色置信区间的具体计算方法,之后提出了将Bootstrap方法与小样本区间估计方法相结合的灰色区间估计方法。利用Bootstrap方法对小样本数据进行重抽样,获得多个与原样本具有相同样本量的相似样本。然后利用灰色置信度理论,计算各个样本满足一定灰色置信度的灰色置信区间。之后对各个灰色置信区间求交集,即可得到原始小样本的更加精确、范围更小的灰色置信区间。最后通过算例仿真,验证了上述方法的有效性。
1 相关定义及理论 1.1 重抽样方法 关于Bootstrap重抽样的方法有很多,本文采用对经验分布进行抽样[4, 12]的方式:
1) 取η=R(0, 1) ,R(0, 1) 可以产生[0,1]>内的任意小数。
2) 定义P=η(n-1) ,M=[P],[·]表示向最近的整数取整,并且满足
 | (1) |
3) 则再生样本的产生方式为
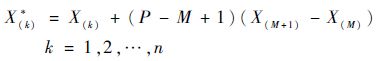 | (2) |
1.2 灰色系统理论 灰色系统理论[13-14]是研究传统概率统计、模糊数学等理论难以解决的“少数据”、“贫信息”的不确定性问题。通过发掘数据之间的潜在关系,获得新的信息,用于解决新问题。
定义1 给定样本空间X={x1, x2, …, xn}∈Rn,xi与yi的距离为
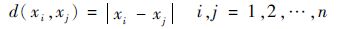 | (3) |
定义2 对于给定的数据样本空间X={x1, x2, …, xn}∈Rn,样本X的灰色估计值为
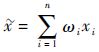 | (4) |
式中:ωi为样本元素xi在灰色估计值
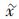
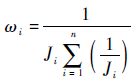 | (5) |
式中:Ji为元素xi与其他元素之间的平均距离,其定义为
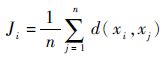 | (6) |
注1 式(5) 中的权重与样本之间的距离是相关的。当式(6) 中的平均距离越大,则式(5) 中的权重越小。这也就意味着,样本元素在样本空间越密集,则相应的样本元素的权重越大。相对于文献[15-16],这里的定义考虑的因素更全面。
定义3 设样本空间X={x1, x2, …, xn}∈Rn,其灰色估计值为
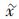
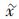
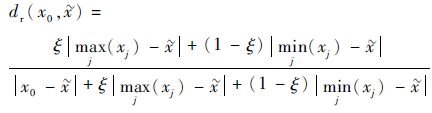 | (7) |
式中:
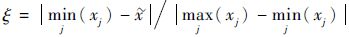
注2 式(7) 定义的灰色置信度考虑了样本元素的密度对灰色权重的影响,而不同于文献[16]只考虑了样本拓扑。当样本中的最大元素
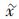
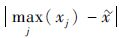
定义4 设定一个灰色置信度α,则根据该置信度求得的被估计参数x0的取值区间称为满足灰色置信度α的灰色置信区间[16-17]。
定理1 对于已知数据样本X={x1, x2, …, xn},给定一个灰色置信度α,则灰色置信区间为
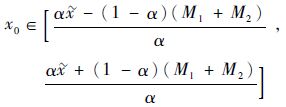 | (8) |
式中:
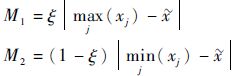 |
证明根据灰色置信度的概念,可得
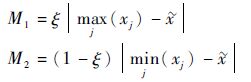 | (9) |
将式(7) 代入式(9) 中,有
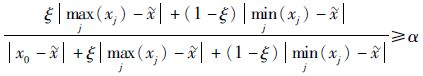 | (10) |
方程式(10) 可进一步转化为
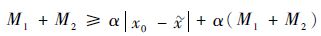 | (11) |
当x0-
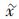
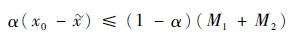 | (12) |
则有
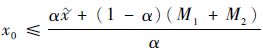 | (13) |
当x0-
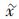
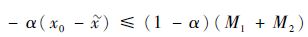 | (14) |
则
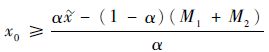 | (15) |
因此,对于x0的灰色置信区间为
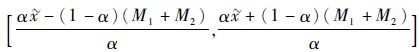
证毕
注3 式(13) 是灰色置信区间的上限,记为x0u;式(15) 是灰色置信区间的下限,记为x0l。则式(8) 可进一步表达为x0∈x0l, x0u。
注4 根据定理1,如果任一元素落入某一灰色置信区间内,则可以获知该元素的灰色置信度。因此,对于给定的样本空间中的任意元素,可以计算它的灰色置信度。
2 算法及步骤 2.1 算法的基本思想 基于小样本的区间估计方法可以求得满足一定灰色置信度的灰色置信区间。但该计算是在小样本数据的基础上进行的,小样本数据覆盖的信息量少,所以求得的灰色置信区间可能偏差较大。本文借助重抽样方法的思想,对求得的灰色置信区间进行了修正。
利用Bootstrap的重抽样方法对原始小样本作有放回的重抽样,获得N组具有相同样本量的相似样本;然后分别计算各个样本满足一定灰色置信度的灰色置信区间;最后将各个灰色置信区间求交集,即可得到原始小样本的精度更高、范围更为准确的灰色置信区间。
2.2 算法的计算步骤 设给定的小样本数据为X={x1, x2, …, xn},则利用改进的算法计算满足一定灰色置信度的灰色置信区间的具体步骤如下:
步骤1 利用Bootstrap方法对小样本X进行重复抽样,获得N组样本,记为Xk={xk1, xk2, …, xkn},k=1, 2, …, N,每组中的样本个数与原小样本X中的样本个数相同。
步骤2 对于第k组样本,计算样本中某一元素xki(i=1, 2, …,n)相对于该样本中其他元素的灰色距离
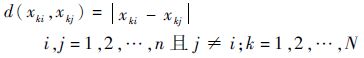 | (16) |
步骤3 计算元素xki相对于其他各元素的平均灰色距离,即
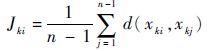 | (17) |
步骤4 计算元素xki在小样本中的灰色权重
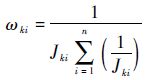 | (18) |
步骤5 计算第k组样本的灰色估计值
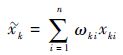 | (19) |
步骤6 取灰色置信度α,根据定理1可得第k组样本的灰色置信区间为
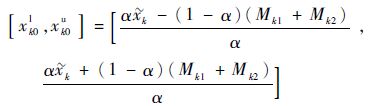 | (20) |
式中:
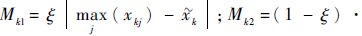

步骤7 重复上述步骤,可求得(N+1) 组(包括原始样本)样本的(N+1) 个灰色置信区间,将各区间求交集,则原小样本X的满足置信度α的灰色置信区间为
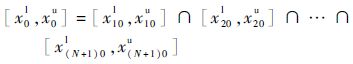 | (21) |
3 仿真分析 仿真1 取试验数据样本X={10.6,10.8,9.9,10.3,10.4,11.0,9.7,11.2,11.4,10.5,9.3,9.6,10.6,10.2,10.9,9.6},共16个数据。
1) 用传统概率统计方法求置信区间
假设数据服从正态分布,则样本X的均值和方差分别为
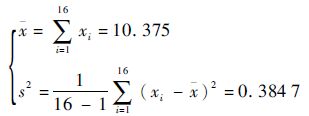 | (22) |
取置信度95%,则求得的置信区间为[10.071 1, 10.678 9]。
2) 用本文方法求灰色置信区间
利用Bootstrap方法对样本X作重复抽样,获得4组相似样本如下:
 |
按2.2节中的步骤,取灰色置信度95%,则计算得到原始样本、4个抽样样本的置信区间及最终的置信区间如表 1所示。
表 1 各样本的灰色置信区间 Table 1 Grey confidence interval of each sample
| 样本 | 灰色置信区间 | 区间宽度 |
| X | [10.005 5, 10.605 5] | 0.600 0 |
| X1 | [10.043 3, 10.601 5] | 0.558 2 |
| X2 | [10.132 1, 10.692 0] | 0.559 9 |
| X3 | [9.993 5, 10.548 4] | 0.554 9 |
| X4 | [10.111 0, 10.672 2] | 0.561 2 |
| 最终区间 | [10.132 1, 10.548 4] | 0.416 3 |
表选项
对比表 1中的最终的灰色置信区间与传统概率统计方法求得的置信区间,可见二者很接近。由此说明,在样本量较大的情况下,本文的方法与传统概率统计方法在求置信区间问题上是等效的。同时也证明了本文方法的有效性。图 1给出了传统概率分布曲线与本文方法的灰色置信区间曲线的对比。
 |
| 图 1 传统概率分布曲线与灰色置信区间曲线对比 Fig. 1 Comparison between traditional probability distribution curve and grey confidence interval curve |
| 图选项 |
图 1中的传统概率分布曲线是满足样本条件的概率密度函数曲线的归一化形式。从图 1可见,两种方法的置信度与样本值关系的分布趋势是相同的,置信度最大处的样本取值也基本一致。进一步证明了本文方法的合理性。
此外,表 1中给出了只利用原始样本X的数据求得的灰色置信区间[10.005 5 , 10.605 5],与最终的置信区间[10.132 1, 10.548 4]相比,前者的区间宽度要宽。在相同的灰色置信度下,后者则更加精确。
仿真2 取小样本数据X′={10.4,9.7,11.2,9.3}。由于样本量过少,不能采用传统概率统计方法进行区间估计,只能采用本文的灰色区间估计方法。用Bootstrap方法生成4 组相似小样本分别为
 |
取灰色置信度95%,则计算得到原始样本、4个抽样样本的置信区间及最终的置信区间如表 2所示。
表 2 各小样本的灰色置信区间 Table 2 Grey confidence interval of each small sample
| 样本 | 置信区间 | 区间宽度 |
| X′ | [9.765 0, 10.354 5] | 0.589 5 |
| X′1 | [9.965 1, 10.509 9] | 0.544 8 |
| X′2 | [10.055 4, 10.605 4] | 0.550 0 |
| X′3 | [9.999 5, 10.546 9] | 0.547 4 |
| X′4 | [9.704 9, 10.244 4] | 0.539 5 |
| 最终区间 | [10.055 4, 10.244 4] | 0.189 0 |
表选项
从表 2中可见,经过求交集后,最终的置信区间宽度减小为0.189 0,区间更窄,相对精度进一步提高。各小样本灰色置信区间曲线对比如图 2所示。
从图 2中可见,各小样本的灰色置信区间相互交错,通过取交集的方式可以获得较为精确的置信区间,排除随机误差等因素对结果的影响。
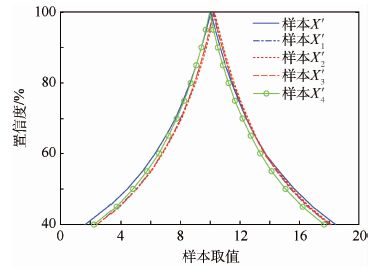 |
| 图 2 灰色置信区间曲线对比 Fig. 2 Comparison of grey confidence interval curves |
| 图选项 |
在同样的小样本数据条件下,利用文献[10]中的计算方法,计算得到的灰色置信区间为[9.979 3, 10.568 8],相比于表 2中的最终区间,这个区间要更宽。因此,其精确度就差一些。另外,用文献[10]中的方法计算样本的灰色估计值为10.274 0,而利用本文中的方法计算的灰色估计值为10.149 9。对比两个灰色估计值可看到,本文中的灰色估计值离样本元素密集的区域更近一些,因此也验证了定义2的有效性。
为了将本文方法与文献[10]中的方法做更多方面的对比说明,分别计算了两种方法在不同置信水平下的置信区间,如表 3所示。
表 3 不同置信度时两种方法对比 Table 3 Comparison of two methods at different confidence levels
| 置信度/% | 本文方法置信区间 | 文献[10]方法置信区间 |
| 75 | [9.966 0, 10.598 6] | [8.407 4, 12.140 7] |
| 80 | [10.045 1, 10.519 5] | [8.874 0, 11.674 0] |
| 90 | [10.176 8, 10.387 7] | [9.651 8, 10.896 3] |
表选项
从表 3可见,每一种方法的置信区间宽度均随着置信水平的提高而变得更窄。同时,在每一个置信水平下,本文方法计算得到的置信区间均包含于文献[10]方法计算得到的置信区间中,再次说明了本文所提出的方法计算精度更高一些。
仿真3 设在某新型导弹试验系统中,由于多种不确定因素的存在,建立了5种不同的导弹模型,但尚没有统一的标准确定哪一种模型更可信,需要先通过仿真初步评估各个模型的可信度。通过仿真给各个模型相同的输入量,则在某一时刻获得的各个模型的输出结果为{3.2, 2.6, 1.3, 1.8, 2.9}。将这5个输出数据作为小样本数据,采用本文的方法进行评估。
当灰色置信度选择90%时,根据2.2节,计算得到的灰色置信区间为[x0l, x0u]=[2.015 5, 2.808 6]。由此说明,如果某个模型的输出结果处于上述区间内时,该模型输出结果的可信度为90%,进而可得该模型的相对可信度为90%。
当采取不同的灰色置信度时,则相应的灰色置信区间如表 4所示。
表 4 不同置信度下的置信区间 Table 4 Confidence interval of different confidence levels
| 置信度/% | 置信区间 | 区间宽度 |
| 75 | [1.794 6, 2.880 7] | 1.086 1 |
| 80 | [1.823 6, 2.863 3] | 1.039 7 |
| 90 | [1.872 0, 2.834 3] | 0.962 3 |
| 95 | [1.892 3, 2.822 0] | 0.929 7 |
表选项
由表 4可见,随着置信度的提高,置信区间变得越来越小,这与传统的概率统计结果是相似的。
此外,根据本文计算方法,可得到原始样本中各个元素的可信度,如表 5所示。
表 5 各个输出结果的可信度 Table 5 Credibility of each output result
| 输出值 | 3.2 | 2.6 | 1.3 | 1.8 | 2.9 |
| 可信度/% | 53 | 98 | 43 | 69 | 75 |
表选项
由表 5可见,第2个导弹模型具有最高的可信度,而第3个导弹模型的可信度最低。这样就通过仿真计算对导弹的模型可信度做了初步评估。在此基础上可根据试验数据、工程经验等对导弹模型做进一步的评估。
综合上述3组仿真,本文提出的基于重抽样的小样本区间估计方法能够达到小样本区间估计的目的,通过与传统概率统计方法的对比,并结合实际工程问题的仿真,证明了本文方法的合理性和有效性。
4 结论 1) 针对工程中的小样本试验数据量小、信息量不足的特点,提出了基于重抽样的小样本试验系统可信度灰色评估方法。
2) 在小样本区间估计方法的基础上,采用Bootstrap重抽样理论,产生多个相似小样本,最后将各小样本的灰色置信区间求交集,可获得更为精确的置信区间,同时可排除一些随机干扰等因素对估计结果的影响。
3) 通过与传统概率统计方法的仿真对比,并结合导弹模型验证仿真,证明了本文方法的有效性和合理性,可为工程中的系统评估提供一定指导。
参考文献
| [1] | 李裕奇, 赵联文, 王沁, 等. 概率论与数理统计[M].3版.北京: 国防工业出版社, 2009: 202-280.LI Y Q, ZHAO L W, WANG Q, et al. Probability and mathematical statistics[M].3rd ed.Beijing: National Defence Industry Press, 2009: 202-280.(in Chinese) |
| [2] | 游文杰, 吉国力, 袁明顺, 等. 一类小样本的统计方法建模及其可视化[J].数学的实践与认识, 2013, 43(7): 68–75.YOU W J, JI G L, YUAN M S, et al. A small-sample modeling and visualization on statistical methods[J].Mathematics in Practice and Theory, 2013, 43(7): 68–75.(in Chinese) |
| [3] | 罗为, 刘鲁. 基于偏最小二乘法的军用无人机研制费用预测[J].北京航空航天大学学报, 2010, 36(6): 667–670.LUO W, LIU L. Prediction of military UAV development cost based on partial least square regression method[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(6): 667–670.(in Chinese) |
| [4] | 张守玉, 封伟书. 基于Bootstrap方法的正态分布样本数据生成研究[J].装备指挥技术学院学报, 2009, 20(2): 97–100.ZHANG S Y, FENG W S. Study of sampled data creation for norm distribution on Bootstrap method[J].Journal of Academy of Equipment Command & Technology, 2009, 20(2): 97–100.(in Chinese) |
| [5] | 段晓君, 王正明. 小子样下的Bootstrap方法[J].弹道学报, 2003, 15(3): 1–5.DUAN X J, WANG Z M. Applicability of Bootstrap method in small sample case[J].Journal of Ballistics, 2003, 15(3): 1–5.(in Chinese) |
| [6] | MARIEKE E T, CAJO J F, TER B. Bootstrap confidence intervals for principal response curves[J].Computational Statistics & Data Analysis, 2008, 52(4): 1837–1849. |
| [7] | 胡正东, 曹渊, 张士峰, 等. 特小子样试验下导弹精度评定的Bootstrap方法[J].系统工程与电子技术, 2008, 30(8): 1493–1497.HU Z D, CAO Y, ZHANG S F, et al. Bootstrap method for missile precision evaluation under extreme small sample test[J].Systems Engineering and Electronics, 2008, 30(8): 1493–1497.(in Chinese) |
| [8] | DENG J L. Control problems of grey systems[J].Systems & Control Letters, 1982, 1(5): 288–294. |
| [9] | 曾波, 刘思峰. 基于灰色关联度的小样本预测模型[J].统计与信息论坛, 2009, 24(12): 22–26.ZENG B, LIU S F. Small sample prediction model based on grey incidence degree[J].Statistics & Information Forum, 2009, 24(12): 22–26.(in Chinese) |
| [10] | 刘义, 王国玉, 柯宏发. 一种基于灰色距离测度的小样本数据区间估计方法[J].系统工程与电子技术, 2008, 30(1): 116–119.LIU Y, WANG G Y, KE H F. Approach of parameter estimation for small samples based on grey distance measure[J].Systems Engineering and Electronics, 2008, 30(1): 116–119.(in Chinese) |
| [11] | 刘恒, 梅卫, 单甘霖. 小样本数据的三种区间估计方法性能分析[J].系统工程与电子技术, 2014, 36(10): 1929–1933.LIU H, MEI W, SHAN G L. Analysis on performance of three interval estimation methods for small samples[J].Systems Engineering and Electronics, 2014, 36(10): 1929–1933.(in Chinese) |
| [12] | JACK P C K, DAVID D. Validation of regression metamodels in simulation:Bootstrap approach[J].European Journal of Operational Research, 2006, 170(1): 120–131.DOI:10.1016/j.ejor.2004.06.018 |
| [13] | 邓聚龙. 灰色系统理论教程[M].武汉: 华中理工大学出版社, 1990: 5-84.DENG J L. The grey system theory tutorial[M].Wuhan: Huazhong University of Science Press, 1990: 5-84.(in Chinese) |
| [14] | 刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用[M].7版.北京: 科学出版社, 2014: 2-20.LIU S F, YANG Y J, WU L F, et al. The grey system theory and its application[M].7th ed.Beijing: Science Press, 2014: 2-20.(in Chinese) |
| [15] | LIAN Z W,DANG Y G,WANG Z X,et al.Grey distance incidence degree and its properties [C]//Proceedings of 2009 IEEE International Conference on Grey Systems.Piscataway,NJ:IEEE Press,2009:37-41. |
| [16] | 刘义, 王国玉, 柯宏发, 等. 一种应用于外场实验数据处理的非概率参数估计方法[J].信号处理, 2009, 25(1): 113–117.LIU Y, WANG G Y, KE H F, et al. A non-statistical approach of parameter estimation for field data processing[J].Signal Processing, 2009, 25(1): 113–117.(in Chinese) |
| [17] | KE H F, CHEN Y G, LIU Y. Data processing of small samples based on grey distance information approach[J].Journal of Systems Engineering and Electronics, 2007, 18(2): 281–289.DOI:10.1016/S1004-4132(07)60088-7 |
