由于实际工程中被控对象的动态特性一般难以用精确的数学模型来描述,存在不确定性和外部干扰,因此在容错控制系统设计中同时考虑系统的容错性和鲁棒性具有重要意义。鲁棒容错控制能够在被控对象具有不确定性的情况下,依然保证闭环系统的联立镇定和完整性,并且系统的性能指标能够达到设计要求。文献[3]针对航空发动机,设计了基于特征结构配置方法的容错控制系统,但没有考虑输入矩阵不确定性的影响。文献[4]采用基于滑模观测器的控制方法对航天器的飞轮故障进行了鲁棒容错控制。文献[5-6]利用自适应理论设计了高超声速飞行器的鲁棒容错控制器,但无论是自适应理论还是基于观测器的方法实质上都属于主动容错控制,需要对故障进行实时准确的检测,因此其应用具有一定的局限性。由于H∞指标既考虑了自身参数摄动的影响,又刻画了抗外界扰动的能力,因此基于H∞指标的容错控制方法也得到了广泛的研究。文献[7]利用Riccati方程来求解鲁棒容错控制器,求得的控制器不仅能够保证闭环系统的渐近稳定性,还保证了H∞性能,但在Riccati方程的求解过程中缺乏有效的方法来确定待定参数的最佳值,这给控制器设计带来了很大的保守性。文献[8]利用结构H∞和旋翼状态反馈(Rotor State Feedback,RSF)控制理论对旋翼的传感器故障进行了鲁棒容错控制。随着线性矩阵不等式(Linear Matrix Inequality,LMI)技术的发展,利用LMI来解决鲁棒H∞容错控制问题成为发展趋势[9-15],其核心是寻找一个闭环系统的二次型Lyapunov函数,从而保证系统具有渐近稳定性,为了方便计算需要对所有的系统状态使用不同的Lyapunov变量,这会导致控制器的求解变为非凸优化。针对该问题,文献[9-11]对所有的故障情况采用同一种Lyapunov变量,显然由此得到的控制器具有较大的保守性;文献[12-15]利用扩展LMI技术,引入松弛变量,使得Lyapunov变量和系统矩阵解耦,但松弛变量的引入在增加设计自由度的同时也会增加LMI维数。
本文针对一类考虑执行器失效故障和范数有界参数不确定的系统,研究了一种用来求解鲁棒H∞容错跟踪控制问题的迭代LMI算法。该算法允许所有的系统状态使用不同的Lyapunov变量,从而降低了控制系统的保守性;相比于扩展LMI技术,该算法无需额外增加LMI的阶数,就可以解决Lyapunov变量和系统矩阵的耦合问题。通过该算法求得的控制器能够保证闭环系统的鲁棒性小于给定的H∞范数上界;无论在正常和故障情况下都可以实现跟踪控制,并且正常情况下的系统性能最优,从而实现了系统的鲁棒容错控制。
1 问题描述 考虑如下线性系统:
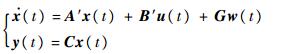 | (1) |
式中:x(t)∈Rn, y(t)∈Rp, u(t)∈Rm, w(t)∈Rh分别为系统状态、输出、输入和外部干扰;A和B分别为合适维数的系统矩阵和输入矩阵,A′=A+ΔA(t),B′=B+ΔB(t),ΔA(t)=EaΣ(t)Fa和ΔB(t)=EbΣ(t)Fb为范数有界不确定参数,Ea、Fa、Eb和Fb为维数合适矩阵,ΣT(t)Σ(t)≤I为时变不确定变量。
在系统式(1)中加入执行器故障,可得系统故障模型为
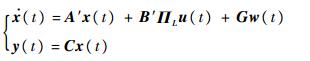 | (2) |
式中:ΠL=diag(πL1, πL2, …, πLm)为执行器效率矩阵,L=0, 1, …, 2m-1。
在控制系统中往往需要对输入指令r(t)进行跟踪,即使系统式(2)的跟踪误差e(t)=r(t)-Csy(t)满足
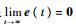
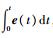
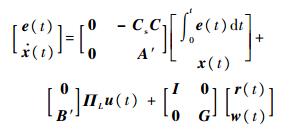 | (3) |
不妨记增广系统状态和系统外部扰动为
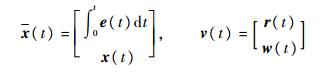 | (4) |
于是可得
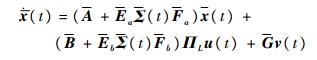 | (5) |
式中:
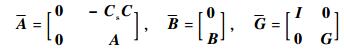 | (6) |
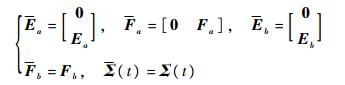 | (7) |
本文控制的目的是:针对增广系统式(6)设计一种控制器使得闭环系统能够渐近稳定。如果只考虑系统的稳定性,可能会导致控制器输出信号u(t)变得很大以致无法实现。为此,需要在设计过程中考虑对控制信号的度量。根据以上设计思想,在增广系统中引入包含系统状态和控制信号的关注输出z(t),于是可得
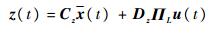 | (8) |
式中:Cz和Dz为加权矩阵,用来平衡跟踪误差和控制能量。
考虑如下状态反馈控制器:
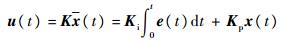 | (9) |
式中:K=[Ki?Kp]∈Rm×(l+n)为需求解的控制增益。
将式(9)代入式(6)、式(8),可得带有执行器故障的闭环系统为
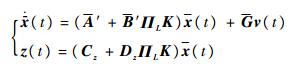 | (10) |
式中:
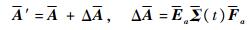 | (11) |
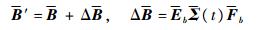 | (12) |
本文设计的控制器需要使得闭环系统式(10)满足以下要求:
1)无论在正常或故障情况下,控制器均能够保证闭环系统渐近稳定。
2)对于带有范数有界不确定性系统式(10),所设计的控制器满足设定的性能指标,同时保证无故障时系统性能最优。
3)无论在正常或故障情况下,输出信号Csy(t)与参考信号r(t)之间无稳态误差。
为了方便下文的描述,给出如下引理。
引理1??Schur补引理。对给定的对称矩阵
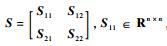
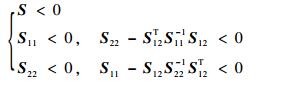 | (13) |
引理2[12, 16-17]??设E、F和Ψ为给定矩阵,Ψ为对称矩阵,且时变参数矩阵Σ(t)满足ΣT(t)·Σ(t)≤I。当
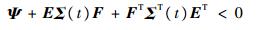 | (14) |
成立时,那么必定存在一个正常数ε满足:
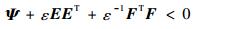 | (15) |
推论??对于实矩阵X、Y,其维数符合相乘法则,存在ε>0使得如下不等式成立:
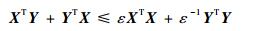 | (16) |
证明??只需令Ψ=0, Σ(t)=I且E=XT, F=Y,即可得结论式(16)。??证毕
H∞范数指标是最优控制理论中最有效的性能指标之一,其主要用来刻画系统抗外来干扰的能力,同时也考虑了对自身参数摄动的抑制能力。H∞范数指标数学描述如下。
考虑如下系统:
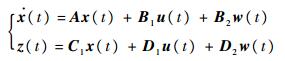 | (17) |
式(17)中,外界干扰w(t)是能量有界信号。H∞控制问题可以表述为:设计一个控制器使得闭环系统渐近稳定,同时关注输出z(t)能量要小于γ倍外部干扰信号的能量,即‖z(t)‖22 < γ‖w(t)‖22,γ为给定正数。由控制理论可知,这实质上就是要求z(t)到w(t)传递函数的无穷范数小于给定的γ值,即‖G(jω)‖∞ < γ。
下面将给出一个将H∞控制问题转化为LMI表达式的重要引理——有界实引理。
引理3??对于可控系统式(17),如果存在一个正定对称矩阵P满足如下不等式:
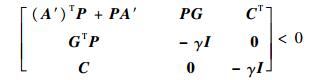 | (18) |
那么该系统是渐近稳定的,且满足‖Gzw(jω)‖∞ < γ。
2 鲁棒容错跟踪控制器设计 为了将本文所要求的鲁棒控制器设计转换为LMI描述,将闭环系统式(10)代入引理3可得
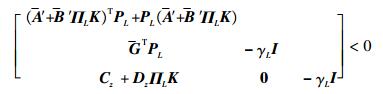 | (19) |
式中:PL和γL分别表示不同故障状态下的Lyapunov变量和鲁棒性能指标。
为了分离出式(19)中不确定参数
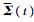
 | (20) |
易得式(20)中不等式右边第1项为对称矩阵,则由引理2可得必存在正标量ε1、ε2,满足:
 | (21) |
由引理1进一步可得
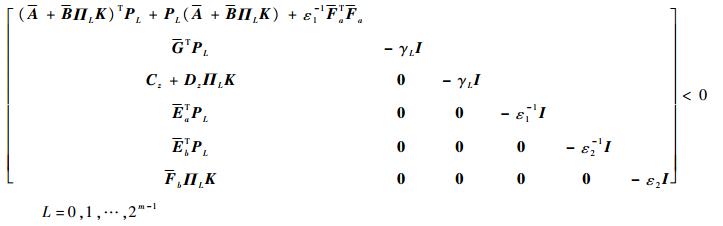 | (22) |
注意式(22)中没有包含不确定参数
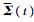
易知式(22)仍属于非凸优化,无法利用现有的LMI工具求解。因此,本文发展了一种迭代LMI算法来解决此问题,为保证该迭代算法的有效运行,需要给出一个合适的初值。文献[19]利用互补线性化方法求解初始控制器,但在多参数线性化过程中,该方法往往无解。因此,本文给出了一种初始控制器求解方法。为了方便叙述,将执行器故障模型进行改写。记:
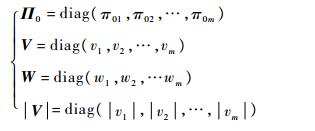 | (23) |
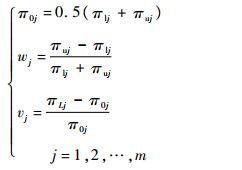 | (24) |
式中:πlj、πuj分别为控制效率矩阵的上、下界。
将式(24)代入式(23),即可得执行器效率矩阵为
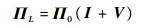 | (25) |
并且易得|V|≤W≤I。
定理1考虑闭环扩维系统式(10),对于给定的H∞范数上界γ,如果存在对称正定矩阵X,矩阵Y、Z和正标量?1~?5,满足:
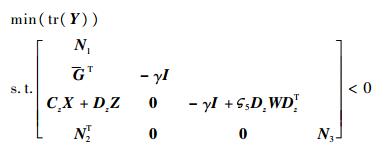 | (26) |
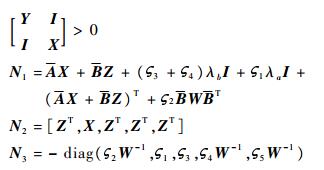 | (27) |
则由此获得的状态反馈增益矩阵K=Π0-1ZX-1必能够保证闭环系统式(10)是渐近稳定的,闭环系统的鲁棒性能小于给定的H∞范数上界。
证明?由引理3可知,闭环系统是渐近稳定的,且满足‖Gzw(jω)‖∞ < γ的充要条件是式(19)成立。不妨对所有的故障情况均使用同一个Lyapunov函数变量P,且对式(19)左右两边同乘以diag(P-1, I, I),并记X=P-1,于是可得
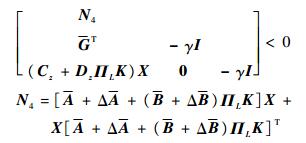 | (28) |
将式(28)进行分解可得
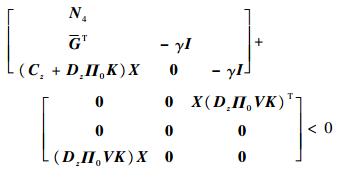 | (29) |
令Z=Π0KX,同时由引理2的推论可得
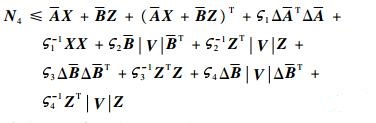 | (30) |
将式(25)代入式(30)可得
 | (31) |
其中
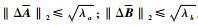
同理可得
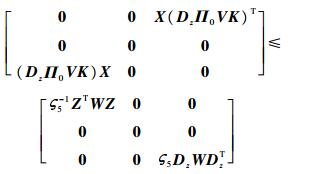 | (32) |
于是可得
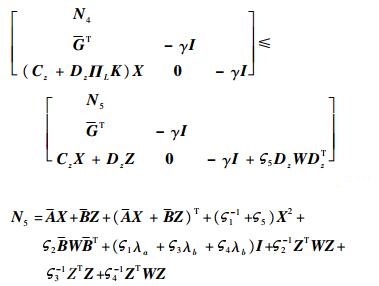 | (33) |
由此可知,不等式(33)右边是式(28)的一个强约束条件,因此不等式
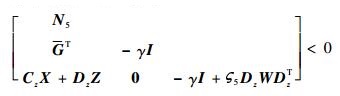 | (34) |
的解也是不等式(28)的解, 进一步由引理1可知,式(34)和式(26)等价,即若有矩阵变量(X, Z)使得不等式(26)成立,则P=X-1必然是引理3所要求的LMI的解,因而由此得到的控制器就能保证闭环系统是渐近稳定的,且鲁棒性能小于给定的H∞范数上界,这就是式(26)的物理意义。
对式(27)应用引理1,可得X-1 < Y等价于P < Y,因此要求tr(Y)极小就是要求tr(P)极小,由保性能控制理论可知,这样做可以保证系统的性能最优,这也就是式(27)的物理意义。??证毕
根据得到的初始控制器K=Π0-1ZX-1, 利用下面给出的迭代LMI算法用来解决式(22)中的非凸求解问题。
Step 1??选择合适的H∞范数上界γ,根据定理1计算初始控制器K0=Π0-1Z0(X0)-1。
Step 2??令K=K0,由LMI式(22)所约束的优化问题,计算得到对应不同故障情况的初始Lyapunov变量PL0。
Step 3??在第j步迭代(j>0)。
1)将PL=PLj-1代入不等式(22),求解其中的优化问题,得到第j步的控制器增益Koptj。
2)将K=Koptj代入不等式(22),求解其中的优化问题,得到第j步的Lyapunov变量PjL。
Step 4??给定一个足够小的阈值σ,若|tr(P0j-P0j-1)| < σ,输出的Kopt=Kjopt作为最优H∞鲁棒容错控制器增益,算法结束。否则,令j=j+1,返回Step 3。
算法的收敛性证明可以参看文献[20]。从迭代算法的步骤中可以看出,本文算法实质是通过两步优化方法实现了Lyapunov变量和控制增益的解耦,从而将非凸优化转化为凸优化。本文算法相比于扩展LMI算法,由于没有引入松弛变量,因此大大降低了LMI表达式的阶数,降低了LMI的求解难度,提高了运算效率;付出的代价是需要对低阶LMI(相对于扩展LMI算法)进行循环求解,但考虑到控制器的计算是离线的,因此这样的代价是可以接受的。
3 仿真实例 为了验证本文算法的有效性,以多操纵面高超声速飞行器X-33为对象,设计了飞行跟踪控制器。关于X-33模型的详细内容可以参考文献[21]。本文选取再入段做仿真研究,飞行器的系统状态x(t)=[β, Φ, α, p, q, r]T, 分别为侧滑角、滚转角、迎角、滚转角速率、俯仰角速率和偏航角速率;飞行器的输出y(t)=x(t);舵面输入u(t)=[δir, δil, δfr, δfl, δrr, δrl, δor, δol]T,分别为右侧内升降副翼、左侧内升降副翼、右侧襟翼、左侧襟翼、右侧方向舵、左侧方向舵、右侧外升降副翼和左侧外升降副翼。在控制器设计过程中,考虑2种故障,分别为右侧内升降副翼完全失效和右侧方向舵完全失效,即令相应的πLi=0。考虑系统的不确定性,系统矩阵摄动40%。飞行器需要跟踪的指令信号r(t)=[βcmd, Φcmd, αcmd]T;选择加权矩阵:
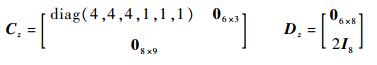 |
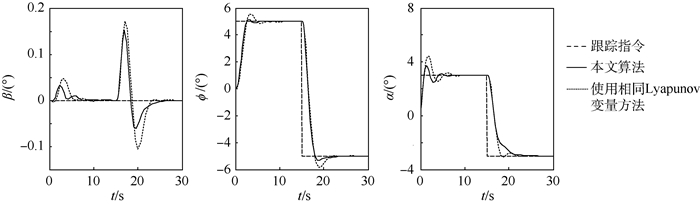
根据本文算法求出的鲁棒容错跟踪控制器如式(35)所示。为了验证本文算法的优越性,将其与所有故障状态均使用同一个Lyapunov变量的方法进行对比(也即本文算法的初值)。图 1给出了不存在故障时系统动态跟踪响应,此时2种控制器均能够很好地跟踪参考信号。图 2和图 3分别给出了右侧内升降副翼和右侧方向舵失效故障时仿真结果,此时2种控制器仍然能够跟踪控制指令,但很明显无迭代优化情况的超调量比较大,控制效果显然不如本文算法。图 4给出了右侧内升降副翼和右侧方向舵同时失效故障时的仿真结果。可以看出,此时使用相同Lyapunov变量方法得到的控制器有较为明显的振荡,几乎无法跟踪指令,而本文算法的控制器虽然也有一些波动,但依然能够得到较好的稳定系统,这充分说明了本文算法可以有效削弱控制器的保守性。
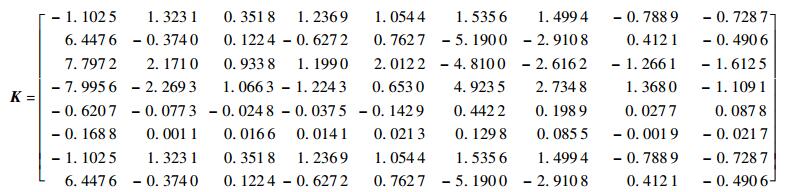 | (35) |
 |
| 图 1 无故障时飞行器指令响应曲线 Fig. 1 Command response curves of vehicle without fault |
| 图选项 |
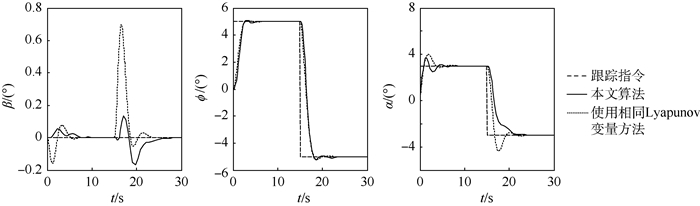 |
| 图 2 右侧内升降副翼失效时飞行器指令响应曲线 Fig. 2 Command response curves of vehicle under actuator outage of right inboard elevon |
| 图选项 |
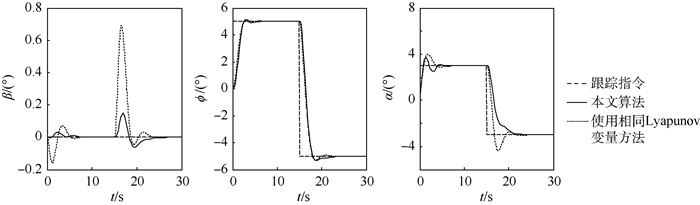 |
| 图 3 右侧方向舵失效时飞行器指令响应曲线 Fig. 3 Command response curves of vehicle under actuator outage of right rudder |
| 图选项 |
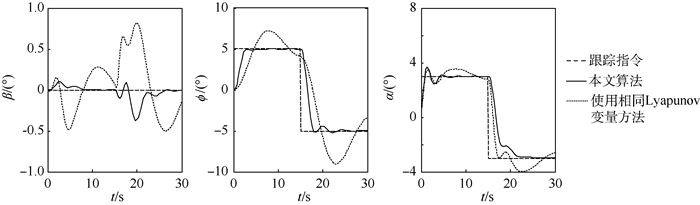 |
| 图 4 右侧内升降副翼和右侧方向舵同时失效时飞行器指令响应曲线 Fig. 4 Command response curves of vehicle under actuators outage of both right inboard elevon and right rudder |
| 图选项 |
4 结论 本文研究了一种迭代LMI算法,用来解决鲁棒容错控制器设计过程中存在的非凸优化问题。通过在高超声速飞行器X-33上的仿真实验, 得到了以下结论:
1)所设计的控制器不仅可以保证对指令的跟踪,而且能够使得正常情况下的跟踪性能最优,在故障情况下也能够保证对指令的跟踪。
2)与所有故障状态均使用同一个Lyapunov变量方法相比,本文算法可以降低控制器设计的保守性,提高系统的动态性能,并且闭环系统系统具有较好的鲁棒性, 甚至在多故障情况下仍能够保持较好的跟踪性能,从而验证了本文算法的正确性。
参考文献
| [1] | JI Y, ZHOU H L, ZONG Q. Adaptive active fault-tolerant control of generic hypersonic flight vehicles[J].Journal of Systems and Control Engineering, 2015, 229(2): 130–138. |
| [2] | ZHANG P, LIU H H T, LI X B, et al. Fault tolerance of cooperative interception using multiple flight vehicles[J].Journal of the Franklin Institute, 2013, 350(9): 2373–2395.DOI:10.1016/j.jfranklin.2013.02.022 |
| [3] | 傅强. 航空发动机被动容错控制系统鲁棒性设计[J].测控技术, 2013, 32(5): 32–34.FU Q. Robustness design of passive fault tolerant control system for aero engine[J].Measurement & Control Technology, 2013, 32(5): 32–34.(in Chinese) |
| [4] | 张爱华, 胡庆雷, 霍星, 等. 过驱动航天器飞轮故障重构与姿态容错控制[J].宇航学报, 2013, 34(3): 369–376.ZHANG A H, HU Q L, HUO X, et al. Fault reconstruction and fault tolerant attitude control for over-activated spacecraft under reaction wheel failure[J].Journal of Astronautics, 2013, 34(3): 369–376.(in Chinese) |
| [5] | CHEN F Y, WANG Z, TAO G, et al. Robust adaptive fault-tolerant control for hypersonic flight vehicles with multiple faults[J].Journal of Aerospace Engineering, 2015, 28(4): 04014111.DOI:http://html.rhhz.net/BJHKHTDXXBZRB/10.1061/(ASCE)AS.1943-5525.0000449 |
| [6] | HE J J, QI R Y, JIANG B.Adaptive fault-tolerant control design for hypersonic flight vehicles based on feedback linearization[C]//33rd Chinese Control Conference.Piscataway, NJ: IEEE Press, 2014:3197-3202.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6895464&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D6895464 |
| [7] | YANG G H, ZHANG S Y, LAM J, et al. Reliable control using redundant controllers[J].IEEE Transactions on Automatic Control, 1998, 43(11): 1588–1593.DOI:10.1109/9.728875 |
| [8] | PANZA S, LOVERA M.Rotor state feedback in helicopter flight control: Robustness and fault tolerance[C]//2014 IEEE Conference on Control Applications.Piscataway, NJ:IEEE Press, 2014:451-456.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6981387&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D6981387 |
| [9] | 陈雪芹, 耿云海, 张迎春, 等. 基于LMI的鲁棒容错控制及其在卫星姿态控制中的应用[J].控制理论与应用, 2008, 25(1): 95–99.CHEN X Q, GENG Y H, ZHANG Y C, et al. Robust fault-tolerant control based on LMI approach and application in satellite attitude control system[J].Control Theory & Applications, 2008, 25(1): 95–99.(in Chinese) |
| [10] | 陈明, 童朝南. 不确定系统鲁棒容错控制的LMI设计方法[J].控制与决策, 2009, 24(4): 526–531.CHEN M, TONG C N. LMI approach to robust fault-tolerant H-infinity control for uncertain systems[J].Control and Decision, 2009, 24(4): 526–531.(in Chinese) |
| [11] | 杨冬梅, 孙俊娜. 不确定时滞线性离散系统的鲁棒容错控制[J].东北大学学报(自然科学版), 2012, 33(2): 161–164.YANG D M, SUN J N. Robust fault tolerant control for uncertain linear discrete systems with time-delay[J].Journal of Northeastern University(Natural Science), 2012, 33(2): 161–164.(in Chinese) |
| [12] | YE S J, ZHANG Y M, WANG X M, et al.An improved LMI approach for static output feedback fault-tolerant control with application to flight tracking control[C]//4th IEEE Conference on Industrial Electronics and Applications.Piscataway, NJ:IEEE Press, 2009:35-40.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5138166&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5138166 |
| [13] | 欧阳高翔, 倪茂林, 孙承启. 视故障为结构不确定项的鲁棒可靠跟踪控制器设计[J].控制理论与应用, 2009, 26(1): 80–84.OUYANG G X, NI M L, SUN C Q. Robust reliable tracking controller design when the fault is viewed as a structural uncertainty[J].Control Theory & Applications, 2009, 26(1): 80–84.(in Chinese) |
| [14] | ZHANG Q J, YE S J, LI Y, et al. An enhanced LMI approach for mixed H2/H∞ flight tracking control[J].Chinese Journal of Aeronautics, 2011, 24(3): 324–328.DOI:10.1016/S1000-9361(11)60038-1 |
| [15] | 王明昊, 刘刚, 杨述华. 高超声速飞行器的多胞LPV系统控制器设计[J].空间控制技术与应用, 2013, 39(1): 15–22.WANG M H, LIU G, YANG S H. Polytopic-LPV-system-based control design for hypersonic vehicle[J].Aerospace Control and Application, 2013, 39(1): 15–22.(in Chinese) |
| [16] | XIE L. Output feedback H∞ control of systems with parameter uncertainty[J].International Journal of Control, 1996, 63(4): 741–750.DOI:10.1080/00207179608921866 |
| [17] | 俞立, 陈国定, 杨马英. 不确定系统具有圆盘区域极点约束的鲁棒控制[J].自动化学报, 2000, 26(l): 116–120.YU L, CHEN G D, YANG M Y. Robust control of uncertain linear system with disk pole constraints[J].Acta Automatica Sinica, 2000, 26(l): 116–120.(in Chinese) |
| [18] | HAN X D, LIU J G, XIE D X, et al. Robust H∞ guaranteed cost satisfactory fault-tolerant control for discrete-time systems with quadratic D stabilizability[J].Journal of Systems Engineering and Electronics, 2010, 21(3): 496–502.DOI:10.3969/j.issn.1004-4132.2010.03.022 |
| [19] | HE Y, WANG Q G. An improved ILMI method for static output feedback control with application to multivariable PID control[J].IEEE Transactions on Automatic Control, 2006, 51(10): 1678–1683.DOI:10.1109/TAC.2006.883029 |
| [20] | CAO Y Y, LAM J, SUN Y X. Static output feedback stabilization: An ILMI approach[J].Automatica, 1998, 34(12): 1641–1645.DOI:10.1016/S0005-1098(98)80021-6 |
| [21] | HOLLIS B R, THOMPSON R A, MURPHY K J, et al. X-33 aerodynamic computations and comparisons with wind-tunnel data[J].Journal of Spacecraft and Rockets, 2001, 38(5): 684–691.DOI:10.2514/2.3753 |
