常见的无位置传感器无刷直流电机控制方法主要有反电动势(BEMF)法[1-4]、续流二极管法[5]、磁链法[6]、滑模观测器法[7]和电流注入法[8]等。以上各种无位置传感器无刷直流电机控制方法均需要通过电机参数及运行状态得到转子的位置信息,该位置信息的准确性是影响无位置传感器控制方式能否高效运行的关键。但是任意一种无位置传感器无刷直流电机控制方法都无法保证其得到的位置信息绝对准确,电机参数的误差、温度、外界环境的变化、滤波及干扰因素的影响等都会导致提取到的转子位置信息出现偏差。文献[9]提出了一种以非导通相续流电流偏差为反馈量,以控制非导通相续流电流对称为目标的位置信号闭环控制策略,但是该控制策略只能在特定斩波方式下使用,且无法考虑绕组电感导致的电流相位滞后问题。文献[10]提出了一种通过端电压对称校正换相位置的方法,以端电压差值作为偏差量,以换相位置补偿角作为被控制量,建立比例积分(PI)调节器,校正换相位置,该方法可以有效校正位置信号检测误差,但是无法补偿由绕组电感引起的电流相位滞后误差。文献[11]通过实验检测不同转速下测得的位置信号和实际位置之间的相位误差,建立表格,然后通过查表法补偿误差,该方法可以在一定程度上减小换相误差,但是该补偿过程是开环控制的,无法根据电机运行状态实时调节换相位置补偿角,当电机运行参数与建立表格时运行参数不同时,可能会导致换相偏差增大,甚至导致运行失败。文献[12-13]分析了超前滞后换相对电流的影响,指出了超前或滞后换相都会引起导通相电流增大甚至非导通相导通,而电流的增加必然导致损耗的增加。
无位置传感器无刷直流电机换相位置的准确性,不仅包含提取到的转子位置信息的准确性,还须考虑电机绕组电感引起的电流滞后[14-16]。因此,换相位置准确与否包括2个方面:①检测到的转子位置是否准确;②能否准确计算绕组电感引起的电流滞后角度。一般的转子位置补偿策略通常只考虑检测到的转子位置信号的准确性,而未考虑绕组电感引起的电流相位滞后。
本文通过推导无刷直流电机换相位置与母线电流的数学关系,构造了以换相位置补偿角为控制对象,以母线电流随换相角度的变化率为偏差量的PI调节器,并在此基础上提出了一种无刷直流电机换相位置优化策略,该策略可以同时校正位置信号检测和绕组电感引起的换相误差,无需将两者分开计算。经实验验证,该策略能够以简单的优化过程实现良好的优化效果,有效提高了无刷直流电机的运行效率。
1 换相位置对母线电流的影响 无刷直流电机输出的电磁功率等于反电动势与电枢电流的数量积,换相位置不准确会引起电枢电流与反电动势相位不一致,造成功率因数降低,进而导致无刷直流电机效率下降,而对换相位置优化的最终目的是使电枢电流与反电动势相位保持一致。为了简化计算,设梯形波反电动势的平顶宽度为120°,将电枢电流等效为标准的方波电流,不考虑弱磁增磁作用的影响。
1.1 电枢电流与反电动势同相时的功率 图 1所示为a相电枢电流与反电动势同相位时的波形。此时无刷直流电机处于最佳运行状态,其力矩波动最小,效率最高。
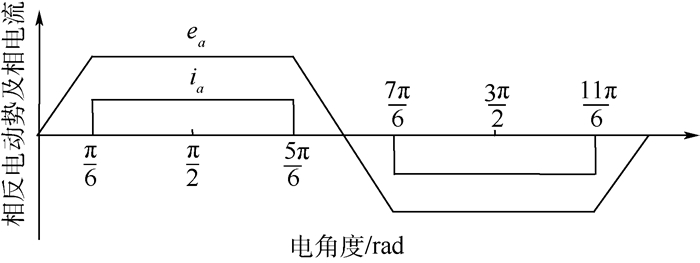 |
| 图 1 无相位差时a相电枢电流与反电动势波形 Fig. 1 Armature current and BEMF waveform of phase a with no commutation error |
| 图选项 |
选取图 1中一个换相周期π/6~π/2为分析对象,在π/6~π/2期间,无刷直流电机输出的电磁功率P0为
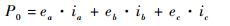 | (1) |
式中:ea、eb和ec为相反电动势;ia、ib和ic为相电流。在此换相周期内,有ea=-eb=E,ia=-ib=I0,E为相反电动势最大值,I0为相电流和相反电动势同相位时的直流母线电流,ic=0。
由式(1)可知:
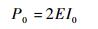 | (2) |
1.2 电枢电流与反电动势不同相时的功率 图 2所示为电枢电流与反电动势存在相位差θ时的三相反电动势和电流波形。θ为负时,表示电流超前,θ为正时,表示电流滞后。取一个换相周期(π/6+θ)~(π/2+θ)作为分析对象,该换相周期内输出的电磁功率Pθ为
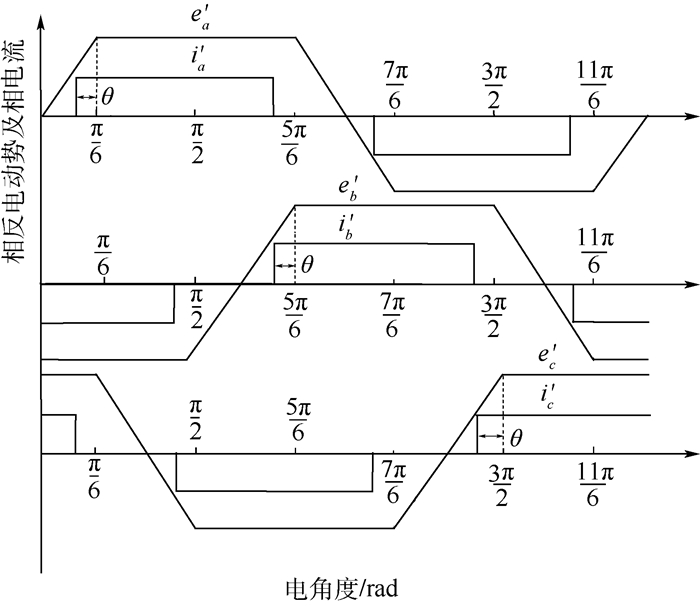 |
| 图 2 不同相时三相电枢电流与反电动势波形 Fig. 2 Armature current and BEMF waveform of triphase with commutation error |
| 图选项 |
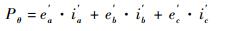 | (3) |
式中:ea′、eb′和ec′为存在相位差θ时的相反电动势;ia′、ib′和ic′为存在相位差θ时的相电流。在此换相周期内,有ia′=-ib′=Iθ,ic′=0,Iθ为存在相位差θ时的母线电流。
因此,可由式(3)得
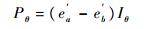 | (4) |
1.3 换相角度偏差对母线电流的影响 无刷直流电机在固定转速、固定功率运行时,在每一个换相周期内输出的电磁功相同,因此有
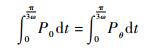 | (5) |
式中:ω为电角速度。
由图 2可知,θ < 0时,换相周期(π/6+θ)~(π/2+θ)内各相反电动势的值为
 | (6a) |
 | (6b) |
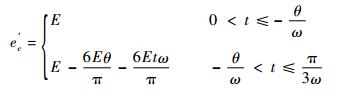 | (6c) |
θ > 0时,该换相周期内各相反电动势的值为
 | (7a) |
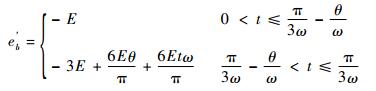 | (7b) |
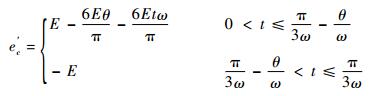 | (7c) |
以π/6+θ对应的时刻作为式(5)中积分的零时刻,由式(2)、式(4)~式(6)或式(2)、式(4)、式(5)、式(7)均可得,换相超前和滞后时的母线电流Iθ均满足:
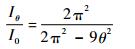 | (8) |
随着电流超前滞后角的增大,得到的母线电流Iθ会增大,其最小值为I0,为相电流和相反电动势同相位时的直流母线电流,其值不受换相角度偏差的影响,I0的具体值对后续换相位置优化策略影响较小,因此无需计算其精确值,用该转速下的额定电流近似代替即可。
式(8)是在(π/6+θ)~(π/2+θ)换相周期计算得到的,但由于三相对称的无刷直流电机6个换相周期是等价的,因此在无刷直流电机运行期间,换相角度偏差和母线电流之间恒满足式(8)。
母线电流与换相角度偏差的关系如图 3所示。随着换相角度偏差增大,母线电流增加越来越明显,θ为0时,表示无刷直流电机相电流和相反电势同相位。由于换相位置偏差超过π/3时,无刷直流电机已经失步,此时其已无法正常运行,因此上述分析均在-π/3 < θ <π/3区间进行。
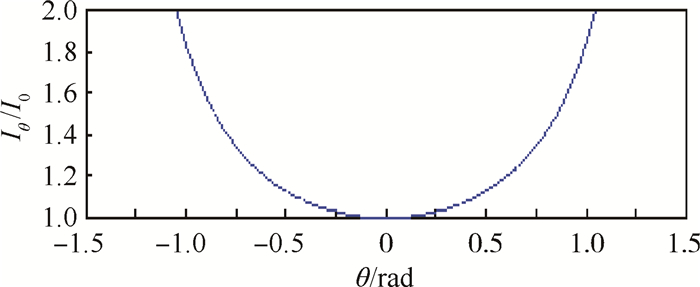 |
| 图 3 母线电流与换相角度偏差的关系 Fig. 3 Relationship between bus current and angular commutation deviation |
| 图选项 |
2 换相位置优化策略在驱动系统中的实现 2.1 构建PI调节器 由第1.3节分析可知,Iθ是随换相角度偏差θ变化的值,取Iθ对θ的变化率记为
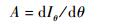 | (9) |
母线电流变化率与换相角度偏差的关系如图 4所示。θ越接近0,A的绝对值越小;反之,A的绝对值越大,且电流超前时A为负值,电流滞后时A为正值。
 |
| 图 4 母线电流变化率与换相角度偏差的关系 Fig. 4 Relationship between bus current gradient and angular commutation deviation |
| 图选项 |
通过上述数学分析,可以构造以A为偏差量,以换相位置补偿角α作为被控制量的PI调节器。构建的A和α的关系为
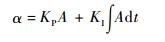 | (10) |
式中:KP为比例系数;KI为积分系数。
以无位置传感器反电动势法为例,实际工作中,通过反电动势法得到的反电动势过零点信号与实际换相位置并非直接对应(采用30°或90°相位延时),通常需要外加一定延时角度τ,最终延时角度φ可以表示为
 | (11) |
式中:τ为综合考虑信号滤波电路引起的相位延时、电感引起的电流滞后、电压比较器和光耦等芯片引起的延时及计算过程引起的延时等得到的相位延时角。
由图 4可知,取KP < 0,KI < 0,当电流超前于反电动势时,θ < 0,A < 0,根据式(10)得α > 0,由式(11)可得延时角度φ增大,从而减小电流与反电动势的相位差;反之,延时角度φ减小。
将式(11)按照增量式PI调节器离散化后可以得到
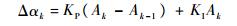 | (12) |
式中:Ak为第k次进入PI调节时的A值;Δαk为第k次换相位置补偿角的变化量;k为正整数。
离散化以后的软件延时角度可以表示为
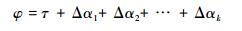 | (13) |
2.2 调速系统逻辑框图 本文通过分析母线电流与换相角度偏差之间的关系提出了以母线电流变化率为基础的换相位置优化策略。图 5为采用该换相位置优化策略的调速系统控制逻辑框图。图中:ω0为给定的参考速度;PID为速度环的比例积分微分调节器;BUCK为用于调节转速的降压电路。与传统的无刷直流电机调速系统相比,采用换相位置优化策略的调速系统增加了母线电流检测、计算A值和PI调节三部分。该控制系统中,首先通过三相端电压分压、滤波和比较等环节得到反电动势过零点;然后根据转速、绕组电感、滤波电路和计算耗时等估算
 |
| 图 5 采用换相位置优化策略的调速系统逻辑框图 Fig. 5 Logic diagram of speed control system using commutation position optimization strategy |
| 图选项 |
延时时间;最后在估算延时的基础上通过本文提出的换相位置优化策略进行PI调节,得到换相位置补偿角,进一步优化换相位置。
3 实验验证 3.1 实验装置 实验对象为氢燃料电池汽车高速离心式空气压缩机。空气压缩机属于风机类型负载,其输出转矩及功率随转速升高而增加,叶轮克服空气阻力做功即其有效输出功。实验装置如图 6所示。
 |
| 图 6 实验装置 Fig. 6 Experimental devices |
| 图选项 |
驱动器原理框图如图 7所示。图中:Vi为直流电源的输入电压;Va、Vb和Vc为三相的端电压;JTAG为调试接口;CAN总线为控制器局域网总线。通过BUCK变换器输出的直流电压Vo调节无刷直流电机转速,通过反电动势法提取转子位置信号,母线上装有电流传感器,通过单片机的AD转换模块采集电流传感器输出的信号用于A的计算。
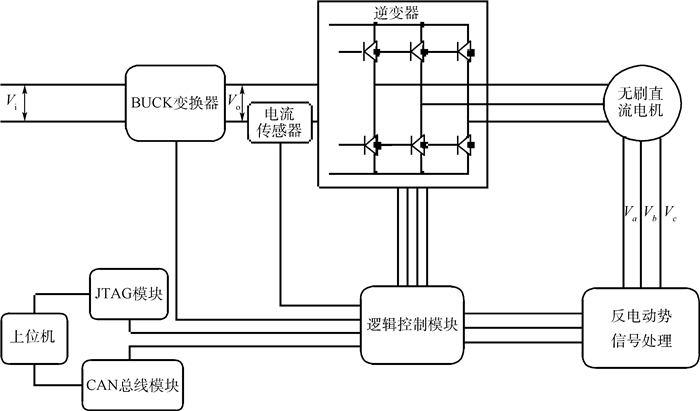 |
| 图 7 实验用驱动器原理框图 Fig. 7 Principle diagram of experimental drive |
| 图选项 |
氢燃料电池汽车高速电动离心式空气压缩机的电机参数如表 1所示。
表 1 空气压缩机电机参数 Table 1 Parameters of electric machine as air compressor
| 电机参数 | 数值 |
| 额定功率/kW | 10 |
| 额定转速/(r·min-1) | 100 000 |
| 待机转速/(r·min-1) | 15 000 |
| 极对数 | 1 |
| 线电感/μH | 80 |
| 线电阻/mΩ | 40 |
| 额定电流/A | 50 |
| 额定电压/V | 250 |
表选项
3.2 稳态实验分析 图 8为30 000 r/min时a相电流及端电压波形。上半屏为a相电流波形,下半屏为a相对地的端电压波形。由图 8(a)可知,当换相超前时,a相导通前,S1处的反电动势明显小于a相关断后S2处的反电动势;由图 8(b)可知,当换相滞后时,S1处的反电动势大于S2处的反电动势;由图 8(c)可知,经过换相位置优化以后,S1与S2处的反电动势大致相同。通过端电压波形对比可以看出,该换相位置优化策略能有效补偿换相位置偏差。
 |
| 图 8 a相电流及端电压波形 Fig. 8 Current and terminal voltage waveforms of phase a |
| 图选项 |
为了进一步验证该换相位置优化策略的优化效果,实验中将式(11)所示换相延时公式改为
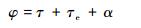 | (14) |
式中:τe为验证该换相位置优化策略的优化效果而额外增加的延时。实验中,τe从-10°到20°每隔2°做一次实验,记录换相位置优化前后的母线电流值,优化前α取值为0,优化后其值为通过该换相位置优化策略得到的值。在转速15 000、20 000、25 000、30 000 r/min得到的4组实验结果如图 9所示。通过实验结果可以看出,在不同转速下,优化前的母线电流随换相位置的变化规律符合式(8),因而该实验可以进一步证明本文建立的母线电流与换相位置的数学关系的正确性。
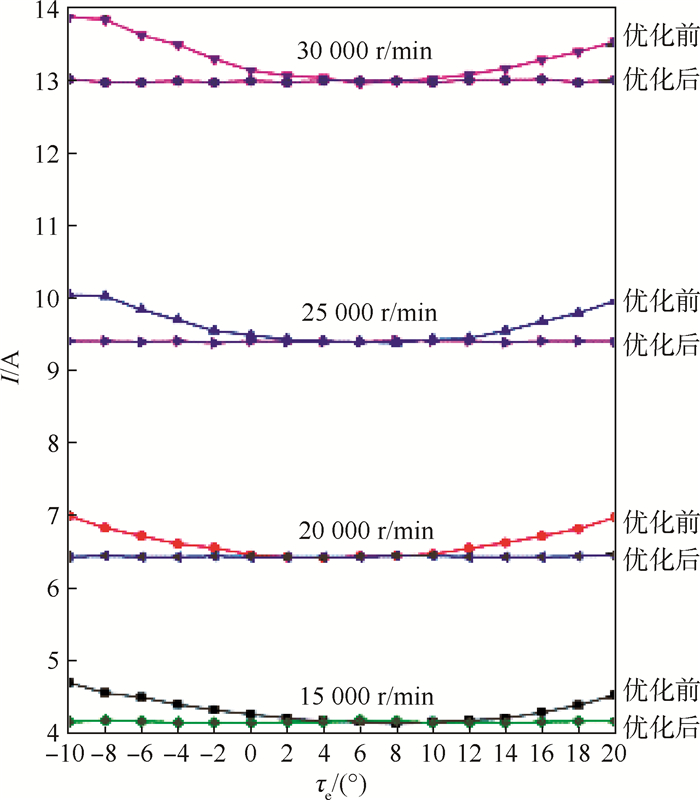 |
| 图 9 换相位置优化前后母线电流 Fig. 9 Bus current before and after commutation position optimization |
| 图选项 |
从图 9中25 000 r/min和30 000 r/min换相位置优化前的电流曲线可以发现,在τe=-10°时得到的母线电流值与τe=-8°时基本相同,这是因为换相位置优化前,在τe=-8°时得到的φ已经接近于0,当τe=-10°时,通过式(14)得到φ为负值,而φ为负值在实际换相位置调整中是无法实现的,在程序中,当得到φ为负值时,将其调整为0。
通过不同转速下换相位置优化前后的数据对比,可以确定出各个转速下最佳换相点的位置和换相位置优化策略可以达到的换相延时区间,如表 2所示。
表 2 不同转速下换相位置优化结果 Table 2 Commutation position optimization results at different rotating speeds
| 转速/(r·min-1) | 最佳换相延时/(°) | 换相延时区间/(°) |
| 15 000 | τ+8 | (τ+4)~(τ+12) |
| 20 000 | τ+4 | (τ+2)~(τ+8) |
| 25 000 | τ+6 | (τ+4)~(τ+10) |
| 30 000 | τ+6 | (τ+4)~(τ+8) |
表选项
表 2中,最佳换相延时指通过换相位置优化前的曲线得到的母线电流最小时的换相延时角度。换相延时区间指通过换相位置优化策略可以达到的换相角度范围。以图 9中15 000 r/min为例,在-10°~20°范围内优化后的电流值均小于优化前(τ+4°)和(τ+12°)时的电流值,这就意味着换相位置优化策略可以将换相位置由任意角度调节到(τ+4°)~(τ+12°)之间,因此,15 000 r/min时的换相延时区间即为(τ+4°)~(τ+12°)。
从表 2可以看出,15 000 r/min时优化后的换相延时区间为8°,随着转速的升高,母线电流值的增加,在30 000 r/min时,优化后的换相延时区间减小到4°,换相位置优化策略的优化效果随母线电流值的增加逐渐提高。
3.3 动态实验分析 为验证动态条件下的换相位置优化效果,分别测量换相位置优化前后15 000~20 000 r/min,20 000~25 000 r/min,25 000~30 000 r/min加速过程的母线电流有效值及加速时间,加速过程采用同样的控制参数,是否进行位置优化通过CAN总线进行设置,转速达到设定值时立刻停止输出,以便于区分加速阶段与稳态运行阶段,实验结果如表 3所示。
表 3 优化前后母线电流及加速时间 Table 3 Bus current and accelerating time before and after optimization
| 加速过程转速/ (r·min-1) | 加速时间/s | 加速过程电流/A | |||
| 优化前 | 优化后 | 优化前 | 优化后 | ||
| 15 000~20 000 | 3.6 | 3.4 | 6.37 | 6.29 | |
| 20 000~25 000 | 3.2 | 3.0 | 9.27 | 9.19 | |
| 25 000~30 000 | 3.4 | 3.0 | 12.87 | 12.69 | |
表选项
通过表 3可以看出,换相位置优化后的加速时间小于优化前,同时其母线电流的有效值也小于换相位置优化前,说明在加速过程中通过换相位置优化策略提高了无刷直流电机运行的效率,因此可以从侧面证明该换相位置优化策略对于动态过程同样具有良好效果。25 000~30 000 r/min优化前后加速过程如图 10所示。
 |
| 图 10 换相位置优化前后实验波形 Fig. 10 Experimental waveform before and after commutation position optimization |
| 图选项 |
4 结论 本文通过综合分析换相位置偏差与母线电流的关系,提出了以母线电流对换相角度变化率为基础的换相位置优化策略,通过理论分析及实验表明:
1)该策略可以准确调节换相位置到最优换相点,有效减小母线电流,改善相电流及端电压波形,提高无刷直流电机运行效率。
2)可以同时校正位置信号检测误差和绕组电感引起的电流相位滞后,避免了采用换相位置优化策略时无法进行相位超前角控制的问题。
3)无需计算偏差的具体值,而是通过PI调节使换相位置在最优换相点附近小幅波动,因此无需复杂的计算,简化了优化过程。
4)通过采样母线电流作为调节依据,无需检测每次换相时的电流或电压,对运算速度及采样频率要求较低,可以节约CPU资源,适用于高速驱动场合。
本文提出的换相位置优化策略在稳态时优化效果良好,在动态时对换相位置也可以进行相应的优化,但是当负载波动频率与该换相位置优化策略调节的频率接近时,优化效果并不理想,因此,仍需进一步改进控制策略以提高其在各种工况下的优化效果。
致谢
感谢同济大学汽车学院对本文研究工作的支持与帮助。
参考文献
| [1] | ACARNLEY P P, WATSON J F. Review of position-sensorless operation of brushless permanent-magnet machines[J].IEEE Transactions on Industrial Electronics, 2006, 53(2): 352–362.DOI:10.1109/TIE.2006.870868 |
| [2] | DAMODHARAN P, VASUDEVAN K. Sensorless brushless DC motor drive based on the zero-crossing detection of back electromotive force(EMF) from the line voltage difference[J].IEEE Transactions on Energy Conversion, 2010, 25(3): 661–668.DOI:10.1109/TEC.2010.2041781 |
| [3] | BI C, HLA N P, JIANG Q, et al. Back-EMF ZCP error induced by electromagnetic structure of spindle motor[J].IEEE Transactions on Magnetics, 2011, 47(7): 1899–1905.DOI:10.1109/TMAG.2011.2157895 |
| [4] | ZWYSSIG C, KOLAR J W, ROUND S D. Megaspeed drive systems:Pushing beyond 1 million r/min[J].IEEE/ASME Transactions on Mechatronics, 2009, 14(5): 564–574.DOI:10.1109/TMECH.2008.2009310 |
| [5] | OGASAWARA S, AKAGI H. An approach to position sensorless drive for brushless DC motors[J].IEEE Transactions on Industry Applications, 1991, 27(5): 928–933.DOI:10.1109/28.90349 |
| [6] | ERTUGRUL N, ACARNLEY P. A new algorithm for sensorless operation of permanent magnet motors[J].IEEE Transactions on Industry Applications, 1994, 30(1): 126–133.DOI:10.1109/28.273630 |
| [7] | FAKHAM H, DJEMAI M, BUSAWON K. Design and practical implementation of a back-EMF sliding-mode observer for a brushless DC motor[J].IET Electric Power Applications, 2008, 2(6): 353–361.DOI:10.1049/iet-epa:20070242 |
| [8] | KASA N, WATANABE H. A mechanical sensorless control system for salient-pole brushless DC motor with autocalibration of estimated position angles[J].IEEE Transactions on Power Electronics, 2000, 47(2): 389–395. |
| [9] | 宋飞, 周波, 吴小婧. 校正无位置传感器无刷直流电机位置信号相位的闭环控制策略[J].中国电机工程学报, 2009, 29(12): 52–57.SONG F, ZHOU B, WU X J. Closed loop control method to correct position phase for sensorless brushless DC motor[J].Proceedings of the CSEE, 2009, 29(12): 52–57.(in Chinese) |
| [10] | 吴小婧, 周波, 宋飞. 基于端电压对称的无位置传感器无刷直流电机位置信号相位校正[J].电工技术学报, 2009, 24(4): 54–60.WU X J, ZHOU B, SONG F. A new control method to correct position phase for sensorless brushless DC motor[J].Transactions of China Electrotechnical Society, 2009, 24(4): 54–60.(in Chinese) |
| [11] | 韦鲲, 任军军, 张仲超. 三次谐波检测无刷直流电机转子位置的研究[J].中国电机工程学报, 2004, 24(5): 163–167.WEI K, REN J J, ZHANG Z C. Research on the scheme of sensing rotor position of BLDCM based on the third harmonic component[J].Proceedings of the CSEE, 2004, 24(5): 163–167.(in Chinese) |
| [12] | LIN M Y, LI Q, GU W G.Effect of rotor position error on commutation in sensorless BLDC motor drives[C]//8th International Conference on Electrical Machines and Systems(ICEMS 2005).Piscataway, NJ:IEEE Press, 2005. |
| [13] | SAMOYLENKO N, HAN Q, JATSKEVICH J.Balancing hall-effect signals in low-precision brushless DC motors[C]//Applied Power Electronics Conference(APEC 2007).Piscataway, NJ:IEEE Press, 2007. |
| [14] | JIANG Q, BI C, HUANG R Y. A new phase-delay-free method to detect back EMF zero-crossing points for sensorless control of spindle motros[J].IEEE Transactions on Magnetics, 2005, 41(7): 2287–2294.DOI:10.1109/TMAG.2005.851841 |
| [15] | SHEN J X, TSENG K J. Analysis and compensation of rotor position detection error in sensorless PM brushelss DC motor drives[J].IEEE Transactions on Energy Conversion, 2003, 18(1): 87–93.DOI:10.1109/TEC.2002.808339 |
| [16] | HAN Q, SAMOYLENKO N, JATSKEVICH J. Average-value modeling of brushless DC motors with 120° voltage source inverter[J].IEEE Transactions on Energy Conversion, 2008, 23(2): 423–432.DOI:10.1109/TEC.2008.918628 |
