自Sherbrooke[1-3]提出经典的备件多层级库存理论以来,国内外****在此基础上对其进行了大量扩展和模型改进。Levner[4]和Samouei[5]等主要采用网络维修流程图的方法,以最小总库存和运输成本为目标,同时考虑各保障站点之间的依赖性和相互作用,对备件多层级库存问题进行了分析;Caglar等[6]建立了以响应时间为约束,以库存费用最小为目标的价格昂贵备件多级库存模型;Costantino等[7]以备件短缺数最小和系统可用度最大为限制条件,依据不同维修站点具备不同维修能力,运用边际效应法对备件多层级库存进行了优化;Topan和Bayindir[8]采用(NQ, R)库存策略,对服从泊松分布的2级备件携带方案进行了优化;Dada[9]以库存费用最小为目标,建立了低需求率且昂贵备件的2级库存模型;Sleptchenko等[10]改进了VARI-METRIC模型中无限维修能力的假设条件;Al Hanbali和van der Heijden[11]采用对系统可用度分区间的形式,对2级备件库存进行了优化,并验证了算法的精确性;Lau等[12]提出了可用度随时间变化的多级库存模型;Topan等[13]以平均供应时间为约束,以最小化库存为目标,采用(Q, R)策略对多个备件2级库存配制进行了建模分析;Basten[14]和樊九九[15]等将故障件修理级别分析引入到多级库存模型中,在降低总库存成本方面取得了显著效果;王睿等[16]以战时舰艇编队任务成功性为约束条件,以保障费用最小为目标,运用边际效应法求出3级库存保障方案;孙蕾和左洪福[17]以费用为约束条件,以系统可用度最大为目标,对航空类备件多级库存进行了优化;刘任洋等[18]以可用度为约束条件,以费用最小为目标,建立了基于横向转运的可修件3级库存优化模型。
可以看出,尽管目前对备件多级库存优化问题的研究非常深入,但在具体工程实践中都存在以下问题:①大部分研究的约束条件都为1个[4-18],当约束条件增加为2个或以上时,就无法再使用已有的模型和方法求出备件多层级最优库存携带方案。②目前研究多是多层或多级备件库存问题,而对工程实践中出现的多个约束条件下备件多层和多级联合的最优库存问题,截止目前很少有研究提及。③目前多级库存研究大部分从商业供应链的角度,以费用最小为评价指标[4-6, 9, 13, 16],而部队工程实践中,使用方多以系统可用度为装备效能评估指标,评价指标体系范围有待扩充。④本文产生的工程背景是舰艇索马里护航备件携带利用率非常低的问题(利用率大概为20%左右[19]),舰艇编队备件携带要受到舰艇载荷、保障经费及仓库体积等多个约束因素影响,已有模型主要针对陆地装备,以降低保障经费[4-6, 9, 13-18]为目标,并未考虑海军部队中常见的载荷和库存体积方面约束,无法满足海军部队工程实践的需要。⑤备件多层多级混合库存问题是研究的难点和热点。
因此,本文以舰艇保障经费、载荷和仓库体积为约束条件,以舰艇编队期望短缺数最小和可用度最大为目标函数,以舰艇编队索马里护航备件携带为研究背景,建立了相应库存模型,并给出了模型求解步骤和方法,通过案例分析验证了模型可为解决此类问题提供有效借鉴。
1 模型描述 本文产生的工程背景是舰艇编队索马里护航备件携带问题,文献[19]指出编队携带备件大概有80%被原封不动的带回,这种低备件利用率必然引起使用方的重视,故舰艇编队在出海之前,对其携带备件方案进行优化是非常有必要的,且具有重大的经济意义。
编队组成一般为1艘伴随综合保障舰和2艘最新型护卫舰或驱逐舰[20]。伴随综合保障舰具有中继级的维修能力,相当于1个海上“移动式”后方仓库,因新型驱逐舰或护卫舰配备了专门的修理中队,相当于1个保障基地,这样整个编队便组成了1个后方仓库和2个基地的2级器材保障模式。
新型舰船由很多大型且复杂装备组成,其备件携带方案必然要分2个层级来综合权衡制定,这样才能更好满足工程实践的需要。本文将备件分为外场可更换单元(Line-Replaceable Unit, LRU)和内场可更换单元(Shop-Replaceable Unit, SRU)。因而编队组成了2层2级的保障模式,由于舰艇备件携带受舰艇载荷及仓库体积的限制,在考虑备件费用约束的同时,还必须考虑备件质量和备件体积约束。为了简化模型求解过程和步骤,对模型的影响条件进行了一些合理的假设:
1)后方仓库或基地内部不进行串件拚修。
2)后方仓库或基地间不进行横向供应。
3)故障件修理工作相对独立,不相互影响。
4)现场可对故障件进行拆卸和定位。
5)维修渠道无限,不存在备件排队等待问题。
6)补给舰和舰艇之间距离很近,一般只有几链,故可以忽略伴随补给舰到舰艇的备件供应时间。
7)假设所有备件重要性相同。
8)所有的SRU都可以在后方仓库进行修理。
2 需求率的确定 2.1 备件需求率模型 不考虑故障间隔时间、误报警率等维修参数的影响,依据备件k单装备配置数量Zk、装备在现场配置数量Nj、故障间隔时间MTBFk及执行任务周期Tk等参数可以得出故障现场需求率为
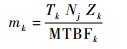 | (1) |
式中:j为基地编号,j=1, 2, …, J(0=后方仓库);k为LRU的项目编号, k=1, 2, …, K。
依据mk可以求出后方仓库或基地的LRU和SRU的需求率。
2.2 各级站点需求率的求解方法 多层多级备件需求率求解过程始于LRU失效并送到基地供应站。如果基地供应站有1件LRU备件,就进行更换,否则基地就发生1次LRU短缺。LRU故障件在基地修理有一定概率:如果LRU设备太复杂,往往就会被送到后方仓库进行修理,同时基地会安排向后方仓库申请该LRU 1件。
若LRU在基地进行修理,则设想将发现1件且仅为1件SRU发生故障。若基地现有库存有1件SRU备件就进行更换,将其安装到LRU,就完成了LRU的修理。基地能否修理SRU有一定概率:在基地修理能力范围之内,就在基地进行修理,反之,则发往后方仓库进行修理,同时向后方仓库提出该SRU的申请。
当完成了1件LRU的送修和补给时,即使还存在任何未解决的问题,但1次备件满足得到了供应;否则,LRU的现有库存就增加1件。若LRU未在基地进行修理,在后方仓库就发生SRU送修的类似过程。
根据基地LRU需求率,再结合给定备件各种参数(如修理概率等),可以计算出基地j相应SRU任务期内的需求量及后方仓库LRU和SRU的需求量,具体备件需求和供应渠道流程如图 1所示。
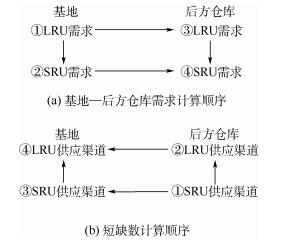 |
| 图 1 备件需求及供应渠道流程 Fig. 1 Flowsheet of spares demand and supply channels |
| 图选项 |
基地j的SRUi任务周期内需求量为
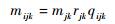 | (2) |
式中:mijk为基地j的SRUi任务周期内需求量;mjk为基地j的LRUk任务周期内的需求量;rjk为基地j的LRUk在本地修理的概率;qijk为LRUk修理产生SRUi需求的概率。
后方仓库LRUk任务周期内的需求量为各基地发生的对后方仓库补给申请的LRUk需求之和:
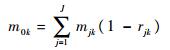 | (3) |
式中:m0k为后方仓库LRUk任务周期内的需求量。
后方仓库SRUi任务周期内的需求量为所有基地补给需求量之和加上后方级修理对应LRU所需的SRU件数(在MOD-METRIC标准模型中忽略了SRU的来源),即
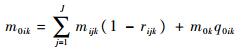 | (4) |
式中:rijk为基地j的SRUi在本基地维修的概率;q0ik为LRUk在中心仓库修理产生SRUi需求的概率;m0ik为后方仓库SRUi任务周期需求量。
图 1(b)为供应渠道及短缺数顺序需要计算基地的期望短缺数。这点正是计算需求量的反向顺序。依据单个使用现场装备可用度与备件短缺数的关系,可以得出单个装备的备件可用度。本文重点是依据本节给的1组备件(1件LRU及其所属第2层级的若干SRU)在基地和后方仓库的需求量计算,相应地可以计算出K组备件在基地和后方仓库的需求率。
3 备件库存优化模型 3.1 装备效能评估指标的确定 装备效能评估指标是衡量备件保障方案配置好坏程度的重要参数,常用的指标有可用度和备件期望短缺数等。
备件短缺数是指某一时间内装备不能满足备件需求的个数。若发生一次备件需求不能被满足,则记为备件短缺一次。备件短缺数定义如下:
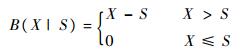 | (5) |
式中:S为备件库存量;X为备件需求量;B为备件短缺函数。
备件短缺数的确定需要通过备件存储量S和补给件或需要修理件DI的稳态概率分布来确定。若DI小于库存S时,表示库存S能够满足备件需求,不会产生备件短缺;只要DI需求超过S时,库存无法满足备件需求,就会出现备件短缺。假设某一随机时刻待收库存数为(S+L)件时,就会出现L件短缺,此时备件期望短缺数
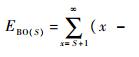
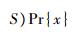
后方仓库或基地库存S、后方仓库或基地现有库存量OH、备件短缺数BO及待收件数DI满足如下关系:
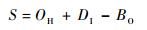 | (6) |
在备件模型中,备件期望短缺数为EBO(S)=
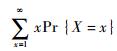
此时,还需要一个衡量所有随机x偏离E(x)程度的变量,这一衡量与均值偏离程度的变量称为方差,即Var(x)=E(x2)-(E(x))2,E(x2)为x2的期望值,也可以称为x的2阶样本距。
Pr(x)属于何种分布,可以用方差除以均值得到差均比VTMR来确定。当VTMR=1时,分布函数Pr(x)服从泊松分布;当0 < VTMR < 1时,分布函数Pr(x)服从二项分布;当VTMR > 1时,分布函数Pr(x)服从负二项分布[21]。VTMR的定义为
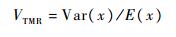 | (7) |
可用度的数学定义是任一时刻装备能够正常工作的程度,装备可用度求解公式为
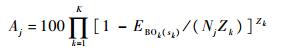 | (8) |
式(8)求单个基地可用度最大值,对式(8)两边取对数:
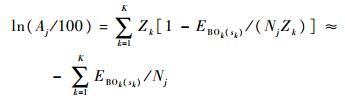 | (9) |
后方仓库和基地组成的整个系统的平均可用度为
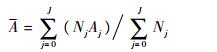 | (10) |
A式中:为系统平均可用度。
3.2 目标函数和约束条件 本文将编队期望短缺数最小和可用度最大作为目标函数,舰艇有效载荷、保障经费及仓库体积作为约束条件。
后方仓库所有备件体积之和必须小于或等于后方仓库体积上限,即
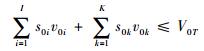 | (11) |
式中:s0i为后方仓库中备件SRUi的存储数量;v0i为后方仓库中备件SRUi的体积;s0k为后方仓库中备件LRUk的存储数量;v0k为为后方仓库中备件LRUk的体积;V0T为后方仓库体积指标的上限值。
基地j所有备件体积之和必须小于或等于基地仓库体积上限,即
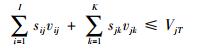 | (12) |
式中:sij为基地j仓库中备件SRUi的存储数量;vij为基地j仓库中备件SRUi的体积;sjk为基地j仓库中备件LRUk的存储数量;vjk为基地j仓库中备件LRUk的体积;VjT为基地j仓库体积指标的上限值。
后方仓库所有备件质量之和必须小于或等于后方仓库质量指标上限,即
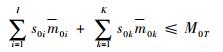 | (13) |
式中:m0i为后方仓库中备件SRUi的质量;m0k为后方仓库中备件LRUk的质量;M0T为后方仓库质量指标的上限值。
基地j所有备件质量之和必须小于或等于基地仓库质量指标上限,即
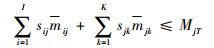 | (14) |
式中:m0i为基地j仓库中备件SRUi的质量;mjk为基地j仓库中备件LRUk的质量;MjT为基地j仓库质量指标的上限值。
后方仓库所有备件费用之和必须小于或等于后方仓库费用指标上限,即
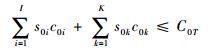 | (15) |
式中:c0i为后方仓库中备件SRUi的费用;c0k为后方仓库中备件LRUk的费用;C0T为后方仓库保障经费总指标的上限值。
基地j所有备件质量之和必须小于或等于基地仓库质量指标上限,即
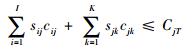 | (16) |
式中:cij为基地j仓库中备件SRUi的费用;cjk为基地j仓库中备件LRUk的费用;CjT为基地j保障经费总指标的上限值。依据式(11)~式(16),可以得出本文建立的模型为
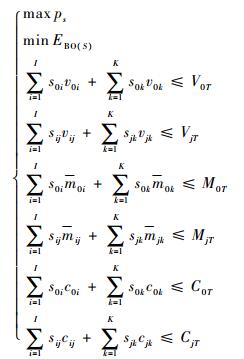 | (17) |
主要采用拉格朗日乘子法和边际效应法相结合对模型进行求解和优化。
3.3 库存优化方法 编队在出海执行任务准备阶段,备件携带受到后勤保障经费、载荷及仓库体积的限制,不可能不限品种和数量的携带舰船所需的所有备件,必须要对备件携带方案进行优化,达到在满足所有约束指标的基础上,使编队可用度最大及期望短缺数最小。
本文库存优化方法主要思想是用拉格朗日乘子[22]将影响库存配置的3个因素转换为拉格朗日乘子,然后采用边际效应分析[3]求出库存最优分配方案。一方面,拉格朗日乘子法能将影响库存配置方案的3个因素转换为1个拉格朗日乘子,这为使用边际效应分析奠定了基础;另一方面,边际效应分析具备求解速度快、操作方便及结论精度高的特点,是库存优化中常见的方法。方法开始时,假设所有层级站点备件初始库存量都为0,在每次迭代计算过程中,通过比较边际效应值的大小,确定备件携带种类和数量。模型具体求解步骤如下:
步骤1 由于编队备件携带涉及的影响因素非常多,此种情况下,边际效应法无法使用,引入拉格朗日乘子法,将所有影响因素转换为拉格朗日乘子,即
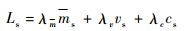 | (18) |
式中:λm为备件质量因子;λc为备件购置费用因子;λv为备件体积因子;ms为备件质量;cs为备件购置费用;vs为备件体积。
步骤2只考虑一种约束因素,运用边际效应法求出此时备件携带方案。
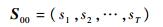 | (19) |
步骤3 据此求出后方仓库或基地总备件质量、体积及费用,从而可求出质量因子、体积因子和费用因子。以费用为例进行说明。
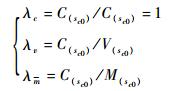 | (20) |
依据式(20)便可求出相应的拉格朗日乘子。
步骤4依据式(14)~式(18)构建后方仓库或基地的LRU和SRU拉格朗日乘子组合,即
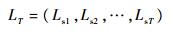 | (21) |
步骤5重新构建Ls为自变量,Pr(Ls)为因变量的函数,并做1阶差分,此时边际增量为
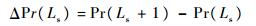 | (22) |
步骤6依据式(21)和式(22),计算得到边际效应值,即
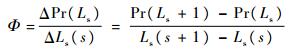 | (23) |
步骤7重复步骤1~步骤6,直到再增加1件最优备件时,就会有某个约束值超过给定指标上限,此时停止(只要有1个超过指标上限时就停止)。
4 实例分析 以某舰艇编队准备去索马里执行为期3个月护航任务备件清单中的7项电子类备件为例,构成了1个中心仓库和3个保障基地的2层2级后勤保障组织结构形式,对应备件参数及各项属性值如表 1所示。
表 1 备件参数及属性 Table 1 Paremeters and attributes of spare parts
| 备件编号 | Z | MTBF/h | c/万元 | m/kg | v/m3 | r1 | r2 | r3 |
| LRU1 | 1 | 1 026 | 3.7 | 29.8 | 2.4 | 0.8 | 0.7 | 0.8 |
| LRU2 | 1 | 978 | 7.5 | 18.7 | 3.6 | 0.9 | 0.9 | 0.8 |
| LRU3 | 1 | 1 134 | 3.2 | 11.6 | 0.9 | 0.8 | 0.8 | 0.7 |
| LRU4 | 1 | 654 | 7.3 | 32.6 | 1.1 | 0.9 | 0.7 | 0.7 |
| LRU5 | 2 | 885 | 1.8 | 10.5 | 0.6 | 0.6 | 0.5 | 0.5 |
| SRU1 | 1 | 2 217 | 0.7 | 10.8 | 0.4 | 0.6 | 0.5 | 0.4 |
| SRU2 | 1 | 1 893 | 2.7 | 2.8 | 1.1 | 0.5 | 0.5 | 0.6 |
| ??注:Z—单机安装数量;ri(i=1, 2, 3)—设备LRU或SRU故障后能在第ri个基地或仓库被修好的概率。 | ||||||||
表选项
索马里护航是中国最新型的舰艇,动力装置、武备及特装等都是目前各自领域的最先进装备,绝大部分装备是一样的或相似度非常高,故其备件差异性并不大。舰艇备件数以万计,出于对本文方法介绍的目的,选取了1组相同装备,以1个中心仓库和1条舰艇为例进行研究,并对备件属性值进行了适当的处理,但计算方法和原理是一样的。
依据表 1,按照第2节方法,可以得到基地备件需求率为(1.754 4, 1.840 5,1.587 3, 2.752 3, 4.067 8, 0.811 9, 0.950 9),后方仓库备件需求率为(1.228 1, 0.736 2, 1.111 0, 1.926 6, 5.694 9, 1.217 9, 1.331 3)。此次索马里护航每条舰艇对于这7项备件分配的保障经费、载荷和仓库体积的指标上限为155万元、710 kg及58.5 m3,伴随综合保障船对应指标为150万元、775 kg及61.5 m3。依据文献[3]的边际效应法,循环100次得到在费用约束下的最优备件携带方案,基地和后方仓库分别为8,4,5,5,8,9,8和10,2,4,4,11,12,10。依据备件携带方案,计算此时总的备件质量、费用和体积(见表 2)。
表 2 费用约束条件下备件方案结果 Table 2 Results of spare parts project under cost constraint
| 备件方案 | c/万元 | m/kg | v/m3 | 方案结果是否确定 |
| 基地 | 154.4 | 737.8 | 60.8 | 否 |
| 后方仓库 | 149.2 | 758.3 | 61.6 | 否 |
表选项
分析表 2中的数据可知,基地的备件费用为154.4万元,小于指标上限155万元,符合要求;但质量为737.8kg,超过指标上限27.8kg,同时基地备件体积为60.8m3,超过指标上限2.3m3,备件质量和体积都不满足要求;后方仓库的备件费用为149.2万元,小于指标150万元上限,符合要求;质量为758.3kg,小于指标775kg上限,符合要求;同时基地备件体积为61.6m3,超过指标上限0.1m3,备件体积指标不满足要求。
携带方案成立的前提条件是所有约束条件同时满足要求,若有一项约束值超过了指标上限,备件携带方案就不符合要求,需按第3.3节的模型和库存优化方法重新计算。
按照第3.3节模型和库存优化原理重新计算得到基地和后方仓库的费用拉格朗日乘子分别为(16.0310, 20.5555, 7.9131, 16.9156, 5.5210, 3.9759, 6.0794)和(15.1747, 19.7723, 7.5838, 16.1580, 5.2482, 3.7207, 5.8963),按步骤1~步骤6循环98次得到基地和仓库备件携带方案分别为7,4,5,5,8,9,8和10,2,4,4,11,11,10。此时备件费用、质量和体积如表 3所示。
表 3 多约束条件下备件方案结果 Table 3 Results of spare parts project under multi-constraints
| 备件方案 | c/万元 | m/kg | v/m3 | 方案结果是否确定 |
| 基地 | 150.7 | 708.0 | 58.4 | 是 |
| 后方仓库 | 148.5 | 774.5 | 61.2 | 是 |
表选项
此时基地备件费用、质量和体积分别为150.7万元、708.0kg和58.4 m3,分别小于对应指标155万元、710kg及58.5m3的上限,满足要求。后方仓库的备件费用、质量和体积分别为148.5万元,774.5 kg和61.2 m3,分别小于对应指标150万元、775kg及61.5m3上限,满足要求。
下面分别给出上述2种情况下的备件期望短缺数EBO和费用c之间的关系,如图 2和图 3所示。
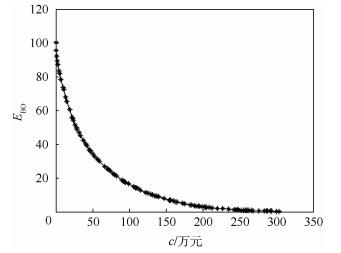 |
| 图 2 费用约束条件下的最优短缺数曲线 Fig. 2 Optimal curve of expect back order under cost constraints |
| 图选项 |
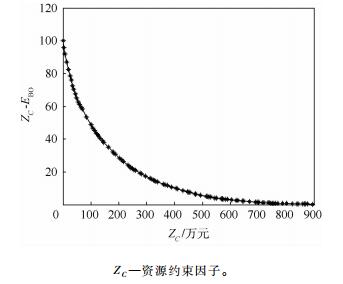 |
| 图 3 多约束条件下的最优短缺数曲线 Fig. 3 Optimal curve of expect back order under multi-constraints |
| 图选项 |
从图 2和图 3可以得出:
1)舰艇编队备件携带方案受到的影响因素非常多,只考虑费用约束,在此基础上得到的备件携带方案并不是最优方案(有2个约束值超标)。
2)备件短缺数曲线上的各个离散点是在各约束因素下的最优值,且相当于该短缺数下最低指标值。
3)短缺数最优曲线能够为方案制定者和决策者制定编队备件携带方案提供参考和依据。以图 3为例,当备件短缺数为0.3954时,后方仓库备件费用、质量和体积的值分别为141万元、775.8kg和57.6m3,这是设定约束指标的最低值。
编队可用度在备件期望短缺数基础之上,依据式(8)~式(10)即可得到,限于篇幅原因,不再赘述。
5 结论 1)本文以舰艇保障经费、载荷和仓库体积为约束条件,以备件期望短缺数和可用度为优化函数,采用拉格朗日乘子和边际效应相结合的方法,建立了多影响因素下的备件多层多级库存优化模型,得到了最优方案。
2)只考虑一种约束因素,运用边际效应法得到的备件携带方案往往只是对应影响因素下的最优方案,未考虑的影响因素有可能会超过指标上限,这种方案显然是欠妥的,运用本文提供的模型和方法,求解出的备件库存方案满足所有影响因素指标要求。
3)解决了多约束因素下多级多层混合的备件库存优化问题,可为索马里护航备件携带方案制定者提供理论参考依据,使制定的备件携带方案更加符合工程实践情况。
4)主要针对定量约束因素进行研究,若在工程实践中遇到定性因素时,需要对本文模型进行适当调整,但求解方法和思路相同(如运用专家群打分法将定性条件转换为定量约束条件,转入第3.3节进行求解,因篇幅有限,这里不再详细叙述)。
5)本文模型是建立在不进行横向转运和串件拚修基础之上的,备件横向转运和串件拚修是提高保障效能指标及降低保障费用的有效手段,这将是下一步的研究重点和进一步的研究方向。
参考文献
| [1] | SHERBROOKE C C. METRIC:A multi-echelon technique for recoverable item control[J].Operations Research, 1968, 16(1): 122–141.DOI:10.1287/opre.16.1.122 |
| [2] | SHERBROOKE C C. An evaluator for the number of operationally ready aircraft in a multilevel supply system[J].Operations Research, 1971, 19(3): 618–635.DOI:10.1287/opre.19.3.618 |
| [3] | SHERBROOKEC C. Optimal inventory modeling of systems:Multi-echelon techniques[M].Netherland: Springer Science & Business Media, 2006: 6-10. |
| [4] | LEVNER E, PERLMAN Y, CHENG T C E, et al. A network approach to modeling the multi-echelon spare-part inventory system with backorders and interval-valued demand[J].International Journal of Production Economics, 2011, 132(1): 43–51.DOI:10.1016/j.ijpe.2011.03.004 |
| [5] | SAMOUEI P, KHEIRKHAH A S, FATTAHI P. A network approach modeling of multi-echelon spare-part inventory system with backorders and quantity discount[J].Annals of Operations Research, 2015, 226(1): 551–563.DOI:10.1007/s10479-014-1718-z |
| [6] | CAGLAR D, LI C L, SIMCHI-LEVI D. Two-echelon spare parts inventory system subject to a service constraint[J].IIE Transactions, 2004, 36(7): 655–666.DOI:10.1080/07408170490278265 |
| [7] | COSTANTINO F, DI GRAVIO G, TRONCI M. Multi-echelon, multi-indenture spare parts inventory control subject to system availability and budget constraints[J].Reliability Engineer-ing & System Safety, 2013, 119: 95–101. |
| [8] | TOPAN E, BAYINDIR Z P. Multi-item two-echelon spare parts inventory control problem with batch ordering in the central warehouse under compound Poisson demand[J].Journal of the Operational Research Society, 2012, 63(8): 1143–1152.DOI:10.1057/jors.2011.125 |
| [9] | DADA M. A two-echelon inventory system with priority shipments[J].Management Science, 1992, 38(8): 1140–1153.DOI:10.1287/mnsc.38.8.1140 |
| [10] | SLEPTCHENKO A, VAN DER HEIJDEN M C, VAN HARTEN A. Effects of finite repair capacity in multi-echelon, multi-indenture service part supply systems[J].International Journal of Production Economics, 2002, 79(3): 209–230.DOI:10.1016/S0925-5273(02)00155-X |
| [11] | AL HANBALI A, VAN DER HEIJDEN M. Interval availability analysis of a two-echelon, multi-item system[J].European Journal of Operational Research, 2013, 228(3): 494–503.DOI:10.1016/j.ejor.2013.02.009 |
| [12] | LAU H C, SONG H, SEE C T, et al. Evaluation of time-varying availability in multi-echelon spare parts systems with passivation[J].European Journal of Operational Research, 2006, 170(1): 91–105.DOI:10.1016/j.ejor.2004.06.022 |
| [13] | TOPAN E, BAYINDIR Z P, TAN T. An exact solution procedure for multi-item two-echelon spare parts inventory control problem with batch ordering in the central warehouse[J].Operations Research Letters, 2010, 38(5): 454–461.DOI:10.1016/j.orl.2010.05.006 |
| [14] | BASTEN R J I, VAN DER HEIJDEN M C, SCHUTTEN J M J. Joint optimization of level of repair analysis and spare parts stocks[J].European Journal of Operational Research, 2012, 222(3): 474–483.DOI:10.1016/j.ejor.2012.05.045 |
| [15] | 樊九九, 郭霖瀚, 杨懿, 等. 考虑维修效能的修理级别优化[J].北京航空航天大学学报, 2015, 41(2): 351–357.FAN J J, GUO L H, YANG Y, et al. Optimization of repair level considering maintenance effectiveness[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(2): 351–357.(in Chinese) |
| [16] | 王睿, 雷红伟, 彭英武, 等. 战时任务条件下舰艇装备多级备件优化[J].上海交通大学学报, 2013, 47(3): 398–403.WANG R, LEI H W, PENG Y W, et al. Optimization of warship spare parts in the scenario of wartime mission[J].Journal of Shanghai Jiao Tong University, 2013, 47(3): 398–403.(in Chinese) |
| [17] | SUN L, ZUO H F. Optimal inventory modeling of multi-echelon system for aircraft spares parts[J].Information Technology Journal, 2013, 12(4): 688–695.DOI:10.3923/itj.2013.688.695 |
| [18] | 刘任洋, 李庆民, 李华. 基于横向转运策略的可修件三级库存优化模型[J].航空学报, 2014, 35(12): 3341–3349.LIU R Y, LI Q M, LI H. Optimal model of three-echelon inventory for repairable spare parts with lateral transshipments strategy[J].Acta Aeronautica et Astronatica Sinica, 2014, 35(12): 3341–3349.(in Chinese) |
| [19] | 李予阳.大数据:开启智能船舶时代[N].经济日报, 2014-10-20(14).LI Y Y.Big data:Open the era of intelligent ship[N].Economic Daily, 2014-10-20(14)(in Chinese). |
| [20] | 悬崖. 中国海军用费效比考量反海盗护航任务[J].舰载武器, 2014(6): 23–27.XUAN Y. Chinese navy's cost-effectiveness evaluation in counter piracy and escort operation[J].Shipborne Weapons, 2014(6): 23–27.(in Chinese) |
| [21] | 孙蕾, 左洪福. 基于METRIC的民机初始备件数量确定及配置模型[J].中国机械工程, 2013, 24(23): 3200–3205.SUN L, ZUO H F. Optimal allocation modeling for initial spare parts of civil aircraft based on METRIC[J].China Mechanical Engineering, 2013, 24(23): 3200–3205.(in Chinese) |
| [22] | 王乃超, 康锐. 多约束条件下备件库存优化模型及分解算法[J].兵工学报, 2009, 30(2): 247–251.WANG N C, KANG R. An optimization model for inventory spares under multi-constraints and its decomposition algorithm[J].Acta Armamentarii, 2009, 30(2): 247–251.(in Chinese) |
