现有LPV控制方法在应用中的关键问题在于如何建立准确、计算复杂度低的LPV模型。目前LPV建模较常用的方法为Bounding box方法[3-4],该方法先将系统转化为仿射参数依赖型,然后分析选取系统矩阵中对系统特性影响较大的变量作为变参数,并直接选取变参数的上下界形成顶点系统,此方法变参数的选取依赖于设计人员的经验,所建立的LPV模型在非顶点处的误差没有定量描述,且存在一定的保守性。文献[5]运用Qhull算法在包线范围内基于实际的工作点求取LPV多胞顶点,相较于Bounding box方法,此方法所求得的多胞形区域更小,保守性降低。对于不具备仿射参数依赖型的LPV系统,文献[6]提出了一种张量积分解方法求解顶点系统,此方法要求系统矩阵可表示为状态变量的显示函数,由于高超声速飞行器的强非线性以及气动参数的不确定性,系统矩阵的函数表达式是很难得到的。文献[7-8]采用文献[6]提出的张量积分解理论,先将飞行器在包线范围内线性化得到一系列线性时不变(LTI)系统,选取状态变量中的变量作为变参数,然后进行数值拟合得到LPV模型,进而应用高阶奇异值分解(HOSVD)理论选取顶点,此方法数值拟合难度较大,且精度也很难保证。在飞行器LPV多胞系统建模过程中,如何同时兼顾到建模准确性、复杂性、保守性以及控制器阶数是值得研究的问题。
本文提出了一种基于网格化张量及HOSVD的凸多胞LPV模型建模方法,避免了LPV系统矩阵函数表达式的拟合过程,给出了奇异值与建模精度和多胞顶点数量的关系,可减少工作量和对设计人员经验的依赖,在保证建模精度的前提下控制顶点数量,提高建模过程的自动化程度。
1 大包线对象的LPV建模问题 设对象在整个飞行包线内的模型可表述为如式(1)所示的非线性形式:
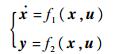 | (1) |
式中:x∈Rm为系统状态;u∈Rn为系统输入信号;y∈Rl为系统输出信号,则非线性系统可转化为如下的LPV形式:
 | (2) |
式中:ρ(t)=[ρ1(t) ρ2(t)…ρN(t)]T为随飞行状态或飞行包线变化的未知但可测量或估计的参数。
非线性系统的LPV描述形式不是唯一的,其直接影响控制系统的设计复杂度。现有LPV系统的控制器综合一般是基于线性变参数轨迹上的一组线性矩阵不等式(LMI),其控制器可以由LMI的解来构造,LMI的数量直接影响到控制器的计算复杂度,若LPV系统具有多胞形结构,由于多胞形是凸集,LPV系统可以由顶点完全描述[9],则只需对顶点进行控制器的设计即可。因此凸多胞LPV系统是解决大包线控制器设计问题的合适的LPV描述形式。
定义1仿射参数依赖型LPV多胞系统。
由变参数ρ(t)描述的多胞系统为
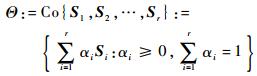 | (3) |
式中:r=2N为顶点数;Si为多胞系统的顶点;αi为多胞系统的凸分解系数。当LPV系统的系统矩阵A(ρ(t))、B(ρ(t))、C(ρ(t))、D(ρ(t))仿射依赖于时变参数向量ρ(t),且ρ(t)变化于多胞Θ内,称LPV系统为多胞系统。
LPV多胞系统的系统矩阵分解形式为
 | (4) |
式中:Ai、Bi、Ci和Di为LPV系统多胞顶点模型系统矩阵;凸分解系数为变参数的函数,可表示为αi(t)=f(ρ(t))。当变参数轨迹在多胞Θ内时,则LPV控制器系统矩阵Ak(ρ(t))、Bk(ρ(t))、Ck(ρ(t))和Dk(ρ(t))分解形式为
 | (5) |
大包线高超声速飞行器LPV建模的核心问题可以归结为:①如何获得合适的多胞LPV顶点模型及凸分解系数,在保证建模精度的前提下求解最少的多胞顶点和低维度准确的凸分解系数。顶点数量的减少不仅可以降低建模的保守性同时可以降低控制器的阶数,低维度准确的凸分解系数可降低系统的数据存储量、提高在线增益调度时的计算速度,有利于工程化实现。②如何定量描述所求多胞模型的建模精度,使得对于变参数的任意一固定点,满足如下精度要求:
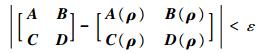 | (6) |
式中:ε为系统允许的建模误差大小,式(6)描述了原系统与所求多胞系统的差异化程度。
2 基于HOSVD的LPV多胞顶点建模 HOSVD理论[10]应用于LPV系统可以有效地将系统近似为一系列的LTI模型,这些LTI模型对应于LPV多胞系统的顶点。根据多胞系统的顶点性质和实有界定理,设计控制器时只要对其顶点进行设计即可。因此基于HOSVD的LPV多胞顶点建模方法是LPV控制理论中极其重要的部分,其建模精度与复杂度直接影响到LPV控制器的设计。HOSVD理论是将奇异值分解的思想应用于高维张量数据中的一种降维方法,其理论基础是张量展开。
2.1 HOSVD理论 定义2 (张量展开)若AE为一个(I1×I2×…×IN)维实张量,张量中元素可以表示为AEi1i2…iN={ai1i2…iN},则其沿第n模展开为矩阵A(n)E,且ai1i2…iN出现在矩阵A(n)E的第in行第j列。
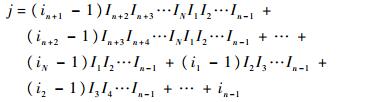 |
定义3 (HOSVD)对于一个(I1×I2×…×IN)维实张量AE可表示为乘积形式:
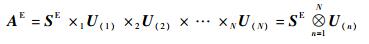 | (7) |
式中:U(n)=[u1(n)u2(n)…uIn(n)]为(In×In)维矩阵,n=1, 2, …, N,ui(n)为第i个n模奇异向量;SE为一个(I1×I2×…×IN)维实张量,且其子张量满足条件:
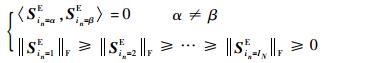 |
弗罗贝尼乌斯范数定义为
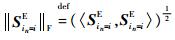
定理1对一个n秩为Rn(1≤n≤N)的张量AE进行HOSVD,将分解后得到的n模奇异值σIn′+1n(n), σIn′+2n(n)…, σRn(n)的相应元素变为0,得到一个新的张量
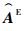
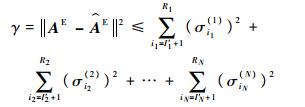 | (8) |
HOSVD是基于张量展开应用奇异值分解理论来解决高维数据主成分提取问题的方法。相较于仿射参数依赖型LPV系统的经验选取法,HOSVD方法的误差来源于舍弃的奇异值与特征向量,误差有确切的计算方法,可由式(8)直接计算出来,有利于控制误差的大小,同时也能够控制顶点数量降低控制器的阶数,更利于工程化实现。
2.2 基于网格化张量的HOSVD方法改进 高超声速飞行器气动参数非线性剧烈变化,很难用状态转换法以及函数替换法写出LPV模型的具体表达式。相比而言,Jacobian线性化法更适合于求解高超声速飞行器的LPV模型[11],其理论基础是一阶Taylor展开。
在整个飞行包线内对ρ(t)中每一个变参数进行网格化划分,设划分个数分别为I1, I2, …, IN,则在网格化的参数空间内,可得到变参数的网格化张量形式ρE∈RI1×I2×…×IN。设非线性系统式(1)在全包线内存在一系列平衡点xe(ρeE), ue(ρeE),满足f(xe(ρeE), ue(ρeE))=0,则非线性系统可写成网格化线性模型组的形式:
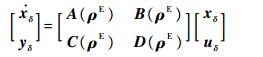 | (9) |
式中:
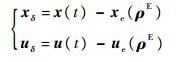 | (10) |
其中系统状态矩阵为方程偏导数在平衡点处的值:
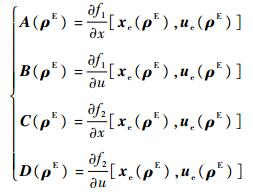 | (11) |
则在每一个固定点ρ,系统式(9)描述了非线性系统式(1)在该点的局部特性。
在网格化的参数空间内,一系列平衡点线性化得到张量形式的系统描述,其中:
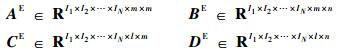 |
将得到的张量形式的系统描述重新组合成一个张量GE∈RI1×I2×…×IN×(m+l)×(m+n),GE中的每一个元素均为与变参数相关的变量:
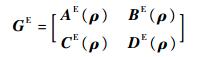 | (12) |
对张量GE进行高阶奇异值分解,分别舍弃前N(变参数的个数)模中较小的奇异值和对应的特征向量,设1-N模的奇异值中保留的个数分别为a1, a2, …, aN,得到的顶点个数为M=a1×a2×…×aN,可以得到LPV系统多胞形描述为
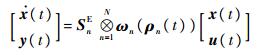 | (13) |
式(13)也可表示为
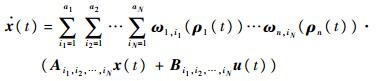 | (14) |
式中:权重函数ωn, i应满足条件
 | (15) |
由式(13)和式(14)可得到顶点张量SnE与所求顶点矩阵的对应关系,式(3)中凸分解系数α与式(13)中的权重函数ω的关系为
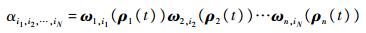 |
在误差允许的范围内离散的系统矩阵可由求解出的顶点系统和权重矩阵Un还原
 | (16) |
式中:Un包含每一个变参数对应的权重函数ωn,误差γ可表示为
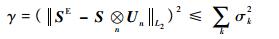 | (17) |
与式(3)仿射参数依赖型LPV多胞模型的结构类似,基于HOSVD建立多胞模型的方法也是由顶点的凸分解得到整个多胞模型,两者的区别在于多胞顶点和凸分解系数的求取方法。相较于仿射参数依赖型LPV模型选取变参数上下界组合的方法,本文提出的方法无需依赖于设计者的经验,同时也没有复杂的数据拟合过程,参数的设定只涉及到每一模保留奇异值的个数,在误差允许的范围内选定顶点个数,整个设计过程可以很容易地实现自动化设计。
综上,基于HOSVD方法的多胞LPV顶点系统的设计流程如图 1所示。
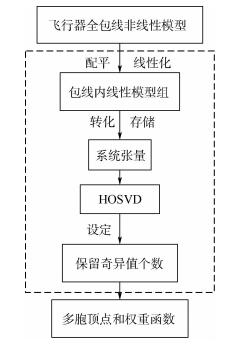 |
| 图 1 基于HOSVD的LPV多胞系统设计流程 Fig. 1 Flowchart of polytopic LPV system design based on HOSVD |
| 图选项 |
根据上述分析,如图 1所示,可以得到基于HOSVD的高超声速飞行器LPV系统多胞分解的一般步骤:
1)针对飞行器非线性模型,给定变参数、变量范围、变量划分网格数,在网格化的飞行包线内进行线性化得到线性模型组。
2)将离散化的系统数据转化为可用于HOSVD方法的张量GE形式。
3)对GE应用HOSVD方法,在每一模中舍弃较小的奇异值以及与之相对应的奇异值向量,得到多胞顶点系统。
4)由HOSVD得到的权重矩阵Un的第in(in=1, 2,…, In)个列向量un便确定了变量ρn(t)的权重函数ωn, in(ρn(t)),进而得到凸分解系数。
建模的误差大小与LTI顶点的个数成反比,选择保留的奇异值数量越多得到的顶点个数越多,模型越精确。一般情况下,为了便于控制器的分析与设计,同时降低控制器阶数,根据系统可容忍的误差大小,选择有限个LTI顶点系统。
3 鲁棒LPV自增益控制器设计 3.1 多胞LPV系统鲁棒控制器设计 对于某型航天飞机[12]六自由度非线性模型,选取再入包线:高度H为30~40km,马赫数Ma为3~5。由于航天飞机采用倾斜转弯(Bank-To-Turn,BTT)控制方式,侧滑较小,气动特性除高度、马赫数外,受迎角α影响最大,因此选取H、Ma和α作为LPV系统的变参数。对变参数进行网格化的划分,网格的划分依据对象的特性与包线的范围,将变参数分别划分6、3、7等份。本文选取C=I,D=0,得到网格化的张量形式GE=[AEBE],对得到的网格化的张量GE∈R6×3×7×6×9进行高阶奇异值分解,得到的HOSVD结果如表 1所示。
表 1 HOSVD结果 Table 1 Results of HOSVD
| 奇异值阶数 | 一维展开 | 二维展开 | 三维展开 |
| 一阶 | 81.5175 | 81.5185 | 81.4868 |
| 二阶 | 0.4546 | 0.2115 | 2.2289 |
| 三阶 | 0.0006 | 0.0795 | 0.4736 |
| 四阶 | 0.0003 | 0.1174 | |
| 五阶 | 0.0001 | 0.0852 | |
| 六阶 | 0.00008 | 0.0151 |
表选项
本文设定系统顶点建模误差小于0.1,根据表 1中的分解结果,每一维上分别保留2、2、3个奇异值,通过误差计算式(8)得到实际的误差为0.028,满足设计要求。在整个顶点选取过程中,只需设定每一维上保留较大奇异值的个数,实现了本文对系统自动选取顶点的要求,并得到一个12个顶点的多胞LPV系统模型。得到各变参数对应的权重函数曲线如图 2所示。
图 2中的曲线描述了权重函数随变参数的实时变化情况,高度、马赫数、迎角对应的权重函数维数与每一维上保留的奇异值个数正好对应。
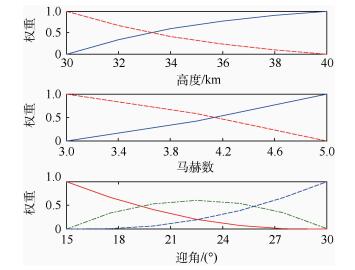 |
| 图 2 变参数的权重函数 Fig. 2 Weighting functions of varying-parameter |
| 图选项 |
本文基于上述HOSVD过程得到的顶点系统与凸分解系数,对各顶点设计控制器。在考虑系统参数不确定性的情况下,可将每个顶点系统模型描述为增广系统状态空间形式[13],对增广系统应用H∞鲁棒控制中的混合灵敏度设计方法[14],求使系统内稳定且满足闭环性能指标的控制器。基于此方法设计高超声速飞行器的自增益调度控制系统,控制系统结构如图 3所示,变参数反馈给在线调参模块可由变参数对应的权重函数求解得到凸分解系数,实时选择各顶点控制器所占权重,从而得到全包线控制器。
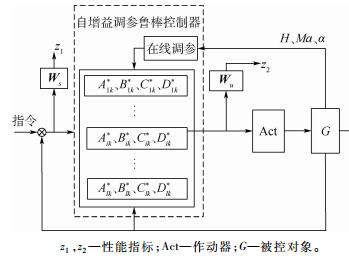 |
| 图 3 基于鲁棒混合灵敏度增益调度控制系统 Fig. 3 Gain scheduling control system based on robust mixed sensitivity |
| 图选项 |
H∞混合灵敏度设计的难点在于如何将系统的闭环性能指标要求表示在尽量简单的加权函数中。本文依据回路成形理论[15]选择期望的回路传递函数为ωs/s,结合闭环系统性能的要求对回路进行频域整形,选取合适的混合灵敏度加权函数阵,得到多胞顶点的鲁棒控制器。高超声速飞行器三通道的混合灵敏度加权函数阵选取为
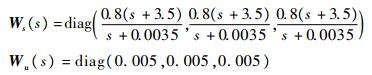 |
当LPV系统的顶点控制器确定以后,LPV控制器可由顶点的凸组合求得,全包线控制器形式如式(5)所示,其凸组合是由变参数ρ(t)在多胞Θ中的位置决定的。
3.2 仿真与分析 在飞行包线区域内选择一状态点H=35km, Ma=4, α=20°,在三通道加入姿态阶跃指令信号进行仿真验证,仿真结果如图 4所示。
 |
| 图 4 三通道阶跃指令响应 Fig. 4 Three channels' step order response curves |
| 图选项 |
仿真结果表明,在不考虑不确定性的情况下控制器能精确跟踪迎角、侧滑角、滚转角阶跃指令信号,三通道姿态角能够在2s之内跟踪指令信号,响应速度较快,且没有超调量。同时可看出所设计的控制器受通道之间耦合的影响较小。当考虑如表 2所示的气动力系数、气动力矩系数、动压、转动惯量、质量的不确定性,对闭环系统进行100次蒙特卡罗仿真,仿真结果如图 5所示。
表 2 不确定性 Table 2 Uncertainty
| 不确定性项 | 不确定性范围 |
| 气动力系数 | -20%~+20% |
| 气动力矩系数 | -20%~+20% |
| 动压 | -30%~+30% |
| 转动惯量 | -5%~+5% |
| 质量 | -3%~+3% |
表选项
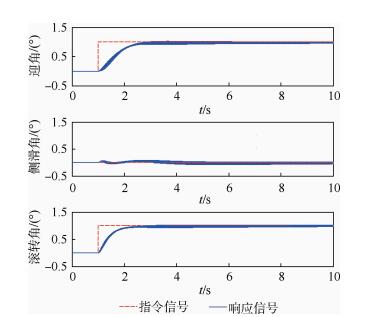 |
| 图 5 100次蒙特卡罗仿真结果 Fig. 5 Results of 100 Monte-Carlo simulation |
| 图选项 |
从仿真结果可以看出,在强不确定性因素的影响下,100次蒙特卡罗仿真的控制器跟踪性能与标称情况下相近,不确定性对控制器的动态性能影响较小,说明本文设计的LPV变增益控制器对不确定性系统具有良好的跟踪性能和鲁棒性。
根据航天飞机的飞行指令,在包线区域内(见图 6)对系统进行仿真,迎角响应如图 7所示。
 |
| 图 6 飞行包线 Fig. 6 Flight envelope |
| 图选项 |
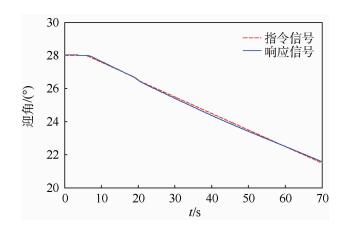 |
| 图 7 迎角指令跟踪仿真 Fig. 7 Angle of attack command tracking simulation |
| 图选项 |
图 7中的仿真结果表明在整个飞行包线内能够精确跟踪姿态指令,验证了控制器的增益调度能力。图 8中的曲线对应于12个多胞顶点的凸分解系数,其描述了整个在线增益调度过程中各顶点所占实时状态点的权重,以及顶点控制器所占全包线控制器的权重。
 |
| 图 8 凸分解系数仿真结果 Fig. 8 Results of onvex parameter decomposition simulation |
| 图选项 |
4 结论 本文针对航天飞机再入段大包线对象提出了一种基于网格化张量及HOSVD的LPV多胞模型建模方法,并设计了LPV鲁棒控制器,仿真验证表明:
1)基于网格化张量的HOSVD方法能够完成LPV多胞模型的建模,在保证建模精度的前提下控制顶点数量,并给出误差的计算方法。
2)相较于传统的建模方法,基于网格化张量及HOSVD方法能够降低对设计人员经验的依赖,大幅提高建模过程的自动化程度,有利于工程化应用。
3)基于回路成形理论设计的鲁棒混合灵敏度控制器能够实现在线增益调度,并具有很好的鲁棒性。
参考文献
| [1] | 白辰, 任章, 樊垚, 等. 基于模糊神经网络扰动观测器的RLV动态逆再入姿态控制[J].中南大学学报(自然科学版), 2013, 7(1): 58–62.BAI C, REN Z, FAN Y, et al. Dynamic inversion control for RLV reentry attitude based on fuzzy-neural disturbance observer[J].Journal of Central South University(Natural Scicence), 2013, 7(1): 58–62.(in Chinese) |
| [2] | HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance Control and Dynamics, 2006, 29(6): 1315–1328.DOI:10.2514/1.20151 |
| [3] | LIND R. Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects[J].Journal of Guidance Control and Dynamics, 2002, 25(4): 733–739.DOI:10.2514/2.4940 |
| [4] | YUSUKE Y, TAKASHI S.Attitude control of spacecraft with VSCMGs using LPV modeling technique[C]//SICE Annual Conference.Tokyo:Waseda University, 2011:2678-2683.http://www.doc88.com/p-8058933636668.html |
| [5] | KUMAR A.Convex modeling techniques for aircraft control[D].Virginia:Virginia Polytechnic Institute and State University, 2000:1-5.http://arc.aiaa.org/doi/pdf/10.2514/6.2000-4458 |
| [6] | PETRES Z.Polytopic decomposition of linear parameter-varying models by tensor-product model transformation[D].Budapest:Budapest University of Technology and Economics, 2006:25-89.http://cn.bing.com/academic/profile?id=2096926384&encoded=0&v=paper_preview&mkt=zh-cn |
| [7] | 秦伟伟, 郑志强, 刘刚, 等. 高超声速飞行器的LPV鲁棒变增益控制[J].系统工程与电子技术, 2011, 33(6): 1327–1331.QIN W W, ZHENG Z Q, LIU G, et al. Robust variable gain control for hypersonic vehicles based on LPV[J].Systems Engineering and Electronics, 2011, 33(6): 1327–1331.(in Chinese) |
| [8] | 王明昊, 刘刚, 杨述华. 高超声速飞行器的多胞LPV系统控制器设计[J].空间控制技术与应用, 2013, 39(1): 15–22.WANG M H, LIU G, YANG S H. Polytopic-LPV-system-based control design for hypersonic vehicle[J].Aerospace Control and Application, 2013, 39(1): 15–22.(in Chinese) |
| [9] | HE C F, YANG L Y, WANG Z C, et al.Linear parameter-varying attitude controller design for a reusable launch vehicle during reentry[C]//Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference.Piscataway, NJ:IEEE Press, 2014:2723-2728. |
| [10] | RAJWADE A, RANGARAJAN A, BANERJEE A. Image denoising using the higher order singular value decomposition[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2013, 35(4): 849–862.DOI:10.1109/TPAMI.2012.140 |
| [11] | OHARA A, YAMAGUCHI Y, MORITO T.LPV modeling and gain scheduled control of reentry vehicle in approach and landing phase[C]//AIAA Guidance, Navigation, Control and Conference and Exhibit.Reston:AIAA, 2001:1-11.http://link.springer.com/10.1007/978-3-642-36110-4_1 |
| [12] | Aerodynamic design data book, Volume 1M:Orbiter vehicle STS-1: SD72-SH-0060 [R].[S.l.]:Rockwell International, 1980.http://arc.aiaa.org/doi/pdf/10.2514/3.25879 |
| [13] | 王振超, 杨凌宇, 张晶, 等. 面向大包线导弹的分回路LPV姿态控制器设计[J].航空兵器, 2015, 1(2): 14–20.WANG Z C, YANG L Y, ZHANG J, et al. Loop separate LPV attitude controller design for large envelope missile[J].Aero Weaponry, 2015, 1(2): 14–20.(in Chinese) |
| [14] | 夏文艳, 高嵩, 王洁, 等. 基于H∞混合灵敏度的导弹解耦控制器设计方法[J].电子设计工程, 2009, 17(11): 43–45.XIA W Y, GAO S, WANG J, et al. Decoupling based on the H∞ mixed sensitivity controller for missile design method[J].Electronic and Engineering, 2009, 17(11): 43–45.(in Chinese) |
| [15] | 傅彩芬, 谭文, 刘吉臻. 基于回路成形的鲁棒增益调度控制器设计[J].信息与控制, 2005, 34(2): 152–156.FU C F, TAN W, LIU J Z. Robust gain scheduling controller based on loop shaping[J].Information and Control, 2005, 34(2): 152–156.(in Chinese) |
