对于RLV飞行控制系统的设计,当前国内外采用了非线性跟踪控制[2]、神经网络自适应控制[3]、滑模干扰观测器控制[4]、模型参考变结构控制[5]及轨迹线性化[6]等非线性控制方法。但由于采用经典控制理论设计的控制器具有物理意义明确、结构简单及鲁棒性强等优点,因此目前工程上仍常采用经典控制理论设计各类飞行器控制律。文献[7]在拉平段采用PID控制,通过控制升降舵实现升降速度控制,进而实现了飞行器安全着陆,该控制方案常用于有动力飞行器着陆。无动力RLV在采用文献[7]的控制方案时,飞行器接地时刻的升降速度可满足接地要求,但缺点是接地点散布较大,易超出安全范围。为保证在复杂的风干扰或参数不确定情况下RLV仍具有较好的接地性能,在拉平段通过升降舵进行高度控制也是一种控制方案,但该控制方案的难点是RLV如何精确跟踪由圆弧拉起/指数拉起/浅下滑轨迹组成的拉平着陆轨迹[8]。RLV拉平着陆轨迹的高度给定指令可视为加速度输入函数,由于采用PID控制的高度跟踪控制系统为Ⅱ型系统,因而系统存在加速度静差,为此可通过提高系统的型别来消除系统加速度稳态静差。文献[9-10]研究了弹射座椅和导弹的飞行控制系统,采用鲁棒伺服线性二次型调节器(Linear Quadratic Regulator,LQR)理论在外回路增加积分环节提高了系统的型别,实现了控制系统对输入指令的精确跟踪,该方法的难点是加权矩阵Q、R的选取需依赖于设计者的经验,缺点是易导致系统稳定性恶化。除在反馈回路增加积分环节提高系统的型别外,还可通过引入前馈校正装置来提高系统的跟踪精度。文献[11]采用经典控制理论在反馈系统中引入前馈校正装置实现了火炮系统对输入指令的精确跟踪,具有较强的工程实用性。
针对无动力RLV的拉平纵向控制问题,本文基于经典控制理论中前馈控制思想,提出一种按输入补偿的高度跟踪复合控制律设计方法。首先基于线性模型设计反馈回路控制律参数,然后采用平衡截断法[12]对由姿态回路构成的等效飞行器传递函数进行模型降阶,最后基于时间加权高度跟踪误差/误差变化率平方积分性能指标设计前馈校正环节参数。对于起落架释放前后2组控制律的切换问题,提出一种基于积分器初值的控制律平滑切换方法。通过算例验证控制策略与控制结构的合理性,以及控制律设计和控制律平滑切换方法的有效性。
1 RLV纵向数学模型 RLV进场着陆为无动力着陆,仅通过操纵相关的气动舵面跟踪期望的着陆轨迹,在规定的接地状态范围内实现安全着陆。根据理论力学中刚体质心运动及转动运动定理,RLV的纵向动力学模型[13]为
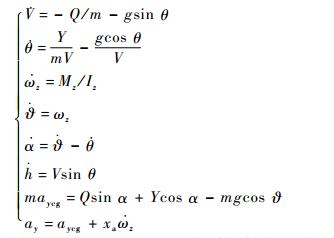 | (1) |
式中:h、V、θ、α、υ和ωz分别为高度、速度、轨迹倾角、迎角、俯仰角和俯仰角速率;xa为加速度计安装在飞行器对称面内距重心的距离,置于重心前时xa定义为正,反之为负;aycg和ay分别为飞行器重心处的法向加速度和加速度计安装处的法向加速度;m和g分别为飞行器质量和重力加速度;Iz为俯仰转动惯量;Q、Y和Mz分别为阻力、升力和俯仰力矩,其值通常取决于飞行器的速度、迎角及各气动舵面偏角,可用以下形式表述:
 | (2) |
其中:δ=[δe, δea, δsb]T,δe、δea和δsb分别为升降舵、襟翼和阻力板;q=ρV2/2为动压,ρ为空气密度;Ma、S和bA分别为马赫数、参考面积和平均气动弦长;Cx、Cy和mz分别为阻力系数、升力系数和俯仰力矩系数;Cx0、Cy0和mz0分别为基准点阻力系数、升力系数和俯仰力矩系数;Cx*、Cy*和mz*为气动导数,*为式(2)中相关参数。
为便于分析问题,在基准点为铅垂面内固定轨迹倾角恒定动压飞行的条件下,对非线性系统式(1)进行小扰动线性化,考虑θ、υ和α之间的线性关系θ=υ-α,得到RLV的线性化模型:
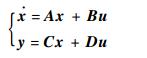 | (3) |
式中:
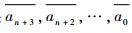
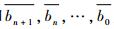
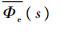
 |
其中:θ*、V*为基准运动对应的轨迹倾角、空速;I5×5为单位矩阵;05×3为零矩阵。
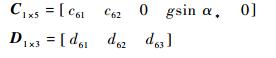 |
式中:
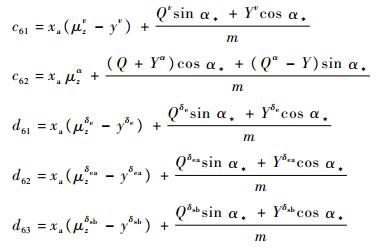 |
其中:α*为基准运动对应的迎角;参数xv、xα、xδ*、yv、yα、yωz、yδ*、μzv、μzα、μzωz、μzδ*、Qv、Qα、Qδ*、Yv、Yα和Yδ*的具体表述形式见文献[13],δ*为相应的气动舵面。
2 拉平纵向控制策略与控制结构 RLV进入拉平段后,以飞行器高度与期望着陆轨迹高度之差为引导信号,将高度跟踪误差输入给着陆控制系统,通过控制升降舵偏转实现高度跟踪控制。在常规控制方案中,升降舵通道由姿态控制内回路和高度跟踪控制外回路组成。其中,姿态控制内回路由俯仰角反馈、俯仰角速度反馈和法向加速度反馈构成,用于得到升降舵偏角指令,通过控制升降舵偏转使飞行器产生俯仰运动,改变迎角,从而改变升力使飞行器产生升降运动,实现高度跟踪控制;高度跟踪控制外回路由高度反馈构成PID控制,用于得到内回路所需要的俯仰角给定指令。由于常规控制方案中升降舵通道的系统为Ⅱ型系统,对于深下滑段,高度给定指令为斜坡输入信号的情况下,高度跟踪静差为零,但对于拉平段,此时高度给定指令变为拉平段的圆弧和指数信号,将致使飞行器无法及时跟踪上期望拉平轨迹,因此将产生较大的高度跟踪误差。为此,RLV进入拉平段后,在常规控制方案中高度跟踪控制外回路的基础上引入前馈校正装置,相当于引入输入量的微分信号,根据轨迹变化对俯仰角给定指令进行超前修正,然后经过内回路控制律改变飞行器升降舵偏角指令,使得飞行器获得抬头力矩具有一定的超前量,从而有利于消除高次轨迹指令下的高度跟踪误差。
另外,襟翼和阻力板的舵面偏转对飞行器安全着陆也起到关键作用。襟翼偏转用于增加飞行器的升力,有利于减小拉平高度跟踪误差,同时还便于使飞行器的接地状态满足性能指标。阻力板偏转用于控制飞行器动压,为轨迹跟踪控制提供动压保障。
RLV拉平纵向控制律结构如图 1所示。图中:Hg、Vbg和υg分别为高度给定指令、表速给定指令和俯仰角给定指令;Vb为表速;Kph、Kih和Kdh为高度跟踪控制外回路PID控制比例系数;Kυ、Kωz和Kay为姿态控制内回路的比例系数。图 1中,由于RLV具有纵向静不稳定性特性,引入法向加速度ay反馈用以增加RLV的纵向静稳定性;υ反馈和ωz反馈用于改善RLV的长周期和短周期模态动态性能;对高度进行PID控制和输入补偿前馈校正,实现飞行器在加速度输入信号情况下高度跟踪静差为零。对于襟翼舵面,为增升需要,襟翼偏角将由拉平起始点偏角δea0随时间t匀速下偏至规定偏角δea1。阻力板通道为表速控制,采用PI控制形式实现表速无静差跟踪控制。
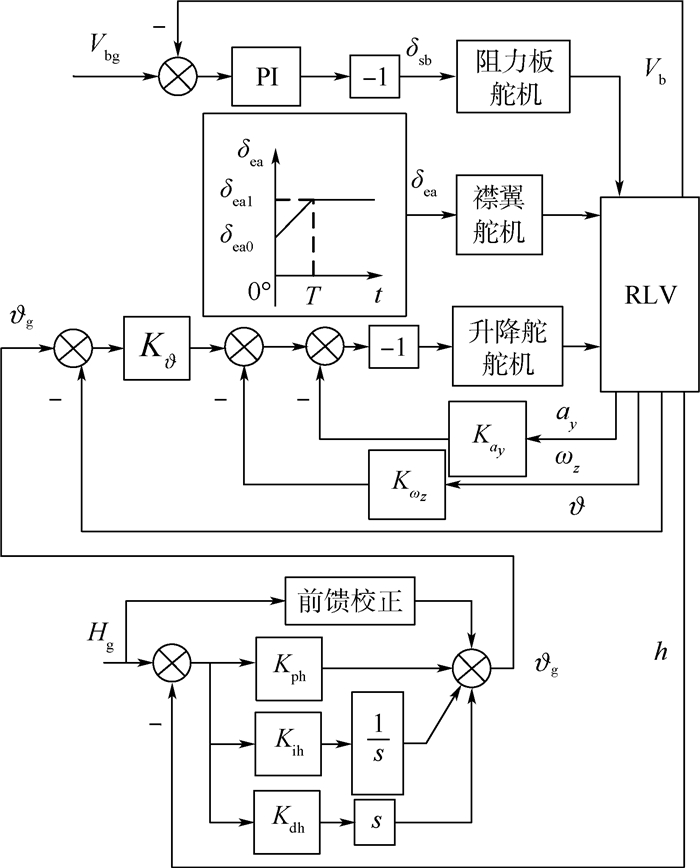 |
| 图 1 RLV拉平纵向控制律结构 Fig. 1 Flare longitudinal control law structure of RLV |
| 图选项 |
拉平纵向各通道的控制律表达式为
 | (4) |
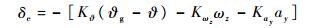 | (5) |
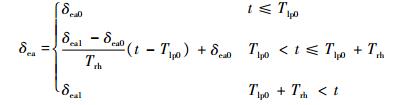 | (6) |
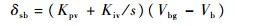 | (7) |
式中:s为拉普拉斯算子;Gf(s)为前馈校正环节;Kpv和Kiv为表速回路PI控制比例系数;Tlp0为RLV进入拉平段的时刻; Trh为襟翼偏角软化时间。
3 拉平纵向控制律参数设计 RLV拉平纵向控制律参数可归纳为2类参数:一类是反馈控制律参数(如Kph、Kih、Kdh、Kυ、Kωz、Kay、Kpv和Kiv);另一类是前馈校正环节参数。在控制律设计过程中,先将反馈控制律参数设计问题转换为多参数多约束优化设计问题,再利用MATLAB提供的SISO Design Tool工具箱[14]对反馈控制律参数在可能的取值范围内寻优。根据这种设计方法,首先优化设计升降舵通道内回路反馈控制律参数,然后优化设计外回路反馈控制律参数,其次基于时间加权高度跟踪误差/误差变化率平方积分指标优化设计前馈校正环节参数,最后在升降舵通道控制律参数基础上再优化设计阻力板通道控制律参数。本文重点讨论如何优化设计升降舵通道前馈校正环节参数,使复合系统既能消除加速度静差,又能改善系统的动态跟踪性能。
将图 1中升降舵回路控制结构简化为图 2所示的2种形式。图中:Gp(s)为输入是俯仰角给定指令、输出是飞行高度的传递函数,由姿态控制内回路传递函数与飞行器传递函数组成;Gc(s)为校正装置传递函数;Gf1(s)和Gf2(s)为前馈校正环节;E(s)为误差传递函数。
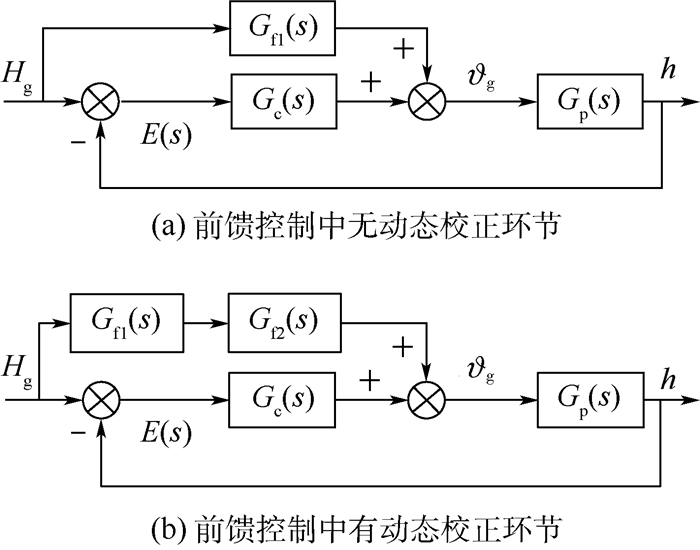 |
| 图 2 升降舵回路控制结构简化图 Fig. 2 Simplified graph of elevator loop control structure |
| 图选项 |
等效飞行器传递函数Gp(s)的一般表达形式如式(8)所示,传递函数Gc(s)、Gf1(s)和Gf2(s)的表达式如式(9)和式(10)所示。
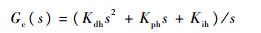 | (9) |
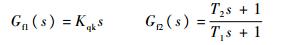 | (10) |
式中:an, an-1, …, a0和bn-1, bn-2, …, b0为Gp(s)的系数;Kqk为静态前馈系数;T1和T2为动态前馈控制器时间常数。Gf1(s)的作用是使复合系统等效为更高型别的系统,使系统加速度误差为零; Gf2(s的作用是提高复合系统的动态响应性能。
对于升阻比大、飞行速度较小和着陆轨迹较缓的常规无动力飞行器,采用图 2(a)所示前馈控制中无动态校正环节的控制结构,即可实现对拉平着陆轨迹的跟踪控制。但对于升阻比小、飞行速度较大和着陆轨迹较陡的RLV,若仍采用图 2(a)所示的控制结构,可能无法快速地跟踪上期望轨迹,进而致使RLV无法安全着陆;若采用图 2(b)所示的前馈控制中有动态校正环节的控制结构,则能改善系统的动态特性,在能消除系统加速度误差的同时,还能快速减小RLV的轨迹跟踪误差。
设计参数Kqk、T1和T2时,首先设计参数Kqk,然后在此基础上再设计参数T1和T2。
设计参数Kqk时,令Gf2(s)=1,则前馈校正环节为Gf(s)=Kqks。
复合系统的闭环传递函数Φ(s)为
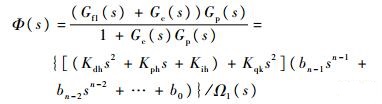 | (11) |
式中:
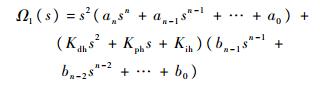 |
复合系统的误差传递函数为
 | (12) |
取Kqk=a0/b0。当输入信号为r(t)=t2/2时,利用终值定理推导可得系统的稳态误差为
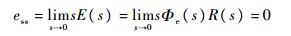 | (13) |
式中:R(s)为输入传递函数。
可见,复合系统的加速度稳态误差为零,复合系统可等效为Ⅲ型系统。
设计完参数Kqk后,再设计参数T1和T2。前馈校正环节变为
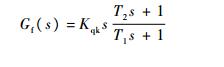 | (14) |
复合系统的闭环传递函数变为
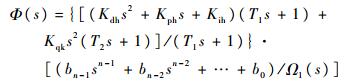 | (15) |
可见,引入前馈校正环节Gf(s)后的闭环系统特征方程增加了1个闭环极点-1/T1。T1的值直接影响系统的控制性能,为尽量减小闭环极点-1/T1对系统稳定性的影响,根据以下原则选取T1的值:
1) T1大于零,以保证闭环极点-1/T1位于左半s平面,从而对系统的稳定性没有影响。
2) T1尽量小,使闭环极点-1/T1远离虚轴,从而降低-1/T1对系统动态性能的影响。
3) T1不宜过小,需结合飞控计算机的运行周期确定。
设计完参数Kqk和T1后,再基于时间加权高度跟踪误差e(t)/误差变化率(t)平方积分指标设计参数T2。
时间加权高度跟踪误差e(t)/误差变化率(t)平方积分指标形式如下:
 | (16) |
式中:λ1和λ2为加权系数。
性能指标J总为正值,J越小表明系统的动态跟踪性能越好。性能指标J中引入误差变化率(t)有利于限制过渡过程中误差的起伏变化,提高系统的动态跟踪性能。时间t的加权,有利于降低动态误差的持续时间。
复合系统的误差传递函数为
 | (17) |
将式(8)~式(10)代入式(17),整理为一般形式,即
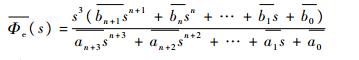 |
则
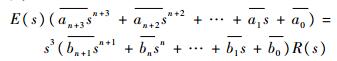 | (18) |
式中:
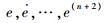
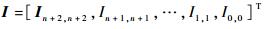
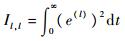
系统误差函数e(t)的微分方程为
 | (19) |
将加速度输入信号r(t)=t2/2代入式(19),得
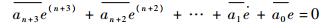 | (20) |
依次将
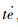
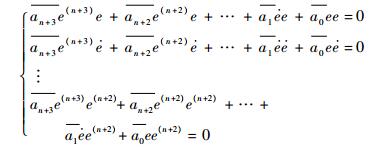 | (21) |
在区间[0, ∞)上分别对等式(21)两边积分,为书写方便,令
 | (22) |
则
 | (23) |
对于Ii, j,当i≠j时,Ii, j通过分部积分法化简,可用Il, l、初值e(l)(0)和终值e(l)(∞)表示,其中, l=0, 1, …, n+2。
由于系统为稳定系统,则终值e(l)(∞)=0。
初值e(l)(0)可由拉普拉斯变换微分公式(24)和初值定理式(25)求得:
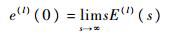 | (25) |
将式(23)整理为矩阵和向量的形式,即
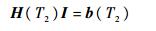 | (26) |
式中:
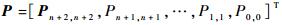
整理式(26),可得到
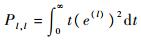
同理,依次将te,
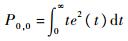
 | (27) |
在区间[0, ∞)上分别对等式(27)左右两边积分,为书写方便,令
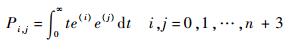 | (28) |
则
 | (29) |
对于Pi, j,当i≠j时,Pi, j通过分部积分法化简,可用Il, l、Pl, l和初值e(l)(0)表示,其中,l=0, 1, …, n+2。
将式(29)整理成矩阵和向量的形式:
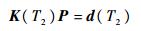 | (30) |
式中:
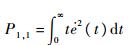
通过整理式(30),得到
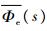
联立
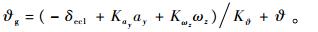

综上可知,等效系统Gp(s)的阶数越高,则误差传递函数
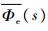
4 控制律平滑切换 RLV进入拉平段后,襟翼偏角开始随时间线性偏转至某规定位置,当RLV满足起落架释放条件后,起落架开始放下。襟翼偏角变化和起落架释放称为构型变化,构型变化对飞行器气动有较大影响。为保证构型变化后的着陆控制系统仍具有较好的控制性能,在控制结构不变的情况下,需重新设计控制律参数。
起落架释放前后升降舵通道控制律参数的不同,必然面临着2组控制律之间的切换问题。控制律之间的切换可能会引起升降舵舵面瞬间跳变,从而产生较大的俯仰力矩,致使飞行器姿态剧烈变化,因此需采用抑制措施,避免舵面瞬变。目前,常采用双模态同步运算瞬变抑制法或单模态运算瞬变抑制法[15]在一定时间内对2组控制律采用淡入/淡出的方式抑制舵面瞬变,但这2种方法均依赖设计者经验,通过调节特定的参数达到较好的控制效果。为避免上述方法经验试凑,提高切换效率,以下基于积分器初值提出一种新的控制律平滑切换方法。
根据控制律中积分器的工作原理,飞控计算机在控制律切换后的第1个运算周期,积分器输出值为其初值xInit0,在之后的运算周期,积分器输出值为初值xInit0累加积分器输入值得到的值。根据积分器的该特性,在控制律切换后的第1个运算周期,可通过对新控制律中积分器赋初值,从而使2组控制律得到的升降舵偏角指令相等。
对于图 1所示的控制结构,通过对高度跟踪控制外回路PID控制中积分器进行赋初值xInit0,以实现控制律平滑切换。由于控制律切换前一个运行周期的舵面偏角δec1已知,飞行器的飞行状态已知,新的控制律参数已知,采用从后向前推导的原则,推导出积分器初值xInit0的表达式为
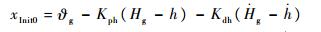 | (31) |
式中

赋入积分器初值后,便可实现2组控制律之间的平滑切换。
5 仿真算例 以某RLV为研究对象,按本文方法进行拉平纵向控制律设计。对RLV进行气动特性分析,确定在拉平起始点襟翼舵面偏角δea0为0°,进入拉平后襟翼偏角δea1保持在15°,襟翼偏角软化时间Trh为5 s。要求RLV的接地状态满足:飞行器接地点距理想接地点纵向偏差不超过±200 m;升降速度小于3 m/s;俯仰角在3°~12°范围内。
根据RLV起落架状态变化过程,选取拉平起始点为起落架收起状态时的控制律设计点,选取起落架释放起始点距地面的中间高度点为起落架放下状态时的控制律设计点。起落架收起和放下状态控制律设计点对应的RLV飞行状态分别为:q=10 142 Pa,h=423 m,α=3.1°,θ=-21°,ωz=0°/s,δe=-4.3°,δea=0°,δsb=35°;q=6 724 Pa,h=216 m,α=8.6°,θ=-9.2°,ωz=6.2°/s,δe=-6.5°,δea=15°,δsb=17°。
在设计点处建立飞行器线性化模型,设计控制律参数,使RLV线性控制系统的时域/频域性能满足控制目标,并使RLV的接地状态接近理想接地状态。其中,RLV理想接地状态为:接地纵向偏差为0 m,升降速度为1.5 m/s,俯仰角为7.5°。
根据第3节中方法设计拉平纵向控制律,性能指标式(16)中的加权系数λ1和λ2分别取0.6和0.4。控制律参数如下所示:
1)起落架释放前。Kph=1.14, Kih=0.33, Kdh=1.25, Kυ=1.81, Kωz=1.21, Kay=0.71, Kpv=8.2, Kiv=0.75, Kqk=0.42, T1=0.5, T2=6。
2)起落架释放后。Kph=1.43, Kih=0.26, Kdh=1.88, Kυ=2.74, Kωz=1.71, Kay=0.7, Kpv=8.2, Kiv=0.75, Kqk=0.53, T1=0.5, T2=0.3。
起落架开始释放时,根据第3节中方法实现起落架释放前后不同控制律之间的平滑切换。
为检验本文提出的控制律设计方法的合理性和有效性,以下分别采用图 2(a)所示前馈控制中无动态校正环节和图 2(b)所示前馈控制中有动态校正环节2种控制结构进行非线性全量仿真,记录并画出RLV的飞行高度、高度跟踪误差(正误差表示期望高度大于实际飞行高度)、升降速度、俯仰角和升降舵响应曲线, 见图 3~图 7,图中横坐标xd为RLV距理想接地点的距离。
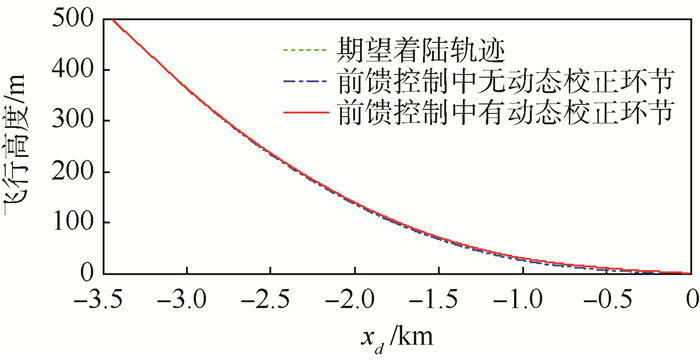 |
| 图 3 飞行高度响应曲线 Fig. 3 Flight altitude response curves |
| 图选项 |
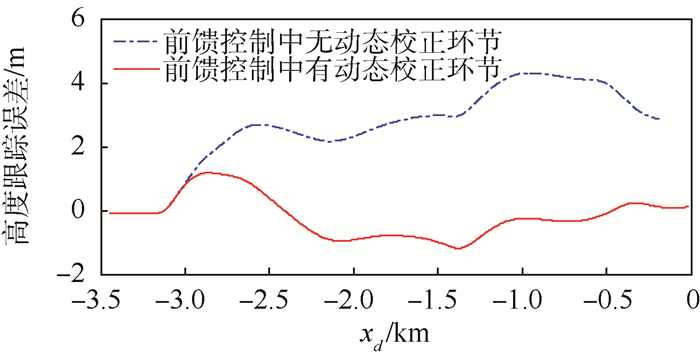 |
| 图 4 高度跟踪误差响应曲线 Fig. 4 Altitude tracking error response curves |
| 图选项 |
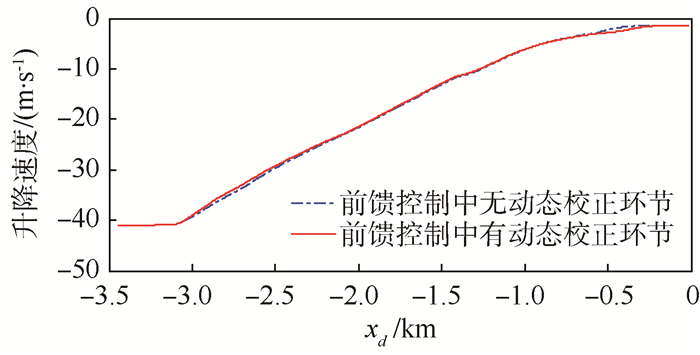 |
| 图 5 升降速度响应曲线 Fig. 5 Vertical speed response curves |
| 图选项 |
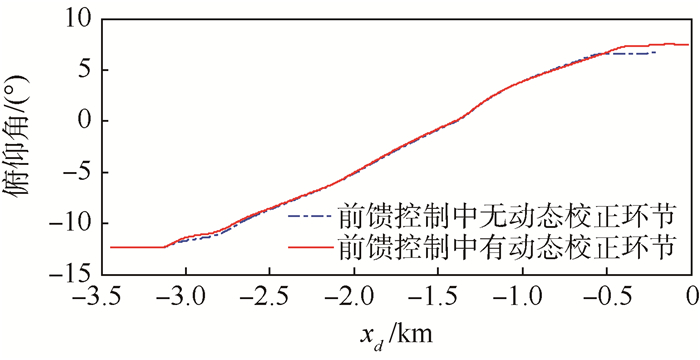 |
| 图 6 俯仰角响应曲线 Fig. 6 Pitch angle response curves |
| 图选项 |
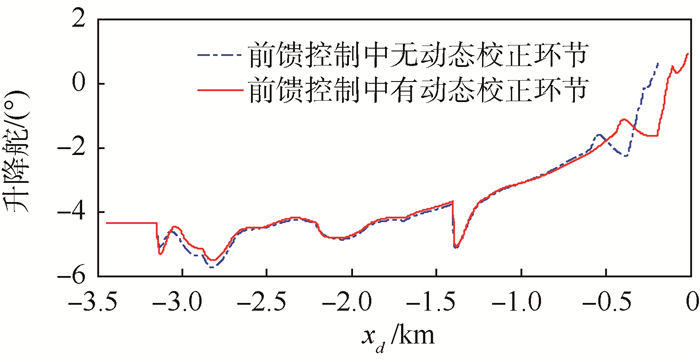 |
| 图 7 升降舵响应曲线 Fig. 7 Elevator response curves |
| 图选项 |
由图 3~图 7可见,采用图 2(a)所示的控制结构时,虽然RLV接地时刻的升降速度(1.3 m/s)和俯仰角(6.7°)均落在要求的范围内,但RLV对期望着陆轨迹的跟踪精度较差(最大高度跟踪误差为4.3 m),致使RLV的实际接地点距理想接地点的纵向偏差较大(-193.8 m);采用图 2(b)所示的控制结构时,RLV对期望着陆轨迹的跟踪精度较高(最大高度跟踪误差仅为1.18 m),RLV各接地状态(升降速度为1.37 m/s,俯仰角为7.46°,接地纵向偏差为-19.1 m)均接近理想接地状态。另外,采用本文提出的控制律平滑切换方法,也实现了起落架释放前后2组控制律之间的平滑切换。
6 结论 本文根据RLV拉平着陆的轨迹跟踪纵向控制需求,提出了一种常规反馈控制与按输入补偿的前馈控制相结合的复合控制方案。
1)提高了RLV的轨迹跟踪精度,减小了飞行器的接地散布。
2)基于时间加权高度跟踪误差/误差变化率平方积分指标的前馈控制律参数设计方法是有效的。
3)通过对新的控制律中积分器赋初值,实现了不同控制律之间的平滑切换。
参考文献
| [1] | KLUEVER C A, NEAL D A. Approach and landing range guidance for an unpowered reusable launch vehicle[J].Journal of Guidance, Control, and Dynamics, 2015, 38(11): 2057–2066.DOI:10.2514/1.G000909 |
| [2] | SUN H F, YANG Z L, ZENG J P. New tracking-control strategy for airbreathing hypersonic vehicles[J].Journal of Guidance, Control, and Dynamics, 2013, 36(3): 846–859.DOI:10.2514/1.57739 |
| [3] | XU H J, MIRMIRANI M, IOANNOU P A.Robust neural adaptive control of a hypersonic aircraft[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2003:1-8. |
| [4] | HALL C E, SHTESSEL Y B. Sliding mode disturbance observer-based control for a reusable launch vehicle[J].Journal of Guidance, Control, and Dynamics, 2006, 29(6): 1315–1328.DOI:10.2514/1.20151 |
| [5] | 潘彦鹏, 周军, 呼卫军. 临近空间飞行器再入段复合控制律设计[J].系统工程与电子技术, 2013, 35(11): 2364–2369.PAN Y P, ZHOU J, HU W J. Design of compound control law for near space vehicle reentry[J].Systems Engineering and Electronics, 2013, 35(11): 2364–2369.(in Chinese) |
| [6] | BEVACQUA T, BEST E, HUIZERGA A, et al.Improved trajectory linearization flight controller for reusable launch vehicles[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2004:875-887. |
| [7] | LIU Z, WANG Y, HAO X W.Coordinated landing control of unmanned aerial vehicle[C]//2011 International Conference on Electronics, Communications and Control.Piscataway, NJ:IEEE Press, 2011:1965-1970. |
| [8] | 郝现伟, 王勇, 杨业, 等. 变构型多操纵面RLV进场着陆轨迹优化设计[J].北京航空航天大学学报, 2015, 41(12): 2232–2239.HAO X W, WANG Y, YANG Y, et al. Optimization design of approach and landing trajectory for variable configuration RLV with muti-control surfaces[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(12): 2232–2239.(in Chinese) |
| [9] | WISE K A, BRINKER J S. Linear quadratic flight control for ejection seats[J].Journal of Guidance, Control, and Dynamics, 1996, 19(1): 15–22.DOI:10.2514/3.21574 |
| [10] | WISE K A.A trade study on missile autopilot design using optimal control theory:AIAA-2007-6673[R].Reston:AIAA, 2007.http://arc.aiaa.org/doi/abs/10.2514/6.2007-6673 |
| [11] | 姜文, 贺昱曜, 贺恭性. 改进火炮拖动随动系统跟随特性的方法[J].火力与指挥控制, 2009, 34(3): 92–95.JIANG W, HE Y Y, HE G X. An improved method for the following character of gun servo system[J].Fire Control and Command Control, 2009, 34(3): 92–95.(in Chinese) |
| [12] | GUGERCIN S, ANTOULAS A C. A survey of model reduction by balanced truncation and some new results[J].International Journal of Control, 2004, 77(8): 748–766.DOI:10.1080/00207170410001713448 |
| [13] | 肖业伦. 飞行器运动方程[M].北京: 航空工业出版社, 1987: 64-81.XIAO Y L. Model of aerocraft[M].Beijing: Aviation Industry Press, 1987: 64-81.(in Chinese) |
| [14] | 薛定宇. 控制系统计算机辅助设计——Matlab语言与应用[M].3版北京: 清华大学出版社, 2012: 284-290.XUE D Y. Computer aided control systems design using Matlab language[M].3rd edBeijing: Tsinghua University Press, 2012: 284-290.(in Chinese) |
| [15] | 杨一栋, 牛佩翼, 江浩. 飞行控制系统模态转换瞬变抑制技术的研究[J].航空学报, 1990, 11(1): 88–92.YANG Y D, NIU P Y, JIANG H. The study of transient suppression techniques for multimode flight control system[J].Acta Aeronautica et Astronautica Sinica, 1990, 11(1): 88–92.(in Chinese) |
