为解决动态故障树中备份门的定量计算问题,Wang等[11]提出了一种冷备份系统的可靠性近似计算方法,该方法适用于系统单元的寿命服从非指数分布;Boudali和Dugan[12]提出了一种将温备份故障树转化为贝叶斯网络进行计算的方法。但这些方法都未考虑主件发生故障时系统能否及时转换到备份件工作的不完全覆盖问题。不完全覆盖问题指系统因冗余管理功能失效导致系统不能正常检测、隔离以及调整失效组件,进而导致整个系统发生故障的现象。而冗余结构的不完全覆盖问题是影响系统可靠性的重要因素。Myers[13]论证了不完全覆盖对于k/n冗余系统可靠性的影响,并提出4种不完全覆盖模型下系统可靠度的计算方法,但未考虑冗余部件的动态失效特征。邢留冬等[14]针对不完全覆盖k/n系统提出了一种基于全概率和条件概率的计算方法,对系统多阶段任务可靠性进行了分析,但是该方法将冗余部件简单地作为冷备份处理。
本文在文献[12]的基础上,给出了考虑不完全覆盖时温备份系统的可靠性计算方法,并通过某机载电子设备论证了该方法的可行性,并与传统计算方法进行比较,该方法计算结果更合理,为复杂动态系统的可靠性分析奠定了一定的基础。
1 动态故障树基础 随着系统复杂程度的增加,系统部件失效通常存在时间顺序和功能相关性等特征。文献[4-5]提出一组动态逻辑门来描述部件失效的动态特征,然后通过建立动态故障树来分析系统的可靠性。动态逻辑门是动态故障树的基础,包括优先与门(PAND)、功能相关门(FDEP)、顺序相关门(SEQ)和备件门(SP)。备件门是系统设计中应用最广泛的动态门,一般用于提高系统的可靠性和安全性。下面重点介绍备件门。
备件门通常包括一个主输入部件和若干个备份部件,备件与主件一般具有相同的功能,但失效率可能不同。根据备件失效机理的不同,备件门可分为3类:冷备份门(CSP)、温备份门(WSP)、热备份门(HSP),其图形符号如图 1所示。
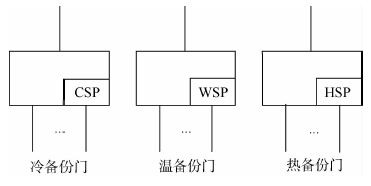 |
| 图 1 3种备份门图形符号 Fig. 1 Graphic symbols for three spare gates |
| 图选项 |
冷备份门包括主件和冷备件。主件在系统开始运作时就进入工作状态,而冷备件处于非工作状态;只有当主件失效后,冷备件才进入工作状态,当冷备件失效时系统失效。
温备份门与冷备份门的区别在于,冷备件在进入工作状态前视为无耗损,而温备件却可能已经失效,但其进入工作前的贮备失效率与工作状态失效率不同。因此系统失效存在两种可能:①温备件保持贮备状态,当主件失效,备件转为工作状态,直至备件失效则系统失效;②温备件比主件先失效,此时当主件失效则意味着整个冗余系统失效。
热备份门是在主件工作的同时,备件也处于工作状态。
2 温备份门的输入分析 相对于冷备份门和热备份门,温备份门的失效过程更复杂,定量计算更困难。本文主要针对温备份门提出一种可靠性定量计算方法,计算中只考虑备件数量为1的情况。为更方便描述温备份门的失效,引用两种特殊函数:阶梯函数和脉冲函数[15]。
2.1 阶梯函数 阶梯函数定义为
 | (1) |
式中:t、τ为非负实数。u(t-τ)在t=τ时不连续,根据其定义,可理解为在某时刻t,若t <τ,则基本事件将不发生。
2.2 脉冲函数 脉冲函数定义为
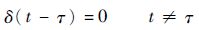 | (2) |
且
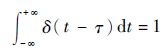 | (3) |
根据脉冲函数的定义以及t、τ为非负实数,式(3) 可化简为
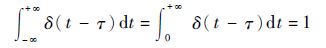 | (4) |
参考文献[15],可得到一个重要推论:
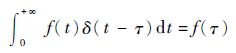 | (5) |
2.3 主件与备件的失效关联分析 某两单元温备份门,部件A、B是备份门的输入,X是备份门的输出,如图 2所示。
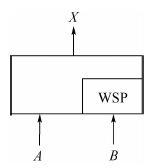 |
| 图 2 两单元温备份门结构简图 Fig. 2 Structure diagram of warm spare gate with two units |
| 图选项 |
主件A工作状态的失效率为λA(a);备件B处于单独工作状态时,其失效率λBi(b)。在温备份系统中,当备件B处于休眠状态时,休眠系数为α(0<α<1) ,其失效率为αλBi(b),当其进入工作状态时,其失效率为λBi(b)。
利用阶梯函数,备件B的条件失效率可表示为
 | (6) |
根据失效密度函数与失效率的关系,备件B的条件概率密度函数为
 | (7) |
3 不完全覆盖的温备份门输出分析 由于检测技术及转换装置的原因,未必能成功检测到主件A的失效并成功切换到备件B工作。对于冗余结构的不完全覆盖问题,通常用覆盖参数c来表征系统发生故障或错误发生时能自动恢复正常工作的能力[16]。系统的覆盖参数与系统发生故障时的监测、定位以及恢复正常工作等紧密相关,其定量关系为c=cd×cl ×cr ,其中cd、cl和cr分别为成功监测到故障发生、准确定位故障发生部位、成功切换到备份件工作的概率[17]。假定温备份系统的覆盖参数为c(0≤c<1)。
利用阶梯函数和脉冲函数,则输出X的条件概率密度函数:
 | (8) |
等式右边u(a-b)δ(x-a)表示备件B先于主件A失效;cu(b-a)δ(x-b) 表示主件A先于备件B失效而且及时检测到A失效,并成功切换到B工作;(1-c)u(b-a)δ(x-a)表示虽然主件A先于备件B失效,但是不能检测到或不能切换到B。
其联合概率密度函数为
 | (9) |
因此,X的概率密度函数为
 | (10) |
将式(8) 代入式(10) 可得
 | (11) |
式中:
 | (12) |
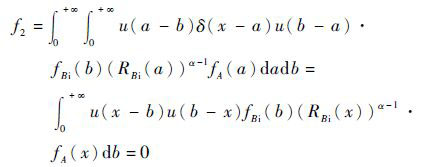 | (13) |
同理,可得
 | (14) |
 | (15) |
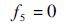 | (16) |
 | (17) |
将式(12) ~式(17) 相加,可得X的概率密度函数:
 | (18) |
式(18) 适用于主件A和备份件B寿命服从各种分布类型时温备份门的输出定量计算。
特别地,当单元A、B寿命均服从指数分布,即
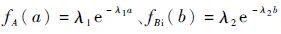
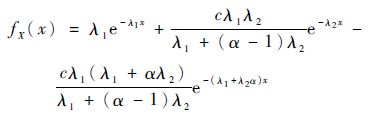 | (19) |
4 实例分析 以某机载电子设备为例,电子设备的核心包括两个并联的数据处理器,设备供电由飞机发动机提供,同时配有应急电源以保证发动机故障时电子设备的正常工作,发动机M、应急电源N寿命为指数分布,其失效率分别为λ1=2×10-4h-1、λ2=10-4h-1, 两个数据处理器C、D服从相同参数的指数分布,其失效率λ3=8×10-5h-1。当应急电源处于休眠状态时,其休眠因子α=0.2。发动机与应急电源组成的冗余结构覆盖参数c=0.95。
4.1 可靠性分析 根据相关建树要求,建立机载电子设备系统的动态故障树,如图 3所示。
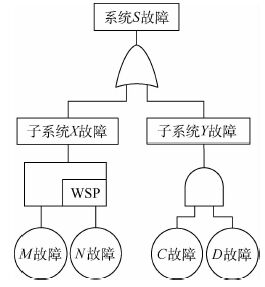 |
| 图 3 系统的动态故障树 Fig. 3 Dynamic fault tree of system |
| 图选项 |
对于温备份子系统X,失效密度函数可由式(18) 得到。
对于与门子系统Y,失效密度函数为
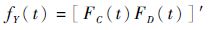 | (20) |
对于或门系统S,失效密度函数为
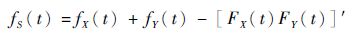 | (21) |
代入相关数据可得系统S的失效密度为
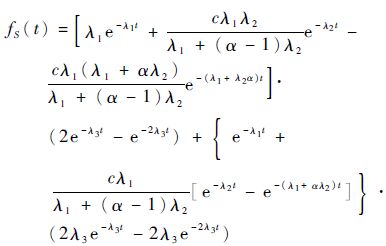 | (22) |
利用MATLAB软件比较本文方法与文献[12]不考虑覆盖问题的方法的系统失效密度随时间变化的曲线,如图 4所示。
 |
| 图 4 系统失效密度函数随时间变化的曲线 Fig. 4 Curves of system failure probability density function changing with time |
| 图选项 |
系统S的可靠度函数为
 | (23) |
同样,可得本文方法与文献[12]方法的系统S可靠度随时间的变化曲线,如图 5所示。
 |
| 图 5 系统可靠度随时间变化的曲线 Fig. 5 Curves of system reliability changing with time |
| 图选项 |
本文方法下系统S的平均故障前时间(MTTF):
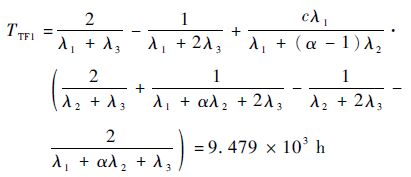 |
采用文献[12]方法得系统平均故障前时间:TTF2=9.748×103 h
根据图 5和系统平均故障前时间(MTTF)计算结果可知,两种计算方法结果基本一致,但是本文考虑不完全覆盖问题更符合实际情况,得到的温备份系统的可靠度比传统方法更合理。
文献[18]在考虑不完全覆盖问题,采用双重积分来描述温备份逻辑门的输出,并通过离散化方法进行了定量分析。相比于文献[18],本文得到更简捷的温备份门输出表达式,有利于进一步对系统进行灵敏度和不确定性分析。
4.2 灵敏度分析 将系统可靠度R看作λ1、λ2、λ3、α, c的函数,在t=5 000 h 时,系统S的可靠度R=0.714 1。
系统S可靠度随单个参数变化的曲线如图 6所示。
将λ1=2×10-4, λ2=10-4, λ3=8×10-5,α=0.2,c=0.95,t=5 000 h作为状态O,在状态点O分别将可靠度R对各变量求偏导,结果如表 1所示。
分析图 6变化趋势和表 1结果可知:
1) 表 1中负数项表示随着该变量的增大,系统可靠度R会降低,正数项则表示系统可靠度R与该变量成正相关,会随着变量的增大而增大。
2) 系统可靠度对于失效率λ3更敏感,若要提高系统可靠度,应首先降低部件C、D的失效率。对于部件M、N组成的温备份系统,降低备件B的失效率更有利于提高系统的可靠度。
3) 相比于休眠系数α,覆盖参数c对于系统可靠性影响更明显。
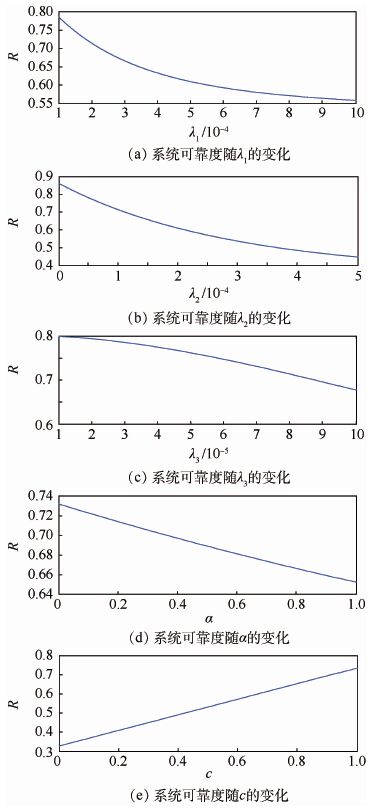 |
| 图 6 系统可靠度随单个参数变化的曲线 Fig. 6 Curves of system reliability changing with one of variables |
| 图选项 |
表 1 系统可靠度对各变量的偏导数 Table 1 Partial derivatives of system reliability to variables
| 变量的偏导数 | 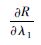 | 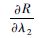 | 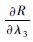 | 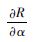 | 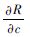 |
| 数值 | -578 | -1 235.4 | -1 770.5 | -0.087 | 0. 406 5 |
表选项
5 结论 1) 考虑冗余系统的不完全覆盖问题,提出了一种动态故障树温备份门的定量分析方法,该方法适用于多种分布类型的温备份门计算。
2) 对系统进行灵敏度分析,得到了各部件对于系统可靠度的影响显著程度,并提出了提高系统可靠性的措施。
3) 通过与传统方法的比较,阐明了非完全覆盖对系统可靠性的影响。
因此,在实际工程的冗余系统中,进行系统可靠性分析时必须考虑非完全覆盖问题,提高失效检测与定位技术对于保障系统安全可靠运行具有重大意义。
参考文献
| [1] | LENG L, LIU Y. Fault tree reliability analysis for passive medium pressure safety injection system in nuclear power plant[J].Energy and Power Engineering, 2013, 5(4): 264–268.DOI:10.4236/epe.2013.54B051 |
| [2] | DOBRIVOJE C, MILOMIR G, MILE S, et al. Fault tree analysis of hydraulic power-steering system[J].International Journal of Vehicle Design, 2014, 64(1): 26–45.DOI:10.1504/IJVD.2014.057774 |
| [3] | SHI X,BAZZI A M.Fault tree reliability analysis of a micro-grid using Monte Carlo simulations[C]//Power and Energy Conference at Illinois (PECI).Piscataway,NJ:IEEE Press,2015:1-5. |
| [4] | DUGAN J B, BAVUSO S J, BOYD M A. Dynamic fault-tree for fault-tolerant computer systems[J].IEEE Transactions on Reliability, 1992, 41(3): 363–376.DOI:10.1109/24.159800 |
| [5] | DUGAN J B, SULLIVAN K J, COPPIT D. Developing a low-cost high-quality software tool for dynamic fault-tree analysis[J].IEEE Transactions on Reliability, 2000, 49(1): 49–59.DOI:10.1109/24.855536 |
| [6] | SMOTHERMAN M K, ZEMIUDEH K. A non-homogenedous Makrov model for phased-mission reliability analysis[J].IEEE Transaciton on Reliability, 1989, 38(5): 585–590.DOI:10.1109/24.46486 |
| [7] | DUGAN J B.Galileo:A tool for dynamic fault tree analysis[C]//Proceedings of the 11th International Conference on Computer Performance Evaluation:Modelling Techniques and Tools.Berlin Heidelberg:Springer-Verlag,2000:328-331. |
| [8] | AMARI S,DILL G,HOWALD E.A new approach to solve dynamic fault trees[C]// Proceedings of Annual IEEE Reliability and Maintainability symposium(RAMS 2003).Piscataway,NJ:IEEE Press,2003:374-379. |
| [9] | RAO K D, GOPIKA V, RAO V V S S, et al. Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment[J].Reliability Engineering and System Safety, 2009, 94(4): 872–883.DOI:10.1016/j.ress.2008.09.007 |
| [10] | BOUDALI H,DUGAN J B.A new Bayesian network approach to solve dynamic fault trees[C]//Reliability and Maintainability Symposium,2005.Piscataway,NJ:IEEE Press,2005:451-456. |
| [11] | WANG C, XING L, AMARI S V. A fast approximation method for reliability analysis of cold-standby systems[J].Reliability Engineering and System Safety, 2012, 106(4): 119–126. |
| [12] | BOUDALI H, DUGAN J B. A continuous-time bayesian network reliability modeling and analysis framework[J].IEEE Transactions on Reliability, 2006, 55(1): 86–97.DOI:10.1109/TR.2005.859228 |
| [13] | MYERS A F. k-out-of-n:G system reliability with imperfect fault coverage[J].IEEE Transactions on Reliability, 2007, 56(3): 464–473.DOI:10.1109/TR.2007.903229 |
| [14] | XING L D, AMARI S V, WANG C. Reliability of k-out-of-n systems with phased-mission requirements and imperfect fault coverage[J].Reliability Engineering and System Safety, 2012, 103(3): 45–50. |
| [15] | SPANIER J, OLDHAM K B. An Atlas of functions[M].2nd ed.New York: Springer-Verlag, 2009: 75-78. |
| [16] | BOURICIUS W G,CARTER W C,SCHNEIDER P R.Reliability modeling techniques for self-repairing computer systems[C]//Proceedings of 24th National Conference of ACM,1969.New York:ACM Press,1969:295-309. |
| [17] | DUGAN J B, TRIVEDI K S. Coverage modeling for dependability analysis of fault-tolerant systems[J].IEEE Transactions on Computers, 1989, 38(6): 775–787.DOI:10.1109/12.24286 |
| [18] | SUN J,LI Y F,LIU Y,et al.A numerical model with age reduction factor for warm spare[C]//Quality,Reliability,Risk,Maintenance,and Safety Engineering (ICQR2MSE),2011.Piscataway,NJ:IEEE Press,2011:275-280. |
