国外研究人员在20世纪90年代已将舵机伺服纳入颤振分析框架[1],主要由韩国****Lee等[2]主导,典型工作是考虑舵机动刚度和间隙非线性的颤振分析。国内的相关研究也一直在跟进,如张新榃等[3]发展了一种可考虑舵机动刚度的颤振分析方法,并提出一种通过改变舵机控制律来调节舵机动刚度,从而实现颤振抑制的方法[4];杨宁等[5]分析了结构非线性和舵机动刚度对舵系统颤振的综合影响。典型结论是动刚度改变了系统阻尼,从而影响到颤振边界;间隙会削弱舵面的支持刚度,还会带来极限环振荡或混沌效应,对系统颤振有不利影响。
在文献[1-5]中提到的动刚度及非线性因素之外,还有一种因素一直没有引起关注,那就是接触刚度。接触刚度广泛存在于发生力接触的两物体之间,它是作用力的函数,表现出强非线性特征。无论是经典的Hertz接触理论,还是考虑了接触表面粗糙度的GW模型[6],或是更精细的分型模型[7],都证明了这一结论。在舵机减速器内部,接触无处不在,如键与槽的接触,齿轮轮齿间的接触和滚珠和丝杠的接触等。其中,尤以滚珠丝杠副这类点接触最“软”,加上它位置靠近输出级这一因素,足以对舵面旋转频率造成极大影响,直接影响舵系统整体颤振特性。
现有文献有关接触刚度的报道多集中于机械加工过程[8-12],其中有关滚珠丝杠的研究也多是数控机床中的长程丝杠[8-10],其结构特征、承载形式和工作环境,都与舵机减速器中的丝杠有很大差别。本文将以某电动伺服舵系统为对象,探索接触刚度对舵机动力学的影响。从地面振动试验现象出发,分析舵机内部可能起主导作用的非线性因素,并以此建立舵机动力学模型;将仿真和试验结果进行对比,验证建模方法的可行性;最后建立舵系统颤振时域分析模型,对接触刚度和间隙联合作用下舵系统的响应行为展开研究。
1 研究对象 研究对象为某电动伺服舵系统,其结构如图 1所示。舵系统由电动舵机和全动梯形舵组成。舵机内含两级减速器,第1级为齿轮副,第2级为滚珠丝杠副。舵轴下方设有可调阻尼器。
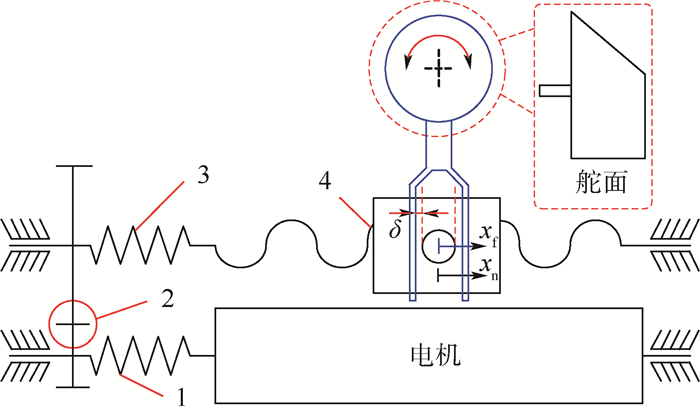 |
| δ—拨叉和螺母连接处的一个“综合间隙”半宽度,为减速器中各零部件配合处间隙统一向拨叉螺母处归集的一个等效间隙;xf—螺母位移;xn—拨叉位移;1,3—扭转刚度;2—啮合刚度; 4—接触+拉压刚度。 图 1 舵系统结构 Fig. 1 Structure of fin-actuator system |
| 图选项 |
对于这类舵系统,舵机对舵面的支持作用十分关键。当转角指令被给定时,舵机处于位置保持状态。此时,舵面若受外力作用迫使舵机转角偏移,电机会产生回复力矩进行纠偏。这种作用类似于扭转弹簧,不同点在于扭转弹簧的刚度是一个定值,而舵机因为有能量源存在,其刚度会随激励频率变化而变化,是带有相位的复值。
2 试 验 从地面振动试验中获取了舵面模态、频率以及舵机频响(FRF)特性。考虑到舵机的分散性,选择了多组舵机进行试验。试验方案如图 2所示。
 |
| 图 2 地面振动试验方案 Fig. 2 Scheme of ground vibration test |
| 图选项 |
进行带有力反馈的步进正弦扫频,以激振力(Ff)为输入,激振点处加速度为输出,得到舵系统频响曲线。将激振力在40~120 N之间的一组典型频响曲线绘于图 3。发现随着激振力的提高,舵面旋转频率从70 Hz向84 Hz迁移,表明舵机刚度随激励力的变化发生变化。
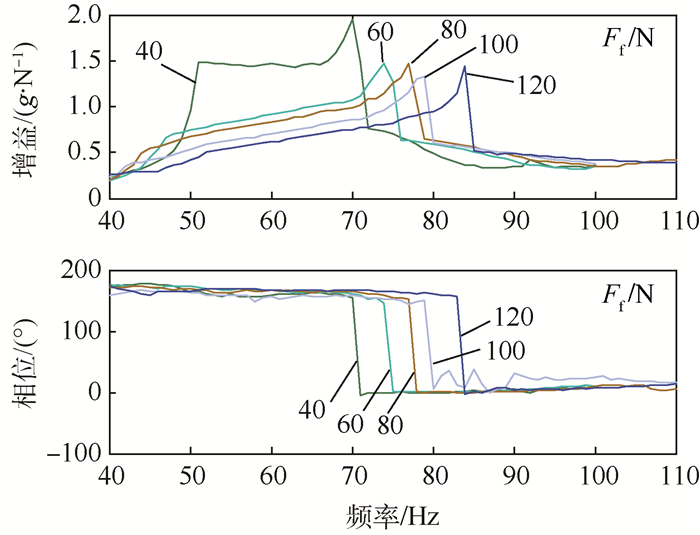 |
| 图 3 不同激振力下舵面频响曲线 Fig. 3 FRF curves of fin under different excitation forces |
| 图选项 |
变换多组舵机进行相同测试,将其中4台(1#~4#)的舵面旋转频率随激振力变化趋势绘于图 4。4条曲线走势相同,说明舵机一致性较好。舵面旋转频率随着激振力的增大而提高,且增速渐缓,显示出典型的多项式刚度特性。
 |
| 图 4 舵面旋转频率随激振力的变化趋势 Fig. 4 Change trend of rotational frequency of fin according to excitation force |
| 图选项 |
根据图 1所示舵系统结构,分析造成这一现象的可能原因。电机输出轴以键连接方式与小齿轮相连,存在轴扭转刚度;小齿轮与大齿轮间存在啮合刚度;丝杠存在轴扭转刚度和拉压刚度;滚珠丝杠副存在接触刚度;其余部位刚度或量级较高,或位置远离舵轴,对舵面旋转频率不构成主要影响,可不予考虑;各零部件配合处有间隙存在,尤以拨叉和滑动螺母相接处最大。所有这些因素中,造成非线性刚度的关键因素可能是滚珠丝杠接触刚度及间隙。
3 理论建模 3.1 舵机动力学及运动学建模 将减速器结构等效为多自由度质量-阻尼-弹簧系统,逐级建立其动力学方程为
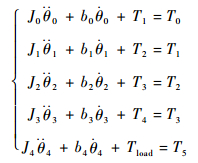 | (1) |
式中:J0~J4分别为电机转子惯量、小齿轮惯量、大齿轮惯量、丝杠旋转惯量和轴套旋转惯量;θ0~θ4和b0~b4分别为电机转子、小齿轮、大齿轮、丝杠和轴套的旋转角与旋转方向的摩擦阻尼系数;T0为作用于电机转子上的洛伦兹力;Tload为舵机受到的外部作用力矩。其余参数定义为
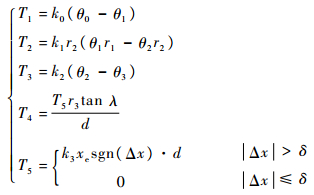 | (2) |
式中:r1~r3分别为小齿轮、大齿轮和丝杠节圆半径;k0~k2分别为电机转子轴扭转刚度、大小齿轮啮合刚度和丝杠扭转刚度;
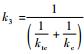
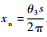
需要说明的是,啮合刚度k1虽是随旋转运动周期变化的刚度,但舵机处于位置保持状态时的啮合刚度变化幅度很小,所以k1可按常数处理。
关于接触刚度kc,其来源及受力关系如图 5所示。Hertz接触理论认为,滚珠和曲面之间的接触是点接触,有负荷Q作用时,接触点将扩展成为一个椭圆接触面(见图 5(a))。对于丝杠-滚珠-螺母副,滚珠沿螺旋滚道运动,受到来自螺母和丝杠滚道的双向挤压(见图 5(b)),滚珠和滚道在接触点处同时发生弹性变形。
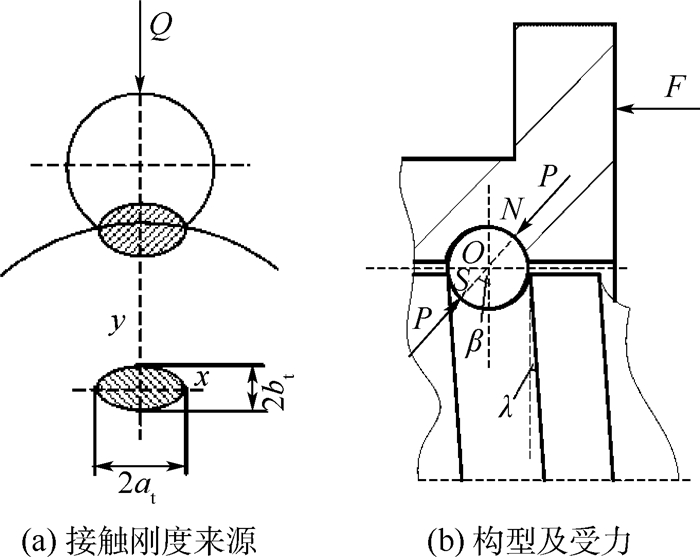 |
| at—椭圆长轴半径;bt—椭圆短轴半径;N—滚珠与螺母接触点;S—滚珠与丝杠接触点;P—法向接触力;F—轴向载荷。 图 5 丝杠-滚珠-螺母副受力与接触模型 Fig. 5 Force and contact model of screw-ball-nut pair |
| 图选项 |
假设螺母受到的轴向载荷为F,丝杠-滚珠-螺母副因接触刚度导致的轴向变形量为δa,由Hertz接触理论知理想接触情况下轴向变形δa与轴向工作载荷F间的关系为
 | (3) |
式中:z为工作滚珠数;β为滚珠丝杠副接触角;K(e)为与椭圆偏心率有关的第一类完全椭圆积分;enp为滚珠与螺母滚道椭圆接触面的偏心率;manp为该接触面的长半轴系数;ρnp为该接触面的主曲率;E′为当量弹性模量;esp为滚珠与丝杠滚道椭圆接触面的偏心率;masp为该接触面的长半轴系数;ρsp为该接触面的主曲率。
将式(3)简写为
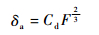 | (4) |
当接触副的结构形式和制造材料确定后,轴向接触变形系数Cd就是一个确定值。可见接触副的轴向接触变形与轴向载荷的
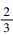
由式(4)进一步得到接触副轴向接触刚度kc的表达式为
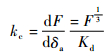 | (5) |
式中:
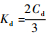
可知丝杠-滚珠-螺母副的轴向接触刚度随着轴向载荷的增大而增大,呈非线性关系。实际当中,因为几乎不存在赫兹接触理论中的理想接触,所以kc和F之间的关系通常表示为
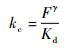 | (6) |
式中:次方数γ不会严格等于
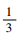
电机电路部分建模可参见文献[13],图 6直接给出基于前述理论建立的舵机综合模型Simulink框图。其中虚线框部分为电机电路模型,减速器子系统根据式(1)的动力学方程建立。
 |
| s—Laplace变量;L—电感;R—电阻;Ki—电流反馈系数;Ke—反电动势系数;K—力矩系数。 图 6 舵机Simulink框图 Fig. 6 Simulink block diagram of synthesized fin-actuator system |
| 图选项 |
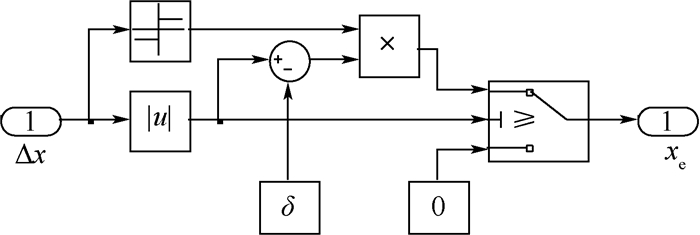
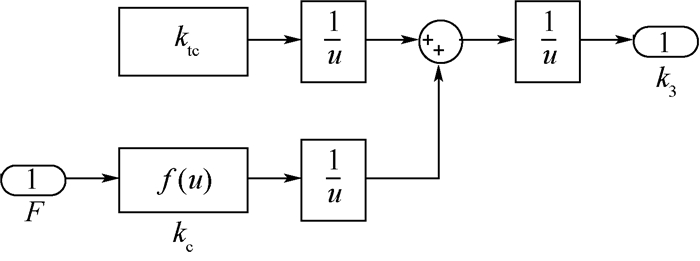
对于减速器内部结构,仅给出丝杠-滚珠-螺母副这一关键部位的详细模型,其余部分比较常规,不再赘述。图 7为螺母和拨叉结合处的间隙模型。图 8为由丝杠拉压刚度和接触刚度合成的综合刚度模型。图 9为丝杠-滚珠-螺母副力学模型,其中间隙模型如图 7所示,刚度模型如图 8所示。
 |
| u-输入值。 图 7 间隙模型 Fig. 7 Freeplay model |
| 图选项 |
 |
| 图 8 丝杠-滚珠-螺母副刚度模型 Fig. 8 Stiffness model of screw-ball-nut pair |
| 图选项 |
 |
| Fn-F的新值;Fo-F的旧值。 图 9 丝杠-滚珠-螺母副力学模型 Fig. 9 Force model of screw-ball-nut pair |
| 图选项 |
3.2 颤振时域建模 为了舵面颤振方程中引入舵机的“复杂”支持,基于分支模态法[14]对方程进行改写。取舵轴根部固支情况下的舵面弹性模态作为弹性分支,舵轴根部放开旋转自由度得到的舵面刚体旋转模态作为刚体分支,得
 | (7) |
式中:
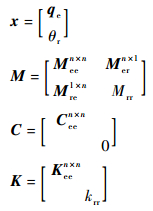 | (1) |
其中:Meen×n、Ceen×n和Keen×n分别为舵面弹性分支n阶模态对应的广义质量、阻尼和刚度阵,均为对角阵;qe为广义坐标;Mrr、krr和θr分别为刚体分支旋转模态对应的物理惯量、刚度以及坐标;Mern×1为Mre1×n的转置,代表弹性和刚体分支的耦合质量;Fa为气动力。
在计算Fa时,输入模态为舵面弹性模态和刚体模态分支的集合,即1阶刚体旋转模态和n阶弹性模态的组合。
频域下舵面广义非定常气动力表达式为
 | (8) |
式中:q∞=ρV2/2为飞行动压,ρ为大气密度,V为来流速度;Af为气动力影响系数矩阵,其为减缩频率k=ωb/V的函数,ω为圆频率,b为参考弦长。
时域下的气动力影响系数矩阵可借助最小状态(Minimum-State,MS)[15]法进行拟合。先给出拉氏域下的气动力影响系数矩阵:
 | (9) |
式中:p=bs/V;A0~A2、
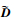
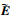
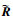
略去滞后根的影响,则时域下非定常气动力可近似为
 | (10) |
式中:

将式(10)代入式(7),并将式(7)写成状态空间的形式:
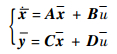 | (11) |
式中:
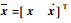
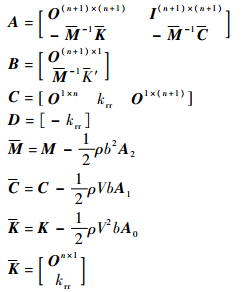 | (2) |
最终建立如图 10所示的舵系统颤振时域综合模型。舵系统对应式(11)的舵面+气动力子系统,舵机对应图 6所示的舵机子系统。
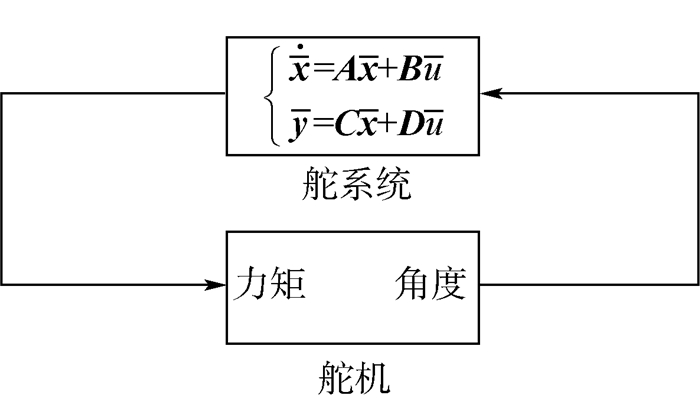 |
| 图 10 舵系统颤振模型Simulink框图 Fig. 10 Simulink block diagram of fin-actuator flutter model |
| 图选项 |
4 结果与讨论 舵系统虽涉及诸多参数,但其中大部分参数是确定的或可测的,如控制系统和电机电路参数、舵机零部件质量(或惯量)、舵轴阻尼器阻尼系数等。表 1列出的是仿真计算过程中用到的主要参数,这些参数都是确定的。
表 1 仿真参数 Table 1 Simulation parameters
| 类目 | 参数 | 数值 |
| 电机 | 电阻R/Ω | 1.1 |
| 电感L/H | 6.53×10-4 | |
| 力矩系数kt/(N·m·A-1) | 0.034 | |
| 反电动势系数kemf/(V·rad-1·s-1) | 0.034 | |
| 转子惯量J0/(kg·m2) | 1.09×10-6 | |
| 转子阻尼系数b0/(N·m·rad-1·s-1) | 0.003 | |
| 减速器 | 小齿轮惯量J1/(kg·m2) | 2.4×10-8 |
| 小齿轮节圆半径r1/mm | 5.0 | |
| 大齿轮惯量J2/(kg·m2) | 4.0×10-6 | |
| 大齿轮节圆半径r2/mm | 22.5 | |
| 丝杠惯量J3/(kg·m2) | 3.18×10-5 | |
| 丝杠螺旋角λ/(°) | 6.06 | |
| 丝杠导程ss/mm | 4.0 | |
| 丝杠节圆半径r3/mm | 6.0 | |
| 舵轴与丝杠距离d/mm | 28.5 | |
| 轴套惯量J4/(kg·m2) | 4.1×10-5 | |
| 阻尼器阻尼系数b4/(N·m·rad-1·s-1) | 0.25 | |
| 舵面 | 旋转惯量Mrr/(kg·m2) | 9.95×10-3 |
表选项
其他非确定参数主要根据理论或试验方法进行估算。如k0~k3这4个刚度参数先用材料力学方法进行计算,然后根据试验结果进行修正。除舵轴阻尼器外的其余各处阻尼系数是根据工程经验进行设置的。
图 11~图 14中的仿真曲线,是用快速傅里叶变换(Fast Fourier Transform,FFT)的方法对Simulink模型的“仿真扫频力”输入和“舵轴转角”输出求频响所得。
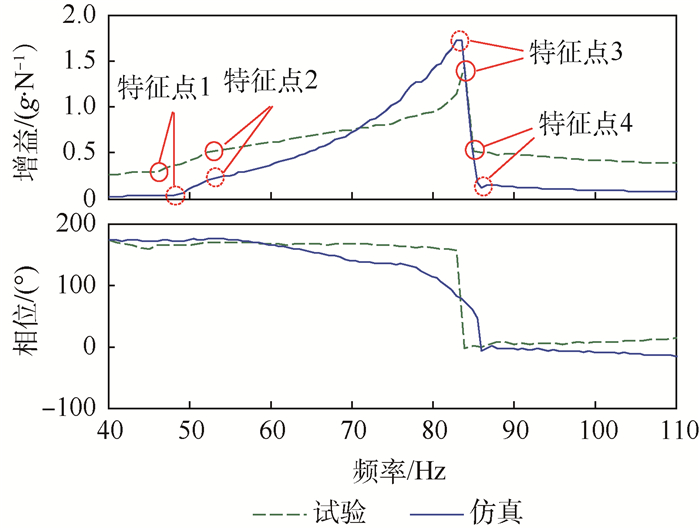 |
| 图 11 试验和仿真频响对比(带接触刚度和间隙) Fig. 11 Comparison of FRFs from simulation and test (with contact stiffness and freeplay) |
| 图选项 |
 |
| 图 12 接触刚度和常数刚度下仿真频响对比(带间隙) Fig. 12 Comparison of FRFs from simulations under contact stiffness and constant stiffness (with freeplay) |
| 图选项 |
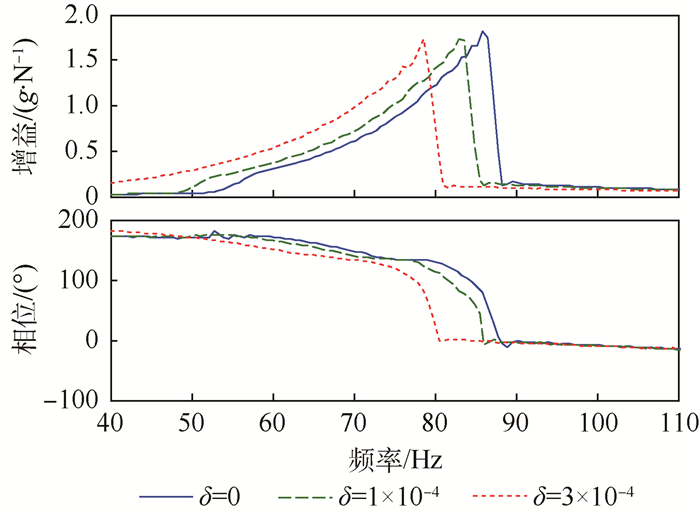 |
| 图 13 不同δ下频响对比(带接触刚度) Fig. 13 Comparison of FRFs under different δ (with contact stiffness) |
| 图选项 |
 |
| 图 14 不同激振力下仿真频响对比 Fig. 14 Comparison of FRFs from simulations under different excitation forces |
| 图选项 |
图 11是激振力为120 N时,得到的试验和仿真频响对比。仿真频响准确地捕捉到了试验频响中的4处特征点(响应突变点)。
作为对照,图 12给出了考虑接触刚度和不考虑接触刚度时的2组仿真曲线。这里不考虑接触刚度指用舵面旋转频率为84 Hz对应的常数刚度代替接触刚度。可以看出常数刚度下,频响曲线体现出典型的二阶系统特征,完全失去接触刚度下的几处特征。
图 13考察的是间隙对舵面旋转频率的影响。随着间隙半宽度δ值的增大,频率呈下降趋势。δ为1×10-4时,换算得到的舵轴间隙大概为0.1°。
图 14是不同激振力Ff下系统仿真频响曲线的对比。对照图 3,可以看到仿真结果和试验结果规律一致。
图 15将不同激振力下舵面旋转频率的仿真结果和图 4中4组舵机(1#~4#)的试验结果进行对比,同样能够看到一致规律。
 |
| 图 15 仿真和试验旋转频率随激振力变化的对比 Fig. 15 Comparison of simulation and experimental data for change trend of fin rotational frequency according to excitation force |
| 图选项 |
在颤振分析环节,主要对比舵系统在接触刚度和常数刚度2种假设下,气动弹性响应的不同。
舵机模型取经试验数据修正过的模型。常数刚度假设下,舵面刚体旋转频率依然保持84 Hz(对应接触刚度假设下激振力为120 N时的频率)。舵面弹性分支仅保留一阶弯曲模态,固有频率72 Hz。非定常气动力算法取超音速偶极子网格法。
对于非线性系统,变量的初始状态对系统稳定性影响很大。飞行器快速机动时,经常会令舵面快速打出偏角,以下点考察这类阶跃指令角和来流速度联合作用下舵系统的稳定性。
讨论之前,首先定义2个概念:
临界角:当前风速下,系统处于发散和极限环(Limit Cycle Oscillation,LCO)(或收敛)交界的舵机指令角。
临界速度:无论舵机指令角多小,系统都会发散的最小速度。
图 16所示是舵轴旋转角间隙为0.1°(对应δ=1×10-4)时,接触刚度和常数刚度假设下的稳定边界对比。横轴为无量纲速度来流速度,纵轴为舵机指令角大小。
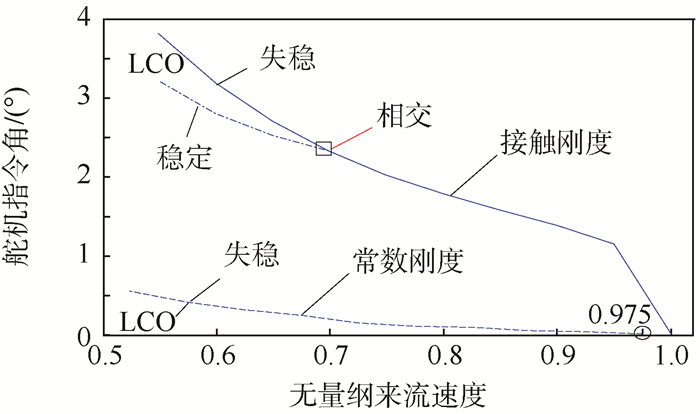 |
| 图 16 接触刚度和常数刚度假设下舵系统稳定边界对比(间隙:0.1°) Fig. 16 Comparison of stable boundaries of fin-actuator system under contact stiffness and constant stiffness (freeplay: 0.1°) |
| 图选项 |
从图 16中看到,常数刚度下系统响应存在LCO和失稳2个域,且随着风速提高,临界角渐小;接触刚度下,临界角同样随风速提高而渐小,但与前者相比系统响应多了一个稳定域,这样系统在LCO域上下就存在2个边界。当风速大于0.7时,两边界重合,LCO域消失。对比两种假设的失稳边界发现,相同风速下,接触刚度的临界角更大。在0.1°间隙下,常数刚度的临界速度比接触刚度小2.5%。
图 17、图 18所示是不同工况下的舵偏角响应曲线。图中标记S、E分别代表振动起始点和终止点(发散情况下为过程点)。
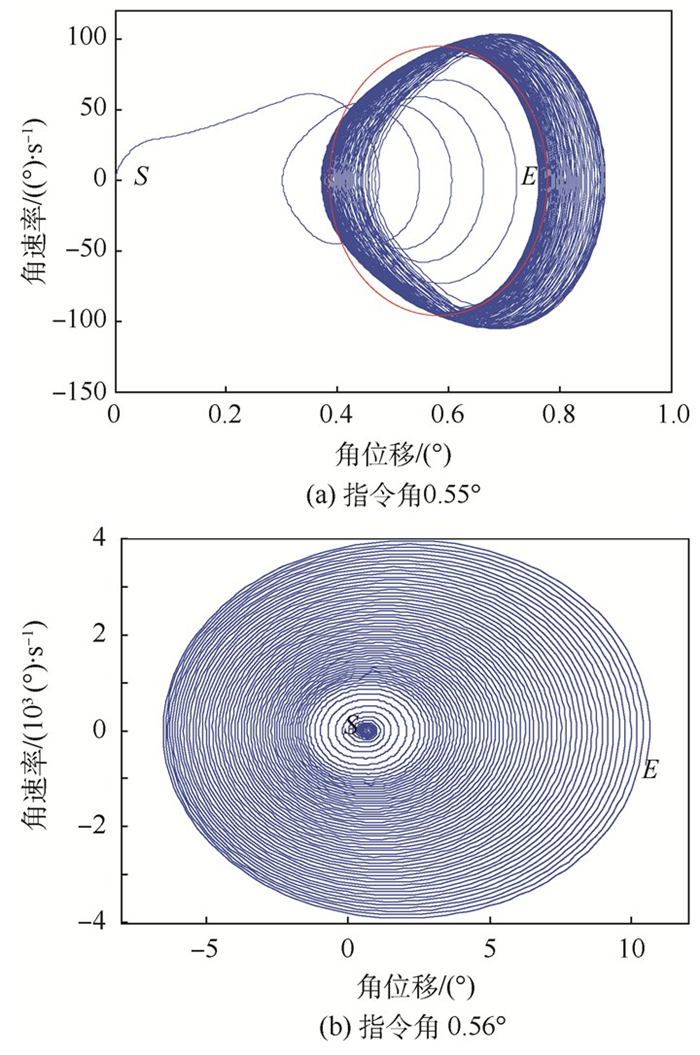 |
| 图 17 舵偏角相图(常数刚度,速度:0.52,间隙:0.1°) Fig. 17 Phase diagram of fin shaft angle (constant stiffness, velocity: 0.52, freeplay: 0.1°) |
| 图选项 |
 |
| 图 18 舵偏角相图(接触刚度,速度0.55,间隙:0.1°) Fig. 18 Phase diagram of fin shaft angle (contact stiffnessvelocity: 0.55, freeplay: 0.1°) |
| 图选项 |
图 17为常数刚度,风速0.52,间隙0.1°时,不同指令角下的舵机转角响应相图。阶跃指令角为0.55°时,系统维持稳定的LCO运动。当指令角增加到0.56°时,系统响应发散。同时也看到常数刚度假设下没有收敛域出现。图 18为接触刚度,风速0.55,间隙0.1°,指令角分别为2.5°、3.5 °和4.5°时的舵机转角响应相图。系统分别处于收敛、LCO和发散状态。其中发散状态特征不同于常数刚度假设,舵偏角没有逐渐打向90°,而是在到达68°之后,振荡发散。
图 19所示是接触刚度和常数刚度下舵系统稳定边界在不同间隙下的变化趋势对比。图中箭头所示为趋势走向。可以看到,相同风速下,随着间隙的增大,常数刚度假设的临界角增大。其临界速度在3种间隙下均位于0.975处,保持不变;对于接触刚度假设,当风速小于0.75时,临界角随间隙增大而增大。但当风速大于0.75时,临界角却是减小的。系统的临界速度也会随间隙的增大而减小。此外,还发现系统的LCO域下边界不会受间隙的影响。
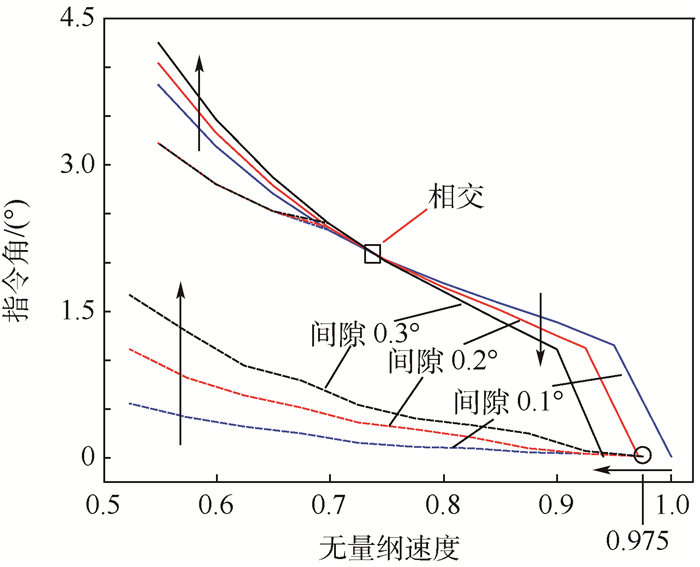 |
| 图 19 接触刚度和常数刚度假设下舵系统稳定边界与间隙大小的关系 Fig. 19 Relations between freeplays and stable boundaries of fin-actuator system under contact stiffness and constant stiffness |
| 图选项 |
5 结 论 1) 考虑接触刚度和间隙的舵系统动力学模型,准确捕捉到了地面振动试验中的非线性现象:随着激振力的增大,舵面旋转频率逐渐升高,舵机提供的支持刚度在提高。说明以接触刚度为主,间隙为辅的非线性因素组合,共同主导了舵系统整体的动力学行为。
2) 接触刚度下的舵系统气动弹性响应存在稳定、LCO和失稳3个域。当风速大于0.7时,LCO域上下边界重合,LCO域消失。而常数刚度下,系统仅存在LCO和失稳2个域。
3) 2种刚度假设下,随着风速的提高,系统边界角均减小。相同风速下,接触刚度下的边界角一般大于常数刚度下的边界角,更加稳定。
4) 常数刚度下,边界角随间隙增大而增大;接触刚度下,风速低于0.75时,边界角与间隙正相关。风速高于0.75时,反之。
5) 常数刚度下,边界速度不随间隙变化;而接触刚度下,间隙越大,边界速度越低,甚至会低于常数刚度下的边界速度。
6) 本文舵面模态频率为弯低旋高。随风速提高,舵机受力增大,此时接触刚度会提高舵机整体刚度,从而拉大舵面弯旋频率差,改善系统稳定性。倘若是弯高旋低的情形,接触刚度的作用很可能是相反的,需谨慎对待。
综上,鉴于2种刚度假设下,舵系统动力学行为及气动弹性响应的多处不同,认为工程分析中,应当对舵机的支持特性引起足够重视,尤其要关注接触刚度和其他非线性因素联合作用下可能带来的不利影响。
参考文献
| [1] | YEHEZKELY E, KARPEL M. Nonlinear flutter analysis of missiles with pneumatic fin actuators[J].Journal of Guidance, Control, and Dynamics, 1996, 19(3): 664–670.DOI:10.2514/3.21672 |
| [2] | SHIN W H, LEE I, SHIN Y S, et al. Nonlinear aeroelastic analysis for a control fin with an actuator[J].Journal of Aircraft, 2007, 44(2): 597–605.DOI:10.2514/1.24721 |
| [3] | 张新榃, 吴志刚, 杨超. 考虑舵机动力学的舵系统颤振分析[J].北京航空航天大学学报, 2011, 37(8): 927–932.ZHANG X T, WU Z G, YANG C. Flutter analysis for rudder considering actuator's dynamics[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(8): 927–932.(in Chinese) |
| [4] | ZHANG X T, WU Z G, YANG C. New flutter-suppression method for a missile fin with an actuator[J].Journal of Aircraft, 2013, 50(3): 989–994.DOI:10.2514/1.C031961 |
| [5] | YANG N, WU Z G, YANG C. Structural nonlinear flutter characteristics analysis for an actuator-fin system with dynamic stiffness[J].Chinese Journal of Aeronautics, 2011, 24(5): 590–599.DOI:10.1016/S1000-9361(11)60069-1 |
| [6] | VALENTIN L P. Contact mechanics and frictions[M].Berlin: Springer Berlin Heidelberg, 1987: 64-68. |
| [7] | 张学良, 黄玉美, 傅卫平, 等. 粗糙表面法向接触刚度的分形模型[J].应用力学学报, 2000, 17(2): 31–35.ZHANG X L, HUANG Y M, FU W P, et al. Fractal model of normal contact stiffness between rough surfaces[J].Chinese Journal of Applied Mechanics, 2000, 17(2): 31–35.(in Chinese) |
| [8] | KATUHIRO N, KAZUKI T. Stiffness of a pre-loaded ball screw[J].Transactions of the Japan Society of Mechanical Engineers, 1987, 53(492): 1898–1904.DOI:10.1299/kikaic.53.1898 |
| [9] | KRIPA K V, SAMIR A N. The dynamics of lead-screw drives: Low-order modeling and experiments[J].Journal of Dynamic Systems, Measurement, and Control, 2004, 126(2): 388–396.DOI:10.1115/1.1771690 |
| [10] | XIAO H, BRENNAN M J, SHAO Y M. On the undamped free vibration of a mass interacting with a Hertzian contact stiffness[J].Mechanics Research Communications, 2011, 38(8): 560–564.DOI:10.1016/j.mechrescom.2011.07.012 |
| [11] | KONO D, INAGAKI T, MATSUBARA A, et al. Stiffness model of machine tool supports using contact stiffness[J].Precision Engineering, 2013, 37(3): 650–657.DOI:10.1016/j.precisioneng.2013.01.010 |
| [12] | KONO D, NISHIO S, YAMAJI I, et al. A method for stiffness tuning of machine tool supports considering contact stiffness[J].International Journal of Machine Tools and Manufacture, 2015, 90: 50–59.DOI:10.1016/j.ijmachtools.2015.01.001 |
| [13] | ZHANG R J, WU Z G, YANG C. Fin-actuator system modeling and experimental validating for aeroelastic research[C]//56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2015. |
| [14] | GLADWELL G M L. Branch mode analysis of vibrating systems[J].Journal of Sound and Vibration, 1964, 1(1): 41–59.DOI:10.1016/0022-460X(64)90006-9 |
| [15] | KARPEL M. Extensions to the minimum-state aeroelastic modeling method[J].AIAA Journal, 1991, 29(11): 2007–2009.DOI:10.2514/3.10832 |
