针对无刷直流电机转矩脉动的研究主要集中在电机结构优化和改进控制策略2个方面[1]。MSRF无刷直流电机一般采用无齿槽结构,基本消除了齿槽转矩脉动[2],已经实现了优化。在改进控制策略方面,可进一步细分为分散控制策略和整体控制策略。前者主要针对引起转矩脉动的具体因素,比如换相、非导通相续流、非理想梯形波和电枢反应等;后者主要采用直接转矩控制(Direct Torque Control, DTC)、自抗扰控制、模糊控制和神经网络控制等方法抑制整体转矩脉动。分散控制策略中,重叠换相法[3]、PWM斩波法、滞环电流法[4-5]和电流预测法[6]等都是针对无刷直流电机换相转矩脉动进行抑制的,并取得了一定效果,但是方法作用区域都是在无刷直流电机的换相阶段或者换相阶段前后,受到换相时间的限制。除换相过程外,非理想反电动势(Electromotive Force,EMF)、非导通相续流等问题均会引起转矩脉动,针对这些因素,也有很多****进行了研究[7-10]。但分散控制策略都是针对具体因素,如果对引起无刷直流电机转矩脉动的因素分别进行处理,算法会很复杂,而且有些造成转矩脉动的因素无法进行数学建模和对应的转矩脉动抑制,较好的处理方法是对电机转矩进行估计和控制。
在整体抑制转矩脉动的控制策略中,自抗扰控制、模糊控制和神经网络控制等方法存在参数整定困难、计算复杂和实时性差等缺点,不利于实现。直接转矩控制以电磁转矩作为直接反馈控制量,通过选择适当的定子电压矢量把转矩和定子磁链误差限制在滞环内[1]。该方法因受不确定的转矩脉动影响小,得到致力于抑制无刷直流电机转矩脉动工作者的青睐,也得到了广泛深入的研究。
文献[11]指出,120°导通工作方式下无刷直流电机控制特性使其磁链形状为带有6个尖角的不规则圆形,导致传统直接转矩控制对磁链幅值控制精度不高,基于此,文献[12]结合无刷直流电机120°导通工作方式的特点,提出了一种无磁链反馈直接转矩控制方案,因为控制结构简单,为无刷直流电机直接转矩控制普遍采用,本文也采用无磁链反馈直接转矩控制对电机转矩进行控制。
直接转矩控制首先需要对转矩进行估计,滑模观测器(Sliding Mode Observer, SMO)因受电机参数影响小、易于实现,得到了广泛研究和应用。文献[13]在无磁链反馈直接转矩控制的基础上,采用滑模观测器对反电动势进行观测,提高了转矩的观测精度和控制精度,并对存在抖振的反电动势观测结果进行滤波处理,但是没有考虑滤波器导致的相移问题,使反电动势观测不准确。文献[14]针对滑模观测器出现的抖振问题,提出一种分段式滑模变结构直接转矩控制,减小了系统抖振,提高了对反电动势的估计精度,但是该方法难以确定参数,而且影响了稳定精度。文献[15-16]将电阻和电感进行自适应辨识,提高了滑模变观测器对反电动势的估计精度,转矩的控制精度有所提高,但是控制算法复杂。
为了提高直接转矩控制对转矩的控制精度,文献[17]将6个电压矢量增加到12个,得到了平稳的转矩,但控制复杂度增加,而且只是单纯增加电压矢量个数,没有对施加的电压矢量进行限幅,对转矩脉动抑制效果的提高改善不大。文献[18]将传统按照数学模型调制开关管的PWM方法与直接转矩控制方法相结合,实现了转矩脉动的最小化,有效抑制了转矩脉动,但是调制开关管的PWM占空比需要提前计算,在运行时进行查表操作,实现复杂。文献[19-20]分别利用模糊控制方法、神经网络控制方法改善直接转矩控制的效果,但其主要问题是算法复杂,不易实现。
传统直接转矩控制的bang-bang控制器对大电感无刷直流电机控制效果较好,但对小电感无刷直流电机作用较差,而MSRF无刷直流电机典型特点就是电感较小,因此必须对传统直接转矩控制的bang-bang控制器进行改进。基于此,本文首先针对引起转矩脉动的换相和非导通相续流建立了数学模型,分析得到电机转矩与绕组电流关系函数,提出了一种判断电机状态,按数学模型进行转矩预测的转矩控制方法,能够在保持转矩响应速度的情况下减小转矩脉动。同时为减弱传统滑模观测器对反电动势观测过程中出现的抖振,提出一种参数可调的光滑连续函数替换符号函数,大幅削弱了抖振,实现了绕组反电动势以及转矩的精确估计。这2种方法结合形成了一种改进转矩控制方法,仿真和实验结果表明,该方法相对于传统直接转矩控制能大幅度减小无刷直流电机在非换相阶段转矩脉动,对换相阶段转矩脉动也有一定的抑制效果。
1 无刷直流电机的数学模型 1.1 基本数学模型 图 1为无刷直流电机三相绕组等效模型及驱动模型。假设电机三相绕组完全对称。图中:R为每相绕组的电阻;L为每相绕组等效电感;U0为中性点电压;Ud为直流母线电压;eA、eB和eC分别为对应A、B和C相的反电动势;iA、iB和iC分别为A、B和C相的电流;uA、uB和uC分别为A、B和C相绕组端电压。正方向如图 1所示。
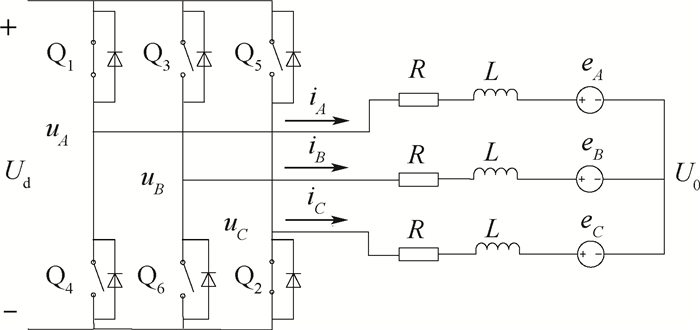 |
| 图 1 无刷直流电机等效模型及驱动模型 Fig. 1 Equivalent model of BLDCM and inverter model |
| 图选项 |
根据图 1得无刷直流电机电压平衡方程为
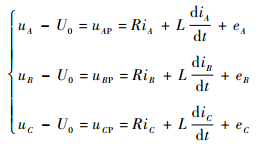 | (1) |
式中:uAP、uBP和uCP为三相绕组相电压。
1.2 绕组不同导通状态下数学模型 MSRF无刷直流电机在运行过程中,造成电机输出力矩脉动的因素主要有:① 换相;② 非导通相续流;③ 三相绕组反电动势不是标准梯形波;④ 其他因素。前2种因素能够引起转矩脉动,是因为电机导通状态发生变化。由于MSRF无刷直流电机结构经过设计,其磁密均匀而且转速一般不高,可在建立数学模型时不考虑非理想梯形波的影响。下面对无刷直流电机正常运行状态、换相状态和非导通相续流状态进行数学建模。
1.2.1 正常运行状态 无刷直流电机正常运行时,电机绕组只有两相导通。根据图 1所示,电机状态为AC相导通,有
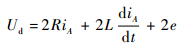 | (1) |
同时有
 | (2) |
式中:e=eA;ω为转子机械角速度;Te为电机电磁转矩。
1.2.2 换相状态 对于实际的无刷直流电机来说,较常见的情况往往是换相转矩减小的情况[6],因此本文对换相过程中关断相电流下降速率小于开通相电流上升速率的情况不予研究。电机换相有开关管上管导通和下管导通2种,分别以AB→AC、AC→BC换相过程为例进行分析。这2种情况下电机导通状态如图 2所示。
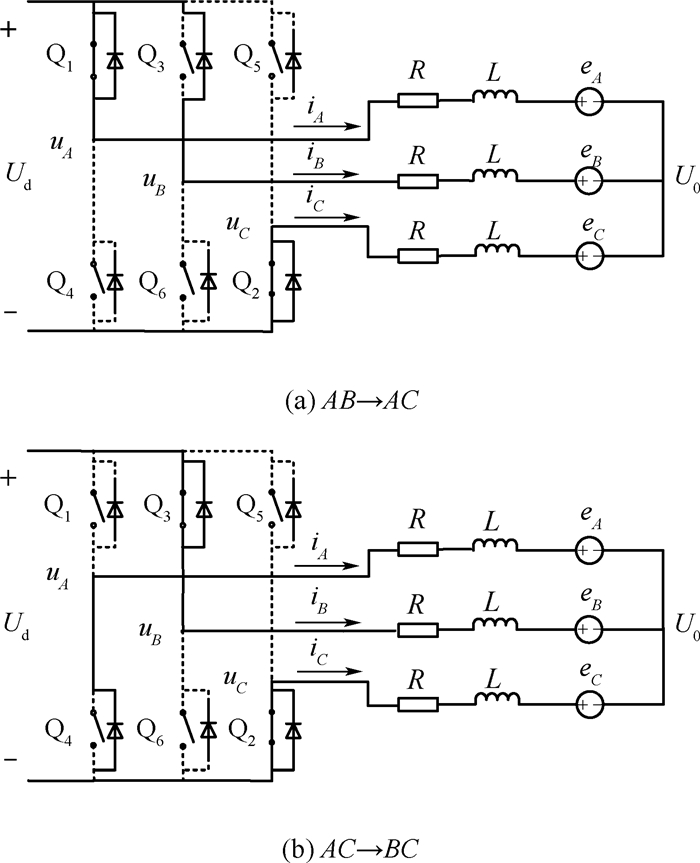 |
| 图 2 AB→AC、AC→BC换相过程无刷直流电机等效电路 Fig. 2 Equivalent circuits of BLDCM in commutation period of AB→AC,AC→BC |
| 图选项 |
根据图 2(a),有
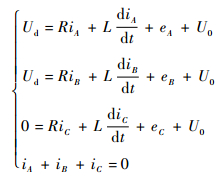 | (3) |
则
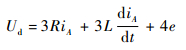 | (4) |
式中:e=eA。
同时有
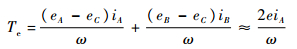 | (2) |
考虑到MSRF无刷直流电机电感很小,换相时间很短,可忽略换相期间反电动势变化。分析式(2),前一项(eA-eC)iA/ω与非换相相电流成正比,后一项(eB-eC)iB/ω与关断相电流成正比,而关断相电流下降速率非常快,同时换相期间,eB、eC相差不大,可将后一项忽略。
同理,得到AC→BC换相期间有
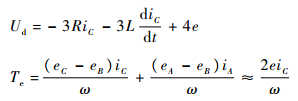 | (5) |
式中:e=eC。
其他换相情况以此类推。
电机换相状态的识别,自霍尔信号发生变化到关断相电流降为零为换相阶段。
1.2.3 非导通相续流状态 根据文献[10],非导通相续流是因换相延迟引起。非导通相续流有2种形式:上管旁路导通和下管旁路导通。图 3分别为CB相导通换相至AB相导通时换相延迟和BC相导通换相至BA相导通时换相延迟引起的非导通相续流时三相绕组等效电路。
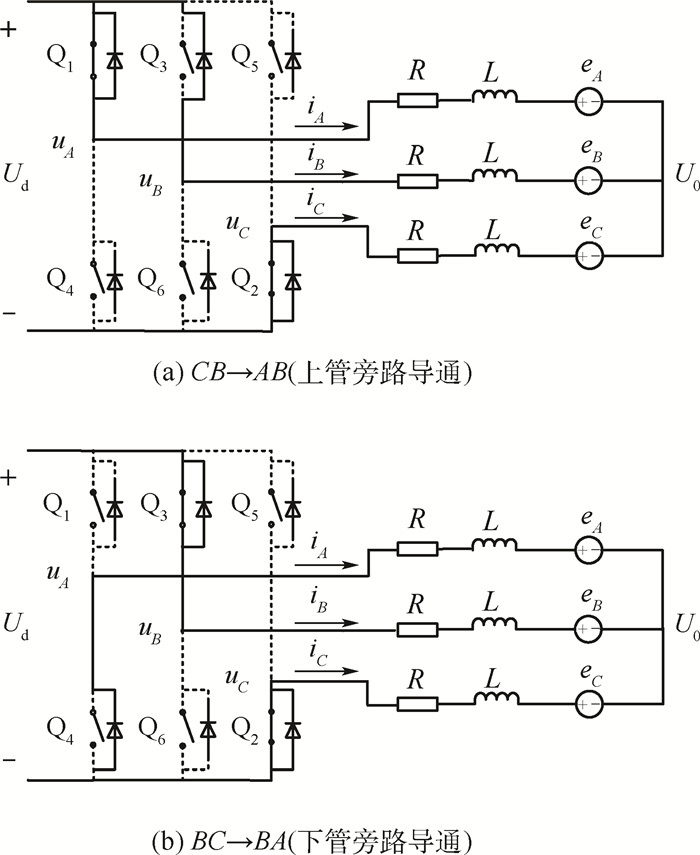 |
| 图 3 不同非导通相续流情况下无刷直流电机等效电路 Fig. 3 Equivalent circuits of BLDCM with diode freewheeling of different inactive phases |
| 图选项 |
从图 3可以看出,上管旁路导通时,电机绕组导通状态同上管换相,下管旁路导通时,电机绕组导通状态同下管换相。因此,非导通相续流时,可以认为电机“换相”,非导通相为开通相。例如,CB导通换相至AB导通换相延迟时,可认为A为开通相,C为关断相。在这种假设下,非导通相续流与正常换相情况完全相同。非导通相续流判断条件为非导通相端电压小于零电压(下管旁路导通)或者大于直流母线电压(上管旁路导通)。
综上,不同电机绕组导通状态下数学模型可合并如下:
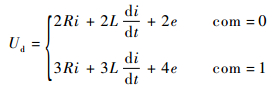 | (3) |
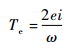 | (4) |
式中:com=0为电机处于两相导通状态,i为上管导通相电流,e为上管导通相反电动势;com=1为电机处于换相状态或者非导通相续流状态,i为非换相相电流,e为非换相相反电动势。
2 改进型滑模观测器 考虑到三相绕组反电动势有可能不是标准梯形波,而且滑模观测器具有对电机参数不敏感、鲁棒性强的优点,选用滑模观测器对绕组反电动势进行估计。
将式(3)经过Clark变换,得到静止坐标系下电压方程如下:
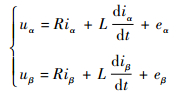 | (5) |
式中:uα、uβ、iα、iβ、eα和eβ分别为αβ坐标系下的绕组定子电压、定子电流和绕组反电动势。
于是,在两相静止坐标系下无刷直流电机电磁转矩为[14]
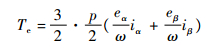 | (6) |
式中:p为电机极数。
考虑到MSRF转动惯量大,认为采样过程中,转子转速不变,即αβ坐标系下绕组反电动势不变。以
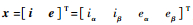
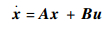 | (7) |
式中:
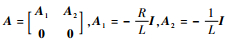
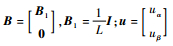
所提出的改进型滑模观测器假设电机绕组电阻和等效绕组电感不变,根据式(7)建立反电动势滑模观测器如下:
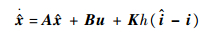 | (8) |
式中:
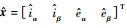
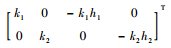
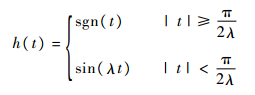 | (6) |
其中:λ为函数参数;sgn(·)为符号函数。
h(t)波形如图 4所示。可知,函数h(t)为奇函数,且t>0时,h(t)>0,t<0时,h(t)<0。此特点与符号函数类似,将符号函数替换为h(t)函数后依旧会使滑模观测器具有状态切换功能。函数h(t)有1个参数,可以根据系统需求调节λ的大小。h(t)函数在t=0处收敛至0。在系统状态进入滑模区域后,相当于减小了滑模观测器的滑模增益,减小抖振现象。
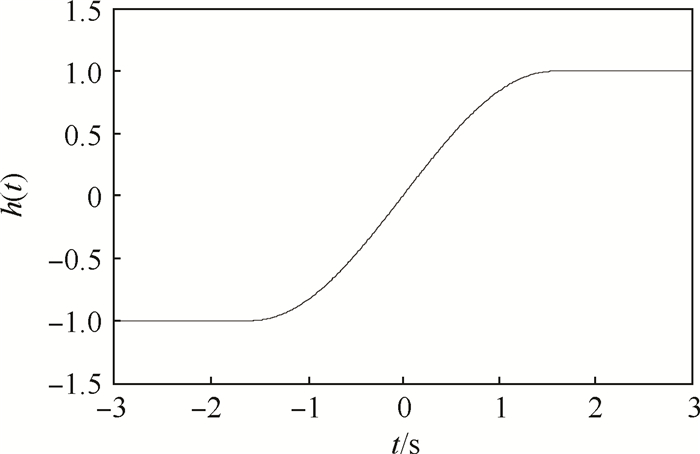 |
| 图 4 h(t)波形(λ=1) Fig. 4 Waveform of h(t) (λ=1) |
| 图选项 |
式(8)减去式(7)得到
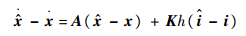 | (9) |
选取滑模面
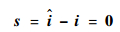 | (7) |
于是滑模观测器如下:
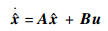 | (10) |
根据观测器进入滑模条件:
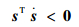 | (8) |
即
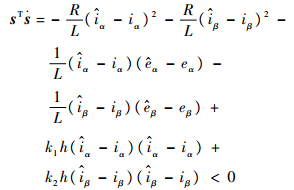 | (11) |
又h(t)与t符号相同,且h(t)<1。只需保证:
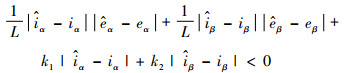 | (12) |
即可保证式(11)成立,可取:
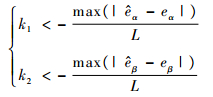 | (13) |
按式(13)选取k1、k2,可保证所设计的观测器进入滑模状态。根据等效输入理论,观测器进入滑模区域后,有
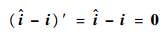 | (9) |
结合式(9)得到
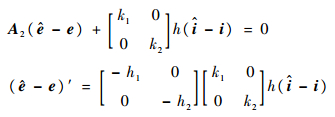 | (10) |
则
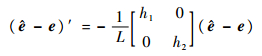 | (14) |
于是,当h1>0,h2>0时,反电动势观测误差会以指数形式收敛到零,实现对绕组反电动势估计。
参数λ主要影响抖振的收敛速度。对无刷直流电机而言,滑模观测器跟踪的iα、iβ信号具有连续阶跃的特点,设iα、iβ信号的最大阶跃值为I,则λ值的经验取值范围为:
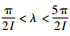
3 转矩控制器 3.1 基于转矩预测的转矩控制器设计 由于采样周期很短,将式(3)、式(4)在k时刻进行离散化,有
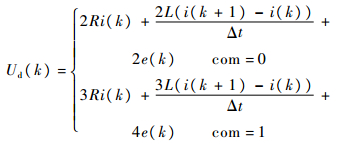 | (15) |
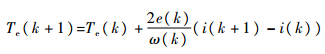 | (16) |
式(15)表明,电机在不同运行状态下,可以通过控制k时刻直流母线电压来控制k+1时刻电机上管导通相电流i(k+1)。根据式(16)可知,通过控制k时刻直流母线电压可进而间接控制k+1时刻电机转矩。
同时,i(k)、ω(k)可以通过传感器得到,e(k)、Te(k)可以通过改进滑模观测器得到。电机状态判断方法在第1.2.2 节和第1.2.3节已说明。
令Te(k+1)=Te*,Te*为参考转矩。即使每个下一时刻期望转矩均为参考力矩,有
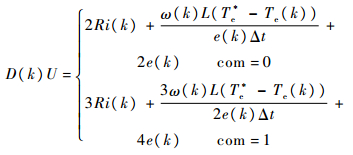 | (17) |
式中:D(k)为电机不同状态下,使k+1时刻电机转矩理论上为期望转矩时,需要对电机供电电压的调制占空比。
式(17)说明,根据电机状态,按照不同数学模型得出的对电机的供电电压U进行占空比为D(k)的占空比调制,可以在理论上使得k+1时刻电机转矩为期望转矩。
图 5为实际应用的一种无刷直流电机驱动等效电路。图中:U为额定电压;二极管D0、电感Lf、电容C0和开关管Q7构成Buck电路。可以看出,通过Q7可以调制电机供电电压,调制后通过电感Lf、电容C0构成的低通滤波器滤波,使实际作用于三相绕组的Ud近似于直流电压。如果按式(17)对Q7输入占空比为D(k)的数字信号,就可以实现对转矩的控制。
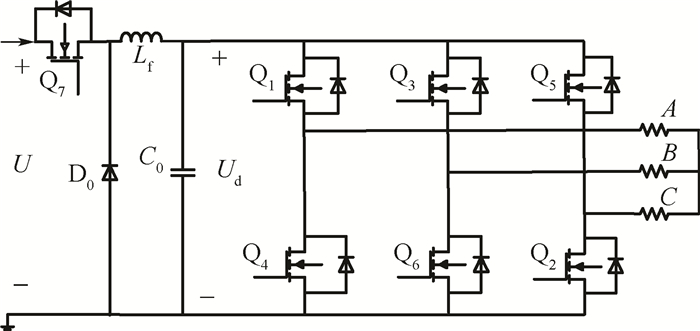 |
| 图 5 实际应用的无刷直流电机驱动等效电路 Fig. 5 Actual used equivalent circuit of inverter of BLDCM |
| 图选项 |
3.2 控制器稳定性和鲁棒性 由式(3)可知,无刷直流电机在换相阶段与非换相阶段数学模型类似,只证明非换相阶段基于转矩补偿策略的转矩控制器的收敛性。
无刷直流电机数学模型是对实际系统的近似,考虑电机参数估计误差,根据式(3)可假设实际系统方程为
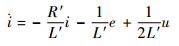 | (18) |
式中:u为系统输入电压;R′和L′分别为无刷直流电机实际绕组电阻和绕组等效电感。
忽略滑模观测器对电机反电动势的估计误差,则转矩补偿策略对应的系统方程为
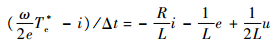 | (19) |
综合式(18)、式(19),可得
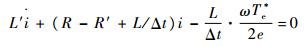 | (11) |
假设收敛过程中电机转速不变,且设:
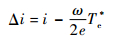 | (12) |
则有
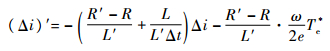 | (20) |
由式(20)可知,系统在R′=R时稳定,系统在稳定的前提下,控制器对电机电感参数具有鲁棒性;在电机参数估计准确的情况下,有
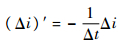 | (13) |
即电流误差以指数形式收敛到零,系统稳定,且收敛速度与系统控制周期有关。
4 总体控制方案 图 6为本文提出的无刷直流电机改进转矩控制系统框图。无刷直流电机利用本身的位置传感器确认转子位置,控制逆变器开关管。采样电机任意两相的电流和绕组端电压以及中性点电压,经过Clark变换得到αβ坐标系下定子电流与定子电压。利用滑模观测器对绕组反电动势进行估计,进而估计电机转矩。根据此时电机绕组导通状态对应的数学模型,输出电源额定电压的调制占空比,使下一时刻理论电磁转矩为期望电磁转矩。为了保证系统稳定,采用离线绕组电阻测量方案,即利用绕组中热敏电阻测量绕组温度,将不同温度下绕组电阻值存于程序表格中,程序运行时进行查询。图中:N*和N分别为无刷直流电机的参考转速和实际转速。
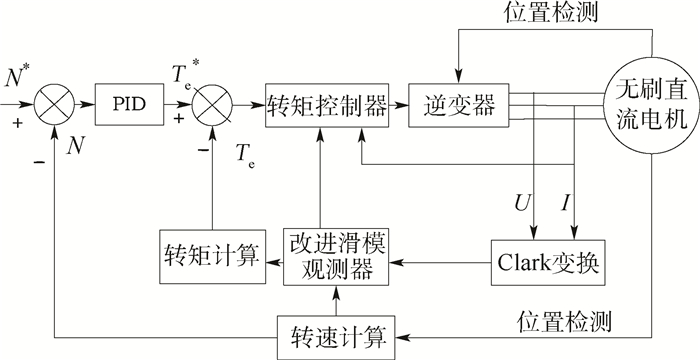 |
| 图 6 改进转矩控制方法的结构框图 Fig. 6 Control framework of advanced torque control method |
| 图选项 |
5 仿真和实验验证 5.1 仿真验证 根据实际应用的MSRF无刷直流电机参数,利用MATLAB建立无刷直流电机模型。参数为:额定电压U=28 V,相绕组电阻为0.17 Ω,相绕组自感为0.78 mH,相绕组互感为0.15 mH,极对数为4,黏滞系数为0.000 2 N·m/(rad·s-1),额定负载转矩为0.02 N·m,反电动势系数为0.007 9 V/(r·min-1),转子转动惯量为0.027 3 kg·m2,电机加速阶段最大参考力矩为0.302 N·m。
为验证改进滑模观测器能否削弱传统滑模观测器存在的抖振,在指令转速为400 r/min、仿真(采样、控制)频率为50 kHz条件下进行仿真验证,eβ的观测误差
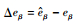
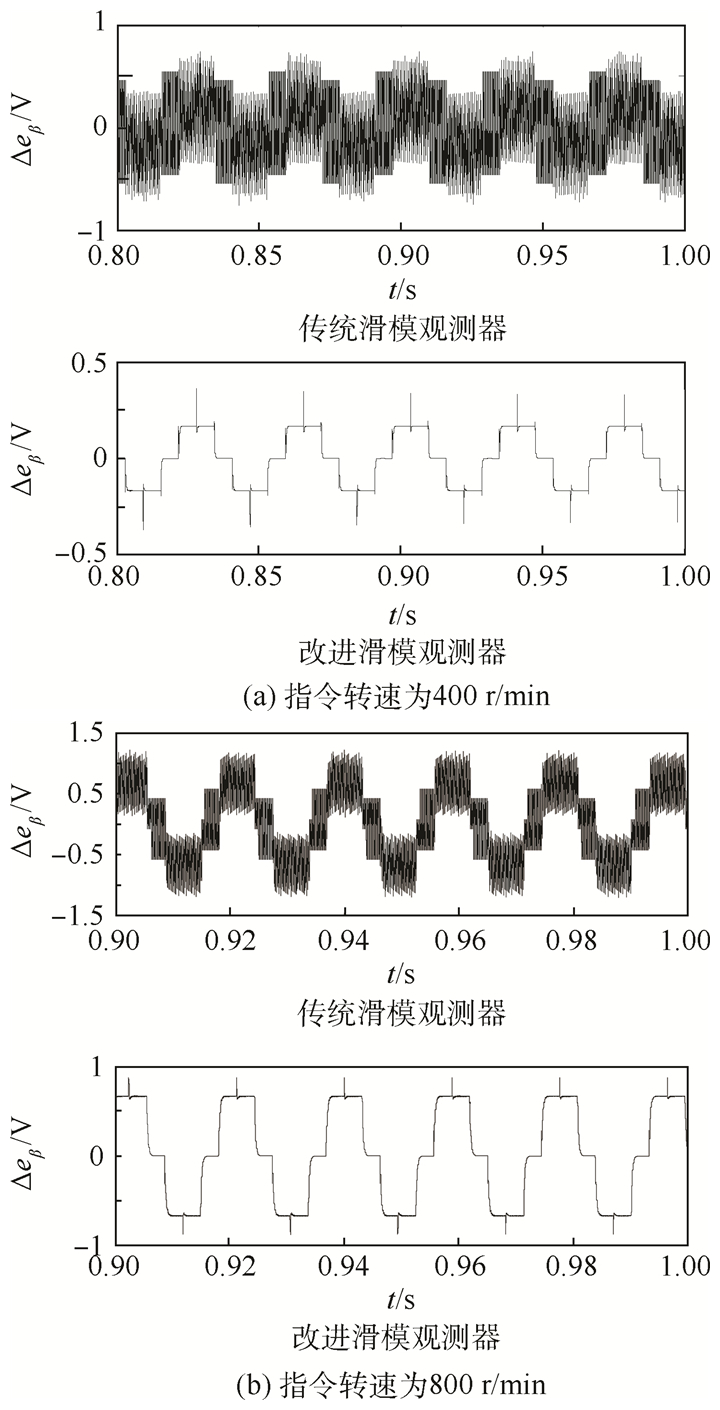 |
| 图 7 400 r/min与800 r/min指令转速下绕组反电动势估计误差仿真结果 Fig. 7 Simulation results of back-EMF estimation error under command speeds of 400 r/min and 800 r/min |
| 图选项 |
更改指令转速为800 r/min,再次仿真,结果见图 7(b)。滑模增益参数保持不变。
从图 7可知,利用所提出的改进滑模观测器相对传统滑模观测器对定子绕组反电动势的估计值更平滑,基本消除了抖振现象。由于滑模观测器跟踪的实际电流基本上是阶段性阶跃电流,造成了滑模观测器对eβ的观测存在阶跃性的观测误差。
再验证基于转矩预测的转矩控制方法(称改进方法)是否相对于传统无磁链反馈直接转矩控制方法(称传统DTC方法)能够更好地抑制转矩脉动。2种方法都采用改进滑模观测器,滑模增益参数不变,设传统DTC方法的转矩滞环宽度为0.005 N·m,仿真频率为50 kHz。图 8为指令转速为400 r/min(初始转速350 r/min)时转矩仿真结果。可以得到,电机转速为350~400 r/min情况下,传统DTC方法转矩脉动36.7%(按加速阶段计算),改进方法转矩脉动在换相时为16.7%(按加速阶段计算)。
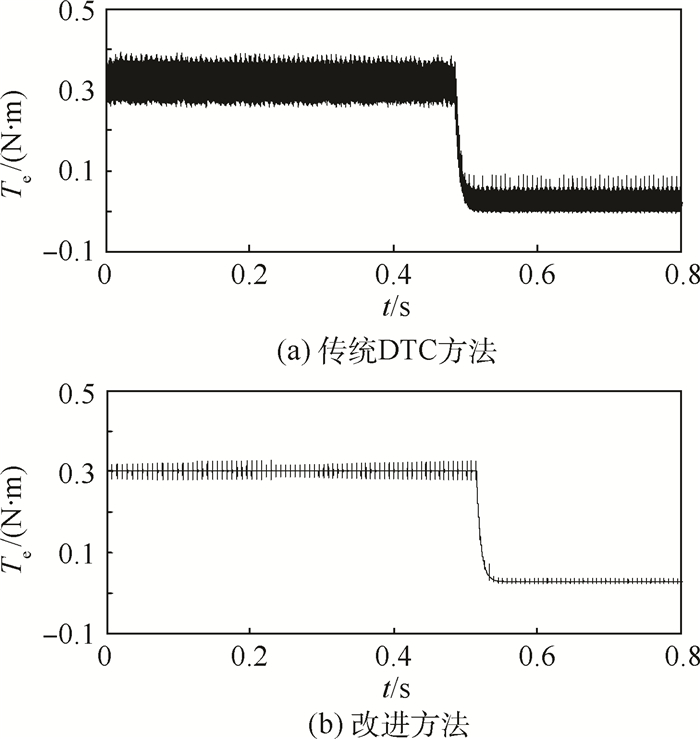 |
| 图 8 指令转速为400 r/min时转矩仿真结果 Fig. 8 Simulation results of torque under command speed of 400 r/min |
| 图选项 |
将图 8一个周期内细节展开如图 9所示,且加入电机状态信号、2种方法的控制器输出信号进行对比。图 9(a)中纵坐标表示电机运行状态,1为换相阶段,0为非换相阶段,可以看出,传统DTC控制器输出电压在0和28 V间跳变,转矩波形明显超过了设定的转矩滞环宽度。改进方法在换相阶段对电机转矩进行补偿后,在换相阶段完成后0.000 5 s内收敛到参考转矩0.302 N·m,在换相阶段由于转矩估计误差的存在,使转矩控制精度较差,超过了参考转矩,形成了新的脉动。但是总体来说,改进方法能够减小整个运行阶段的转矩脉动,尤其在非换相阶段相对于传统DTC方法得到平稳的转矩。
 |
| 图 9 单位周期内2种方法转矩结果与输出电压对比 Fig. 9 Comparison of torque and ouput voltage in one unit cycle between two methods |
| 图选项 |
图 10为指令转速为800 r/min(初始转速为750 r/min)时2种转矩控制方法的转矩仿真结果。可以看出,改进方法在加速阶段和稳速阶段均比传统DTC方法转矩控制精度高。
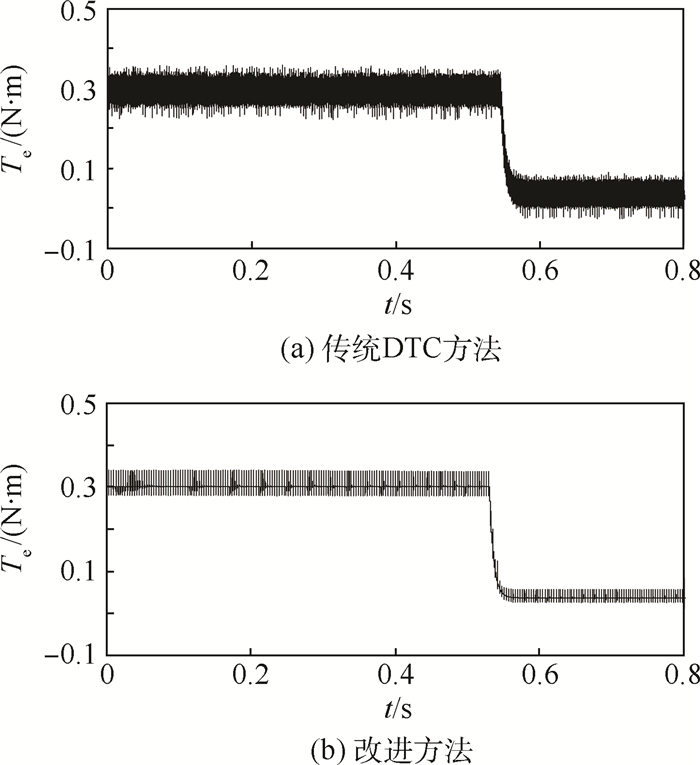 |
| 图 10 指令转速为800 r/min时转矩仿真结果 Fig. 10 Simulation results of torque under command speed of 800 r/min |
| 图选项 |
图 10细节以及对应的控制器输出电压如图 11所示。可以看出,0.200~0.210 s之间,电机转矩上限边界很整齐,这是由于电机转速提高,改进方法为补偿跌落转矩,而输出的电压相等,在基本相同转速下,对转矩的补偿效果相同。同样,改进方法作用下非换相阶段转矩很平稳。
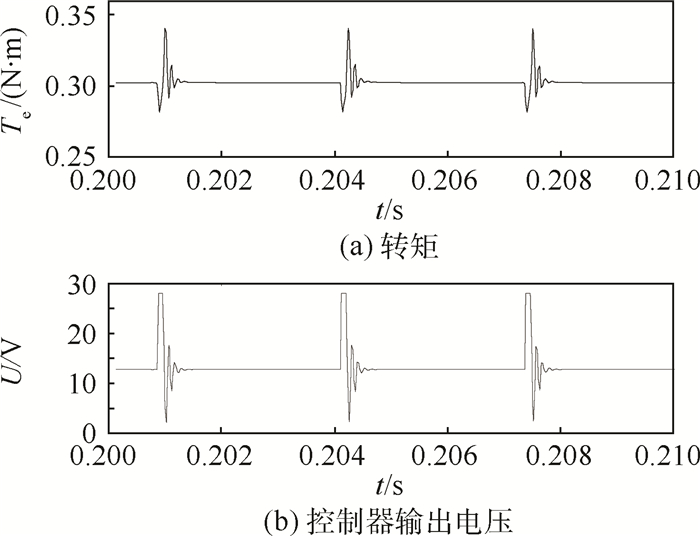 |
| 图 11 改进方法转矩和控制器输出电压波形 Fig. 11 Torque and output voltage waveform of controller by advanced methool |
| 图选项 |
为了验证相对于传统DTC方法,改进方法是否会大幅度降低转矩响应速度,在电机转速稳定为600 r/min时,负载转矩从0.02 N·m突变为0.10 N·m,2种方法作用下转矩响应结果见图 12。可以得到,传统DTC方法和改进方法在负载力矩突变时,响应时间均在0.02 s左右,说明改进方法相对于传统DTC方法没有大幅度降低转矩响应速度。
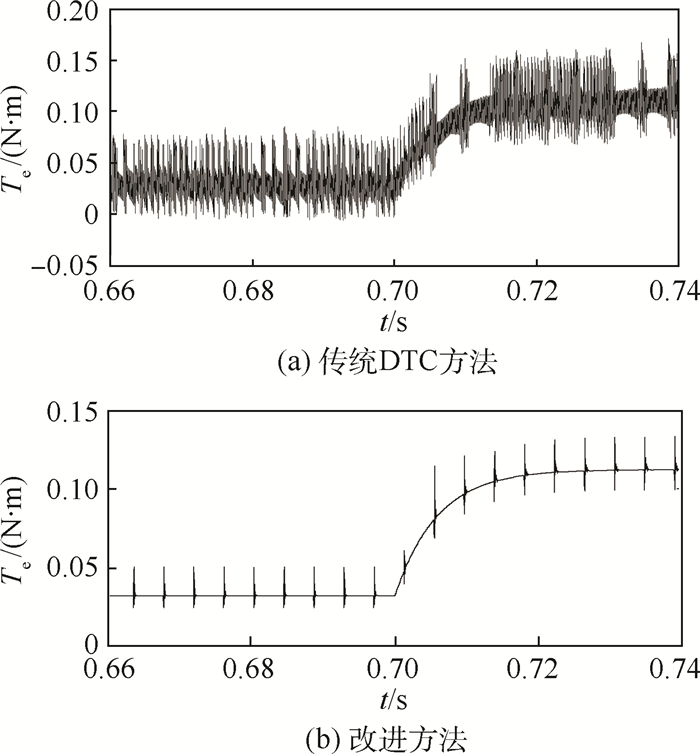 |
| 图 12 负载突变时转矩响应仿真结果 Fig. 12 Simulation results of torque response with step load |
| 图选项 |
5.2 实验验证 为了进一步验证所提基于改进滑模观测器和转矩预测的转矩控制方法的有效性,在MSRF无刷直流电机上进行实验。实验用MSRF无刷直流电机参数与所建立的仿真电机模型相同。由于电机的绕组反电动势和转矩均无法直接测量,因此在实验中,选择将电机的估计定子电流、估计绕组反电动势和估计转矩通过串口上传至上位机,然后利用MATLAB绘制图像。
首先验证所提出的改进滑模观测器能否减小传统滑模观测器中的系统抖振。在电机加速阶段(转速接近600 r/min)进行实验,得到传统滑模观测器与改进滑模观测器的iβ跟踪结果见图 13,2种方法对eβ的估计波形见图 14。
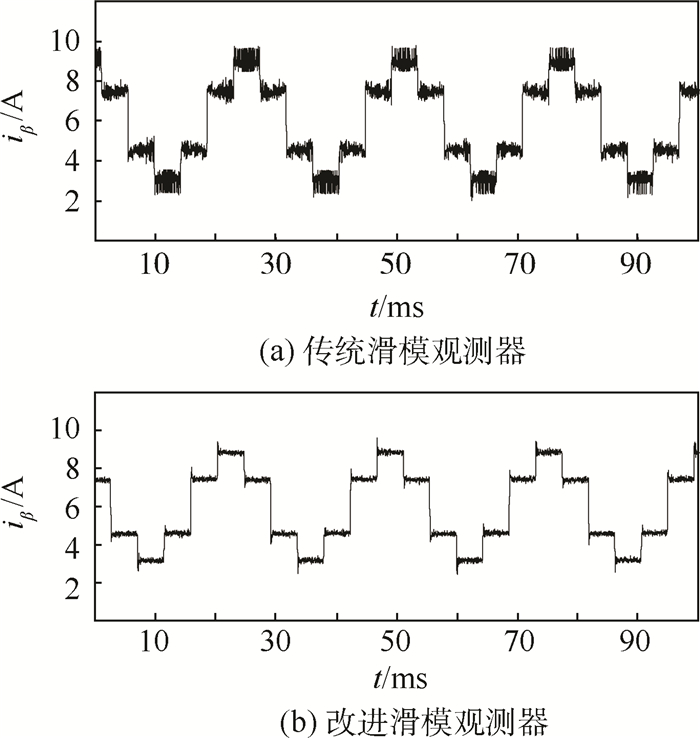 |
| 图 13 传统和改进滑模观测器的iβ跟踪结果 Fig. 13 Tracking results of iβ by traditional and advanced SMOs |
| 图选项 |
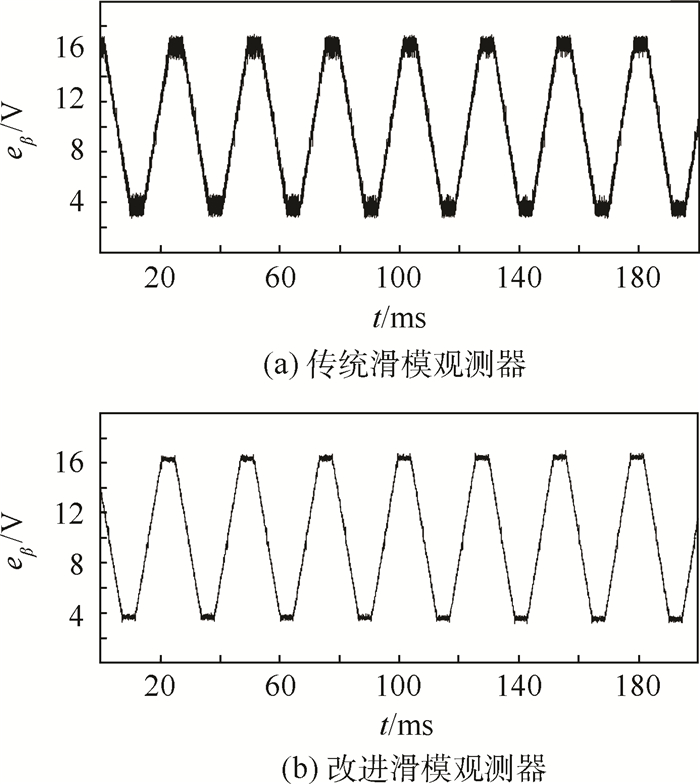 |
| 图 14 传统和改进滑模观测器对eβ的估计结果 Fig. 14 Estimation results of eβ by traditional and advanced SMOs |
| 图选项 |
从图 13可以看出,实验条件下,传统滑模观测器对iβ的跟踪效果中存在很大的抖振,抖振幅度达到1.5 A,改进滑模观测器作用下,iβ的抖振幅度降到了0.4 A左右。这种情况下,改进滑模观测器相对于传统滑模观测器能够更准确地估计绕组反电动势,图 14的实验结果也说明了此问题。明显,利用新提出的函数替换符号函数的改进滑模观测器能够有效抑制系统抖振。同时由于三相电流和电压测量误差、滑模观测器的参数整定不准确,以及滑模观测器原理上无法消除跟踪误差、系统外来干扰等问题的存在,改进滑模观测器对iβ的跟踪仍旧存在一定的抖振。
为了验证改进方法相对于传统DTC方法能否更好地抑制转矩脉动,在电机处于加速阶段(转速接近600 r/min)时,进行实验验证。传统DTC方法也采用改进滑模观测器估计绕组反电动势,进而估计电机转矩,转矩滞环宽度为0.005 N·m。图 15为2种方法作用下转矩实验结果。
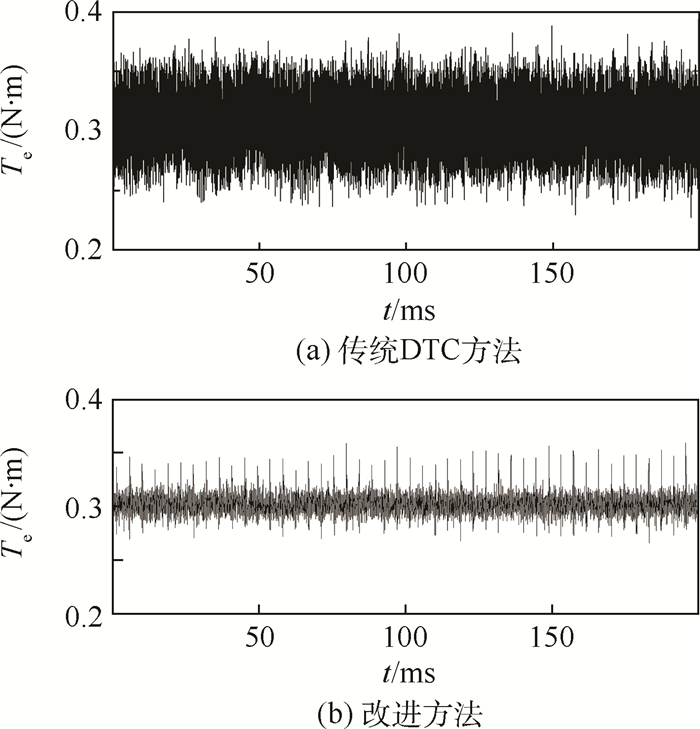 |
| 图 15 传统DTC方法和改进方法转矩实验波形 Fig. 15 Tow experimental curves of troque by traditional DTC method and advanced method |
| 图选项 |
从图 15可以看出,实验条件下,传统DTC方法作用下,电机转矩脉动为40%左右,改进方法作用下,在换相阶段转矩脉动近似为26%,非换相阶段转矩脉动近似为12%。由于实验条件下传统DTC方法也采用改进滑模观测器对转矩进行估计,实验结果说明,改进方法能够有效地改进传统DTC方法的bang-bang观测器的缺陷,进而更好地抑制转矩脉动。
在实验条件下,电机转矩三相电流以及电压的测量误差和测量时间差的存在造成对转矩的估计是不准确的,而且改进滑模观测器不可能完全消除系统抖振,进而消除绕组反电动势的估计误差,造成电机的转矩估计存在误差。另外,实验对象电机绕组的电阻参数不对称、逆变器开关器件正向导通电阻和二极管续流导通电阻的存在也影响所提方法的精度。本实验系统中采用的集成逆变器芯片MSK4300在使用过程中的发热问题也会影响系统的参数。这些原因导致实验条件下所提出的改进方法转矩脉动抑制效果相对于仿真条件有所下降。
为了验证所提出的改进方法的转矩响应速度是否下降,在实验条件下,电机处于加速状态时,在电机转速超过600 r/min时,将给定最大参考转矩从0.07 N·m增大至0.32 N·m,实验结果如图 16所示。
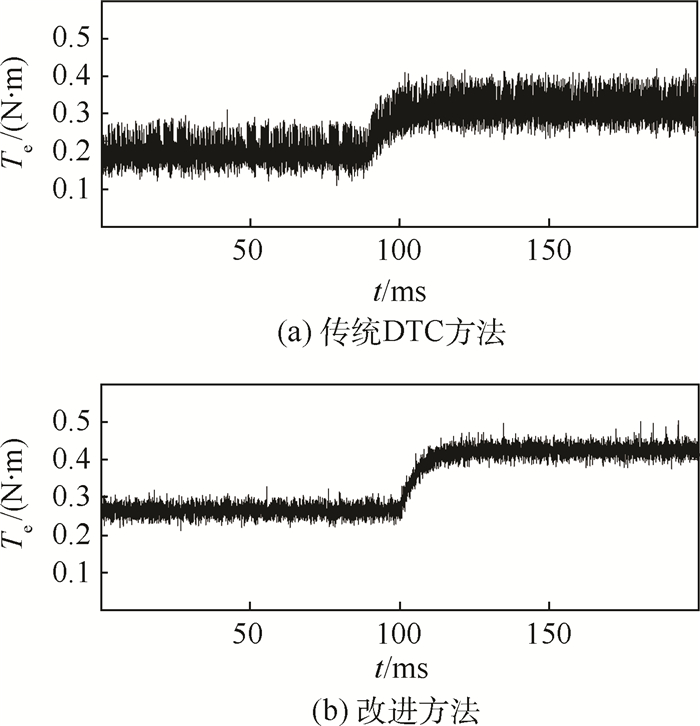 |
| 图 16 实验条件下负载突变时转矩响应曲线 Fig. 16 Response curves of torque under mutation loads in the condition of experiment |
| 图选项 |
从图 16可以看出,在实验条件下,传统DTC方法和改进方法基本都在20 ms左右完成转矩的重新稳定,2种方法具有基本相同的转矩响应速度,这与仿真结果相符。
6 结 论 本文针对造成转矩脉动的换相过程和非导通相续流建立了数学模型,提出了一种基于数学模型的转矩预测的转矩控制方法。针对传统滑模观测器的抖振问题,提出了一种含参数的光滑连续函数代替符号函数,形成了一种改进滑模观测器。仿真和实验结果说明:
1) 改进滑模观测器能够有效抑制系统抖振,提高了绕组反电动势和转矩的估计精度。
2) 基于改进型滑模观测器和转矩预测相结合的改进转矩控制方法能够有效抑制MSRF无刷直流电机运行过程中的转矩脉动,提高了输出力矩的稳定性。
参考文献
| [1] | 巫庆辉, 邵诚, 徐占国. 直接转矩控制技术的研究现状与发展趋势[J].信息与控制, 2005, 34(4): 444–450.WU Q H, SHAO C, XU Z G. Survey of research status quo and development trends about direct torque control[J].Information and Control, 2005, 34(4): 444–450.(in Chinese) |
| [2] | 王志强, 赵波, 周新秀. 反作用飞轮电机换相转矩脉动分析[J].微特电机, 2010, 38(10): 1–4.WANG Z Q, ZHAO B, ZHOU X X. Commutation torque ripple analysis of brushless DC motor for reaction flywheels[J].Small & Spacial Electrical Machines, 2010, 38(10): 1–4.(in Chinese) |
| [3] | YOSHIDA M, MURAI Y, TAKADA M. Noise reduction by torque ripple suppression in brushless DC motor[C]//29th Annual IEEE Power Eletrionics Specialist Conference. Piscataway, NJ: IEEE Press, 1998, 2: 1397-1401. |
| [4] | KIM G H, KANG S J, WON J S. Analysis of the commutation torque ripple effect for BLDCM fed by HCRPWMVSI[C]//7th Annual Applied Power Electronics Conference and Exposition. Piscataway, NJ: IEEE Press, 1992: 277-284. |
| [5] | 杨进, 杨向宇. 一种减小无刷直流电机纹波转矩的新方法[J].微电机, 2005, 38(1): 9–11.YANG J, YANG X Y. The application of tysteresis control in reducing ripple torque of brushless DC motor[J].Micromotors, 2005, 38(1): 9–11.(in Chinese) |
| [6] | 林平, 韦鲲, 张仲超. 新型无刷直流电机换相转矩脉动抑制控制方法[J].中国电机工程学报, 2006, 26(3): 153–158.LIN P, WEI K, ZHANG Z C. A novel control scheme to suppress the commutation torque ripple in BLDCM[J].Proceedings of the CSEE, 2006, 26(3): 153–158.(in Chinese) |
| [7] | SONG J H, CHOY I. Commutation torque ripple reduction in brushless DC motor drives using a single DC current sensor[J].IEEE Transactions on Power Electronics, 2004, 19(2): 312–319.DOI:10.1109/TPEL.2003.823177 |
| [8] | 任军军. 永磁无刷直流电机的转矩脉动抑制的控制策略研究[D]. 杭州: 浙江大学, 2004.REN J J. Research on torque ripple minimization techniques for PM brushless DC motor[D]. Hangzhou: Zhejiang University, 2004(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10613-1013106653.htm |
| [9] | 陈冬, 房建成. 非理想梯形波反电动势永磁无刷直流电机换相转矩抑制方法[J].中国电机工程学报, 2008, 28(30): 79–83.CHEN D, FANG J C. Commutation torque ripple reduction in PM brushless DC motor with nonideal trapezoidal back EMF[J].Proceedings of the CSEE, 2008, 28(30): 79–83.(in Chinese) |
| [10] | 郭方正, 韩邦成, 刘刚. PAM调制方式下高速无刷直流电机非导通相续流抑制方法研究[J].微电机, 2009, 42(8): 42–46.GUO F Z, HAN B C, LIU G. Research on suppression for diode freewheeling of inactive phase in high-speed BLDCM using PAM strategy[J].Micromotors, 2009, 42(8): 42–46.(in Chinese) |
| [11] | OZTURK S B, TOLIYAT H A. Direct torque control of brushless DC motor with non-sinusoidal back-EMF[C]//IEEE IEMDC 2007: Proceedings of the International Electric Machines and Drives Conference. Piscataway, NJ: IEEE Press, 2007. |
| [12] | 林海, 梁中, 闫茂德, 等. 无刷直流电机改进型直接转矩控制研究[J].电气传动, 2014, 44(8): 11–14.LIN H, LIANG Z, YAN M D, et al. Improved direct torque control in brushless DC motor drives[J].Electric Drive, 2014, 44(8): 11–14.(in Chinese) |
| [13] | 安群涛, 孙立志, 刘超, 等. 无刷直流电机的磁链自控直接转矩控制[J].中国电机工程学报, 2010, 30(12): 86–92.AN Q T, SUN L Z, LIU C, et al. Flux linkage self-control based direct torque control of brushless DC motor[J].Proceedings of the CSEE, 2010, 30(12): 86–92.(in Chinese) |
| [14] | 朱俊杰, 粟梅, 王湘中, 等. 分段式滑模变结构无刷直流电机直接转矩控制[J].仪器仪表学报, 2013, 34(11): 2634–2640.ZHU J J, SU M, WANG X Z, et al. Direct-torque-control of brushless DC motors based on segmented sliding-mode-variable-structure[J].Chinese Journal of Scientific Instrument, 2013, 34(11): 2634–2640.(in Chinese) |
| [15] | 郭鸿浩, 周波, 左广杰, 等. 无刷直流电机反电势自适应滑模观测[J].中国电机工程学报, 2011, 31(21): 142–149.GUO H H, ZHOU B, ZUO G J, et al. Adaptive sliding-mode observer for back electromotive force estimation of brushless DC motor[J].Proceedings of the CSEE, 2011, 31(21): 142–149.(in Chinese) |
| [16] | 郭鸿浩, 周波, 左广杰, 等. 无刷直流电机转矩观测与电感自适应辨识[J].中国电机工程学报, 2011, 31(33): 151–158.GUO H H, ZHOU B, ZUO G J, et al. Torque estimation and adaptive inductance identication for brushless DC motor[J].Proceedings of the CSEE, 2011, 31(33): 151–158.(in Chinese) |
| [17] | 周衍, 张兴华. 一种简易的无刷直流电动机直接转矩控制[J].微特电机, 2014, 42(7): 54–60.ZHOU Y, ZHANG X H. A kind of simplified direct torque control for brushless DC motor[J].Small & Spacial Electrical Machines, 2014, 42(7): 54–60.(in Chinese) |
| [18] | 李珍国, 章松发, 周生海, 等. 考虑转矩脉动最小化的无刷直流电机直接转矩控制系统[J].电工技术学报, 2014, 29(1): 139–146.LI Z G, ZHANG S F, ZHOU S H, et al. Direct torque control of brushless DC motor considering torque ripple minimization[J].Transaction of China Electrotechnical Sociaty, 2014, 29(1): 139–146.(in Chinese) |
| [19] | 王晓远, 田亮, 冯华. 无刷直流电机直接转矩模糊控制研究[J].中国电机工程学报, 2006, 26(15): 134–138.WANG X Y, TIAN L, FENG H. Study of the fuzzy control on direct torque control for brushless BLDCM[J].Proceedings of the CSEE, 2006, 26(15): 134–138.(in Chinese) |
| [20] | 许鹏, 郭桂芳, 曹军义, 等. 直流无刷电机神经网络直接转矩控制[J].中国电机工程学报, 2009, 29(Suppl.): 192–196.XU P, GUO G F, CAO J Y, et al. Neural network control on direct torque control for brushless DC motor[J].Proceedings of the CSEE, 2009, 29(Suppl.): 192–196.(in Chinese) |
