为提高EHA动态性能,许多****基于非线性控制理论来设计其控制器,如滑模变结构控制[5-7]、自适应控制[8-10]和模糊控制[11]等,并取得了一定的成果。在这些非线性控制策略中,滑模变结构控制由于设计简单且对系统参数摄动和外界扰动强鲁棒性而深受重视[12]。对非线性系统而言,在设计滑模变结构控制器时,应取非线性的切换函数,但目前大多采用线性的切换函数,这将降低系统的控制性能,且滑模变结构控制由于其本质上的不连续特性将引起系统的抖振,这种抖振不仅增加了控制器的负担,而且有可能使系统跟踪误差在零点附近产生抖动,从而增大稳态误差,有时甚至会造成系统的不稳定[13]。反馈线性化是一种非线性控制设计方法,其基本思想是:通过适当的非线性状态变换和反馈变换,使非线性系统实现全部或部分的精确线性化,以方便应用熟知的线性控制方法进行设计,但其需要精确的模型信息,无法克服干扰,鲁棒性较差。
基于以上原因,本文以EHA为研究对象,将反馈线性化与滑模变结构控制相结合:一方面利用滑模变结构对外界干扰强鲁棒性特点,减弱反馈线性化对精确模型的依赖,以提高EHA控制系统的鲁棒性;另一方面将EHA的非线性模型反馈线性化后,可建立线性滑模切换函数,并应用线性理论来改善其动态性能;同时引入了模糊控制算法来削弱系统的抖振。最后,对EHA的跟踪控制进行了仿真,通过仿真验证了本文所提方法的有效性。
1 EHA非线性建模 1.1 系统描述 EHA系统组成原理如图 1所示,该系统执行元件为对称双作用液压缸,液压泵为双向定排量泵,动力源为永磁同步电机。EHA控制器通过比较指令位移与实际位移的大小,来改变电机的转速和转向,从而达到控制作动器位移的目的。
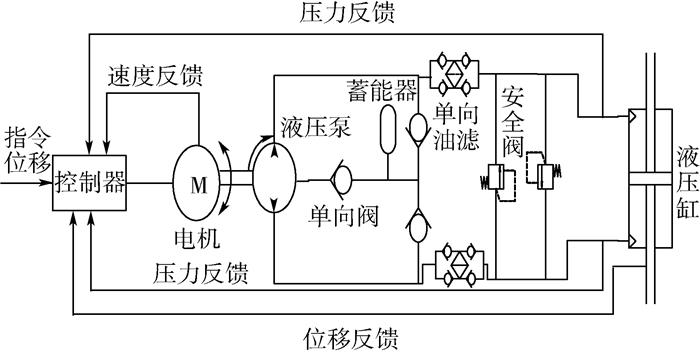 |
| 图 1 EHA系统组成原理 Fig. 1 Composition principle of EHA system |
| 图选项 |
1.2 系统的非线性模型
1.2.1 永磁同步电机模型 永磁同步电机分梯形波和正弦波2种,后者比前者调速范围大、力矩脉动小,且考虑现有飞机主电源为交流电源,故本文中选择正弦波永磁同步电机作为动力源。为建模方便,假设铁心不饱和,且忽略气隙中高次谐波和磁损耗,电机采用id=0矢量控制,其在dq坐标系有以下方程:
电机q轴定子电压方程为
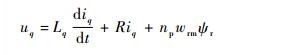 | (1) |
电机运动方程为
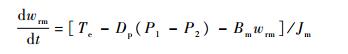 | (2) |
电磁转矩方程为
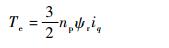 | (3) |
式中:uq、Lq和iq分别为q轴的定子电压、电感和电流;R为定子电阻;np为电机极对数;wrm为电机转速;ψr为永磁体产生的磁链;Dp为定量泵排量;P1、P2分别为液压泵高、低压腔压力;Bm和Jm分别为电机阻尼系数和转动惯量;Te为电机电磁转矩。
1.2.2 泵控缸模型 根据文献[14],泵控缸流量连续方程为
 | (4) |
式中:A为液压缸液压杆活塞面积;xt为液压缸液压杆的位移;V0为液压管路和液压缸平均体积;βe为液压油等效容积弹性模数;ξ、Lext分别为液压泵内、外泄漏系数;Ppipe为液压管路压降。
在式(4)中,液压管路压降Ppipe大小与流量大小有关,根据Darcy管流动方程,其与流量的关系近似为
 | (5) |
式中:Kpipe为黏性系数。
液压缸力平衡方程为
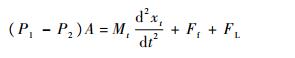 | (6) |
式中:Mt为液压缸液压杆及负载等效到其的总质量;Ff为摩擦力;FL为作用在液压杆的外负载力。
在式(6)中,摩擦力Ff通常认为由静摩擦力、库仑摩擦力和黏性摩擦力组成[15],可表示为
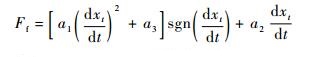 | (7) |
式中:a1、a2和a3为摩擦系数。
1.3 系统的非线性模型状态空间描述 取q轴定子电压uq作为模型输入量。此时令u=uq,x1=iq,x2=wrm,x3=P1-P2,x4=xt,x5=dxt/dt,通过式(1)~式(7),可得EHA非线性模型状态空间描述为
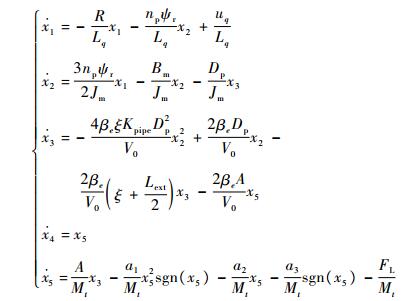 | (8) |
由式(8)可以看出,EHA模型呈强非线性且特征参数多,计算量大,直接求解比较困难,需要对其进行线性化。
2 非线性模型反馈线性化 EHA非线性模型状态空间描述形式所对应的仿射非线性系统的标准形式为
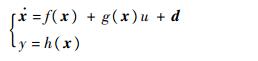 | (9) |
式中:f(x)和g(x)为充分光滑的向量场;d为系统所受干扰量;y为系统输出量;h(x)为系统输出函数。
因此,EHA非线性模型可改写为
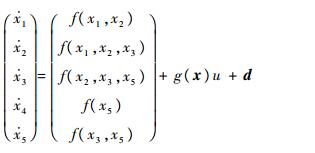 | (10) |
式中:
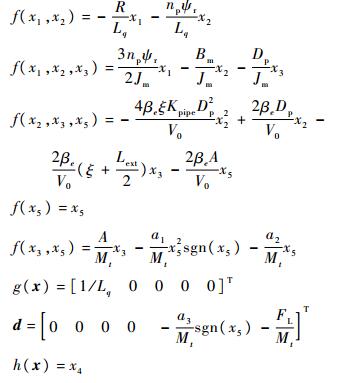 |
2.1 反馈线性化条件 在对EHA非线性模型反馈线性化之前,要验证其是否满足反馈线性化的条件。按照相关定义[16-17]:对原点附近的所有x,矩阵[g adfg…adfn-1g]的秩等于系统维数n且集合{g, adfg,…,adfn-2g}是非奇异对合分布(f、g为向量函数f(x)、g(x)的缩写),则其满足非线性模型状态反馈线性化条件。当矩阵的秩小于n时,可以实现部分线性化,但此时需保证零动态子系统的稳定性。
2.2 反馈线性化求解 设EHA系统相对阶为r,则根据式(11)计算其相对阶:
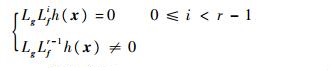 | (11) |
根据式(11)计算得到:Lgh(x)=0,LgLfh(x)=0,LgLf2h(x)=0,LgLf3h(x)=0,LgLf4h(x)=
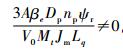
 | (12) |
 | (13) |
式(12)中,z6为新取的控制量,通过式(12)和式(13),EHA非线性系统可转换为如下线性系统:
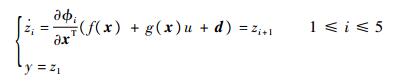 | (14) |
3 模糊滑模控制器设计 3.1 最优滑模面的滑模控制
3.1.1 滑模面函数及其参数确定 EHA的控制目标是使作动器状态向量z跟踪期望状态向量zr,因此定义跟踪误差向量为
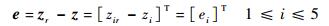 | (15) |
式中:ei为跟踪误差向量e的各个分量形式。
对EHA模型进行微分流形变换后得
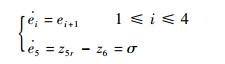 | (16) |
为在下文中方便表示和书写,定义z5r-z6=σ。将式(16)表示为误差状态方程为
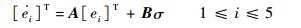 | (17) |
式中:
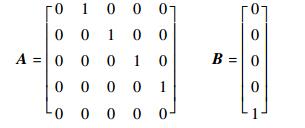 |
选取线性切换面:
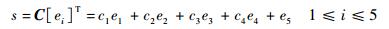 | (18) |
式中:C=[c
为使滑模具有良好的动态品质和鲁棒性,本文采用最优控制方法确定滑模切换面的参数值。由于(A, B)完全能控,可将式(17)和式(18)化为标准型,即
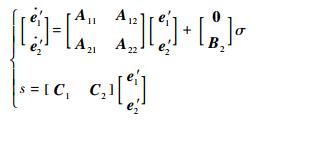 | (19) |
式中:
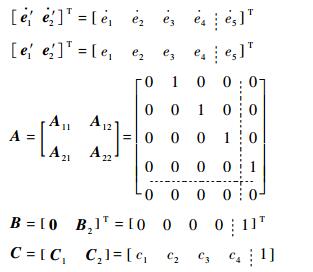 |
当系统在滑模面上运动时:
 | (20) |
根据线性系统最优跟踪问题性能指标定义[18],同时考虑到系统在滑模面运动时与控制量无关,此时定义系统性能指标函数为
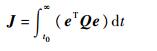 | (21) |
式中:Q为给定的正定矩阵,取
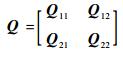
故二次型展开后可表示为
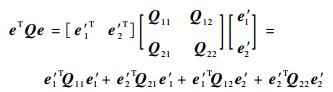 | (22) |
令H=Q22-1Q21e1′+e2′,则式(22)可表示为
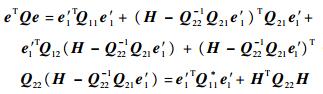 | (23) |
则式(19)可表示为
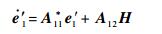 | (24) |
联立式(23)和式(24),得到一个等价的典型二次型性能指标最优控制问题,其中, Q11*=Q11-Q12Q22-1Q21;A11*=A11-A12Q22-1Q21。
由(A, B)可控和Q正定,可得出(A11, A12)可控和Q22及Q11*正定,故上面所描述的最优问题有解。根据二次型性能指标最优控制解法可得
 | (25) |
式中:P可根据黎卡提方程PA11*+A11*TP-PA12Q22-1A12TP +Q11*=0解得。
根据式(25)得
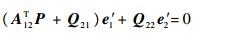 | (26) |
从而得到
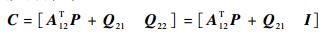 | (27) |
3.1.2 滑模控制器设计 为了实现作动器对不确定性和外界干扰的鲁棒控制,设计如下滑模控制:
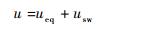 | (28) |
式中:ueq为滑模控制中等效控制部分;usw为滑模控制中切换部分。
将式(12)中的LdLf4h(x)看作外部干扰,先不考虑其影响,令
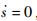
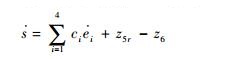 | (29) |
将式(12)代入式(29)得
 | (30) |
从而可以得到
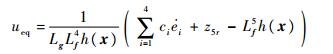 | (31) |
切换控制表示为
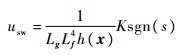 | (32) |
式中:K为切换控制中的控制增益,K=LdLf4h(x)+η,η>0。
构造Lyapunov函数V(s)=s2/2,显然V(0)=0,当s≠0时,V(s)>0,故V(s)为正定函数,对其求导可得
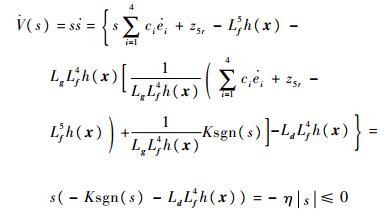 | (33) |
由Lyapunov稳定判别定理可知系统是稳定的。
3.2 模糊控制器设计
3.2.1 切换控制增益的模糊控制 在滑模控制中,切换控制中的控制增益用于补偿系统的不确定性及外界干扰,取较大的控制增益可使系统有较好的鲁棒性,但会造成较大抖振。为了保证系统鲁棒性同时削弱抖振,控制增益应随着系统不确定性及外界干扰变化而变化。鉴于此,本文引入模糊控制,通过调节切换控制增益大小的方法,从而减弱抖振。
由指定参数滑模(即第3节所设计最优滑模面)发生条件得
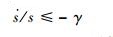 | (34) |
式中:γ为正常数。
定义
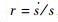
1)当r≤-γ时,系统满足指定滑模发生条件,无需改变K的大小,即ΔK=0。
2)当-γ < r < 0时,系统满足滑模发生条件,但不满足指定滑模发生条件,需要K有较小的改变。ΔK的正负与LdLf4h(x)和s有关,不失一般性,设LdLf4h(x)>0,此时系统已趋向滑模面,则s>0时,应有ΔK>0,以使


3)当r=0时,系统不满足滑模发生条件,需要K有较大的改变。ΔK的正负分析同上。
4)当r>0时,系统不满足滑模发生条件,且远离滑模面运动,需要K有很大的改变。ΔK的正负分析同上。
根据上述分析,设计的模糊控制器以r为输入,|ΔK|为输出,将|ΔK|乘以sgn(s)即得到其真实变化量。因此定义模糊集:
r={NB, NM, NS, ZO, P}
ΔK={ZO, VS, S, M, B}
式中:NB为负大;NM为负中;NS为负小;ZO为零;P为正;VS为很小;S为小;M为中;B为大。隶属度函数采用Sigmoid型与三角形函数结合获得。
具体模糊规则如下:
1)规则1。若r为NB,则|ΔK|为ZO。
2)规则2。若r为NM,则|ΔK|为VS。
3)规则3。若r为NS,则|ΔK|为S。
4)规则4。若r为ZO,则|ΔK|为M。
5)规则5。若r为P,则|ΔK|为B。
采用积分的方法对
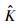
 | (35) |
式中:G为比例系数,且G>0。
从而切换控制器为
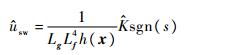 | (36) |
则模糊滑模控制器为
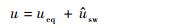 | (37) |
3.2.2 切换项的模糊控制 为进一步削弱抖振,可对切换项模糊化。根据滑模控制特点可知,当s为零时,控制器为等效控制;当s非零时,控制器为等效控制加切换控制。
根据上述分析,取

s={N, ZO, P}
μ={N, ZO, P}
式中:N为负。隶属度函数采用三角函数。
具体模糊规则如下:
1)规则1。若s为N,则μ为P。
2)规则2。若s为ZO,则μ为ZO。
3)规则3。若s为P,则μ为P。
因此控制律为
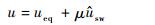 | (38) |
式中:当μ=1时,
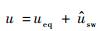
4 仿真验证 为验证本文所设计的控制器的有效性,在MATLAB/Simulink环境下将EHA系统模型式(8)和控制算法实现,对EHA位移跟踪控制进行仿真。EHA相关参数如下:Lq=2 mH,R=0.2Ω,np=2,ψr=0.186 Wb,Dp=1.0×10-6 m3/rad,Bm=3×10-4 N·m/(rad·s-1),Jm=1.5×10-3 kg·m2,A=1.8×10-3 m2,V0=1.4×10-4 m3,βe=6.8×108 N/m2,ξ=Lext=1.02×10-12 m3/(s·Pa),Mt=1.4 kg。
EHA理想跟踪轨迹设置为yd=sin(2πt),初始位置设置为0.8,外界干扰主要考虑外负载力,其采用高斯函数表示为FL=aexp[-(t-c)2/2b2],a决定负载力大小,b表示负载力作用时间范围,c表示负载力的中心,a=10 kN,b=0.5,c=1.5。同时由于作动器工作频宽为0~3 Hz,故本文所设计控制器对跟踪轨迹为yd=sin(4πt)和yd=sin(6πt)信号进行了仿真。
仿真结果如图 2~图 6所示。图 2为反馈线性化控制仿真结果,图 3为反馈线性化滑模控制仿真结果,图 4为反馈线性化模糊滑模控制仿真结果,图 5为反馈线性化最优滑模面双模糊滑模控制仿真结果,图 6为4种控制方法跟踪误差的对比,图 7为本文方法在跟踪信号频率为2 Hz和3 Hz下的跟踪误差对比。
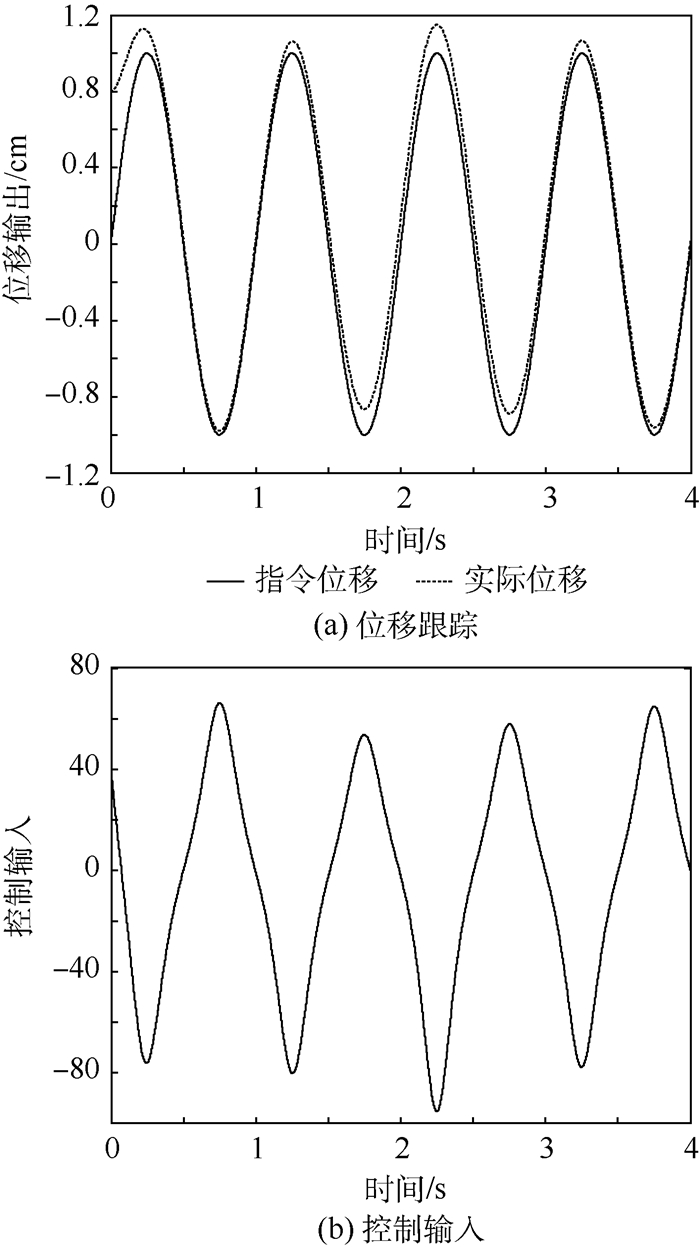 |
| 图 2 反馈线性化控制仿真结果 Fig. 2 Simulation results of feedback linearization control |
| 图选项 |
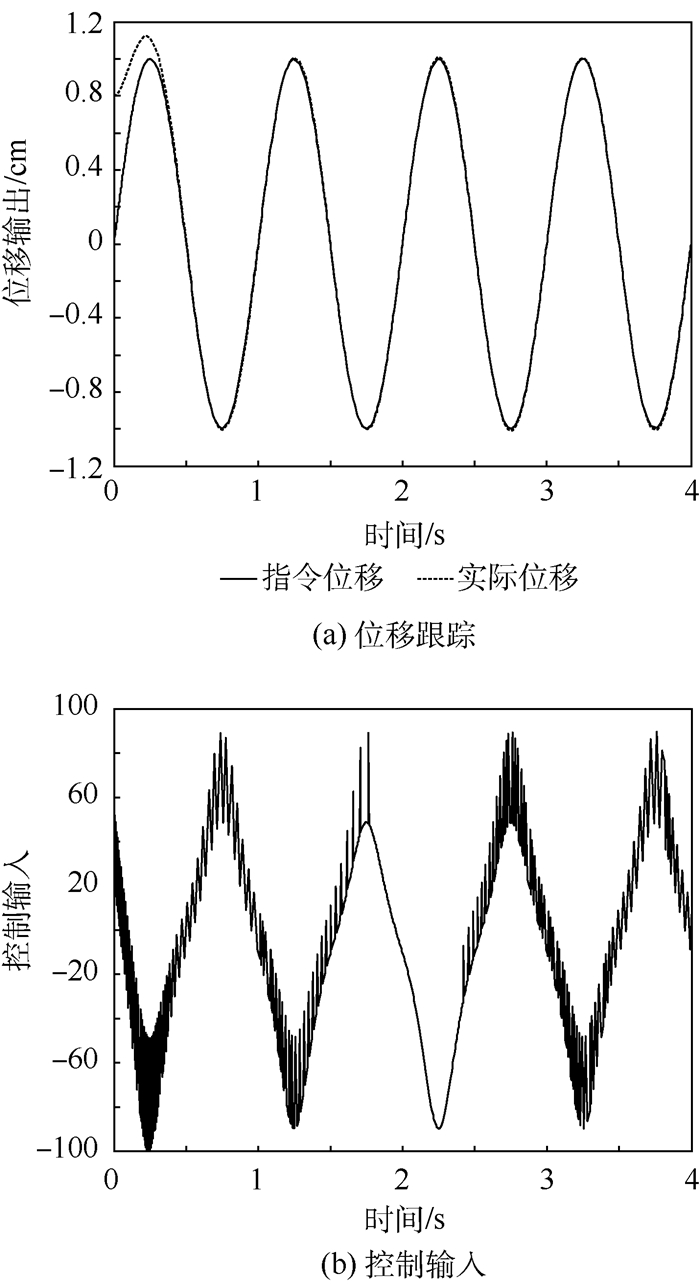 |
| 图 3 反馈线性化滑模控制仿真结果 Fig. 3 Simulation results of sliding mode control based on feedback linearization |
| 图选项 |
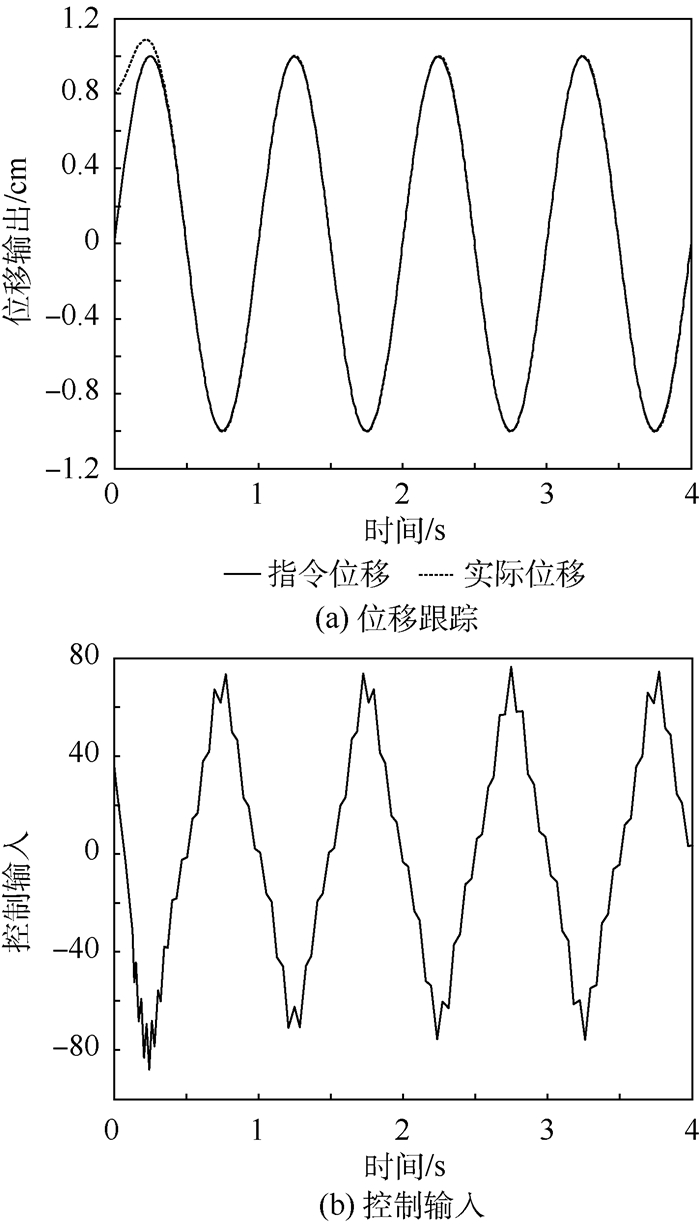 |
| 图 4 反馈线性化模糊滑模控制仿真结果 Fig. 4 Simulation results of fuzzy sliding mode control based on feedback linearization |
| 图选项 |
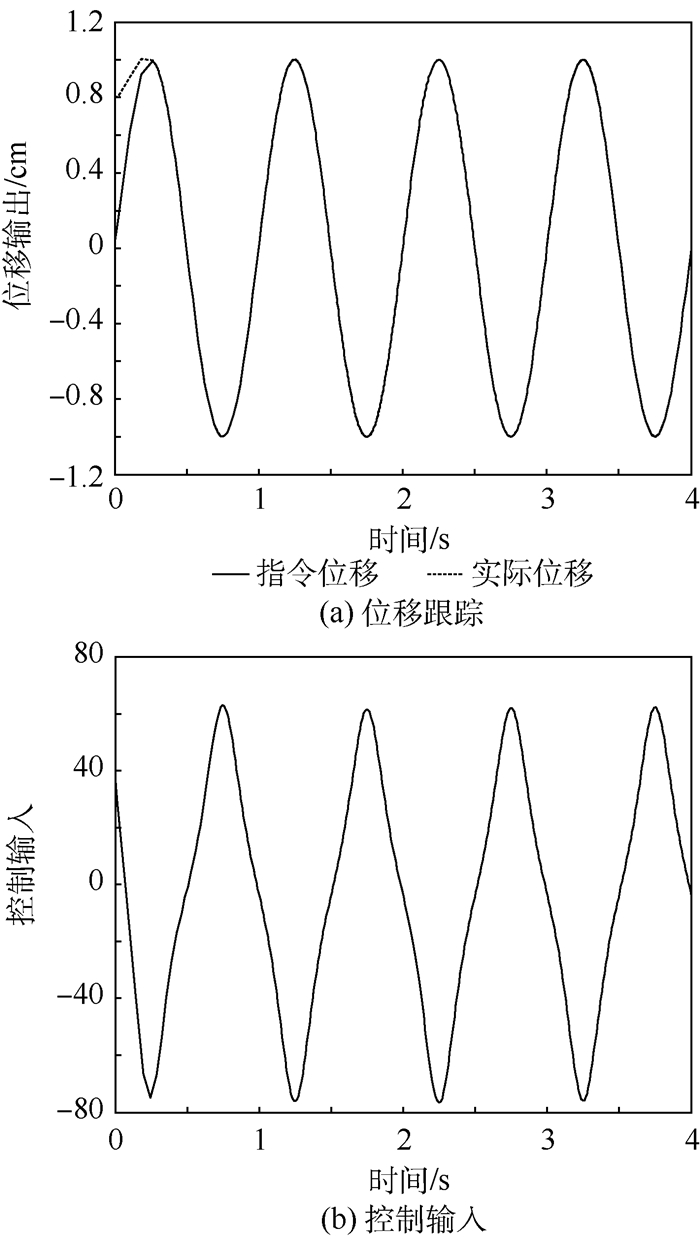 |
| 图 5 反馈线性化最优滑模面双模糊滑模控制仿真结果 Fig. 5 Simulation results of double fuzzy sliding mode control with optimal sliding surface based on feedback linearization |
| 图选项 |
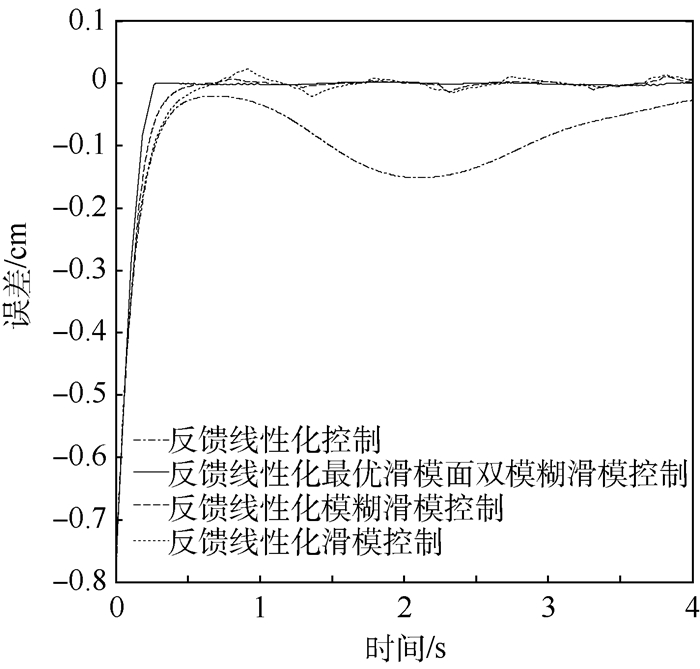 |
| 图 6 4种控制方法跟踪误差的对比 Fig. 6 Tracking errors of four control schemes |
| 图选项 |
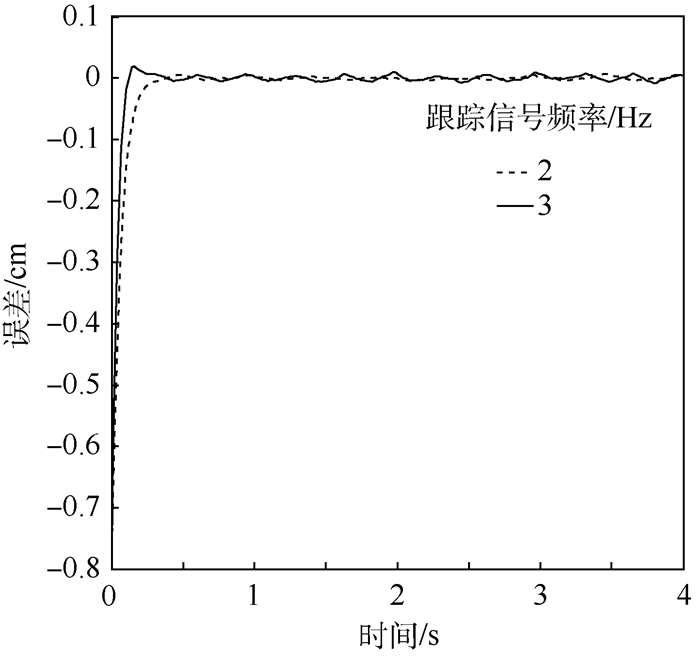 |
| 图 7 不同频率跟踪信号下的跟踪误差的对比 Fig. 7 Tracking errors under different frequency tracking signals |
| 图选项 |
从图 2和图 6中可以看出,在有外界干扰的情况下,反馈线性化控制会有较大的误差,而有滑模控制的则不受外界干扰的影响,说明其有较好的鲁棒性,从而实现系统控制的鲁棒性目标。
结合图 3~图 5可知,滑模控制虽具有较好的鲁棒性,但存在抖振,造成控制输入及跟踪误差曲线在零点附近的抖动。模糊滑模控制削弱了抖振,而本文所提出的方法更进一步地削弱了抖振;同时可以看出本文所提方法的调整时间大概在0.3 s左右,而另外3种方法的调整时间大概在0.5 s左右,因此本文所提出方法还减少了调整时间,提高了响应速度。
从图 6和图 7中可以看出,在高频率下跟踪误差会变大,这是因为在高频率下更易引起滑模控制的抖振,从而造成跟踪误差曲线的抖动;同时,可以看出其跟踪误差幅值基本在0.05 mm之内,可以满足EHA控制要求。
通过仿真结果的对比分析可知,本文所提方法不仅提高了系统的鲁棒性,而且通过反馈线性化建立最优滑模切换函数提高了系统的响应速度,同时通过双模糊控制器的设计削弱了系统的抖振,可以满足EHA控制精度要求,说明本文所提出方法是有效的。
5 结论 本文针对EHA存在的强非线性和外界干扰,设计了一种新型控制器,仿真结果证明:
1)本文所提控制算法与反馈线性化控制相比具有较好鲁棒性,与传统的滑模和模糊滑模控制相比进一步削弱了抖振且提高了响应速度。
2)在EHA工作频宽范围内,可以满足其控制精度要求。
本文方法同样适用于类似的非线性控制系统,尤其是在航空、航天等对控制精度要求较高的领域。
参考文献
| [1] | QI H T, FU Y L, QI X Y, et al. Architecture optimization of more electric aircraft actuation system[J].Chinese Journal of Aeronautics, 2011, 24(4): 506–513.DOI:10.1016/S1000-9361(11)60058-7 |
| [2] | DE LUCENA S E, SUZUKI E Y.Electro-hydraulic actuator tester for fly-by-wire aircrafts[C]//2007 IEEE Instrumentation and Measurement Technology Conference.Piscataway, NJ:IEEE Press, 2007:59-64.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=4258493&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Ficp.jsp%3Farnumber%3D4258493 |
| [3] | YU S, GANEV E. Next generation power and thermal management system[J].SAE International Journal of Aerospace, 2008, 1(1): 1107–1121.DOI:10.4271/2008-01-2934 |
| [4] | TAKAHASHI N, KONDO T, TAKADA M, et al.Development of prototype electro-hydrostatic actuator for landing gear extension and retraction system[C]//Proceedings of the 7th JFPS International Symposium on Fluid Power.Piscataway, NJ:IEEE Press, 2008:165-168.https://www.researchgate.net/publication/271302109_DEVELOPMENT_OF_PROTOTYPE_ELECTRO-HYDROSTATIC_ACTUATOR_FOR_LANDING_GEAR_EXTENSION_AND_RETRACTION_SYSTEM |
| [5] | WANG S, BURTON R, HABIBI S. Sliding mode controller and filter applied to a model of an electro-hydrostatic actuator system[J].Journal of Dynamic Systems, Measurement, and Control, 2011, 133(3): 024504-1–024504-7. |
| [6] | GHAZALI R, SAM Y M, RAHMAT M F, et al.Two-degree-of-freedom robust control for a non-minimum phase electro-hydraulic system[C]//Proceedings of 24th Chinese Control and Decision Conference.Piscataway, NJ:IEEE Press, 2012:1184-1190.http://cpfd.cnki.com.cn/Article/CPFDTOTAL-KZJC201205001227.htm |
| [7] | YANG L, YANG S, BURTON R. Modeling and robust discrete time sliding mode control design for a fluid power electro-hydraulic actuator system[J].IEEE/ASME Transactions on Mechatronics, 2013, 18(1): 1–10.DOI:10.1109/TMECH.2011.2160959 |
| [8] | LEE J M, KIM H M, PARK S H, et al.A position control of electro-hydraulic actuator systems using the adaptive control scheme[C]//Proceedings of the 7th Asian Control Conference.Piscataway, NJ:IEEE Press, 2009:21-26.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5276319&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Ficp.jsp%3Farnumber%3D5276319 |
| [9] | SEO I S, SHIN J M, HAN M K, et al.Adaptive position control scheme with neural networks for electro-hydrostatic actuator systems[C]//Proceedings of the 2010 IEEE International Conference on Mechatronics and Automation.Piscataway, NJ:IEEE Press, 2010:501-506.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=5588597&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D5588597 |
| [10] | LING T G, RAHMAT M F, HUSAIN A R.ANFIS modeling and direct ANFIS inverse control of an electro-hydraulic actuator system[C]//Proceedings of 8th Conference on Industrial Electronics and Applications.Piscataway, NJ:IEEE Press, 2013:370-375.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=6566397&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D6566397 |
| [11] | AHN K K, TRUONG D Q, SOO Y H.Self-tuning fuzzy PID control for hydraulic load simulator[C]//Proceedings of IEEE International Conference on Control, Automation and Systems.Piscataway, NJ:IEEE Press, 2007:2098-2102.http://ieeexplore.ieee.org/xpl/login.jsp?tp=&arnumber=4406935&url=http%3A%2F%2Fieeexplore.ieee.org%2Fxpls%2Fabs_all.jsp%3Farnumber%3D4406935 |
| [12] | XU Z, RAHMAN M F.Direct torque and flux control of an IPM synchronous motor using variable structure control approach[C]//The 30th Annual Conference of the IEEE Industrial Electronic Society. Piscataway, NJ:IEEE Press, 2004:2733-2738.https://www.researchgate.net/publication/3281338_Direct_Torque_and_Flux_Regulation_of_an_IPM_Synchronous_Motor_Drive_Using_Variable_Structure_Control_Approach |
| [13] | HA Q P, NGUYEN Q H, RYE D C. Fuzzy sliding-mode controllers with applications[J].IEEE Transactions on Industrial Electronics, 2001, 48(1): 38–46.DOI:10.1109/41.904548 |
| [14] | 康荣杰, 焦宗夏, JEANC M, 等. 电动静液作动器非线性框图建模与鲁棒控制方法[J].航空学报, 2009, 30(3): 518–525.KANG R J, JIAO Z X, JEAN C M, et al. Nonlinear block diagram model and robust control of electro-hydrostatic actuator[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(3): 518–525.(in Chinese) |
| [15] | CHINNIAH Y A.Fault detection in the electrohydraulic actuator using extended Kalman filter[D].Saskatoon:University of Saskatchewan, 2004:170-183. |
| [16] | HEY Y, YANM D. Nonlinear control theory and application[M].Xi'an: Electronic Science and Technology University Press, 2007: 115-119. |
| [17] | 李殿璞. 非线性控制系统理论基础[M].北京: 清华大学出版社, 2014: 188-215.LI D P. Theoretical basis of nonlinear control system[M].Beijing: Tsinghua University Press, 2014: 188-215.(in Chinese) |
| [18] | 于长官. 现代控制理论及应用[M].哈尔滨: 哈尔滨工业大学出版社, 2005: 170-176.YU C G. Modern control theory and application[M].Harbin: Harbin Institute of Technology Press, 2005: 170-176.(in Chinese) |
