随着信息技术的飞速发展和应用需求的不断扩展，现代嵌入式实时系统所承载功能的规模和复杂性呈现爆发式增长。为了适应日益庞大且复杂的系统功能需求，同时满足嵌入式实时系统对本身尺寸、重量和功率(Size, Weight and Power, SWaP)等多方面的限制，在统一的共享资源平台上整合多种不同系统功能已经成为当前嵌入式实时系统的发展趋势^[1]。而多核处理器技术的诞生及其迅速发展，在极大程度提升处理器性能的同时，也为实时系统的综合集成化设计提供了硬件平台支持。
然而，不同功能应用对系统的重要性不一样，相应地其认证需求也有区别，比如安全关键应用需要经过权威认证机构(Certification Authorities, CA)的严格检验，而非关键应用的正确性保障一般由设计者提供。功能应用的关键性级别越高，认证时所作假设越趋严格，以计算任务的最坏情况执行时间(Worst Case Execution Time, WCET)为例，CA得出的WCET估计值可能远远大于任务正常情况下的执行时间。对于这种不同关键性功能共存的“混合关键性系统”(Mixed-Criticality System, MCS)，实时调度和可信性认证等问题更为复杂和困难，如果按照保守的设计准则采用传统的经典调度理论，会造成不恰当的资源浪费。如何在满足不同关键性功能认证需求的同时提高资源利用率对混合关键性系统的设计与应用至关重要，也为实时系统理论研究提出了新的挑战^[2]。
Vestal^[3]最先提出了混合关键性系统中的实时任务调度问题，假设每个任务具有多个最坏情况执行时间并引入了混合关键性偶发任务模型。之后，大量的研究工作投入到混合关键性系统调度问题中，并且涌现出了很多单处理器任务调度算法^[3-10]。其中，Baruah等^[5]提出的最早虚拟截止期优先(Earliest Deadline First by Virtual Deadline，EDF-VD)算法，是经典EDF算法在混合关键性系统中的适应性扩展，其特点是可通过对系统资源利用率的计算来进行任务可调度性判定，时间复杂度低，便于实现在线分析。
针对多处理器平台中的混合关键性调度问题，Mollison等^[11]提出了基于关键性单调优先级分配的分层调度算法，按照任务的关键性级别将任务划分到不同分区。文献^[12]研究了基于固定优先级调度算法的划分调度问题，对比分析了不同任务划分策略对调度性能的影响。而文献^[13]研究了基于动态优先级调度算法的划分调度问题，允许系统在关键性模式切换时对实时任务集进行重新划分。Pathan^[14]将传统(非混合关键性)的全局固定优先级调度算法扩展到混合关键性系统中，提出了基于最坏响应时间的可调度性分析方法。Li和Baruah^[15-16]等研究了前述EDF-VD算法在多处理器平台中的扩展，分别提出基于EDF-VD的全局调度算法和划分调度算法。
值得注意的是，文献^[15]中混合关键性全局调度算法是适用于单处理器混合关键性任务调度的EDF-VD算法^[5]和传统(非混合关键)任务全局调度算法fixed-priority and Earliest Deadline First ( fpEDF )^[17]的结合，为了便于表述，将其记为fpEDF-VD。利用fpEDF算法基于资源利用率的可调度性条件，Li和Baruah^[15]给出了fpEDF-VD算法的两种可调度性判定方法。然而，研究发现该方法不能有效地判定系统可调度性，且文献^[15]中实验结果存在差错。针对这种缺陷及局限性，本文通过函数图像分析研究不同关键性级别的系统可调度性需求，在此基础上提出一种更精确的基于资源利用率的可调度性判定方法，并将其与已有方法进行了比较分析。
1 系统模型与定义 本节给出混合关键性实时任务系统模型的形式化定义，并阐述相关的基本术语和概念。
1.1 混合关键性系统 设定多处理器平台由m个单位速率的同构处理器组成，记为Π={π_i|1≤i≤m}。混合关键性任务系统定义为由一组有限数量且相互独立的混合关键性偶发实时任务构成的集合Γ={τ_i|1≤i≤n}，其中，每个任务都将产生任意可能次序的无限数量混合关键性作业序列。假设任务具有隐式截止期，可抢占执行。
混合关键性偶发任务模型是对传统偶发任务模型的一般化扩展，每个任务τ_i由一个四元组(T_i, D_i, ξ_i, C_i)描述，其中各元素的具体含义如下：
1) T_i∈N⁺表示任意两个连续释放作业间的最小时间间隔，也称任务周期。
2) D_i∈N⁺为任务相对截止期限，满足D_i=T_i。
3) ξ_i∈{1, 2, …, K}表示任务的既定关键性级别，约定ξ_i值越大任务的关键性级别越高，其中K为系统中关键性级别的最大值。
4) C_i表示任务在不同关键性级别下的WCET，是一个大小为K的向量，C_i(l)为关键性级别l对应的WCET，满足C_i(l)≤C_i(l+1) 且?l>ξ_i, C_i(l)=C_i(ξ_i)。
1.2 系统运行时行为及可调度性 WCET是任务执行时间的保守上限，任务释放的作业的准确执行时间只有在其运行完成时才能通过系统运行时监视功能获知，进而确定系统当前的运行关键性级别。假定系统不会经历错误运行时行为，即任何作业J_i^k的实际执行时间δ_i^k都不会超过C_i(K)，定义系统运行时行为的关键性级别λ为

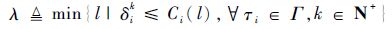(1)

式中：Γ为混合关键任务系统。
混合关键性系统的调度正确性具有多重认证需求，即对每个关键性级别都要进行独立的运行时可调度性验证。基于以上原则，引入混合关键性任务系统可调度性定义。
定义1 给定一种调度算法，混合关键性任务系统Γ可调度的充分必要条件是：对于任意可能的系统运行时关键性级别λ(1≤λ≤K)，系统中所有既定关键性级别高于或等于λ的任务释放的作业都在截止期之前执行完成。
上述定义意味着设计者只须保证系统中所有既定关键性级别高于或等于当前系统运行时关键性级别λ的任务释放的作业都满足其截止期限，而不必关心既定关键性级别低于系统运行时关键性级别λ的任务的执行情况。这里假设当系统运行时关键性级别从λ提升到λ+1时，所有既定关键性级别低于λ+1的任务直接被放弃执行。
1.3 系统处理器利用率 任务的处理器利用率定义为其WCET与周期的比值；而系统的处理器利用率则定义为系统中所有任务的处理器利用率的总和。由于混合关键性系统中每个任务的WCET与系统运行时关键性级别有关，因此需要考虑不同关键性级别下的处理器利用率。对于任务τ_i，当系统处于λ关键性级别时，其相应处理器利用率定义为

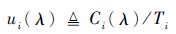(2)

如1.2节所述，混合关键性系统调度过程中，只有既定关键性级别高于或等于系统运行时关键性级别的任务才能获得执行。即系统在不同关键性级别下执行的任务集不同，相应地系统处理器利用率也会不同。类似地，定义U_x^y为系统关键性级别为y时，既定关键性级别等于x的任务子集的处理器利用率总和：

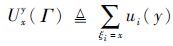(3)

为了简化系统的描述和算法分析，本文只研究双关键性系统模型即设定K=2，并分别用L和H表示低和高关键性级别，且仅考虑系统运行时关键性级别提升的情况。多关键性级别以及运行时关键性级别下降的情况留待以后讨论。
2 调度算法描述 2.1 fpEDF算法 传统任务全局调度算法fpEDF是在同构多处理器平台上的Global EDF算法^[18]的改进版本，其结合固定优先级FP和最早截止期优先EDF两种算法的优势，针对不同负载任务采用不同优先级分配策略，从而提高系统的可调度性。具体来说，处理器利用率最大的前m－1个任务中利用率大于0.5的任务所释放的作业被赋予最高优先级，其余任务释放的作业按传统EDF赋予优先级^[17]。
假设传统偶发任务υ_i用二元组(周期T_i, 最坏情况执行时间C_i)表征，且每个任务的相对截止期限都等于各自的周期。针对fpEDF算法，Baruah^[17]提出了一种简单的基于处理器利用率的充分可调度性判定条件。
定理1 ^[17] 传统任务系统Λ={υ_i|1≤i≤n}在单位速率同构多处理器平台Π={π_i|1≤i≤m}上使用fpEDF算法可正确调度的充分条件是系统处理器利用率满足：

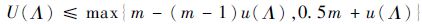(4)

式中:为系统中所有任务的利用率总和；为系统中单个任务的最大利用率。
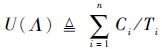
2.2 混合关键性全局调度算法fpEDF-VD 根据系统运行时的不同关键性级别，单处理器混合关键性调度算法EDF-VD为任务设定不同的虚拟截止期限，并按照传统EDF对任务进行实时调度。特别地，当系统运行在低关键性级别时，对混合关键性任务τ_i，如果ξ_i=H，则其虚拟相对截止期为；当系统切换到高关键性级别时，如果ξ_i=H，则τ_i的虚拟相对截止期为被放弃执行。其中x∈(0, 1) 为虚拟相对截止期调整参数。
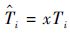
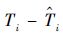
采用fpEDF算法的优先级赋予规则，混合关键性全局调度算法fpEDF-VD将上述EDF-VD的基本原理扩展到多处理器平台，其调度机制具体描述如下：
1) 在系统运行前的预处理阶段，基于处理器利用率判断系统可调度性(可调度性判定方法在3.4节给出)：若系统可调度，计算虚拟相对截止期调整参数x；否则，返回fpEDF-VD算法不能成功调度系统。
2) 系统初始时为低关键性级别，即λ=L。
① 低关键性任务释放的作业的虚拟相对截止期为T_i，高关键性任务释放的作业的虚拟相对截止期为_i=xT_i。
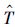
② 依据全局调度算法fpEDF赋予作业优先级并选择优先级最高的作业执行。
③ 若任意高关键性任务τ_i释放的一个作业执行C_i(L)单位时间后仍未完成，则系统切换到高关键性级别。
3) 一旦系统处于高关键性级别，即λ=H。
① 放弃所有低关键性级别任务释放的作业，包括当前活动的作业。
② 高关键性任务当前活动作业的截止期在原来的基础上扩大T_i－_i，新释放的作业的虚拟相对截止期为T_i－_i。
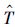
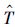
③ 依据全局调度算法fpEDF赋予作业优先级并选择优先级最高的作业执行。
3 可调度性分析 与EDF-VD算法类似，采用fpEDF-VD算法的系统可调度性取决于预处理阶段能否找到合适的虚拟相对截止期调整参数x，使系统运行在不同关键性级别时均能满足相应任务集的截止期要求。显而易见，调整参数x越小，低关键性级别下任务的虚拟相对截止期越紧迫，系统可调度性越难保证；相反地，调整参数x越大，高关键性级别下任务的虚拟相对截止期越紧迫，系统可调度性越难保证。针对fpEDF-VD算法，综合分析系统在不同关键性级别下的可调度性需求，本节给出一种新的改进的基于处理器利用率的混合关键性系统可调度性判定方法。
3.1 fpEDF算法可调度区域 依据定理1中传统任务系统可调度条件，图 1描述了基于处理器利用率的系统可调度区域，其中横轴表示单个任务的最大利用率u，纵轴表示系统的总利用率U。可调度区域Rgn定义为：折线段XYZW以及XYZW与横轴、纵轴构成的平面区域。这意味着，对于传统任务系统Λ，如果其处理器利用率对应的点(u(Λ), U(Λ))位于可调度区域Rgn内，则fpEDF算法可以成功调度该系统。

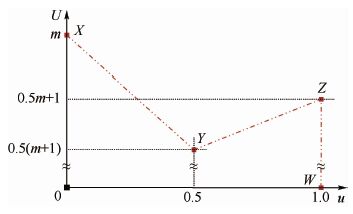图 1 基于利用率的可调度区域 Fig. 1 Utilization-based schedulability region

图选项

3.2 低关键性系统行为可调度条件 依据fpEDF-VD调度算法，系统在低关键性级别可调度意味着所有任务都能满足调整后的截止期要求。考虑到_i≤T_i以及fpEDF调度的可延展性^[19]，上述要求成立的一个充分条件是fpEDF算法可以在m个单位速率同构处理器上成功调度传统任务系统Γ^L，其定义如下：

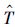
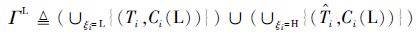(5)

对于式(5) 定义的传统任务系统Γ^L，所有任务的利用率总和为

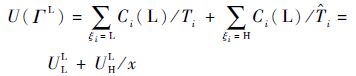(6)

单个任务的最大利用率为

(7)

式中：表示系统在低关键性级别下单个低关键性任务的最大利用率；u_H^L=max{u_i(L)|ξ_i=H}表示系统在低关键性级别下单个高关键性任务的最大利用率。为保证每个任务的利用率都不大于1，从式(7) 可知，调整参数x应满足x≥u_H^L。
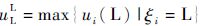
根据以上定义，传统任务系统Γ^L的具体配置取决于调整参数x，相应地，U(Γ^L)和u(Γ^L)都可看作是参数x的一元函数，更进一步地也可以将U(Γ^L)表示为u(Γ^L)的函数，其中u(Γ^L)的定义范围由参数x确定。基于上述分析，图 2中的折线段ABC描述了以u(Γ^L)为自变量的函数U(Γ^L)的图像，也即系统总利用率和单个任务最大利用率确定的点P(u(Γ^L), U(Γ^L))随参数x的变化趋势。
1) u^L_L>u_H^L：当x∈(u_H^L/u_L^L, 1) 时，则有u(Γ^L)与参数x无关，即u(Γ^L)=u_L^L，对应线段BA；当x∈[u_H^L, u_H^L/u_L^L]时，依据式(6) 和式(7) 可知U(Γ^L)为u(Γ^L)的一次函数，即U(Γ^L)=ku(Γ^L)+b，其中k=U_H^L/u_H^L≥1，b=U_L^L，对应线段CB。
2) u_L^L≤u_H^L：对?x∈[u_H^L, 1) 有u(Γ^L)=u_H^L/x∈[u_H^L, 1]，同1) 类似，U(Γ^L)为u(Γ^L)的一次函数，对应线段CB。

图 2 低关键性级别可调度性与参数x关系 Fig. 2 Relationship between low-criticality schedulability and parameter x

图选项

考虑到参数x的取值决定点P(u(Γ^L), U(Γ^L))在折线段ABC上的位置，结合3.1节中系统可调度区域Rgn的定义，可以得到如下的低关键性系统行为可调度充分条件。
定理2 在折线段ABC上，若调整参数x使得其对应点P(u(Γ^L), U(Γ^L))位于可调度区域Rgn内，则fpEDF-VD算法保证混合关键系统Γ的低关键性级别行为可调度。
3.3 高关键性系统行为可调度条件 依据fpEDF-VD调度算法，系统在高关键性级别下只须保证高关键性任务释放的作业的截止期要求。对于关键性级别提升时正活动的高关键性任务τ_i释放的作业，其虚拟截止期限和实际截止期限之间的间隔为T_i－_i，未完成部分需要的执行时间不大于C_i(H)；对于关键性级别提升后高关键性任务τ_i释放的作业，需要在相对截止期限T_i－_i之前执行C_i(H)单位时间。考虑到T_i－_i≤T_i以及fpEDF调度的可延展性^[19]，同样地，高关键性系统行为可调度的一个充分条件为fpEDF算法在m个单位速率同构处理器上成功调度传统任务系统Γ^H，其定义如下：

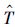
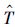
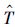
(8)

对于式(8) 定义的传统任务系统Γ^H，所有任务的利用率总和为

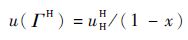(9)

单个任务的最大利用率为

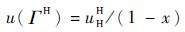(10)

式中：u_H^H=max{u_i(H)|ξ_i=H}表示系统在高关键性级别下单个高关键性任务的最大利用率。为保证每个任务的利用率都不大于1，从式(10) 可知，调整参数x应满足x≤(1－u_H^H)。
与传统任务系统Γ^L类似，Γ^H的具体配置同样取决于调整参数x，相应地，U(Γ^H)和u(Γ^H)都可看作是参数x的一元函数，更进一步地，也可以将U(Γ^H)表示为u(Γ^H)的函数，其中u(Γ^H)的定义范围由参数x确定。基于上述分析，图 3中的线段DE描述了以u(Γ^H)为自变量的函数U(Γ^H)的图像，也即系统总利用率和任务最大利用率确定的点Q(u(Γ^H), U(Γ^H))随参数x的变化趋势：对?x∈(0, 1－u_H^H］有u(Γ^H)∈[u_H^H, 1) ，依据式(9) 和式(10) 可知U(Γ^H)为u(Γ^H)的一次函数，即U(Γ^H)=ku(Γ^H)，k=U_H^H/u_H^H≥1，对应线段DE。

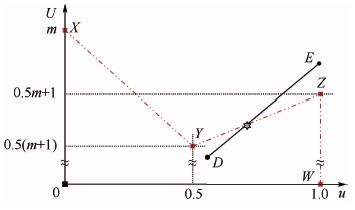图 3 高关键性级别可调度性与参数x关系 Fig. 3 Relationship between high-criticality schedulability and parameter x

图选项

考虑到参数x的取值决定点Q(u(Γ^H), U(Γ^H))在折线段DE上的位置，结合3.1节中系统可调度区域Rgn的定义，可以得到如下的高关键性系统行为可调度充分条件。
定理3 在线段DE上，若调整参数x使得其对应的点Q(u(Γ^H), U(Γ^H))位于可调度区域Rgn内，则fpEDF-VD算法保证混合关键系统Γ的高关键性级别行为可调度。
3.4 改进的系统可调度性判定方法 如前所述，调整参数x越小，低关键性级别系统可调度性越难保证。定理2给出了混合关键性系统Γ的低关键性级别行为可调度要求，值得注意的是，u(Γ^L)和U(Γ^L)都是调整参数x的单调递减函数。因此，折线段ABC与可调度区域边界XYZW的交点对应的x值即为其可行最小值x₁。同理，调整参数x越大，高关键性级别系统可调度性越难保证。定理3给出混合关键性系统Γ的高关键性级别行为可调度要求，其中u(Γ^H)和U(Γ^H)都是调整参数x的单调递增函数。因此，折线段DE与XYZW的交点对应的x值即为其可行最大值x₂。
综合上述不同关键性级别的系统行为可调度性对调整参数x的要求，图 4给出fpEDF-VD算法的可调度性判定方法GLOBAL-MINMAX。其中Step 1采用最坏情况资源预留方法初步判断系统可调度性；Step 2对应低关键性级别系统可调度性要求，即?x₁且x≥x₁；Step 3对应高关键性级别系统可调度性要求，即?x₂且x≤x₂；Step 4给出混合关键性系统可调度条件，即x₁≤x₂。

图 4 fpEDF-VD算法可调度性判定方法 Fig. 4 Schedulability testing approach for fpEDF-VD algorithm

图选项

3.5 可调度性判定方法比较 与文献^[15]中给出的混合关键性系统可调度性判定方法GLOBAL和GLOBAL-PRAGMATIC相同，GLOBAL-MINMAX也采用最坏情况资源预留方法初步判断系统可调度性，并基于定理1中传统系统可调度条件判断是否存在可行的虚拟相对截止期调整参数。然而，GLOBAL和GLOBAL-PRAGMATIC方法仅测试有限的调整参数候选值，而本文提出的GLOBAL-MINMAX能准确地计算可行调整参数的确切范围。也就是说，对于给定的混合关键性任务系统，如果GLOBAL或GLOBAL-PRAGMATIC可以找到可行的虚拟截止期调整参数x，那么根据GLOBAL-MINMAX必定存在可行调整参数的最小值x₁和最大值x₂，且满足x₁≤x≤x₂；反之不成立。
推论1 混合关键性任务系统可调度性判定方法GLOBAL-MINMAX严格优于GLOBAL和GLOBAL-PRAGMATIC。
此外，需要指出的是，虽然GLOBAL仅测试一个调整参数候选值而GLOBAL-PRAGMATIC测试多个候选值，但是GLOBAL-PRAGMATIC的可调度性能不一定优于GLOBAL。本文将在仿真实验中对此进一步说明。
为了方便理解，给出表 1中所示的双处理器平台上的混合关键性任务集实例，分别采用上述3种方法进行可调度性判定。依据GLOBAL方法，调整参数候选值x=0.231，任务集可调度；依据GLOBAL-PRAGMATIC方法，调整参数候选值x∈{0.10, 0.12, 0.16, 0.18}，但任务集不可调度；依据GLOBAL-MINMAX方法，调整参数候选值x∈[0.181, 0.550]，任务集可调度。
表 1 混合关键性任务集实例(m=2) Table 1 An example of mixed-criticality task set (m=2)

任务	Ti=Di	ξi	Ci(L)	Ci(H)
τ1	100	L	17	17
τ2	100	L	68	68
τ3	100	H	6	45
τ4	100	H	9	42

表选项






4 实验仿真与结果分析 针对隐式截止期双关键性偶发任务模型和单位速率同构多处理器平台，本节采用随机生成任务集可调度比率(即接受率)作为评价指标，通过仿真实验对比分析混合关键性全局调度算法fpEDF-VD的不同可调度性判定方法的有效性。
1) GLOBAL-MINMAX：本文提出的可调度性判定方法，如图 4所示。
2) GLOBAL：文献^[15]中描述的基础可调度性判定方法。
3) GLOBAL-PRAGMATIC：文献^[15]中描述的改进后可调度性判定方法。
4) REGULAR-EDF：最坏情况资源预留方法，使用Global EDF算法调度传统任务系统∪_i{(T_i, C_i(ξ_i))}，并依据定理1判定系统可调度性。
4.1 随机任务集生成方法 采用与文献^[15]类似的混合关键性随机任务集生成方法，任务集的生成主要受以下参数控制：
1) 期望的任务集利用率U_G。
2) 随机任务为高关键性任务的概率P。
3) 任务在高关键性下处理器利用率的最小值U₁和最大值U₂。
4) 任务在高关键性级别下的处理器利用率与低关键性级别下的处理器利用率的最小比例R₁和最大比例R₂。
图 5描述了任务集生成方法：初始时任务集被设置为空集，然后逐次将随机生成的新任务添加到任务集中，直到任务集的利用率满足max(U_L^L+U_H^L, U_H^H)=U_G。若生成的随机任务集中所有任务的关键性级别均相同，则舍弃整个任务集并从空集开始重新生成任务集。

图 5 随机任务集生成方法 Fig. 5 Random task sets generation method

图选项

任务集中每个随机任务根据如下步骤产生:
1) 任务关键性级别ξ_i在H和L间随机选择，满足生成高关键性任务的概率为P。
2) 高关键性级别下任务的处理器利用率u_i(H)在区间[U₁, U₂]上均匀分布。
3) 低关键性级别下任务的处理器利用率u_i(L)=u_i(H)/r，其中比率r的取值在区间[R₁, R₂]上均匀分布。
4.2 结果及分析 图 6给出了在不同处理器平台和任务生成参数配置下，上述4种可调度性判定方法的随机任务集可调度比率的对比结果。其中，横轴表示规范化任务集利用率U_G/m，纵轴接受率表示成功调度的任务集个数与生成的总任务集个数的百分比。对于不同的任务集利用率水平，图中每个数据点代表基于10 000个随机生成任务集的统计结果。

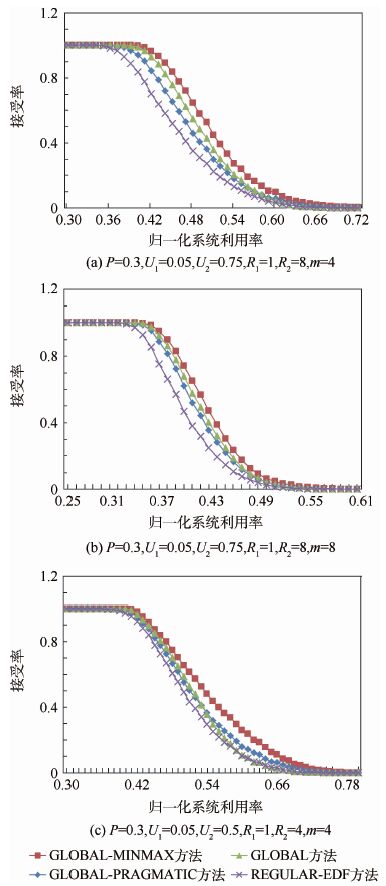图 6 不同任务集生成参数下4种方法的接受率比较 Fig. 6 Acceptance ratio comparison of four approaches with different parameters of task set generation

图选项

从图 6中可以发现，本文提出的可调度性判定方法GLOBAL-MINMAX的可调度性能优于文献^[15]中的方法，在不同处理器平台或不同任务生成参数配置下，均具有更高的接受率。例如，在图 6(c)中，当任务集利用率U_G/m=0.5时，上述4种可调度性判定方法的接受率从高到低分别为：0.526、0.431、0.360和0.274。
此外，从图 6(c)中可以明显看出：有些条件下GLOBAL-PRAGMATIC方法的可调度性能优于GLOBAL方法，而有些情况下的结果却相反。这与前面的理论分析结论一致。且经过与文献^[15]作者交流，证实其实验分析不够全面，给出的统计结果是基于错误的前提假设，即GLOBAL-PRAGMATIC方法严格优于GLOBAL方法。
5 结论 本文研究多处理器平台混合关键性全局调度算法fpEDF-VD的可调度性分析问题，在分析现有可调度性判定方法的缺陷及局限性的基础上，完成了以下工作：
1) 利用函数图像分析提出改进的可调度判定方法GLOBAL-MINMAX。
2) 通过实例分析和对比验证了该方法的正确性和高效性。
3) 实验结果与理论分析一致，表明GLOBAL-MINMAX具有更优的可调度性能。

参考文献

[1]	BARHORST J,BELOTE T,BINNS P,et al.White paper:A research agenda for mixed-criticality systems:88ABW-2009-1383 [R].San Francisco:Cyber-Physical Systems Week,2009.
[2]	BARUAH S K,LI H,STOUGIE L.Towards the design of certifiable mixed-criticality systems[C]//Real-Time and Embedded Technology and Applications Symposium.Piscataway,NJ:IEEE Press,2010:13-22.
[3]	VESTAL S.Preemptive scheduling of multi-criticality systems with varying degrees of execution time assurance[C]//Real-Time Systems Symposium.Piscataway,NJ:IEEE Press,2007:239-243.
[4]	BARUAH S K,BURNS A,DAVIS R.Response-time analysis for mixed criticality systems[C]//Real-Time Systems Symposium.Piscataway,NJ:IEEE Press,2011:33-43.
[5]	BARUAH S K,BONIFACI V,D'ANGELO G,et al.Mixed-criticality scheduling of sporadic task systems[C]//European Symposium on Algorithms.Heidelberg:Springer Verlag,2011:555-566.
[6]	BARUAH S K,FOHLER G.Certification-cognizant time-triggered scheduling of mixed-criticality systems[C]//Real-Time Systems Symposium.Piscataway,NJ:IEEE Press,2011:3-12.
[7]	GUAN N,EKBERG P,STIGGE M,et al.Effective and efficient scheduling of certifiable mixed-criticality sporadic task systems[C]//Real-Time Systems Symposium.Piscataway,NJ:IEEE Press,2011:13-23.
[8]	BARUAH S K,BONIFACI V,D'ANGELO G,et al.The preemptive uniprocessor scheduling of mixed-criticality implicit-deadline sporadic task systems[C]//Proceedings of Euromicro Conference on Real-Time Systems.Piscataway,NJ:IEEE Press,2012:145-154.
[9]	PONTUS E,WANG Y.Bounding and shaping the demand of mixed-criticality sporadic tasks[C]//Proceedings of Euromicro Conference on Real-Time Systems.Piscataway,NJ:IEEE Press,2012:135-144.
[10]	PONTUS E, WANG Y. Bounding and shaping the demand of generalized mixed-criticality sporadic task systems[J].Real-Time Systems, 2014, 50(1): 48–86.DOI:10.1007/s11241-013-9187-z
[11]	MOLLISON M S,ERICKSON J P,ANDERSON J H,et al.Mixed-criticality real-time scheduling for multicore systems[C]//International Conference on Computer and Information Technology.Piscataway,NJ:IEEE Press,2010:1864-1871.
[12]	KELLY O R,AYDIN H,ZHAO B.On partitioned scheduling of fixed-priority mixed-criticality task sets[C]//International Conference on Trust Security and Privacy in Computing and Communications.Piscataway,NJ:IEEE Press,2011:1051-1059.
[13]	谷传才, 关楠, 于金铭, 等. 多处理器混合关键性系统中的划分调度策略[J].软件学报, 2014, 25(2): 284–297.GU C C, GUAN N, YU J M, et al. Partitioned scheduling policies on multi-processor mixed-criticality systems[J].Journal of Software, 2014, 25(2): 284–297.(in Chinese)
[14]	PATHAN R.Schedulability analysis of mixed-criticality systems on multiprocessors[C]//Proceedings of Euromicro Conference on Real-Time Systems.Piscataway,NJ:IEEE Press,2012:309-320.
[15]	LI H,BARUAH S K.Global mixed-criticality scheduling on multiprocessors[C]//Proceedings of Euromicro Conference on Real-Time Systems.Piscataway,NJ:IEEE Press,2012:166-175.
[16]	BARUAH S K, CHATTOPADHYAY B, LI H, et al. Mixed-criticality scheduling on multiprocessors[J].Real-Time Systems, 2014, 50(1): 142–177.DOI:10.1007/s11241-013-9184-2
[17]	BARUAH S K. Optimal utilization bounds for the fixed-priority scheduling of periodic task systems on identical multiprocessors[J].IEEE Transactions on Computers, 2004, 53(6): 781–784.DOI:10.1109/TC.2004.16
[18]	GOOSSENS J, FUNK S, BARUAH S K. Priority-driven scheduling of periodic task systems on multiprocessors[J].Real-time Systems, 2003, 25(2-3): 187–205.
[19]	BAKER T P,BARUAH S K.Sustainable multiprocessor scheduling of sporadic task systems[C]//Proceedings of Euromicro Conference on Real-Time Systems.Piscataway,NJ:IEEE Press,2009:141-150.