随着航空技术的发展,新型飞行器的机动能力显著提升,意味着对舵系统的动态性能要求越来越高,舵面受到的载荷力矩变化也愈加复杂,而传统的机械式和电液式负载模拟器性能缺陷日益明显[4]。随着电机驱动及控制技术的发展,以电机为驱动的EDLS得到了广泛的研究和应用[5]。EDLS是典型的被动式力矩加载系统,在加载过程中,舵机在位置控制指令下工作,而加载电机与其固连在一起,因此,由于惯量、摩擦、齿隙和弹性形变等因素,不可避免地产生加载电机与舵机运动不同步,产生多余力矩。多余力矩的存在严重影响加载的精度,降低加载系统的灵敏度和稳定性,故多余力矩的消除是保证EDLS性能的关键问题[4-5]。
目前,国内外诸多****对EDLS多余力矩的消除进行了研究,现有多余力矩消除主要从两个方面入手:①从驱动器选型及EDLS结构设计方面,尽量减小EDLS引入的转动惯量或改变轴系统刚度[6-7];②采用先进的控制策略对多余力矩补偿消除,是目前减小多余力矩的主要方式。现主要算法有舵机速度前馈补偿或位置前馈补偿法[4-5]、神经网络补偿法[8-10]、观测器补偿法[11]和迭代学习补偿法[12-13]等。文献[4]基于不变性原理分别引入舵机的速度和位置前馈来补偿多余力矩,其不足之处在于需要系统精确的逆模型;文献[9]提出了一种改进自适应学习率新型小脑模型(BOWA-CMAC)的复合控制策略,试图分析各个参数对系统的影响,采用图表法进行参数寻优;文献[10]提出采用非均匀量化思想对CMAC进行改进,但CMAC网络结构设计缺乏理论指导,推广和应用较为困难;文献[11]基于扰动观测的双回路控制方法,采用混合灵敏度优化的DOB方法设计鲁棒控制器;文献[12]提出一种将PID反馈控制与迭代补偿相结合的复合控制策略,简化了系统设计;文献[13]针对正弦负载的实验,提出幅值和相位修正的迭代学习控制策略,解决加载力矩跟踪精度和相位滞后问题。但上述研究中,力矩反馈回路中一般采用常规PID控制策略,尽管采用各种补偿控制策略,往往难以得到满意的控制效果。
分数阶控制自Oustaloup等[14]提出以来,得到了广泛研究和应用。与传统整数阶微积分相比,分数阶微积分更加细腻,且具有记忆功能和遗传特性。因此,分数阶控制具有更好的动态性能和鲁棒性[15]。目前,常用的分数阶控制器有分数阶PIλDμ控制[16]、分数阶滑模控制[17]和分数阶迭代学习控制[18-19]等。与整数阶控制器相比,分数阶控制器引入微分和积分两个可变自由度参数,使控制器设计更加灵活,如分数阶PIλDμ控制器,与整数阶PID控制器相比,微分阶次μ和积分阶次λ能够调整闭环系统的滞后和超前角度,从而在兼顾系统稳定性和动态性能的前提下提高稳态性能,达到控制性能要求。文献[15]提出一种分数阶PIλDμ参数整定方法,应用于两个相互耦合的存储系统;文献[16]给出离散分数阶PIλDμ的定义、整定、数字实现和应用;文献[18-19]针对分数阶系统提出P型和PD型分数阶迭代学习控制,并给出收敛性证明。
针对EDLS一类复杂的负载模拟问题,即正弦载荷和梯形波载荷,提出一种以分数阶PIλDμ控制器作为反馈控制、分数阶迭代学习控制器(Fractional Order Iterative Learning Control, FO-ILC)作为补偿控制的复合控制策略,将分数阶微积分理论应用到PID和迭代学习控制中,抑制EDLS中的多余力矩及各种非线性因素干扰,提高加载系统的动态性能和稳态精度,并进行实际系统加载实验验证本文方法的有效性。
1 EDLS结构和数学模型 1.1 EDLS结构 EDLS的系统结构如图 1所示。EDLS测试台主要由加载电机(永磁同步电机)、膜片型联轴器、力矩传感器、舵机位置传感器和舵机组成。永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有功率密度大、可靠性高和转矩动态性能好等诸多优点[12],因此,选择采用PMSM作为ELDS的驱动元件。加载电机通过膜片型联轴器与力矩传感器、舵机系统相连,膜片型联轴器具有零回转间隙、体积小等优点,避免引入齿隙等非线性因素。力矩传感器用来实时测量EDLS和舵机系统组成的轴系统上的负载力矩,舵机位置及电机位置的测量均采用光电编码器实现。
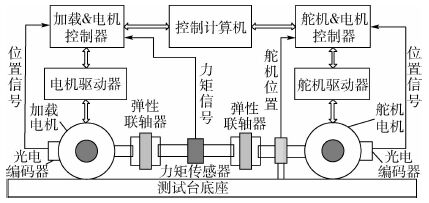 |
| 图 1 EDLS结构 Fig. 1 Structure of EDLS |
| 图选项 |
由图 1可以看出,EDLS系统与舵机系统通过联轴器刚性连接,EDLS在对舵机加载的同时又随之在一定角度内往复运动,舵机的运动会导致EDLS产生扰动力矩,即多余力矩[10-12]。
1.2 EDLS数学模型 为保证电机转矩的动态性能,PMSM采用直接转矩控制(Direct Torque Control, DTC)方式,其力矩传递函数为
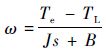 | (1) |
式中:Te为PMSM输出电磁转矩;J为整个轴系统的转动惯量;B为摩擦系数;TL为传感器测量的力矩值,也是负载力矩值;ω为加载PMSM的转速。
由于力矩传感器的转动惯量非常小,在其量程工作范围内,可认为是一个比例环节[13],即
 | (2) |
式中:KG为力矩传感器的刚度系数;θ为EDLS位置输出;θ1为舵机系统位置输出。
结合式(1) 和式(2) ,可得到EDLS的力矩传递函数为
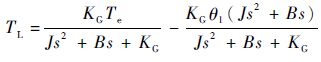 | (3) |
文献[9-10]所推导出的EDLS模型为3阶系统,而本文得到的是2阶模型,原因是文献[9-10]加载电机采用力矩电机或PMSM采用矢量控制方式,在EDLS模型推导过程中必须考虑电流环参数的设计,而DTC鲁棒性强,其控制性能不受参数的影响[20],此时可将转矩环认为是1的环节。与文献[9-10]中的EDLS模型相比,PMSM采用DTC方式建立的EDLS模型降低了模型阶次,减少控制器参数设计的数量。
2 控制器设计 2.1 分数阶PIλDμ控制器设计 EDLS系统工作时,被加载舵机和加载电机分别动作,舵机按照指令角度进行位置伺服控制,加载力矩信号是基于舵机位置和加载梯度进行设置给定。由式(2) 和式(3) 中可看出,负载力矩的形成由加载电机位置和舵机位置两个因素决定,即EDLS具有两个输入:①加载电机控制输入;②舵机实际角度,舵机实际角度输入可视为扰动输入。为有效抑制舵机位置输入的干扰,一般负载模拟器控制系统采用位置反馈作为内环、力矩环作为外环的闭环结构形式[13],如图 2所示。图中:Te*为加载电机控制输入;Gθ(s)为位置控制器传递函数;GT(s)为力矩控制器传递函数;DTC控制环增益为1;TL*为给定力矩;Uin(θ*)为力矩控制器的输出,即为位置控制器的输入。Gθ(s)和GT(s)通常采用经典整数阶PID控制器实现,而分数阶PIλDμ控制器是整数阶PID控制器的广义形式,增加了两个可调节参数,参数整定范围变大,控制能力更加灵活,控制效果更佳。整数阶PID控制器和分数阶PIλDμ控制器的取值范围如图 3所示。
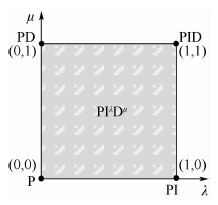 |
| 图 3 整数阶PID控制器和分数阶PIλDμ控制器示意图 Fig. 3 Schematic diagram of integer order PID control and fractional order PIλDμ control |
| 图选项 |
图 3中,经典P、PI、PD和PID仅表示4个离散的点,分数阶PIλDμ为整个阴影部分,即分数阶PIλDμ控制器的积分阶次λ和微分阶次μ取不同的值,也可演变成整数阶P、PD、PI和PID等控制器。因此,分数阶PIλDμ控制器更具有一般形式。
 |
| 图 2 EDLS控制结构 Fig. 2 Control structure of EDLS |
| 图选项 |
设计分数阶PIλDμ控制器的传递函数为
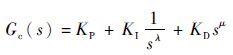 | (4) |
式中:KP为比例增益;KI为积分常数;KD为微分常数。
图 2中位置闭环控制器Gθ(s)和力矩闭环控制器GT(s)均采用式(4) 所设计的控制器形式实现,分数阶PIλDμ控制器中各个参数的设计和整定原理采用幅值裕量法及相位裕量法,具体整定原理详见参考文献[21-22]。
2.2 分数阶迭代学习控制器设计 一般为了验证舵机的性能,常用的负载模拟力矩有正弦载荷和梯形波载荷[12],正弦载荷用来测试舵机的控制性能,梯形波载荷用来测试载荷突变的恶劣环境下,舵机的功能是否正常。而正弦和梯形波载荷具有周期重复性,迭代学习控制适合具有重复运动性质的被控对象,以系统的实际输出与给定轨迹的偏差信号修正不理想的控制信号,提高系统的跟踪性能,实现有限时间上的完全跟踪任务。与常规迭代学习控制相比,分数阶迭代学习控制能够获得更好的收敛速度和更高的控制精度[18-19]。
对于系统式(3) ,设计采用分数阶PDγ型迭代学习控制器,其形式为
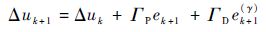 | (5) |
式中:ΓP和ΓD分别为迭代学习的比例增益和分数阶微分增益;Δuk和Δuk+1分别为上一个迭代学习周期和当前迭代学习周期的迭代补偿控制量;ek+1(γ)为当前迭代学习周期误差ek+1的γ阶微分。
式(5) 在频域下的传递函数为
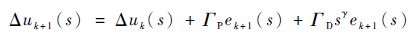 | (6) |
则基于分数阶迭代学习控制的复合控制框图如图 4所示。
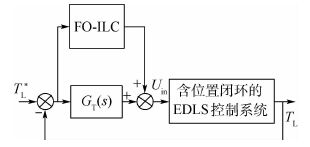 |
| 图 4 基于分数阶迭代学习控制的EDLS控制结构 Fig. 4 Control structure of EDLS based on FO-ILC |
| 图选项 |
根据图 2和式(3) ,可得到含有位置闭环EDLS控制系统的开环传递函数为
 | (7) |
式中:Uin为力矩闭环的输出,其物理意义为位置角度的给定。
将式(7) 写成标准形式为
 | (8) |
式中:
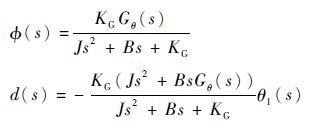 |
其中:d(s)为EDLS的周期性扰动输入。从d(s)的表达式中可以看出,设计合适的控制器Gθ(s),能够对舵机位置扰动进行抑制,即d(s)≤dmax。
定理1 将分数阶PD型迭代学习控制律式(6) 施加于EDLS系统式(8) 中,系统中周期性干扰满足d(s)≤dmax,选取适当的学习增益ΓP和ΓD,若满足谱半径
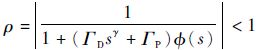
证明取系统式(8) 的期望输入为Yd(s),Yk(s)为第k次运行后输出,ek(s)为学习误差,Δuk(s)为第k次的控制输入,k次修正后的控制为Δuk+1(s),则第k+1次时,系统控制误差为
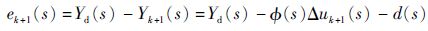 | (9) |
将控制律式(6) 代入式(9) ,整理可得
 | (10) |
将式(10) 进行整理可得
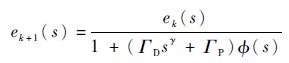 | (11) |
对式(11) 两边取绝对值可得
 | (12) |
递推可得
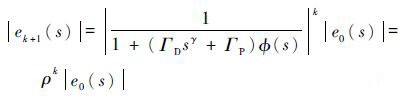 | (13) |
由于
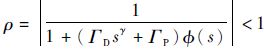
注1 由定理1可知,理论上仅采用分数阶迭代学习控制方法就能够实现对EDLS的高精度控制,因此,图 4中的位置闭环控制和力矩闭环控制的作用是提高系统的收敛速度,减少分数阶迭代学习的学习周期。
2.3 分数阶微积分的实现 目前精确计算分数阶微积分的值较为困难,一般利用有限的整数阶微积分进行数值逼近,主要有傅里叶级数法、Grunwald-Letnikov定义直接计算法、频域滤波算法和数字滤波算法。本文采用改进型Oustaloup方法进行分数阶微积分的数值计算,具体计算方式为[15-16]
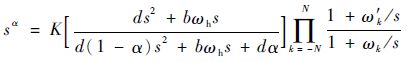 | (14) |
式中:N为正整数,2N+1为系统式(14) 的近似阶次,一般N取值为3;K=(ωbωh)α,ωh和ωb分别为截止频率的上限和下限,其值根据系统的控制周期或频率进行选取;b和d为引入的系数;α为微积分阶次;第k个零点ω′k和极点ωk分别为
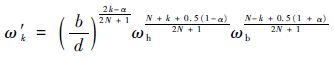 | (15) |
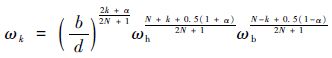 | (16) |
则分数阶微积分计算步骤如下:
1) 选定近似频率段范围(ωb, ωh)和阶次2N+1。
2) 根据微积分的阶次α,由式(15) 和式(16) 计算零点和极点,以及K值。
3) 根据式(14) 计算出近似化的有理传递函数。
式(14) 仅针对0 <α<1范围内的分数阶微分有效,当α>1,如微分阶次α=1.4,此时采用s1.4=ss0.4;当α<0,即使用分数阶积分时,如α=-0.4,此时用式s-0.4=s0.6/s代替计算。
3 验证实验 为验证本文所提方法的有效性,在自行研制的实验平台上进行力矩加载实验,实验平台如图 5所示。加载电机的驱动及DTC的实现采用ABB公司的ACS800伺服驱动控制器实现,位置闭环、力矩闭环和迭代学习控制采用DSP2812实现。
 |
| 图 5 EDLS实验平台 Fig. 5 Experimental platform of EDLS |
| 图选项 |
实验中,位置闭环采用分数阶PIλ控制,力矩闭环采用分数阶PIλDμ控制,分数阶迭代学习控制采用PDγ型控制,各控制器参数如下:位置闭环:Pθ=5.8,Iθ=0.35,λθ=0.9;力矩闭环:PT=2.7,IT=0.75,DT=0.001,λT=μT=0.9;迭代学习控制器:PILC=0.2,DILC=0.002,γ=0.8。分数阶微积分的计算相关参数为:N=3,ωb=0.001,ωh=1 000,b=10,d=9。
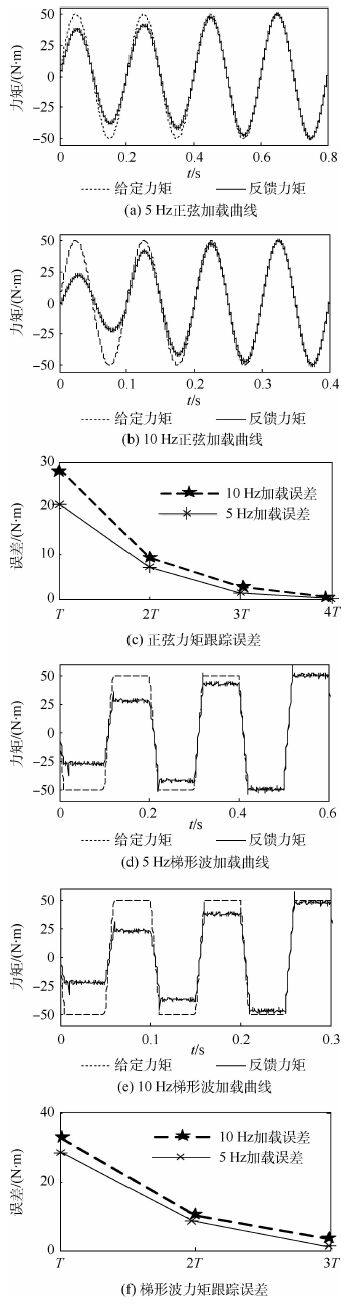
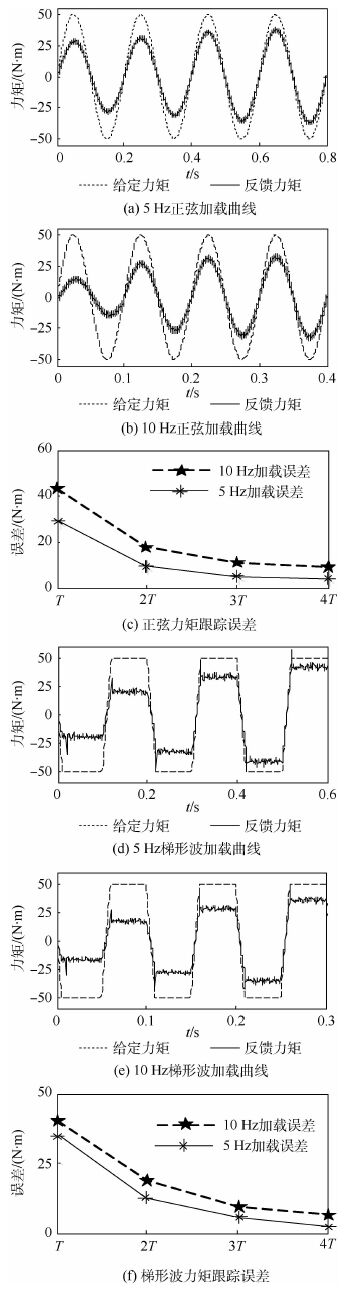
3.1 力矩加载实验 舵机按照正弦规律工作,工作幅值为10°,选择5 Hz和10 Hz两种频率为工作频率,加载力矩给定幅值为50 N·m,正弦载荷和梯形波载荷的频率与舵机工作频率相同,相位超前180°。为验证分数阶复合控制的有效性,分别对整数阶PID+整数阶ILC和分数阶PIλDμ+分数阶ILC两种控制方法进行对比。实验过程中运行数据暂时保存在DSP内部的RAM中,实验后通过DSP仿真器将存储的数据读出,然后用于MATLAB绘图。分数阶PIλDμ+分数阶ILC的实验结果如图 6所示,而整数阶PID+整数阶ILC的实验结果如图 7所示。
图 6、图 7中,力矩跟踪曲线结果中,迭代学习周期即为给定载荷的周期T。对于EDLS,采用每个正弦(梯形波)周期最大力矩加载误差的绝对值来评价力矩的跟踪性能。在分数阶PIλDμ+分数阶ILC的控制方式下,对正弦载荷30 N·m,5 Hz工况下,[0, T]时间范围内最大加载误差绝对值为20 N·m,而10 Hz时接近30 N·m;梯形波负载条件下,在[0, T]时间范围内,5 Hz和10 Hz的力矩误差分别为28 N·m和35 N·m,表明多余力矩随着舵机运行频率的增加而变大,而无论是5 Hz,还是10 Hz的期望载荷,随着迭代学习控制器的补偿,EDLS力矩输出误差逐渐减小,当运行到[2T, 3T]控制周期时,加载力矩误差的最大值为4 N·m,幅值误差为8%,当达到[3T, 4T]时,力矩跟踪误差收敛到1 N·m以内,力矩跟踪误差达到2%,跟踪效果大大提升。
 |
| 图 6 分数阶复合控制结果 Fig. 6 Results of fractional order composite control |
| 图选项 |
 |
| 图 7 整数阶复合控制结果 Fig. 7 Results of integer order composite control |
| 图选项 |
从图 7整数阶PID+整数阶ILC控制方式下的实验结果可以看出,在正弦载荷30 N·m,5 Hz工况下,[0, T]时间范围内整数阶PID+整数阶ILC控制方法下的最大加载误差绝对值为30 N·m,10 Hz条件下的力矩误差为45 N·m;梯形波负载条件下,在[0, T]时间范围内5 Hz和10 Hz的力矩误差分别为35 N·m和45 N·m。与本文方法相比,其在[0, T]时间范围内,无论是正弦负载还是梯形波负载,误差均大于本文方法的结果。在收敛时间方面,本文方法在[3T, 4T]范围内已达到较高精度,而整数阶PID+整数阶ILC的控制结果在[3T, 4T]仍存在较大误差。由上述结果分析可以看出,本文方法的收敛速度和控制精度均高于整数阶PID+整数阶ILC的控制方式。
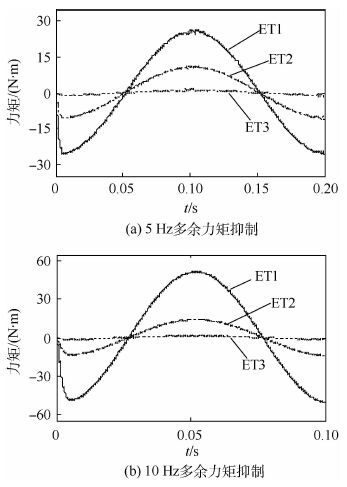
3.2 多余力矩抑制实验 多余力矩的测量一般是指EDLS开环给定力矩为零,舵机系统按照指定轨迹运行时,力矩传感器反馈的力矩值。因此,将EDLS系统开环给定0 N·m载荷,舵机在5 Hz、10 Hz两种频率,正弦幅值为10°。为比较不同控制器下的控制效果,将本文方法与文献[4-5]中舵机位置前馈补偿的控制方法进行对比,实验结果如图 8所示。图中:ET1为开环状态下的多余力矩曲线;ET2为舵机前馈补偿下的多余力矩曲线;ET3为本文方法在[3T, 4T]时的多余力矩曲线。
 |
| 图 8 多余力矩抑制效果对比 Fig. 8 Comparison of surplus torque suppression effect |
| 图选项 |
图 8中不同舵机频率和控制方法的多余力矩最大值对应如表 1所示,结果表明,在5 Hz和10 Hz条件下运行时,舵机位置前馈控制方式下的多余力矩的消除率分别为 56.6%、71.8%;而采用本文分数阶PIλDμ+分数阶ILC控制方式时,多余力矩的消除率分别达到97.8%、95.7%,抑制效果显著。
表 1 多余力矩抑制最大值 Table 1 Maximum values of surplus torque suppression
| 频率/Hz | ET1max/(N·m) | ET2max/(N·m) | ET3max/(N·m) |
| 5 | 28.5 | 12.37 | 0.62 |
| 10 | 54.7 | 15.45 | 2.34 |
表选项
4 结论 针对电动加载系统存在多余力矩等问题,提出一种分数阶PIλDμ+分数阶迭代学习控制的复合控制策略,并通过实验验证,得出以下结论:
1) 利用分数阶微积分的信息记忆特性,将分数阶PIλDμ引入到电动加载系统中,提高电动加载系统的动态性能和鲁棒性。
2) 针对具有周期性的力矩加载曲线,设计分数阶迭代学习控制器,并证明系统的收敛性,结果表明该方法能够有效抑制电动加载系统中存在的多余力矩。
3) 为降低系统模型建模复杂度和提高转矩的动态响应,内环采用直接转矩控制方式。
参考文献
| [1] | NAM Y, HONG S K. Force control system design for aerodynamic load simulator[J].Control Engineering Practice, 2002, 10(5): 549–558.DOI:10.1016/S0967-0661(02)00004-7 |
| [2] | YALLA S K, KAREEM A. Dynamic load simulator:Actuation strategies and applications[J].Journal of Engineering Mechanics, 2007, 133(8): 855–863.DOI:10.1061/(ASCE)0733-9399(2007)133:8(855) |
| [3] | 齐蓉, 林辉, 陈明. 被动式电动加载系统多余力的研究[J].控制与决策, 2006, 21(2): 225–228.QI R, LIN H, CHEN M. Research on surplus torque in passive electric loading system[J].Control and Design, 2006, 21(2): 225–228.(in Chinese) |
| [4] | 李成功, 靳红涛, 焦宗夏. 电动负载模拟器多余力矩产生机理及抑制[J].北京航空航天大学学报, 2006, 32(2): 204–208.LI C G, JIN H T, JIAO Z X. Mechanism and suppression of extraneous torque of motor driver load simulator[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(2): 204–208.(in Chinese) |
| [5] | 张立勋, 孟庆鑫, 刘庆和, 等. 位置同步补偿克服负载模拟器干扰力矩及提高系统频宽的理论与实验研究[J].宇航学报, 1997, 18(1): 121–124.ZHANG L X, MENG Q X, LIU Q H, et al. Experimental and theoretic study on eliminating the disturbance torque and widening the frequency band width of the load simulator using position synchro compensation[J].Journal of Astronautics, 1997, 18(1): 121–124.(in Chinese) |
| [6] | 齐蓉, 林辉. 弹翼电动加载系统多余力矩分析与消除[J].西北工业大学学报, 2005, 23(6): 759–763.QI R, LIN H. Analysis and elimination of surplus torque in missile wing electric loading system[J].Journal of Northwestern Polytechnical University, 2005, 23(6): 759–763.(in Chinese) |
| [7] | 王鑫, 冯冬竹. 引入弹簧杆的电动负载模拟器实验研究[J].电机与控制学报, 2012, 16(9): 91–94.WANG X, FENG D Z. Experimental research on DC load simulator test bed with elastic rod[J].Electric Machines and Control, 2012, 16(9): 91–94.(in Chinese) |
| [8] | 沈东凯, 华清, 王占林. 基于神经网络的电动加载系统[J].航空学报, 2002, 23(6): 525–529.SHEN D K, HUA Q, WANG Z L. Motor-driven load system based on neural networks[J].Acta Aeronautica et Astronautica Sinica, 2002, 23(6): 525–529.(in Chinese) |
| [9] | 杨波, 黄耀达, 台钰莹. 基于BOWA小脑模型的高精度稳定电动加载系统[J].航空学报, 2012, 33(4): 734–743.YANG B, HUANG Y D, TAI Y Y. High precision and stable electric loading system based on BOWA-CMAC[J].Acta Aeronautica et Astronautica Sinica, 2012, 33(4): 734–743.(in Chinese) |
| [10] | 杨波, 王哲. 新型小脑模型关联控制器复合控制在电动加载系统中的结构及算法[J].控制理论与应用, 2011, 28(6): 827–833.YANG B, WANG Z. Structure and algorithm of hybrid control in cerebella model articulation controller for electric loading system[J].Control Theory & Applications, 2011, 28(6): 827–833.(in Chinese) |
| [11] | 方强, 马杰, 毕运波, 等. 基于扰动观测器的电动负载模拟器控制系统设计[J].浙江大学学报(工学版), 2009, 43(11): 1958–1964.FANG Q, MA J, BI Y B, et al. Disturbance observer based controller design for electric dynamic load simulator[J].Journal of Zhejiang University(Engineering Science), 2009, 43(11): 1958–1964.(in Chinese) |
| [12] | 王明彦, 郭奔. 基于迭代学习控制的电动伺服负载模拟器[J].中国电机工程学报, 2003, 23(12): 123–126.WANG M Y, GUO B. Electric servo load simulator based on iterative learning control[J].Proceedings of the CSEE, 2003, 23(12): 123–126.(in Chinese) |
| [13] | 牛国臣, 王巍, 宗光华. 基于迭代学习的电动负载模拟器复合控制[J].控制理论与应用, 2014, 31(12): 1740–1747.NIU G C, WANG W, ZONG G H. Composite control for electric load simulator based on iterative learning[J].Control Theory & Applications, 2014, 31(12): 1740–1747.(in Chinese) |
| [14] | OUSTALOUP A, MOREAU X, NOUILLANT M. The CRONE suspension[J].Control Engineering Practice, 1996, 4(8): 1101–1108.DOI:10.1016/0967-0661(96)00109-8 |
| [15] | TEPLJAKOV A,PETLENKOV E,BELIKOV J,et al.Design and implementation of fractional-order PID controllers for a fluid tank system[C]//American Control Conference.Piscataway,NJ:IEEE Press,2013:1777-1782. |
| [16] | MERRIKH-BAYAT F, MIREBRAHIMI N, KHALILI M R. Discrete-time fractional-order PID controller:Definition,tuning,digital realization and some applications[J].International Journal of Control Automation and Systems, 2015, 13(1): 81–90.DOI:10.1007/s12555-013-0335-y |
| [17] | DADRAS S, MOMENI H R. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty[J].Communications in Nonlinear Science and Numerical Simulation, 2012, 17(1): 367–377.DOI:10.1016/j.cnsns.2011.04.032 |
| [18] | LI Y, CHEN Y Q, AHN H S, et al. A survey on fractional-order iterative learning control[J].Journal of Optimization Theory and Applications, 2013, 156(1): 127–140.DOI:10.1007/s10957-012-0229-9 |
| [19] | LI Y, CHEN Y Q, AHN H S. Fractional-order iterative learning control for fractional-order linear systems[J].Asian Journal of Control, 2011, 13(1): 54–63.DOI:10.1002/asjc.253 |
| [20] | REN Y, ZHU Z Q, LIU J M. Direct torque control of permanent magnet synchronous machine drives with a simple duty ratio regulator[J].IEEE Transactions on Industrial Electronics, 2014, 61(10): 5249–5258.DOI:10.1109/TIE.2014.2300070 |
| [21] | 张邦楚, 王少锋, 韩子鹏, 等. 飞航导弹分数阶PID控制及其数字实现[J].宇航学报, 2005, 26(5): 653–656.ZHANG B C, WANG S F, HAN Z P, et al. Using fractional-order PID controller for control of aerodynamic missile[J].Journal of Astronautics, 2005, 26(5): 653–656.(in Chinese) |
| [22] | 薛定宇, 赵春娜. 分数阶系统的分数阶PID控制器设计[J].控制理论与应用, 2007, 24(5): 771–776.XUE D Y, ZHAO C N. Fractional order PID controller design for fractional order system[J].Control Theory & Applications, 2007, 24(5): 771–776.(in Chinese) |
