最新四旋翼无人机(UAV)吸引了来自不同领域相关机构的兴趣，旋翼类飞机适合军事侦察、货物运输和其他一些对敏捷和精确性要求高的任务^[1-2]。无人机具有6个自由度和4个输入，是典型的非线性欠驱动系统^[3]。Mistler等^[4]先将无人机线性化，再使用动态反馈法实现了对无人机的控制，Xu和?zgüner^[5]通过变换分解，将整个飞行器系统分解为完全驱动系统和欠驱动系统，通过滑模控制实现精确控制。Dierks和Jagannathan^[6]设计了估计速度的神经网络观测器，观测值用于控制输入的设计，Coza和Macnab^[7]使用模糊系统实现了对无人机的控制。
四旋翼无人机的姿态子系统不包括位置子系统的信息，因此大部分文献采用的是时标分离方法，所谓时标分离方法是指无人机的姿态子系统和位置子系统分开设计控制器，时标分离方法的应用是在假设姿态子系统的收敛速度比位置子系统快的前提下提出的，但是姿态子系统的快速收敛是基于高增益的参数，在控制过程中，高增益参数可能会使控制输入过大，超过控制器的输出范围，此外，在整个系统的稳定性分析上缺乏明确的证明。
高增益观测器在非线性系统中应用广泛，其具有设计简单的特点，通过调节增益保证观测器全局指数渐进收敛^[8-9]。
反演法是将复杂的非线性系统分解成不超过系统阶数的子系统^[10]，为每个子系统设计李雅普诺夫函数和中间虚拟控制量，通过设计单个李雅普诺夫函数逐步完成整个系统的李雅普诺夫函数设计。Bouabdallah和Siegwart^[11]将反演和滑模结合，用于控制室内小型直升机，Madani和 Benallegue^[12]使用反演法和状态估计器来控制无人飞行器。反步法在实现不确定性非线性系统鲁棒控制和自适应控制方面效果很好，由于对虚拟控制求导的过程中可能会出现“微分爆炸”的现象，反步法在高阶系统的应用将会面临“微分爆炸”的不利影响。采用动态面可以消除微分项的膨胀^[13]，一般是引入一阶滤波器来获得虚拟控制的导数项^[14]，将滤波器的输出作为虚拟信号使控制律设计简化，消除控制律微分项的膨胀。此外，动态面控制的引入能给出四旋翼无人机整个系统稳定性分析。
1 无人机系统动态模型 如图 1为四旋冀无人机结构图，其中Oxyz为惯性坐标系，飞行器由4个螺旋桨控制位置和欧拉角，l为飞行器半臂长，F_i(i=1,2,3,4)为螺旋桨推力形成的扭转力矩，m为无人机质量,g为重力加速度。

图 1 四旋翼无人机结构图 Fig. 1 Structure of quadrotor UAV

图选项

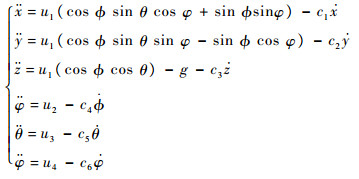(1)

式中:x、y和z为位置信息；θ、ф和φ分别为俯仰角、滚转角和偏航角；c_i(i=1,2,…,6)为系统参数；u_i(i=1,2,3,4)为系统输入。
UAV具有6个自由度和4个输入，是典型的非线性欠驱动系统。由于欠驱动特性的存在，因此不可能完成对6个自由度变量的全部控制。一般选择控制位置子系统的3个量(x,y,z)和在姿态子系统中选择1个变量进行控制，一般选择偏航角φ，最终实现对4个变量的控制，剩下的2个变量保持镇定即可。
时标分离方法的应用是在假设姿态子系统的收敛速度比位置子系统快的前提下提出的，但是姿态子系统的快速收敛是基于高增益的参数，在控制过程中，高增益参数可能会使控制输入过大，超过控制器的输出范围。另外，从理论上来说，在混合控制器结构中，2个子系统渐近稳定并不代表系统整体渐近稳定，而动态面的引入正好能解决系统整体全局稳定性的证明问题。
2 高增益观测器 飞行器UAV的位置和欧拉角可以通过传感器来测量，但是UAV 的速度和角速度难以测量，可以通过设计观测器来获取速度和角速度的估计值。令=。观测器设计如下：

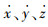
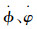
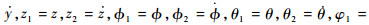
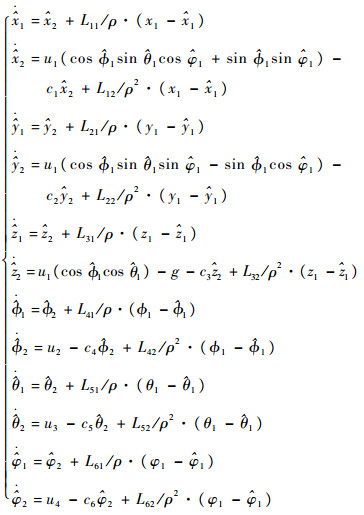(2)

式中：L为增益；ρ为收敛参数。
设系统所有的状态变量为

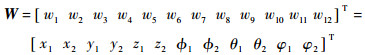定义观测器误差：

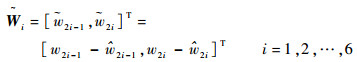由式(2)可得

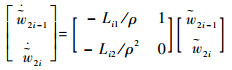(3)

式中:ρ为很小的正实数。
由式(3)可知，存在正数γ₀和?₀，满足

(4)

式中：t₀为初始时间。
3 动态面控制设计 动态面与反演法都是采用“递进式”设计方法，由于对虚拟控制求导的过程中可能会出现“微分爆炸”的现象，反演法在高阶系统的应用将会面临“微分爆炸”的不利影响。动态面通过引入一阶滤波器来获得虚拟控制的导数项，避免虚拟控制求导，使整个系统的控制律设计简洁化。动态面控制设计如下。
1) 定义第1个位置误差为

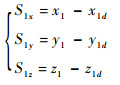(5)

式中:x_1d，y_1d，z_1d为位置跟踪信号，则，。设计第1个Lyapunov函数为

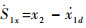
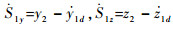
(6)

可得

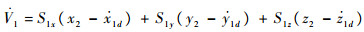设计虚拟控制为

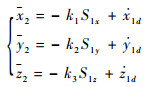(7)

式中：k₁，k₂，k₃>0，为了避免求时出现微分爆炸，将分别输入到如下低通滤波器中。

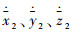
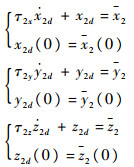2) 定义第2个误差

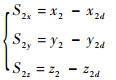(8)

可得


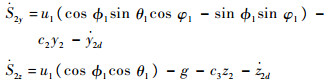则设计第2个Lyapunov函数为

(9)

因为UAV为欠驱动系统，控制目标选取为跟踪位置和偏航角，保持俯仰角和滚转角有界。位置子系统只有一个控制输入u₁，选取中间指令来间接控制位置变量，偏航角φ₁跟踪目标角度φ₁，设计虚拟控制为

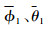
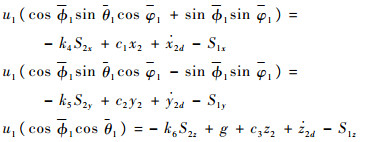其中：k₄，k₅，k₆>0，设

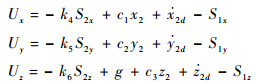求解方程可得

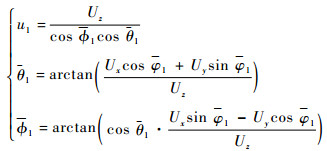(10)

由式(10)可知，中间指令表达式由位置子系统变量和偏航角构成，整个系统的控制目标为控制位置子系统和偏航角跟踪目标信号，因此当位置子系统和偏航角跟踪上目标信号时，中间指令信号是有界的，进而能保证俯仰角和滚转角有界。
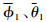
设

将输入到如下低通滤波器中，


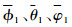
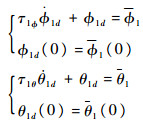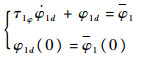3)定义第3个误差

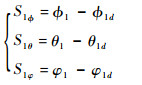(11)

可得。
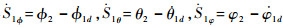
设计第3个Lyapunov函数为

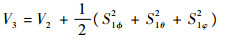(12)

设计虚拟控制为

(13)

式中：k₇，k₈，k₉>0，将输入到如下低通滤波器中：

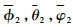
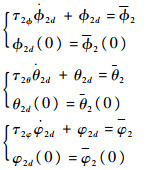4)定义第4个误差

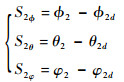(14)

可得

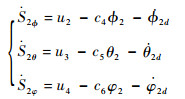设计第4个Lyapunov函数为

设计控制律为

(15)

式中：k₁₀，k₁₁，k₁₂>0。
稳定性分析：由于四旋翼无人机具有6个自由度，需要设计3组一阶滤波器，因此全局稳定性分析难度增加。定义边界层误差为

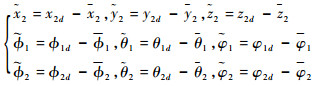(16)

由低通滤波器表达式，可得

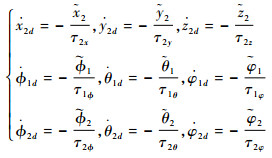(17)

由于

由边界层误差，可得

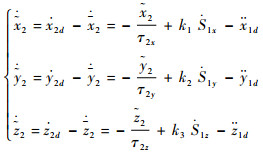(18)

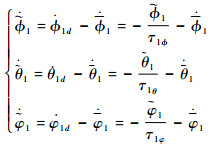(19)

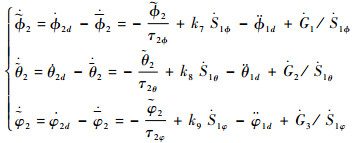(20)

由式(18)~式(20)可知，变量为误差和边界层误差的连续函数,设计整个系统的Lyapunov函数为

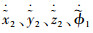
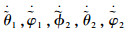
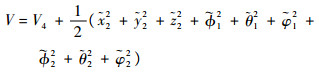由式(18)~式(20)可知，存在非负连续函数B_2x,B_2y,B_2z,B_1ф,B_1θ,B_1φ,B_2ф,B_2θ,B_2φ满足式(21)~式(23)：

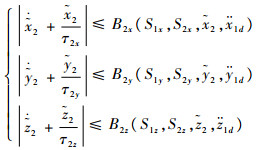(21)

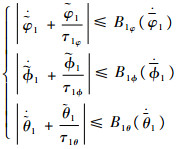(22)

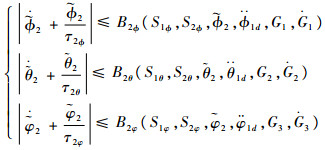(23)

假设1 四旋翼的状态变量是可测的并可用于控制律设计。
假设2 跟踪目标x_1d是有界的，存在正数χ₁使得成立；跟踪目标y_1d是有界的，存在正数χ₂使得成立；跟踪目标z_1d是有界的，存在正数χ₃使得成立；跟踪目标是有界的，存在正数χ₄使得成立。
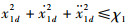
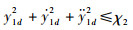
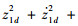
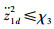
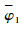
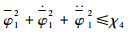
定理1 对于四旋翼无人机系统，采用控制律对四旋翼无人机进行控制。在假设1和假设2的基础上，系统初始值V(0)≤p，p为任意正常数。那么可以通过调节参数k_i(i=1,2,…,12)、B_2x,B_2y,B_2z,B_1ф,B_1θ,B_1φ,B_2ф,B_2θ,B_2φ使整个闭环系统半全局一致有界，并且跟踪误差收敛到任意小残集内。
证明 在V≤p成立的基础上，考虑以下紧集

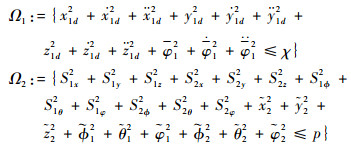可知Ω₁×Ω₂也是紧集。在V≤p成立时，B_2x,B_2y,B_2z,B_1ф,B_1θ,B_1φ,B_2ф,B_2θ,B_2φ在Ω₁×Ω₂上有最大值，记为：M_2x,M_2y,M_2z,M_1ф，M_1θ,M_1φ,M_2ф,M_2θ,M_2φ。
对V求导，可得

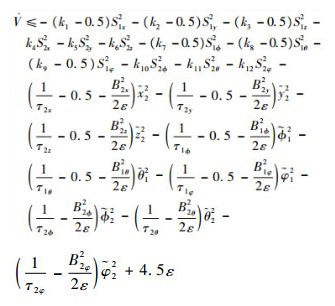(24)

选取系统的控制参数如下：k₁≥0.5+r，k₂≥。
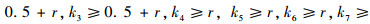
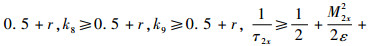
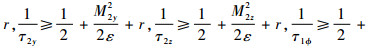
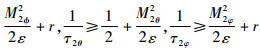
选取r≥(4.5η)/(2p)。当V=p时，由于B_*≤M_*(*=2x,2y,2z,1ф,1θ,1φ,2ф,2θ,2φ)，可得。因此可知V≤p为不变集，另外当V(0)≤p，即对任意t>0都有V(t)≤p。由定理1可知V(0)≤p，可得

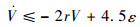(25)

求解式(25)可得

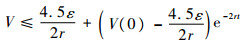(26)

因此闭环系统的所有信号是有界的，而且

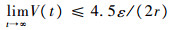(27)

由式(27)可知，可通过调节参数k_i(i=1,2,…,12)、B_2x,B_2y,B_2z,B_1ф,B_1θ,B_1φ,B_2ф,B_2θ,B_2φ和ε使得r任意大，即跟踪误差任意小。
需要说明的是，由于本文高增益观测器和系统非线性函数满足分离定理条件^[15-16]，因此可把观测器的观测值直接作为状态反馈，可以保证控制系统的稳定性，即控制律设计中不能直接测量得到的速度和角速度变量用观测器估计值替换,而无需再次证明闭环系统的稳定性，即，仍然可以得到式(25)~式(27)，即基于高增益观测器控制的闭环系统的所有信号是半全局一致有界的。
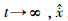
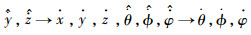
4 仿真研究 取动态面控制的参考航迹，，设定初始位置为(0.5,0.5,0.5)，初始姿态角为(0,0,0.5)。为了完成跟踪目标，参数选取τ_2x=τ_2y=τ_2z=τ_1ф=τ_1θ=τ_1φ=τ_2ф=τ_2θ=τ_2φ=0.02，k_i=5(i=1,2,…,12)，取观测器的初值为0，观测器参数选取L₁₁=L₂₁=L₃₁=L₄₁=L₅₁=L₆₁=1，L₁₂=L₂₂=L₃₂=L₄₂=L₅₂=L₆₂=1,ρ=0.1。
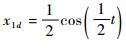
图 2反映无人机跟踪效果图，图 3为参数c_i(i=1,2,…,6)在10 s时刻迅速减小5倍，观测器和路径跟踪误差仍保持着较高的精度。

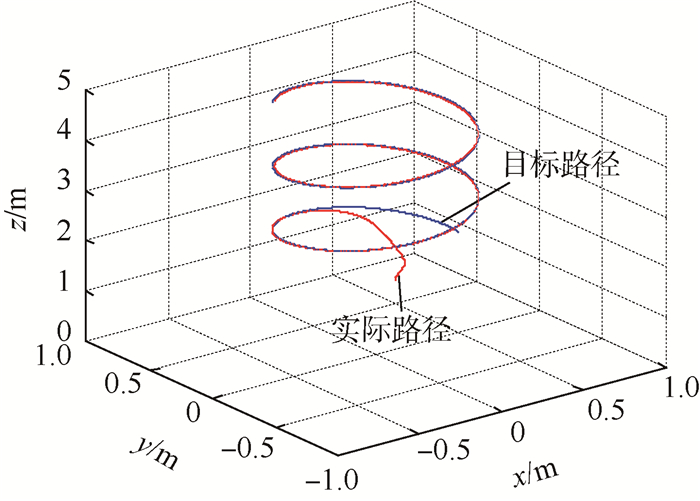图 2 无人机路径跟踪控制 Fig. 2 Path tracking control of quadrotor UAV

图选项

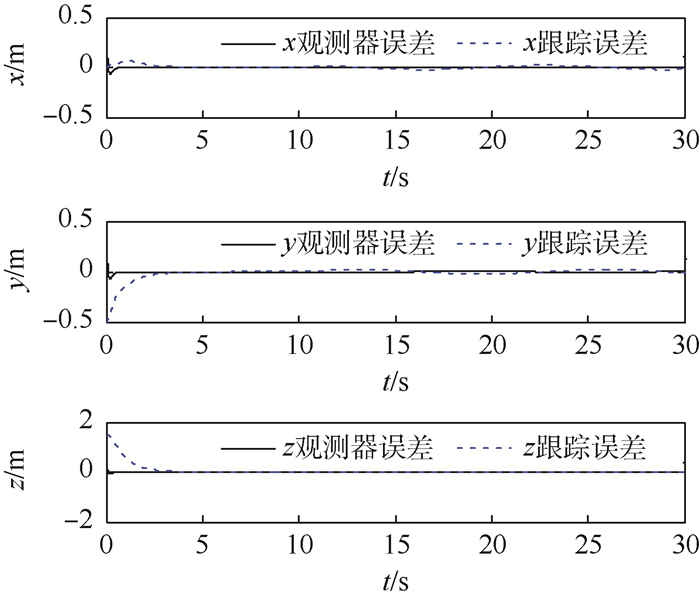图 3 参数变化下观测器和路径跟踪控制误差 Fig. 3 Tracking errors of observer and path with changed parameters

图选项

图 4 为x方向位置、速度观测值和跟踪效果，图 5 为y方向位置、速度观测值和跟踪效果，图 6为z方向位置、速度观测值和跟踪效果，图 7为偏航角、角速度观测值和跟踪效果，图 8为俯仰角和滚转角变化。

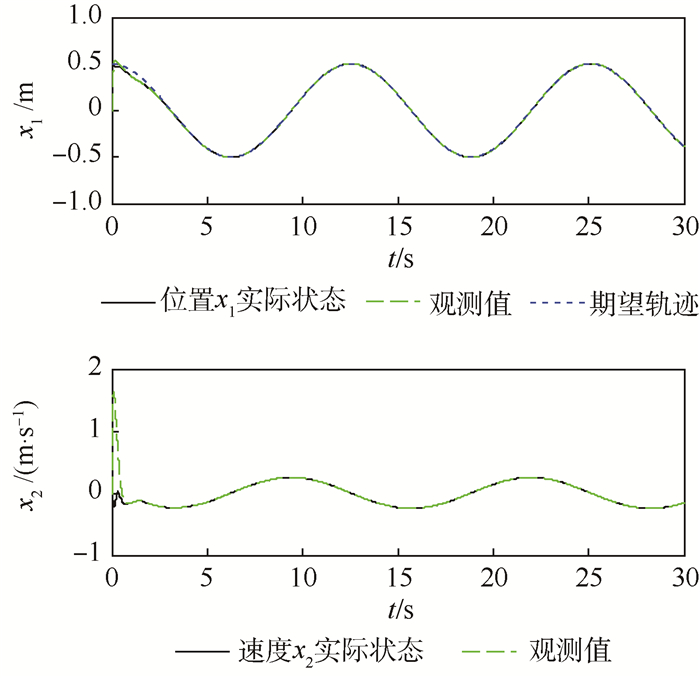图 4 水平方向位置、速度观测值和路径跟踪控制 Fig. 4 Path tracking control and observed values of position and velocity of horizon direction

图选项

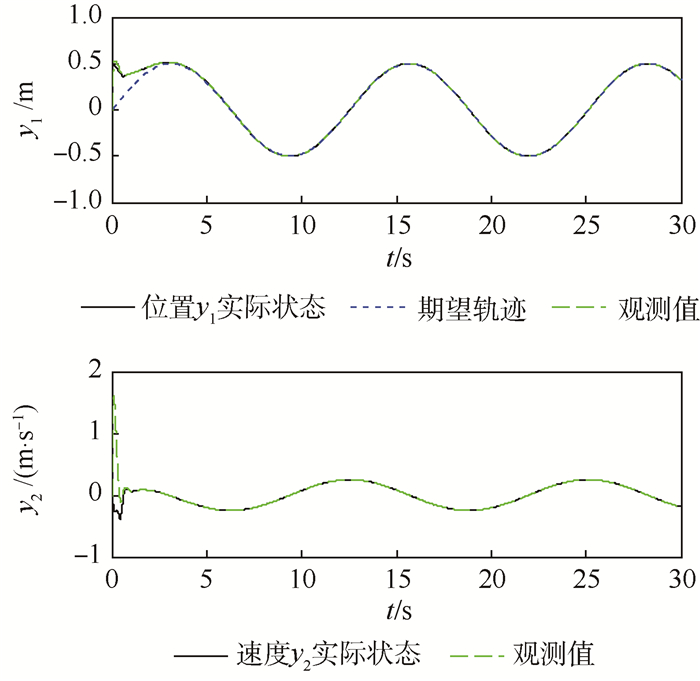图 5 纵向位置、速度观测值和路径跟踪控制 Fig. 5 Path tracking control and observed values of position and velocity of longitude direction

图选项

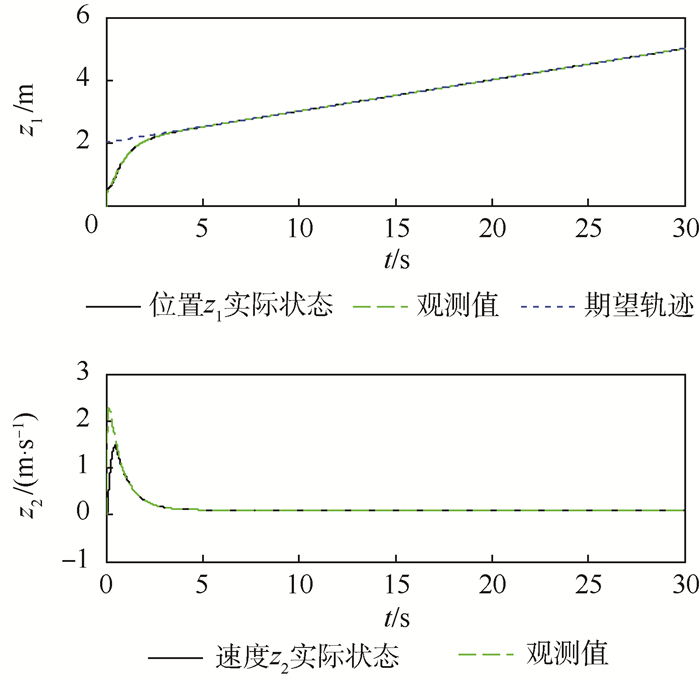图 6 垂直方向位置、速度观测值和路径跟踪控制 Fig. 6 Path tracking control and observed values of position and velocity of vertical direction

图选项

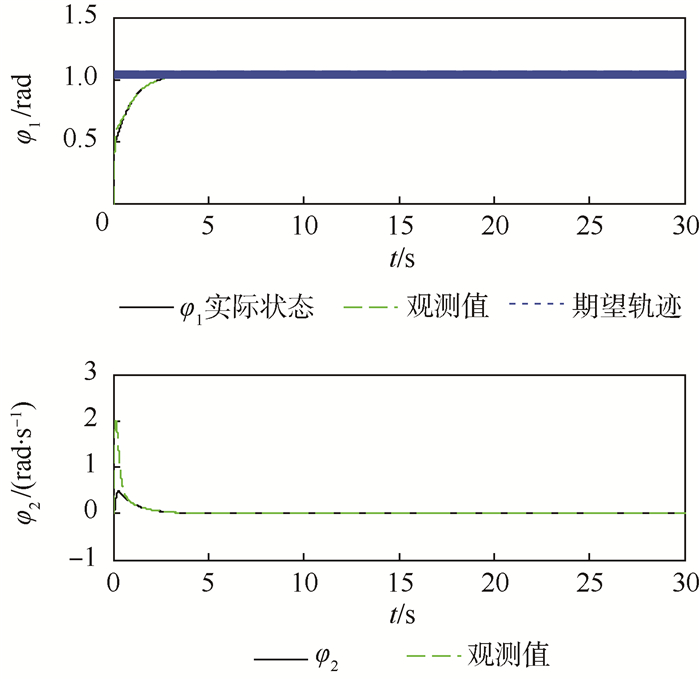图 7 偏航角、偏航角速度观测值和路径跟踪控制 Fig. 7 Path tracking control and observed values of gaw angle and angular velocity of yaw

图选项

由图 3~图 8可以看出，在0.5 s后观测值逼近真实值，因此可在0.5 s后加入动态面控制，动态面控制可以使飞行器的位置和偏航角快速跟踪上期望轨迹，并保证滚转角和俯仰角是有界的。

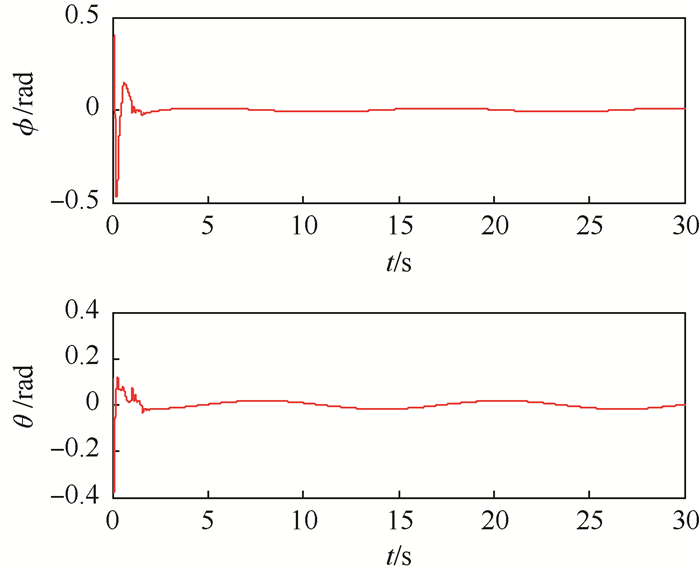图 8 俯仰角和滚转角变化 Fig. 8 Change of pitch and roll angles

图选项

5 结 论 本文针对四旋翼无人机飞行器系统，利用动态面技术设计控制器，保证了系统的全局稳定性：
1) 利用高增益观测器得到位置速度和姿态加速度估计值，解决了速度信号难以获得的问题。由于高增益观测器对未建模部分及系统参数不确定性具有鲁棒性，因此对模型参数精确性要求降低。
2) 利用动态面设计控制器，通过引入滤波器来求取控制信号中的系统状态的导数项，避免了出现系统状态导数项数值过大的现象。并且利用分离定理来解决观测器与控制器的联合使用问题。
3) 能够解决系统稳定性整体证明问题，不是基于常用的时标分离假设进行稳定性分析，而是从全局的角度给出了系统全局稳定性分析。

参考文献

[1]	RAFFO G V, ORTEGA M G, RUBIO F R. An integral predictive/nonlinear H∞ control structure for a quadrotor helicopter[J].Automatica, 2010, 46(1): 29–39.DOI:10.1016/j.automatica.2009.10.018
[2]	PAN Y, LIU Y, WANG P, et al. Research of UAV control system based on DSP[J].Electronic Measurement Technology, 2014, 15(2): 101–121.
[3]	LEE D B,NATARAJ C,BURG T C,et al.Adaptive tracking control of an underactuated aerial vehicle[C]//Proceedings of the 2011 American Control Conference (ACC 2011) American Control Conference.Piscataway,NJ:IEEE Press,2011:2326-2331.
[4]	MISTLER V,BENALLEGUE A,M'SIRDI N K.Exact linearization and noninteracting control of a 4 rotors helicopter via dynamic feedback[C]]//10th IEEE International Workshop on Robot and Human Interactive Communication (ROMAN 2001).Piscataway,NJ:IEEE Press,2001:586-593.
[5]	XU R, ?ZGüNER ü. Sliding mode control of a class of underactuated systems[J].Automatica, 2008, 44(1): 233–241.DOI:10.1016/j.automatica.2007.05.014
[6]	DIERKS T, JAGANNATHAN S. Output feedback control of a quadrotor UAV using neural networks[J].IEEE Transactions on Neural Networks, 2010, 21(1): 50–66.DOI:10.1109/TNN.2009.2034145
[7]	COZA C,MACNAB C J B.A new robust adaptive-fuzzy control method applied to quadrotor helicopter stabilization[C]//2006 Annual meeting of the North American on Fuzzy Information Processing Society.Piscataway,NJ:IEEE Press,2006:475-479.
[8]	RAKHTALA S M. Control of oxygen excess ratio in a PEM fuel cell system using high-order sliding-mode controller and observer[J].Turkish Journal of Electrical Engineering & Computer Sciences, 2015, 23(1): 255–278.
[9]	ZHOU Y, SOH Y C, SHEN J X. High-gain observer with higher order sliding mode for state and unknown disturbance estimations[J].International Journal of Robust & Nonlinear Control, 2014, 24(15): 2136–2151.
[10]	CHEN M A, ZHAO G, FENG S. Design of integrated guidance and control based on wavelet neural network backsteppting method[J].Journal of Projectiles Rockets Missiles & Guidance, 2015, 21(1): 36–45.
[11]	BOUABDALLAH S,SIEGWART R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor[C]//Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Piscataway,NJ:IEEE Press,2005:2247-2252
[12]	MADANI T,BENALLEGUE A.Backstepping control with exact 2-sliding mode estimation for a quadrotor unmanned aerial vehicle[C]//Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS 2007).Piscataway,NJ:IEEE Press,2007:141-146.
[13]	HUANG J T. Global adaptive neural dynamic surface control of strict-feedback systems[J].Neurocomputing, 2015, 17(1): 403–413.
[14]	YU Z, LI S, LI F. Observer-based adaptive neural dynamic surface control for a class of non-strict-feedback stochastic nonlinear systems[J].International Journal of Systems Science, 2015, 12(2): 122–129.
[15]	ATASSI A N, KHALIl H K. A separation principle for the stabilization of a class of nonlinear systems[J].IEEE Transactions on Automatic Control, 1999, 44(9): 1672–1687.DOI:10.1109/9.788534
[16]	ZHOU Y, SOH Y C, SHEN J X. High-gain observer with higher order sliding mode for state and unknown disturbance estimations[J].International Journal of Robust & Nonlinear Control, 2014, 24(15): 2136–2151.