当前在高轨道卫星的自主导航研究中,主要集中在2个方面:一是采用天体敏感器的天文导航;二是采用星载卫星导航接收机的全球导航卫星系统(GNSS)导航。前者是用光学敏感器测得的天体(如月球、地球、太阳、其他行星和恒星)信息进行载体位置的解算,但是由于高轨道观测地平精度有限,导致单一使用天文导航方法进行高轨道卫星位置确定精度较低。而后者主要是研究 GPS 高轨道卫星的自主定轨,此方法也存在着导航星星数不足和信号几何覆盖差等缺点[1]。
X射线脉冲星导航(XNAV)是一种全新的航天器自主导航方法,是以遥远的天体X射线脉冲星体作为定位的基准,并具有相当高的准确性和可靠性。同时它以太阳系为参考物,因此具有为中、高轨道卫星提供自主确定时间、位置和姿态的能力,这为高轨道卫星的自主导航提供一条新的解决途径[2]。目前,脉冲星导航系统的研制仍处于试验的初级阶段。由于X射线探测器的成本和技术风险都较高,而现有的导航算法大多是同时观测3~4颗脉冲星来进行导航解算,这样将大大增加了航天器有效载荷的负担和功耗,同时对航天器姿态精度要求也很高。因此,近年来提出了单X射线探测器导航方法[3],尽管该单脉冲星导航系统有诸多优点,但可观测性较差,很难单独应用于长期自主定轨过程中。笔者前期研究工作提出了分时段实时观测脉冲星的单探测器导航方法[4],该方法有效解决了单脉冲星系统可观性差的问题,但由于每一时段导航观测信息不够充分,使得导航精度相比多星观测有一定降低。
针对上述问题,本文提出一种基于虚拟观测值的高精度单脉冲星与星光组合的新方法。该方法的基本思想是:在长周期的X射线脉冲星的信号(脉冲轮廓)形成期间,利用算法构建虚拟观测值,使其观测周期与星光观测周期同步。由此使单脉冲星与星光组合的滤波器的每一时刻均有3个观测值参与解算,即相当于导航系统始终能够观测到3个观测量信息,从而大大地提高了导航系统精度。
1 单脉冲星导航系统 1.1 脉冲星高阶时间传播方程 图 1为太阳系质心(SSB )参考系内X射线脉冲星脉冲传播示意图[5]。图中: n 为脉冲星方向单位向量; d 和 rSSB 分别为脉冲星和SSB相对于太阳质心的位置矢量; rsat 为卫星相对于 SSB 的位置矢量。
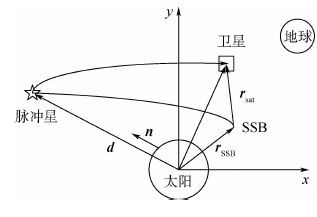 |
| 图 1 X射线脉冲星脉冲传播示意图[5] Fig. 1 Schematic diagram of pulsar propagation of X-ray pulsar[5] |
| 图选项 |
在脉冲星导航中最重要的量就是脉冲到达航天器的时间(Time of Arrival,TOA),位置导航中利用这个量和预计的到达时间之差解算出真实位置和预计位置之差,利用差值对预计位置进行校正。脉冲星脉冲从卫星传播到 SSB 的时间延迟量最主要的延迟是由几何距离引起的[6]。由于脉冲传播过程中受到太阳系引力场作用,因此传播的延迟量需要考虑引力场的广义相对论效应。反映时间延迟量的数学模型就是脉冲星脉冲传播方程。在实际脉冲星导航中,受到宇宙引力场的作用,光是弯曲传播的,即相对论效应的影响不可忽略[7-8]。对脉冲星到达时间进行2次积分,一次沿脉冲星到SSB的光信号传播路径,一次沿脉冲星到航天器的光信号传播路径,2组积分得到的解做差,不考虑脉冲自行速度,可得同一个X 射线脉冲从卫星到 SSB 的传播时间为
 | (1) |
式中: tSSB 和 tsat 分别为同一个 X 射线脉冲到达 SSB和卫星的时间;c为光速; d0 为脉冲星的距离。式(1)等式右边第1项为几何延迟,第2、第3项为Roamer 延迟,是周年视差影响的修正。对于高轨道卫星,几何距离延迟为最主要的因素,第2项为10-7 s量级,等效距离在10~100 m范围内,第3项为10-9 s量级,等效距离在1 m以下[9]。由于目前高轨道卫星自主导航的精度指标通常在几百m范围,因此第2和第3项的影响不可忽略。
1.2 状态方程 选择地球同步卫星轨道研究高轨道卫星的导航系统。以航天器的位置和速度作为状态变量,其状态方程为
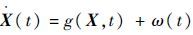 | (2) |
式中: X(t)=[x y z vxvyvz]T 为状态变量,x、y和z分别为航天器三轴位置变量,vx、vy和vz分别为航天器的三轴速度变量; g(X,t) 为状态动力学的非线性函数; ω(t) 为噪声项。考虑地球非球形引力主要的J2、J3项的带谐项摄动,太阳引力产生的加速度以及月球引力产生的加速度,动力学方程如下[10]:
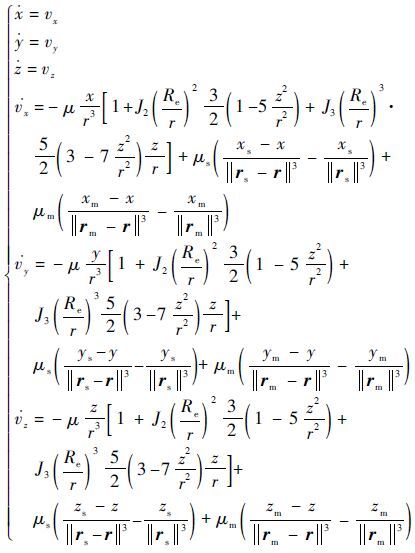 | (3) |
式中: r=(x,y,z) 为航天器相对于地球质心的位置矢量; r 为航天器相对地球质心的距离; Re 为地球半径; rs=(xs,ys,zs) 和 rm=(xm,ym,zm) 分别为航天器相对于太阳和月亮质心的位置矢量; (vx,vy,vz) 为航天器相对于地球质心的速度;μ为地球引力常数;μm为月亮引力常数;μs为太阳引力常数。余下未考虑的高阶摄动将作为系统噪声,一般情况下做高斯白噪声处理。方程式(3)的解可直接用四阶Runge-Kutta法数值计算得到。
1.3 量测方程 根据 X 射线脉冲 TOA 传播方程式(1),脉冲 TOA 与卫星位置之间存在着以下关系[11-12]:
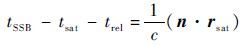 | (4) |
式中: trel 为式(1)中的高阶项。SSB、地球和卫星三者的位置关系如下:
 | (5) |
式中: rE 为地球相对SSB的位置,由太阳系行星历表(如 JPL 的 DE405 等)给出。
将式(5)代入式(4)有
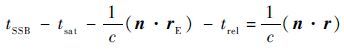 | (6) |
式(6)为根据 X 射线脉冲传播方程推导得到的 XNAV 系统基本观测方程,该方程采用脉冲TOA 作为基本观测量,换算得到导航结算需要的观测量。要得到卫星的位置 r ,需要计算出 trel ,由于 trel 是卫星位置r的函数,为解决时序矛盾,用预报得到的卫星位置 计算得到 trel 的估计值 rel :
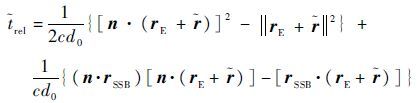 | (7) |
因此用X射线脉冲星量测方程可记为
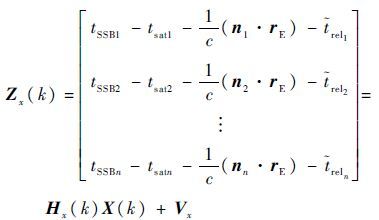 | (8) |
式中: tSSBi 为第i颗脉冲星到达SSB的时间; tsati、reli 和 ni 分别为第i颗脉冲星到达航天器的时间、高阶项估计时间和脉冲方向矢量,i=1,2,…,n; Vx 为X射线量测噪声; Hx 为量测矩阵,其定义为
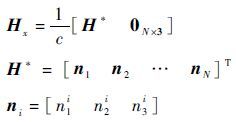 |
对于单脉冲星导航,取N=1,得
 | (9) |
2 单脉冲星与星光融合滤波器 2.1 滤波器设计 航天器携带单个X射线探测器、两个星敏感器及地平仪进行观测[13]。导航子系统探测器选取及观测量如表 1所示。
表 1 导航子系统探测器选取及观测量 Table 1 Selection of detector and observation of navigation subsystem
| 子系统 | 探测器 | 观测量 |
| 脉冲星 | X射线探测器 | 脉冲到达时间差Δt |
| 星光1 | 地平仪/星敏感器 | 星光仰角 α1 |
| 星光2 | 地平仪/星敏感器 | 星光仰角 α2 |
表选项
则组合系统量测方程为
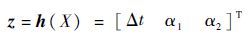 | (10) |
式中:Δt为 tSSB 与 tsat 的差值,见式(6); α1和α2 分别为同时观测的2颗导航恒星的星光仰角:
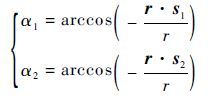 | (11) |
式中: s1=[s1xs1ys1z] 为第1颗导航星星光方向矢量; s2=[s2xs2ys2z] 为第2颗导航星星光方向矢量。集中式卡尔曼滤波算法设计如图 2所示,能够获得导航位置的全局最优估计[14]。
 |
| 图 2 X射线单脉冲星与星光导航集中式卡尔曼滤波设计 Fig. 2 Design of centralized Kalman filter of integrated single X-ray pulsar and starlight navigation |
| 图选项 |
2.2 可观性证明与分析 离散轨道动力学模型[15]为
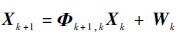 | (12) |
式中: Xk+1和Xk 分别为k+1时刻和k时刻的状态量; Φk+1,k 为k时刻到k+1时刻的一步转移矩阵; Wk 为模型噪声 。
利用简化的J2模型式[15]得到
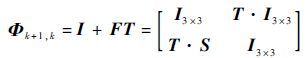 | (13) |
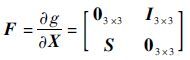 | (14) |
 | (15) |
式中:
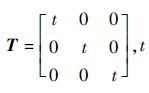
由式(6)离散的观测方程[15]为
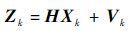 | (16) |
式中: Zk 为k时刻观测矩阵; Vk 为量测噪声。
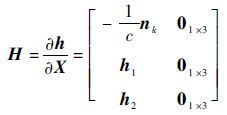 | (17) |
式中: nk=[nxnynz] 为脉冲星的视线方向矢量;
 |
此时系统的可观性矩阵 V 表示为
 | (18) |
将式(13)和式(17)代入式(18)整理,由于 S 中每个元素的量级为
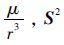
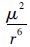
分析式(19)有
1) 当 nk≠0,h1≠0,h2≠0 ,则rank(V)=6,系统同时可以接收到单脉冲星及两颗星光信号,系统完全可观。
2) 当 nk=0 ,则 rank(V)=4 ,此时,脉冲轮廓在形成过程中,无完整的脉冲星信号被接受,系统不可观。
 | (19) |
3 神经网络预测方法 3.1 虚拟观测值的预测 对X射线脉冲星导航,脉冲星信号探测器的输出受X射线源能流密度影响,需要长时间的观测才能获得较高的测量精度,因此,X射线脉冲星观测的采样周期一般要在几百s以上,而星光观测的采样周期可以达到几s的量级。图 3描述了X射线脉冲星与星光的量测时序的关系。
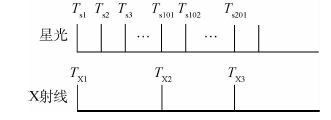 |
| 图 3 X射线单脉冲星与星光组合导航时序图 Fig. 3 Sequence diagram of integrated single X-ray pulsar and starlight navigation |
| 图选项 |
图 3中Tsi为星光的量测时间点(周期为5 s),TXi为X射线脉冲星的量测时间点(周期为500 s)。可以看到,在X射线脉冲星信号的两次采样期间,能够对星光进行多次观测,如:TX1和TX2 2个时间点之间,可以在Ts2,Ts3,…,Ts101等多点处高频率地获得星光观测值,具体观测值根据式(8)给出。基于“时间配准”概念,利用神经网络的推演技术对低采样频率的X射线脉冲星信号进行虚拟观测值再生,其基本思想是:假设X射线脉冲星采样周期的2个时间点TX1和TX2,其观测值分别为ZX1和ZX2。在TX1和TX2之间对应星光高频率观测时间点虚拟一组X射线脉冲星观测值 ZX1n=Z^X11Z^X12…Z^X1n 其时序如图 4所示。
 |
| 图 4 虚拟观测值时序图 Fig. 4 Sequence diagram of virtual observation value |
| 图选项 |
预测观测值 Z^X1i 为
 | (20) |
式中:hX1为非线性观测函数,可通过神经网络对实际观测值ZX1学习得到; X^i 为第i时刻状态估计值; vi 为观测误差。同理,系统根据实际观测值ZX2得到下一组预测观测值 ZX2n=[Z^X21Z^X22…Z^X2n] ,依次类推。
由图 2的集中式卡尔曼滤波算法看到,当对单脉冲星虚拟观测值后,滤波系统的每一时刻均可获得3个观测值,再根据2.2节可观性分析可知,此时导航系统完全可观,同时,由于每一时刻多个观测值参与滤波,系统精度得到大大提高。
3.2 神经网络预测虚拟观测值 根据式(8)可知,观测方程是非线性的,引入具有自适应学习能力的神经网络对观测值进行估计。误差反向传播(BP)神经网络是一种对非线性可微函数进行权值训练的单向传播多层前向网络。理论研究表明:BP神经网络能够以任意精度逼近任何连续可微函数。设计BP神经网络,将 [x y z vxvyvz] 6个状态量作为输入神经元,并以观测值 Z^X1i 为网络层输出元。首先用当前实际得到的X射线脉冲星观测值信息进行学习,调整权值;再用该学习调整好的权值对后面的观测值进行预测[16],具体步骤如下:
1) 神经网络的前向计算
神经元输入 o :k时刻的状态值 Xk 。
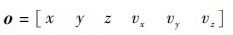 |
输出层输入:
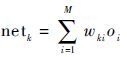 | (21) |
输出层输出 ok :
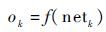 | (22) |
式中: f(·) 为活化函数,这里取 f(x)=x;wki 为神经网络加权系数 。
2) 误差反向传播和加权系数的调整
引入二次型误差函数
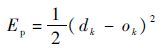 | (23) |
式中: dk 为期望输出,此处为X射线观测值 Zk 。
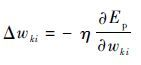 | (24) |
式中: η 为学习速率, η >0
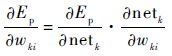 | (25) |
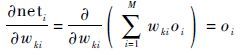 | (26) |
式中:
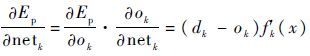
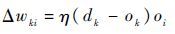 | (27) |
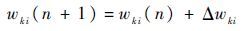 | (28) |
式中:fk(x)为当前时刻k的活化函数。
3) BP神经网络工作流程如图 5所示。
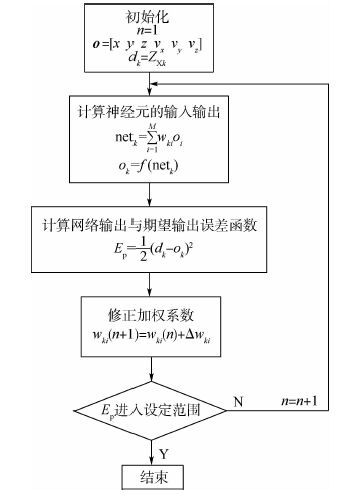 |
| 图 5 BP神经网络流程图 Fig. 5 Flowchart BP neural network |
| 图选项 |
通过图5神经网络预测的观测值满足:
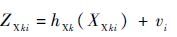 | (29) |
式中: hXk 由神经网络根据k时刻的实际观测值 ZXk 以及对状态值 Xk 学习得到的权值 wk 组合得到。
4 仿真验证及分析 4.1 仿真条件 1) 选用J2000.0地心赤道惯性坐标系。
轨道信息:卫星标称轨道数据由STK软件产生。轨道半长轴为42 164 km,偏心率为0.000 2,轨道倾角为0°,近地点辐角为0°,升交点赤经为193°。
2) 初始误差:三轴位置初始位置误差为500 m,速度误差为5 m/s。
3) 探测器参数:X射线探测器观测时间为500 s;星光探测器观测时间为5 s。
4) 探测器精度:X射线探测器精度为0.1 μs;星光探测器精度为10-5 rad。
4.2 仿真结果 根据3.2节算法对2.1节的集中式组合滤波系统中X射线脉冲信号观测值虚拟,并进行导航解算,其结果如图 6所示。
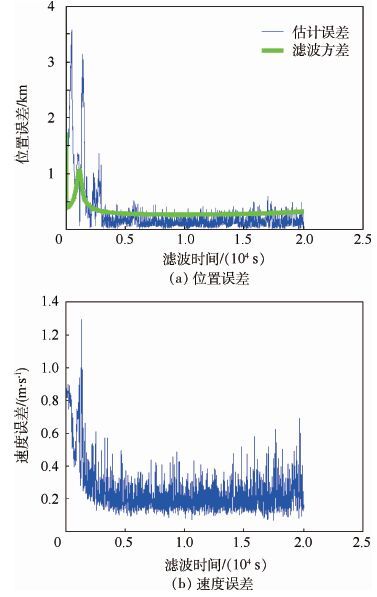 |
| 图 6 基于神经网络虚拟观测值的组合导航位置误差与速度误差 Fig. 6 Position error and speed error of integrated navigation based on virtual observation value using neural network |
| 图选项 |
由图 6可见,通过增加了虚拟的观测值使滤波结果快速收敛,并达到了259.79 m的高导航精度。图 7为没有对X射线脉冲星进行观测值虚拟的联邦滤波组合导航的位置误差结果。对比看出,尽管联邦滤波解决了系统可观测性问题,但在X射线脉冲星500 s周期(形成完整脉冲时间)内由于仅能使用星光观测值进行导航滤波,从而降低了导航精度。表 2展示了2种导航滤波在各轴上的位置误差,可以看到,通过增加虚拟观测值使各轴上的位置误差均得到了较好的抑制。
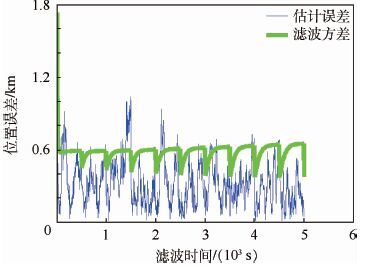 |
| 图 7 联邦滤波组合导航位置误差 Fig. 7 Position error of integrated navigation using federated filter |
| 图选项 |
为验证基于神经网络的虚拟观测值的正确性,将虚拟观测值与实际观测值进行比较,见图 8。
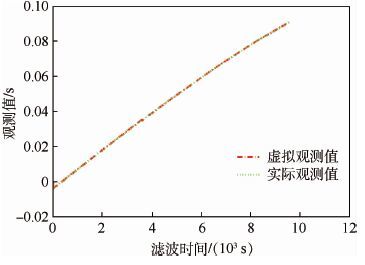 |
| 图 8 神经网络预测观测值与实际观测值比较 Fig. 8 Comparison of virtual observation values using neural network and real observation values |
| 图选项 |
表 2 X脉冲星预测观测值与无预测观测值的导航结果比较 Table 2 Comparison of navigation results between predi-cted and non-predicted observation value of X-ray pulsar
| 参数 | 位置估计误差/m | |||
| x轴 | y轴 | z轴 | Er | |
| 观测值预测 | 194.36 | 67.48 | 158.62 | 259.79 |
| 无观测值预测 | 227.94 | 167.39 | 187.93 | 339.55 |
| 注:Er为总位置误差(3轴误差的均方根)。 | ||||
表选项
由图 8可知,神经网络预测的虚拟观测值与实际观测值基本完全一致,说明用神经网络预测的观测值具有很高的准确度。图 9为5个周期内的虚拟观测值与实际观测值的差值,误差均控制在10-7量级内,说明每个周期内虚拟观测值都在实际观测值附近很小的范围内波动。
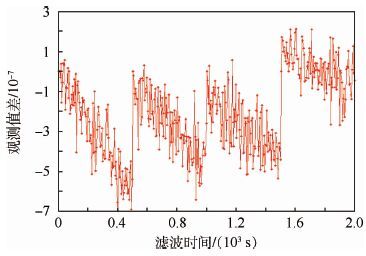 |
| 图 9 神经网络虚拟观测值与实际观测值之差 Fig. 9 Difference between virtual observationvalue using neural network and real observation value |
| 图选项 |
图 10是分别利用神经网络和动力学递推2种方法对X射线脉冲星虚拟观测值的精度比较。可以看出,通过神经网络虚拟的观测值的精度平均能够达到10-7量级,相较于观测值误差范围为0.001%~0.003%,而动力学递推虚拟的观测值的精度平均为10-6量级。这是因为较大的初始误差和系统随机误差,难以使用动力学准确递推观测值。而神经网络通过足够多样本训练后,将具有准确逼近真实观测值的能力。因此,前者不仅精度较后者高,而且预测值平稳,滤波系统可靠性强。
 |
| 图 10 神经网络与动力学递推虚拟观测值方法精度比较 Fig. 10 Accuracy comparison of neural network and dynamic prediction method of virtual observation value |
| 图选项 |
将虚拟观测值周期分别取为5、50和250 s,并通过2.1节的集中式组合滤波系统进行导航解算,其结果比较如图 11所示。
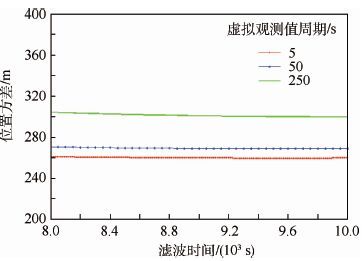 |
| 图 11 虚拟观测值周期对导航精度的影响 Fig. 11 Influence of period of virtual observation value on navigation accuracy |
| 图选项 |
从图 11中看到,虚拟观测值的周期越小,其导航精度越高。表 3详细列出了不同虚拟观测值周期的导航系统各轴上的位置精度。可以看出,随着虚拟观测值周期逐渐加大,各轴上的导航精度均有明显下降。
表 3 不同虚拟观测值周期对应的各轴上的导航位置误差 Table 3 Navigation position error of each axis corresponding to different virtual observation value periods
| 滤波周期/s | 位置估计误差/m | |||
| x轴 | y轴 | z轴 | Er | |
| 5 | 194.36 | 67.48 | 158.62 | 259.79 |
| 20 | 197.72 | 70.67 | 161.23 | 264.73 |
| 50 | 200.45 | 72.45 | 164.78 | 269.41 |
| 250 | 223.46 | 81.78 | 184.86 | 301.32 |
| 500 | 234.78 | 86.32 | 193.36 | 316.17 |
表选项
为了分析量测精度对导航结果的影响,分别针对X射线导航和星光导航取不同的量测精度,其中X射线导航观测量为时间差,精度一般为μs量级,即10-7~10-6 s,星光导航观测量为星光仰角,精度一般为10-4~10-5 rad,得到的导航结果如图 12和图 13所示。
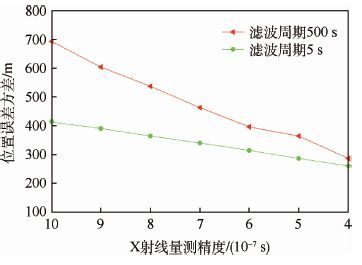 |
| 图 12 X射线量测精度对导航精度的影响 Fig. 12 Influence of X-ray measurement accuracy on navigation accuracy |
| 图选项 |
图 12和图 13分别描述了X射线和星光2个子系统的观测精度对导航系统的影响,量测误差越小,则导航误差越小。比较图 12中2条曲线,可以看出,在同等量测精度的条件下,周期越小精度越高,也可以说对于同样的导航精度需求,导航周期越小,则对探测器的量测精度需求越低。若采用本文的增加虚拟观测值的方法,可以达到高精度测量设备的相同效果,由此大大降低了导航系统的使用成本。
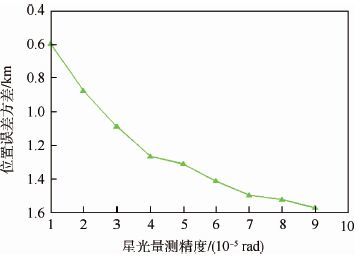 |
| 图 13 星光量测精度对导航精度的影响 Fig. 13 Influence of starlight measurement accuracy on navigation accuracy |
| 图选项 |
图 14给出了单脉冲星与星光组合导航系统精度与各子系统量测精度之间的变化关系。可以看出,对于单脉冲星与星光组合导航,星光的融合主要是解决了系统可观测差的问题,而导航系统的精度则主要取决X射线脉冲星的导航精度。
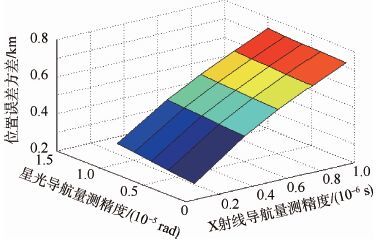 |
| 图 14 子系统量测精度对导航精度的影响 Fig. 14 Influence of measurement accuracy of subsystem on navigation accuracy |
| 图选项 |
表 4为几种组合导航系统的精度对比。比较看出,直接敏感地平的星光导航系统的精度较低。利用3颗X射线脉冲星的导航精度较高,但需要较多的X射线探测器,可实现性较差。采用2颗星光加1颗脉冲星的联邦滤波组合导航方法,可以弥补单一星光的低精度和重量大的X射线探测器的不足。尽管如此,由于联邦滤波器在X脉冲星500 s的脉冲周期中仅能使用星光观测值,因而,导航精度并不理想。
表 4 几种组合导航系统的精度对比 Table 4 Accuracy comparison of several integrated navigation systems
| 导航方式 | 导航周期/s | 预测精度 | 导航精度/m |
| 星光导航(直接敏感地平) | 5 | 1 435 | |
| X射线导航(3颗星) | 500 | 167.67 | |
| 联邦滤波组合导航 | 500 | 316.17 | |
| 动力学递推虚拟观测值 | 5 | 1.00×10-6 | 297.51 |
| 神经网络虚拟观测值 | 5 | 1.00×10-7 | 259.79 |
表选项
从表 4中可以看到,通过在X射线脉冲星长周期的脉冲积累过程中增加虚拟观测值,可以大大提高导航精度。尤其是通过神经网络方法虚拟观测值具有更高的导航精度,这是因为神经网络的优秀预测能力。
5 结 论 本文提出的虚拟观测值的X射线单星与星光组合导航方法,通过理论研究及仿真验证得到主要结论如下:
1) 在X射线脉冲星的长周期内增加虚拟观测值可以实现单脉冲星与星光集中式组合滤波的高精度导航算法,导航精度达到259.79 m。
2) 利用神经网络虚拟观测值的方法优于动力学递推虚拟观测值的方法,观测值估计精度可提高一个数量级,达到10-7量级。
3) 虚拟观测值的周期对导航精度有显著影响。随着虚拟观测值周期加长,组合滤波系统的导航精度明显下降。通过虚拟短周期的观测值,能够补偿由于探测器误差造成的导航误差。
参考文献
| [1] | 乔黎.X射线脉冲星高轨道卫星自主导航及其应用技术研究[D].南京:南京航空航天大学,2010:35-47. QIAO L.X-ray pulsar-based autonomous navigation and its application to high earth orbits satellites[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:35-47(in Chinese).(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [2] | SHEIKH S I, PINES D J, RAY P S, et al. Spacecraft navigation using X-ray pulsars[J]. Journal of Guidance,Control,and Dynamics,2006, 29(1): 50–63. |
| Click to display the text | |
| [3] | 帅平, 李明, 陈绍龙, 等. X射线脉冲星导航系统原理与方法[J]. 北京:中国宇航出版社,2009: 23–27.SHUAI P, LI M, CHEN S L, et al. Principle and method of X-ray pulsars navigation system[J]. Beijing:China Astronautic Publishing House,2009: 23–27.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [4] | 杨博, 张睿, 孙晖, 等. 分时段实时观测脉冲星的单探测器导航方法[J]. 北京航空航天大学学报,2014, 40(9): 1183–1188.YANG B, ZHANG R, SUN H, et al. Navigation method using a single detector based on the observation of X-ray pulsar in different time interval[J]. Journal of Beijing University of Aeronautics and Astronautics,2014, 40(9): 1183–1188.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [5] | EMADZADEH A A, SPEYER J L. X-ray pulsar-based navigation[M].Beijing: National Defence of Industry Press, 2013: 5-15. |
| Click to display the text | |
| [6] | 杨廷高. X射线脉冲星脉冲到达航天器时间测量[J]. 空间科学学报,2008, 28(4): 330–334.YANG T G. Spacecraft X-ray pulsar pulse time measurement[J]. Journal of Space Science,2008, 28(4): 330–334.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [7] | ANDERSON K D,PINES D J.Experimental validation of pulse phase tracking for X-ray pulsar based spacecraft navigation:AIAA-2013-5202[R].Reston:AIAA,2013. |
| Click to display the text | |
| [8] | SHEIKH S I,HELLINGS R W,MATZNER R A.High-order pulsar timing for navigation[C]//Proceedings of the 63rd Annual Meeting of the Institute of Navigation.Fairfax,VA:ION,2007:432-443. |
| Click to display the text | |
| [9] | GOLSHAN A R,SHEIKH S I.On pulse phase estimation and tracking of variable celestial X-ray sources[C]//Proceedings of the 63rd Annual Meeting of the Institute of Navigation.Fairfax,VA:ION,2007:413-422. |
| Click to display the text | |
| [10] | 刘林, 胡松杰, 王歆. 航天动力学引论[M].南京: 南京大学出版社, 2006: 125-156.LIU L, HU S J, WANG X. Introduction of aerospace dynamics[M].Nanjing: Nanjing University Press, 2006: 125-156.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [11] | SUNEEL I S.The use of variable celestial X-ray sources for spacecraft navigation[D].Maryland:University of Maryland,2005:26-37. |
| Click to display the text | |
| [12] | JASON W M, MUNTHER A H,LUKE M B W,et al.SEXTANT-Station explorer for X-ray timing and navigation technology:AIAA-2015-0865[R].Reston:AIAA,2015. |
| Click to display the text | |
| [13] | 房建成, 宁晓琳, 田玉龙. 航天器自主天文导航原理与方法[M].北京: 国防工业出版社, 2010: 77-80.FANG J C, NING X L, TIAN Y L. Principle and method of the spacecraft autonomous celestial navigation[M].Beijing: National Defence of Industry Press, 2010: 77-80.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [14] | 刘劲, 马杰, 田金文. 利用X射线脉冲星和多普勒频移的组合导航[J]. 宇航学报,2010, 31(6): 1552–1556.LIU J, MA J, TIAN J W. Integrated X-ray and doppler shift navigation[J]. Journal of Astronautics,2010, 31(6): 1552–1556.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [15] | 毛悦, 宋小勇, 冯来平. X射线脉冲星导航可见性分析[J]. 武汉大学学报,2009, 34(2): 222–225.MAO Y, SONG X Y, FENG L P. Visibility analysis of X-ray pulsar navigation[J]. Journal of Wuhan University,2009, 34(2): 222–225.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
| [16] | 卞鸿巍, 李安, 覃方军, 等. 现代信息融合技术在组合导航中的应用[M].北京: 国防工业出版社, 2010: 123-126.BIAN H W, LI A, QIN F J, et al. Modern information fusion technology in the application of the integrated navigation[M].Beijing: National Defence of Industry Press, 2010: 123-126.(in Chinese). |
| Cited By in Cnki (0) | Click to display the text | |
