目前解决Allan方差法估计误差大、震荡剧烈的理论有很多,包括#1理论方差[2]、ThêoH方差[3]、总方差[4]和重叠Allan方差法[5]等。其中总方差法是通过镜像映射的方法对数据进行延拓,新数据序列约为原始序列的3倍,增加了数据自由度和估计值稳定性,很好地解决了Allan方差法估计值震荡剧烈的问题。
动态Allan方差法[6-8]使用窗函数截取数据,再对窗内数据进行Allan方差分析,得到原始信号局部的随机误差特性,随着窗函数的移动就可以观测到整个数据段的随机误差特性。这就相当于在原始数据上使用了显微镜来观察其局部特性,然后在时间轴上滑动“显微镜”得到随机误差特性随时间的动态变化。
本文融合总方差法延拓数据和动态Allan方差法加窗的思想,提出动态总方差法。首先使用窗函数对原始随机序列进行分割,然后对窗内数据进行镜像映射来延拓数据,再对延拓后数据进行总方差分析,得到此时总方差值和各随机误差组分系数。随着窗函数的移动,就可得到总方差的二维分布图和各随机误差系数随时间的变化规律。最后针对动态总方差法计算量大、分析速度慢的问题,又推导了动态总方差法的递推公式和初值计算式,从而给出了动态总方差法的快速算法。
1 Allan方差及陀螺随机误差分析 1.1 Allan方差法原理 本节主要从Allan方差的定义、误差和功率谱关系等3个方面对Allan方差法进行分析。Allan方差法就是不断改变数据采集频率的一个过程,假设原始数据的采样周期为Ts,共采集了N个数据,则采集时间为N·Ts,记原始数据序列为{Ωi},i=1, 2, …, N。将采集频率增大为m·Ts,那么就需要对相邻的m个数据取平均值作为更改采样频率后的输出,而且求平均值时数据不允许重叠,那么改变采样频率后的数据长度为K=
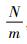
 | (1) |
式中:k为数据重新分组后Ω的序列。
则Allan方差的计算式为
 | (2) |
式中:τ=m·Ts为相关时间,m为平均因子;j为Ω(m)的序列号。需要强调的是式(2)给出的是Allan方差计算式,而不是定义式。那么计算值相对于真实值的相对误差为
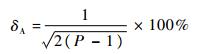 | (3) |
式中:P为重新采样后的输出数据数量,也可以理解为原始数据进行分组得到的组数;而P-1为Allan方差估计的独立数,由式(3)可以看出,Allan方差计算值的相对误差取决于P值,当采样频率过小(即输出数据量P很小)时,估计值相对误差δA就会很大,这就是长相关时间下误差大、震荡剧烈的原因。
参考文献[9]可知,Allan方差与功率谱密度的关系式为
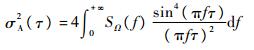 | (4) |
式中:SΩ(f)为功率谱密度,f为信号频率。可以将
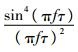
1.2 陀螺随机误差 一般来讲,将陀螺随机误差[10-11]分为角度随机游走(Angular Random Walk,ARW)、零偏不稳定性(Bias Instability,BI)、速率随机游走(Rate Random Walk,RRW)、速率斜坡(Rate Ramp,RR)和量化噪声(Quantization Noise,QN)。为了避免重复,只简要介绍其功率谱密度。
1)角度随机游走
角度随机游走的功率谱密度表达式为
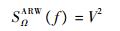 | (5) |
式中:V为角度随机游走系数,式(5)代入式(4)可得其Allen方差为
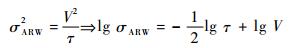 | (6) |
容易看出在Allan方差的双对数曲线中,斜率为

2)零偏不稳定性
零偏不稳定性的功率谱密度表达式为
 | (7) |
式中:B为零偏不稳定性系数,式(7)代入式(4)可得其Allen方差为
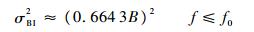 | (8) |
容易看出此时Allan方差为一常值,所以在Allan方差的双对数曲线中,斜率为0的噪声为零偏不稳定性。
3)速率随机游走
速率随机游走的功率谱密度表达式为
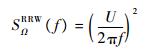 | (9) |
式中:U为速率随机游走系数,式(9)代入式(4)可得其Allen方差为
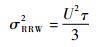 | (10) |
容易看出在Allan方差的双对数曲线中,斜率为

4)速率斜坡
速率斜坡的功率谱密度表达式为
 | (11) |
式中:R为速率斜坡系数,式(11)代入式(4)可得其Allen方差为
 | (12) |
容易看出在Allan方差的双对数曲线中,斜率为1的噪声为速率斜坡。
5)量化噪声
量化噪声的功率谱密度表达式为
 | (13) |
式中:Q为量化噪声系数,式(13)代入到式(4)可得其Allen方差为
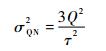 | (14) |
容易看出在Allan方差的双对数曲线中,斜率为-1的噪声为速率斜坡。
1.3 Allan方差法的缺陷 为了找出Allan方差的缺陷,分别仿真出平稳白噪声和方差渐大的白噪声如图 1所示,然后使用Allan方差法进行分析,分析结果如图 2所示。
 |
| 图 1 平稳白噪声和方差渐大白噪声 Fig. 1 Stationary white noise and white noise with gradually bigger variance |
| 图选项 |
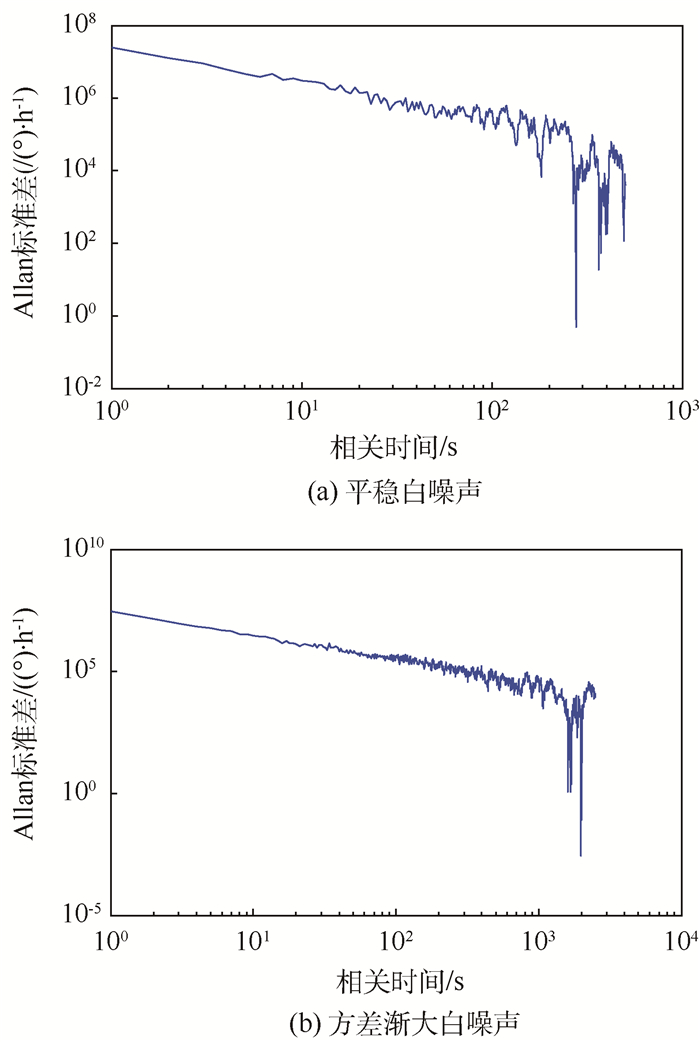 |
| 图 2 平稳白噪声和方差渐大白噪声Allan方差分析 Fig. 2 Allan variance analysis of stationary white noise and white noise with gradually bigger variance |
| 图选项 |
对比图 2的Allan方差分析结果,可以分析出Allan方差的2点缺陷:
1)在长相关时间下,由于Allan方差估计的自由度比较小,导致Allan方差估计值置信度比较低,相对误差比较大,震荡非常严重。
2)平稳白噪声和方差渐大白噪声分析结果相同,说明Allan方差无法跟踪随机序列的动态变化(即无法跟踪信号的方差变化)。
2 总方差法原理分析 Allan方差法存在的第1个缺陷是由于估计值的自由度比较小,那么很自然的一个想法就是通过数据延拓的方法增加数据的自由度。总方差(total variance)法就是通过镜像映射将原始数据进行延长,达到增加估计值置信度、稳定估计值的效果。
假设原始数据序列为{Ωi},序列长度为N,通过镜像映射后的序列为{Ωi*},其映射规则[12]为
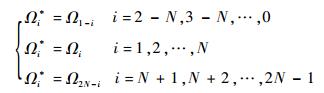 | (15) |
延拓后的序列长度为3N-2,约为原始数据的3倍。
总方差的计算式[13]为
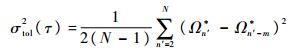 | (16) |
对比式(16)与式(1)和式(2)可以看出,总方差法没有重新采样的过程,而是直接使用原始数据,使数据的利用效率增加了。在总方差中,τ的最大值为N-1,在Allan方差中,τ的最大值为
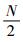
总方差的估计值相对误差[13]为
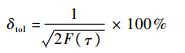 | (17) |
式中:F(τ)为相关时间为τ时的等效自由度, 其计算式为
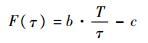 | (18) |
其中:T为数据采集的总时间,
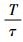
表 1 3种随机误差组分的偏差系数 Table 1 Deviation coefficients of three random error components
| 随机误差组分 | b | c | F(τ) |
| 零偏不稳定性 | 3/2 | 0 | 3.000 |
| 角度随机游走 | 24(ln 2)2/π2 | 0.222 | 2.097 |
| 量化噪声 | 140/151 | 0.358 | 1.514 |
表选项
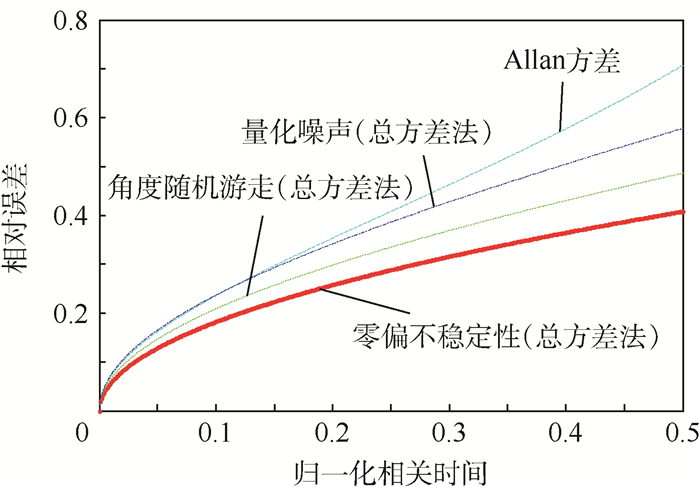
使用式(3)和式(17)计算出Allan方差法和总方差法在不同相关时间下的相对误差。为了便于统一和比较,将相关时间进行归一化处理τ/T,计算结果如图 3所示。
 |
| 图 3 Allan方差与总方差相对误差 Fig. 3 Relative error of Allan variance and total variance |
| 图选项 |
从图 3中可以看出,在相关时间较小的情况下,Allan方差和总方差法的相对误差相差不大;但是在相关时间较大的情况下,总方差法的相对误差比Allan方差法的相对误差小很多;当归一化相关时间为0.5时(即在Allan方差法中将所有数据分为2组),Allan方差估计值的相对误差为70.71%,量化噪声的总方差估计值相对误差为57.81%,角度随机游走的总方差估计值相对误差为40.82%,零偏不稳定性的总方差估计值相对误差为48.63%,说明了当归一化相关时间为0.5时,总方差法的估计值依然有效,其精度远远高于Allan方差法。
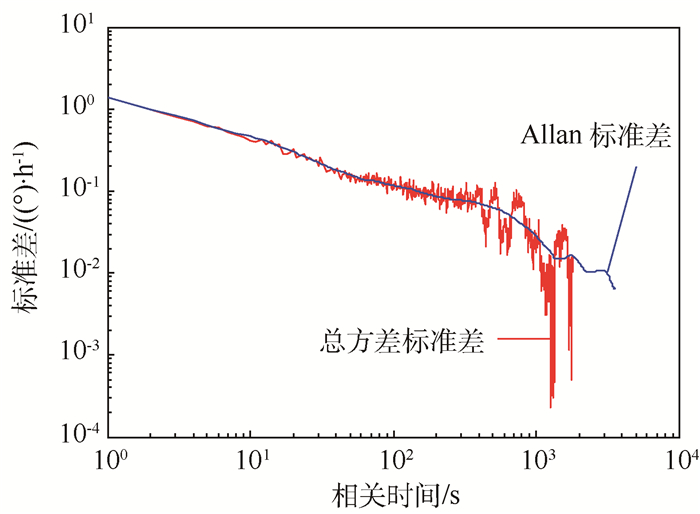
同时使用Allan方差法和总方差法对图 1(b)所示的随机序列进行分析,分析结果如图 4所示,从图中可以看出,总方差法在长相关时间下依然保持了较好的稳定性,解决了Allan方差法在长相关时间下震荡较大的问题。
 |
| 图 4 随机序列的Allan方差和总方差分析 Fig. 4 Allan variance and total variance analysis of random sequence |
| 图选项 |
3 动态Allan方差法分析 Allan方差法的第2个缺陷是无法跟踪信号的非平稳变化,那么可以用窗函数的方法,逐段截取数据对其进行Allan方差分析,窗函数就像显微镜一般,显微出原始数据的局部特性,然后将这些特性在时间轴上展开就可以得到随机特性随时间的变化,这就是动态Allan方差法的理论基础。动态Allan方差法的具体实现步骤[14-15]为
1)确定原始数据的分析时间起点t1和窗函数宽度W,要求
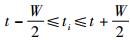
2)用中心点为t1、宽度为W的窗函数截断原始信号Ω(t)。
3)计算窗口内数据的Allan方差值σA2(t1, τ),并使用最小二乘拟合的方法得到此时的随机误差系数。
4)将窗口滑动到下一个时刻t2,要求以t2为中心的窗要与以t1为中心的窗互相重叠。重复步骤2)和步骤3),得到此时窗口内的Allan方差值σA2(t2, τ)和随机误差系数。
5)以此类推,重复上述过程,得到Allan方差值的集合{σA2(ti, τ)}(i=1, 2, …, n)和随机误差系数序列。以t和τ为变量,将Allan方差值的变化展现在三维分布图上,就得到了动态Allan分析的结果;将各时刻的随机误差系数在时间轴上展开,得到随机误差特性的动态变化过程。
使用动态Allan方差法分别分析图 1(a)和图 1(b)中的2种信号,分析结果如图 5所示。图中图形灰度的变化表示方差大小的变化,从图 5(b)中可以看出,随着原始信号方差的增大,动态Allan方差的灰度越来越深,可以很好地跟踪原始数据的动态变化。说明动态Allan方差法解决了Allan方差的第2个缺陷。
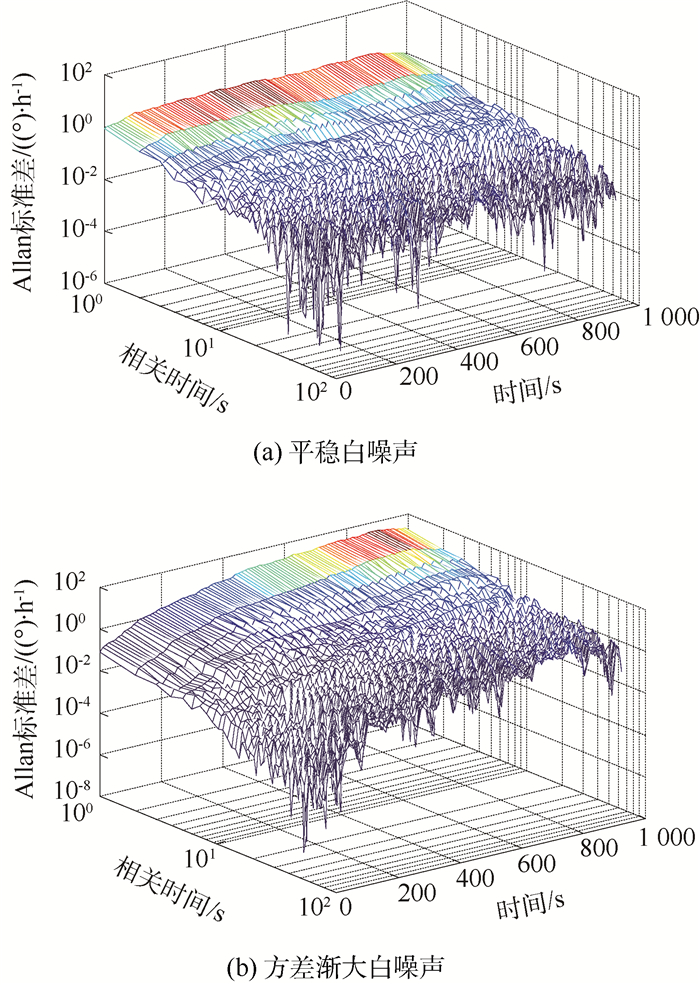 |
| 图 5 平稳白噪声和方差渐大白噪声动态Allan方差分析 Fig. 5 Dynamic Allan variance analysis of stationary white noise and white noise with gradually bigger variance |
| 图选项 |
4 动态总方差法设计 总方差法解决了Allan方差法长相关时间下震荡较大的问题;动态Allan方差法解决了Allan方差法无法跟踪随机信号动态变化的缺陷。结合2种算法的优势,本文提出了动态总方差法,其基本思想是:首先利用窗函数截取原始数据,然后对窗口内的数据进行镜像映射来延拓数据,再对延拓后的数据计算其总方差值,最终得到原始数据的动态总方差图和随机误差系数随时间的变化规律。
动态总方差法的具体实现步骤包括:
1)确定原始数据的分析起点t1和窗口宽度L。
2)用中心点为t1、宽度为L窗函数截取原始信号Ω(t),得到窗口截断信号ΩT(t1),支撑变量描述窗内渐逝的时间,记为t′,则
 | (19) |
记窗函数为PW(t′),则窗内信号为
 | (20) |
3)将窗内信号ΩT(t1, t′)按式(15)给出的方式进行镜像映射,得到延拓序列ΩT*(t1, t′)。
4)按照式(16)给出的总方差法计算式计算得到t1时刻的总方差值σtol2(t1, τ),同时使用最小二乘拟合得到t1时刻的随机误差系数。
5)将窗口滑动到t2,重复步骤2)~步骤4)得到t2时刻的动态总方差值σtol2(t2, τ)和随机误差系数。以此类推,得到动态总方差法序列{σtol2(ti, τ)}(i=1, 2, …, N)和各时刻的随机误差系数。
6)将动态总方差值展示在σtol-τ-t三维图中来分析信号的非平稳特征;将随机误差系数在时间轴上展开得到随机误差随时间的变化规律。
离散情况下,第n个窗截得的数据序列动态总方差的计算公式为
 | (21) |
式中:Ωj*[M]为第j个Ω*[M];Ωj-M*[M]为第j-M个Ω*[M]。
5 动态试验验证 为了验证所设计的动态总方差法的有效性,本文设计了半球谐振陀螺的线振动试验。线振动的初始加速度为5 g,采用弦函数方式施加在陀螺上。陀螺数据采集的频率为10 kHz,共采集了4 200个数据。首先去除输出信号中的趋势项而得到随机信号,如图 6所示,其动态总方差法分析如图 7所示。
 |
| 图 6 原始随机信号 Fig. 6 Original random signal |
| 图选项 |
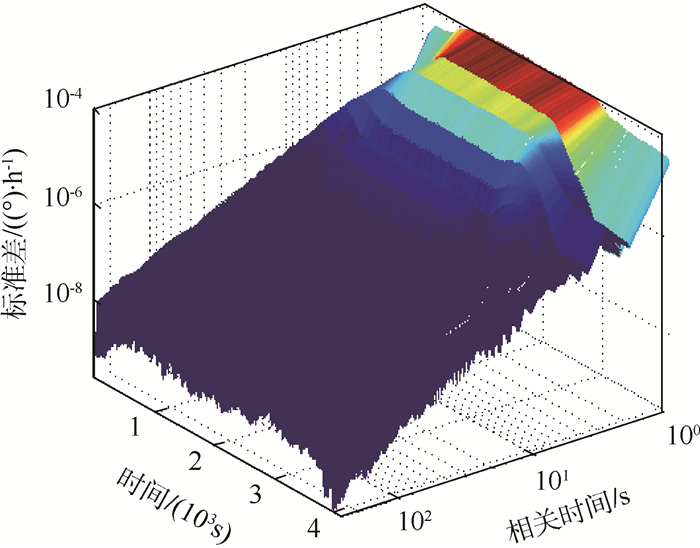 |
| 图 7 陀螺输出的动态总方差分析 Fig. 7 Dynamic total variance analysis of gyro output |
| 图选项 |
从图 7中可以看出灰度的变化,这是由于原始数据方差的变化引起的,说明动态总方差法可以跟踪信号的非平稳性变化。为了观察信号中随机误差组分的变化,分别使用动态Allan方差法和动态总方差法分析原始数据中的量化噪声系数Q、角度随机游走系数N、零偏不稳定性B,结果如图 8和图 9所示,图中t为时间。
 |
| 图 8 动态Allan方差分析结果 Fig. 8 Results of dynamic Allan variance analysis |
| 图选项 |
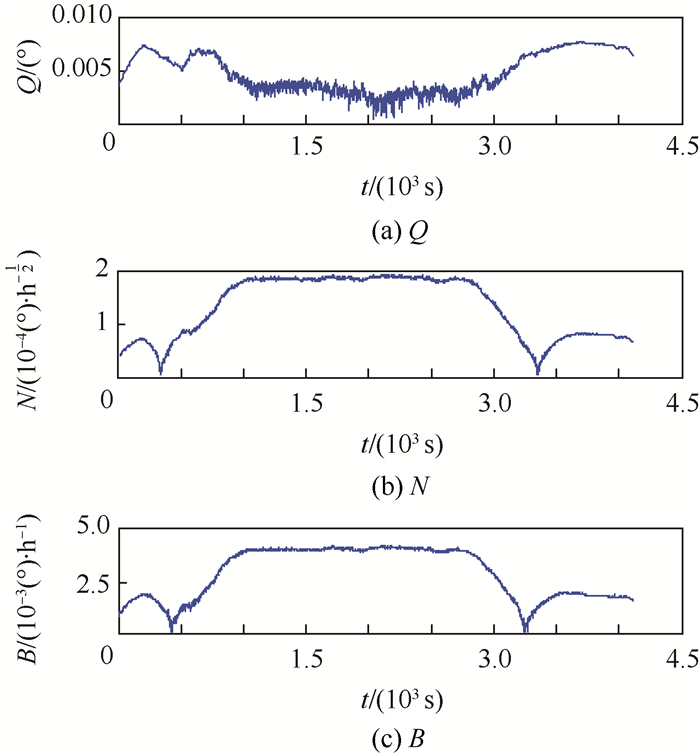 |
| 图 9 动态总方差法分析结果 Fig. 9 Results of dynamic total variance analysis |
| 图选项 |
对比图 8和图 9的处理结果可以得到:
1)从数量级上来讲,动态总方差法分析精度比动态Allan方差法至少高一个数量级。
2)角度随机游走和零偏不稳定性系数在振动过程中增大,而量化噪声系数在振动过程中减小,说明周期性振动弥补了量化噪声的周期性误差。
为了对比动态总方差法和动态Allan方差法的数据处理精度,选取1 000~2 600段数据,共1 600个。对这1 600个数据进行Allan方差分析,然后使用长度为401的窗口分割数据,分别进行动态Allan方差和动态总方差分析。由于Allan方差分析使用了1 600个点,具有数据量上的绝对优势,所以可以将其作为评价动态Allan方差法和动态总方差法的一个标准值。处理结果如表 2所示。
表 2 振动条件下陀螺噪声系数分析结果 Table 2 Noise coefficient analysis result of gyro in vibration condition
| 处理算法 | Q | N | B | V | R |
| Allan方差(1 600) | 3.8×10-3 | 1.8×10-4 | 3.8×10-3 | 2.8×10-2 | 6.7×10-2 |
| 动态总方差(401) | 3.2×10-3 | 1.9×10-4 | 3.9×10-3 | 2.9×10-2 | 7.5×10-2 |
| 动态Allan(401) | 4.8×10-2 | 2.5×10-3 | 3.7×10-2 | 0.4 | 1.2 |
表选项
以表 2中Allan方差法得到的结果作为标准,可以看出使用401点的动态总方差法处理结果与标准结果精度一致,说明在同等精度下,动态总方差法使用的数据约为Allan方差法的1/4;比较动态Allan方差法和动态总方差法处理结果可以看出,使用同等数据量时,动态总方差法达到的精度比动态Allan方差法高一个数量级。
6 动态总方差快速算法 从上面的分析可以看出,动态总方差法同时解决了Allan方差法存在的2个缺陷,而且在分析精度和使用数据量上也有了很大提高。但是动态总方差法使用窗函数截取数据,需要对每个窗函数内的数据进行总方差分析,计算量非常大,算法运行需要的时间特别长。针对这个问题,本文推导了基于递推公式的快速算法。
从第n个窗内数据的动态总方差计算式开始推导,其计算式为式(21),则第n+1个窗内数据的动态总方差计算式为
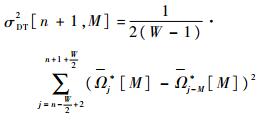 | (22) |
将式(22)变形为
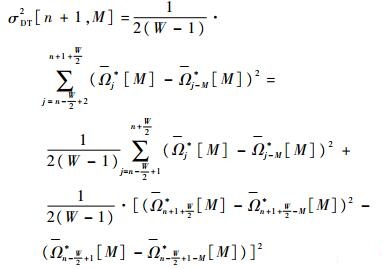 | (23) |
式中:第2个等号后的第1项即为σDT2[n, M],所以动态总方差法的递推公式为
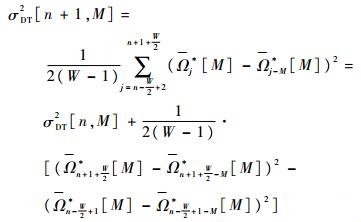 | (24) |
此递推公式的初始项即为第一个窗口的动态总方差值,设其为第n0个窗函数,其值需要按照定义式进行计算,即为
 | (25) |
式(25)和式(24)分别给出了动态总方差快速算法的初始值和递推公式。式(24)和式(25)组合在一起就是动态总方差法的快速算法。
通过对比总方差法的定义式和递推公式可以看出,按照定义式进行计算时,每个窗口需要计算W+1次乘法、2W-1次加法;而按照递推公式进行计算时,每个窗口需要计算3次乘法、4次加法。而整个分析过程共有N-W+1个窗口,那么快速算法就会大大节约算法的运行时间。
为了对上述分析结果进行验证,将窗函数固定为
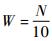
表 3 传统算法与快速算法运行时间 Table 3 Runtime of traditional and fast algorithms
| 数据长度 | 运行时间/s | |
| 传统算法 | 快速算法 | |
| 102 | 3.0×10-3 | 3.1×10-4 |
| 103 | 0.30 | 4.5×10-3 |
| 104 | 118 | 0.25 |
表选项
从表 3给出的结果可以看出,快速算法相对于定义式算法大大节约了运行时间;而且随着数据量的增加,2种算法运行的时间相差也越来越大,快速算法的优势也越明显。
7 结论 1)本文设计了动态总方差法,当使用相同的数据量进行分析时,动态总方差法相对于动态Allan方差法的分析精度至少提高了一个数量级;当分析精度一致时,动态总方差法需要的数据量是Allan方差法的1/4。
2)本文设计了动态总方差法的快速算法,对比快速算法和定义式算法的运行时间可以看出,快速算法极大地减少了算法的运行时间,而且原始数据量越大,则快速算法的优势越明显。
参考文献
| [1] | Gyro and Accelerometer Panel of the IEEE Aerospace and Electronic Systems Society.IEEE standard specification format guide and test procedure for single-axis interferometric fiber optic gyros:IEEE STD 952TM-1997[S].Piscataway, NJ:IEEE Standards Board, 1998. |
| [2] | 程旭维, 汤霞清, 黄湘远. 基于#1理论方差的光学陀螺长期随机误差分析[J].中国激光, 2014, 41(10): 146–153.CHENG X W, TANG X Q, HUANG X Y. Investigation on random error properties of optic gyroscope based on theoretical variance #1[J].Chinese Journal of Lasers, 2014, 41(10): 146–153.(in Chinese) |
| [3] | HOWE D A. Thêo H:A hybrid, high-confidence statistic that improves on the Allan deviation[J].Metrologia, 2006, 43: 322–331.DOI:10.1088/0026-1394/43/4/S20 |
| [4] | HOWE D A. The total deviation approach to long-term characterization of frequency stability[J].IEEE Transactions on Ultrasonic, Ferroelectrics, and Frequency Control, 2000, 47(5): 1102–1110.DOI:10.1109/58.869040 |
| [5] | RILEY W J.Techniques for frequency stability analysis[C]//IEEE International Frequency Control Symposium.Piscataway, NJ:IEEE Press, 2003. |
| [6] | GALLEANI L. The dynamic Allan variance III:Confidence and detection surfaces[J].IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2011, 58(8): 1550–1558.DOI:10.1109/TUFFC.2011.1982 |
| [7] | DOBROGOWSKI A, KASZNIA M.Real-time assessment of dynamic Allan deviation and dynamic time deviation[C]//Proceeding of the 2012 European Frequency and Time Forum.Piscataway, NJ:IEEE Press, 2012:247-252. |
| [8] | GALLEANI L, TAVELLA P. The dynamic Allan variance[J].IEEE Transaction on Ultrasonics, Ferroelectrics, and Frequency Control, 2009, 56(3): 450–460.DOI:10.1109/TUFFC.2009.1064 |
| [9] | 李颖.慢光光纤陀螺关键技术研究[D].哈尔滨:哈尔滨工业大学, 2009.LI Y.Key techniques for the slow light fiber optic gyroscope[D].Harbin:Harbin Institute of Technology, 2009(in Chinese). |
| [10] | 吕琳, 全伟. 基于GP+GA的陀螺随机误差建模分析[J].北京航空航天大学学报, 2015, 41(6): 1135–1140.LYU L, QUAN W. Modeling and analysis of gyroscope's random drift based on GP+GA method[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(6): 1135–1140.(in Chinese) |
| [11] | 祁家毅, 任顺清, 冯士伟, 等. 半球谐振陀螺随机误差分析[J].中国惯性技术学报, 2009, 17(1): 98–101.QI J Y, REN S Q, FENG S W, et al. Random error analysis of hemispherical resonator gyro[J].Journal of Chinese Inertial Technology, 2009, 17(1): 98–101.(in Chinese) |
| [12] | 韩军良, 葛升民, 沈毅. 基于总方差方法的光纤陀螺随机误差特性研究[J].哈尔滨工业大学学报, 2007, 39(5): 708–711.HAN J L, GE S M, SHEN Y. Research on the random error properties of FOG based on total variance[J].Journal of Harbin Institute of Technology, 2007, 39(5): 708–711.(in Chinese) |
| [13] | 石国祥, 陈坚, 叶军, 等. 总方差方法在光纤陀螺随机误差分析中的应用[J].光电工程, 2012, 39(1): 63–67.SHI G X, CHEN J, YE J, et al. Applications of total variance method in random error analysis of the fiber optic gyro signal[J].Opto-Electronic Engineering, 2012, 39(1): 63–67.(in Chinese) |
| [14] | 李冀辰, 高凤岐, 王广龙, 等. 光纤陀螺振动和变温条件下的DAVAR分析[J].中国激光, 2013, 40(9): 184–190.LI J C, GAO F Q, WANG G L, et al. Analysis of dynamic allan variance for fiber optic gyro under vibration and variable temperature conditions[J].Chinese Journal of Laser, 2013, 40(9): 184–190.(in Chinese) |
| [15] | ZHANG C X, WANG L, GAO S, et al. Dynamic Allan variance analysis for stochastic errors of fiber optic gyroscope[J].Infrared and Laser Engineering, 2014, 43(9): 3081–3088. |
