许多****已就压电风扇问题进行了多方面的研究。Toda[1]从实验和理论两方面研究了压电风扇产生的流场,得出了流量与各个参数之间的关系。Kim等[2]通过实验,使用粒子图像测速仪(PIV)研究了悬臂板以其一阶固有频率振动时诱导的流场,同时将理论推导出的流场漩涡特性与实验结果进行对比。Kimber等[3-4]通过红外照相机观察压电风扇的散热效果, 并研究了振动薄片与流场之间的耦合作用。Yoo等[5]通过实验研究振动薄片的材料和尺寸对压电风扇散热效果的影响。给出了在一定的情况下,压电风扇最优的制作材料和尺寸。Wu和Ro[6]用有限元方法分析了实验中所使用的振动薄片的固有频率,进而用流动显示实验研究了热源与振动薄片的距离等因素对流场发展以及散热效率的影响。Florio和Harnoy[7]用数值模拟的方法,研究了包括压电风扇在内的多种散热方式相结合产生的散热效率。Aikalin等[8-9]同时使用实验和数值模拟的方法,研究了多种参数对压电风扇散热效率的影响。还将制作的压电风扇原型装入笔记本电脑。通过测量温度验证了压电风扇的散热效果。Schmidt[10]研究了双振动薄片组成的压电风扇的质量传导特性。另外,贾丽杰[11]、Qureshi[12]和朱熹育[13]等对压电驱动器原理以及相关的控制问题等进行了多方面的研究。
本文的研究目的,即选择几种提高压电风扇性能的可能方案,探究相关因素对压电风扇性能的影响规律并分析其原因,为压电风扇的设计提供指导性的意见和建议。本文主要研究了两个方面的内容,一方面研究了压电风扇振动薄片高阶固有振型的影响,另一方面研究了两种压电风扇振动薄片的排布形式对压电风扇性能的影响。研究使用FLUENT商用软件以及动网格技术。通过用户自定义函数(User-Defined Functions,UDF)控制流场边界运动,模拟压电风扇振动薄片的振动并进行计算。采集处理压电风扇出口风速数据,得出各个因素对压电风扇出口风速的影响。通过分析流场的发展情况,给出各个因素对压电风扇性能影响的成因。
1 计算模型与数据处理 1.1 计算模型 压电风扇主要结构包括由压电材料制成的驱动器和振动薄片。根据实际中压电风扇的外形特征,将压电风扇设计成如图 1所示的结构。
 |
| 图 1 压电风扇结构剖面 Fig. 1 Cross section of a piezoelectric fan |
| 图选项 |
压电风扇整体为管状结构,观察压电风扇的剖面图(图 1所示)。四周黑色部分是压电风扇的外壳及支撑结构;白色长条状结构是振动薄片,振动薄片左侧插入支撑结构中;振动薄片根部灰色方块状结构是由压电材料制作的驱动器,驱动器与振动薄片紧密贴合。当通以交流电时,驱动器会产生周期性的伸长和缩短,从而激励振动薄片振动。振动薄片振动扇动周围空气流动进而产生持续的气流。
为简化计算,在FLUENT软件中,将压电风扇简化为如图 2所示的二维计算模型,悬臂板模型简化为悬臂梁模型,并删除驱动器结构和支撑结构的多余部分。模型尺寸参数和坐标方向如图 2中标注所示。
 |
| 图 2 标准模型计算域示意图 Fig. 2 Schematic of computational domain for standard model |
| 图选项 |
计算中,空气沿图中箭头方向流动。入口和出口分别为流场的压力入口和压力出口边界,上下壁面分别为流场的上下边界。其他参数保持默认值。振动薄片位于流场Y方向的中间位置。流场高度为H,振动薄片厚度为h,振动薄片的长度为l,流场的长度为L。使用UDF控制振动薄片上、下和右边界运动,以此来模拟振动薄片的振动过程。
由于本文中涉及到的计算模型较多,为研究方便,在此定义标准计算模型,将具有以下尺寸的单振动薄片模型称为标准模型:总长L=50.0 mm, 高H=10.0 mm, 振动薄片长l=40.0 mm, 厚度h=0.5 mm。并以标准模型的计算结果作为其他模型计算结果的参照。
注意到本文的研究目的,综合考虑计算精度和计算效率,计算模型的网格划分情况如图 3所示。该模型与图 2所示模型相同。
 |
| 图 3 FLUENT中使用的网格示意图 Fig. 3 Schematic of grid used in FLUENT |
| 图选项 |
本文的研究着眼于参数对压电风扇性能的影响规律,主要关注相应流场的发展情况。通过与相关文献[2, 9, 14]对比,确保本文计算结果的准确性与可信性。在后面的内容中将有具体说明。
1.2 数据处理 使用FLUENT软件提供的Monitor功能,实时采集使用质量加权方法(mass-weighted method)得到的出口边界风速的平均值。考虑到散热效果主要与X方向的空气流量有关,采集出口边界上X方向的风速分量数据并进行处理。
下面说明数据处理方法,以压电风扇标准模型在50 Hz的频率下工作的计算结果为例,说明数据处理方法。根据上一段中描述的方法,画出在一段时间内,流场出口边界X方向的实时风速值, 如图 4所示。
 |
| 图 4 流动时间与出口风速 Fig. 4 Wind velocity at outlet versus flow time |
| 图选项 |
在图 4中,选择一段较长的风速变化平稳的区间,计算该区间内所有时刻对应风速的平均值,将这一数值作为衡量该计算模型散热效率的度量。
2 不同因素对出口风速的影响 2.1 高阶固有振型 压电风扇利用了共振原理,让激振频率等于振动薄片的固有频率,使得振动薄片在很小的载荷下达到较大的振幅。
已有的研究也多令振动薄片以其一阶固有频率振动。此时,出口风速与振动薄片的振动频率成正比[15]。相比一阶固有频率,振动薄片的高阶固有频率更高。如果让振动薄片以其高阶固有频率振动,则可以大幅度提高振动薄片的振动频率。此时,振动薄片将以其高阶固有振型振动。本节的研究目的即探究高阶固有振型对流场的影响。
需要说明的是,不同的振动薄片,其固有频率不同。在本文中,为了计算和建模的方便,不再为每种振动频率分别建立计算模型,而是通过修改UDF直接改变振动薄片的振动频率。为了方便理解,在此假定本文所有算例中为振动薄片设定的振动频率等于其相应阶数的固有频率,并且振动薄片按照相应阶数的振型振动。
当施以正弦激励时,振动薄片上各点在Y方向上以正弦规律运动[16]。因此,将振动薄片上各点的振动形式设为[14]
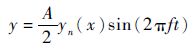 | (1) |
式中:x为振动薄片上各点的横坐标;y为各点的纵坐标;f为振动薄片的振动频率;yn(x)为振型函数,n为振型的阶数;A为振动薄片右端点的振幅(本文中A=4.0 mm保持不变);t为振动时间。通过设置yn(x), 为振动薄片选取不同的振型函数。根据振动理论[17],悬臂梁的固有振型函数为
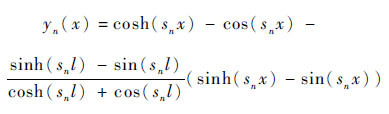 | (2) |
其中:sn为频率方程式(3) 的解;l为振动薄片的长度。
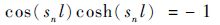 | (3) |
其中方程式(3) 的解为snl=1.875 1,4.694 1,7.854 8,10.995 5,14.137 2,…。
分别计算标准模型以各阶固有振型振动时,在不同振动频率下得到的出口风速。计算结果如图 5所示。
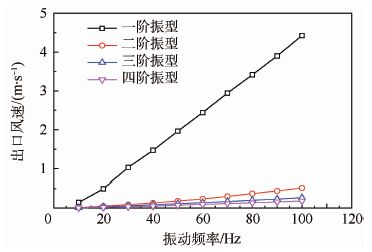 |
| 图 5 不同振型下的出口风速与频率 Fig. 5 Wind velocity at outlet versus frequency for models with different flexural modes |
| 图选项 |
由图 5可以看出,使用一阶固有振型计算得到的出口风速远远大于高阶振型得到的风速。在下面的计算中,振动薄片都是以一阶固有振型振动。
2.2 双振动薄片纵向布置 为了提高压电风扇的散热效率,本文提出了两种可能方案:双振动薄片横向布置和纵向布置。本节和2.3节将研究双振动薄片同时振动对压电风扇性能的影响。
本节研究双振动薄片纵向布置形式对出口风速的影响。纵向布置双振动薄片模型主要结构示意图(剖面图)如图 6所示。
图 6中各结构的名称和颜色与图 1中相同,在此不再赘述。
 |
| 图 6 纵向布置双振动薄片模型结构示意图 Fig. 6 Schematic of model structure with two vibrating plates oriented in vertical direction |
| 图选项 |
计算域如图 7所示。
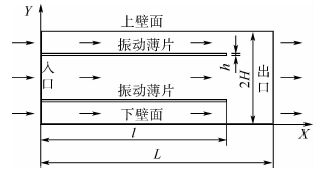 |
| 图 7 纵向布置双振动薄片模型计算域示意图 Fig. 7 Schematic of computational domain for model with two vibrating plates oriented in vertical direction |
| 图选项 |
与标准模型对比,纵向布置双振动薄片模型的高度是标准模型的2倍,即2H。振动薄片分别布置在纵向高度的1/4和3/4处。其他参数相同,两振动薄片以相同频率振动。
两振动薄片同时以相同频率振动时,相位差是该问题中一个不确定因素。因此,先确定两振动薄片的振动相位差对出口风速的影响。计算当振动薄片以50 Hz和100 Hz振动,相位差分别取0,0.1π,…,π,…,1.9π,2π时对应的出口风速。相位差等于上方振动薄片的振动相位减去下方振动薄片的相位。以相位差为横坐标,出口风速为纵坐标画图,如图 8所示。注意,图中横坐标与π相乘后才是对应的相位差。
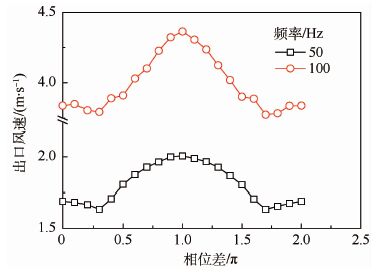 |
| 图 8 频率为50 Hz和100 Hz时相位差与出口风速(纵向布置) Fig. 8 Wind velocity at outlet versus phase difference for frequencies of 50 Hz and 100 Hz (plates oriented in vertical direction) |
| 图选项 |
由图 8可以看出,当两个振动薄片的振动相位差为π时,出口风速最大;当相位差约为0.3π和1.7π时,出口风速最小。
下面来比较纵向布置双振动薄片模型与单振动薄片模型的出口风速。根据周期性原理,相位差取0.3π和1.7π时,计算结果完全相同,在此只选取相位差为0.3π的情况计算。取振动薄片振动相位差为0.3π和π,计算具有两种振动相位差的模型在不同振动频率下的出口风速。将计算结果与单振动薄片模型在相同振动频率下的计算结果对比,计算结果如图 9所示。
 |
| 图 9 3种模型出口风速比较(纵向布置) Fig. 9 Comparison of wind velocity at outlet among three models (plates oriented in vertical direction) |
| 图选项 |
由图 9可以看出,两振动薄片的振动相位差为π时,其出口风速与单振动薄片模型的基本相同。当振动相位差为0.3π时,其出口风速较上述两种模型更小。
2.3 双振动薄片横向布置 本节研究双振动薄片横向布置形式对出口风速的影响。横向布置双振动薄片模型结构示意图(剖面图)如图 10所示。
图 10中各结构的名称和颜色与图 1中相同,在此不再赘述。
 |
| 图 10 横向布置双振动薄片模型结构示意图 Fig. 10 Schematic of model structure with two vibrating plates oriented in horizontal direction |
| 图选项 |
计算域如图 11所示。
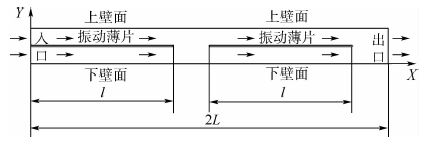 |
| 图 11 横向布置双振动薄片模型计算域示意图 Fig. 11 Schematic of computational domain for model with two vibrating plates oriented in horizontal direction |
| 图选项 |
与标准模型对比,横向布置双振动薄片模型的长度是标准模型的2倍,即2L。振动薄片都布置在纵向高度的1/2处。其他参数相同,两振动薄片以相同频率振动。
与2.2节相同,先确定两振动薄片的振动相位差对出口风速的影响。计算当振动薄片以50 Hz和100 Hz振动,相位差分别取0,0.1π,…,π,…,1.9π,2π时对应的出口风速的大小。本节中,相位差等于右方振动薄片的振动相位减去左方振动薄片的振动相位。以相位差为横坐标,出口风速为纵坐标画图,如图 12所示。注意,图中横坐标与π相乘后才是对应的相位差。
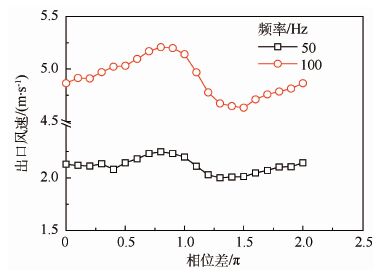 |
| 图 12 频率为50 Hz和100 Hz时相位差与出口风速(横向布置) Fig. 12 Wind velocity at outlet versus phase difference for frequencies of 50 Hz and 100 Hz (plates oriented in horizontal direction) |
| 图选项 |
从图 12中可以看出,当振动薄片的振动相位差为0.8π时,出口风速最大,当相位差约为1.4π时,出口风速最小。
下面来比较横向布置双振动薄片模型与单振动薄片模型的出口风速。取振动相位差为0.8π和1.4π,计算具有2种相位差的模型在不同振动频率下的出口风速。将2种模型的计算结果与单振动薄片模型的对比,计算结果如图 13所示。
由图 13可以看出,双振动薄片横向布置时,不论振动薄片的相位差取多少,模型的出口风速均大于相同振动频率下单振动薄片模型的出口风速。但是,这种布置方式对风速的提升作用有限。
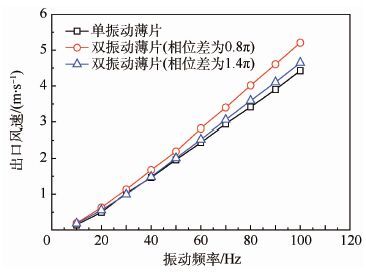 |
| 图 13 3种模型出口风速比较(横向布置) Fig. 13 Comparison of wind velocity at outlet among three models (plates oriented in horizontal direction) |
| 图选项 |
3 计算结果分析 在解释相关因素的影响作用之前,先明确压电风扇的工作原理即其能产生持续气流的原因。
研究表明,压电风扇的出口风速与压电风扇流场中产生的漩涡密切相关[14]。由于在流场中不断有漩涡产生,且产生的漩涡随即被推向出口方向,故而压电风扇能产生持续不断的气流。下面来具体说明这一过程。观察压电风扇流场漩涡示意图,如图 14所示。
 |
| 图 14 具有一阶固有振型的模型风速分布 Fig. 14 Wind velocity distribution for model with first order fundamental flexural modes |
| 图选项 |
图 14展示了标准模型在一个振动周期T内T/2时刻的流场速度分布图(振动薄片以一阶固有振型振动)。此时振动薄片过平衡位置向下运动并在其上侧产生一个漩涡。
在一个振动周期T内,从0时刻到T/4时刻,振动薄片由平衡位置向上运动,在振动薄片自由端下侧产生一个漩涡。从T/4时刻到3T/4时刻,振动薄片向下运动,挤压振动薄片下侧的漩涡并推动漩涡向出口方向运动。同时,在振动薄片自由端上侧产生另一个漩涡。从3T/4时刻到T时刻,振动薄片向上运动,推动振动薄片上方的漩涡向出口方向运动。振动薄片周期性上下振动,不断产生新的漩涡并随后将产生的漩涡推向出口方向从而产生了沿X轴正方向的持续不断的气流。
而漩涡的产生又与流场低压区有关。一个周期T内T/2时刻流场压强分布如图 15所示。图中,暖色区压强高,冷色区压强低,下同。
 |
| 图 15 具有一阶固有振型的模型压强分布 Fig. 15 Pressure distribution for model with first order fundamental flexural mode |
| 图选项 |
对比图 14和图 15可以看出,漩涡的直接成因是振动薄片运动在流场中产生了低压区,低压区与周围区域形成压强差进而卷吸周围空气产生漩涡。
以上关于压电风扇流场发展的模拟结果,与文献[14]通过数值模拟得到的结果以及文献[2, 9]通过流场显示实验观测到的结果基本一致。在此可以确定,本文对流场的模拟计算结果具有较高的可信度。
下面来说明计算结果的成因即相关因素对压电风扇性能的影响作用。
3.1 高阶固有振型 计算结果表明:振动薄片应以其一阶固有振型振动,即激振频率应等于振动薄片的一阶固有频率。
以上结论的成因主要与高阶固有振型的节点(不动点)位置有关。由于节点的存在,在高阶固有振型对应的流场中,没有明显的漩涡产生。因此,相应的压电风扇产生的出口风速非常小。下面来具体分析。
观察标准模型,当振动薄片以二阶固有振型振动时计算得到的流场速度分布图,如图 16所示。
 |
| 图 16 具有二阶固有振型的模型速度分布 Fig. 16 Velocity distribution for model with second order fundamental flexural mode |
| 图选项 |
图 16对应一个振动周期T内T/2时刻,振动薄片的振动频率为50 Hz。
对比图 14和图 16可以看出,在二阶固有振型对应的流场中,由于节点的存在,气流在振动薄片的推动下绕着节点往复运动。此时流场中没有图 14所示的漩涡产生,因此无法产生较大的沿X方向的出口风速。
与二阶固有振型相比,二阶以上固有振型只在节点数量方面与之不同。其对应流场的发展规律与二阶固有振型完全类似,故而也无法产生较大的出口风速。
3.2 双振动薄片纵向布置 计算结果表明:对于纵向布置双振动薄片模型,两个振动薄片振动相位差为π时,出口风速最大,且等于相同振动频率下单振动薄片模型的出口风速。当振动相位差为0.3π时出口风速最小。
造成以上计算结果的原因有两个:对称性和孤立漩涡。当振动相位差为π时,由于对称性,该情况对应的流场与单振动薄片的非常类似,产生的出口风速也与之几乎相同。当振动相位差为0.3π时,由于振动的非对称性,相同时间内流场产生的漩涡数量比较少。同时,每个振动薄片都通过孤立漩涡干扰另一个振动薄片产生漩涡(此漩涡即图 14所示的与出口风速直接相关的漩涡)。因此,振动相位差为0.3π的双振动薄片模型的出口风速最小。下面详细说明这一过程。
首先说明对称性的作用原理。观察振动相位差为0和π时,在一个振动周期T内T/2时刻的流场速度分布,如图 17所示。其中,振动薄片的振动频率是50 Hz。
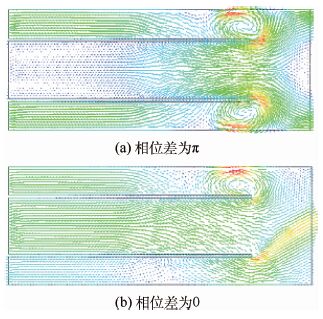 |
| 图 17 流场速度分布比较(纵向布置) Fig. 17 Comparison of flow field velocity distribution(plates oriented in vertical direction) |
| 图选项 |
由图 17可以看出,反相振动双振动薄片模型的流场(图 17(a))关于流场横向中轴线对称,且每一半镜像与单振动薄片模型的流场(图 14)几乎完全相同。流场发展过程的高度相似性,导致其出口风速与单振动薄片模型的几乎完全相同。
观察图 17(b),由于振动薄片运动的非对称性,同一时刻流场中只产生一个漩涡,而反相振动时(图 17(a))是两个。数量较少的漩涡,单位时间内携带的空气总量较少,导致其出口风速比较小。
下面说明孤立漩涡的影响作用。当振动相位差为0.3π时,将其流场与同相振动时的流场对比,流场速度分布如图 18所示。
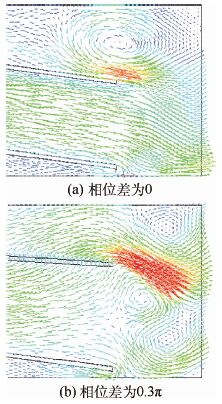 |
| 图 18 具有不同相位差的两种模型速度分布(纵向布置) Fig. 18 Velocity distribution for two models with different phase differences (plates oriented in vertical direction) |
| 图选项 |
图 18(a) 和图 18(b) 分别对应下方振动薄片运动到最低点时刻,振动薄片自由端附近流场的速度分布图。相位差为0.3π时(图 18(b)),当下方振动薄片到达最低位置开始反方向运动时,在其下侧产生一个漩涡(称为主漩涡)。于此同时,上方振动薄片产生的孤立漩涡会不断向下运动,并最终与主漩涡融合。在孤立漩涡的影响下,主漩涡卷吸空气能力下降。最终导致出口风速减小。因此,双振动薄片模型,相位差为0.3π时对应出口风速小于相位差为0时的出口风速。
3.3 双振动薄片横向布置 计算结果表明:对于横向布置双振动薄片模型,当振动相位差为0.8π时,出口风速最大。当振动相位差约为1.4π时,出口风速最小。但是,不论相位差取何值,横向布置双振动薄片模型的出口风速均大于相同振动频率下单振动薄片模型的出口风速。
研究表明,以上结论主要与气流通过压电风扇时的流畅程度有关。当振动相位差不同时,流场中高压区和低压区的相对位置不同,这会对气流产生加强或者阻碍的作用,从而对压电风扇出口风速产生影响。下面将对以上解释做详细说明。
在50 Hz的频率下振动时,观察相位差为0.8π和1.4π的两种压电风扇计算模型,当左方振动薄片运动到最高点时,左方振动薄片自由端附近的流场速度分布图和压强分布图,如图 19和图 20所示。
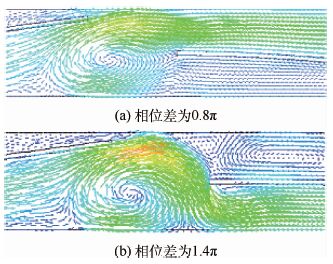 |
| 图 19 具有不同相位差的两种模型速度分布(横向布置) Fig. 19 Velocity distribution for two models with different phase differences (plates oriented in horizontal direction) |
| 图选项 |
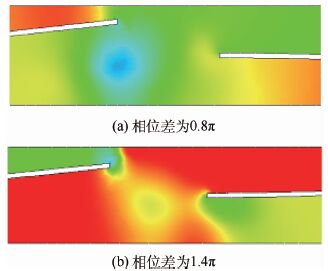 |
| 图 20 具有不同相位差的两种模型压强分布(横向布置) Fig. 20 Pressure distribution for two models with different phase differences (plates oriented in horizontal direction) |
| 图选项 |
当左方振动薄片运动到最高位置时,其下侧漩涡的旋转方向均为顺时针。对于相位差为0.8π的模型(图 19(a)和图 20(a)),其右方振动薄片此时向下运动,在其上侧形成低压区,低压区顺势卷吸漩涡。对于相位差为1.4π的模型(图 19(b)和图 20(b)),其右方振动薄片此时向上运动,在其上侧形成高压区,高压区阻碍了顺时针旋转的气流的流动并迫使其流向右方振动薄片下侧的低压区。与此同时,气流动能减小,流速降低。然而,左方振动薄片的存在,总会使得右方振动薄片流场的进场气流初始速度大于零,对气流产生加速作用。
对于横向布置双振动薄片模型,两振动薄片必须以合适的相位差振动,该相位差的取值与漩涡的转速以及两振动薄片之间的距离有关。不同的压电风扇,其最佳取值不同。
4 结论 本文分析研究了多个因素对压电风扇性能的影响,得到以下结论。
1) 驱动器的激振频率应等于振动薄片的一阶固有频率,即振动薄片应以其一阶固有振型振动。此时计算得到的出口风速远大于以高阶振型计算得到的出口风速。
2) 纵向布置双振动薄片模型,振动频率不变时,两振动薄片振动相位差为π时出口风速最大,相位差为0.3π或者1.7π时出口风速最小。最大出口风速与相同振动频率下的单振动薄片模型的出口风速相同。
3) 横向布置双振动薄片模型,振动频率不变时,两振动薄片振动相位差为0.8π时出口风速最大,相位差约为1.4π时出口风速最小。不论相位差取何值,横向布置双振动薄片模型的出口风速均大于相同振动频率下的单振动薄片模型的出口风速。
参考文献
| [1] | TODA M. Theory of air flow generation by a resonant type PVF2 bimorph cantilever vibrator[J].Ferroelectrics, 1978, 22(1): 911–918.DOI:10.1080/00150197908239445 |
| [2] | KIM Y H, WERELEY S T, CHUN C H. Phase-resolved flow field produced by a vibrating cantilever plate between two endplates[J].Physics of Fluids (1994-present), 2003, 16(1): 145–162. |
| [3] | KIMBER M, GARIMELLA S V, RAMAN A. Local heat transfer coefficients induced by piezoelectrically actuated vibrating cantilevers[J].Journal of Heat Transfer, 2007, 129(9): 1168–1176.DOI:10.1115/1.2740655 |
| [4] | KIMBER M,GARIMELLA S V,RAMAN A.An experimental study of fluidic coupling between multiple piezoelectric fans[C]//10th Intersociety Conference on Thermal and Thermomechanical Phenomena and Emerging Technologies in Electronic Systems,ITherm 2006.Piscataway,NJ:IEEE Press,2006:333-340. |
| [5] | YOO J H, HONG J I, CAO W. Piezoelectric ceramic bimorph coupled to thin metal plate as cooling fan for electronic devices[J].Sensors and Actuators A:Physical, 2000, 79(1): 8–12.DOI:10.1016/S0924-4247(99)00249-6 |
| [6] | WU T, RO P I. Heat transfer performance of a cooling system using vibrating piezoelectric beams[J].Journal of Micromechanics and Microengineering, 2005, 15(1): 213–220.DOI:10.1088/0960-1317/15/1/030 |
| [7] | FLORIO L A, HARNOY A. Combination technique for improving natural convection cooling in electronics[J].International Journal of Thermal Sciences, 2007, 46(1): 76–92.DOI:10.1016/j.ijthermalsci.2006.03.007 |
| [8] | A?IKALIN T, GARIMELLA S V, RAMAN A, et al. Characterization and optimization of the thermal performance of miniature piezoelectric fans[J].International Journal of Heat and Fluid Flow, 2007, 28(4): 806–820.DOI:10.1016/j.ijheatfluidflow.2006.10.003 |
| [9] | A?IKALIN T, WAIT S M, GARIMELLA S V, et al. Experimental investigation of the thermal performance of piezoelectric fans[J].Heat Transfer Engineering, 2004, 25(1): 4–14.DOI:10.1080/01457630490248223 |
| [10] | SCHMIDT R R.Local and average transfer coefficients on a vertical surface due to convection from a piezoelectric fan[C]//Proceedings of the Intersociety Conference on Thermal Phenomena in Electronic Systems.Piscataway,NJ:IEEE Press,1994:41-49. |
| [11] | 贾丽杰, 李敏, 陈伟民. 压电驱动器应变传递模型分析[J].工程力学, 2010, 27(8): 205–210.JIA L J, LI M, CHEN W M. The model analysis of strain transfer in the application of piezoelectric actuators[J].Engineering Mechanics, 2010, 27(8): 205–210.(in Chinese) |
| [12] | QURESHI E M, SHEN X, CHEN J J. Vibration control laws via shunted piezoelectric transducers:A review[J].International Journal of Aeronautical and Space Sciences, 2014, 15(1): 1–19.DOI:10.5139/IJASS.2014.15.1.1 |
| [13] | 朱熹育, 王社良, 朱军强. 基于Sugeno型模糊神经网络的空间杆系结构的压电驱动器主动控制[J].工程力学, 2013, 30(8): 272–277.ZHU X Y, WANG S L, ZHU J Q. Sugeno-type fuzzy neural network active control of space frame structure based on piezoelectric actuator[J].Engineering Mechanics, 2013, 30(8): 272–277.(in Chinese) |
| [14] | 谭蕾, 谭晓茗, 张靖周. 压电风扇激励非定常流动和换热特性数值研究[J].航空学报, 2013, 34(6): 1277–1284.TAN L, TAN X M, ZHANG J Z. Numerical investigation on unsteady flow and heat transfer characteristics of piezoelectric fan[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1277–1284.(in Chinese) |
| [15] | 孔岳, 李敏, 吴蒙蒙. 压电风扇非定常流场速度分布的数值研究[J].工程力学, 2016, 33(1): 209–216.KONG Y, LI M, WU M M. Numerical investigation on the velocity of unsteady flow field induced by piezoelectric fan[J].Engineering Mechanics, 2016, 33(1): 209–216.(in Chinese) |
| [16] | HU H, CLEMONS L, IGARASHI H. An experimental study of the unsteady vortex structures in the wake of a root-fixed flapping wing[J].Experiments in Fluids, 2011, 51(2): 347–359.DOI:10.1007/s00348-011-1052-z |
| [17] | 刑誉峰, 李敏. 工程振动基础[M].2版.北京: 北京航空航天大学出版社, 2011: 136-144.XING Y F, LI M. Engineering vibration[M].2nd ed.Beijing: Beihang University Press, 2011: 136-144.(in Chinese) |
