20世纪60年代英国****Rosenbrock等便研究了多变量系统频域法与时域法之间的联系,提出了对角优势的解耦方法[4]。随着****们的深入研究,涌现出了大量的针对全包线飞行下的多变量控制算法。如Ang等[5]对PID算法进行了多变量控制问题研究,提出了PID解耦控制算法并给出了应用。Meng等[6]给出了多变量控制系统下针对控制器参数优化的一种自适应规律研究。Ding和Yang[7]针对线性离散系统下反馈控制进行了研究。国内****也纷纷进行了相关研究,如王元等[8]以NSGA型发动机为背景进行了LQ/H∞全包线下多变量控制器设计研究。聂聆聪等[9]给出了一种针对几何可调液体冲压发动机的多变量控制算法。张海波等[10]针对航空发动机多变量耦合问题,给出了自抗扰解耦控制律设计方法等。由此可见,近年来许多****从不同角度对多变量控制和发动机全包线控制问题进行了研究分析,并取得了一定的成果。针对航空发动机KQ控制,国外****如Lii[11]和Boje[12]等作了大量研究,而相比国外,国内科研人员所做工作相对较少,如朱玉斌和方中祥[13]针对KQ控制基本原理进行了分析,以某型涡扇发动机为背景建立了稳态控制器,并针对某一点进行了控制器仿真,因此需进一步开展研究工作。KQ算法与其他方法相比,能够有效降低控制器阶次,且不需要复杂的自适应算法等,更利于真实发动机的实时控制[14-15],且高精度的全包线控制更是提高发动机飞行整体性能的最佳途径[16-17],因此本文进行了某型双转子、双涵道混合排气式涡扇发动机的多变量KQ变增益控制器设计与应用研究。
1 KQ多变量控制方法 1.1 KQ基本原理 设广义被控对象的传递函数阵G为l×m维,有l个输出变量和m个输入变量,控制器的传递函数阵K为m×l维。则实际系统的闭环传递函数阵为
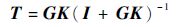 | (1) |
式中:I为单位矩阵。
期望的传递函数阵为Tt,则相应于Tt,期望的控制器Kt应满足:
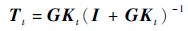 | (2) |
即对应于期望控制器Kt,应满足:
 | (3) |
如果K不等于Kt,则T与Tt之间存在偏差。
定义偏差函数为
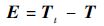 | (4) |
根据Kt和K之间的差异,不难推导出:
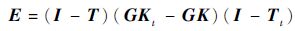 | (5) |
如果E的范数
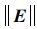
 | (6) |
从而根据式(6) 将问题转换为求取K,进而将式(6) 改为
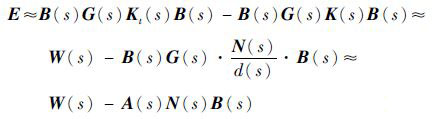 | (7) |
按E的二次型范数为极小值为目标得E的二次型范数为
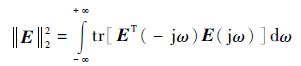 | (8) |
通常可在ω由-∞至+∞的整个范围内选择所考虑频带中的若干个点,这样可使计算简单一些,此问题即为一个线性最小二乘问题。
1.2 KQ优化算法 将式(7) 化为最小二乘求解形式,即
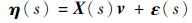 | (9) |
式中:η(s)为已知向量;X(s)为已知矩阵;v为未知参数向量;ε(s)为偏差向量。
而式(7) 中,W(s)、N(s)和E(s)都是m个列向量组成的矩阵:
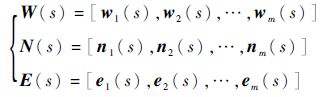 | (10) |
式中:wi(s)、ni(s)和ei(s)分别为构成矩阵W(s)、N(s)和E(s)的列向量。
引入Kronecker积方法,用?代表Kronecker求积运算。将式(8) 的各组列向量分别自上而下堆列,转化为标准式。
其中,Kronecker积的定义:对于两个矩阵P=(pij)p×q和Q=(qij)r×s,P和Q的Kronecker积为
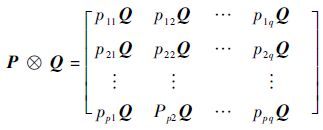 |
根据Kronecker积定义和Kronecker积的性质解决KQ控制器的参数优化的问题,令vec(n)为矩阵n的列拉直,vec称为拉直算子:
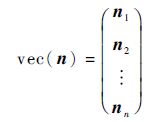 | (11) |
式中:
 |
由式(7) 得
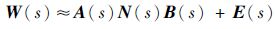 | (12) |
用列拉直运算可得
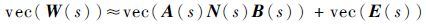 |
即
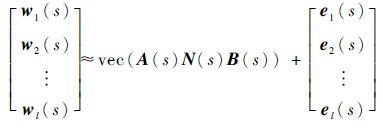 | (13) |
又因为:
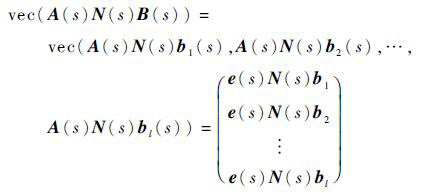 | (14) |
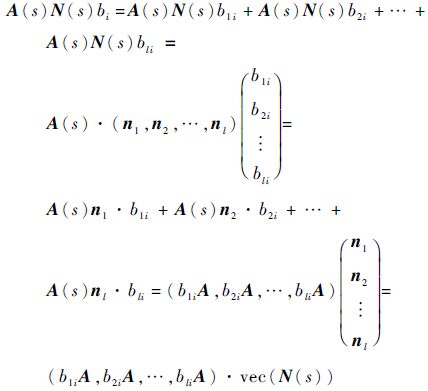 |
故:
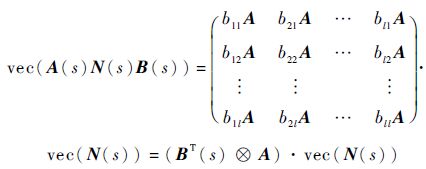 |
由上述可得
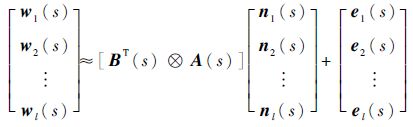 | (15) |
假定:
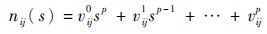 | (16) |
式中:p为正整数,且为多项式nij(s)的次数,设nij(s)的次数相同。这个假设并不会带来限制,因为vijx(x=1, 2, …, P)皆可以为零。
则根据式(16) 可得
 |
定义Σ(s)为
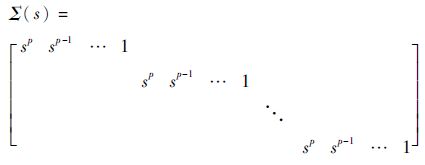 |
则
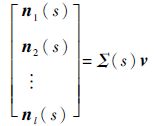 |
式中:
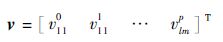 |
因此
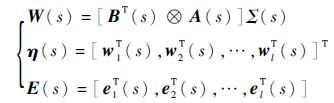 |
则式(15) 转化为式(9) 的标准格式。
令s=jωi, i=1, 2, …, μ处计算η(s)和X(s)(如式(9) 定义),并用式(17) 近似
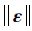
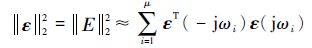 | (17) |
其中,式(17) 的标准最小二乘解为
 |
为改变复数参数值,引入约束条件Im{
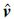
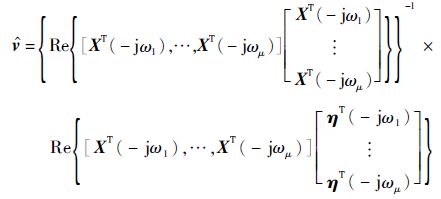 | (18) |
由此可见,算法的有效性根本上取决于参数向量的E2范数的大小。由这一点出发,可以找出改进v^的有效途径,即
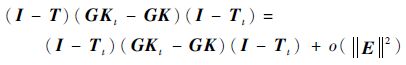 | (19) |
令式(19) 所得控制器为Ki,并假定另一控制器:
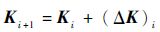 | (20) |
采用这两种控制器的闭环传递函数阵将分别是Ti和Ti+1,令
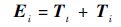 | (21) |
则由式(5) 可知:
 | (22) |
 | (23) |
假定Ti+1≈Ti,则将以式(22) 和式(23) 相减后可得
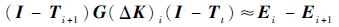 | (24) |
式(24) 中除了(ΔK)i和Ei+1两项外,其他各项都是已知的。通过调整(ΔK)i,以便

1.3 闭环期望函数选择 假定对象为n输入n输出系统,因此控制系统传递函数矩阵为n维矩阵。为了实现闭环控制系统解耦,根据期望闭环传递函数的选择原则,期望闭环传递函数矩阵应选择为对角阵。同时期望闭环传递函数矩阵的每一元素tij结构应尽可能简单,同时考虑到系统快速响应要求,tij的极点在s平面的位置应离虚轴有一定距离。通过上述分析,即可选定闭环期望传递函数。
根据系统线性数学模型的无穷零点的个数、快速推力响应和要求闭环系统具有良好的解耦性能,假设系统的稳定时间是1 s,从而确定主导极点;由于要求期望的闭环系统得到完全解耦,故非对角元素都取0。根据上述分析及T5(涡轮出口温度)、πT(发动机的压比)的特点,选取闭环系统的期望传递函数为
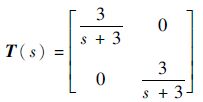 | (25) |
1.4 控制器结构选择 KQ方法对于控制器结构的选择较其他方法有一定的优势,可以采用PI、PID或者高阶控制器,其能够自由选择控制器阶次。
根据系统的闭环传递函数矩阵,如式(2) 所示,可得到系统期望的理想控制器,如式(26)
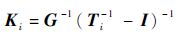 | (26) |
通过式(26) 可确定Ki,即
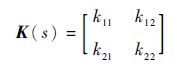 | (27) |
1.5 控制器参数优化 优化控制器参数时,为了使控制器严格正定,故使vij2=0(其中vij2为控制器矩阵系数)。通过最小二乘法进行控制器参数优化,从而使实际控制器的频率响应尽可能地接近期望控制器的性能。
2 稳定性验证与奇异值分析 根据以上分析,利用闭环稳定性判定,以某型涡扇发动机为背景,在指定的频率范围(ω=0.01~35)内作系统逆Nyquist阵列,式(28) 与式(29) 分别为控制器设计点(1, 1) 与(2, 2) 处的传递函数,给出此处系统带有Gershgorin带的逆Nyquist结果如图 1所示,其中对角元素局部放大图如图 2所示。
 | (28) |
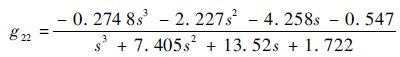 | (29) |
由图 1、图 2可以看出加入控制器后的系统各对角元素的Gershgorin带均不包含原点,故控制后的系统为对角占优系统,其单位反馈系统是闭环稳定的。
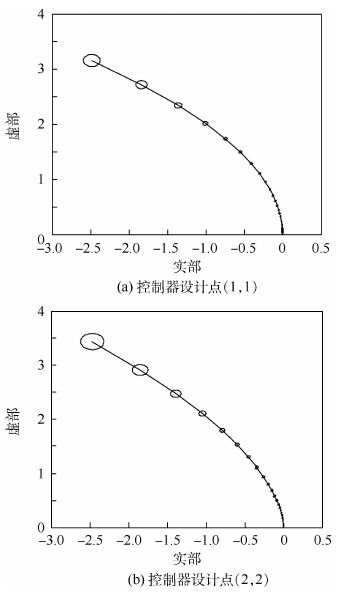 |
| 图 1 加入控制器后系统带有Gershgorin带的逆Nyquist图 Fig. 1 Inverse Nyquist band diagrams with Gershgorin bands when controller is added |
| 图选项 |
 |
| 图 2 加入控制器后系统带有Gershgorin带对角元素的逆Nyquist局部放大图 Fig. 2 Diagonal elements’ enlarged inverse Nyquist band diagrams with Gershgorin bands when controller is added |
| 图选项 |
同时,为了验证系统对指令跟踪、传感器噪声、干扰抑制能力和高频未建模动态的鲁棒稳定性能,给出了该KQ控制器的闭环传递函数奇异值图、回路传递函数的奇异值图和灵敏度传递函数的奇异值图,分别如图 3、图 4和图 5所示。
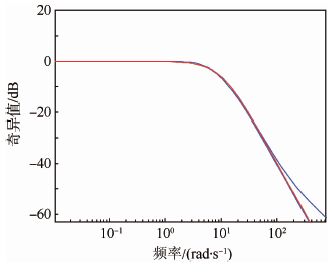 |
| 图 3 闭环传递函数GK(I+GK)-1奇异值 Fig. 3 Singular value of closed-loop transfer function GK(I+GK)-1 |
| 图选项 |
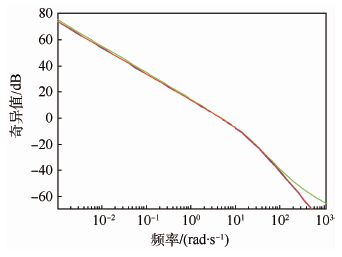 |
| 图 4 回路传递函数GK的奇异值 Fig. 4 Singular value of closed-loop transfer function GK |
| 图选项 |
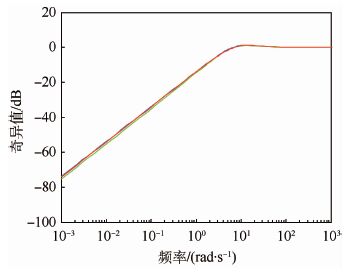 |
| 图 5 灵敏度传递函数(I+GK)-1的奇异值 Fig. 5 Singular value of sensitivity transfer function (I+GK)-1 |
| 图选项 |
图 3为闭环传递函数GK(I+GK)-1的奇异值曲线,图中可以看出,系统具有对高频未建模动态的鲁棒性。
图 4给出了回路传递函数GK奇异值曲线,从中可以看出,由于最小奇异值σ(GK)在低于期望穿越频率(相对于幅值等于1或0 dB)时比较大,因此系统具有满意的指令跟踪和干扰抑制能力;而频率在大于期望穿越频率时,最大奇异值
图 5为灵敏度传递函数矩阵(I+GK)-1的奇异值曲线,由于最大奇异值
综上,所设计的KQ控制器使系统具有满意的低频指令跟踪、干扰抑制能力、传感器噪声的抑制、高频未建模动态的鲁棒稳定性和低频发动机建模误差不敏感等性能,能够满足发动机控制的要求。
3 某型涡扇发动机控制器设计 3.1 调度变量选择 调度变量可以是状态变量也可以是输出参数,还可以是拟定的轨迹或者它们和内部参数的混合。调度参数要能反映工作状态的变化,从而可以通过调度参数切换控制器,对系统进行控制[18]。
以某型双转子、双涵道混合排气式涡扇发动机作为研究对象,以下将以飞行条件高度H=11 km、马赫数Ma=1.2、低压转子百分比转速nL=96%为仿真算例进行设计点控制器设计。其中,该状态下,该型发动机相对增量形式线性数学模型为
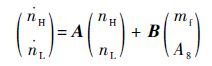 | (30) |
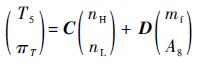 | (31) |
式中:控制量为主燃烧室供油量mf和尾喷管喉部面积A8;被控参数为高压涡轮出口温度T5和发动机的压比πT=P6/P2。由于高压转子转速nH、nL、mf、A8、T5、πT随飞行条件(H、Ma)和nL的变化。飞行条件和nL决定了发动机的状态,根据涡扇发动机的特点和调度变量的选择原则,故可选择H、Ma和nL作为调度变量。如式(32) :
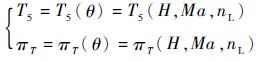 | (32) |
由于系统模型随H、Ma和nL变化而变化,故控制器K可表示为
 | (33) |
对于二阶控制器,其kij为
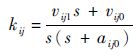 | (34) |
式中:
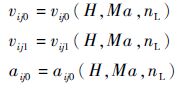 |
通过计算频域中给定的一系列传递函数矩阵,从而计算K中系数的Bode图,利用Bode图近似估计出K的结构形式及其极点位置。最终确定,该系统的期望控制器一个极点为s=0,另一个为s=0.8。确定多变量控制器结构形式为
 |
3.2 设计点控制器设计 通过调度变量的选择后,需要进行设计点控制器设计和设计点控制器参数计算,以及系统性能检测等,从而实现该型涡扇发动机模型的多变量KQ变增益调度控制,进而使得KQ控制器在全包线下满足发动机控制要求[19]。
将该型涡扇发动机的飞行包线分为几段,选取了以下工作点作为典型工作点。由于飞行高度对发动机模型影响相对较小,因此把高度分成H=3,7,11,15,18 km等5段,其中补充H=0 km时控制器参数值。飞行速度的划分是根据不同的高度进行确定的。例如对于H=11 km,飞行速度划分为Ma=0.9, 1.2, 1.5, 1.7,而对于H=3 km则划分为Ma=0, 0.3, 0.5, 0.7,其他高度也进行了相应的划分;由于发动机低压转子转速对发动机数学模型影响相对较大,故把低压转子转速nL划分为9个状态,即nL=96%, 94%, 92%, 90%, 88%, 86%, 84%, 82%, 80%。设计点确定后,根据多变量KQ算法,设计每个设计点控制器。以下将以飞行条件为H=11 km、Ma=1.2、nL=96%时的仿真算例进行设计点控制器设计。此条件下小偏离相对增量形式线性数学模型为
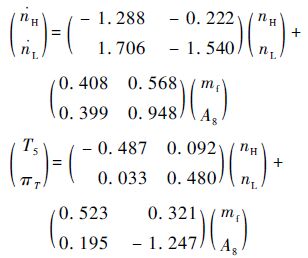 |
如表 1所示,给出了优化后的控制器参数。通过表 1中的参数,实现KQ控制器设计。
表 1 优化后的控制参数 Table 1 Optimized control parameters
| 参数 | 控制器1 | 控制器2 | ||||||
| v111 | v121 | v110 | v120 | v211 | v221 | v210 | v220 | |
| 数值 | 7.231 | 1.754 | 5.842 | 1.661 | -1.022 | -2.926 | 3.093 | -3.200 |
表选项
3.3 非设计点控制器设计 变增益控制器设计最重要的是非设计点控制器参数计算[20]。其中,需要利用设计点控制器参数值计算非设计点控制器参数。
由于KQ多变量控制器不能在线设计,因此无法根据线性变参数(LPV)系统得到当前的发动机线性数学模型,然后根据线性数学模型在线设计多变量控制器。同时,由于KQ控制器的参数较多(每一个控制器K包括k11、k12、k21、k22,每一个kij又包括vij1、vij0和aij0,即每一组控制器需要确定9个参数),而多维曲面拟合,需要控制器参数具有一定的实现规律。通过多维三次B样条拟合控制器参数发现,KQ控制器的参数拟合误差较大,以控制器参数的最大误差为尺度,其最小误差达到7.9%,难以满足控制需要。
为了解决上述问题,采用插值的方法进行增益调度控制系统设计。具体算法是,根据飞行高度和飞行速度确定当前所处于的飞行条件领域(每一个飞行条件领域定义为ΔH<2 km、ΔMa<0.2) ,进而根据发动机当前低压转子转速确定控制器参数值。若当前低压转子转速为设计点数值,即nL=96%,94%,92%,90%,88%,86%,84%,82%,80%等,则采用设计点控制器参数值;若当前低压转子转速不在设计点,例如当前低压转子转速为95%,根据当前飞行条件领域,并利用nL=96%和nL=94%控制器参数值,用一维线性插值方法得到nL=95%的控制器参数。
4 航空发动机仿真 通过上述过程的研究,给出了针对某型双转子、双涵道混合排气式涡扇发动机部件级气动非线性数学模型为仿真平台的KQ变增益控制器应用。对其进行系统仿真,以验证性能。
为了在发动机全包线、全状态下验证增益调度控制器性能,现给出设计点以及包线内随机选取的几个非设计点仿真结果。依次是:设计点H=11 km、Ma=1.2、nL=96%;非设计点H=4 km、Ma=0.3,nL=95%;非设计点 H=13 km、Ma=1.3,nL=93%等。图 6~图 8分别给出了在上述工作点下,T5, r阶跃1%、πT, r阶跃1%时,仿真响应结果。
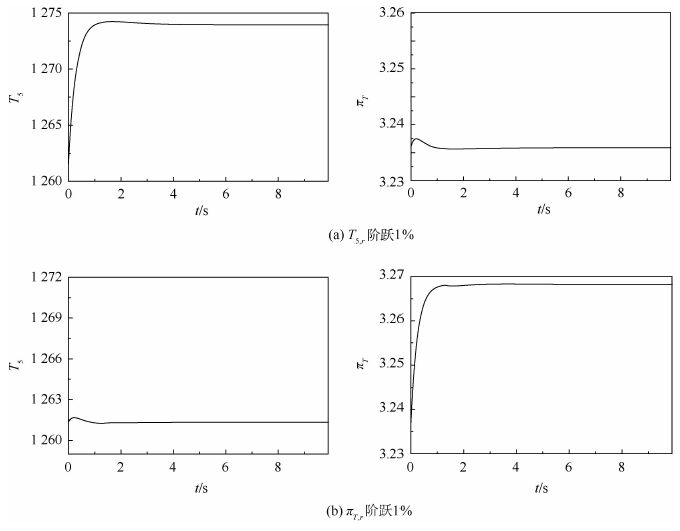 |
| 图 6 H=11 km、Ma=1.2、nL=96%时 T5和πT的响应 Fig. 6 Responses of T5 and πT when H=11 km, Ma= 1.2, nL=96% |
| 图选项 |
 |
| 图 7 H=4 km、Ma=0.3、nL=95%时T5和πT的响应 Fig. 7 Responses of T5 and πT when H= 4 km, Ma=0.3, nL=95% |
| 图选项 |
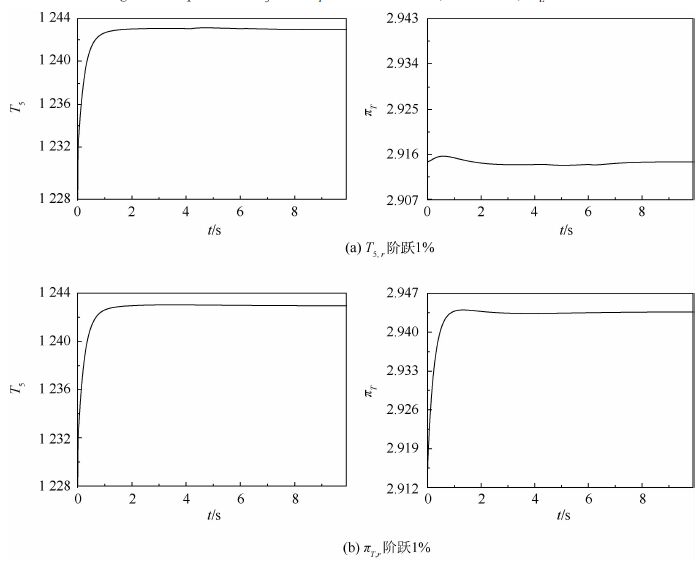 |
| 图 8 H=13 km、Ma=1.3、nL=93%时T5和πT的响应 Fig. 8 Responses of T5 and πT when H=13 km, Ma=1.3, nL=93% |
| 图选项 |
从图 6~图 8中可以看出,T5, r阶跃1%时,控制器作用使πT, r的耦合影响较小,系统的最大耦合影响小于6%,T5, r和πT, r被控参数响应很快,调节时间小于1 s,T5, r没有出现超调量;从图 6(b)可以看出,πT, r阶跃1%时,控制器作用使T5, r的耦合影响较小,系统的最大耦合影响小于2%,T5, r和πT, r被控参数响应很快,调节时间小于1 s;由非线性部件级数学模型仿真结果可以看出,基于KQ的多变量控制器在该设计点的系统的性能较好,能够满足航空发动机控制系统的设计要求。
图 7和图 8分别给出了随机选取的H=4 km、Ma=0.3、nL=95%以及H=13 km、Ma=1.3、nL=93%等非设计点的仿真结果,可以看出,非设计点时控制性能较好,系统超调量较小,被控参数的响应时间很快,耦合影响也较小,各个动态指标满足控制要求。通过不同包线下的仿真结果表明利用插值方法得到的KQ变增益控制器参数
值能够很好地实现该型涡扇发动机全包线控制,系统具有较好的性能,能够满足系统控制性能要求。
同时,为了考察当低压转子转速和低压涡轮出口温度受到意外瞬态扰动的情况下,控制系统对这些扰动的调节能力,进行了在高度、马赫数变化时系统分别加入低压转子转速和低压涡轮转速阶跃扰动时的仿真研究。如图 9~图 11所示,分别给出了不同飞行条件下系统引入干扰时的仿真结果。
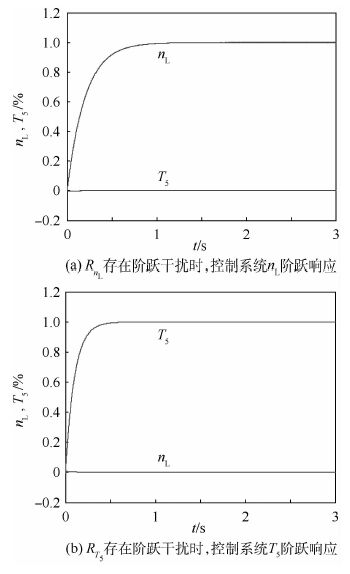 |
| 图 9 H=3 km、Ma=0.2, 系统引入干扰时的仿真结果 Fig. 9 Simulation results when system is introduced (H=3 km, Ma=0.2) |
| 图选项 |
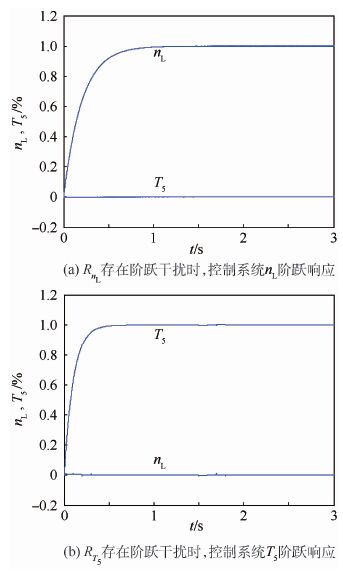 |
| 图 10 H=10 km、Ma=1.1,系统引入干扰时的仿真结果 Fig. 10 Simulation results when system is introduced (H=10 km,Ma=1.1) |
| 图选项 |
 |
| 图 11 H=13 km、Ma=0.3,系统引入干扰时的仿真结果 Fig. 11 Simulation results when system is introduced (H=13 km,Ma=0.3) |
| 图选项 |
仿真曲线说明,当系统分别引入发动机低压转子转速和低压涡轮出口温度阶跃扰动后,随着高度、马赫数变化时,控制系统响应均存在一定微小变化,但是各个条件下均保持了系统的稳定性,表明该控制系统对外界干扰具有很好的鲁棒性。
5 结论 以某型双转子、双涵道混合排气式涡扇发动机为背景,进行了多变量KQ变增益调度控制器设计与应用研究。主要结论为:
1) 阐明了KQ控制器的基本原理和算法,并给出了KQ控制器的设计步骤。通过KQ控制器期望函数的选择、控制结构确定以及控制器参数优化进行了KQ控制器设计。
2) 对所设计的多变量KQ控制器进行了稳定性分析和奇异值分析,结果表明,该KQ控制器能够使得系统闭环稳定且具有满意的低频指令跟踪、干扰抑制能力、传感器噪声的抑制、高频未建模动态的鲁棒稳定性和低频发动机建模误差不敏感等性能。
3) 基于某型双转子、双涵道混合排气式涡扇发动机的部件级非线性模型,通过调度变量选取、设计点控制器设计以及非设计点控制器设计进行了其全包线下的多变量KQ变增益控制器设计与仿真验证。通过设计点和随机选取的非设计点仿真结果表明:所设计的KQ变增益控制器在设计点和非设计点均具有良好的动态特性,满足系统控制性能要求,能够实现该型发动机全包线下的控制需求。
通过研究结果证明,多变量KQ方法能够使系统具有较好的解耦和跟踪能力。
参考文献
| [1] | 樊思齐. 航空发动机控制[M].西安: 西北工业大学出版社, 2008: 179-183.FAN S Q. Engine control[M].Xi'an: Northwestern Polytechnical University Press, 2008: 179-183.(in Chinese) |
| [2] | 周宗才. 某型飞机推进系统控制[M].西安: 空军工程大学, 1997: 110-115.ZHOU Z C. Aircraft propulsion system control of a certain type[M].Xi'an: Air Force Engineering University, 1997: 110-115.(in Chinese) |
| [3] | JAW L C, MATTINGLY J D. Aircraft engine control:Design,system analysis,and health monitoring[M].Reston: AIAA, 2012: 58-63. |
| [4] | 阙志宏, 罗健, 周凤岐, 等. 线性系统理论[M].西安: 西北工业大学出版社, 1994: 153-158.QUE Z H, LUO J, ZHOU F Q, et al. The linear system theory[M].Xi'an: Northwestern Polytechnical University Press, 1994: 153-158.(in Chinese) |
| [5] | ANG K H, CHONG G, LI Y. PID control system analysis,design,and technology[J].IEEE Transactions on Control Systems Technology, 2005, 13(4): 559–576.DOI:10.1109/TCST.2005.847331 |
| [6] | MENG A B, YE L Q, YIN H, et al. Application of genetic algorithm in adaptive governor with variable PID parameters[J].Control Theory & Applications, 2004, 21(3): 398–404. |
| [7] | DING D W, YANG G H. Static output feedback control for discrete-time piecewise linear systems:An LMI approach[J].Acta Automatica Sinica, 2009, 35(4): 337–344.DOI:10.1016/S1874-1029(08)60080-4 |
| [8] | 王元, 李秋红, 黄向华. 基于改进NSGA的航空发动机LQ/H∞控制器设计[J].航空动力学报, 2015, 30(4): 985–991.WANG Y, LI Q H, HUANG X H. LQ/H∞ controller design for aero-engine based on improved NSGA[J].Journal of Aerospace Power, 2015, 30(4): 985–991.(in Chinese) |
| [9] | 聂聆聪, 朴胜志, 吴智锋, 等. 几何可调液体冲压发动机多变量控制算法研究[J].推进技术, 2013, 34(12): 1690–1695.NIE L C, PIAO S Z, WU Z F, et al. Study on multi-variable control system for variable geometry liquid ramjet engine[J].Journal of Propulsion Technology, 2013, 34(12): 1690–1695.(in Chinese) |
| [10] | 张海波, 王健康, 王日先, 等. 一种航空发动机多变量自抗扰解耦控制律设计[J].推进技术, 2012, 33(1): 78–83.ZHANG H B, WANG J K, WANG R X, et al. Design of an active disturbance rejection decoupling multivariable control scheme for aero-engine[J].Journal of Propulsion Technology, 2012, 33(1): 78–83.(in Chinese) |
| [11] | LⅡ A S, BROWN H. Control of jet engines[J].Control Engineering Practice, 1999, 7(9): 1043–1059.DOI:10.1016/S0967-0661(99)00078-7 |
| [12] | BOJE E, OSITA D I. Quantitative multivariable feedback design for turbofan engine with forward path decoupling[J].International Journal of Robust Nonlinear Control, 1999, 9(12): 857–882.DOI:10.1002/(ISSN)1099-1239 |
| [13] | 朱玉斌, 方中祥. 基于KQ的航空发动机多变量控制算法研究[J].测控技术, 2011, 30(10): 70–76.ZHU Y B, FANG Z X. Multivariable control algorithm research based on KQ for aeroengine[J].Journal of Test Technology, 2011, 30(10): 70–76.(in Chinese) |
| [14] | 樊思齐. 航空推进系统控制[M].西安: 西北工业大学出版社, 1995: 30-34.FAN S Q. Aerospace propulsion system control[M].Xi'an: Northwestern Polytechnical University Press, 1995: 30-34.(in Chinese) |
| [15] | 陆军, 郭迎清, 陈小磊. 线性拟合法建立航空发动机状态变量模型[J].航空动力学报, 2011, 26(5): 1172–1177.LU J, GUO Y Q, CHEN X L. Establishment of aero-engine state variable model based on linear fitting method[J].Journal of Aerospace Power, 2011, 26(5): 1172–1177.(in Chinese) |
| [16] | 孙建国, 李秋红, 杨刚, 等. 航空燃气涡轮发动机控制[M].上海: 上海交通大学出版社, 2014: 78-83.SUN J G, LI Q H, YANG G, et al. Aviation gas turbine engine control[M].Shanghai: Shanghai Jiao Tong University Press, 2014: 78-83.(in Chinese) |
| [17] | 佘云峰, 黄金泉, 鲁峰. 涡轴发动机自适应混合诊断模型高斯加权类聚方法[J].航空动力学报, 2011, 26(5): 1178–1184.SHE Y F, HUANG J Q, LU F. Gaussian weighted sum clustering method of adaptive hybrid diagnostic method for turbo-shaft engine[J].Journal of Aerospace Power, 2011, 26(5): 1178–1184.(in Chinese) |
| [18] | LAU K W, WU Q H. Local prediction of non-linear time series using support vectors regression[J].Pattern Recognition, 2008, 41(5): 1539–1547.DOI:10.1016/j.patcog.2007.08.013 |
| [19] | JAW L C, MATTINGLY J D. Aircraft engine control:Design,system analysis,and health monitoring[M].Reston: AIAA, 2009: 33-36. |
| [20] | PISANO A D,RUFLETH B.The CEDAR project-commercial engine damage assessment and reconfiguration:AIAA-2007-2809[R].Reston:AIAA,2007. |
