近年来,随着分数阶微积分理论的不断完善与成熟,分数阶微积分已经逐渐被应用到控制工程领域。将分数阶微积分理论同传统滑模控制策略相结合构成分数阶滑模控制器,往往能使系统获得更好的动静态性能,为此国内外****进行了大量研究。文献[5]针对一类2阶非线性系统,设计了PD型分数阶滑模控制器,并采用模糊方法确定切换增益以减小抖动。文献[6]设计了一种分数阶终端滑模控制器,实现了有限时间收敛,但是控制器存在奇异问题。文献[7]设计了基于分数阶趋近律的滑模控制器,并将其应用于二自由度机械臂控制。文献[8-9]将PID型分数阶滑模控制器分别应用于电子降压转换器和火炮控制,但是并未给出滑模面的稳定性证明。文献[10]将分数阶滑模控制器应用于航天器的姿态跟踪控制,取得了比整数阶控制器更好的控制性能。文献[11]首次将一种PD型分数阶滑模控制器应用于永磁同步电机的调速系统,文献[12]则采用了PI型分数阶滑模控制器,但这2篇文献仅仅从分数阶滑模面的收敛速度层面分析了消抖的作用,而控制量中仍然含有切换项,抖振现象依然存在,其次两者也不能保证系统在有限时间内收敛。此外,控制器中含有被控量误差的高阶分数阶微分项,易引入噪声,限制了分数阶阶数的取值范围。文献[13]将PI型分数阶滑模控制应用于阀控马达的角度控制,但仅仅同整数阶滑模控制做了控制精度的对比,未涉及消抖问题。事实上,滑模控制器的鲁棒性和系统的快速性往往与消抖的目标是互相矛盾的,抗扰性能越强,则要求切换增益越大,造成的结果必然是抖振幅值增大。针对以上问题,本文所构建的新型分数阶滑模控制器(NFOSMC)可以保证系统状态能在有限时间内收敛到平衡点,并通过设计使控制器中直接包含切换项的分数阶积分项消除抖振,实现无抖振控制,保证在减小抖振的同时允许选择更大的切换增益,很好地解决了上述矛盾。
为了提高系统抗扰能力,利用扰动观测器对系统内扰和外扰实时观测并加以前馈补偿是一种常用方法。目前一些常用的观测方法有Luenberger观测器[14]、扩展Kalman滤波器[15]和滑模观测器[16]等。其中,Luenberger观测器要求系统模型精确已知,鲁棒性较差;扩展Kalman滤波器存在计算复杂、整定参数多的问题;而传统滑模观测器的观测值中又包含由抖振造成的高频噪声。
本文设计了一种分数阶扰动观测器(FODOB),采用分数阶微分方程描述扰动动态特性,利用分数阶系统的稳定定理保证扰动误差的收敛性,通过调节分数阶阶数滤除观测值中的高频抖振成分,实现对扰动的无抖振准确观测。
1 电液伺服泵工作原理 图 1为一种永磁同步伺服电机和轴向柱塞泵融合而成的电液伺服泵的工作原理[17]。其基本工作原理如下:由电源接线座引入三相交流电产生旋转磁场,该旋转磁场与转子表面永磁体产生的磁场相互作用驱动转子旋转,此时转子中的柱塞通过和斜盘、配流盘配合产生往复直线运动,从而完成吸排油过程,其中旋转变压器用来检测转子磁极的位置。可以看出,电液伺服泵的工作原理与传统的伺服电机通过联轴器再驱动泵的方式是相同的,但是在结构上实现了伺服电机和液压泵的高度融合,两者共转子、共壳体。
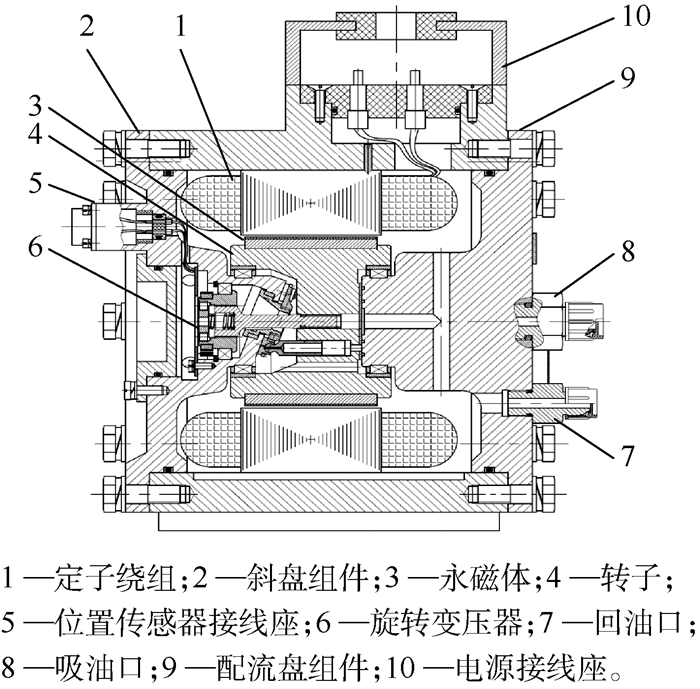 |
| 图 1 电液伺服泵工作原理[17] Fig. 1 Working principle of IEHSP[17] |
| 图选项 |
2 电液伺服泵建模 虽然电液伺服泵定转子之间为油隙而非气隙,但油隙并不改变转子永磁体产生的磁密形状,因此仍然可以假设磁密形状为正弦状,定子绕组反电动势波形也为正弦,转子永磁体为表贴式,在旋转dq坐标系中的电压方程可写为
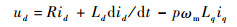 | (1) |
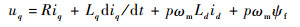 | (2) |
式中:ud、uq分别为d、q轴电压分量;id、iq分别为d、q轴电流分量;Ld、Lq分别为d、q轴等效电感;R为定子绕阻电阻;ψf为转子永磁体磁链;p为极对数;ωm为转子机械角速度。
电液伺服泵电磁转矩为
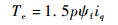 | (3) |
由于电液伺服泵定转子之间为油隙,因此需要考虑转子旋转时与油液产生的摩擦转矩,根据Pertoff定理[18],油隙摩擦转矩为
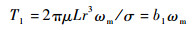 | (4) |
式中:μ为液压油液动力黏度;L为电液伺服泵转子长度;r为电液伺服泵转子半径;σ为定转子间的油隙厚度;b1为油隙摩擦系数。
电液伺服泵三大运动副产生的摩擦转矩为T2=b2ωm,b2为电液伺服泵运动副摩擦系数。电液伺服泵运动方程可写为
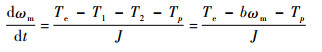 | (5) |
式中:J为转动惯量;Tp为外负载转矩;b=b1+b2为等效的总黏性摩擦系数。
电液伺服泵输出流量为
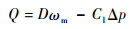 |
式中: D为电液伺服泵排量;Cl为泄漏系数;Δp为电液伺服泵进出口压差。
选取状态变量X=[id??iq??ωm]T,考虑系统模型中参数摄动和外扰,将iq看作ωm的输入量,此时系统状态方程可写为
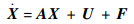 | (6) |
式中:
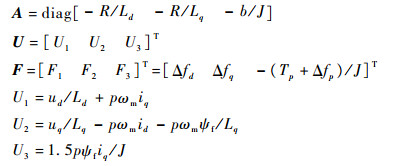 |
其中:Δfd、Δfq和Δfp为参数摄动造成的扰动。
3 分数阶滑模控制器设计 3.1 Riemann-Liouville分数阶微积分定义 目前,常用的分数阶微积分定义有Grunwald-Letnikov定义、Riemann-Liouville(RL)定义和Caputo定义3种,本文采用RL定义,下面给出RL分数阶微积分的定义[19]。
RL分数阶积分:
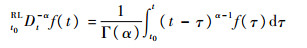 | (7) |
RL分数阶微分:
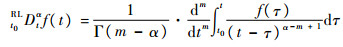 | (8) |
式中:t0RLDtα和t0RLDt-α分别为RL微积分算子;t0和t分别为积分下限和上限;α>0为分数阶微积分阶数;m为大于α的最小正整数;Γ(·)为Gamma函数。
性质1[20-21]??RL分数阶微分具有以下性质:
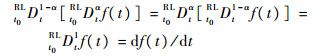 |
为了简便,下文中用Dα表示t0RLDtα。
3.2 分数阶速度滑模控制器设计 设给定角速度为ωd,定义电液伺服泵的角速度误差为e=ωm-ωd。
设计如下分数阶滑模面:
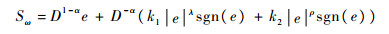 | (9) |
式中:α∈[0, 1];ρ∈(0, 1);λ∈(1, 2), k1, k2∈(0, ∞);sgn(·)为符号函数。
对式(9)求导并利用性质1,可得
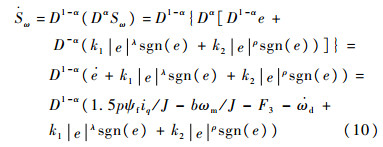 | (10) |
选用指数趋近律,令
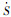
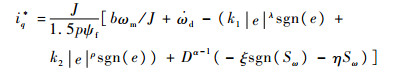 | (11) |
定理1??选用式(9)表示的滑模面和式(11)表示的控制律,可以保证系统状态e从任意初始值开始,都将在有限时间内到达滑模面Sω=0,并在之后的滑模运动中保证误差e在有限时间内收敛到零。
证明??滑模面有限时间稳定性证明:令Sω=0,利用性质1并对式(9)两边进行α阶微分,可得
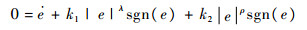 |
由此可得
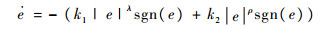 | (12) |
选择Lyapunov函数V1=e2/2,求导并将式(12)代入可得
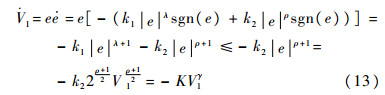 | (13) |
式中:K>0;0?γ?1。
假设t=tr时误差状态e到达滑模面Sω=0,根据有限时间稳定性定理[22],误差状态e将在tr之后的有限时间te内收敛到零,其中收敛时间为te≤V1-γe(tr)/K(1-γ)。
可达性证明:选择Lyapunov函数V2=Sω2/2,求导并代入式(10)和式(11),得
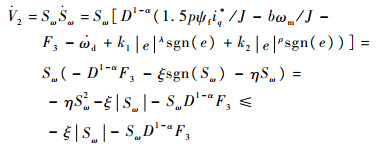 |
此时如果|D1-αF3|≤δ,选择参数ξ=ξ1+δ,ξ1>0, 则
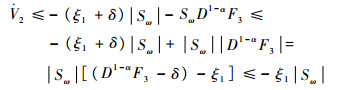 |
根据有限时间稳定性收敛定理,可以保证系统在有限时间内到达滑模面Sω=0,假设在t=tr时到达滑模面,则tr≤-|Sω(0)|/ξ1。????证毕
由式(9)和式(11)可以看出,所设计的分数阶滑模控制器具有以下特点:
1)?滑模面Sω中含有误差e的终端吸引子eρ,因此可以保证e在到达滑模面后在有限时间内收敛到零,由方程式(12)解得收敛时间[23]为
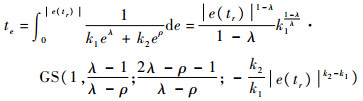 |
式中:GS(·)为高斯超几何函数。
2)?控制量中包含有Dα-1(-ξsgn(Sω)-ηSω),该项是切换项sgn(Sω)的分数阶积分,可以起到平滑滤波作用,有效去除抖振。同时可以保证在滤除抖振的情况下允许选择尽可能大ξ和η,以加快到达滑模面的速度。
3)?到达滑模面后,e的动态行为由微分方程式(12)决定,e(tr)较大时,收敛速度主要由k1|e|λsgn(e)项决定,当e(tr)较小时,收敛速度主要由k1|e|ρsgn(e)项决定,因此保证了e在滑模面上能够全程快速收敛。特别的,当α=1时,滑模面蜕变为普通的整数阶滑模面:
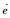
3.3 分数阶q、d轴电流滑模控制器设计 定义1??q、d轴电流跟踪误差分别为eq=iq-iq*,ed=id-id*,采用id*=0的矢量控制方式,分数阶滑模面分别为
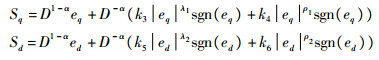 |
式中:λ1∈(1, 2);ρ1∈(0, 1);k3, k4∈(0, ∞);λ2∈(1, 2);ρ2∈(0, 1);k5, k6∈(0, ∞)。
同样选用指数趋近律,可得控制率为
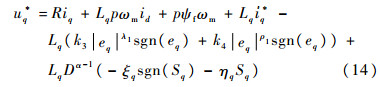 | (14) |
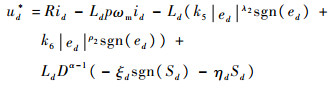 | (15) |
4 分数阶扰动观测器 通过观测器实时观测扰动量F1、F2和F3,将观测值
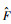
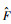
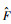
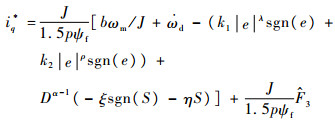 | (16) |
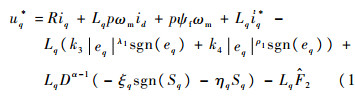 | (17) |
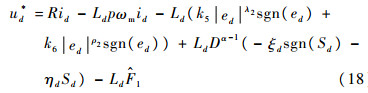 | (18) |
扰动F1、F2和F3通常由定子绕阻电阻R、电感Ld和Lq、磁链ψf等参数和外负载的变化产生,而这些参数的变化本身就是一个缓慢变化的过程而非突变,另外控制器的控制周期很短,所以在一个控制周期内可以把F1、F2和F3看作慢时变量,根据分数阶微分的衰减记忆特性,采用分数阶微分方程DεF=03×1, ε∈(0, 1]来描述这一慢时变过程更为贴切,由此可得系统扩展状态方程为
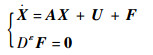 | (19) |
设计如下观测器:
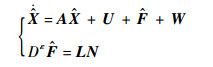 | (20) |
式中:
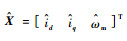
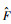
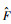
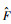
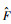
将式(19)和式(20)相减,得到
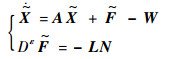 | (21) |
式中:
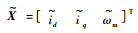
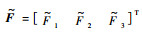
选取滑模超平面Se=
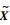
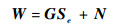 |
式中:N=Hsgn(Se), H=diag[h1 h2 h3]为系数矩阵;G=diag[g1??g2??g3]为系数矩阵。
如果能选取合适的参数矩阵G和H,满足可达性条件SeT
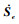
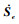
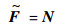 |
根据以上分析,选择Lyapunov函数为V3=SeTSe/2,求导得
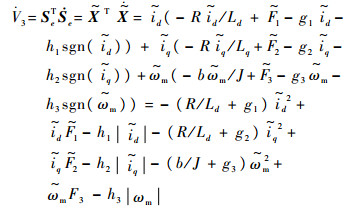 |
此时如果矩阵G正定,则
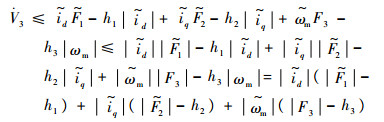 |
所以只要保证h1>
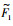
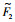
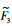
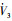
到达滑模面后,扰动观测器误差分数阶微分方程为
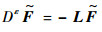 | (22) |
根据分数阶线性系统的稳定性定理[24],只要保证|arg(eig(-L))|>επ/2,
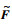
需要注意的是,N中含有切换项sgn(Se),因此N可以看成是真正的扰动误差
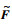
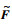
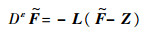 | (23) |
进行分数阶Laplace变换[25],求得分数阶传递函数矩阵为
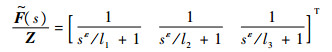 | (24) |
可以看出,通过调节系数矩阵L和分数阶阶数ε可有效滤除高频分量Z,从而实现对扰动的准确观测。
5 仿真分析 为了验证本文设计的控制器的有效性,将其与PI控制、文献[11]中提出的传统分数阶滑模控制器(CFOSMC)以及整数阶滑模控制器(IOSMC)分析比较,IOSMC是指NFOSMC中分数阶阶数α=1时对应的情况。根据文献[11],得出CFO-SMC相应的控制律为
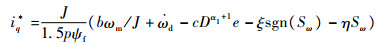 | (25) |
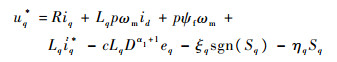 | (26) |
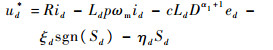 | (27) |
电液伺服泵相关参数为:直流侧母线电压UDC=270 V,额定功率PN=20 kW,额定电流IN=80 A,额定转速nN=8 000 r/min,额定扭矩TN=24 N·m,排量D=5 mL/r,泄漏系数Cl=2×10-13 m3/s/Pa,定子绕组电阻R=0.025 Ω,电感Ld=Lq=0.161 mH,转子永磁磁链ψf=0.056 4 Wb,转动惯量J=0.004 kg·m2,摩擦系数b=0.001 07+0.000 2=0.001 27 N·m/rad/s,极对数p=3,q轴电流限幅值iqm=100 A。
NFOSMC控制器仿真参数为:α=0.2,λ=λ1=λ2=1.5,ρ=ρ1=ρ2=0.6,k1=0.25,k2=0.5,k3=0.01,k4=0.02,k5=1,k6=2,ξ=2 000,η=150,ξd=100,ηd=20,ξq=500,ηq=50。
CFOSMC控制器仿真参数为:α1=0.2,ξ=2 000,η=150, ξd=100,ηd=20,ξq=500,ηq=50,c=0.01。
FODOB仿真参数为:ε=0.6,L=diag[70??100??100],G=diag[2 000??3 000??3 000]。
电液伺服泵控制结构如图 2所示。采用MATLAB/Simulink软件,仿真在以下2种情况下进行:
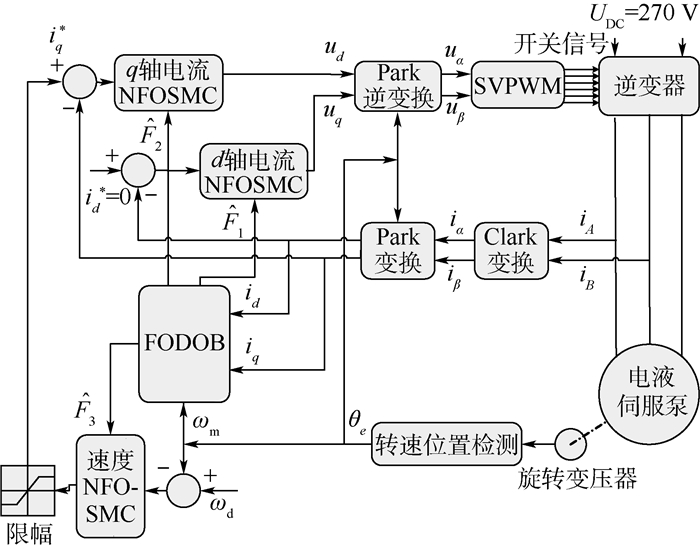 |
| 图 2 电液伺服泵控制结构 Fig. 2 Control structure diagram of IEHSP |
| 图选项 |
1)?电液伺服泵无外负载,给定转速为额定值nd=8 000 r/min。为了防止Windup现象,PI控制采用文献[26]中的Anti-Windup方法,其中速度环参数为:KP1=0.5,KI1=5,KC=15;q轴电流环参数为:KP2=4,KI2=10;d轴电流环参数为:KP3=10,KI3=150。
图 3为NFOSMC和PI控制的仿真对比。从图 3(a)的速度阶跃响应曲线可以看出,NFOSMC的转速响应速度要稍快于PI控制,而且可以做到无超调跟随,PI控制由于采用了Anti-Windup方法,转速超调虽然一定程度上得到了抑制,但仍然存在超调,且收敛速度较慢。从图 3(b)的q轴电流响应曲线可以发现,在加速阶段,实际上q轴电流给定值iq*已经达到限幅值100 A,但是NFOSMC仍然可以很好地跟随限幅值,而PI控制由于Anti-Windup方法的使用,速度环过早地退出了饱和,因此已经不能跟随iq*,说明NFOSMC在加速阶段可以产生更大的加速扭矩,这也正是NFOSMC转速响应速度要快于PI的原因。从图 3(c)的d轴电流响应控制曲线可以明显看出,PI控制的直轴电流id虽然可以收敛于id*=0,但是存在一定的动态波动,而采用NFOSMC时,id可快速跟随指令id*=0,几乎无波动。
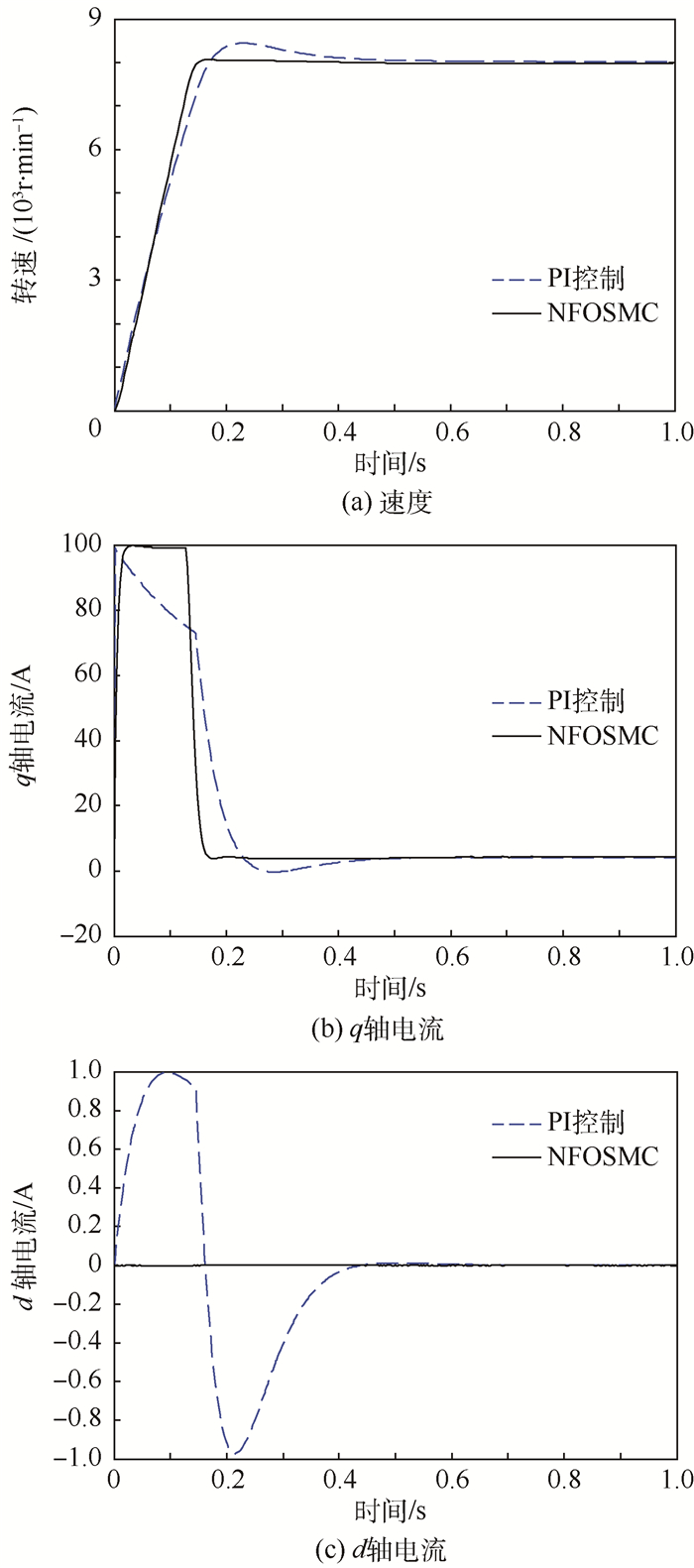 |
| 图 3 NFOSMC与PI控制速度和电流响应对比曲线 Fig. 3 Speed and current response curves comparisonbetween NFOSMC and PI control |
| 图选项 |
图 4为NFOSMC与CFOSMC、IOSMC的仿真对比。从图 4(a)可以看出,三者均能无超调跟随nd,NFOSMC速度稍快于CFOSMC、IOSMC。图 4(b)、图 4(c)表明,CFOSMC、IOSMC均产生了严重的抖振,其中速度环输出信号iq*的抖振幅值范围为-25~35 A,IOSMC的uq抖振幅值范围为120~160 V,CFOSMC的uq抖振幅值范围为100~180 V,而采用NFOSMC时iq*和uq均非常平滑,几乎无抖振。另外,由式(25)~式(27)可以看出,CFOSMC控制率中含有误差e的高阶微分项Dα1+1e,经过多次仿真发现α1的取值范围仅仅为0≤α1≤0.2,取值范围很窄,否则很容易引入噪声,而NFOSMC的分数阶阶数α的取值范围为0≤α≤1时都能保证系统稳定收敛。
 |
| 图 4 NFOSMC与CFOSMC、IOSMC速度响应和控制信号对比曲线 Fig. 4 Speed response and control signal curves comparisonbetween CFOSMC, IOSMC and NFOSMC |
| 图选项 |
2)?为了验证NFOSMC的抗扰能力和FODOB的观测性能,电液伺服泵空载起动,给定转速为额定值nd=8 000 r/min,在t=0.5 s时加入20 N·m的外负载,t=1.5 s时减小为10 N·m,并且在t=2 s时通过让定子绕组增大为额定值的1.2倍,即0.03 Ω来模拟参数摄动。图 5为FODOB观测结果。可以看出,FODOB对于扰动F1、F2和F3均可平滑、准确观测,而且据此还可计算出外加负载的估计值
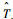
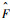
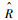
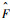
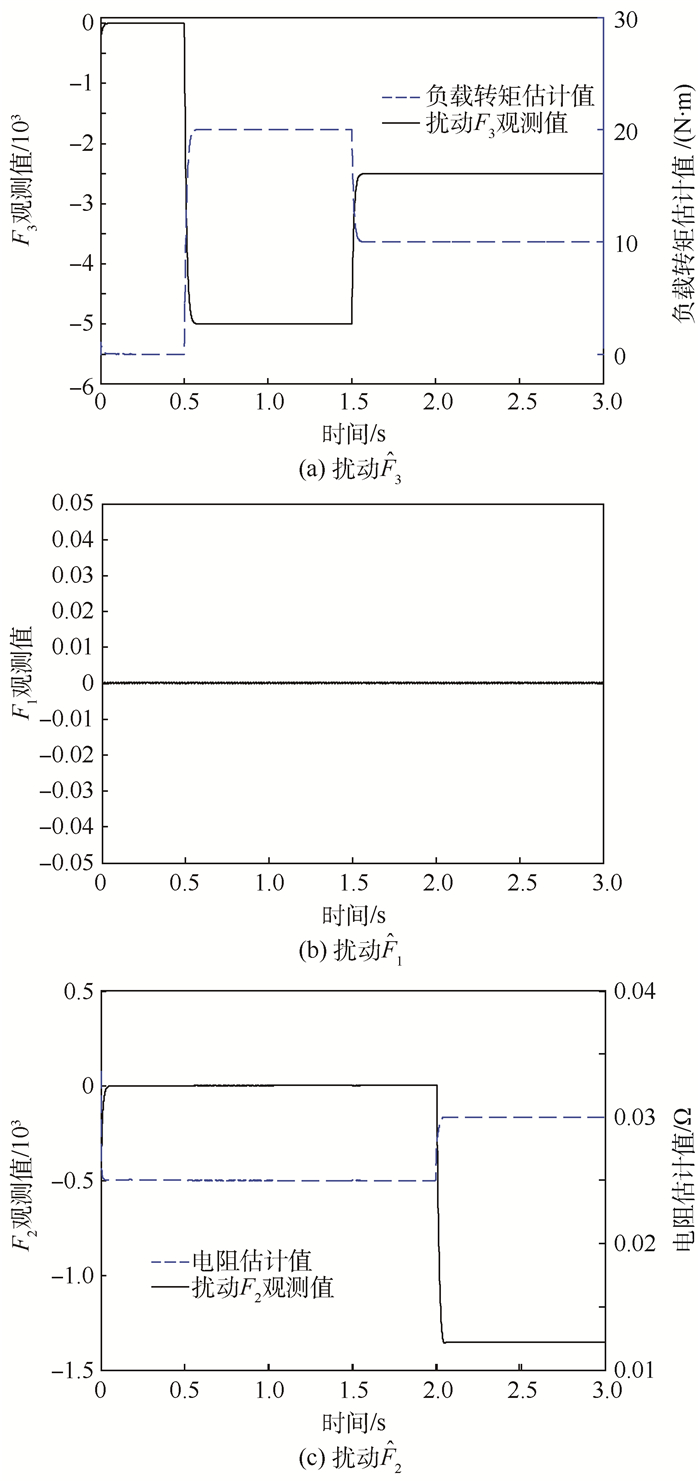 |
| 图 5 FODOB观测结果 Fig. 5 Observed results of FODOB |
| 图选项 |
图 6(a)为受扰时NFOSMC和PI控制的对比曲线。可以看出,当电阻发生20%的波动时,转速在2种策略下都未出现太大波动,主要是由于电液伺服泵的电感很小,该参数扰动PI控制器就可以快速消除,但是从图 5(c)中可以发现FODOB仍可以准确地观测到这一电阻参数波动。而当突加外负载时,图 6(a)表明PI控制时转速波动很大,最大转速降几乎已经达到1 000 r/min,而采用NFOSMC且无FODOB补偿时,相比较PI控制,转速降减小,转速收敛速度加快,说明抗扰能力要强于PI控制。而在采用FODOB扰动补偿后,抗扰能力进一步增强。
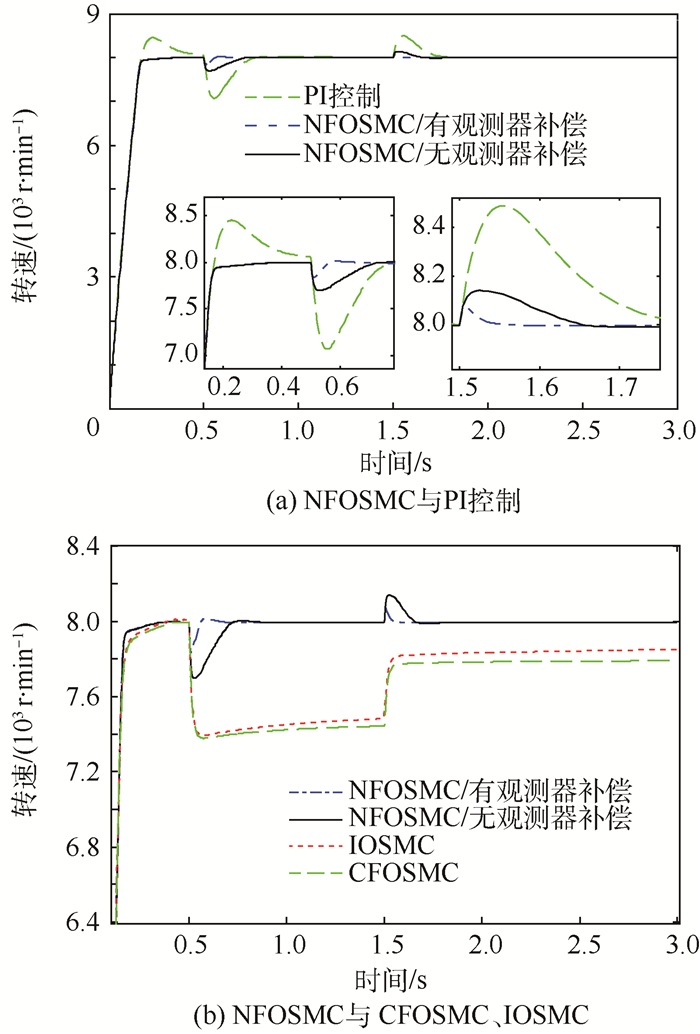 |
| 图 6 NFOSMC与CFOSMC、IOSMC抗扰性能对比曲线 Fig. 6 Comparison curves of anti-disturbance performance between CFOSMC, IOSMC and NFOSMC |
| 图选项 |
图 6(b)为受扰时NFOSMC与CFOSMC、IOSMC的对比曲线。可以看出,当受到外负载扰动时,切换增益仍取ξ=2 000,由于该值较小,对于CFOSMC和IOSMC来说已经不能满足可达性条件,滑模变量只能到达滑模面的一个邻域内,因此转速出现了较大的稳态误差,如果要满足可达性条件,必须选择更大的切换增益ξ,实际上当外部扰动为20 N·m时,可以计算出此时切换增益至少应为ξ=20/J=20/0.004=5 000,而这势必会造成抖振进一步增大。而NFOSMC在无FODOB补偿时,切换增益同样取ξ=2 000,转速仍能够跟随nd,说明NFOSMC自身的抗扰能力要强于CFOSMC和IOSMC,主要原因是由于NFOSMC的切换增益是根据扰动的分数阶上界|D1-αF3|确定,而CFOSMC和IOSMC的切换增益是直接根据扰动|F3|的上界确定,随着时间推移,分数阶上界|D1-αF3|的值是变化的,根据分数阶微分的衰减记忆特性,该值必然会小于|F3|,这就说明相比较CFOSMC和IOSMC,NFOSMC可以用同样大的切换增益抵御更大的扰动。同样,NFOSMC在通过FODOB扰动补偿后,抗扰能力进一步提高。
6 结?论 本文设计了一种新型分数阶滑模控制器(NFOSMC)和扰动观测器(FODOB),通过Lyapunov稳定性定理证明了控制器能在有限时间内收敛,并将其应用于电液伺服泵的速度环和电流环控制,通过分别与PI控制、整数阶滑模控制器(IOSMC)和传统的分数阶滑模控制器(CFOSMC)对比分析, 可以得出以下结论:
1)?相较于PI控制,转速的收敛速度要快于PI控制,而且可无超调跟随转速;对于q、d轴电流的跟踪速度更快、更加平稳。
2)?相较于整数阶滑模控制器和传统的PD型分数阶滑模控制器,转速的收敛速度要略快于两者。利用切换项的分数阶积分滤波作用,去抖振效果明显,可以实现平滑无抖振滑模控制;去除了传统PD型分数阶滑模控制器中的高阶分数阶微分项,避免了噪声引入,扩大了分数阶阶数取值范围。
3)?抗扰性方面,即使没有观测器补偿,本文控制器的抗扰能力也要强于三者。设计的分数阶扰动观测器也能平滑、准确观测扰动,通过前馈补偿抗扰能力能够得到进一步提高。
4)?应该注意到目前分数阶微积分的实现基本都是通过Oustaloup滤波器法[27]近似为整数阶来实现的,而整数阶阶数至少为4阶,因此需进一步研究相应的最优降阶算法,以降低分数阶控制器的应用难度。
参考文献
| [1] | 付永领, 李祝锋, 祁晓野, 等. 轴向柱塞式电液泵能量转化效率研究[J].机械工程学报, 2014, 50(14): 204–212.FU Y L, LI Z F, QI X Y, et al. Research on the energy conversion efficiency of axial pisto electro-hydraulic pump[J].Journal of Mechanical Engineering, 2014, 50(14): 204–212.DOI:10.3901/JME.2014.14.204(in Chinese) |
| [2] | BAIK I C, KIM K H, YOUN M J. Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J].IEEE Transactions on Control Systems Technology, 2000, 8(1): 47–54.DOI:10.1109/87.817691 |
| [3] | 皇甫宜耿, LAGHROUCHES, 刘卫国, 等. 高阶滑模消抖控制在永磁同步电动机中的应用[J].电机与控制学报, 2012, 16(2): 7–11.HUANGFU Y G, LAGHROUCHE S, LIU W G, et al. Chattering avoidance high order sliding mode control for permanent magnet synchronous motor[J].Electric Machines and Control, 2012, 16(2): 7–11.(in Chinese) |
| [4] | 童克文, 张兴, 张昱, 等. 基于新型趋近律的永磁同步电动机滑模变结构控制[J].中国电机工程学报, 2008, 28(21): 102–106.TONG K W, ZHANG X, ZHANG Y, et al. Sliding mode variable structure control of permanent magnet synchronous machine based on a novel reaching law[J].Proceedings of the CSEE, 2008, 28(21): 102–106.(in Chinese) |
| [5] | DELAVARI H, GHADERI R, RANJBAR A, et al. Fuzzy fractional order sliding mode controller for nonlinear systems[J].Communications in Nonlinear Science & Numerical Simulation, 2010, 15(4): 963–978. |
| [6] | DADRAS S, MOMENI H R. Fractional terminal sliding mode control design for a class of dynamical systems with uncertainty[J].Communications in Nonlinear Science & Numerical Simulation, 2012, 17(1): 367–377. |
| [7] | EFE M O.A fractional order adaptation law for integer order sliding mode control of a 2D OF robot[M]//BALEANU D, GUVENC Z B, MACHADO J A T.New trends in nanotechnology and fractional calculus applications.Amsterdam:Springer, 2010:471-478. |
| [8] | CALDERóN A J, VINAGRE B M, FELIU V, et al. Fractional order control strategies for power electronic buck converters[J].Signal Processing, 2006, 86(10): 2803–2819.DOI:10.1016/j.sigpro.2006.02.022 |
| [9] | 高强, 侯润民, 杨国来, 等. 基于分数阶神经滑模的某顶置火炮调炮控制[J].兵工学报, 2013, 34(10): 1311–1317.GAO Q, HOU R M, YANG G L, et al. Adjustment and control of a certain top-mounted gun based on a novel fractional order neural sliding mode strategy[J].Acta Armamentarii, 2013, 34(10): 1311–1317.(in Chinese) |
| [10] | 邓立为, 宋申民. 基于分数阶滑模的挠性航天器姿态鲁棒跟踪控制[J].航空学报, 2013, 34(8): 1915–1923.DENG L W, SONG S M. Flexible spacecraft attitude robust tracking control based on fractional order sliding mode[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(8): 1915–1923.(in Chinese) |
| [11] | ZHANG B T, PI Y G, LUO Y. Fractional order sliding-mode control based on parameters auto-tuning for velocity control of permanent magnet synchronous motor[J].ISA Transactions, 2012, 51(5): 649–656.DOI:10.1016/j.isatra.2012.04.006 |
| [12] | 黄家才, 施昕昕, 李宏胜, 等. 永磁同步电机调速系统的分数阶积分滑模控制[J].吉林大学学报(工学版), 2014, 44(6): 1736–1742.HUANG J C, SHI X X, LI H S, et al. Speed control of PMSM using fractional order integral sliding mode controller[J].Journal of Jilin University(Engineering and Technology Edition), 2014, 44(6): 1736–1742.(in Chinese) |
| [13] | 韩松杉, 焦宗夏, 汪成文, 等. 电液飞行转台的分数阶积分滑模非线性控制[J].北京航空航天大学学报, 2014, 40(10): 1411–1416.HAN S S, JIAO Z X, WANG C W, et al. Fractional integral sliding mode nonlinear controller of electrical-hydraulic flight simulator[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(10): 1411–1416.(in Chinese) |
| [14] | 陈荣, 邓智泉, 严仰光. 基于负载观测的伺服系统抗扰研究[J].中国电机工程学报, 2004, 24(8): 103–108.CHEN R, DENG Z Q, YAN Y G. Research on resist-disturbance performance of servosystem based on load observer[J].Proceedings of the CSEE, 2004, 24(8): 103–108.(in Chinese) |
| [15] | 郑泽东, 李永东, FADELM, 等. 基于扩展Kalman滤波器的PMSM高性能控制系统[J].电工技术学报, 2007, 22(10): 18–23.ZHENG Z D, LI Y D, FADEL M, et al. High performance PMSM control system based on extended Kalman filter[J].Transactions of China Electrotechnical Society, 2007, 22(10): 18–23.(in Chinese) |
| [16] | KIM H, SON J, LEE J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J].IEEE Transactions on Industrial Electronics, 2011, 58(9): 4069–4077.DOI:10.1109/TIE.2010.2098357 |
| [17] | 付永领, 李祝峰, 薛晶, 等.一种带转速反馈的永磁轴向柱塞式电液泵:ZL201320520163.3[P].2014-02-05.FU Y L, LI Z F, XUE J, et al.A kind of permanent magnet axial piston integrated electro-hydraulic pump with speed feedback:ZL201320520163.3[P].2014-02-05(in Chinese). |
| [18] | PONOMAREV P, POLIKARPOVA M, HEINIKAINEN O, et al.Design of integrated electro-hydraulic power unit for hybrid mobile working machines[C]//Proceedings of the 14th European Conference on Power Electronics and Applications (EPE2011).Piscataway, NJ:IEEE Press, 2011:1-10. |
| [19] | PODLUBNY I. Fractional differential equations:An introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications[M].New York: Academic Press, 1999: 62-63. |
| [20] | LI C, QIAN D, CHEN Y. On Riemann-Liouville and caputo derivatives[J].Discrete Dynamics in Nature & Society, 2011, 15(1): 309–323. |
| [21] | AGHABABAM P. A novel terminal sliding mode controller for a class of non-autonomous fractional-order systems[J].Nonlinear Dynamics, 2013, 73(1-2): 679–688.DOI:10.1007/s11071-013-0822-y |
| [22] | BHAT S P, BERNSTEIN D S. Continuous finite-time stabilization of the translational and rotational double integrators[J].IEEE Transactions on Automatic Control, 1998, 43(5): 678–682.DOI:10.1109/9.668834 |
| [23] | YANG L, YANG J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems[J].International Journal of Robust and Nonlinear Control, 2011, 21(16): 1865–1879.DOI:10.1002/rnc.v21.16 |
| [24] | QIAN D, LI C, AGARWAL R P, et al. Stability analysis of fractional differential system with Riemann-Liouville derivative[J].Mathematical & Computer Modelling, 2010, 52(5-6): 862–874. |
| [25] | CHEN Y Q, PETRAS I, XUE D.Fractional order control-A tutorial[C]//Proceedings of the American Control Conference.Piscataway, NJ:IEEE Press, 2009:1397-1411. |
| [26] | 于艳君, 柴凤, 高宏伟, 等. 基于Anti-Windup控制器的永磁同步电机控制系统设计[J].电工技术学报, 2009, 24(4): 66–70.YU Y J, CHAI F, GAO H W, et al. Design of PMSM system based on Anti-Windup controller[J].Transactions of China Electrotechnical Society, 2009, 24(4): 66–70.(in Chinese) |
| [27] | OUSTALOUP A, LEVRON F, MATHIEU B, et al. Frequency-band complex noninteger differentiator:Characterization and synthesis[J].IEEE Transactions on Circuits & Systems-I:Fundamental Theory & Applications, 2000, 47(1): 25–39. |
