近年来,在高超声速飞行器控制研究中,应用较多的方法主要包括动态逆法、滑模变结构控制法、自适应控制法、干扰观测器法及反演控制法等。其中,动态逆法主要用于解决高超声速飞行器各个控制输入量与输出量之间的耦合问题[2-4];滑模变结构控制法主要用于改善系统的鲁棒性[5];自适应控制法主要用于解决高超声速飞行器在复杂环境下的飞行器数学模型与实际动力学模型间的非匹配问题[2, 6];干扰观测器法的主要设计思想是对系统受到的干扰进行观测和逼近,并通过补偿解决系统的非匹配性问题[7-8];反演控制法则是采用递归的策略,逐步设计控制指令[9]。在高超声速飞行器控制方法研究中,各个控制方法往往结合使用,协同解决高超声速飞行器的控制问题。
其中,滑模变结构控制作为非线性鲁棒控制的有效手段,目前已广泛应用于各类高超声速飞行器控制器设计。滑模变结构控制可分为趋近滑模面运动和沿滑模面滑动2个部分。滑动模态(简称滑模)是人为设定的经过平衡点的相轨迹,通过适当的系统设计,位于相轨迹外的系统状态在控制作用下可以在有限时间内到达设定的相轨迹,且当系统状态到达相轨迹后会沿着相轨迹渐近稳定到平衡点[4]。滑模变结构控制具有响应速度快、对参数变化及干扰鲁棒性强、无需系统在线辨识及物理实现简单等优点,其主要缺点在于当状态轨迹到达滑模面后,无法沿着滑模面运动至平衡点,而是在滑模面两侧往复穿越运动,即存在所谓的抖振运动[5]。在实际情况下,抖振不可能完全消除,只能尽量将其限制在一定范围内,比较典型的抖振抑制方法是准滑动模态法[10]和趋近律设计法[11]。其中,准滑动模态控制可通过采用饱和函数sat(x)代替开关函数sgn(x)实现。在趋近律设计方面,比较典型的趋近律包括等速趋近率、指数趋近律、幂次趋近律等。其中,指数趋近律能够有效兼顾趋近速度和削弱抖振两方面的需求,同时参数选择较为简单,因此在滑模控制中成为应用主流。
通常情况下,滑模面可以设计为系统状态量及其各阶导数的线性组合。为了获得更好性能,一些****提出终端滑模控制策略和有限时间收敛的概念[12-13]。终端滑模控制在滑模面设计中引入非线性函数,如将滑模面设计为[14-15]
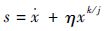 | (1) |
式中:j>k,j和k为正奇数;η>0为滑移面设计参数;x为状态量偏差值。
为了提高远离平衡点时的收敛速度,文献[16]提出了一种全局快速终端滑模面,其滑模面设计为
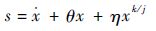 | (2) |
式中:θ为滑移面设计参数。
Wang等[17]在其提出的终端滑模自适应反演姿态控制器中也应用了全局快速终端滑模面。由于在滑模面方程中引入非线性函数,所以在控制律求解时存在奇异点。对此,Feng等[18]探讨了非奇异终端滑模控制器设计问题。近年来,终端滑模控制器凭借有限时间收敛的优良性能逐渐在高超声速飞行器控制研究中引起高度重视[19-21]。
然而,传统的终端滑模控制器仅是在滑模面设计时引入非线性项,能够保证系统状态在沿滑模面运动时有限时间收敛至平衡点,但是却无法保证系统状态运动也能够在有限时间内收敛至滑模面。同时,为了抑制抖振效应,文献[15, 22-24]在设计终端滑模控制器时使用饱和函数sat(s)替换开关函数sgn(s)。文献[14]中的设计虽然能够有效抑制抖振,但是却导致系统状态理论上无法在有限时间内收敛至滑模面,进而造成滑模面趋近阶段的动力学稳定性分析非常困难。
本文以高超声速飞行器绕心动力学模型为研究对象,开展终端滑模变结构控制方法研究,旨在通过优化滑模面的指数趋近律设计,提升系统状态趋近滑模面的速度,同时改善姿态控制精度。
1 预备知识和问题描述 由于高超声速飞行器的绕心运动周期远小于质心运动周期和地球自转运动周期,所以本文在研究高超声速飞行器姿态控制问题时不考虑飞行器的速度、位置变化情况及地球自转角速度。同时,假设飞行器的惯量积远小于转动惯量,进而建模时忽略惯量积的影响。基于上述假设,在飞行器坐标系下建立高超声速飞行器姿态运动简化模型,可描述为[4]
 | (3) |
式中:ωx、ωy和ωz分别为滚动角速度、偏航角速度和俯仰角速度;φ、ψ和γ分别为俯仰角、偏航角和滚动角;Mx、My和Mz分别为滚动力矩、偏航力矩和俯仰力矩;Jx、Jy和Jz分别为x轴、y轴和z轴3个方向的转动惯量。
本文研究所选用的高超声速飞行器模型为NASA兰利研究中心(Langley Research Center)提供的具有轴对称锥形体外形的高超声速飞行器动力学模型[25]。力矩计算表达式为
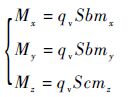 | (4) |
式中:qv=0.5ρv2为动压,ρ为大气密度,v为速度;S为参考面积;b为侧向参考长度;c为纵向参考长度;mx、my和mz分别为滚动力矩系数、偏航力矩系数和俯仰力矩系数。 气动力矩系数表达式由Keshmiri等[26-27]基于CFD 计算数据和风洞测试数据采用多项式拟合方法得到。其中: 滚动力矩系数、偏航力矩系数和俯仰力矩系数可表示为马赫数Ma、攻角α、侧滑角β、左升降舵偏角δe、右升降舵偏角δa和方向舵偏角δr的五阶多项式函数:
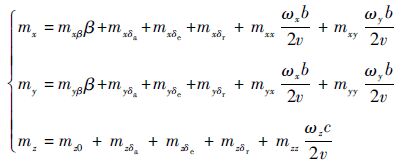 | (5) |
式中:mxβ、mxδa、mxδe、mxδr、mxx和mxy分别为滚转力矩系数mx中β、δa、δe、δr、ωx和ωy的系数表达式;myβ、myδa、myδe、myδr、myx和myy分别为偏航力矩系数my中β、δa、δe、δr、ωx和ωy的系数表达式;mz0为δa、δe、δr、α、β、ωz均为0时的俯仰力矩系数;mzδa、mzδe、mzδr、mzz分别表示俯仰力矩系数mz中的δa、δe、δr、ωz的系数表达式。式(5)等号右侧的各项系数在不同Ma范围内具有不同的表达式。
研究高超声速飞行器姿态控制问题,主要是基于式(3)中的绕心动力学方程,在控制周期内设计合适的控制力矩,使飞行器的姿态角能够保持为期望值。针对本文的研究对象,仿真中通过在有效范围内遍历舵偏角,寻找使三通道控制力矩最接近期望力矩的舵偏角。
2 非线性姿态控制器设计 2.1 动态逆解耦处理 由于高超声速飞行器姿态运动模型式(3)中的状态变量和控制变量间存在非线性关系,所以首先需要对模型进行线性化处理。
在姿态运动模型中,选取俯仰角φ、偏航角ψ和滚动角γ为输出量,记为Θ = [φ?ψ?γ]T。选取俯仰力矩Mz、偏航力矩My和滚动力矩Mx为输入量,记为 U M = [Mx ?My ?Mz]T,则姿态运动模型可表示为
 | (6) |
式中: z = [φ?ψ?γ?ωx ?ωy ?ωz]T; y 为状态观测向量;f()为状态方程。
定理1?[28] 一般非线性系统式(7)在( x 0,u 0)的邻域内可逆的充分必要条件是在此邻域内存在向量相对阶 α = [α1?α2 ?…?αm]T,即( x 0,u 0)为Interactor算法的正则点。
 | (7) |
式中:h()为观测方程。
若记 ω = [ωx?ωy?ωz]T,则飞行器姿态运动模型可改写为
 | (8) |
式中:
 |
 |
利用Interactor算法分析姿态运动模型的可逆性,分别对输出量俯仰角φ、偏航角ψ和滚动角γ进行微分,直到导数中显含控制量Mx、My和Mz(或者其等效控制量为ωx 、ωy 和ωz )为止。
 | (9) |
 | (10) |
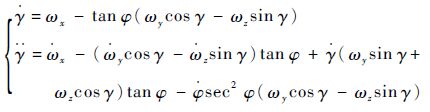 | (11) |
由式(9)~式(11)推导可知俯仰角、偏航角和滚动角的相对阶均为2,姿态运动模型的相对阶(T=2+2+2=6)与系统阶数相等(order=6),由定理1可知姿态运动模型是可逆的,且采用动态逆法可实现模型的完全线性化和三通道解耦。同时,式(9)~式(11)可表示为
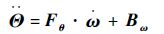 | (12) |
式中:
 |
将式(8)中第2个式子代入式(12)中,可得
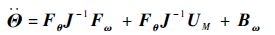 | (13) |
因此,逆系统环节设计为
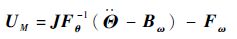 | (14) |
高超声速飞行器姿态控制器组成关系参见图 1。姿态控制器由终端滑模控制器和逆系统组成。控制器的输入φd、ψd、γd分别为俯仰角、偏航角、滚动角的期望值,逆系统环节的输入

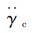
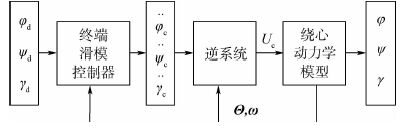 |
| 图 1 姿态控制器 Fig. 1 Attitude controller |
| 图选项 |
2.2 终端滑模控制器设计 终端滑模控制环节选取状态量 Θ 的误差信号 e 为状态量,e = [eφ eψ eγ]T,eφ 、eψ和 eγ分别为俯仰角偏差、偏航角偏差和滚动角偏差。假设制导回路提供的飞行器姿态指令为
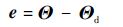 | (15) |
为了保证有限时间收敛特性,滑模面设计为
 | (16) |
式中:si为滑模函数值;ei为被控量偏差;ai>0;bi>0;p和q为正奇数,且满足q<p<2q。
典型的指数趋近律设计为s · = -εsgn(s)-ks的形式,k为s项系数,ε为开关量项sgn(s)系数。为了抑制抖振,通常使用饱和函数取代指数趋近律中的开关函数,即

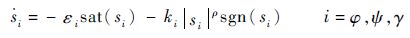 | (17) |
式中:εi,ki(i=φ, ψ, γ)均为正实数;0 <ρ<1;
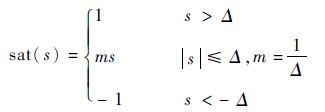 | (18) |
其中:Δ>0为边界层厚度。
在0<ρ<1的情况下,当系统状态远离滑模面(s≥1)时,系统状态趋近滑模面的速度慢于传统的指数趋近律s · = -εsat(s)-ks;在系统状态距离滑模面较近(s<1)时,系统状态趋近滑模面的速度优于基于传统指数趋近律时的趋近速度。
当状态量 Θ 的误差信号ei≠0 (i=φ,ψ,γ)时,对滑模面取一阶导数并结合趋近律表达式(17),可得
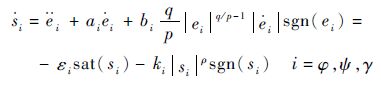 | (19) |
式中:
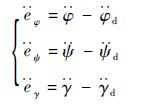 | (20) |
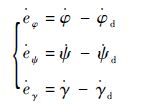 | (21) |
根据表达式(19),可以进一步推导得出
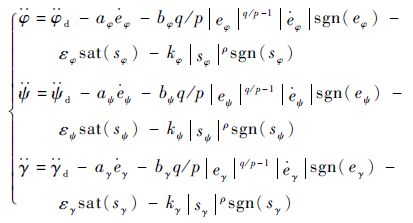 | (22) |
当状态量 Θ 的误差信号ei=0 (i=φ,ψ,γ)时,可得
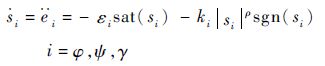 | (23) |
根据式(23),可以进一步推导得出
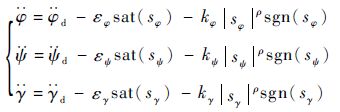 | (24) |
基于式(22)和式(24),最终可得终端滑模控制器输出的俯仰角、偏航角、滚动角二阶导数的期望值为
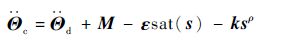 | (25) |
式中:
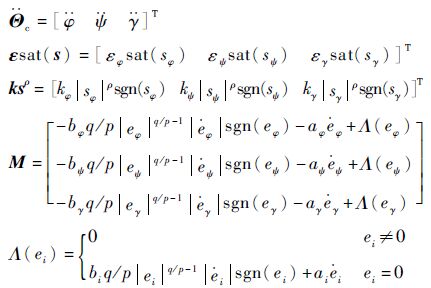 |
式中:Λ(ei)(i=φ,ψ,γ)为一个分段定义符号函数。
最终,可推导得出滚动、偏航和俯仰3个方向的控制力矩向量为
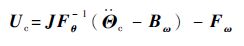 | (26) |
2.3 控制器稳定性证明 定理2?假设存在连续可微函数V:U→ R ,U为函数的定义域,使得其满足下列条件[29-31]:
1) V为正定函数。
2) 存在正实数K>0和μ∈(0,1),以及一个包含原点的开邻域U0,使得下列条件成立:
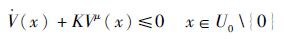 |
则系统为有限时间稳定的;若U =U0 = R n,n为空间维数,则系统为全局有限时间稳定的。且收敛时间满足:
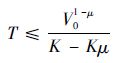 |
式中:V0为初始时刻函数V值。
证明
1) 在滑模面趋近阶段,选取李雅普诺夫函数:
 | (27) |
首先推导滑模面趋近律s · ,由式(16)可得
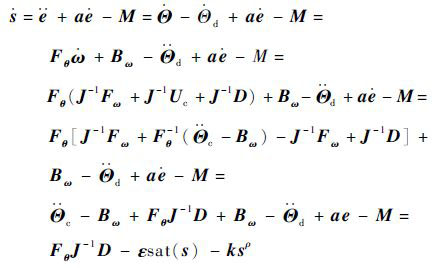 | (28) |
式中: a =diag(aφ, aψ, aγ),aφ、aψ和aγ分别为滑模面中eφ 、eψ和 eγ的系数; D 为外部干扰力矩向量。
在终端滑模控制器鲁棒项增益选择足够大,能够抵消外部干扰力矩的情况下,对V1i求导,可得
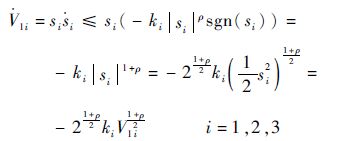 | (29) |
根据定理2,高超声速飞行器姿态运动模型式(3)的状态能够在姿态控制器的控制下在有限时间内收敛至滑模面。收敛时间为
 | (30) |
式中:t0为初始时间;当t>t1i时,si=0。
2) 在沿滑模面滑动阶段,选取李雅普诺夫函数:
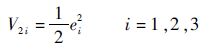 | (31) |
由
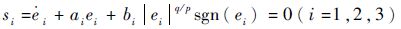
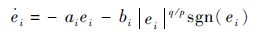 | (32) |
对V2i求导,可得
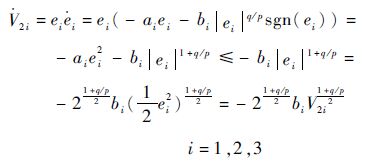 | (33) |
根据定理2,高超声速飞行器姿态运动模型式(3)的状态能够在控制作用下在有限时间内沿滑模面收敛至平衡点。收敛时间为
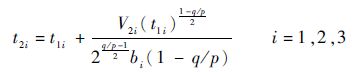 | (34) |
式中:t1i为系统状态到达滑模面的时间。
综合上述1)和2)2个部分证明过程可得,在本文所提出的终端滑模控制器作用下,系统状态收敛至平衡点的过程是全局有限时间收敛的。
3 仿真分析 本节通过仿真验证高超声速飞行器全局有限时间姿态控制方法的有效性。飞行器仿真模型选用NASA兰利研究中心提供的具有轴对称锥形体外形的高超声速飞行器动力学模型[25]。仿真初始条件为φ=1.79°,ψ=4°,γ=-3°,v0=4 590.3 m/s,h=33 528 m,ωx=ωy=ωz=0 (°)/s。姿态控制指令为φd=8°,ψd=0°,γd=0°。飞行器模型升降舵和方向舵的舵偏角范围 为(-30°,30°)。控制器参数设置如下:a1= a2= a3=0.5,b1=b2=b3=0.5,p=15,q=13,ε1=ε2=ε3=2,k1= k2= k3=1,ρ=0.8,Δ1=Δ2=Δ3=1。同时,仿真中转动惯量(Jx,Jy,Jz)的偏差范围设计为[-10%,10%],气动参数(mx,my,mz)偏差范围设计为[-30%,30%],外部干扰设计为
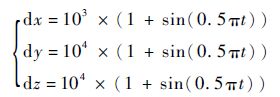 | (35) |
在充分考虑转动惯量和气动参数偏差对控制器可能产生的最大影响的情况下,分别设计了仿真1和仿真2验证控制器的有效性。在仿真1中,选择转动惯量偏差为-10%,气动参数偏差为30%。在此情况下,实际产生的控制效果将比预期值大。仿真结果参见图 2和图 3。图 2表明在存在模型不确定性和外部干扰,以致实际产生的控制效果将比预期值大的情况下,全局有限时间收敛姿态控制方法能够准确跟踪控制指令,取得良好的控制效果。在图 3中,升降舵和方向舵偏角的抖动现象并非滑模控制方法本身的抖振所导致,而是由于当所需舵偏角缓慢变化时,对舵偏角指令进行四舍五入取整导致在相邻整数舵偏角之间抖动。因此,可以认为在本文的控制方法中抖振抑制是有效的。
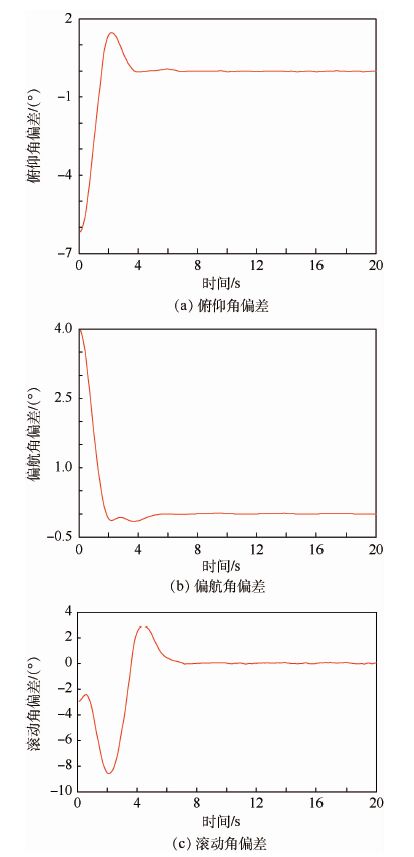 |
| 图 2 仿真1中俯仰角、偏航角及滚动角偏差 Fig. 2 Error of pitch angle,yaw angle androll angle in simulation 1 |
| 图选项 |
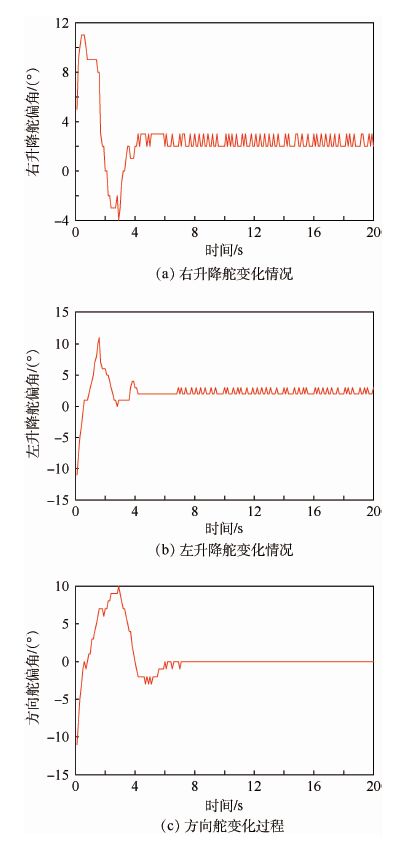 |
| 图 3 仿真1右升降舵、左升降舵及方向舵变化过程 Fig. 3 Changing process of right elevator,left elevator andrudder deflection in simulation 1 |
| 图选项 |
仿真2选择转动惯量偏差为10%,气动参数偏差为-30%。在此情况下,实际产生的控制效果将小于预期值。在仿真结果中,图 4(a)和图 4(b)表明有限时间内在俯仰方向和偏航方向能够准确跟踪控制指令,取得较好的控制效果。在图 4(c)中,滚动角具有一定稳态偏差。由于稳态偏差波动周期与外部干扰周期一致,所以认为该稳态偏差为外部干扰导致。在实际工程中,该偏差仍然在飞行控制可接受的范围内。图 5表明了在仿真2中右升降舵、左升降舵和方向舵偏角变化情况。
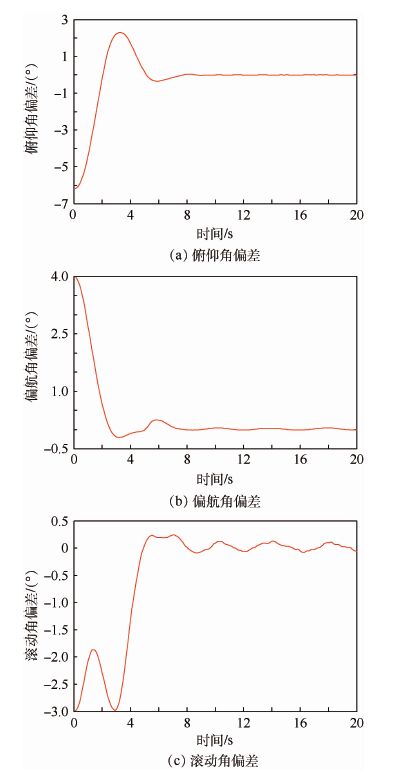 |
| 图 4 仿真2中俯仰角、偏航角及滚动角偏差 Fig. 4 Error of pitch angle,yaw angle androll angle in simulation 2 |
| 图选项 |
 |
| 图 5 仿真2右升降舵、左升降舵及方向舵变化过程 Fig. 5 Changing process of right elevator,left elevator andrudder deflection in simulation 2 |
| 图选项 |
在仿真3中,分别将控制器参数ρ设置为1.0和0.5,其他参数设置同仿真2,进行了两次仿真验 证。其中,当ρ设置为1.0时,趋近律为典型的指数趋近律。在参数ρ分别设置为0.5,0.8和1.0的情况下,控制效果对比情况参见图 6~图 8。其中,图 6(a)、图 7(a)、图 8(a)为俯仰角、偏航角和滚动角的整体控制效果。在图 6(a)和图 7(a)中,在系统状态远离滑模面的情况下,基于传统指数趋近律的终端滑模控制方法使系统状态收敛略快,但是整体性能差异不大。在图 8(a)中,ρ=0.5时的滚动角控制效果相对于其他两种参数设置,性能差异较明显。图 6(b)、图 7(b)和图 8(b)分别将图 6(a)、图 7(a)和图 8(a)中的偏差结果局部放大。从图 6(b)和图 7(b)中可以比较明显的看出,当系统状态距离滑模面较近时,基于本文应用的指数趋近律(

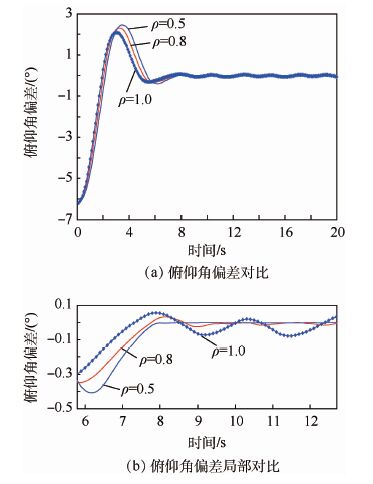 |
| 图 6 仿真3俯仰角偏差对比及其局部对比 Fig. 6 Comparison and local comparison of error ofpitch angle in simulation 3 |
| 图选项 |
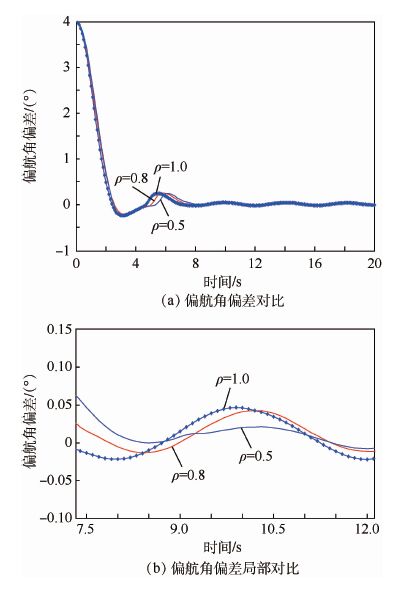 |
| 图 7 仿真3偏航角偏差对比及其局部对比 Fig. 7 Comparison and local comparison of error ofyaw angle in simulation 3 |
| 图选项 |
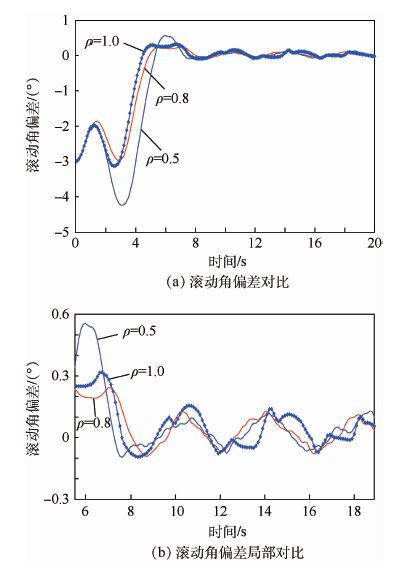 |
| 图 8 仿真3滚动角偏差对比及其局部对比 Fig. 8 Comparison and local comparison of error ofroll angle in simulation 3 |
| 图选项 |
4 结 论 本文以高超声速飞行器绕心运动模型为研究对象,研究了高超声速飞行器姿态控制问题,并提出了一种全局有限时间的姿态控制方法。经仿真实验验证:
1) 在考虑模型不确定性和外部干扰的情况下,全局有限时间终端滑模姿态控制方法具有良好鲁棒性,能够保证系统稳定和姿态控制精度。
2) 动态逆方法对于高超声速飞行器绕心运动模型各输入、输出变量之间的伪线性化处理是有效的。
3) 全局有限时间终端滑模姿态控制方法,基于改进的指数趋近律设计,虽然在理论上可证明其全局有限时间收敛特性,但是在仿真中对比基于典型指数趋近律的终端滑模控制方法在动态性能方面改进效果并不明显。
在后续工作中,将进一步着力于分析趋近律设计对终端滑模变结构控制下运动的影响机理,以便进一步优化终端滑模控制方法中趋近律的设计和应用。
参考文献
| [1] | 吴宏鑫, 孟斌. 高超声速飞行器控制研究综述[J].力学进展, 2009, 39(6): 756–765.WU H X, MENG B. Review on the control of hypersonic flight vehicles[J].Advances in Mechanics, 2009, 39(6): 756–765.(in Chinese) |
| [2] | XU H, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J].Journal of Guidance,Control,and Dynamics, 2004, 27(5): 829–838.DOI:10.2514/1.12596 |
| [3] | LI H F,SUN W C,LI Z Y,et al.Index approach law based sliding control for a hypersonic aircraft:AIAA-2009-1734 [R].Reston:AIAA,2009. |
| [4] | 王鹏.高超声速巡航飞行器姿态控制方法研究[D].长沙:国防科学技术大学,2013.WANG P.Research on attitude control method for hypersonic cruise vehicle[D].Changsha:National University of Defense Technology,2013(in Chinese). |
| [5] | 刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J].控制理论与应用, 2007, 24(3): 407–418.LIU J K, SUN F C. Research and development on theory and algorithms of sliding mode control[J].Control Theory & Applications, 2007, 24(3): 407–418.(in Chinese) |
| [6] | FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance,Control,and Dynamics, 2009, 32(2): 404–416. |
| [7] | WU H N, LIU Z Y, GUO L. Robust L∞-gain fuzzy disturbance observer-based control design with adaptive bounding for a hypersonic vehicle[J].IEEE Transactions on Fuzzy Systems, 2014, 22(6): 1401–1412.DOI:10.1109/TFUZZ.2013.2292976 |
| [8] | YANG J, LI S H, SUN C Y, et al. Nonlinear-disturbance-observer-based robust flight control for airbreathing hypersonic vehicles[J].IEEE Transactions on Fuzzy Systems, 2013, 49(2): 1263–1275. |
| [9] | 黄喜元, 王青, 董朝阳. 基于Backstepping的高超声速飞行器鲁棒自适应控制[J].系统工程与电子技术, 2011, 33(6): 1321–1326.HUANG X Y, WANG Q, DONG C Y. Robust adaptive control of hypersonic vehicles via backstepping method[J].Systems Engineering and Electronics, 2011, 33(6): 1321–1326.(in Chinese) |
| [10] | SLOTINE J J, SASTRY S S. Tracking control of nonlinear sysytems using sliding surfaces with application to robot manipulator[J].International Journal of Control, 1983, 38(2): 465–492.DOI:10.1080/00207178308933088 |
| [11] | 高为炳. 变结构控制的理论及设计方法[M].北京: 科学出版社, 1996: 35-36.GAO W B. Theory and design method of variable structure control[M].Beijing: Science Press, 1996: 35-36.(in Chinese) |
| [12] | YU X H, MAN Z H. Model reference adaptive control systems with terminal sliding modes[J].International Journal of Control, 1996, 64(6): 1165–1176.DOI:10.1080/00207179608921680 |
| [13] | MAN Z H,YU X H.Terminal sliding mode control of mimo linear system[C]//Proceedings of the 25th Conference on Decision and Control.Piscataway,NJ:IEEE Press,1996:4619-4624. |
| [14] | WANG X H, WANG J Z. Partial integrated missile guidance and control with finite time convergence[J].Journal of Guidance,Control,and Dynamics, 2013, 36(5): 1399–1409.DOI:10.2514/1.58983 |
| [15] | WANG Y Y, CHEN J W, GU L Y. Output feedback fractional-order nonsingular terminal sliding mode control of underwater remotely operated vehicles[J].The Scientific World Journal, 2014, 2014: 838019. |
| [16] | YU S H,YU X H.Robust global terminal sliding model control of SISO nonlinear uncertain systems[C]//39th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,2000:2198-2203. |
| [17] | WANG F, ZONG Q, TIAN B L. Adaptive backstepping finite time attitude control of reentry RLV with input constraint[J].Mathematical Problems in Engineering, 2014, 2014: 801747. |
| [18] | FENG Y, YU X H, MAN Z H. Non-singular terminal sliding mode control of rigid manipulators[J].Automatica, 2002, 38(12): 2159–2167.DOI:10.1016/S0005-1098(02)00147-4 |
| [19] | LEE K W,SINGH S N.Multi-input higher-order sliding mode control of aeroelastic systems with uncertainties and gust load[C]//AIAA Guidance,Navigation,and Control Conference.Reston:AIAA,2014:1-16. |
| [20] | WANG J Y, SUN C W. 6-DOF robust adaptive terminal sliding mode control for spacecraft formation flying[J].Acta Astronautica, 2012, 73: 76–87.DOI:10.1016/j.actaastro.2011.12.005 |
| [21] | 熊少锋, 王卫红, 王森. 带攻击角度约束的非奇异快速终端滑模制导律[J].控制理论与应用, 2014, 31(3): 269–278.XIONG S F, WANG W H, WANG S. Nonsingular fast terminal sliding-mode guidance with intercept angle constraint[J].Control Theory & Application, 2014, 31(3): 269–278.(in Chinese) |
| [22] | NEILA M B, TARAK D. Adaptive terminal sliding mode control for rigid robotic manipulators[J].International Journal of Automation and Computing, 2011, 8(2): 215–220.DOI:10.1007/s11633-011-0576-2 |
| [23] | CHEN S Y, L IN, F J. Robust nonsingular terminal sliding-mode control for nonlinear magnetic bearing system[J].IEEE Transactions on Control Systems Technology, 2011, 19(3): 636–643.DOI:10.1109/TCST.2010.2050484 |
| [24] | ZHU Z, XIA Y, FU M. Adaptive sliding mode control for attitude stabilization with actuator saturation[J].IEEE Transactions on Industrial Electronics, 2011, 58(10): 4898–4907.DOI:10.1109/TIE.2011.2107719 |
| [25] | SHAUGHNESSY J D,PINCKNEY S Z,MCMINN J D,et al.Hypersonic vehicle simulation model:Winged-cone configuration:NASA-TM-102610[R].Washington, D.C.:NASA,1990. |
| [26] | KESHMIRI S,COLGREN R,MIRMIRANI M.Development of an aerodynamic database for a generic hypersonic air vehicle:AIAA-2005-6257[R].Reston:AIAA,2005. |
| [27] | KESHMIRI S,COLGREN R, MIRMIRANI M.Six DoF nonlinear equations of motion for a generic hypersonic vehicle:AIAA-2007-6626[R].Reston:AIAA,2007. |
| [28] | 戴先中. 多变量非线性系统的神经网络逆控制方法[M].北京: 科学出版社, 2005: 27-32.DAI X Z. A neural network inverse control method for multivariable nonlinear systems[M].Beijing: Science Press, 2005: 27-32.(in Chinese) |
| [29] | HUANG X Q, LIN W, YANG B. Global finite-time stabilization of a class of uncertain nonlinear systems[J].Automatica, 2005, 41(5): 881–888.DOI:10.1016/j.automatica.2004.11.036 |
| [30] | HONG Y G, HUANG J, XU Y S. On an output feedback finite-time stabilization problem[J].IEEE Transactions on Automatic Control, 2001, 46(2): 305–309.DOI:10.1109/9.905699 |
| [31] | GRUYITCH L T, KOKOSY A. Robot control for robust stability with finite reachability time in the whole[J].Journal of Robotic Systems, 1999, 16(5): 263–283.DOI:10.1002/(ISSN)1097-4563 |
