对于战术拦截导弹，鸭舵控制和尾舵控制方式各有优缺点，如鸭舵控制具有更好的寻的性能^[1],但攻角易饱和,而尾舵控制更适用于中远程导弹等，所研究的双重控制导弹是指具有鸭舵和尾舵两组控制舵面的导弹^[1-3]。该类型导弹将鸭舵控制和尾舵控制相结合，对于增强导弹拦截性能是一种合理的设计折中。文献^[2]针对该类型导弹采用滑模控制方法，提出了一种制导与控制的一体化设计方法，但滑模控制的抖振问题一直是影响其应用的关键因素。文献^[3]基于线性二次型微分对策理论，针对该双重控制导弹进行末制导律的设计和分析，实现了两个控制通道间的最优控制命令分配。基于线性二次型性能指标的最优化制导律^[4-5]，为保证拦截导弹在控制界内运行，对权值系数的选取往往较为保守，同时该类型的制导律在制导末端也往往要求较强的机动性能，对于机动目标的拦截不利^[6]。本文直接将拦截导弹的有界控制性^[7-8]考虑到双重控制导弹制导律的设计当中，避免机动饱和并充分利用导弹的机动能力。
1 问题描述及建模 图 1为制导末端拦截导弹和目标的相对运动关系。图中：二者的相关状态分别采用下标P和E表示；X轴沿初始弹目视线方向；y为二者相对于X轴的位移；γ为航向角；q为弹目视线角。基于以下对导弹和目标的假设条件分析问题：
1) 二者控制动态特性近似线性，且可以沿X轴方向实现线性化。
2) 二者速度大小不变，具有有界的横向加速度。
3) 导弹可对与目标之间的相对运动和本身的部分状态非完全量测，而目标无法获得导弹信息，但可以随机机动规避。

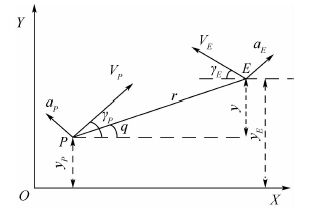图 1 导弹与目标之间的相对运动关系 Fig. 1 Relative movement relationship betweenmissile and target

图选项

参考文献^[1]，导弹鸭舵和尾舵的控制a_Pc、a_Pt分别采用以下传递函数表示：

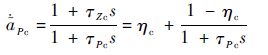(1)

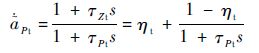(2)

式中：分子分母都为1阶；0＜η_c＜1，-1＜η_t＜0，表示舵面的直接控制部分，一般为小值；a_Pc和a_Pt分别为两组舵面的控制量，对应的控制命令为u_Pc和u_Pt；τ_Pc和τ_Pt为两者控制系统的时间常数；τ_Zc和τ_Zt为系统零点。尾舵产生的作用力与导弹横向机动的方向总是相反的，具有非最小相位的特性。
为便于建立系统模型，式(1)和式(2)可进一步转化为如下形式：

(3)

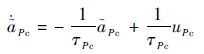(4)

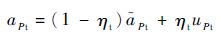(5)

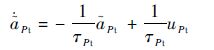(6)

目标控制系统的动态特性表示为

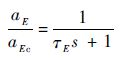(7)

式中：τ_E为目标控制系统的1阶时间常数。
基于假设条件和以上导弹与目标的控制系统模型，定义状态变量：，则所建立的整个系统的状态方程为

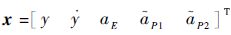
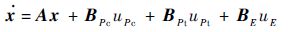(8)

式中：


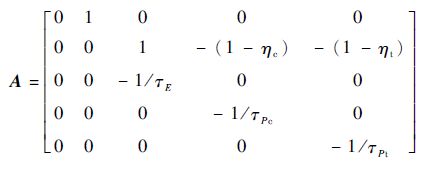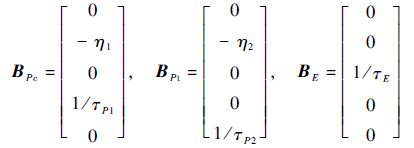由假设1)和假设2)，导弹的飞行时间可由式(9)近似计算：

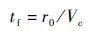(9)

式中：r₀为弹目之间的初始距离；V_c为二者的接近速度，并可近似为V_P+V_E。则整个弹道的剩余飞行时间为

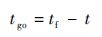(10)

2 微分对策制导律推导 近年来，微分对策理论应用于机动目标拦截方面得到了较为深入的研究^{[3, 6, 9-14]}，导弹和目标追求相反的性能指标，如脱靶量或控制量等的最小化和最大化。定义如下性能指标：

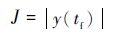(11)

拦截导弹与目标针对最终的脱靶量展开博弈。
基于式(8)，经进一步求解，零控脱靶量Z(t)可表示为

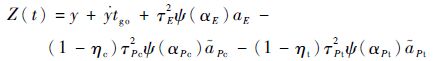(12)

式中：。

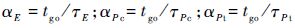
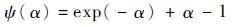(13)

对式(12)两边关于时间t求导，可以得到

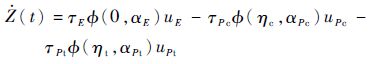(14)

式中：

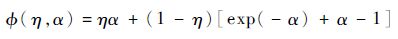(15)

由于Z(t_f/)=y(t_f)，将性能指标式(11)进一步扩展为以下形式：

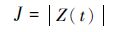(16)

由式(14)和式(16)可以得到，系统式(8)降阶为以零控脱靶量作为状态变量的标量形式，使得制导律的推导大大简化。
结合式(14)，构造哈密顿函数：

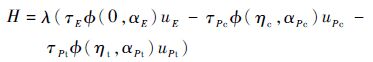(17)

式中：λ为拉格朗日乘子，结合横截条件求解协态方程可得

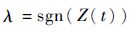(18)

因此，结合上述计算结果，两组舵面和目标的最优控制形式可以表示为

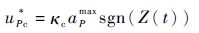(19)

(20)

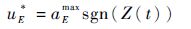(21)

式中：a_P^max和a_E^max分别为导弹和目标的控制上界；κ_c+κ_t=1。由于η_t＜0，与尾舵相关的最优控制命令和Φ(η_t,α_Pt)的符号相关。
由式(15)可以得到

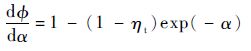(22)

由于α≥0，则η_t≤dΦ/dα＜1。当Φ取最小值的情况下，进一步计算可以求得

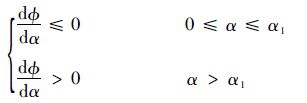(23)

式中：α₁=ln(1-η_t)。由此可以得到，当Φ=0时存在两个解：一个解为α₂=0，另一个解满足：

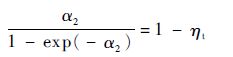(24)

当dΦ/dα>0时，可以得到α₂>ln(1-η_t)=α₁，因此基于上述分析，可以得到

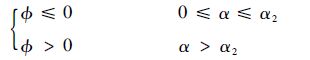(25)

图 2给出了η_t=-0.1条件下Φ的典型分布。

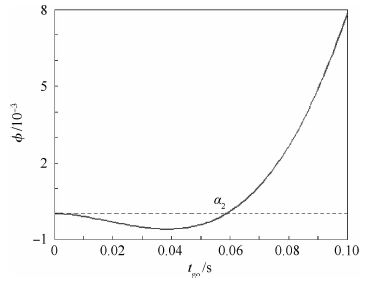图 2 Φ的典型分布曲线(ηt=-0.1) Fig. 2 Typical distribution curve of Φ(ηt=-0.1)

图选项

由上述分析结果，将式(19)~式(21)代入式(14)，并从t到t_f积分，进一步可以求得

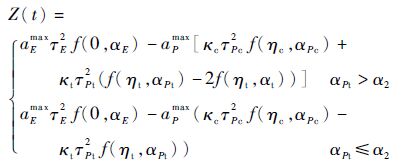(26)

式中：

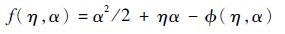(27)

式(19)与式(26)和式(20)与式(26)分别构成了鸭舵和尾舵的最优制导策略，可适用于拦截导弹具有双重控制的情形，而式(21)和式(26)也构成了目标的最优规避策略。在实际作战环境下，目标一般任务单一，对导弹的关键状态信息是无法直接测量的，即使能够意识到被锁定，往往也只能采用随机的规避机动，与最优规避策略恰好吻合的概率很小，甚至接近于零。
3 对策空间分析 假设鸭舵和尾舵采用了类似的控制系统执行机构，具有近似相等的控制系统时间常数，即取τ_Pc=τ_Pt，则α_Pc=α_Pt=α_P，则进一步由式(26)可以得到

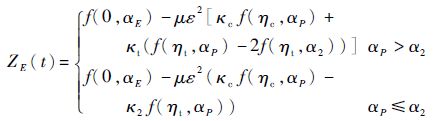(28)

式中：Z_E(t)= Z(t) a_E^maxτ_E² ； μ= a_P^max a_E^max ；ε= τ_P τ_E 。
由式(24)和式(27)可以得到

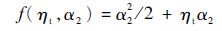(29)

对式(28)求极限，并结合式(29)，可以得到

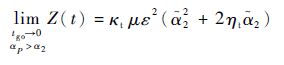(30)

式中：α₂=(t₂-t_f)／τ_P，t₂为对应于α₂的时刻。
由于η_t＜0，基于微分对策理论，系统可能存在共轭点，因此由式(28)，该双边微分对策问题鞍点解的存在条件为

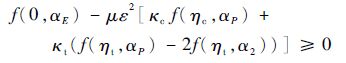(31)

进一步可以得到

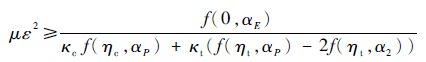(32)

因此，拦截导弹和目标之间的最大机动性能比μ和控制系统时间常数比ε决定了系统是否存在鞍点解。图 3给出了存在鞍点解时，不同ε下μ需要满足的条件。可以看出，当拦截导弹具有较高的控制系统响应速度时，并不要求导弹具有较强的机动性能，反之，控制系统响应速度不足，则可以通过增强机动性能弥补；同时，当拦截导弹和目标控制系统响应速度相当时，所设计的有界控制导弹微分对策制导律并不要求导弹具有较强的机动性能。

图 3 鞍点解的存在条件曲线 Fig. 3 Curves of existence conditions of saddle point solution

图选项

图 4为μ和ε不同取值情况下的对策空间分布。图 4(a)~图 4(c)分别对应不存在共轭点、存在偶共轭点^[3]和存在一般共轭点情况下的微分对策空间。共轭点不存在时，对策值逐渐收敛到零；偶共轭点属于鞍点解的特殊情况，是一种临界状态；存在一般共轭点时，只有在有限的条件下对策值才收敛，如图 4(c)所示，只有当近似t_go＜0.03时，才存在最优弹道使得对策值收敛到零。

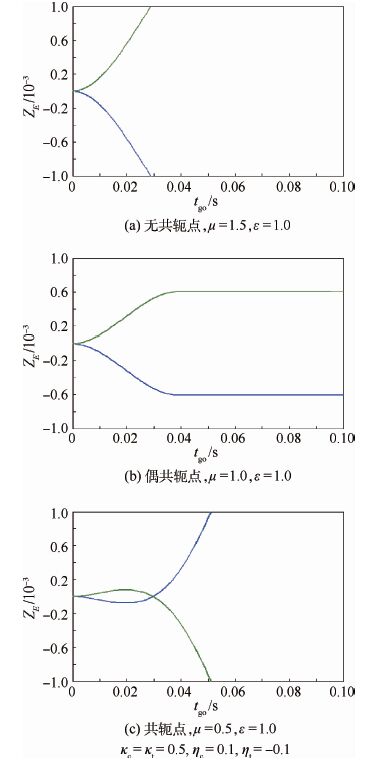图 4 对策空间分布曲线 Fig. 4 Game space distribution curves

图选项

4 目标加速度滤波器和拦截性能衡量指标 4.1 目标加速度滤波器设计 基于式(21)以及文献^[15]的研究结论，目标规避机动的最优方式为转换时间随机的“bang-bang”结构形式。应用成型滤波器方法建模目标的随机机动，采用随机噪声驱动系统，扩展系统状态。对于该类型的目标机动，成型滤波器建模为功率谱密度大小为4(a_E^max)²/t_f的积分环节^[9]。
结合图 1，采用弹上导引头和惯性测量系统可对拦截导弹和目标之间的相对距离r、导弹的横向加速度a_P和弹目视线角q进行测量。r和a_P一般可以较为精确地测量到，而q的测量值是含有噪声的：

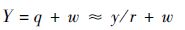(33)

式中：w为符合高斯分布的视线角测量噪声，对应的标准方差为σ_q。
选取目标加速度滤波器状态向量为x=，则其状态方程可建模为

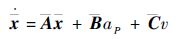(34)

式中：；v为系统噪声；a_Ec为目标机动的控制指令，而其导数建模为功率谱密度大小为4(a_E^max)²/t_f的高斯白噪声。
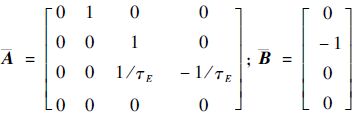
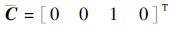
4.2 拦截性能衡量指标 采用单发杀伤概率(Single Shot Kill Probability,SSKP)^[10-11]作为拦截性能的衡量指标。SSKP指标综合考虑了目标随机机动和测量噪声的影响，导弹追求SSKP最大化，而目标则追求SSKP最小化。SSKP可用于衡量给定脱靶量下命中目标的概率，也可以用于衡量给定脱靶概率下命中目标应具有的最小脱靶量。
5 仿真结果及分析 仿真重点针对迎面末端目标拦截情况开展。γ_P(0)≈0,γ_E(0)≈0，其他仿真参数见表 1。鸭舵和尾舵都具有10g的最大机动性能，与目标相当。假设目标的机动为“bang-bang”结构，且仅有一次随机的时间切换^[11]，切换时间采用t_sw表示。
表 1 仿真参数 Table 1 Simulation parameters

参数	数值
导弹飞行速度VP/(m·s-1)	1 200
目标飞行速度VE/(m·s-1)	800
导弹控制系统时间常数τPc,τPt/s	0.2
目标控制系统时间常数τE/s	0.2
导弹最大机动性能aPmax/g	20
目标最大机动性能aEmax/g	10
弹目初始距离r0/m	6 000
量测噪声σq/mrad	1
直接控制系数ηc，ηt	0.1,-0.1
加权系数κc，κt	0.5

表选项






图 5为t_sw=1.5 s时的目标机动命令及其实际值和估计值的曲线。可见，当滤波器收敛时间足够时，可以获得目标加速度的较好估计。图 6和图 7分别为相应的脱靶量曲线和两组舵面的控制量曲线，最终的脱靶量大小为0.488 m。采用本文设计的有界微分对策制导律，鸭舵与尾舵的控制量可以满足导弹最大机动性能指标的要求。

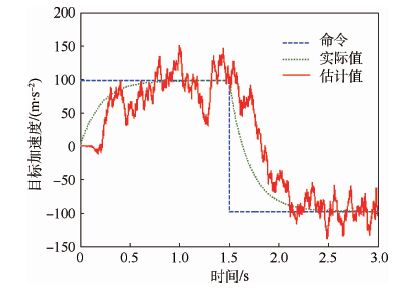图 5 目标加速度和估计值曲线 Fig. 5 Target acceleration and estimation value curves

图选项

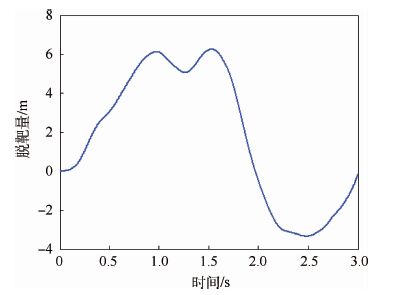图 6 脱靶量变化曲线 Fig. 6 Variation curve of miss distance

图选项

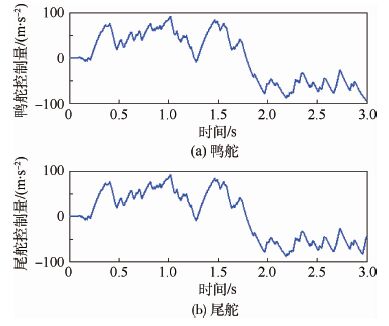图 7 鸭舵和尾舵的控制量曲线 Fig. 7 Curves of control values of canard fin and tail fin

图选项

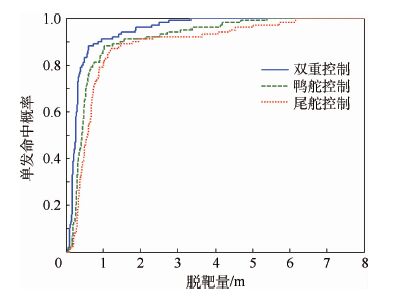图 8 累积脱靶量分布曲线 Fig. 8 Cumulative miss distance distribution curves

图选项

基于Monte Carlo法，对分别采用单一的鸭舵或尾舵控制，以及双重控制的三种微分对策制导律下的拦截性能进行仿真比较，三者取相同的目标机动命令切换时间和噪声随机数产生器种子，仿真次数为500次。如图 8所示，对于给定的SSKP，所设计的双重控制制导律具有最小的脱靶量，进而对弹头杀伤半径要求最小，而对于单一舵面控制方式，鸭舵控制方式的拦截性能优于尾舵方式。
6 结 论 1) 针对具有两组控制舵面的有界控制导弹，完成了微分对策制导律的设计，实现了前后舵面的融合控制和控制指令的优化分配。
2) 对策空间分析明确了鞍点解的存在条件，有利于导弹最大加速度和控制系统时间常数在工程上的初步设计。
3) Monte Carlo仿真结果表明了所设计制导律的优势，不仅命中概率大大提高，且机动性能要求较低。

参考文献

[1]	GUTMAN S. Superiority of canards in homing missiles[J].IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(3): 740–746.DOI:10.1109/TAES.2003.1238732
[2]	IDAN M,SHIMA T,GOLAN O M.Integrated sliding mode autopilot-guidance for dual control missiles:AIAA-2005-6455 [R].Reston:AIAA,2005.
[3]	SHIMA T, GOLAN O M. Linear quadratic differential games guidance law for dual controlled missiles[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(3): 834–842.DOI:10.1109/TAES.2007.4383577
[4]	CHO H, RYOO C K, TSOURDOS A, et al. Optimal impact angle control guidance law based on linearization about collision triangle[J].Journal of Guidance,Control,and Dynamics, 2014, 37(3): 958–964.DOI:10.2514/1.62910
[5]	WEISS M, SHIMA T. Optimal linear-quadratic missile guidance laws with penalty on command variability[J].Journal of Guidance,Control,and Dynamics, 2015, 38(2): 226–237.DOI:10.2514/1.G000738
[6]	花文华, 孟庆龄, 张拥军. 寻的导弹范数型微分对策制导律[J].高技术通讯, 2013, 23(4): 392–399.HUA W H, MENG Q L, ZHANG Y J. Norm differential game guidance law for homing missiles[J].Chinese High Technology Letters, 2013, 23(4): 392–399.(in Chinese)
[7]	TAUB I, SHIMA T. Intercept angle missile guidance under time varying acceleration bounds[J].Journal of Guidance,Control,and Dynamics, 2013, 36(3): 686–699.DOI:10.2514/1.59139
[8]	花文华, 孟庆龄, 张金鹏. 有界控制导弹随机最优制导律[J].固体火箭技术, 2015, 38(1): 7–11.HUA W H, MENG Q L, ZHANG J P. Stochastic optimal guidance law for bounded-control missiles[J].Journal of Solid Rocket Technology, 2015, 38(1): 7–11.(in Chinese)
[9]	花文华, 陈兴林. 变速导弹有界控制非线性微分对策制导律[J].控制与决策, 2011, 26(2): 1886–1890.HUA W H, CHEN X L. Nonlinear bounded-control differential game guidance law for variable-speed missiles[J].Control and Decision, 2011, 26(2): 1886–1890.(in Chinese)
[10]	SHINAR J, TURETSKY V, OSHMAN Y. Integrated estimation/ guidance design approach for improved homing against randomly maneuvering targets[J].Journal of Guidance,Control,and Dynamics, 2007, 30(1): 154–161.DOI:10.2514/1.22916
[11]	SHINAR J, SHIMA T. Nonorthodox guidance law development approach for intercepting maneuvering targets[J].Journal of Guidance,Control, and Dynamics, 2002, 25(4): 658–666.DOI:10.2514/2.4960
[12]	PROKOPOVY O, SHIMA T. Linear quadratic optimal cooperative strategies for active aircraft protection[J].Journal of Guidance,Control,and Dynamics, 2013, 36(3): 753–764.DOI:10.2514/1.58531
[13]	BARDHAN R, GHOSE D. Nonlinear differential games-based impact-angle-constrained guidance law[J].Journal of Guidance,Control,and Dynamics, 2015, 38(3): 384–402.DOI:10.2514/1.G000940
[14]	BASIMANEBOTLHE O,XUE X P.Stochastic optimal control to a nonlinear differential game[EB/J].Advances in Difference Equations,2014[2014-10-14].http://www.advancesindifferenceequations.com/content/2014/1/266.
[15]	SHINAR J, STEINBERG D. Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model[J].Journal of Aircraft, 1977, 14(8): 795–802.DOI:10.2514/3.58855