CTOA是指裂纹尖端附近上下裂纹表面之间的夹角,该参量可以表征出裂纹尖端的局部特征。试验研究及有限元结果表明[2-4]:CTOA在裂纹启裂时比较大,该值在裂纹扩展的初始阶段迅速减小,并在接下来的稳态裂纹扩展中近似保持为常数。在稳态裂纹扩展中,近似为常数的CTOA值即为该厚度下材料的CTOAc。进一步的研究表明:当裂纹长度及非裂纹韧带长度(宽度减去裂纹长度)均大于4倍厚度时,材料的CTOAc只与厚度有关,而与试样的几何构型及加载形式无关[5-7]。因此,CTOAc是一个比较有前途的断裂准则。
ASTM E2472-12[8]给出了2种CTOAc的测量方法:显微镜观测法(Optical Microscopy,OM)和数字图像相关法(Digital Image Correlation,DIC)。这些方法复杂难操作且工作量大进而限制了CTOA的应用。OM与DIC均是通过摄像技术测定CTOAc,而摄像技术复杂难操作且代价高昂,这进而限制了CTOA的应用。找出一种简单、廉价、易操作的CTOAc测量方法成为推广CTOA准则应用的必要条件。
δ5为德国Gteborgs Kungliga Segel Sllskap (GKSS)提出的一种裂纹尖端张开位移(Crack Tip Opening Displacement,CTOD)定义[9],该参量用以建立低约束条件下材料的阻力曲线。进一步的研究表明[10]:当裂纹长度(a)及非裂纹韧带长度达至3~4倍厚度时,材料的δ5-Δa曲线仅与厚度有关,而与试样的几何构型及加载方式无关,Δa为裂纹扩展量。δ5-Δa曲线的可转移性限制条件与CTOAc几乎相同,基于此,GKSS提出了测量CTOAc的CTOD-δ5技术[11]。相较于ASTM规定的常规方法,CTOD-δ5技术的操作更加简单且具有更好的理论基础;Heerens和Schodel[11-12]通过试验验证了CTOD-δ5技术与OM的等效性。尽管如此,寻找更为简单、准确的CTOAc测量方法仍是该准则所面临的问题。
本文根据CTOD-δ5技术及CTOA性质导出了裂纹尖端附近上下表面的轮廓线,并将δ5与vR这两种CTOD定义联系了起来(vR为Dugdale模型定义的CTOD,指裂纹瞬时单侧张开位移)。在此基础上,本文导出了等效于CTOD-δ5技术的CTOAc测量方法,该方法仅需运用ASTM E561-10[13]规定的常规静态拉伸试验即可得到试样厚度下材料的CTOAc。为了验证准静态拉伸试验法的准确性,本文对7B04 M(T)试样进行了静态拉伸试验,并分别采用准静态拉伸试验法与CTOD-δ5技术估算出了7B04的CTOAc;此外,本文根据获得的CTOAc对试样进行了弹塑性有限元模拟,并将得到的F-Δa曲线与试验结果进行了对比,F为外载荷。
1 理论分析 CTOD-δ5技术是指通过测量试样δ5-Δa曲线而导出试样厚度下材料CTOAc的方法,该方法必须同时测量出试样的F-Δa曲线与F-δ5曲线。其中,δ5是指原裂纹尖端上下2.5 mm处的位移[1],见图 1。
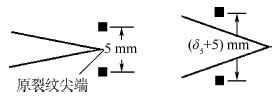 |
| 图 1 δ5定义 Fig. 1 δ5 definition |
| 图选项 |
CTOD-δ5技术认为CTOA近似等于δ5-Δa曲线的斜率[11],即
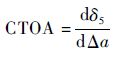 | (1) |
ASTM E2472-12[8]给出了δ5-Δa曲线的拟合形式:
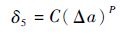 | (2) |
式中:C、P均为小于1的拟合常数。
本文结合文献[1]对式(2) 进行如下修正:
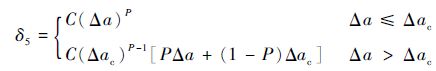 | (3) |
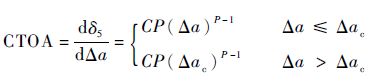 | (4) |
式中:CP(Δac)P-1为材料的CTOAc, Δac为CTOA过渡区长度。
由式(3) 和式(4) 可知:裂纹扩展量Δa达到Δac时,CTOA达至临界值,δ5的值为C(Δac)P;Δa的继续增加并不会引起CTOA的变化;此时裂纹尖端附近的裂纹上下表面开始出现直线区域,该区域斜率的大小等于CTOAc的一半。该直线段上裂纹表面的方程为
 | (5) |
坐标系原点为原裂纹尖端,x方向为裂纹扩展方向,y方向为垂直于裂纹面的方向。
随着裂纹的继续扩展,裂纹尖端后始终存在着如式(5) 所示的直线裂纹表面区域,该区域的方程类似于式(5) ,将此时的裂纹扩展量代替式中的Δac即可。
忽略δ5测量点与原裂纹尖端之间2.5 mm试样段随着裂纹扩展的变形量,则δ5值的变化即可看作原裂纹尖端裂纹上下表面沿y轴方向位移的变化。对式(5) 进一步分析发现:直线纵轴截距小于该裂纹扩展量下δ5值的一半,并因此导出裂纹扩展量大于等于Δac时裂纹上下表面的近似轮廓线,见图 2。图中轮廓线与横坐标的截距表示裂纹扩展量的大小;轮廓线与纵坐标的截距表示δ5的值的一半;此外,图中的每一条曲线代表一个裂纹扩展量下裂纹上表面的轮廓线,a0为原裂纹尺寸,Δa0为初始裂纹扩展量,Δδ50为Δa0导致的附加δ5值。该轮廓线与实际观测到的裂纹表面轮廓相吻合,这也进一步说明了CTOD-δ5技术的准确性。
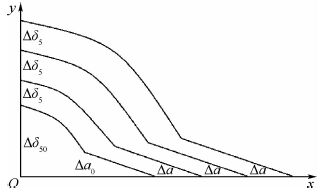 |
| 图 2 CTOD-δ5技术导出裂纹上表面的轮廓线 Fig. 2 Profile on crack’s upper surface derived from CTOD-δ5 technique |
| 图选项 |
根据式(1) ~式(5) 可知:当裂纹扩展量达至Δac时,裂纹尖端附近上下表面出现直线区域,该区域的斜率大小为CTOAc的一半。在此基础上,假设裂纹尖端继续产生了一个无穷小裂纹扩展da,则裂纹尖端将会出现一个位移量dδ,可以认为da产生的新裂纹上下表面为直线,且直线斜率大小为CTOAc的一半。此时,dδ与da有如下关系:
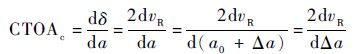 | (6) |
根据式(1) 和式(6) 可知:
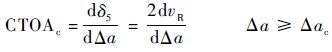 | (7) |
式(7) 只能说明两种CTOD定义随着裂纹扩展量的变化率之间的关系,并不能说明两种CTOD定义本身之间的关系。
根据式(7) 可知:如果能够导出试样的vR-Δa曲线,即可进一步得到材料的CTOAc,且该值与CTOD-δ5技术求得的CTOAc一样准确。
1985年,Newman[14]根据Dugdale模型估算出了7B04试样的vR-Δa曲线。该方法仅仅需要F-Δa曲线即可导出试样的vR-Δa曲线,即只需根据ASTM E561-12[13]对7B04试样进行准静态拉伸试验就可估算出试样厚度下材料的CTOAc。相较于CTOD-δ5技术,准静态拉伸试验法仅需要测量试样的外载荷F及V(裂纹口张开位移CMOD),而CMOD仅需要一个中心孔引伸计即可测量,这样不仅使得操作更加简单而且避免了刀口粘贴偏差导致的误差。Newman[14]导出7B04试样vR-Δa曲线的过程如下。
图 3给出了7B04试样的几何尺寸,假设试样厚度为B;图 4为估算试样vR的DUGDALE模型。图中:ρ为塑性区尺寸,ae为有效裂纹尺寸,流动应力σ0的表达式为
 | (8) |
式中:σs和σb分别为屈服强度及拉伸强度。
首先根据有效裂纹尖端的应力无奇异求得塑性区尺寸ρ。
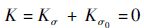 | (9) |
式中:K为裂纹尖端应力强度因子;Kσ为外载荷引起的应力强度因子;Kσ0为流动应力引起的应力强度因子。
由式(9) 可以求得7B04试样的裂纹尖端塑性区尺寸为
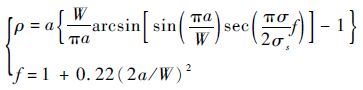 | (10) |
式中:f为修正因子;W为试样宽度。式(10) 的成立条件为:2(a+ρ)/W≤0.85。
估算出塑性区尺寸ρ后,将(F, Δa)数据点代入到DUGDALE模型,应用式(11) 可求得vR。
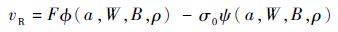 | (11) |
式中:B为试样厚度;其余变量定义如下:
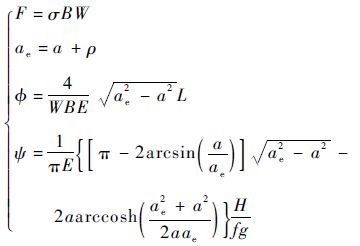 | (12) |
式中:
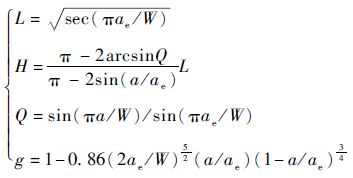 | (13) |
根据式(7) ~式(13) ,可以求出7B04试样的vR-Δa曲线,进而得到试样厚度下材料的CTOAc。
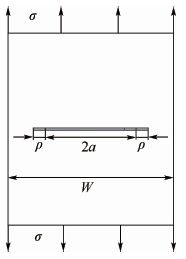 |
| 图 3 7B04模型几何尺寸 Fig. 3 7B04 model geometry |
| 图选项 |
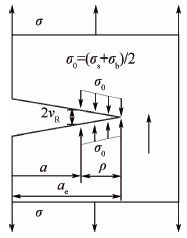 |
| 图 4 DUGDALE模型 Fig. 4 DUGDALE model |
| 图选项 |
2 试验 为了验证准静态拉伸试验方法的准确性,本文对7B04试样进行了静态拉伸试验。铝合金7B04性能数据见表 1。
表 1 铝合金7B04性能数据 Table 1 Material properties of Aluminum Alloy 7B04
| 性能 | E/MPa | ν | n | σs/MPa | σb/MPa |
| 数值 | 74 000 | 0.33 | 0.09 | 410 | 490 |
| 注:E—弹性模量;ν—泊松比;n—应变硬化指数。 | |||||
表选项
7B04试样宽度W为150 mm,有效长度为300 mm,厚度B为5 mm,其几何尺寸见图 5。试样中心具有直径为5 mm的圆孔,该圆孔用以安装测量CMOD的位移引伸计。试样的初始裂纹尺寸包含了该圆孔的直径,本试验室大量的试验数据表明该做法并不影响试验的最终精度。试样的几何尺寸符合ASTM E561-10[13]规定的尺寸,由于试样尺寸较小,不需要对其施加防屈曲装置。
本试验试样件数为10件,试样编号为AL-01~AL-10,初始裂纹2a0均在0.30W~0.35W之间。初始裂纹均由疲劳预裂生成,预裂载荷满足ASTM E561-10[13]要求。试样共有3个位移引伸计,一个测量裂纹口张开位移V, mm;两个测量初始裂纹尖端上下2.5 mm位置处的位移变化量δ5, mm,如图 6所示。对试样施加位移控制载荷,位移加载速率遵循ASTME561-10要求,输出载荷为力载荷,kN。试验共有9件有效试样,除了AL-01外均为有效试样。
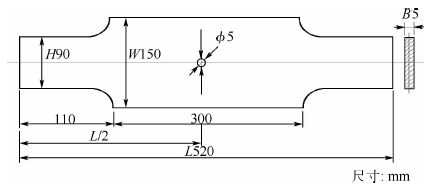 |
| 图 5 7B04试样几何尺寸 Fig. 5 7B04 specimens’ geometry |
| 图选项 |
 |
| 图 6 试样装载及引伸计位置 Fig. 6 Test set-up of specimens and clip gauges |
| 图选项 |
由试验直接测得的数据为F-V、F-δ5曲线,为了使得图更加清晰,本文只给出了AL-03、AL-05、AL-10的曲线图,如图 7所示。F-δ5曲线走势类似于F-V曲线,但δ5较V偏小一些。
采取加载柔度法对F-V曲线进行处理即可得到试样的F-Δa曲线,见图 8;加载柔度法过程类似于卸载柔度法,其具体流程见ASTM E561-10[13];该方法得到的裂纹长度为有效裂纹长度。由于AL-02~AL-04这3件试样的F-Δa曲线代表9件试样的整体趋势,图 8不再罗列出其他试样的F-Δa曲线。
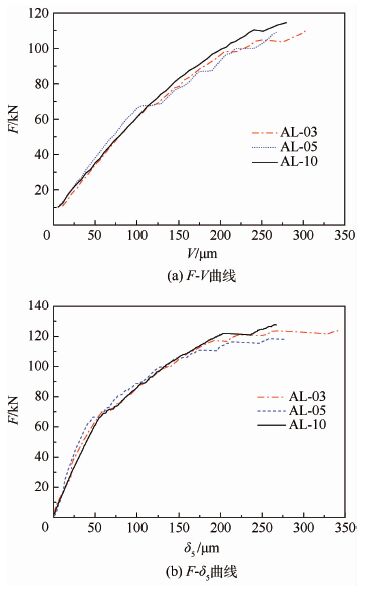 |
| 图 7 F-V、F-δ5 曲线 Fig. 7 F-V,F-δ5 curves |
| 图选项 |
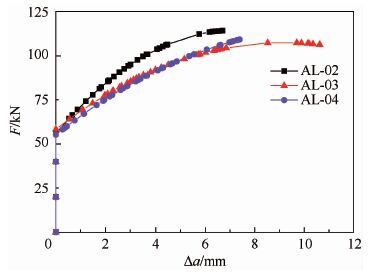 |
| 图 8 F-Δa曲线 Fig. 8 F-Δa curves |
| 图选项 |
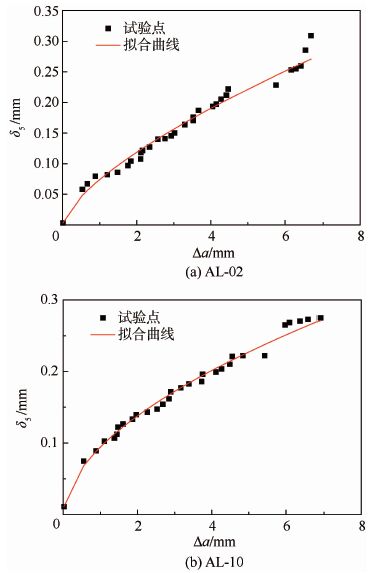
本文首先采用准静态拉伸试验法估算试样厚度下7B04的CTOAc。准静态拉伸试验法首先根据F-Δa曲线得到vR-Δa曲线,并根据式(7) 求得CTOD-Δa曲线,进而求得试样厚度下材料的CTOAc。CTOD-Δa曲线中的CTOD是指瞬时裂纹尖端后1 mm位置处的裂纹尖端张开位移,该值的大小等于CTOA(弧度制)。图 9(a)和图 9(b)分别给出了AL-02、AL-10试样的vR-Δa曲线图。
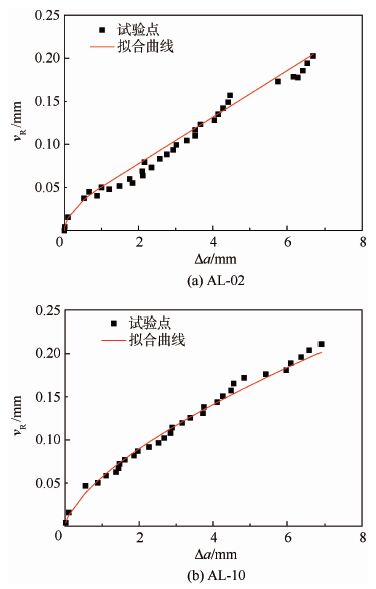 |
| 图 9 AL-02和AL-10的vR-Δa曲线 Fig. 9 vR-Δa curves of AL-02 and AL-10 |
| 图选项 |
vR-Δa曲线的拟合形式为
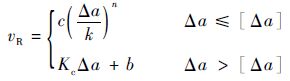 | (14) |
式中:kc =1 mm;[Δa]根据试验数据点进行选取;c、nc为拟合常数。Kc、b与c、nc的关系为
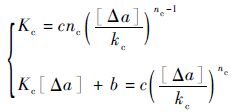 | (15) |
由式(7) 和式 (14) 得到的CTOD-Δa曲线如图 10所示;表 2给出了9个试样的CTOAc,为了方便对比,表中将弧度制的CTOAc转换为度数。
 |
| 图 10 vR-Δa曲线估算出的CTOD-Δa曲线 Fig. 10 CTOD-Δa curves estimated from vR-Δa curves |
| 图选项 |
表 2 准静态拉伸试验估算的CTOAc Table 2 CTOAc estimated from quasi-static tensile test
| 编号 | CTOAc/(°) |
| AL-02 | 3.09 |
| AL-03 | 2.84 |
| AL-04 | 3.08 |
| AL-05 | 2.99 |
| AL-06 | 2.84 |
| AL-07 | 2.81 |
| AL-08 | 3.03 |
| AL-09 | 3.21 |
| AL-10 | 3.11 |
| 平均值 | 3.00 |
表选项
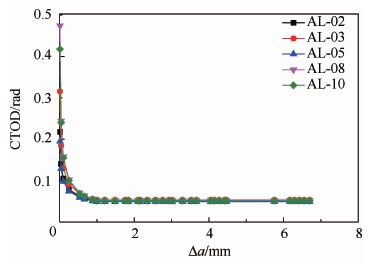
接着采用CTOD-δ5技术估算试样厚度下7B04的CTOAc。CTOD-δ5技术将F-Δa曲线与F-δ5曲线结合获得各试样的δ5-Δa曲线,并根据式(1) ~式(4) 求得各试样的CTOD-Δa曲线,进而得到试样厚度下7B04的CTOAc。CTOD-Δa曲线中的CTOD是指瞬时裂纹尖端后1 mm位置处的裂纹尖端张开位移,该值的大小等于CTOA(弧度制)。图 11给出了AL-02、AL-10的δ5-Δa曲线。
将图 9与图 11进行对比:vR、δ5两种CTOD随着裂纹扩展量变化的趋势十分相近,vR比δ5技术小一些。图 12给出了δ5-Δa曲线导出的CTOD-Δa曲线,表 3给出了CTOD-δ5技术得到的试样厚度下7B04的CTOAc。
 |
| 图 11 AL-02和AL-10的δ5-Δa曲线 Fig. 11 δ5-Δa curve of AL-02 and AL-10 |
| 图选项 |
将表 2、表 3中的数据进行对比发现:准静态拉伸试验法估算的5 mm厚度下铝合金7B04的CTOAc为3°,CTOD-δ5技术估算的CTOAc为2.97°,两种方法得到的CTOAc相差1%。
试验结果验证了准静态拉伸试验法的准确性,即准静态拉伸试验法是一种等于CTOD-δ5技术的CTOAc测量方法(即该方法的准确度等同于CTOD-δ5技术)。此外,准静态拉伸试验法仅需要测量F-V曲线即可得出试样厚度下材料的CTOAc,这不仅简化了试验的操作而且避免了刀口粘贴偏差导致的误差。
 |
| 图 12 δ5-Δa曲线估算出的CTOD-Δa曲线 Fig. 12 CTOD-Δa curves estimated from δ5-Δa curves |
| 图选项 |
表 3 CTOD-δ5法估算的CTOAc Table 3 CTOAc estimated from CTOD-δ5 method
| 编号 | CTOAc/(°) |
| AL-02 | 2.89 |
| AL-03 | 3.06 |
| AL-04 | 3.02 |
| AL-05 | 2.81 |
| AL-06 | 3.11 |
| AL-07 | 2.93 |
| AL-08 | 3.00 |
| AL-09 | 2.97 |
| AL-10 | 2.95 |
| 平均值 | 2.97 |
表选项
3 有限元模拟 为了进一步说明试验,本节根据试验测得的CTOAc对试样进行弹塑性有限元模拟,并将模拟得到的F-Δa曲线与试验测得值进行对比。
本文采用ABAQUS对试样进行有限元模拟。根据圣维南原理忽略试样的夹持段,将试样转换为150 mm×300 mm尺寸的标准M(T)板;由于对称性,本文对1/4M(T)板进行平面二维模拟,即对裂纹扩展平面作为对称面、裂纹扩展方向的1/4试样进行模拟。根据试验可知:载荷与初始裂纹存在着相对应的关系。为了代表9件试件的整体情况,模型的初始裂纹a0选为24 mm(该值为试样初始裂纹的平均值并近似等于初始裂纹的中位数)。此外,本文分别采用平面应力模型、平面应变核模型两种模型对试样进行模拟,其中平面应变核模型[15]是指裂纹尖端附近采用平面应变单元,而远离裂纹的区域应用平面应力单元的模型。
模型的输入数据有CTOAc、材料的真实应力应变曲线,CTOAc已由试验测得,真应力-真应变曲线可根据7B04的材料属性获得,如图 13所示。
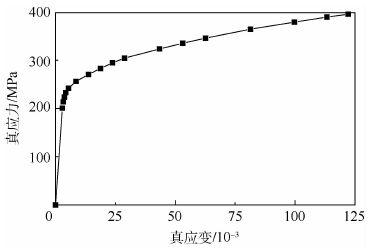 |
| 图 13 7B04真应力-真应变曲线 Fig. 13 True stress-ture strain curve of 7B04 |
| 图选项 |
说明:图 14对应力-真应变曲线进行了一些外推,外推段代替了原M(T)真实应力应变曲线中的下降段。这样的处理手段提高了弹塑性有限元模拟的收敛性,也更符合本文的分析需要。
模型的具体型式如图 14所示,平面应变核的高度取为厚度5 mm(文献[15]建议应变核的高度取为1~3倍的试样厚度,本文选为试样厚度即5 mm),则1/4模型应变核高度为2.5 mm。由于两种模型形状一样,这里只给出平面应变核模型图,平面应力区域单元为CPS4,平面应变区域单元为CPE4(平面应力模型均为CPS4单元)。
模型采用ABAQUS的DEBOND命令模拟裂纹的稳态扩展。CTOAc只受试样厚度的影响,在将CTOAc作为输入数据时,模型已经考虑了试样的厚度影响。此外,为了保证模型的收敛性,本文施加了大小为0.000 2的稳态因子[16]。
图 15给出了有限元模拟出的F-Δa曲线,其中试验点选择初始裂纹尺寸最接近24 mm的试样的试验值。根据图 15可知:裂纹开始扩展时,平面应变核模型的误差在3%,平面应力模型的误差在11%,这是因为裂纹刚开始扩展时裂纹尖端约束对裂纹的影响较大,平面应变核模型更能够模拟裂纹尖端的真实约束;当裂纹扩展量达至1 mm左右时,两个模型与试验值的误差均在2%以内,该结果表示试验方法测得的CTOAc是准确的,此时两个模型是相当的;此外,试验测得的CTOAc过渡区长度近似等于1 mm,该值与初始裂纹扩展段相等,CTOAc的过渡区对平面应力模型的影响更大。
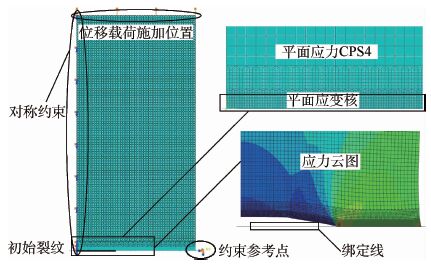 |
| 图 14 有限元模拟图 Fig. 14 Finite element simulated diagram |
| 图选项 |
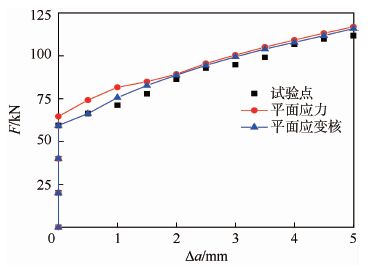 |
| 图 15 F-Δa曲线的对比 Fig. 15 Comparison of F-Δa curves |
| 图选项 |
4 结论 1) 根据CTOD-δ5技术导出了裂纹尖端的轮廓线,并导出了vR、δ5两种CTOD定义之间的关系,进而得出了一种基于准静态拉伸试验的CTOAc测量方法,该方法与CTOD-δ5技术相等效且更加简单。
2) 对铝合金M(T) M(T)试样进行了静态拉伸试验,并分别采用准静态拉伸试验法、CTOD-δ5技术测得了5 mm厚度下铝合金M(T)的CTOAc。试验结果显示:两种方法估算出的CTOAc仅相差1%。准静态拉伸试验法仅需要测量F-V曲线即可得出试样厚度下材料的CTOAc,这不仅简化了试验的操作而且避免了刀口粘贴偏差导致的误差。
3) 根据试验测得的CTOAc对试样进行了弹塑性有限元模拟。分别采用平面应变核模型、平面应力模型对试样进行模拟并得到试样的F-Δa曲线。模拟结果显示:试验测得的CTOAc是准确的;裂纹初始扩展时,平面应变模型更能真实地反映裂纹尖端的约束;当裂纹扩展量大于CTOA的过渡区时,平面应变核模型与平面应力模型是相当的。
参考文献
| [1] | NEWMAN J C, JAMES M A, ZERBST U. A review of the CTOA/CTOD fracture criterion[J].Engineering Fracture Mechanics, 2003, 70(3-4): 371–385.DOI:10.1016/S0013-7944(02)00125-X |
| [2] | NEWMAN J C, DAWICKE D S, SESHADRI B R. Residual strength analyses of stiffened and unstiffened panels-Part I:Laboratory specimens[J].Engineering Fracture Mechanics, 2003, 70(3-4): 493–507.DOI:10.1016/S0013-7944(02)00133-9 |
| [3] | MAHMOUD S, LEASE K. The effect of specimen thickness on the experimental characterization of critical crack tip opening angle in 2024-T351 aluminum alloy[J].Engineering Fracture Mechanics, 2003, 70(3-4): 443–456.DOI:10.1016/S0013-7944(02)00130-3 |
| [4] | MAHMOUD S, LEASE K. Two dimensional and three dimensional finite element analysis of critical crack tip opening angle in 2024-T351 aluminum alloy at four thicknesses[J].Engineering Fracture Mechanics, 2004, 71(9-10): 1379–1391.DOI:10.1016/S0013-7944(03)00167-X |
| [5] | ZHU X K, JOYCE A J. Review of fracture toughness (G,K,J,CTOD,CTOA) testing and standardization[J].Engineering Fracture Mechanics, 2012, 85(1): 1–46. |
| [6] | ZERBST U, HEINIMANN M, DONNE C D, et al. Fracture and damage mechanics modeling of thin-walled structures-An over-view[J].Engineering Fracture Mechanics, 2009, 76(1): 5–43.DOI:10.1016/j.engfracmech.2007.10.005 |
| [7] | NEWMAN J C, CREWS J H, BIGELOW C A, et al. Variations of the global constraint factor in cracked bodies under tension and bending loads[J].ASTM STP, 2002, 1406(1): 279–297. |
| [8] | ASTM Committee.Standard test method for determination of resistance to stable extension under low-constraint conditions:ASTM E2472-12[S].Philadelphia:ASTM,2012:1-26. |
| [9] | SCHWALBE K H. Introduction of δ5 as an operational definition of the CTOD and its practical use[J].ASTM Speical Technical Publication, 1995, 1256(26): 763–778. |
| [10] | SCHWALBE K H, HEERENS J. R-curve testing and its relevance to structural assessment[J].Fatigue & Fracture Engineering Material & Structures, 1998, 21(10): 1259–1271. |
| [11] | HEERENS J, SCHODEL M. On the determination of crack tip opening angle,CTOA,using light microscopy and δ5 measurement technique[J].Engineering Fracture Mechanics, 2003, 70(3-4): 417–426.DOI:10.1016/S0013-7944(02)00128-5 |
| [12] | HEERENS J, SCHODEL M. Characterization of stable crack extension in aluminum sheet material using the crack tip opening angle determined optically and by the δ5 clip gauge technique[J].Engineering Fracture Mechanics, 2009, 76(1): 101–113.DOI:10.1016/j.engfracmech.2008.04.009 |
| [13] | ASTM Committee.Standard test method for K-R curve deter-mination:ASTM E561-10[S].Philadelphia:ASTM,2010:1-16. |
| [14] | NEWMAN J C. Evaluation of the crack tip opening displacement (vR) resistance curve method[M].Berlin: Springer, 1986: 157-176. |
| [15] | PIRONDI A. Modeling strength of cracked friction stir welded panels by means of the crack tip opening angle(CTOA)[J].Engineering Fracture Mechanics, 2010, 77(11): 2091–2099.DOI:10.1016/j.engfracmech.2010.03.021 |
| [16] | PIRONDI A, FERSINI D. Simulation of ductile crack growth in thin panels using the crack opening angle[J].Engineering Fracture Mechanics, 2009, 76(1): 88–100.DOI:10.1016/j.engfracmech.2008.05.008 |
