在航空自组织网络中，随着定位装置和定位算法发展的成熟，基于地理位置信息的主动式路由协议(Optimized Link State Routing protocol，OLSR)由于能主动进行周期性链路探测和路由维护而在动态网络环境下展现出较大的优势^[1]。其中一个关键就是个体之间位置信息的更新和拓扑的维护主要通过HELLO消息的交互^[2-3]。虽然使用较短的更新周期能较快地维护邻居列表和链路信息，但是过短的周期则会增加不必要的控制开销^[4-5]。文献[6]通过实际硬件测试发现，HELLO的更新周期对整个网络吞吐量性能影响非常大。
标准的OLSR协议允许不同的节点具有不同的HELLO更新周期，但是具体的实现方案和操作过程并没有给出。Fast-OLSR^[7]通过增加短周期HELLO信息类型来适应网络节点的高速运动，主要根据节点与邻居节点的高速相对运动基础信息来设定控制信息的更新周期。虽然其在一定程度上减少路由开销，却增加了一个新的HELLO信息类型，而且仅有两种固定周期并不能很好适应链路和拓扑变化情况。文献[8]提出的动态自适应间隔的OLSR协议，即IOLSR协议，其中每个节点都能根据本地的链路状况自适应地调整HELLO周期。虽然这在一定程度上减少了控制开销，却没有适应编队的拓扑结构，即不能很好地适应真正的网络实时需求。文献[9]提出了基于链路中断概率的自适应信标交换算法，主要根据理想运动模型来预测链路，并不适用于实际的节点运动状态。
以上的HELLO更新算法能适应一定的移动环境，却没有考虑编队组网中飞行控制所需要的位置更新需求。目前，无人机编队飞行控制研究主要采用长机-僚机控制方法和一致性协调控制方法。长机-僚机控制方法通过控制长机，按预定轨迹飞行，并由长机对僚机下达命令，使得僚机跟随长机并以固定的编队结构一起飞行。该方法易于理解和实现，但鲁棒性较弱，一旦长机出现故障，则整个编队的控制将失效。一致性协议是多智能体协调控制研究的热点之一，它是指智能体通过邻域中其他智能体的状态信息决定自身的状态，并最终使其状态达到一致的方法^[10]。其中位置信息的周期性相互交换是保证其一致性运动的必要条件。对于编队控制而言，通信上过长的更新周期而导致的位置更新延时可能会导致编队无法收敛到期望的稳定队形^[11-12]。
针对以上问题，本文提出了适应无人机编队组网运动状态的自适应HELLO更新算法(应用该算法的OLSR协议简称为AOLSR)。该算法依据编队状态将HELLO更新分为两部分：收敛到期望队形所能容忍的最大延时作为更新周期依据；稳定飞行状态下依据链路的变化而自适应更新周期。网络自适应地更新HELLO消息既能满足一致性协调控制的需求，又能在及时维护拓扑和链路信息基础上减少网络的控制开销。
本文结构安排如下：第1节介绍编队运动模型并详细推导组成特定稳定编队所能容忍的最大允许延时；第2节根据编队运动状态进行HELLO等控制消息的自适应更新周期设计；第3节分别对编队控制系数对允许延时的影响和网络在自适应HELLO算法下的整体性能进行仿真分析。
1 编队系统模型和延时上限 1.1 编队系统模型 为了表示编队控制和通信的关系，利用图论知识定义无向编队图G=(V, E)，其中V为无人机集合，E?V×V为边集合，表示个体之间的信息流，如果(i, j)∈E，说明个体i和j之间能进行通信。定义邻接矩阵A=(a_ij)_n×n，如果(i, j)∈E，则令a_ij=1，否则令a_ij=0；度矩阵Δ=diag{d₁, d₂, …, d_n}∈R^n×n，其中对角元素。图G的拉普拉斯矩阵定义为L=Δ-A。为了方便后续计算，定义规范化邻接矩阵，则矩阵的每行之和都为1，相应的度矩阵和拉普拉斯矩阵为。
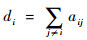
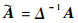
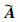
参考文献[13-14]设计的多无人机控制系统模型，每个无人机模型最终可以简化为双积分动态模型：

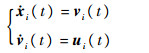(1)

式中：和v_i(t)分别为第i个无人机的位置和速度；u_i(t)为第i个无人机的控制输入，i=1, 2, …, n。
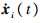
根据一致性理论，控制输入u_i(t)应该是无人机的相对位置误差和相对速度误差的函数，令个体i和j之间的通信延时为τ_ij，设计第i个无人机的反馈控制为

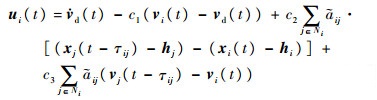(2)

式中：控制系数c₁、c₂和c₃均为常数；v_d(t)为期望速度; h_i为期望位置；N_i为个体i邻居集合。假设v_d(t)为常数v_d，且个体之间的通信延时一致，均为τ，则个体i的闭环控制形式为

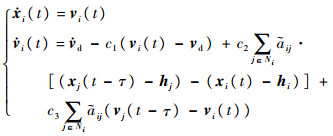(3)

式中：h_i和h_j为无人机的期望位置。
1.2 收敛至期望队形的延时上限 具有式(3)形式的多无人机系统能否形成期望队形，并以期望速度和稳定队形向前运动，不仅与系统拓扑结构相关，同时取决于控制系数和延时的大小，下面求出最大允许延时的上限。令

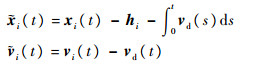则式(3)为

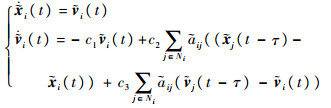(4)

将此系统扩展到所有个体，即令

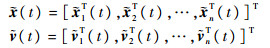则有

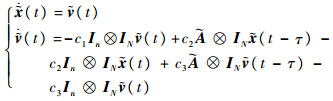(5)

式中：I_n和I_N分别为n×n阶和N×N阶的单位矩阵。
存在正交矩阵U，使得，其中U和λ分别为的特征向量矩阵和特征值构成的对角矩阵，即λ=diag(λ₁, λ₂, …, λ_n)。因此有坐标变换，式(5)进一步写成：

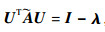
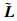
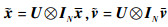
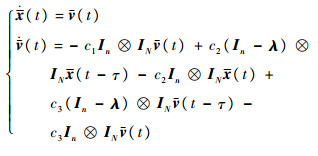(6)

再将式(6)的系统分解为n个独立的子系统，则有

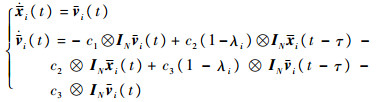(7)

对式(7)进行拉普拉斯变换，得到

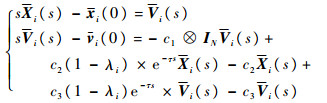(8)

式中: 和分别为和的拉普拉斯变换。
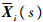
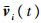
进一步可以得到闭环系统的特征方程：

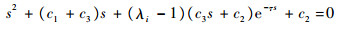(9)

由稳定性理论，编队系统渐近稳定的充要条件是式(9)除了有一个0的特征根外，其余特征根都位于左半复平面。下面求出延时的上限值：
当τ=0时，明显满足稳定条件，不再证明；当τ>0时，令F_i(s)=1+G_i(s)，其中：

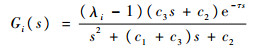(10)

为了满足系统的稳定性，需要证明F_i(s)的零点都在左半复平面。令s=jω，根据Nyquist判据，F_i(s)的零点都在左半复平面的充要条件是：对于所有的ω∈[0, ∞)，G_i(jω)的轨迹不包含复平面的(-1, j0)点。由规范化的编队图可知图中顶点最大的度为1，再根据Gerschgorin圆盘定理可知：拉普拉斯矩阵的特征值λ_i都在以(1, 0)为圆心，1为半径的圆内。又因为是实对称矩阵，所以0≤λ_i≤2，令λ′_i=1-λ_i，则可以得到λ′_i²≤1，由幅值穿越条件G_i(jω)=1，得到

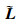
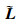
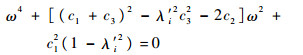(11)

令k_i=(c₁+c₃)²-λ′_i²c₃²-2c₂，对3种情况进行讨论：
1)?当k_i≥0时，只有当λ_i=0或λ_i=2时，方程(11)存在解ω=0，否则方程不存在关于ω>0的实根，即G_i(jω) < 1恒成立，因此，当k_i≥0时，对于任意延时τ>0，当ω∈[0, ∞)，G_i(jω)的轨迹不包含复平面的(-1, j0)点，即F_i(s)的零点都在左半复平面。
2)?当k_i < 0且k_i²-4c₁²(1-λ′_i²) < 0时，方程不存在关于ω的实根，说明|G_i(jω)| < 1恒成立，因此，对于任意延时τ>0，当ω∈［0, ∞)，G_i(jω)的轨迹不包含复平面的(-1, j0)点，即F_i(s)的零点都在左半复平面。
3)?当k_i < 0且k_i²-4c₁²(1-λ′_i²)≥0时，得到方程式(11)的实根，即可得到穿越频率：

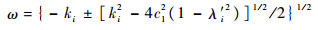(12)

稳定性判据转化为求穿越频率ω下的相位裕度条件：

(13)

当λ′_i≤0时，得

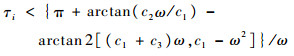(14)

当λ′_i>0时，同理可得

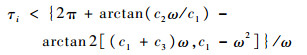(15)

综上，对于任意延时τ < τ_i，当ω∈[0, ∞)，G_i(jω)的轨迹不包含复平面的(-1, j0)点，即F_i(s)的零点都在左半复平面。综上，整个系统的最大允许通信延时为τ_m=min{τ_i}，若能保证当τ < τ_m，则以式(3)为控制系统的无人机编队能最终收敛稳定。
2 自适应HELLO更新策略 在移动无人机编队组网中，本文使用基于位置信息的高动态OLSR路由协议^［1]，该协议通过周期性地交互HELLO消息来感知拓扑和交换组成期望编队过程中所需的地理位置信息。现实环境中，编队组网与随机运动模型组网存在着较大区别：编队组网在形成期望编队过程中需要实时提供位置信息并及时维护路由，这对信标交换的延时要求更高，而在形成稳定队形之后，其拓扑不会有太大的变化，因此不需要发送多余的HELLO等控制消息，频繁地更新位置信息。编队自适应HELLO更新算法可根据运动的场景自适应地调整HELLO消息更新周期，算法流程如图 1所示(其中α为更新指数)，主要分为两步：

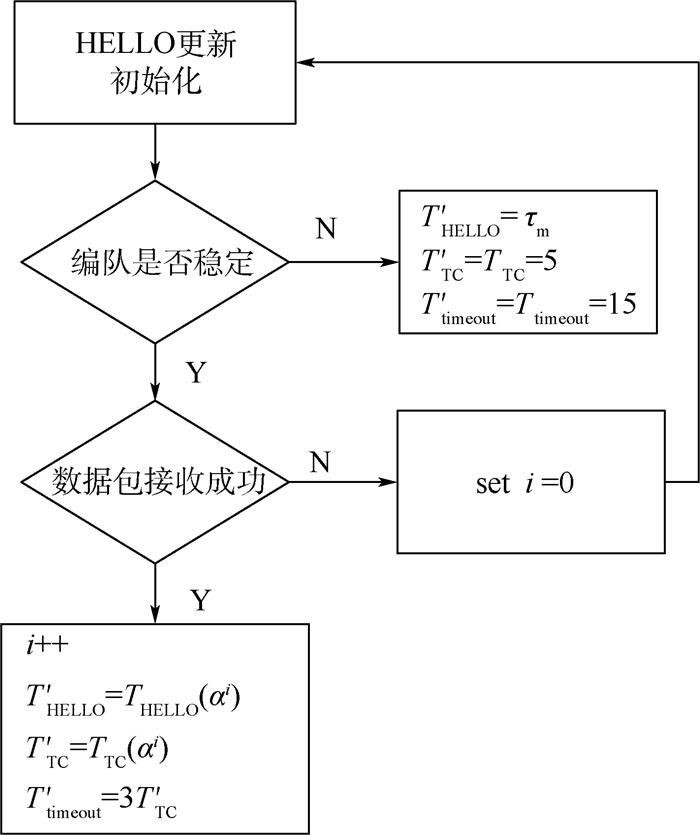图 1 自适应HELLO更新算法的流程图 Fig. 1 Flowchart of adaptive HELLO update algorithm

图选项

1)?当无人机进行组队时，所有个体在接收到组队的指令后，依据收敛至稳定编队的最大允许延时，HELLO消息更新周期设置为

(16)

其中拓扑控制(TC)周期和消息有效时间根据文献[8]分别设定如下：TC周期设定为T_TC=2.5t_m，消息有效时间设定为T_timeout=3T_TC。
2) ?当编队处于稳定状态时，对于位置的实时更新要求不高，这时更注重数据信息传输的有效性，减少不必要的通信开销。因此，本文以网络的链路状况来调整控制信息的更新周期：更新周期以成功接收的相应信息包的个数呈指数次方增加，一旦出现统计失败，立即恢复初始化状态感知拓扑。
3 仿真分析 使用NS2仿真分析AOLSR协议和OLSR协议在编队场景中的性能，仿真参数设置如表 1所示；设置标准：OLSR的HELLO周期分别为2 s和4 s，TC周期设置为5 s和10 s，消息有效时间设置为15 s和30 s。编队运动场景设置为3个阶段：0~400 s随机分布于活动区域，400 s到约600 s为组队过程，向期望位置组成特定编队，600 s后保持队形以期望速度2.5 m/s恒速前进。仿真分为两部分：检验并讨论控制系数c₁、c₂、c₃和拉普拉斯矩阵特征值λ_i与最大允许延时的关系；针对整个网络的吞吐量、交付率、端到端延时、路由开销及控制信息等网络性能进行仿真比较。
表 1 仿真参数 Table 1 Simulation parameters

参数	数值
场景大小/km2	2×1
MAC层	IEEE 802.11
通信半径/m	250
数据类型	CBR 512 bytes
数据包产生速率/(packet·s-1)	10
节点移动速度/(m·s-1)	[0 5]
更新指数α	2

表选项






3.1 控制参数与特征值对允许延时上限的影响 通过MATLAB计算可以得到τ_m与控制系数c₁、c₂、c₃和拉普拉斯矩阵特征值λ_i的关系，如图 2所示。

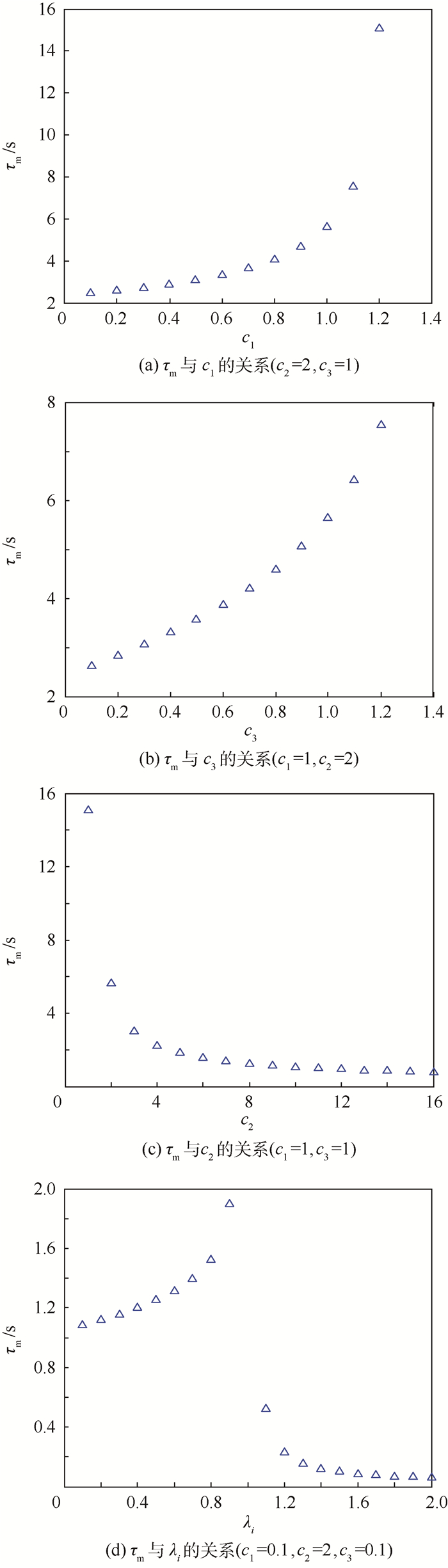图 2 控制系数和编队延时上限的关系 Fig. 2 Relationship between control factors and maximum tolerable delay of formation

图选项

由图 2(a)、图 2(b)可以发现τ_m与c₁、c₃成正比，从图 2(c)可以看出，τ_m与c₂成反比。因此，当组成编队过程中对实时位置信息的更新需求较高时，可以适当选择较大的c₁、c₃和较小c₂的控制参数。为了更大范围的讨论τ_m与特征值λ_i的关系，令c₁=0.1，c₂=2，c₃=0.1，如图 2(d)所示，当λ_i=1时，τ_m趋于无穷大，同样由式(9)可知，当λ_i=1时，方程的根与延时没有关系。
3.2 网络性能 由初始位置、期望位置和速度计算出相应的规范化邻接矩阵和相应拉普拉斯矩阵的特征值，并由式(14)和式(15)计算出编队组队允许的延时上限为2.56 s。首先比较AOLSR和2 s HELLO更新周期和4 s HELLO更新周期的标准OLSR协议(简称2sOLSR，4sOLSR)在上述特定运动状态下实时控制开销和实时吞吐量。
如图 3所示，给出了仿真时间下每50 s统计的路由控制包开销情况。由图 3可发现前400 s的控制开销相对都较为平稳，且2sOLSR开销要明显高于AOLSR；在400~600 s的组队过程中，AOLSR的控制包数量明显增加，而在600 s组队完成后控制开销明显减少且低于4sOLSR控制开销，这说明AOLSR能很好地适应动态拓扑，能根据链路情况调整HELLO等控制消息的周期来维护正常通信。原因有：①在组队过程允许的延时上限为2.56 s，根据本文算法，此阶段的HELLO周期设置为2 s，更新频率较快；②到达期望编队后，编队拓扑基本不变，链路相对稳定，因此，依据自适应更新算法就会逐渐加大更新周期，路由的控制开销也就明显下降。

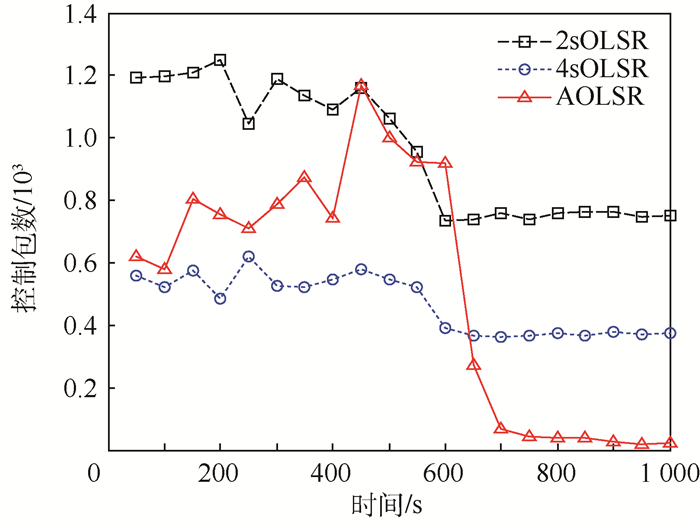图 3 实时路由控制包 Fig. 3 Real time routing control packets

图选项

其次，实时吞吐量通过成功接收的数据包来表示^[15]，由图 4发现，总体上，在静止阶段(0~400 s)由于是跳数较多情况，吞吐量相对于后面组队聚集后的稳定阶段要低(1 000 packets左右)；且三者在组队过程中，都出现吞吐量下降的情况，但是AOLSR却能较快地调整其HELLO等控制消息的周期，维护好网络的链路，其吞吐量能较快地提升上来(约在450 s左右)。虽然另外两种更新周期的OLSR协议在500 s左右也开始上升，但这不是自适应调整的结果，而是组队基本结束才使得链路基本稳定造成的。

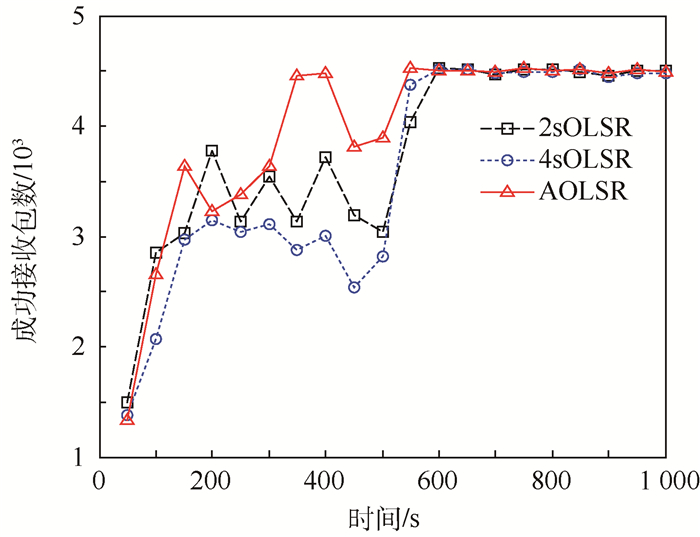图 4 成功接收数据包 Fig. 4 Successfully received packets

图选项

下面主要比较和分析AOLSR和另外两更新周期的OLSR协议在不同链路突发错误条件下控制开销、吞吐量、延时及丢包率方面的性能。如图 5所示。

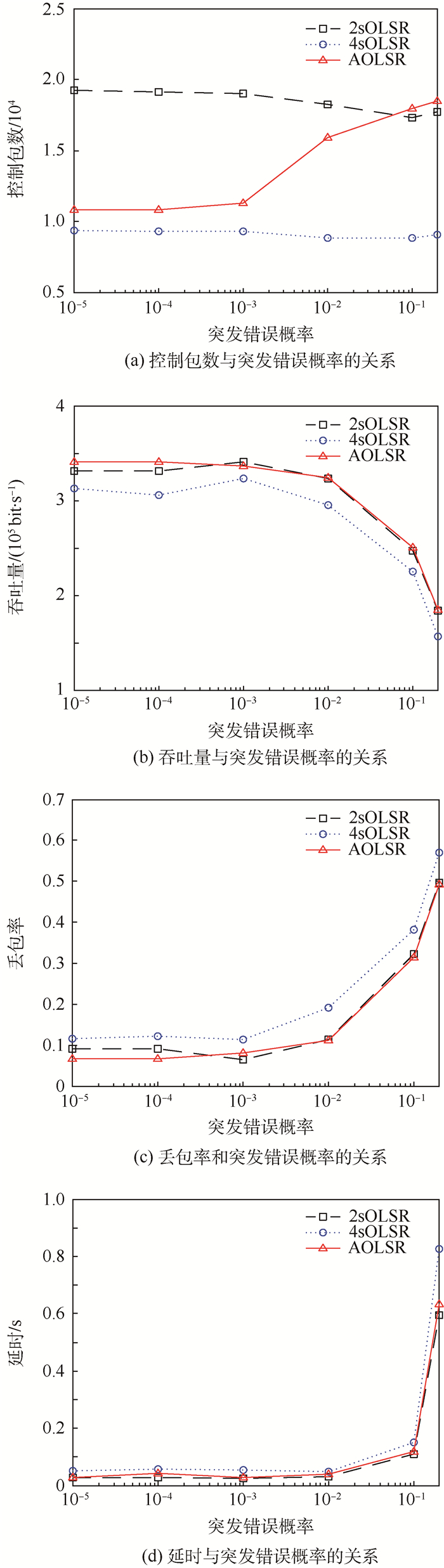图 5 网络控制开销、吞吐量、丢包率和延时的比较 Fig. 5 Comparison of network control overhead, throughput, drop rate and delay

图选项

图 5(a)给出路由控制开销随链路突发错误变化的情况。可以很明显地发现固定更新周期的OLSR协议其控制包数并没有随着链路的突发错误概率的增加而增加。相对标准OLSR，AOLSR控制包数量能根据链路情况增加控制包的发包频率，其控制开销要远远小于2sOLSR协议，减少约为42.6%。虽然4sOLSR协议的开销低于AOLSR，但是其他性能却无法得到保障，下面通过图 5(b)、图 5(c) 及图 5(d) 进行分析：
1)?虽然总体上2sOLSR的吞吐量、丢包率及延时等方面性能和AOLSR协议的相差不大，但是因为没有自适应的控制消息更新周期导致开销远远大于AOLSR。
2)?虽然OLSR增大HELLO周期能减少开销(如图 5(a))，但是由图 5(b)~图 5(d)可以明显发现其在吞吐量、丢包率和延时等方面性能下降比较大，且远远达不到AOLSR和2sOLSR相应的性能。
3)?在链路情况较好(突发错误概率小于10^-4)时，AOLSR的各方面性能都要比另外两者好。
4 结论 针对无人机编队网络环境中HELLO消息更新不合理而出现的编队不稳定和控制开销过大的问题，在传统OLSR协议固定HELLO更新算法基础上，提出基于编队控制的自适应HELLO更新算法，仿真结果表明：
1)?AOLSR的自适应HELLO更新算法引入了编队稳定控制机制，既能为编队组网的一致性协调控制所需的及时位置更新提供保障，又能减少不必要的控制开销，提高网络的吞吐量。
2)?提出的AOLSR与传统OLSR相比，可以有效地适应动态拓扑的变换，合理调整HELLO等控制消息的更新间隔，降低了整个网络控制开销。
3)?在不同的链路环境中，由于AOLSR采用自适应更新策略，能及时维护中断链路，性能较为理想；AOLSR与大周期更新的OLSR相比，虽然在控制开销上不理想，但是吞吐量、丢包率和延时性能很突出；而与小周期更新的OLSR相比，在保持其他性能基本相近的情况下，很大程度上减少了控制开销。

参考文献

[1]	WANG A, ZHU B. Improving MPR selection algorithm in OLSR protocol based on node localization[J].Journal of Intelligent & Robotic Systems, 2014, 9(7): 1674–1681.
[2]	PALANIAMMAL M, LALLI M. Comparative study of routing protocols for MANETs[J].International Journal of Networked and Distributed Computing, 2014, 2(2): 118–127.
[3]	ERNST R, JOPEN S A, BARTELT T.Reducing MANET neighborhood discovery overhead[C]//IEEE 39 th Conference on Local Computer Networks.Piscataway, NJ:IEEE Press, 2014:374-377.
[4]	HAN S Y, LEE D. An adaptive hello messaging scheme for neighbor discovery in on-demand MANET routing protocols[J].IEEE Communications Letters, 2013, 17(5): 1040–1043.DOI:10.1109/LCOMM.2013.040213.130076
[5]	ERNST R, MARTINI P.Adaptive HELLO for the neighborhood discovery protocol[C]//IEEE 37th Conference on Local Computer Networks.Piscataway, NJ:IEEE Press, 2012:470-478.
[6]	HIYAMA M, KULLA E, IKEDA M, et al. Investigation of OLSR behavior for different HELLO packets intervals in a MANET testbed[C]//IEEE 27th International Conference on Advanced Information Networking and Applications.Piscataway, NJ:IEEE Press, 2013:183-188.
[7]	BENZAID M, MINET P, ALAGHA K.Analysis and simulation of fast-OLSR[C]//57th IEEE Semiannual Vehicular Technology Conference.Piscataway, NJ:IEEE Press, 2003, 3:1788-1792.
[8]	LARSEN E, J FATHAGEN, Y PHAM, L Landmark.iOLSR:OLSR for WSNs using dynamically adaptive intervals[C]//Proceedings of the 5th International Conference on Sensor Technologies and Application.Trondheim:IFSA Press, 2011:21-27.
[9]	张衡阳, 郑博, 陈校平, 等. 基于链路断开概率的自适应信标交换算法[J].计算机研究与发展, 2013, 50(3): 472–480.ZHANG H Y, ZHENG B, CHEN X P, et al. An adaptive beacon exchang algorithm baced on link broken probability[J].Journal of Computer Research and Development, 2013, 50(3): 472–480.(in Chinese)
[10]	PENG Z, WEN G, RAHMANI A, et al. Distributed consensus-based formation control for multiple nonholonomic mobile robots with a specified reference trajectory[J].International Journal of Systems Science, 2015, 46(8): 1447–1457.
[11]	DONG X, XI J, LU G, et al. Formation control for high-order linear time-invariant multiagent systems with time delays[J].IEEE Transactions on Control of Network Systems, 2014, 1(3): 232–240.DOI:10.1109/TCNS.2014.2337972
[12]	DONG X, YU B, SHI Z, et al. Time-varying formation control for unmanned aerial vehicles:Theories and application[J].IEEE Transactions on Control of Network Systems, 2015, 23(1): 340–348.
[13]	WANG N, ZHANG T W, XU J Q. Formation control for networked spacecraft in deep space:With or without communication delays and with switching topology[J].Science China Information Sciences, 2011, 54(3): 469–481.DOI:10.1007/s11432-011-4191-1
[14]	姜丽梅, 张汝波. 具有通信延时的多机器人编队控制[J].北京邮电大学学报, 2012, 35(2): 54–58.JIANG L M, ZHANG R B. Multi-robot formation with communication delay[J].Journal of Beijing University of Posts and Telecommunications, 2012, 35(2): 54–58.(in Chinese)
[15]	高先明, 张晓哲, 王宝生, 等. 面向虚拟路由器的基于历史转发开销的资源调度算法[J].电子与信息学报, 2015, 37(3): 686–692.GAO X M, ZHANG X Z, WANG B S, et al. Historical forwarding overhead based the resource scheduling algorithm for the virtual router[J].Journal of Electronics & Information Techonology, 2015, 37(3): 686–692.(in Chinese)