由于μ值难以得到精确解, 通常采用Doyle[1]提出的D-K迭代法进行求解, 基本思想是利用μ的上下界函数对μ进行多次迭代逼近求近似解。传统的D-K迭代采用H∞的方法设计控制器, 涉及Riccati方程的求解, 尽管Riccati方程处理方法可以给出控制器的结构形式便于进行理论分析,但是求解前往往需要确定待定参数, 这些参数的选择直接影响结论的好坏, 此外还无法处理病态状态矩阵系统的鲁棒问题。
针对这些不足, 相关****提出了一些具有发展潜力的新的研究方向。文献[5-6]分别提出了基于非线性矩阵不等式(Nonlinear Matrix Inequality, NMI)和双线性矩阵不等式(Bilinear Matrix Inequality, BMI)的μ方法, 但迄今为止, BMI和NMI的数值算法还未成熟。Chen[7]和Fu[8]等给出了基于线性矩阵不等式(Linear Matrix Inequality,LMI)的μ分析方法, 该方法具有良好的数值性态(多项式时间复杂度), 这使得该方法能够更加有效地处理实际控制工程中的问题。
运用LMI方法进行μ分析的关键在于:针对H∞控制器的求解问题将形如式(7)所示的Riccati不等式根据Schur补的性质等价转化成一个LMI可行性问题, 不但降低了求解难度,可解条件也得到有效放宽。但文献[7-8]的处理方法仍然存在一定的局限性,即只能进行状态反馈控制器设计, 需要附加状态观测器, 当状态信息难以获得时则无能为力。
为了弥补以上所述各种方法不足, 本文在文献[7, 9]的基础上, 进行基于LMI的输出反馈控制器设计, 运用LMI方法给出了问题线性可解的凸约束条件以改善D-K迭代的最优解问题, 并同文献[10]提出的一种改进D-K迭代、PID算法进行比较。数值计算表明解出的控制器具有较好鲁棒稳定性和鲁棒性能, 本方法增强了μ分析对病态状态矩阵系统的适用性。
1 预备知识 1.1 参数摄动模型 μ问题可描述成:对给定不确定量集合Δ, γ∈R+及标称系统G(s)∈H∞空间。
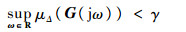 | (1) |
式中:sup为结构奇异值μ的上确界。
系统G(s)有以下状态空间实现:
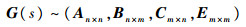 | (2) |
式中:n为状态维数;m为控制输入维数。
在如图 1所示的输出反馈系统中的状态方程:
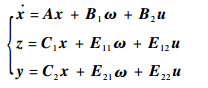 | (3) |
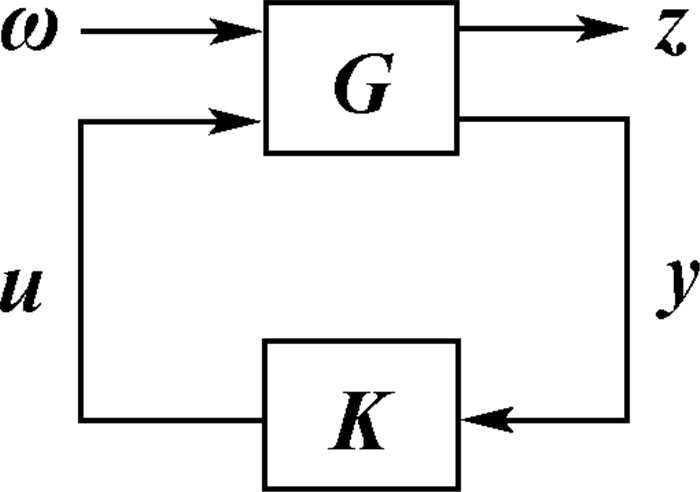 |
| 图 1 输出反馈系统模型 Fig. 1 Output feedback system model |
| 图选项 |
式中:x为状态矢量;ω为外部扰动;z为输出误差;u为控制输入;y为量测输出。
定义1?给定非负整数r、u及非负整数数组
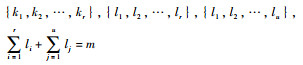
不确定集合
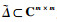
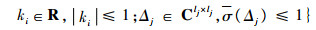 | (4) |
式中:σ(·)表示矩阵奇异值上确界。
结构奇异值定义为
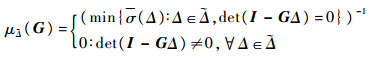 | (5) |
1.2 矩阵不等式
1.2.1 Schur引理[11] 在将NMI转化为LMI的问题中, 常用到矩阵的Schur补性质。具体描述如下:考虑对称矩阵S∈Rn×n, 并将S进行分块:
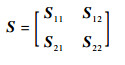 | (6) |
式中: S11为方阵, 则以下条件等价:
1)?S < 0
2)?S11 < 0, S22 -S12 TS11 -1S12 < 0
3)?S22 < 0, S11 -S12 S22 -1S12 T < 0
其中:S22 -S12 TS11 -1S12 或S11 -S12 S22 -1S12 T称为矩阵S的Schur补。当S为线性矩阵变量时上述等价关系也说明了条件2)和3)中的NMI分别定义了一个关于变量的凸约束。在控制问题中经常遇到形如式(7)的Riccati不等式:
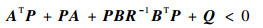 | (7) |
式中:A, B, Q=QT>0, R=RT>0为适当维数的常数矩阵;P为对称矩阵变量。根据Schur补的性质可以将Riccati不等式的问题转化成一个等价的如式(8)所示LMI的可行性问题。
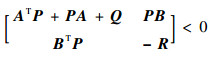 | (8) |
1.2.2 有界实引理 设γ>0, 系统G(s)的状态空间矩阵为(A, B, C, E), 则以下条件等价:
1)?系统渐近稳定, 且||G(s)||∞ < γ
2)?存在一个对称矩阵P>0, 使得
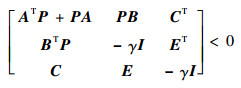 | (9) |
2 D-K迭代的LMI表述 2.1 D求解 现有的D-K迭代算法可描述为
定义集合
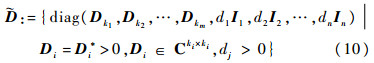 | (10) |
求

为利用LMI并迭代解出优化后的K, 需要得到式(10)的LMI描述, 不仅要用闭环系统系数矩阵表述以方便K求解, 还要将非线性不等式条件转换成线性不等式矩阵的形式。下面利用Schur引理和有界实引理经过推导实现。式(10)的初步等价描述为:求D∈
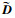
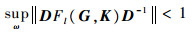 | (11) |
设初始控制器状态矩阵为(Ak, Bk, Ck, Ek), 输出反馈闭环系统状态矩阵为(Acl, Bcl, Ccl, Ecl), 易知
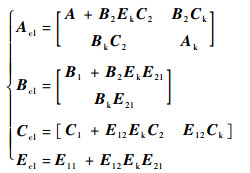 | (12) |
根据有界实引理得到与式(10)等价约束条件:
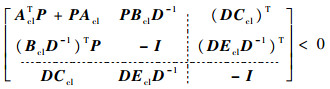 | (13) |
运用Schur引理对式(13)左侧矩阵变量按虚线所示分成4个子矩阵,由条件3)可得式(14), 矩阵分解后得到式(15)和式(16), 因为 D∈,
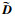
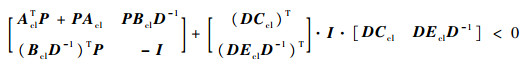 | (14) |
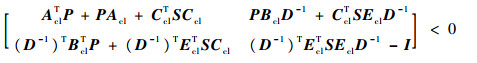 | (15) |
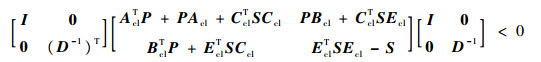 | (16) |
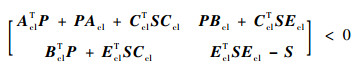 | (17) |
式中:
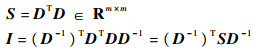 |
由于式(17)是LMI的形式, 进而解出P、S得到D, 可通过MATLAB软件中LMI工具箱凸优化求解器feasp实现。
2.2 输出反馈控制器K求解
2.2.1 输出反馈的LMI表述 首先进行以下假定:①(A, B2, C2)是能稳能检的;②E22=0。条件①对系统的输出反馈镇定是充分必要的, 条件②对一般系统都具有适用性[13]。
设H∞控制器u=Ky应用到系统后得到闭环系统为
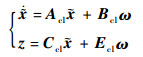 | (18) |
闭环系统是渐近稳定的且从ω到z的传递函数的H∞范数小于1的充分必要条件是存在对称正定矩阵Xk使得
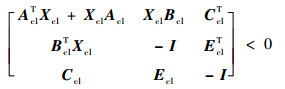 | (19) |
由于Acl、Bcl、Ccl及Ecl依赖于未知的控制器参数, 再加上不确定的矩阵变量Xcl导致矩阵不等式难以像状态反馈情形那样方便解出控制器, 必须对矩阵不等式进行处理使之成为可解的LMI形式。
2.2.2 消元法 通过对式(19)进行矩阵参数替代、消元使之转化成一组LMI可行性问题, 详细推导见文献[9], 下面直接写出求解步骤:
1)?求满足下列条件的矩阵X和Y。
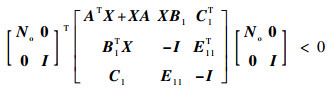 | (20) |
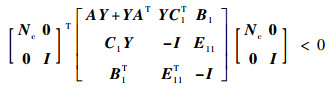 | (21) |
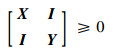 | (22) |
式中:No和Nc分别是以子空间ker([C2 E21])和ker([B2 T E12T])中任意一组向量作为列向量所构成的矩阵, 即满足Im No=ker([C2 E21])和Im Nc=ker([B2T E12T])的矩阵[14]。
2)?求满足X-Y-1=X1X1T的矩阵X1∈Rn×nk, 其中nk为X-Y-1的秩;再通过式(23)构造Xcl, 文献[9]已证明, 只要1)中不等式条件满足且要设计的控制器维数大于等于系统状态量即nk≥n, 就总能找到满足要求的Xcl:
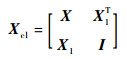 | (23) |
此外将反馈系统系数矩阵按式(24)构造:
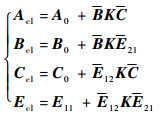 | (24) |
式中:
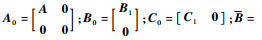
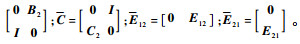
3)?将式(23)、式(24)代入式(19)得到如式(25)的等价表述:
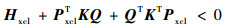 | (25) |
式中:
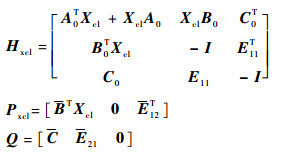 |
式(25)得到只包含矩阵变量K的一个LMI, 通过应用MATLAB软件中的LMI工具箱——mincx求解器可以求出系统的输出反馈最优H∞控制器, 连续时间系统H∞控制器综合问题的求解器是hinflmi, 离散时间系统H∞控制器综合问题的求解器是dinflmi, 本文在数值仿真环节将采用hinflmi求解器进行计算。
3 基于LMI的D-K迭代步骤 结合传统D-K迭代步骤如下:
1)?初始化K, 求解满足
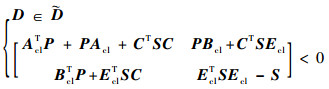 | (26) |
的稳定D(s)。
2)?根据最小化||DMD-1||∞的D(s)矩阵, 设计求解满足min||DMD-1||∞的控制器K, 即
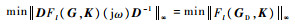 |
定义GD状态矩阵(Ad, Bd, Cd, Ed):
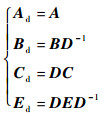 |
其中:
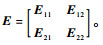
利用消元法求出H∞控制器参数矩阵K。
3)?代入K状态参数, 返回1)继续求解D, 重复迭代直到K满足要求, 得到最优化的μ控制器。
4 数值仿真 考虑如图 2所示参数摄动对象系统模型, 对于系统G,其中(z1, z2, u)分别为输入干扰、建模误差和控制输入, (ω1, ω2, y)为对应输出,(k, τ)为标称系统参数, (w0, w1)为加权函数。注意到该模型代表的广义系统状态矩阵中E12非列满秩不满足Riccati方程解法的正常条件, 由于在实际工程中具有一般性, 不妨定义此类系统为病态状态矩阵系统。
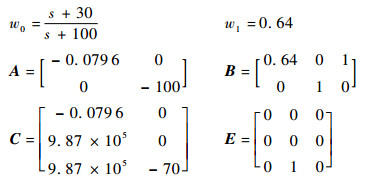 |
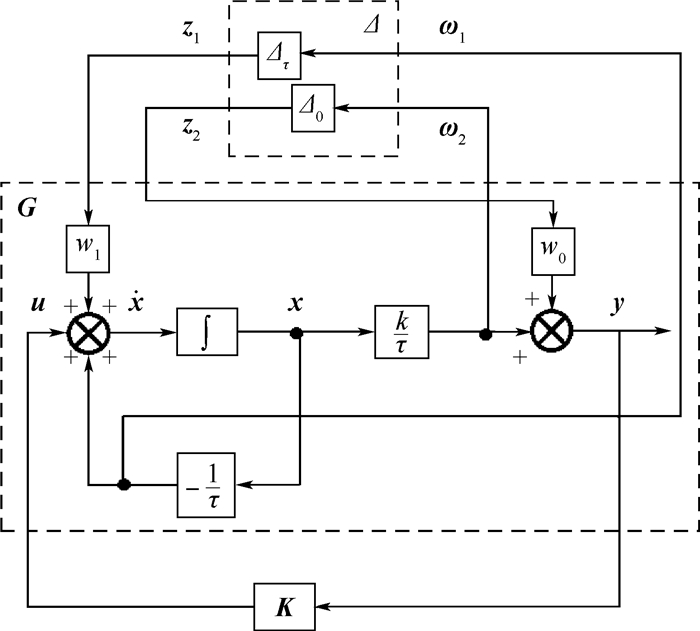 |
| 图 2 参数摄动对象系统模型 Fig. 2 Parameter perturbation model of object system |
| 图选项 |
针对这类系统文献[10]提出一种解决方法, 对E12、E21加入较小修正系数使之满秩, 据此方法得到的μ控制器鲁棒稳定性如图 3所示。此外采用本文提出的基于LMI的D-K迭代进行μ控制器设计。
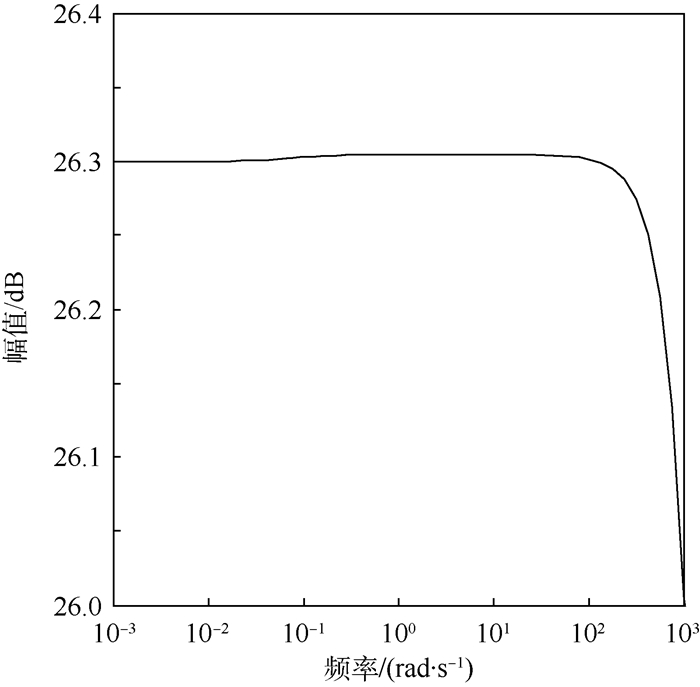 |
| 图 3 μ/文献[10]系统结构奇异值曲线 Fig. 3 Structured singular value curves of μ/Ref.[10] system |
| 图选项 |
经过5次迭代, 最终得到的控制器如下:
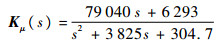 | (27) |
其幅频特性如图 4所示, 此外最优化设计PID控制器[15]如下:
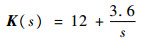 | (28) |
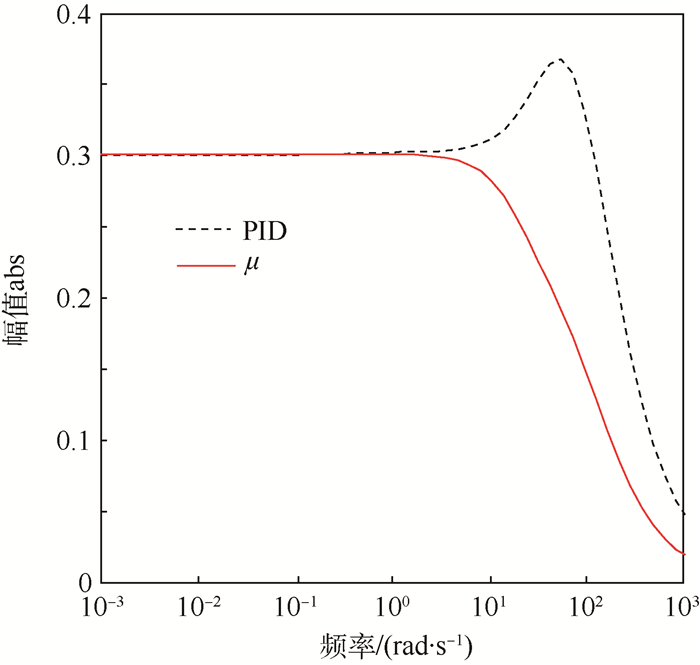 |
| 图 4 μ控制器幅频特性 Fig. 4 Amplitude-frequency characteristic of μ controller |
| 图选项 |
同μ控制器的鲁棒性能进行对比, 对应参数摄动结构的系统矩阵结构奇异值曲线如图 5所示。可知μ控制器系统比PID控制器系统的最大奇异值更小, 曲线过渡也更加平稳, 鲁棒稳定性更好。图 3所示采用文献[10]处理方法求解出的控制器系统与μ控制系统结构奇异值曲线对比, 可知虽然Riccati方程求解条件满足, 但是由于系统矩阵处理后存在一定程度失真, 导致控制器鲁棒稳定性变差, 无法得到最优的鲁棒控制器。
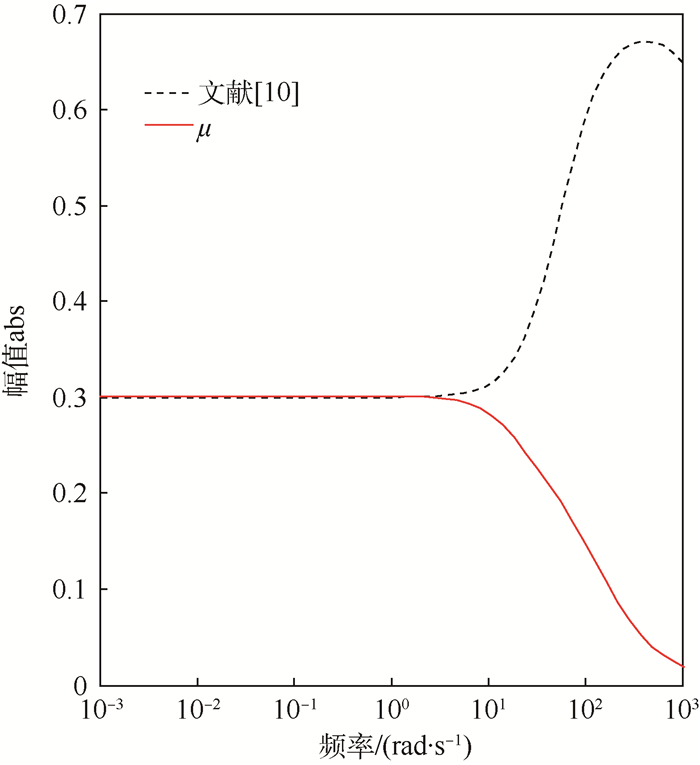 |
| 图 5 μ/PID系统结构奇异值曲线 Fig. 5 Structured singular value curves of μ/PID system |
| 图选项 |
为了检测μ控制器的鲁棒性能, 利用SIMU-LINK进行数值仿真, 设置输出反馈系统, 求解器类型为Gear, 仿真时间为5 s, 输入为电流阶跃信号, 当标称输出25 MPa的压力信号时, 对比PID控制器与μ控制器输出反馈系统的阶跃响应曲线如图 6所示, 可以看到上升时间PID:0.2 s, μ:0.1 s, 说明μ控制器的动态性能略好于PID控制器;当输入信号为强度10%, 频率33 Hz的特征扰动时, PID控制器与μ控制器输出反馈系统的输出曲线如图 7所示, 可以看到μ控制器最大输出0.2 MPa, PID控制器最大输出1.75 MPa, 即μ控制器的干扰抑制性能明显强于PID控制器。
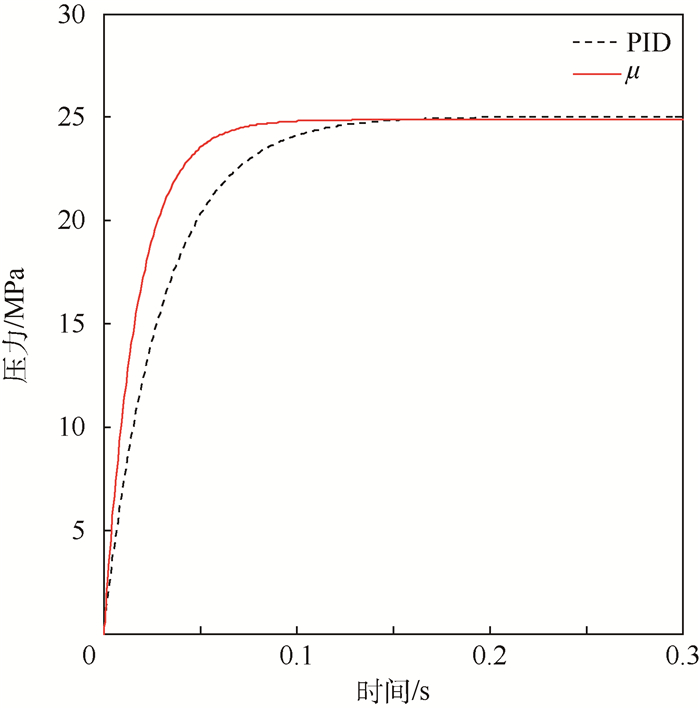 |
| 图 6 μ/PID系统阶跃响应 Fig. 6 Step response of μ/PID system |
| 图选项 |
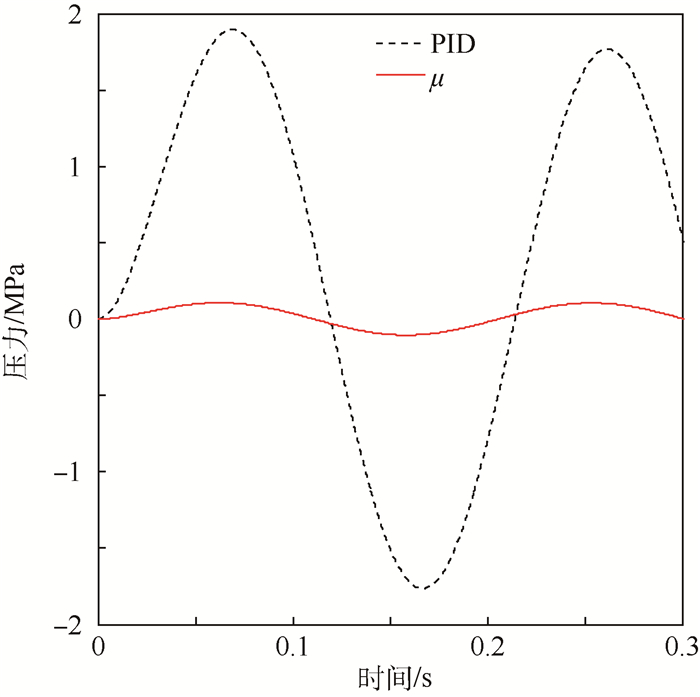 |
| 图 7 干扰输入μ/PID系统输出 Fig. 7 Output of input disturbance μ/PID system |
| 图选项 |
5 结论 针对传统D-K迭代算法在应用上受局限的问题, 本文分别给出D-K算法中对角矩阵D、输出反馈控制器K的矩阵不等式描述。由于μ方法中的D、K求解具有非线性,为了将其转化成LMI的描述形式,文中在Schur引理和有界实引理的基础上对传统D-K算法D求解问题进行线性化处理, 并利用消元法使K设计问题线性化, 并通过构造系数矩阵使得D、K的求解得以交替迭代进行, 突破了LMI方法输出反馈H∞控制器局部最优的局限。本文设计的μ控制器经理论分析和数值仿真表明:
1)?综合了LMI方法适用性广以及D-K算法交替凸优化的优点。
2)?相对于文献[7-8]中的控制器由于无需状态观测器更具有工程实用性。
3)?相较于文献[15]中方法得到的PID控制器具有较好的动态性能以及较好的鲁棒性能; 相较于文献[10]方法解出的μ控制器具有较好的鲁棒稳定性和鲁棒性能。
参考文献
| [1] | DOYLE J C. Analysis of feedback systems with structured uncertainties[J].IEE Proceedings D-Control Theory and Applications, 1982, 129(6): 242–250.DOI:10.1049/ip-d.1982.0053 |
| [2] | SAFONOV M G.Stability margins of diagonally perturbed multivariable feedback systems[C]//IEEE Conference on Decision & Control Including the Symposium on Adaptive Processes.Piscataway, NJ:IEEE Press, 1981:1472-1478.http://digital-library.theiet.org/content/journals/10.1049/ip-d.1982.0054?fmt=text |
| [3] | FAN K H, TITS A L, DOYLE J C. Robustness in the presence of mixed parametric uncertainty and unmodeled dynamics[J].IEEE Transaction on Automatic Control, 1991, 36(1): 25–38.DOI:10.1109/9.62265 |
| [4] | BALAS G J, DOYLE J C, GLOVER K. Analysis and synthesis toolbox[M].Minneapolis: Musyn Incorporated and Mathworks Incorporated, 1998. |
| [5] | COLLINS E G, SADHUKHAN D, WATSON L T. Robust controller synthesis via non-linear matrix inequalities[J].International Journal of Control, 1999, 72(11): 971–980.DOI:10.1080/002071799220515 |
| [6] | CHAMANBAZ M, DABBENCE F, TEMPO R, et al. A statistical learning theory approach for uncertain linear and bilinear matrix inequalities[J].Automatic, 2014, 50(6): 1617–1625.DOI:10.1016/j.automatica.2014.04.005 |
| [7] | CHEN G, SUGIE T L.Analysis and synthesis of state feedback systems based on multipliers and LMI[C]//Proceedings of the American Control Conference.Piscataway, NJ:IEEE Press, 1998:537-541. |
| [8] | FU R, HUANG L. Optimized LMI algorithm for L-analysis and synthesis with application in power system[J].Proceedings of the Chinese Society for Electrical Engineering, 2002, 22(10): 7–11. |
| [9] | 俞立. 鲁棒控制-线性矩阵不等式处理方法[M].北京: 清华大学出版社, 2002: 88-120.YU L. Robust control-linear matrix inequalities approach[M].Beijing: Tsinghua University Press, 2002: 88-120.(in Chinese) |
| [10] | 傅剑, 杨卫东, 李伯群, 等. 基于μ综合的热轧动态设定AGC鲁棒控制[J].北京科技大学学报, 2006, 28(3): 293–298.FU J, YANG W D, LI B Q, et al. Robust control of hot rolling dynamic setting AGC based on μ synthesis[J].Chinese Journal of Engineering, 2006, 28(3): 293–298.(in Chinese) |
| [11] | WANG J L, YANG G H, LIU J. An LMI approach to H-index and mixed H-/H∞ fault detection observer design[J].Automatic, 2007, 43(9): 1656–1665.DOI:10.1016/j.automatica.2007.02.019 |
| [12] | STEIN G, DOYLE J C. Beyond singular values and loop shapes[J].AIAA Journal of Guidance and Control, 1991, 14(1): 5–16.DOI:10.2514/3.20598 |
| [13] | 郑大钟. 线性系统理论[M].北京: 清华大学出版社, 1990: 10.ZHENG D Z. Linear system theory[M].Beijing: Tsinghua University Press, 1990: 10.(in Chinese) |
| [14] | SERRE D. Matrices:Theory and applications[M].New York: Springer, 2002: 6-7. |
| [15] | 何芝强.PID控制器参数整定方法及其应用研究[D].杭州:浙江大学, 2005:35-38.HE Z Q.The PID controller parameter setting method and application research[D].Hangzhou:Zhejiang University, 2005:35-38. |
