在航空航天中存在着大量复杂的薄壁结构，薄壁结构的动态响应与传递特性复杂且受几何建模误差的影响。几何模型的建模误差通常来源于圆角的简化，因此合理建立圆角等效模型对于动态响应分析的精度起着至关重要的作用。在有限元建模过程中，壳单元建立的模型可以大大缩减单元的数量，因此通常采用壳单元进行复杂薄壁结构的建模。在运用壳单元的建模过程中，由于开口薄壁结构存在着大量的圆角，而圆角对开口结构的弯扭性能有很大的影响，因此合理建立圆角的等效模型是壳单元建模过程的关键。
近年来，关于圆角在动力学分析中的建模研究相对较少。但在采用壳单元薄壁结构的建模中，圆角对结构频率与响应的影响不能忽略。
Brown等^[1-2]采用壳单元对结构的圆角进行等效建模，然而这种建模方法仅考虑了圆角对结构面内刚度的贡献而未考虑圆角对结构面外刚度的贡献。因此对于细长梁结构的频率计算精度较低。为了建立与实验结果吻合度较高的精细化模型，本文提出采用壳单元与梁单元组合对圆角进行合理简化建模，这种等效模型同时考虑了圆角的面内效应与面外效应，具有较高的计算精度，且应用范围更加广泛。本文通过理论公式的推导，得到了等效模型参数的计算方法，并通过实例验证了模型的正确性。
1 薄壁梁结构圆角建模 1.1 圆角简化条件 本文圆角简化建模方法采用结构刚度等效原理，等效建模方法适用于计算薄壁梁结构的固有频率与模态振型，本文建模方法不适用于计算结构圆角区域的局部应力。
1.2 圆角面外效应 薄壁梁结构^[3]通常是指壁厚t与截面最大尺寸b之比t/b≤0.1且截面最大尺寸b与杆长l之比b/l≤0.1的等截面直杆。由于这类薄壁结构在设计过程中为了避免局部应力集中，通常会将直角改为圆角，如图 1所示。

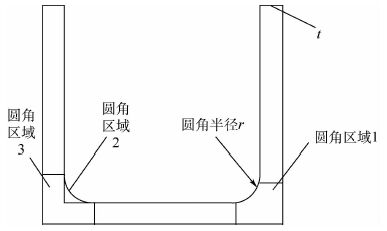图 1 槽型薄壁结构横截面 Fig. 1 Cross section of groove type thin-walled structure

图选项

薄壁梁弯曲时，圆角的面外效应是指在平截面假设下由于整体结构的弯曲而造成圆角区域2的纵向纤维伸长或压缩而体现出梁的效应。而对于薄壁杆件的约束扭转，由于截面翘曲受到抑制，截面上将会产生附加的约束扭转正应力和剪应力，此时圆角区域2沿杆件轴向仍然会体现出梁的性质。因此对于以上2种情况，圆角可以用梁来等效。由于圆角区域2的惯性矩贡献相对于整个截面而言是高阶小量，因此可以忽略不计，而只需考虑其拉压刚度等效，即

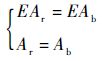(1)

式中：A_r为圆角区域2面积；A_b为等效梁单元的截面面积；E为弹性模量。
开口薄壁结构自由扭转问题属于求解泊松方程的第一边值问题^[4-7]，即求解如下方程：

边界条件为

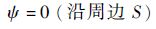(2)

式中：ψ为普朗特应力函数；S为截面的边界。

(3)

式中：M_T为截面扭矩。
式(3) 说明，扭矩M_T为ψ曲面下所包体积的2倍，槽型截面自由扭转时普朗特应力函数分布云图如图 2所示。
由图 2可以看出，圆角区域1对截面的整体抗扭刚度影响较大，圆角区域1的抗扭刚度K_t可以由式(4) 进行计算^[8]：

(4)

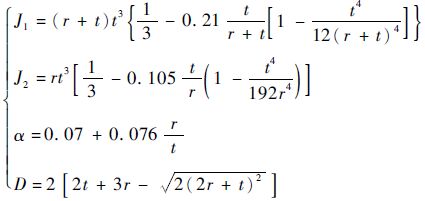(5)

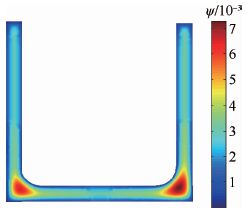图 2 普朗特应力函数分布云图 Fig. 2 Prandtl stress function distribution contour

图选项

式中：G为剪切模量。
图 1中圆角区域3(L形区域)的扭转常数为^[9]

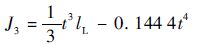(6)

式中：l_L为L形区域中心线的长度。
于是等效梁单元抗扭刚度为

(7)

式中：K_s为附加壳单元对抗扭刚度的贡献，具体表达式见式(34) 。
由式(1) 和式(7) 可以计算等效梁单元的截面参数，梁单元材料与结构材料相同，其余参数均为零。双圆角或单斜角结构得到其抗扭刚度的解析式较为困难，通常可以采用数值解法如有限差分法，通过求解泊松方程的边值问题，获得圆角区域的抗扭刚度，即

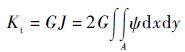(8)

式中：A为周边S所围成的区域;J为扭转惯性矩。
可以采用类似的计算方法得到梁单元截面参数。
1.3 圆角面内效应 对于槽型结构的低频模态，横截面可以近似满足开口薄壁杆件的刚周面假设，但是对于高频模态，刚周面假设将无法满足，截面将会在面内发生变形，此时圆角对其面内刚度会产生较大的影响，因此合理地建立圆角面内模型对于高频动力学分析是必要的。

1.3.1 双圆角建模^[1-2] 对于槽型截面的面内变形，其可以视作平面应变状态，此时壳结构在平面内可以退化为梁结构，结构的面内刚度可以通过广义梁理论^[10]计算。平面应变问题的弹性模量为

(9)

式中：ν为材料泊松比。
双圆角面内等效模型如图 3所示。
用连接圆角切点处的壳单元来近似等效圆角对截面面内刚度的贡献，等效壳单元的厚度与弹性模量可以通过结构面内刚度等效来计算，将图 3所示结构离散为3个欧拉伯努利梁单元，在节点4上施加静态力P和扭矩M可以计算出节点4转角，如图 4所示。

图 3 面内圆角等效示意图 Fig. 3 Equivalent schematic of in-plane fillet

图选项

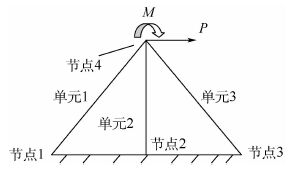图 4 双圆角广义梁单元示意图 Fig. 4 Schematic of generalized beam element of double fillet

图选项

图 4中，单元3和单元1与水平方向的夹角为45°，梁单元的节点1~节点3固定，因此结构的总的自由度数为2，即节点4的水平自由度u_bd和转角自由度θ_bd，结构的刚度矩阵为

(10)

式中：E_bd和t_bd分别为单元1、3的等效弹性模量和厚度；L_d为单元2的长度。
由式(11) 可以计算出结构在力P和扭矩M作用下的静态位移θ_bd。

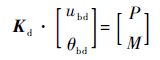(11)

真实结构圆角在力P和扭矩M作用下截面C产生的转角为θ_fd，如图 5所示。

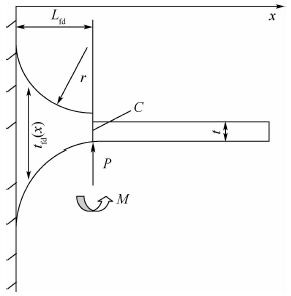图 5 双圆角几何结构与受载 Fig. 5 Double fillet geometry and loading

图选项

单位厚度的圆角结构变形应变能为

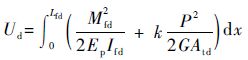(12)

式中： L_fd为圆角区域长度；A_td为图 5中的截面面积；k为剪切系数，对于矩形截面取k=1.2。

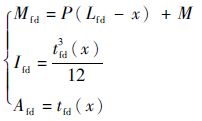(13)

其中：t_fd(x)为变截面面积。
由卡式第二定理可以得到

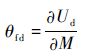(14)

由弯曲刚度等效原理，对于任意的M、P均有

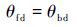(15)

由M、P的任意性可以得到关于E_bd、t_bd的非线性方程组，非线性方程组可以通过数值解法求解，从而求得等效截面参数E_bd、t_bd。

1.3.2 单圆角建模 单圆角建模与双圆角建模方法类似，仍然用连接圆角切点处的壳单元来等效圆角。此时将结构离散成2个欧拉伯努利梁单元，结构在节点3和节点2处受力P和扭矩M作用。结构处于平衡状态，如图 6所示。

图 6 单圆角广义梁单元示意图 Fig. 6 Schematic of generalized beam element of single fillet

图选项

图 6中，单元2与水平方向的夹角为45°，单元1的长度为L_s，由于图 6所示的结构具有对称性，因此结构可以简化为图 7。

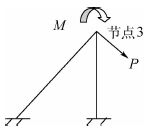图 7 结构简化图 Fig. 7 Structure simplification diagram

图选项

因此，图 7所示结构的总的自由度数为2，即节点3的水平自由度u_bs和转角自由度θ_bs，结构的刚度矩阵为

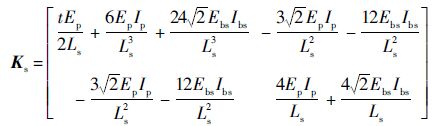(16)

式中：E_bs为单元2的等效弹性模量；E_p和t分别为单元1的弹性模量和厚度。

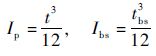(17)

其中：t_bs为单元2的厚度。
由刚度矩阵和外载荷可以求得转角自由度θ_bs, 即

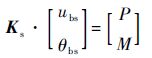(18)

单圆角结构在力P和扭矩M的作用下截面B产生的转角为θ_fs，如图 8所示，由于结构的对称性，因此可以取结构的一半进行分析，这种结构类似于曲梁，其位移与转角可以通过曲梁理论进行计算^[11-15]。图 8中，o为极坐标原点，中心轴为曲梁上下表面的中心线，中心轴的曲率半径为r_c，oC与水平方向的夹角为θ^*，易知曲率半径r_c为

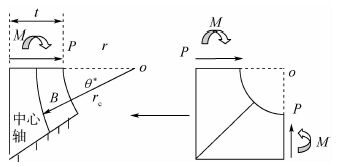图 8 单圆角几何结构与受载 Fig. 8 Single fillet geometry and loading

图选项

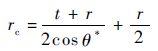(19)

结构在力P与扭矩M作用下的应变能为

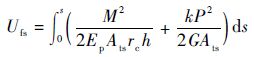(20)

式中：s为沿中心轴的曲线坐标；h为截面的中性轴与中心轴的距离；A_ts为图 8的横截面面积。
由卡式第二定理可以得到

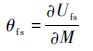(21)

通过将曲梁划分为n段，而每一微段可以用中心轴曲率为常数的曲梁来等效，如图 9所示。

图 9 曲梁微段 Fig. 9 Micro section of curved beam

图选项

图 9为第i个曲梁微段，微段沿曲线坐标长ds_i，微段的曲率半径为r_i。微段所受载荷为M_is, P_is和轴向力N_is由力和力矩的平衡条件可以得到

(22)

式中：θ^*_i为第i段与水平方向的夹角。
第i段中心轴的曲率半径为

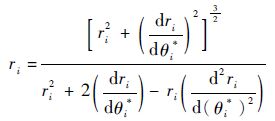(23)

式中：

(24)

由于曲梁为单位厚度，因此第i段的截面面积为

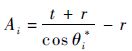(25)

第i段中性轴与截面中心轴的距离为

(26)

微段沿曲线坐标的长为

(27)

结构总应变能为

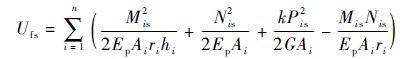(28)

将式(22) ~式(27) 代入式(28) , 并由卡式第二定理可以得到

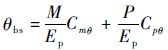(29)

式中：

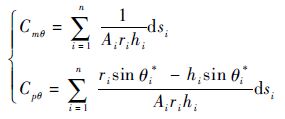(30)

由等效弯曲刚度等效原理，对于任意的M、P均有

(31)

由M、P的任意性可以得到关于E_bs、t_bs的非线性方程组，通过数值解法可以求得E_bs、t_bs。

1.3.3 夹角非直角的圆角建模 第1.3.1节和第1.3.2节分析的2种情况均为夹角为直角时的圆角建模方法，类似的，圆角建模可以推广到任意夹角γ(0 ＜γ＜π)的情况，上述曲梁位移与转角的计算方法具有通用性，对于夹角非垂直的情况，以单圆角为例，离散结构如图 10所示。

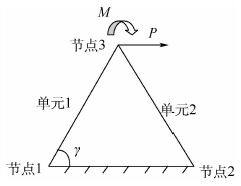图 10 夹角非直角的圆角广义梁单元示意图 Fig. 10 Schematic of generalized beam element of non-right angle fillet

图选项

图 10所示结构的单元刚度矩阵为

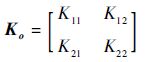(32)

式中：

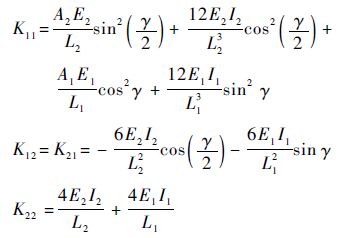其中：A₂、E₂、L₂和I₂分别为单元2的截面积、弹性模量、单元长度和截面惯性矩；A₁、E₁、L₁和I₁分别为单元1的截面积、弹性模量、单元长度和截面惯性矩。
对于单位厚度的圆角而言

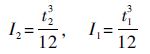(33)

与第1.3.1 节和第1.3.2节的分析过程类似，对于一般的曲梁结构，由于获得解析解的难度较大，因此通常可以通过有限元进行求解载荷作用下的转角，然后用刚度等效原理可以得到E₂、t₂。

1.3.4 壳单元附加抗扭刚度 考虑到附加壳单元会对结构整体抗扭刚度产生影响，壳单元的附加抗扭刚度为

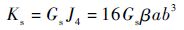(34)

式中：a和b分别为矩形截面的长和宽；β为关于a/b的系数；G_s为壳单元的剪切刚度；J₄为附加壳单元的截面惯性矩。
1.4 圆角等效步骤 圆角等效为梁单元与壳单元的组合结构，梁单元需要计算的等效截面参数为：截面面积A_b可由式(1) 计算。抗扭刚度K_t可由式(7) 计算，梁单元的密度与结构密度相同，由此可以使得等效结构的总质量与原始结构总质量相同。壳单元需要计算的等效截面参数为：等效弹性模量与壳单元厚度E_bs、E_bd、t_bs、t_bd，壳单元的密度为零，根据不同的圆角类型壳单元等效截面参数可以由式(15) 或式(31) 进行计算。
2 仿真算例 2.1 算例 1 槽型薄壁结构长1.5 m，截面宽0.12 m，高0.105 m，截面壁厚0.01 m，圆角半径为0.01 m，弹性模量为71×10⁹ N/m², 密度为2 780 kg/m³，如图 11所示。
结构圆角建模方法如图 12所示，梁的截面参数A=2.146×10^-5 m², J=1.1×10^-10 m⁴,ρ=2 780 kg/m³, 壳单元厚度为0.006 m，弹性模量为4.363×10¹¹ N/m²，泊松比为0.3，其余参数均为零，表 1为各阶模态频率误差。

图 11 槽型薄壁结构 Fig. 11 Groove type thin-walled structure

图选项

图 12 圆角等效建模 Fig. 12 Fillet equivalent modeling

图选项

由表 1可以看出，无圆角的模型刚度明显较实体结构偏低，频率误差超过5%，已经不适用于工程计算。而通过由壳单元和梁单元的组合对圆角建模可将频率的误差降低到2%以内，可以很好地满足工程精度要求。不同模型的频响函数对比如图 13所示。
表 1 频率误差 Table 1 Frequency error

自由模态阶数	实体模型/Hz	圆角模型/Hz	实体模型与圆角模型误差/%	壳模型无圆角/Hz	实体模型与壳模型误差/%
1	104.33	104.20	-0.12	98.67	-5.43
2	185.09	187.70	1.41	177.75	-3.97
3	272.02	273.46	0.53	270.94	-0.40
4	404.16	406.63	0.61	384.10	-4.96
5	451.73	451.40	-0.07	417.40	-7.60
6	464.94	464.35	-0.13	429.81	-7.56
7	506.58	505.22	-0.27	469.05	-7.41
8	563.50	559.62	-0.69	523.50	-7.10
9	613.29	616.31	0.49	585.47	-4.54
10	639.69	638.15	-0.24	606.34	-5.21

表选项

图 13 算例1频响函数对比结果 Fig. 13 Comparison results of frequency response function of Example 1

图选项

图 13中原始模型为未对圆角区域进行建模的模型。由表 1和图 13可以看出，通过这种圆角建模方法可以高精度地模拟真实结构，壳单元和梁单元的建模所需单元数量为1 200，而通过实体单元建模所需的单元数量为58 977。因此这种建模方法可以减少将近98%的单元数量。
2.2 算例 2 薄壁箱型梁^[15]是工程中常见的结构，由于箱型梁具有良好的结构性能，因此常见于航空航天结构。薄壁箱型梁截面如图 14所示。

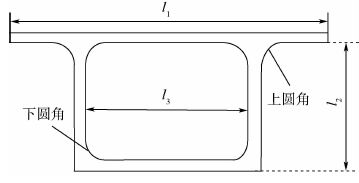图 14 薄壁箱型梁截面 Fig. 14 Thin-walled box girder section

图选项

箱型梁长为0.5 m，截面壁厚为0.002 m，l₁为0.079 m，l₂为0.030 m，l₃为0.035 m，圆角半径为0.003 m。圆角的等效建模方法与算例1相同，对于双圆角，等效梁的截面参数为：A=1.413 7×10^-5 m²，ρ=2 780 kg/m³，J=5.51×10^-11 m⁴，壳单元的弹性模量为1.126×10¹² N/m²，壳单元厚度为0.000 539 m，泊松比为0.3。对于单圆角截面参数为A=7.068 5×10^-6 m²，ρ=2 780 kg/m³，J=3.67×10^-11 m⁴，壳单元厚度0.000 621 m，弹性模量为7.363×10¹¹ N/m²，泊松比为0.3。频率误差如表 2所示。频响函数对比如图 15所示。
表 2 薄壁箱型梁频率误差 Table 2 Frequency error of thin-walled box girder

自由模态阶数	实体模型/Hz	圆角模型/Hz	实体模型与圆角模型误差/%	壳模型无圆角/Hz	实体模型与壳模型误差/%
1	917.56	917.42	-0.02	863.08	-5.89
2	1 278.60	1 270.90	-0.60	1 275.10	-0.23
3	1 848.00	1 836.30	-0.63	1 676.90	-9.31
4	2 171.20	2 160.30	-0.50	2 021.30	-6.91
5	2 339.80	2 303.80	-1.54	2 076.80	-11.24
6	2 379.50	2 333.30	-1.94	2 152.30	-9.54
7	2 499.10	2 460.70	-1.54	2 337.70	-6.48
8	2 686.10	2 658.50	-1.03	2 457.20	-8.23
9	2 702.30	2 677.80	-0.91	2 522.60	-6.67
10	2 740.20	2 707.00	-1.21	2 542.80	-7.23

表选项

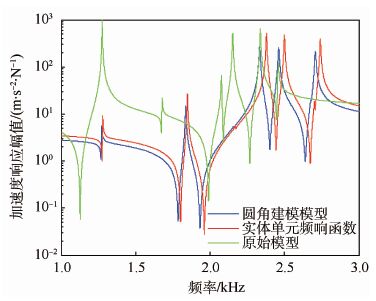图 15 算例2频响函数对比结果 Fig. 15 Comparison results of frequency response function of Example 2

图选项

3 结论 1) 本文提出了一种对于薄壁结构中圆角的等效建模方法，通过梁单元与壳单元的组合建模，同时考虑了圆角的面内效应与面外效应，各阶计算误差在2%以内。
2) 通过壳单元与梁单元组合建模相对于实体单元减少了至少95%的单元数量，有效提高了计算效率。
3) 本文方法相比于其他方法适用范围广，且适用于复杂薄壁结构的圆角建模，由于之前所提出的建模方法基本仅考虑圆角面内效应，因此应用范围有限。
4) 本文详细分析了圆角对结构抗扭刚度的影响，通过梁单元合理模拟了圆角对结构抗扭刚度的贡献，并且通过频响函数曲线验证了模型的正确性与准确性。
5) 本文方法虽有一定的复杂性，但全面考虑了圆角对结构刚度的贡献，对于计算精度要求较高的薄壁结构有一定的工程应用价值，同时合理分析了结构动态特性计算中的误差来源。

参考文献

[1]	SEUGLING R M,BROWN A M.Modeling of fillets in thin-walled structures for dynamic analysis[C]//Proceedings of the 19th International Model Analysis Conference,2001:379-384.
[2]	BROWN A M, SEUGLING R M. Using plate finite elements for modeling fillets in global response analysis[J].Finite Element in Analysis and Design, 2004, 40(13-14): 1963–1975.DOI:10.1016/j.finel.2004.01.008
[3]	包世华, 周坚. 薄壁杆件结构力学[M].北京: 中国建筑工业出版社, 2006: 190-193.BAO S H, ZHOU J. Structural mechanics of thin-walled rod member[M].Beijing: China Building Industry Press, 2006: 190-193.(in Chinese)
[4]	钱伟长. 圣维那扭转问题的物理假定[J].物理学报, 1953, 9(4): 215–220.QIAN W C. Physical assumptions of the Saint Venant torsion problem[J].Journal of Physics, 1953, 9(4): 215–220.(in Chinese)
[5]	钱伟长, 林鸿荪, 胡海昌. 弹性柱体扭转理论[M].北京: 科学出版社, 1956: 178-179.QIAN W C, LIN H S, HU H C. Torsion bar elastic theory[M].Beijing: Science Press, 1956: 178-179.(in Chinese)
[6]	钱伟长. 弹性力学[M].北京: 科学出版社, 1980: 156-158.QIAN W C. Elastic mechanics[M].Beijing: Science Press, 1980: 156-158.(in Chinese)
[7]	王敏中, 王炜, 武际可. 弹性力学教程[M].北京: 北京大学出版社, 2002: 127-134.WANG M Z, WANG W, WU J K. Elastic mechanics course[M].Beijing: Peking University Press, 2002: 127-134.(in Chinese)
[8]	YOUNG W C. Roark's formulas for stress and strain[M].6th ed.New York: McGraw-Hill, 1989: 215-216.
[9]	BORESI A P, SCHMIDT R J, SIDEBOTTOM O M. Advanced mechanics of materials[M].5th ed.New York: Wiley, 1993: 367.
[10]	ROARK R J. Formulas for stress and strain[M].5th ed.New York: McGraw-Hill, 1989: 206.
[11]	赵超燮. 结构矩阵分析原理[M].北京: 高等教育出版社, 1985: 92-93.ZHAO C X. Structure matrix analysis[M].Beijing: Higher Education Press, 1985: 92-93.(in Chinese)
[12]	郑振飞, 彭大文. 抛物线形的曲杆单元刚度矩阵[J].福州大学学报(自然科学版), 1983(4): 76–82.ZHENG Z F, PENG D W. The stiffness matrix of a parabolic curved rod element[J].Journal of Fuzhou University(Natural Science), 1983(4): 76–82.(in Chinese)
[13]	宋俊杰, 刘茂江. 材料力学手册[M].石家庄: 河北科学技术出版社, 1984: 32.SONG J J, LIU M J. Handbook of materials mechanics[M].Shijiazhuang: Hebei Science and Technology Press, 1984: 32.(in Chinese)
[14]	吕子华, 吕令毅. 矩阵结构力学[M].北京: 中国建筑工业出版社, 1997: 77-79.LYU Z H, LYU L Y. Matrix structure mechanics[M].Beijing: China Building Industry Press, 1997: 77-79.(in Chinese)
[15]	罗旗帜. 薄壁曲箱梁桥剪滞效应分析[J].铁道学报, 1999, 21(5): 89–93.LUO Q Z. Analysis of shear lag effect in thin walled curved box girder bridges[J].Journal of the China Railway Society, 1999, 21(5): 89–93.(in Chinese)