文献[7]在宽带组网体制下,详细分析了不同视角观测时旋转对称锥体目标的一维距离像特性,并基于时间距离像分布准确估计出了锥体目标的特征参数。文献[8]通过三站一维距离像融合实现了锥体目标的三维重构及参数提取。文献[9]在窄带组网体制下,推导了不同视角散射中心瞬时频率变化关系,利用频谱熵实现了散射中心的匹配关联,并进一步提出了基于散射中心瞬时频率相关性的目标参数提取算法。然而,上述目标特征提取算法均是在单一体制雷达网中进行的,基于混合体制雷达组网的目标参数提取研究则相对较少。考虑到在实际作战条件下,利用不同体制雷达对目标同时进行观测的可能性较大,且混合体制雷达网较单一雷达网能更好地实现全空域、跨频段的目标联合识别,极大地提高防御系统的反隐身、抗干扰性能,因此,进行混合体制雷达网中的目标识别研究是十分必要的。目前,国内主要处于理论研究阶段,文献[10]在总结基于宽带雷达网和窄带雷达网的目标微动特征提取研究现状的基础上,对基于宽窄带混合体制雷达网的弹道目标识别技术进行了深入探讨,并依据现有雷达工作模式初步提出了2种混合体制雷达网的构成方案。且研究表明[11],对目标同一散射中心而言,窄带雷达获取的微多普勒曲线可以等效为宽带雷达获得的距离像曲线的导函数,文献[12]正是基于此思想对宽窄带混合体制雷达网中旋转目标的微多普勒效应进行分析,并实现了目标三维微动特征的提取。国外,Linde[13]对基于宽窄带混合体制雷达网的非合作目标识别技术进行了深入探讨,并依据现有雷达工作模式初步提出了两种混合体制雷达网的构成方案,其中一种已在美国Senrad雷达上得到了应用,并且针对飞机目标的识别进行了相关测试。
本文在文献[7]的基础上,进一步对宽窄带混合体制雷达网中的目标参数提取进行了研究。首先建立了锥体目标进动模型,详细分析了宽带和窄带体制下进动对回波的调制特性。然后利用微多普勒和差比实现了不同体制下散射中心的匹配关联,并提出了通过一部宽带雷达和一部窄带雷达联合提取目标参数的新方法。最后,仿真分析了散射中心曲线提取误差对目标参数提取精度影响。
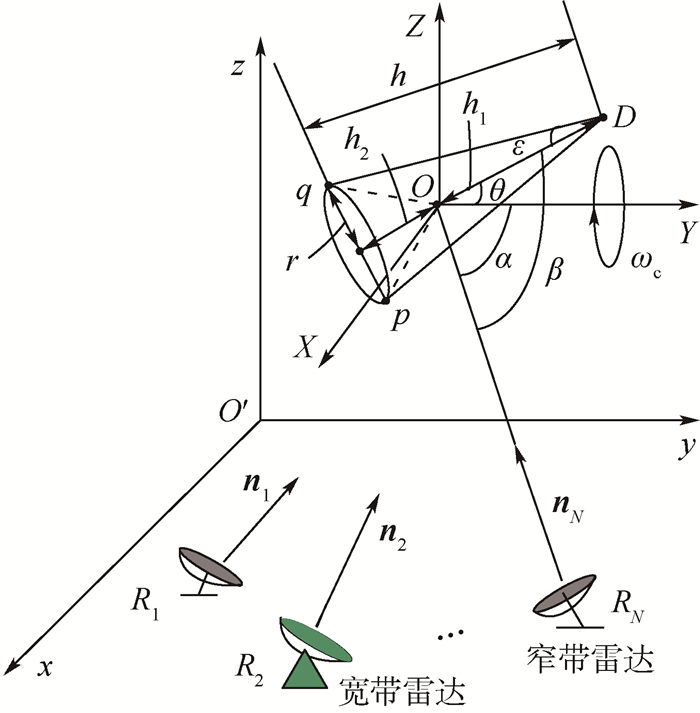
1 进动模型 首先建立宽窄带混合体制雷达网观测模型如图 1所示,O′-xyz为全局坐标系;Ri为雷达网中的第i部单基雷达, i=1, 2, …, N;ni为第i部雷达的单位视线方向。当雷达网探测空间存在多个目标时,本文假设目标匹配已经完成,且各雷达之间的时间同步精度已满足雷达网联合观测要求。现选取其中一部雷达进行分析,O-XYZ为参考坐标系,其构建准则与文献[14]中相同。D、p、q分别为锥体的3个强散射中心,ωc为锥旋角速度,(α, β)分别为雷达视线与目标锥旋轴、对称轴的夹角,θ为进动角,ε为半锥角,h为锥体高度,r为底面半径,h1和h2则分别为O点与锥顶以及底面中心的距离,且在远场条件下,雷达与O点的距离为R0。
 |
| 图 1 组网雷达示意图 Fig. 1 Sketch map of netted radar |
| 图选项 |
对于单部雷达而言,当β满足β∈(0, ε)∪ (π/2, π-ε)时,锥体3个散射中心同时可见,且通常ε较小[7],因此本文主要在视角范围为β∈(π/2, π-ε)内进行算法研究。
t时刻,取锥体对称轴上的单位方向向量为
 | (1) |
式中:φi为初始相位角。
雷达网中,第i部雷达视线方向向量定义为
 | (2) |
式中:αi为第i部雷达视线与锥旋轴的夹角。由式(1)、式(2)可知β满足:
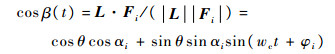 | (3) |
进而可得各散射中心的径向距离表达式分别为[13]
 | (4) |
由式(4)可以看出,锥顶D的径向距离变化服从正弦规律,而p、q的径向距离随进动变化偏离了正弦规律,且三者均与目标的结构参数、进动角、雷达视线角有关,此时如果能准确提取出散射中心径向距离变化曲线参数,便可实现对目标进动和结构特征的求解。
2 信号模型 2.1 宽带信号模型 假设雷达发射线性调频信号为
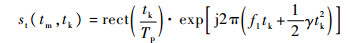 | (5) |
其中:
 | (6) |
式中:

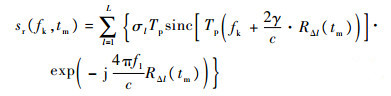 | (7) |
式中:L为目标上等效散射中心的个数;c为光速;σl为第l个散射中心的散射系数,进一步观察可知距离像的峰值出现在:
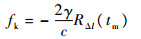 | (8) |
对式(8)两边同时乘以系数因子-c/(2γ),便可实现距离定标,使散射中心在距离像中的峰值位置与微距离变化保持一致。结合式(4)可得第1节中锥体目标各散射中心微距离变化表达式为
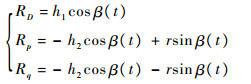 | (9) |
2.2 窄带信号模型 假设雷达发射单频脉冲信号,在高频近似的条件下,目标呈光学区散射特性,目标回波可等效为几个强散射中心回波之和[15],若目标第l个散射中心在t时刻与雷达的距离为Rl(t),经正交双通道解调可以得到回波基带信号为
 | (10) |
式中:f2为载波频率。对式(10)进行时频分析可得第l个散射中心的多普勒变化表达式为
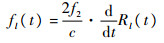 | (11) |
假设目标平动已得到完全补偿,结合式(4)可得第1节中锥体目标各散射中心的微多普勒频率表达式为
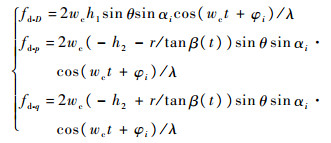 | (12) |
从式(12)可以看出,fd-D服从标准的正弦分布,而fd-p、fd-q的包络还受到r/tanβ(t)项的调制,变化形式复杂,难以直接用于目标参数求解。
进一步观察比较式(9)和式(12)发现,底面两个散射中心的微距离及微多普勒频率均具有对称结构。两散射中心的微距离正弦项同为R1=-h2cosβ(t),微多普勒频率的正弦项同为fd1=-2wch2sinθsin αcos(wct+φi)/λ,而非正弦项则只是正负符号相反,因而本文考虑利用该对称性来简化目标参数求解算法。
3 目标特征参数的宽窄带融合提取 3.1 散射中心关联特性分析 根据第2节分析可知,若利用宽带雷达和窄带雷达分别从不同视角对锥体目标进行观测,在得到的距离像和时频分布图中均将包含3个微动调制分量,由于观测视角及雷达体制不同,各散射中心的排列顺序也将存在差异,因而在对目标特征进行融合提取前,首先要进行散射中心的匹配关联。观察式(9)和式(12)可知,令k1=(Rp+Rq)/RD,k2=(fd-p+fd-q)/fd-D,两者满足:
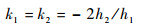 | (13) |
可以看出k1、k2均不随雷达观测视角和观测时间改变,仅与h1、h2有关。对式(9)和式(12)做进一步分析,令Rk=(Rp+Rq)/(Rp-Rq)、fdk=(fd-p+fd-q)/(fd-p-fd-q),推导可得
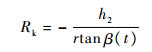 | (14) |
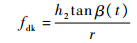 | (15) |
由于本文选取的β∈(π/2, π-ε),于是tan β(t) < 0,且r、h1为目标结构参数均大于零。因此,在观测时间内Rk、fdk分别满足Rk>0,fdk < 0。若调换Rk、fdk假设式中p、q的顺序,结果刚好相反。由此便可实现p、q两点的关联识别。
综上所述,基于微多普勒和差比的宽窄带匹配关联算法步骤如下:
Step 1??径向距离预处理。采用ESPRIT算法[16]提取宽带雷达距离像中某一时刻3个散射中心径向位置,求得其中任意两点径向距离之和与第3点径向距离的比值。
Step 2??瞬时频率预处理。采用峰值法提取窄带雷达时频图中某一时刻3个散射中心瞬时频率值,求得其中任意两点瞬时频率之和与第3点瞬时频率的比值。
Step 3??初步关联出锥顶散射中心。对预处理后的数据进行比较,根据式(13)识别出锥顶散射中心。
Step 4??对2个锥底散射中心进行细分。在区分出锥顶散射中心的基础上,分别求得剩余2个散射中心的径向距离和差比、瞬时频率和差比,借助式(14)、式(15)区分出2个锥底散射中心。
3.2 进动与结构参数提取 在3.1节分析的基础上,现利用一部宽带雷达和一部窄带雷达对目标特征参数进行融合提取。假设雷达1发射线性调频信号,雷达2发射单频脉冲信号,雷达视线角分别为α1和α2,为进一步简化参数求解过程,可分别选取雷达1距离像中时刻t1对应的散射中心径向距离,雷达2时频图中t2时刻对应的散射中心瞬时频率进行计算,且t1和t2分别满足cos(wct1+φ1)=1,cos(wct2+φ2)=1,结合式(3),由式(9)和式(12)可知此时锥顶散射中心径向位置取得均值,瞬时频率取得极值fd-D(t2)为
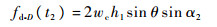 | (16) |
且Rk、fdk的瞬时值分别为
 | (17) |
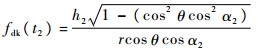 | (18) |
至此,便实现了目标各散射中心微距离和微多普勒频率表达式的联合化简。现采用扩展Hough变换提取雷达1获得的距离像中锥顶散射中心径向距离变化曲线参数,由式(9)可知曲线幅度AD=h1sin θ sin α1,令m1=AD/fd-D(t2),m2=Rk(t1)/fdk(t2),于是得到
 | (19) |
式(19)中包含α1、α2、θ、wc 4个未知量,其中锥旋角频率wc可采用文献[17]中的自相关函数凸包算法求得,这种改进的自相关法对先验信息的要求不高,且适用范围广,对宽、窄带回波分别得到的角频率求平均即可获得角频率的精确估计值
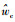
然而,在减少一个未知量的基础上,常规条件仍难以实现其他几个参数的求解。考虑θ∈[5°, 15°]时,cos2θ的取值区间为0.99~0.94,该变化对方程组求解结果影响不大[9, 14]。基于此,现提出参数估计算法如下:
Step 1??对α1、α2进行粗估计。设定θ的取值范围为5°~15°,取值步长为0.5°,由式(19)可求得各θ值所对应的α1、α2,进而求平均可得粗估计值

Step 2??对r、θ进行粗估计。令A=Rp(t1)-Rq(t1),B=fd-p(t2)-fd-q(t2),将


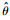
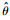

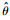
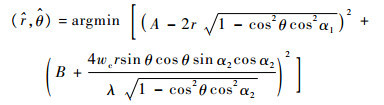 | (20) |
Step 3??通过循环迭代对α1、α2、r、θ进行精估计。在Step 2求得
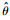
Step 4??估计h1、h2、h。在精确估计出


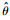

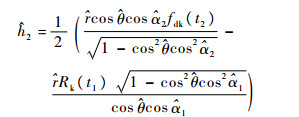 | (21) |
结合式(13),令k=(k1+k2)/2,可以求得
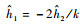

 | (22) |
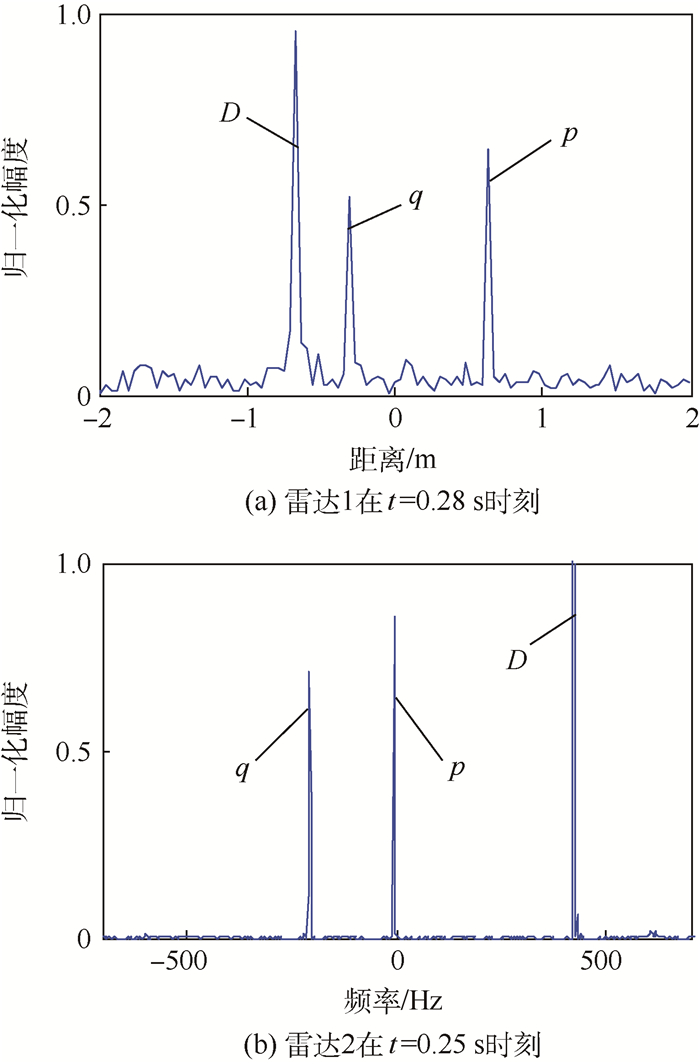
4 仿真分析 4.1 目标参数估计 仿真时设置目标参数为:h1=2 m,h2=0.5 m,r=0.5 m,h=2.5 m,θ=13°,锥旋频率fc=4 Hz。设置雷达参数为:雷达1发射信号载频f1=10 GHz,带宽为4 GHz,脉冲重复频率为1 kHz;雷达2发射信号载频为f2=8 GHz,脉冲重复频率为2 kHz。2部雷达观测视线与旋转轴的夹角分别为α1=120°、α2=135°,积累时间均为1 s,雷达信噪比(SNR)均为10 dB。图 2(a)为雷达1获得的目标回波时间距离像,图 2(b)为雷达2获得的重排谱图,它有效地改善了信号分量的时频聚集性,对提高瞬时频率估计精度具有很大帮助。
 |
| 图 2 不同视角观测结果 Fig. 2 Observation results from different perspectives |
| 图选项 |
对图 2进行采样,并分别借助ESPRIT算法和峰值法提取出雷达1的散射中心径向位置和雷达2的散射中心瞬时频率值,进一步运用3.1节中的散射中心关联匹配准则完成散射中心匹配如图 3所示,表 1为此时提取的各散射中心对应径向位置和瞬时频率值。图 4为采用扩展Hough变换检测图 2(a)中锥顶散射中心径向位置变化曲线所得的曲线振幅、中值二维参数空间,提取得到正弦曲线振幅为0.412 5 m, 相对误差为2.44%。
 |
| 图 3 2部雷达不同时刻采样结果 Fig. 3 Sampling results of two radars at different time |
| 图选项 |
表 1 不同雷达回波散射中心采样结果 Table 1 Sampling results of scattering center in different radar echoes
| 散射点 | 雷达1径向位置/m | 雷达2瞬时频率值/Hz | ||
| 理论值 | 估计值 | 理论值 | 估计值 | |
| D点 | -0.666 5 | -0.653 2 | 426.424 0 | 423.828 1 |
| p点 | 0.638 0 | 0.627 0 | -5.264 7 | -3.906 3 |
| q点 | -0.304 8 | -0.291 4 | -207.947 2 | -205.078 1 |
表选项
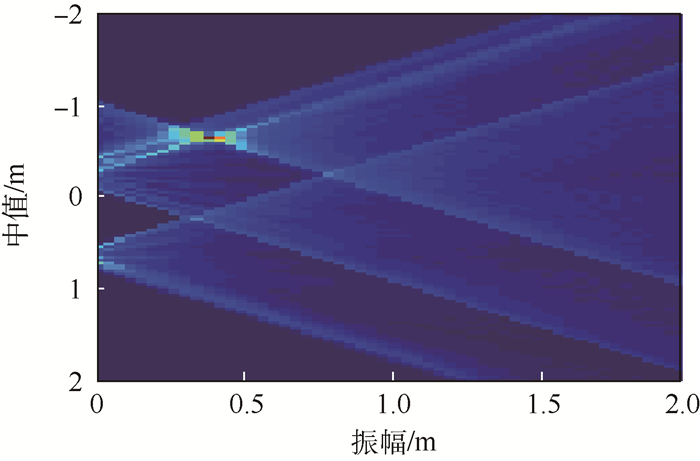 |
| 图 4 扩展Hough变换二维参数空间 Fig. 4 Two-dimensional parametric space of expanded Hough transform |
| 图选项 |
结合表 1,将提取结果代入式(19)中,利用本文3.2节算法可求得目标参数值如表 2所示,其中α1、α2、r、θ的估计精度较高,而h、h1、h2的估计精度相对较低,这主要是由于后三者的估计方法中用到了其他估计参数,产生了误差积累。此外,将本文方法与其他目标参数提取方法进行比较发现,文献[18]通过分布式宽带雷达组网对空间目标的三维进动特征进行提取,提取参数多且性能好,当信噪比为-10 dB时,进动角估计相对误差仅为2.58%,略高于本文的2.38%,但该方法对各雷达时间同步精度和各雷达性能要求很高,在目前装备条件下难以满足; 文献[19]通过泰勒级数展开得到锥体目标底部散射中心回波相位的6阶近似表达式,然后利用各阶系数与目标参数之间的解析关系联立方程组求解目标进动和结构特征,实现难度较大,且易受噪声影响,当信噪比为10 dB时,该算法参数估计精度才刚刚达到85%,明显低于本文参数估计精度,这也充分说明了本文基于宽窄带混合体制雷达网的目标特征提取方法的有效性和可行性。在现有高分辨雷达装备不足的情况下,利用宽带雷达和窄带雷达对目标特征进行联合提取,既能充分发挥窄带雷达的优势,又能保证目标特征提取精度,是一种更为实用的组网方式。
表 2 锥体弹头特征参数估计结果 Table 2 Estimation results of cone-shaped warhead's feature parameters
| 参数 | 理论值 | 估计值 | 相对误差/% |
| α1/(°) | 110 | 111.250 9 | 0.23 |
| α2/(°) | 135 | 134.405 7 | 0.44 |
| θ/(°) | 13 | 13.309 8 | 2.38 |
| r/m | 0.5 | 0.490 7 | 1.86 |
| h1/m | 2 | 1.886 4 | 5.68 |
| h2/m | 0.5 | 0.474 8 | 5.04 |
| h/m | 2.5 | 2.361 2 | 5.55 |
表选项
4.2 算法鲁棒性分析 为了验证本文目标参数提取算法的鲁棒性,分别设置不同曲线参数估计精度对目标特征参数提取精度进行验证。对雷达1而言,由于受雷达发射信号带宽的限制及一维距离像旁瓣的影响,在提取距离像曲线幅度及某一时刻散射点径向位置时必然会引入误差;对于雷达2而言,时频分辨率的不足同样会影响瞬时频率提取精度。而上述误差均会制约方程式(19)的求解精度,因此本文主要分析它们对目标参数估计的影响。为便于分析,定义归一化误差为
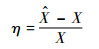 | (23) |
式中:
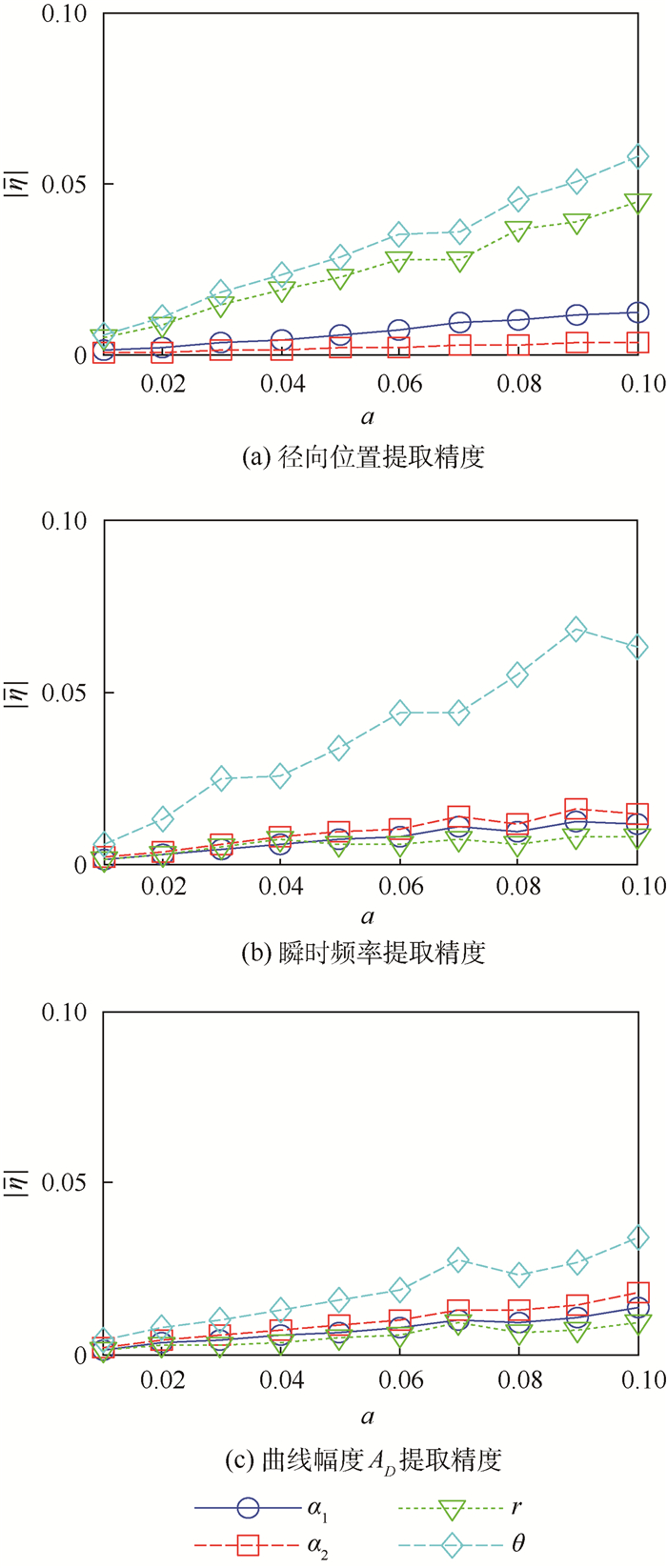 |
| 图 5 不同曲线参数对参数估计的影响 Fig. 5 Influences on parameter estimation caused by different curve parameters |
| 图选项 |
5 结论 本文对基于宽窄带混合体制雷达网的锥体进动目标特征参数联合提取问题展开了研究,经仿真实验验证表明:
1)?在锥体目标3个散射中心同时可见范围内,仅使用一部宽带雷达和一部窄带雷达进行联合观测即可实现对目标进动和结构参数的联合提取。
2)?本文提出的目标参数联合提取算法估计精度较高,在现有高分辨雷达装备不足的情况下,其可以获得比单使用窄带雷达更好的识别性能。
3)?考虑到目前可通过对低分辨雷达加装宽带信号发射装置来实现性能升级,因此下一步将尝试提出基于这种升级版雷达的目标微动参数联合提取算法。
参考文献
| [1] | 贺思三, 周剑雄, 付强. 利用一维距离像序列估计弹道中段目标进动参数[J].信号处理, 2009, 25(6): 925–929.HE S S, ZHOU J X, FU Q. Using HRRP sequence to estimate the precession parameters of midcourse target[J].Signal Processing, 2009, 25(6): 925–929.(in Chinese) |
| [2] | 颜维, 孙文峰, 钱李昌, 等. 基于一维像序列的弹道中段目标进动特征提取[J].空军雷达学院学报, 2011, 25(2): 87–96.YAN W, SUN W F, QIAN L C, et al. Precession feature extraction of ballistic midcourse target based on HRRP sequences[J].Journal of Air Force Radar Academy, 2011, 25(2): 87–96.(in Chinese) |
| [3] | WANG J, LEI P, SUN J P, et al. Spectral characteristics of mixed micro-Doppler time-frequency data sequences in micro-motion and inertial parameter estimation of radar targets[J].IET Radar, Sonar & Navigation, 2014, 8(4): 275–281. |
| [4] | YE C M, XU J, PENG Y N, et al. Key parameter estimation for radar rotating object imaging with multi-aspect observations[J].Science China:Information Sciences, 2010, 53(8): 1641–1652.DOI:10.1007/s11432-010-4028-3 |
| [5] | SMITH G E, WOODBRIDGE K, BAKER C J, et al. Multistatic micro-Doppler radar signatures of personnel targets[J].IET Signal Processing, 2010, 4(3): 224–233.DOI:10.1049/iet-spr.2009.0058 |
| [6] | 贺思三, 赵会宁, 冯存前. 多视角距离像序列弹道目标的进动参数估计[J].信号处理, 2013, 29(8): 1027–1035.HE S S, ZHAO H N, FENG C Q. Precession parameter estimation for ballistic targets based on multi-aspect range-profile sequence[J].Journal of Signal Procession, 2013, 29(8): 1027–1035.(in Chinese) |
| [7] | 艾小锋, 邹小海, 李永桢, 等. 基于时间-距离像分布的锥体目标进动与结构特征提取[J].电子与信息学报, 2011, 33(9): 2083–2088.AI X F, ZOU X H, LI Y Z, et al. Feature extraction of precession and structure of cone-shaped object based on time-HRRP distribution[J].Journal of Electronics & Information Technology, 2011, 33(9): 2083–2088.(in Chinese) |
| [8] | 雷腾, 刘进忙, 杨少春, 等. 基于三站一维距离像融合的弹道目标特征提取方法研究[J].宇航学报, 2012, 33(2): 228–234.LEI T, LIU J M, YANG S C, et al. Study on feature extraction method of ballistic target based on three-station range profiles[J].Journal of Astronautics, 2012, 33(2): 228–234.(in Chinese) |
| [9] | 韩勋, 杜兰, 刘宏伟. 基于窄带雷达组网的空间锥体目标特征提取方法[J].电子与信息学报, 2014, 36(12): 2956–2962.HAN X, DU L, LIU H W. Feature extraction of space cone-shaped target based on narrow-band radar networks[J].Journal of Electronics & Information Technology, 2014, 36(12): 2956–2962.(in Chinese) |
| [10] | 冯存前, 李靖卿, 贺思三, 等. 组网雷达中弹道目标微动特征提取与识别综述[J].雷达学报, 2015, 4(6): 609–620.FENG C Q, LI J Q, HE S S, et al. Micro-Doppler feature extraction and recognition based on netted radar for ballistic targets[J].Journal of Radars, 2015, 4(6): 609–620.(in Chinese) |
| [11] | 张群, 罗迎. 雷达目标微多普勒效应[M].北京: 国防工业出版社, 2013: 22-81.ZHANG Q, LUO Y. The micro-Doppler effect of radar targets[M].Beijing: National Defence Industry Press, 2013: 22-81.(in Chinese) |
| [12] | 李东伟, 罗迎, 张群, 等. 组网雷达中旋转目标微多普勒效应分析及三维微动特征提取[J].空军工程大学学报, 2012, 13(3): 45–49.LI D W, LUO Y, ZHANG Q, et al. Research on micro-Doppler effect and extraction of three-dimensional micro-motion features of rotating targets in netted radar[J].Journal of Air Force Engineering University, 2012, 13(3): 45–49.(in Chinese) |
| [13] | LINDE G.Use of wide-band waveforms for target recognition with surveillance radar[C]//Proceedings of IEEE Radar Conference.Piscataway, NJ:IEEE Press, 2000:128-133. |
| [14] | 赵双, 鲁卫红, 冯存前, 等. 多视角微多普勒融合的进动目标特征提取[J].信号处理, 2016, 32(3): 296–303.ZHAO S, LU W H, FENG C Q, et al. Feature extraction of precession targets based on multi-aspect micro-Doppler fusion[J].Signal Processing, 2016, 32(3): 296–303.(in Chinese) |
| [15] | 关永胜, 左群声, 刘宏伟, 等. 空间进动目标微动参数估计方法[J].电子与信息学报, 2011, 33(10): 2427–2432.GUAN Y S, ZUO Q S, LIU H W, et al. Micro-motion parameters estimation of space precession targets[J].Journal of Astronautics, 2011, 33(10): 2427–2432.(in Chinese) |
| [16] | 张贤达. 现代信号处理[M].北京: 清华大学出版社, 2002: 135-140.ZHANG X D. Modern signal processing[M].Beijing: Tsinghua University Press, 2002: 135-140.(in Chinese) |
| [17] | 肖立, 周剑雄, 何峻, 等. 弹道中段目标进动周期估计的改进自相关法[J].航空学报, 2010, 31(4): 812–818.XIAO L, ZHOU J X, HE J, et al. Improved autocorrelation method for precession period estimation of ballistic target in midcourse[J].Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 812–818.(in Chinese) |
| [18] | LUO Y, YUAN N, ZHU F, et al. Three-dimensional precession feature extraction of space targets[J].IEEE Transactions on Aerospace and Electronic Systems, 2014, 50(2): 1313–1329.DOI:10.1109/TAES.2014.110545 |
| [19] | 韩勋, 杜兰, 刘宏伟. 窄带雷达观测下的锥体目标参数估计方法[J].西安电子科技大学学报, 2015, 42(6): 43–48.HAN X, DU L, LIU H W. Parameter estimation method for cone-shaped target under narrow-band radar observation[J].Journal of Xidian University, 2015, 42(6): 43–48.(in Chinese) |
