删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于信息理论的网络文本组合聚类*

本站小编 Free考研考试/2021-12-25
文本聚类在数据挖掘、信息检索和社交媒体挖掘等领域有着广泛应用，其旨在将文档集划分成若干有意义的类别，这是许多实际应用中的关键环节，如对搜索引擎返回的海量结果进行分类浏览[1]，浏览大型文档集合[2]，以及从用户产生内容中发现未知的观点[3]等。
尽管文本聚类被广泛研究，但其高维性和稀疏性仍是难以解决的问题。随着近几年社会媒体的快速发展，文本数量出现爆炸式增长，同时文本信息更加短促，这些特征加剧了文本聚类的难度。特征操作[4-5]、距离选择[6]及子空间聚类[7]等传统方法在聚类的精度和效率上很难做到均衡。
本文针对文本聚类提出了一种分解-组合算法框架——DIAS。首先通过采用简单随机特征抽样算法分解高维文本，得到多样化的结构知识，同时又规避了大量噪声特征的产生。然后基于信息理论的一致性聚类(Information-theoretic Consensus Clustering，ICC)将多视角基础聚类知识组合起来，得到高质量的一致性划分。
通过在8个真实文本数据集上的实验，证明了DIAS算法相较于其他主流算法在精度上的优势。DIAS算法中的简单随机特征抽样在处理高稀疏文本时更为高效，一个很小的抽样比例(10%)在绝大多数实验数据上即能得到令人满意的效果。此外，实验证明DIAS算法在处理弱基础聚类上具有显著优势，其关键在于充分利用了基础聚类的多样性。由于DIAS算法在分布式计算上的天生优势，其有希望成为大规模文本聚类的主流算法。
1 DIAS算法基本框架 图 1阐述了DIAS算法的3个主要阶段：
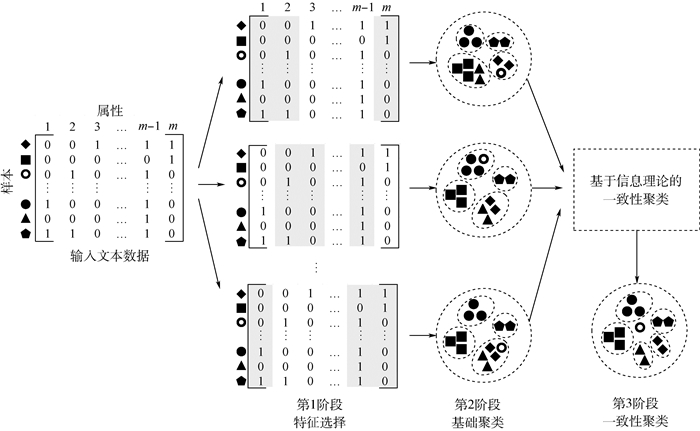图 1 DIAS算法框架 Fig. 1 Framework of DIAS algorithm
图选项




1)?第1阶段进行特征子集选择，将高维文本数据按列划分成小的数据集。划分方法应当快速高效，同时保证数据子集的多样性。实验结果表明，如果采用简单随机特征抽样策略，即使采样率低至10%，DIAS算法的效果仍然不错。详情参见实验部分。
2)?第2阶段针对每个数据子集生成一个基础聚类。尽管理论上可采用任何聚类算法，本文推荐采用K-均值算法，可充分利用其高效性和鲁棒性。
3)?第3阶段是DIAS的关键，即对基础聚类结果进行融合。一致性聚类算法应当是高效和健壮的，并能从大量的弱基础聚类中进行学习。为满足上述要求，本文提出ICC算法。详情参见第2节。
研究发现，DIAS算法在处理海量、高维文本时有天然优势：首先，通过特征选择，DIAS算法既规避了噪声特征，又从文本中得到了多样化的聚类信息，从而降低维度灾难的影响；其次，针对数据子集的聚类适于并行或分布计算，这对于大数据计算是至关重要的。由于DIAS算法的第1、2阶段较为简单，下面主要围绕第3阶段的ICC算法展开研究。
2 基于信息理论的一致性聚类 令D表示文本数据集合，D=n。假设采用硬聚类划分将D划分成K个数据子集，用集合C={Ck|k=1, 2，…, K}表示，Ck∩Ck′=?，?k≠k′，∪k=1KCk=D。令向量π=(Lπ(d1), Lπ(d2), …, Lπ(dn))T，Lπ将文本dl映射到标签集合{1, 2, …, K}中，1≤l≤n。假设有r个基础聚类Π={π1, π2, …, πr}。目标是找到一致性聚类算法以求解下述问题：
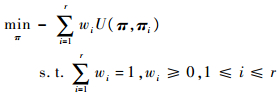(1)

式中：U：Z++n×Z++n|→R为效用函数；w=(w1, w2, …, wr)T为用户给定的基础聚类权重向量。本文默认w1=w2=…=wr=1，主要出于两点考虑：①充分利用各基础聚类结果的多样性(参见第3.2.2节实验部分)；②在一致性聚类前无从得知各基础聚类结果的准确性。若要自动设置w，一种思路是将其L2范式作为约束加入目标函数中。笔者将在未来工作中考虑这个问题。
式(1)是一个非凸优化问题，其核心在于选择一个合适的效用函数U，以高效地得到一个较好的一致性聚类结果。
2.1 基于信息理论的效用函数 DIAS算法的核心是将基础聚类融合成一个聚类结果，这就要求一致性聚类算法必须具有高效性和健壮性。因此本文提出一个基于信息理论的效用函数，并据此构建高效的ICC算法。
根据式(1)，效用函数定义在2个划分π和πi上，因此可视为2个划分的相似度的一个测度。采用表 1的可能性矩阵来辅助效用函数定义。如表 1所示，π和πi分别有K和Ki个簇。nkj(i)表示πi中的簇Cj(i)与π中的簇Ck共同包含的样本数目，则

表 1 可能性矩阵 Table 1 Contingency matrix
簇C1(i)C2(i)…C(i)Ki∑
C1n11(i)n12(i)…n(i)1Kin1+(i)
C2n21(i)n22(i)…n(i)2Kin2+(i)
CKnK1(i)nK2(i)…n(i)KKinK+(i)
∑n+1(i)n+2(i)…n(i)+Kin


表选项






令pkj(i)=nkj(i)/n，pk+(i)=nk+(i)/n，p+j(i)=n+j(i)/n，可得标准化后的可能性矩阵，并据此定义效用函数。令离散分布Pk(i)=(pk1(i)/pk+, pk2(i)/pk+, …, pkKi(i)/pk+), ?k, P(i)=(p+1(i), p+2(i), …, p+j(i), …p(i)+Ki)，由此导出定义1。
定义1????如果函数UH满足式(2)定义，那么称其为基于信息理论的效用函数。
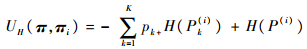(2)

式中：H为香农熵。
因H是凹函数，根据詹森不等式易得

因此，UH≥0。UH越高，效用值越高，说明2种划分的相似度也越高。应注意，UH是非对称的，即如果π≠πi，则UH(π, πi)≠UH(πi, π)。
选择UH作为式(1)中的效用函数的主要原因是：可将关于π的优化问题转化为一个基于信息理论的K-均值聚类问题，这样就能保证高效性和健壮性。为了更好理解转化过程，首先介绍二元矩阵的概念，用于汇总所有基础聚类结果。定义二元矩阵X=(xl, x2, …, xn)T，其中：
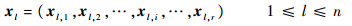(3)

(4)

(5)

很明显, ‖xl, i‖=1，?l, i。
根据UH和X的定义，有如下重要定理。
定理1????假设π是D上K个簇C1, C2, …, CK的一个一致性划分，给定r个基础聚类π1, π2, …, πr和权重向量w，则
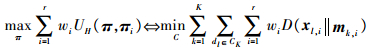(6)

式中：
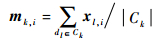(7)

D(xl, i‖mk, i)为从xl, i到mk, i的KL-divergence。
证明????易证

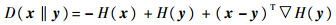因此有

由式(7)易知，，故(β)=0，

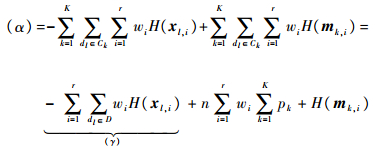易知(γ)为常数，因此有
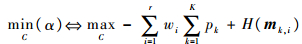(8)

因为

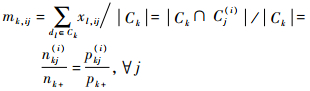得出

如果用Pk(i)代替式(8)中的mk, i，并在等式右侧加入常量，可得

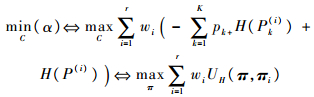证毕
定理1表明，借助从基础聚类中得到的二元矩阵，ICC算法可转换为基于信息理论的K-均值聚类。后者由于具有高效性、健壮性和广泛适用性等优点，因而被公认是非常优秀的算法。事实上，近年来许多文献都将信息理论应用到文本聚类上，如Gokcay和Principe[8]介绍了valley seeking聚类算法，并在其中采用信息论测度估计了数据划分的代价；Dhillon等[9]根据互信息提出了联合聚类算法来进行文本聚类；Cao等[6]最近在基于信息理论的K-均值(IK-means)聚类算法的基础提出了SAIL算法以处理零值困境。
2.2 DIAS算法详解 算法1????DIAS
输入：文本数据D; 簇个数K; 随机特征抽样率rs; 基础聚类权重w。输出：一致性聚类结果π*。
1)?以设定的随机特征抽样率rs从D中抽取数据子集Di，1≤i≤r。
2)?利用K-均值算法对Di进行基础聚类得到πi，1≤i≤r。
3)?从Π={π1, π2, …, πr}中构建二元矩阵X。
4)?调用ICC以计算π*。
5)?返回π*。
算法2????ICC
输入：二元矩阵X; 簇个数K; 权值w。输出：一致性聚类结果π*。
1)?根据X和w的值得到加权二元矩阵X′。
2)?在X′上执行基于信息理论的K-均值算法得到π*。
3)?返回π*。
算法要点如下：
1)?算法1第1行中叙述DIAS算法数据集是通过随机特征选择方案生成的。这不仅是算法高效的原因，更重要的是从特征中寻求多样信息，这对得到多样化基础聚类非常关键。本文倾向于取较小的rs值，比如10%。
2)?本文在DIAS算法中采用K-均值算法进行基础聚类。绝大多数情况下，K-均值聚类是高效、稳定的，能够得到相当好的划分效果。应该避免采用复杂的算法，因为这会严重影响效率，而对一致性聚类的精度贡献往往不大。
3)? ICC算法采用K-均值聚类是非常高效的。其时间复杂度为O(InrK)，I为收敛时迭代的次数(通常不超过20)，因为二元矩阵的特点，数据维度为r。r个基础聚类的时间复杂度为O(rIndrsK)，d为一篇文档包含的平均词数。可以通过采用并行计算以及设定小的rs值来降低复杂度。值得一提的是，ICC算法的空间复杂度因为数据维度由d减为r，从而得到大幅降低；这一点同样适用于基础聚类，因为基础聚类的数据维度也由d减为drs。
3 实验结果 本节检验DIAS算法的效果。主要关注：①影响DIAS算法的主要因素；②DIAS算法相较于其他主流聚类算法的优越性；③ICC算法对主流一致性聚类算法的优势。
3.1 实验设计
3.1.1 实验数据 实验采用8个已经标注的真实文本数据集，它们的主要特征如表 2所示。表中：变异系数(coefficient of variation)用来度量真实簇中样本容量不均衡性；密度为文本数据中非零值比例，用来表征文本的稀疏程度。表格中前5个数据集来源于CLUTO[10]，RCV和News20[11]是有名的标准文本集[12]，Baike[13]则来源于百度百科。
表 2 实验数据集 Table 2 Experimental data sets
数据集样本量属性个数类别数密度最小类样本量最大类样本量变异系数
cacmcisi4 66314 40920.001 2146 03 2030.53
classic7 09441 68140.000 81 0333 2030.55
mm2 521126 37320.001 51 1331 3880.14
reviews4 069126 37350.001 51371 3880.64
sports8 580126 37370.001 01223 4121.02
RCV9 62529 99240.002 52 0222 6380.18
News2018 84626 214200.005 26289990.10
Baike9 809287 986200.002 1271 6011.14


表选项







3.1.2 实验工具 DIAS算法基于MATLAB平台编程实现，参数默认值如下：ICC算法的权值设为等值；随机特征抽样率rs=10%；对每个数据集采用MATLAB的kmeans函数(相似度采用cosine)运行100遍得到r=100个基础聚类；聚类数设置为真实簇个数；运行ICC算法10遍取最好的结果。参与比较的算法包括基于信息理论的K-均值算法、基于互联矩阵的一致性聚类方法(HCC)，均在MATLAB平台实现。为了全面对比，还采用了2个有名的工具：CLUTO[14]和基于图的一致性聚类工具(GCC)[15]。这些工具的参数在实验中根据不同数据集进行优化适配。

3.1.3 聚类有效性评价指标 由于所有数据集的簇标签已知，本文采用正向外部效度(Normalized Mutual Information，NMI, 记为NMI([0, 1])度量聚类的有效性[15]。NMI基于信息理论中的共有信息概念，目前已被广泛应用于聚类分析的外部评价。
3.2 DIAS算法的影响因素分析
3.2.1 质量因素分析 直观来看，基础聚类的好坏应对ICC算法的成功非常重要。问题在于需要多少个高质量的基础聚类才能得到一个好的一致性聚类。DIAS算法采用的简单随机特征抽样算法很难得到大量好的基础聚类。这一推测可以从基础聚类的质量分布中得到验证。从图 2可以看出，无论是cacmcisi还是Baike，大部分基础聚类的质量都比较差。关键在于ICC算法能否利用少量相对高质量的基础聚类得到较好的一致性划分。
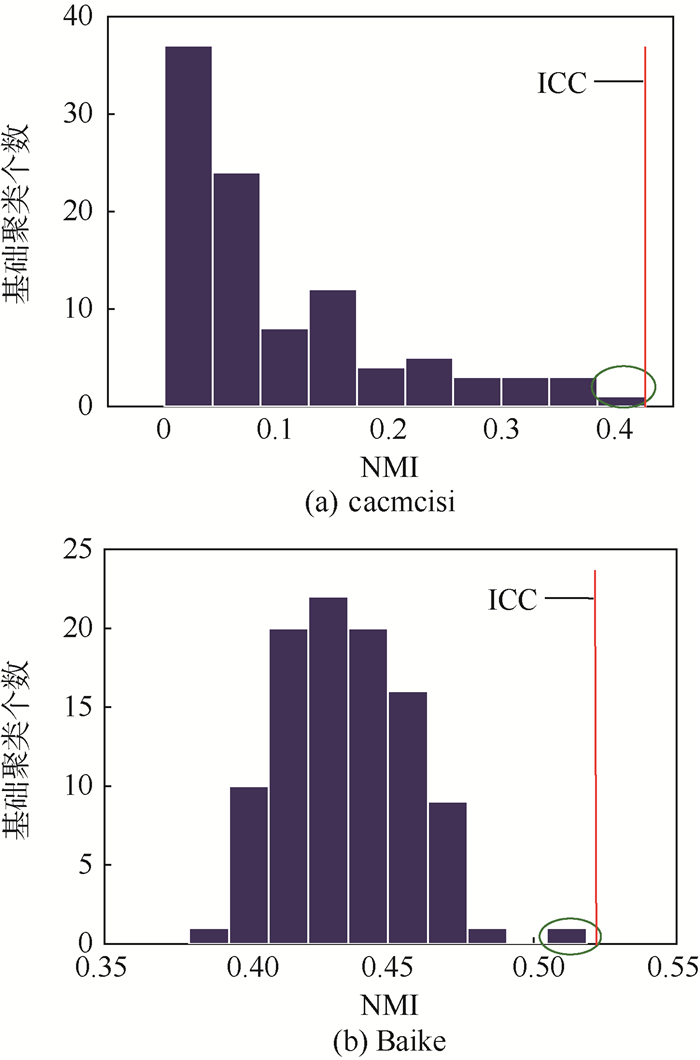图 2 cacmcisi和Baike基础聚类质量 Fig. 2 Quality of basic partitionings of cacmcisi and Baike
图选项




通过实验发现，ICC算法能够利用少量相对高质量的基础聚类得到较好的一致性划分。图 2中右侧竖线表明，ICC算法得到的一致性划分的质量高于基础聚类的平均水平，这证明ICC算法能够从少量相对较高质量的基础聚类提取出簇结构的重要信息。进一步，对cacmcisi数据进行敏感性分析，即按照质量从好到坏的顺序依次移除基础聚类，观测ICC算法效果的变化。如图 3所示，当移除前20的基础聚类时，ICC算法效果出现急剧下降。而按照从坏到好移除基础聚类时，其性能下降要缓和得多。这充分表明ICC算法可以从少数较高质量的基础聚类中学习，以得到较好的一致性划分结果。
图 3 cacmcisi上的逐步删除策略 Fig. 3 Stepwise deletion strategy on cacmcisi
图选项





3.2.2 多样性因素分析 通常情况下，DIAS算法中随机特征抽样算法只能产生弱基础聚类，较好的几乎没有。那么，ICC算法能否从大量弱基础聚类中进行学习以得到较好结果就显得尤为重要。
图 4所示为sports和RCV中的基础聚类结果，所有NMI均小于0.4。通过实验发现，ICC算法能够从这些弱基础聚类中得到较好的一致性划分。图 4右侧垂直线表明由ICC算法得到的一致性划分远好于最好的基础聚类。这说明尽管基础聚类的质量均较差，ICC算法依然可以充分利用其聚类结果的多样性来生成较好的划分。该结论也适用于classic、mm、reviews和News20等数据集，如图 5所示。以上结果表明，基础聚类的多样性是ICC算法成功的关键因素。
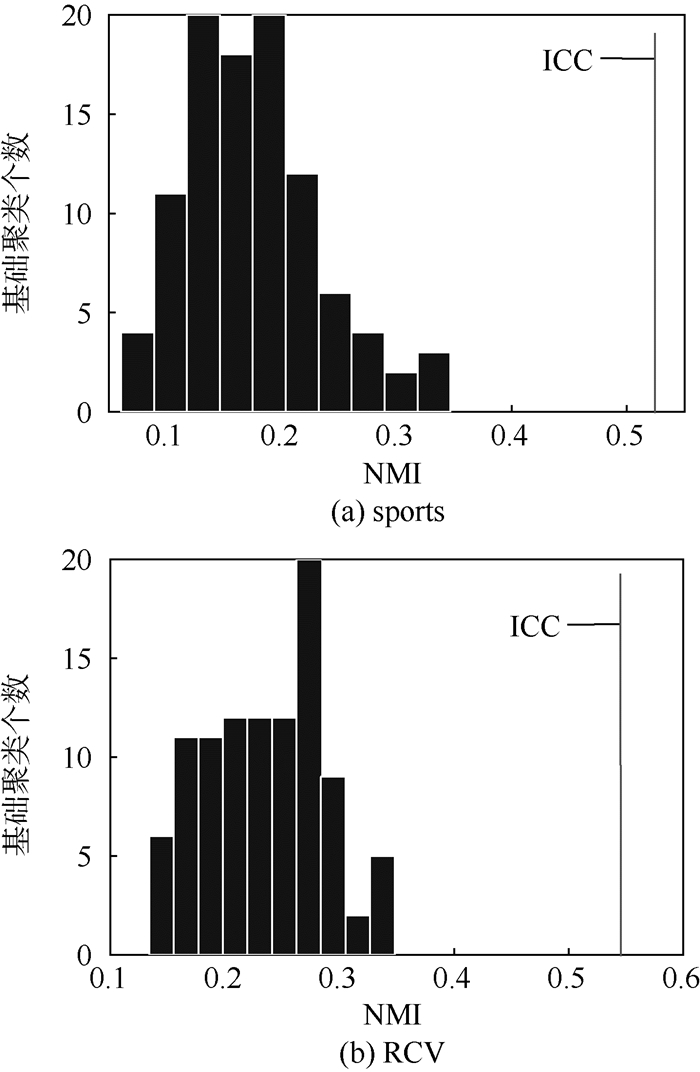图 4 sports和RCV基础聚类质量 Fig. 4 Quality of basic partitionings of sports and RCV
图选项




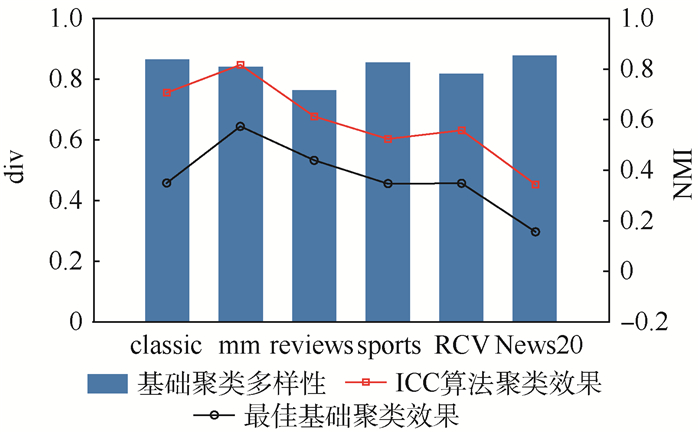图 5 基础聚类的多样性 Fig. 5 Diversity of basic partitionings
图选项




为了更好地理解上述结论，接下来直接度量基础聚类的多样性。令sij=NMI(πi, πj)表示基础聚类πi和πj的相似度。定义关联加权矩阵Mw=[wiwj](1≤i, j≤r)和加权相似度矩阵Ms=[wiwjsij]。F表示矩阵的Frobenius范数。则基础聚类的多样性测度可定义为
(9)

式中：


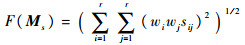div越大，表明基础聚类的多样性越好。借助div，可以研究基础聚类的多样性和一致性划分的质量之间的关系。
图 5展示的是除cacmcisi和Baike之外的所有数据集的实验结果，其中采用每个数据集中最好的基础聚类的质量作为比较研究的基准。如图 5所示，借助基础聚类的多样性，所有数据集的聚类结果都得到了提升。
上述结果揭示了多样性因素对ICC算法的重要性，即在大部分情况下多样性因素相比于质量因素，对文本的一致性聚类影响更大。这尤其适合处理高稀疏性文本，因为文本中往往会充斥着大量弱相关项和无关项，很难期望能从文本数据中得到足够多的高质量基础聚类。

3.2.3 基础聚类的生成策略的影响分析 基础聚类的生成策略对DIAS算法的影响主要归结为以下2个问题：①默认的10%的特征抽样率是否太低；②多少基础聚类是合适的。下面对上述问题进行实验分析。
表 3所示为通过设置DIAS算法中不同的抽样比例来观测聚类性能的变化。如图 6所示，尽管不同数据集要求的最优抽样率均不相同，但10%的策略在除了News20以外的所有数据集上均可得到满意效果。这主要归功于文本中存在大量的噪声特征，而低抽样率恰好可以忽略这些噪声特征。如果更进一步考虑效率和空间的问题，则10%策略在处理大文本数据时更具有优势。比如，当特征抽样率rs≥50%时，拥有32 GB RAM的计算机也会出现内存溢出的情况，如表 3“N/A”所示。
表 3 特征抽样率的敏感性分析 Table 3 sensitivity analysis of feature sampling rate
数据集特征抽样率/%
1030507090
cacmcisi0.423 80.159 90.153 50.160 90.165 9
classic0.708 40.502 10.552 50.523 90.454 5
mm0.816 70.842 60.814 20.777 00.779 3
reviews0.612 90.618 20.618 90.603 60.603 0
sports0.523 80.518 00.417 40.459 70.498 9
RCV0.558 00.566 70.573 30.580 10.500 6
News200.343 80.542 40.573 20.596 80.589 4
Baike0.522 20.540 9N/AN/AN/A


表选项






为研究基础聚类个数的影响，对每个数据集中已生成的100个基础聚类进行随机抽样，以不同的特征抽样率rs得到不同的基础聚类子集，在此基础上采用ICC算法进行一致性聚类。重复实验100次，观测不同rs值下聚类性能的变化。图 6显示了在数据集mm和reviews上的结果。显然，随着rs值越趋近于100时，ICC算法能产生更高质量和更稳定的结果，但其实当rs=50时的结果已经很令人满意了。
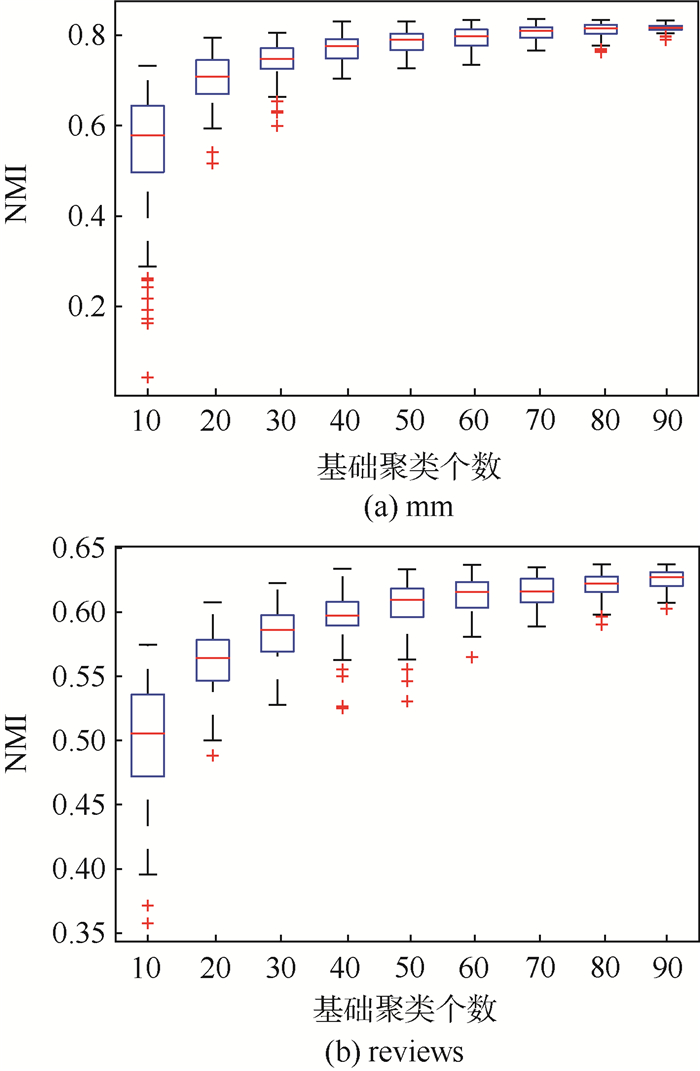图 6 基础聚类数量的影响 Fig. 6 Impact of number of basic partitionings
图选项




3.3 DIAS算法与单聚类算法的比较 将DIAS算法与被广泛认可的文本聚类算法进行比较，如基于余弦距离的K-均值(采用CLUTO)和基于信息理论的K-均值(采用IK-means)。特征处理方法TD-IDF也加入对比实验。
表 4列示了3种算法的聚类结果，其中表现最好的用粗体标示，次好的用下划线标示，内存溢出错误用N/A标示。采用TD-IDF加权的结果用idf表示，没有采用的则用none表示。
表 4 聚类质量的对比 Table 4 Comparison of clustering quality
数据集ICCCLUTOIK-means
noneidfnoneidfnoneidf
cacmcisi0.428 30.488 60.165 00.220 30.460 30.608 1
classic0.706 40.720 90.450 80.547 10.506 40.381 0
mm0.816 70.716 10.781 70.000 00.136 10.111 5
reviews0.612 90.605 30.570 60.529 80.321 80.282 4
sports0.523 80.674 20.472 20.665 40.204 40.124 5
RCV0.558 00.592 70.586 40.594 90.463 70.025 7
News200.343 80.490 90.164 110.058 70.068 5
Baike0.522 20.551 70.501 30.544 1N/AN/A


表选项






表 4所示结果对比明显。首先，采用TF-IDF的方法除了IK-means外，均能有效地提高文本聚类效果。例如，采用TF-IDF的DIAS算法相较于没有TF-IDF的，在8个数据集中的6个能表现得更好。相似情况也发生在CLUTO上。其次，DIAS算法无论在有或没有TF-IDF的情况下，都比广泛使用的CLUTO和基于信息理论的IK-means表现得更好。基于TF-IDF的DIAS算法是所有算法中性能最好的，其在3个数据集上表现最好，在4个数据集上表现次好。
综上所述，DIAS算法与公认较好的文本聚类算法相比，仍具有较强的竞争力。而TF-IDF确实能够提高DIAS的聚类效果。
3.4 ICC算法与其他集成方法的比较 ICC算法是DIAS算法中最重要的一环，但它不是一致性聚类的唯一方法。在文献中还有其他一些诸如GCC[16]和HCC[17]的一致性聚类算法。GCC包括CSPA、HGPA和MCLA 3种不同的算法，本文选择性能最好的算法作比较。HCC算法是一种以互联矩阵为基础、对所有基础聚类进行信息集成的信息凝聚层次聚类算法。本文以默认值运行GCC算法和HCC算法，并将它们的聚类结果与ICC算法进行比较。
如图 7所示，ICC算法相较于其他2种算法具有明显的优势，在cacmcisi、classic、sports和News20这4个数据集上尤为突出。值得注意的是，HCC算法在classic、sports和RCV上表现较差。这表明HCC算法在实际运用中的健壮性不够好，并且其复杂度达到了Ο(n3)，进一步阻碍了其在大规模文本数据集上的应用。相比于HCC算法，GCC算法表现得更为稳定和快速，但和ICC算法相比还是有较大的差距。
图 7 不同一致性聚类算法比较 Fig. 7 Comparison of different consensus clustering algorithms
图选项




4 相关工作 1)?文本聚类方面的相关工作
特征转换和特征选择是文本聚类中2个主要技术[18]。特征转换是将原始高维空间映射到低维空间进行分析处理，方法包括主成分分析[4-5]、隐性语义索引[19]、独立成分分析[20]和随机映射[21]。特征选择也称为子空间聚类，多采用自底而上或自顶而下的搜索策略来发现子集中存在的相关关系。自底而上方法是根据密度的单调性，将邻近区域内密度超过阈值的子空间继续进行聚类，而对原始子空间进行修剪，其得到的子空间集往往涵盖了各式各样的簇类[22-24]，但聚类效果与密度阈值参数紧密相关，而该参数往往又难以确定。自顶而下方法通过属性选择和评价的多次迭代将聚类和子空间选择结合起来[25-27]，其所需要的迭代开销大，耗时长，效率较低。更多细节可以参考文献[7]。
2)?一致性聚类方面的相关工作
一致性聚类通常都会转化成组合优化问题，通过设置一个全局目标函数，采用启发式算法寻找近似解。针对不同的目标函数提出了许多对应的解法，诸如EM算法、非负矩阵分解、核聚类算法和模拟退火等。在这些方法中，最引人注目的当属文献[24]提出的基于二次熵的K-均值聚类算法。在此基础上，文献[7]给出了基于K-均值一致性聚类的算法框架。还有一些方法并没有显式的目标函数。典型算法包括基于图的方法、基于互联矩阵的方法、重标注和投票方法、局部自适应聚类算法以及基于遗传算法的方法等，详情参考文献[28]。文献[29]对一致性聚类给出了综述。
5 结论 本文针对文本聚类问题提出了DIAS算法框架，并对其中核心的基于信息理论的组合聚类算法进行了理论和实验研究，得到如下结论：
1)?通过采用简单随机特征抽样产生基础聚类，DIAS算法可以得到多样化的结构知识并同时减少文本的高维稀疏性带来的噪声特征的影响。
2)?基于信息理论的组合聚类可转化成K-均值聚类问题，大大提高组合学习的效率。
3)?大量数据实验表明，DIAS算法可以从弱基础聚类中学习得到高质量的一致性划分，并能很好地适应分布式计算要求，有望成为未来文本大数据聚类的主流算法之一。

参考文献
[1] ZAMIR O, ETZIONI O, MADANI O, et al.Fast and intuitive clustering of web documents[C]//Proceedings of the 3rd International Conference on Knowledge Discovery and Data Mininge.New York:AIAA, 1997:287-290.
[2] CUTTING D R, KARGER D R, PEDERSEN J O, et al.Scatter/gather:A cluster-based approach to browsing large document collections[C]//Proceedings of 15th ACM International Conference on Research and Development in Information Retrieval.New York:ACM, 1992:318-329.
[3] CHA M, KWAK H, RODRIGUEZ P, et al.I tube, you tube, everybody tubes:Analyzing the world's largest user generated content video system[C]//Proceedings of the 7th ACM SIGCOMM Conference on Internet Measurement.New York:ACM, 2007:1-14.
[4] DUDA R O, HART P E, STORK D G. Pattern classification[M].2nd edNew York: Wiley-Interscience, 2000: 14-15.
[5] JOLLIFFE I T. Principal component analysis[M].2nd edNew York: Springer, 2002: 8-21.
[6] CAO J, WU Z, WU J, et al. Sail:Summation-based incremental learning for information-theoretic text clustering[J].IEEE Transactions on Cybernetics, 2013, 43(2): 570–584.DOI:10.1109/TSMCB.2012.2212430
[7] WU J, LIU H, XIONG H, et al. K-means-based consensus clustering:A unified view[J].IEEE Transactions on Knowledge and Data Engineering, 2015, 27(1): 155–169.DOI:10.1109/TKDE.2014.2316512
[8] GOKCAY E, PRINCIPE J C. Information theoretic clustering[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(2): 158–171.DOI:10.1109/34.982897
[9] DHILLON I, MALLELA S, MODHA D.Information-theoretic co-clustering[C]//Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM, 2003:89-93.
[10] Digitical Technology Center (DTC).CLUTO-Software for clustering high-dimensional datasets[DS/OL].(2006-10-18)[2015-01-30].http://glaros.dtc.umn.edu/gkhome/cluto/cluto/overview.
[11] CAI D.The 20 newgroups data set[DS/OL].(2008-01-14)[2015-01-30].http://www.cad.zju.edu.cn/home/dengcai/Data/TextData.html.
[12] CAI D, WANG X, HE X.Probabilistic dyadic data analysis with local and global consistency[C]//Proceedings of the 26th International Conference on Machine Learning (ICML'09).New York:ACM, 2009:105-112.
[13] LI R L.English text segmentation corpus[DS/OL].(2011-10-30)[2015-1-30].http://www.datatang.com/data/11968.
[14] ZHAO Y, KARYPIS G. Empirical and theoretical comparisons of selected criterion functions for document clustering[J].Machine Learning, 2004, 55(3): 311–331.DOI:10.1023/B:MACH.0000027785.44527.d6
[15] STREHL A, GHOSH J. Cluster ensembles-A knowledge reuse framework for combining partitions[J].Journal of Machine Learning Research, 2003, 3: 583–617.
[16] ZHONG S, GHOSH J. Generative model-based document clustering:A comparative study[J].Knowledge and Information Systems, 2005, 8(3): 374–384.DOI:10.1007/s10115-004-0194-1
[17] FRED A L N, JAIN A K. Combining multiple clusterings using evidence accumulation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(6): 835–850.DOI:10.1109/TPAMI.2005.113
[18] AGGARWAL C C, ZHAI C. Mining text data[M].New York: Springer, 2012: 81-86.
[19] BERRY M W, DUMAIS S T, O'BRIEN G W. Using linear algebra for intelligent information retrieval[J].SIAM Review, 1995, 37(4): 573–595.DOI:10.1137/1037127
[20] HYVARINEN A, OJA E. Independent component analysis:Algorithms and applications[J].Neural Networks, 2000, 13(4-5): 411–430.DOI:10.1016/S0893-6080(00)00026-5
[21] BOUTSIDIS C, ZOUZIAS A, DRINEAS P.Random projections for K-means clustering[C]//Advances in Neural Information Processing Systems.Cambridge:MIT Press, 2010:298-306.
[22] AGRAWAL R, GEHRKE J, GUNOPULOS D, et al.Automatic subspace clustering of high dimensional data for data mining applications[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data.New York:ACM, 1998:94-105.
[23] CHENG C H, FU A W, ZHANG Y.Entropy-based subspace clustering for mining numerical data[C]//Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM, 1999:84-93.
[24] GOIL S, NAGESH H, CHOUDHARY A.MAFIA:Efficient and scalable subspace clustering for very large data sets[C]//Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM, 1999:443-452.
[25] AGGARWAL C C, YU P S.Finding generalized projected clusters in high dimensional spaces[C]//Proceedings of the ACM SIGMOD International Conference on Management of Data.New York:ACM, 2000:70-81.
[26] FRIEDMAN J H, MEULMAN J J. Clustering objects on subsets of attributes[J].Journal of the Royal Statistical Society:Series B-Statistical Methodology, 2004, 66(4): 815–849.DOI:10.1111/rssb.2004.66.issue-4
[27] WOO K G, LEE J H, KIM M H, et al. FINDIT:A fast and intelligent subspace clustering algorithm using dimension voting[J].Information and Software Technology, 2004, 46(4): 255–271.DOI:10.1016/j.infsof.2003.07.003
[28] LI T, DING C, JORDAN M I.Solving consensus and semi-supervised clustering problems using nonnegative matrix factorization[C]//Proceedings of 7th IEEE International Conference on Data Mining.Piscataway, NJ:IEEE Press, 2007:577-582.
[29] 杨燕, 靳蕃, KAMELM. 聚类组合研究的新进展[J].计算机工程与应用, 2008, 44(11): 142–144.YANG Y, JIN F, KAMEL M. Latest development of clustering ensemble[J].Computer Engineering and Applications, 2008, 44(11): 142–144.(in Chinese)


相关话题/基础 数据 信息 实验 质量
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 基于机器学习的管材数控弯曲质量预测*
    管材数控(NumericalControlled，NC)弯曲技术能够实现金属管材塑性弯曲成形过程高精度、高效率、高技术化和对产品轻量化的要求，广泛应用于航空航天、汽车和船舶等工业生产中。数控弯曲过程在材料性能、模具接触和工艺参数等因素的共同作用下，构成了一个复杂的非线性系统，同时产生回弹、起皱和减薄 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于粗糙集-信息熵的辐射源威胁评估方法*
    辐射源威胁评估是电子对抗领域的一个重要研究课题，干扰资源分配、干扰辅助决策都以等级判定作为基础[1]，对于战机完成作战任务与提高生存能力至关重要。机载电子对抗装备可以侦察到5种脉冲描述字(PDW)，威胁评估基于此进行，因而可将辐射源威胁评估作为多属性决策问题。目前机载告警设备的威胁评估方式只是与预先 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 高速切削高温合金GH4169数值模拟与实验*
    镍基高温合金GH4169因其具有高屈服应力和抗疲劳等优良性能，常用于制造燃气轮机的轮盘、航空发动机与叶片等耐热零部件，但由于它同时具有导热系数低、弹性模量小等特点，是典型的难加工材料。对于GH4169这种难加工材料，采用传统的切削加工，效率极低，刀具寿命短，必须建立适合高效切削技术的新理论和研究方法 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 不完备信息条件下的并发故障诊断方法*
    随着技术的发展，现代设备结构日趋复杂，逐渐向大型化、自动化等方向发展，各部件之间联系更加紧密，这就为复杂装备的故障诊断带来了新的挑战。在诊断知识获取过程中，由于被测对象结构复杂、诊断系统采集的信息缺失等原因，致使所得到的故障信息存在不完备的情况；同时，在设备实际运行过程中，常常伴随有并发故障的发生。 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于优化字典学习算法的压缩数据收集*
    无线传感器网络(WirelessSensorNetworks,WSNs)由多个具有无线通信能力的传感器节点组成,部署在特定的监测环境中,对物理环境信息的收集是其主要应用之一[1]。典型的WSNs数据收集过程是:传感器节点周期性地感知物理环境信息,并将采集到的传感器数据通过多跳转发的方式汇聚到基站节点 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 蜻蜓爬升过程飞行特征实验研究*
    微型飞行器(MicroAirVehicle,MAV)的发展和应用使昆虫飞行机理的研究越来越受到相关人员的关注[1]。昆虫在不同飞行状态下身体和翅膀运动参数的准确描述和飞行特征的探究为昆虫飞行机理研究和仿生流体力学的探索提供重要的数据依据。在众多飞行能力出众的昆虫界,蜻蜓又被称为“飞行之王”,有着其独 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 信息缺失的航空发动机传感器数据重构*
    航空发动机是航空飞行器的重要系统,航空发动机状态监视是健康管理的第一步,根据状态监视结果进行故障诊断、故障隔离和剩余寿命周期预测等。状态监视离不开状态参数数据,目前主要使用的有气路数据、滑油数据和孔探数据等,将这些信息融合能够进一步提高健康管理效率和质量。随着传感器技术的发展,面临着传感器数据维度增 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 亚临界雷诺数圆柱绕流远场气动噪声实验研究*
    圆柱绕流是一个典型的流动问题,广泛存在于航空航天、船舶以及风工程[1-2]等实际工程问题中。其流动尾流区域存在卡门涡街、流动分离和层流湍流的转捩等复杂的流动现象[3-4]。长久以来围绕圆柱绕流的流动、减阻等难题进行了深入细致的研究,而对于圆柱绕流噪声的研究却是从1878年Strouhal[5]开始的 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于奇异谱分析的空间环境数据插补方法
    由于受卫星轨道限制、测量设备故障、通信链路中断及人为数据剔除等因素的影响,空间环境测量数据(包括太阳风参数、行星际磁场和高能粒子通量等)经常出现数据缺失现象,而很多分析过程及建模手段都需要连续的数据作为输入,因此,研究空间环境缺失数据插补方法有着重要的现实意义。空间环境数据具有典型的非线性、非平稳特 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 乏信息空间机械臂随机振动信号的灰自助评估
    乏信息是指测量数据具有的测量信息不完整和不充足,如概率分布已知,但只有少量数据可供分析;概率分布未知,测量数据也只有少量;趋势项未知等,都具有乏信息的特征[1]。航空、航天运载系统、载人航天工程系统、战术导弹和飞行姿态控制等行业经常遇到更加复杂的乏信息问题[2,3]。对于空间机械臂而言,振动会影响安 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.