为了对以上缺陷进行预测,相关****们进行了大量研究。林艳等[2]结合起皱能量准则和有限元方法提出了预测起皱的方法, 认为影响薄壁管数控弯曲成形过程起皱发生的主要因素是弯曲半径、相对管径、芯棒伸长量和摩擦因素。Li等[3-5]利用ABAQUS有限元软件研究了管胚与模具之间的接触对多种缺陷尤其是起皱产生的影响。Zhan等[6]使用有限元方法对弯曲回弹的机理和规律进行了分析,认为回弹与弯曲角度的关系分为双线性和线性2个部分,并得到了回弹的回归公式。同时研究认为强度系数越大、硬化指数越小,回弹越大。Jiang等[7]使用多因素分析方法,认为回弹角度与弯曲角度、屈服强度和强度系数正相关,而与弹性模量、硬化指数和各向异性系数负相关。
到目前为止, 预测数控弯管质量的研究大多仅针对定性分析,很难在实际工艺中采用。可靠和快速的弯曲质量预测方法在工业界的应用具有重要价值。机器学习方法具有对非线性系统进行模式识别与函数拟合的能力,提供了较为完备的理论支撑[8-9],因此本研究建立了基于机器学习和有限元相结合的大直径管材数控弯曲质量预测方法,充分考虑材料性能、几何参数和多种工艺参数对成形质量的影响。
1 数控弯管工艺分析与模型 管材数控弯曲是一种数字化精确控制的旋转绕弯法,图 1为管材数控弯曲成形工艺原理。管材跟随夹紧模、弯曲模和镶块围绕弯曲模轴心旋转并发生变形。防皱模在弯曲过程提供压紧力,以防止管材直线段翘起。同时向前进给,利用摩擦力推动管胚补料。芯轴和芯球从管胚内部支持管壁,以防止截面畸变。防皱模位于弯曲模与管胚之间填补空隙,从外侧支撑管胚以防止此区域起皱。
 |
| 图 1 管材数控弯曲成形工艺原理 Fig. 1 Principle of tube numerical controlled bending forming process |
| 图选项 |
成形过程中,管材在外力矩M作用下发生弯曲,变形区的应力-应变状态如图 2所示。当变形程度较小时,变形区仅存在轴向应力σθ。随着弯曲变形程度的增大,管材厚向应力σt与周向应力σD增加,逐渐形成三向应力状态。变形区外侧承受切向拉伸产生的双向拉应力, 内弧面承受三向压应力。假设过程中管胚直径不发生变化,即εD=0, 变形可简化为平面应变状态。根据塑性变形体积不变原理,厚向应变与轴向应变大小相等,方向相反,即εt=-εθ。因此,弯曲变形区的外侧将发生减薄的现象, 内侧管壁将发生增厚,甚至可能发生起皱。当相对弯曲半径(弯曲半径与管材直径的比值R/D)较小时,将增大管材发生起皱的可能性。
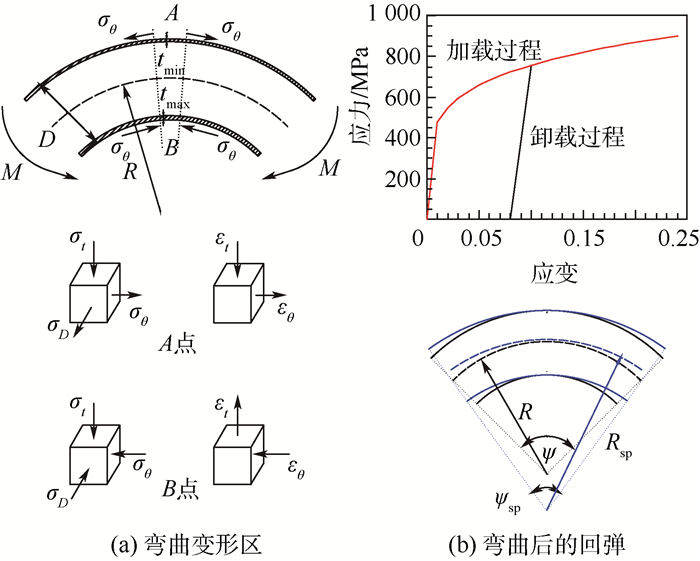 |
| tmin—成形后的管材外壁最薄处的壁厚;tmax—成形后的管材内壁最厚处的壁厚;A—成形后的管材外壁最薄处的位置;B—成形后的管材内壁最厚处的位置。 图 2 管材成形及回弹时的应力-应变状态 Fig. 2 Stress-strain state of tube forming and spring-back |
| 图选项 |
成形完成后模具卸载,外力矩消失,变形过程中的弹性应变释放,管材会不可避免地发生回弹。此时,弯曲半径与弯曲角度ψ都将发生变化。根据胡克定律,得到回弹后的半径Rsp与角度ψsp关系式为
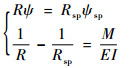 | (1) |
式中:E和I分别为弹性模量与管材截面的弯曲模量。
根据以上的分析,本文使用ABAQUS/Explicit的动力显式有限元算法建立管材数控弯曲过程的数值仿真模型。由于管材厚度与外径的比值较小,管材具有壳体的结构特征。因此,管胚的单元类型采用减缩积分和沙漏控制的4节点有限应变双曲薄壳单元(S4R)。而模具则使用离散刚体,以便参与管材与模具间的接触的分析。管材与模具间的接触约束条件采用罚函数约束算法实现以保证变形体表面的节点不穿透刚性的表面,而接触界面的摩擦使用库仑模型描述:
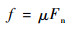 | (2) |
式中:μ为管胚与各模具间的摩擦系数;Fn为接触界面的法相压力。管材的材料模型使用服从Mises屈服准则的各向同性硬化弹塑性材料模型,同时使用Krupkowski-Swift模型描述材料的流动硬化:
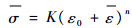 | (3) |
式中:K为强度系数;ε0为初始应变;n为硬化指数;σ和ε分别为应力和应变。
图 3为管材数控弯曲工艺有限元模型。由于回弹过程不存在复杂的接触条件,可以认为回弹过程不是严重非线性过程。因此采用ABAQUS/Standard模块计算,既避免了算法出现不收敛的情况,也可以提高计算的效率。将成形计算的模型导入ABAQUS/Standard模块中,删除管胚模型之外所有模具零件、载荷和边界条件。在管胚直线段的管段添加固定约束,使得回弹以其为基准。
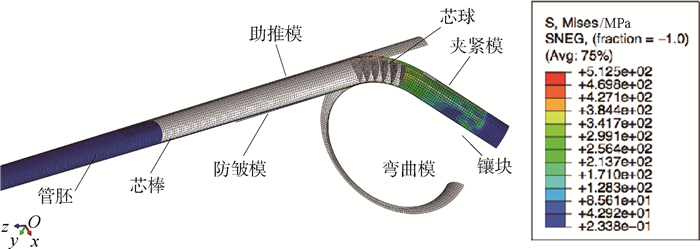 |
| 图 3 管材数控弯曲工艺有限元模型 Fig. 3 Finite element model of tube numerical controlled bending process |
| 图选项 |
2 起皱、减薄和回弹的预测方法 为了衡量管材数控弯曲质量,定义质量标准参数:成形最大减薄率It=(t0-tmin)/t0,用来表示管材减薄程度,t0为初始的管材壁厚[10]。最大起皱因子T/Umin,用来描述管材成形后起皱程度的参数,Umin为管件受压区域的最小起皱能,T为外力所作的功。当T/Umin>1认为管材已经起皱[11]。管材在成形后的回弹一般使用回弹角度Δψ=ψ-ψsp来衡量。
管材数控弯曲的成形质量主要由3个方面因素决定:①管材材料性能,主要包括弹性模量E、泊松比ν、强度系数K、初始应变ε0和硬化指数n等;②弯管的几何形状,主要包括弯曲角度ψ、弯曲半径R和管壁厚度t;③工艺参数,主要包括模具与管胚之间的间隙ga和摩擦系数μ、芯轴伸出量e、芯球个数m、芯球厚度d和助推参数w等。因此最大减薄率、最大起皱因子和最终成形角度可以分别表示为
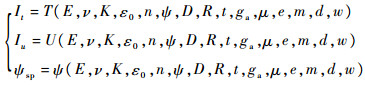 | (4) |
由定义可以知道,在这3个函数中,最大减薄率与最终成形角度是连续函数, 而最大起皱因子是二值函数。因此需要使用不同的方法,对成形质量进行预测。
本文为了预测最大减薄率与最终成形角度,选择使用径向基函数(Radial Basis Function,RBF)神经网络[12-13],如图 4所示。它是一种3层的前向神经网络,其中第1层为输入层,第2层为以RBF为变换函数的隐藏层,而第3层为输出层。输入层与隐藏层之间是权值为1的线性连接,而输出层是对隐藏层激活输出进行线性调节。其基本思想是利用RBF对输入进行变换,将低维的数据转换到高维空间中,使得不可分的问题在高维线性可分。RBF神经网络结构简单,能够逼近任意非线性函数,因此适用于预测连续的成形质量。
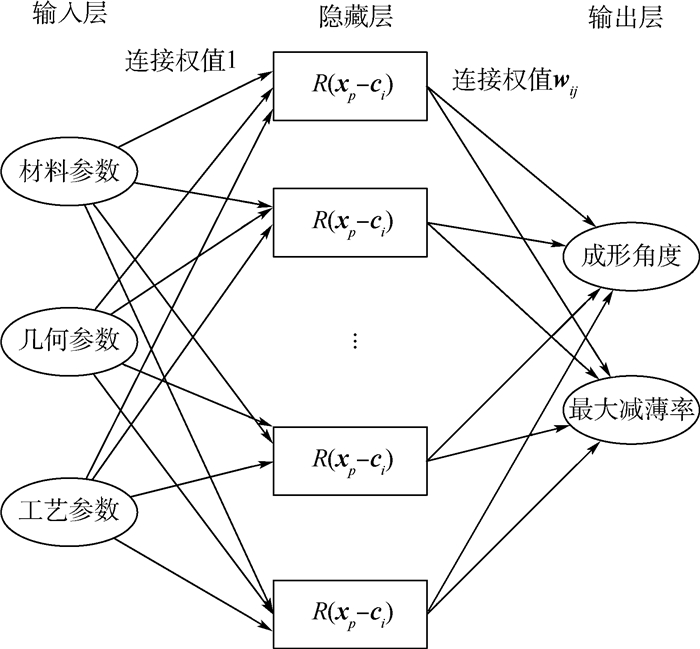 |
| 图 4 RBF神经网络预测回弹角度与最大减薄率 Fig. 4 Prediction of spring-back angle and maximum thinning ratio with RBF neural network |
| 图选项 |
采用高斯函数作为激活函数建立RBF神经网络:
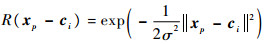 | (5) |
式中:
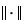
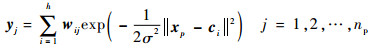 | (6) |
式中:wij为第i个隐藏层与第j个输出的线性连接权重;h为网络隐藏层节点数;np为输出层节点数。
最大起皱因子则采用二分类支持向量机(Support Vector Machine,SVM)进行预测[14-15],如图 5所示。SVM网络具有完善的统计学习理论基础,其主要思想是建立一个超平面作为分类的决策面,使得分类之间的距离最大,是实际风险最小化的实现。
 |
| 图 5 SVM二分类 Fig. 5 Binary classification with SVM |
| 图选项 |
假设样本集{(x1, y1), (x2, y2), …, (xp, yp), …, (xN, yN)}是线性可分的2类问题,N为样本个数,(xp, yp)为m维的输入向量, y∈(-1, +1)为分类号,则该输入空间的分类判别的超平面函数应为
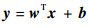 | (7) |
式中:w为m维的线性变换向量;b为线性偏置向量。如果该超平面可以对样本集中所有样本进行正确分类并具有间隔,则该平面需要满足:
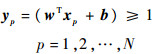 | (8) |
并得到分类间的间隔M=2/||w||。因此,寻找最佳超平面的问题可以表示为
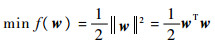 | (9) |
满足yp(wTxp+b)>1。这个约束的最优化问题可以使用Lagrange方法转化为
 | (10) |
满足
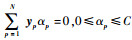
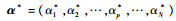
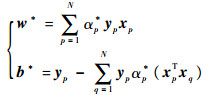 | (11) |
因此最大间隔的分类超平面为
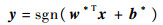 | (12) |
对于本文中的线性不可分情况,SVM将输入向量映射到高维的特征向量空间,并在高维空间构建超平面,即将线性K(xp, xq)=xpTxq利用非线性核函数代替。本文中选择RBF为
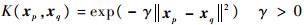 | (13) |
本文的研究重点主要包括材料性能参数和弯曲几何关系与成形质量的关系,因此在建立有限元模型并进行模拟时,摩擦系数为固定值,如表 1所示。表 2为本文主要研究参数的取值范围, 包括几何参数、材料参数和弯曲角度等。同时,其他的主要工艺参数可以通过管材几何尺寸定义,如表 3所示。对于预测模型发生起皱的情况,将不再考虑减薄与回弹。图 6为管材数控弯曲质量预测方法的流程图。
表 1 各接触表面间的摩擦系数 Table 1 Friction coefficients between blank and tools
| 接触表面 | μ |
| 管胚与夹紧模 | 0.70 |
| 管胚与防皱模 | 0.05 |
| 管胚与助推模 | 0.30 |
| 管胚与弯曲模 | 0.30 |
| 管胚与镶块 | 0.30 |
| 管胚与芯轴 | 0.05 |
| 管胚与芯球 | 0.05 |
| 芯轴与芯球 | 0.08 |
表选项
表 2 主要研究参数的取值范围 Table 2 Spans of main research parameters
| 参数名称 | 范围 |
| 管材外径/mm | 70~100 |
| 管壁厚度/mm | 1~3 |
| 弯曲半径/mm | 140~200 |
| 弯曲角度/(°) | 5~90 |
| 弹性模量/GPa | 170~220 |
| 强度系数 | 750~850 |
| 初始应变 | 0.02~0.10 |
| 硬化系数 | 0.0~0.27 |
表选项
表 3 主要工艺参数取值 Table 3 Spans of main processing parameters
| 参数名称 | 取值 |
| 管模间隙/mm | 0.5 |
| 芯球数 | 5 |
| 芯球厚度 | 0.5 D |
| 芯轴伸出量 | |
| 助推系数 | 1.0 |
| 芯球间距 | 0.5 d |
表选项
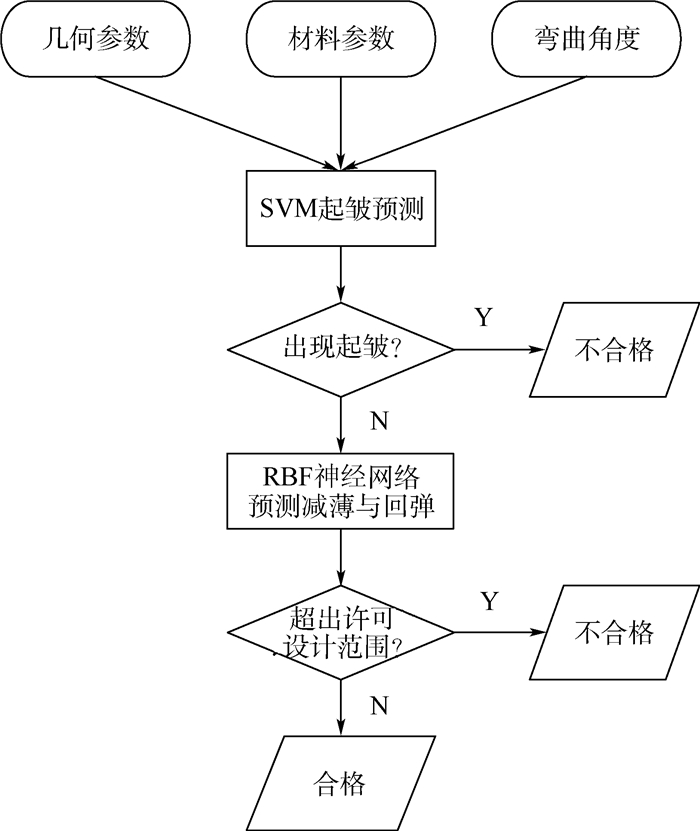 |
| 图 6 弯管质量预测流程 Fig. 6 Flowchart of bending tube quality prediction |
| 图选项 |
3 实验结果与讨论 3.1 实验数据处理 预测数据来源于200组有限元模拟实验。首先将其中的70%作为训练集,30%作为测试集,使用训练集建立了SVM起皱分量模型并使用测试集进行了预测验证。随后选择实验中没有出现起皱的145组模型按照同样的比例划分,用以训练预测减薄与回弹的RBF神经网络。
为了消除不同维数据的输入输出数量级的差异对网络预测产生的较大影响,需要对数据进行归一化,即将所有数据都转化为[0,1]区间之中的数。本文中采用“最大最小”归一化方法,对每一维中的数据进行如下计算:
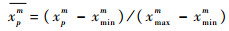 | (14) |
式中:xpm为样本p在m维的值; xmaxm和xminm分别为所有样本中这一维上最大和最小值;xpm为归一化后的值。在通过网络进行预测后需要对输出进行反归一化,得到预测结果。
对输入变量进行主成分分析(Principal Component Analysis,PCA)。PCA是一种对数据进行简化的常用方法,目的是将复杂的模型降维,发现其中数据之间的关联,并且去除可能导致解空间不稳定或不连贯的噪声。图 7所示为起皱预测模型中各变量的成分分析,分布比较均匀,即各因素均对起皱有一定影响。
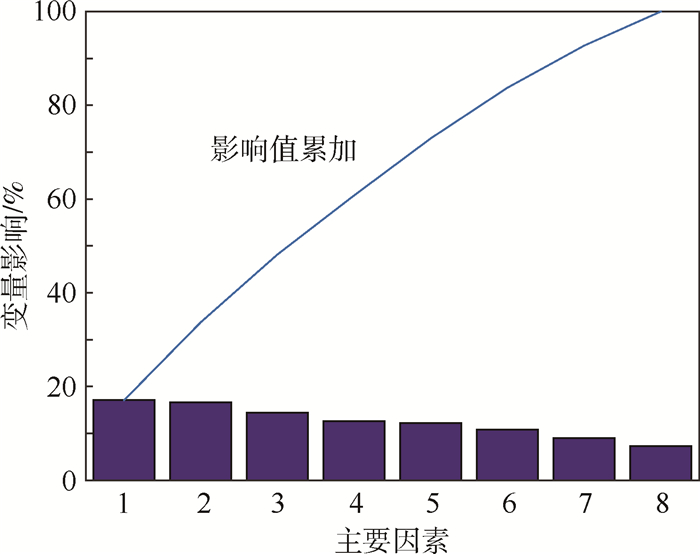 |
| 图 7 起皱预测模型PCA分析 Fig. 7 PCA analysis of wrinkle prediction model |
| 图选项 |
3.2 起皱的预测模型 在起皱预测模型的建立过程中,可以利用交叉验证的方法对SVM的参数g和c进行优化,得到最佳预测模型,预测的准确度达到95%以上,如图 8所示。最佳参数c=147.033 4,g=0.020 617,准确率为96.296 3%。
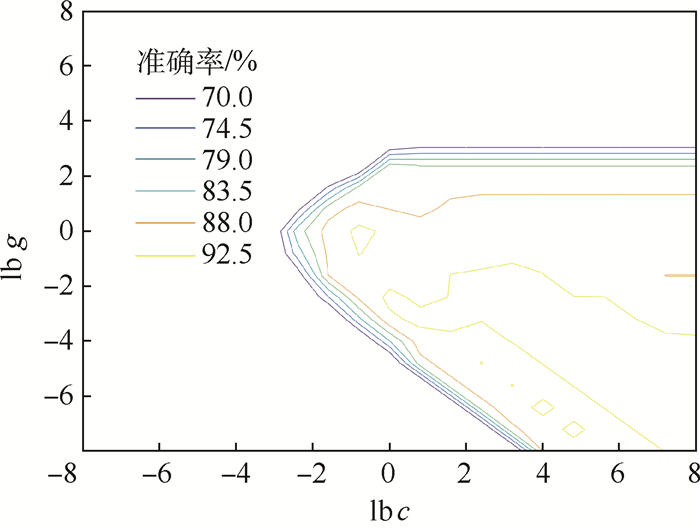 |
| 图 8 SVM参数选择结果等高线 Fig. 8 Contours of SVM parameters' selection |
| 图选项 |
3.3 减薄率与回弹的预测模型 基于RBF神经网络的最大减薄率与回弹角度的实验值与预测值的比较如图 9所示。预测值与实验值的差距基本保持在10%以内,可以认为预测模型能够较为准确地反映各个参数与减薄的函数关系。
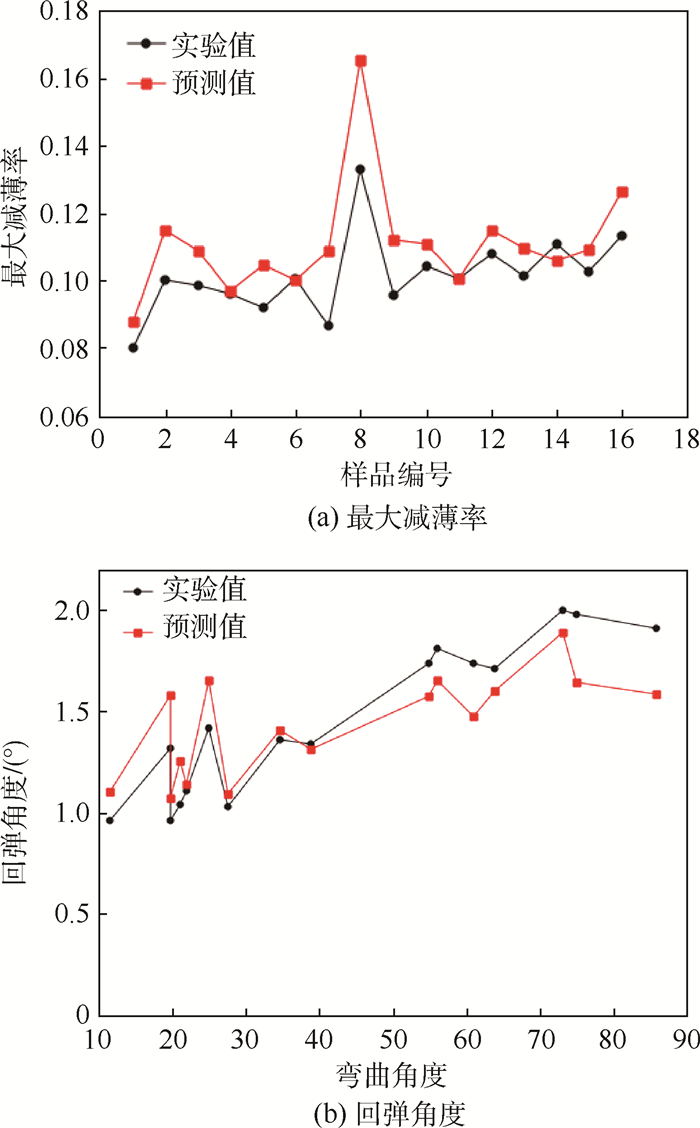 |
| 图 9 最大剪薄率和回弹角度的预测值与实验值比较 Fig. 9 Comparison between predicted and experimental values of maximum thinning ratio and spring-back angle |
| 图选项 |
4 结论 本文结合径向基函数神经网络与支持向量机提出了对管材数控弯曲的成形质量进行预测的方法。经实验验证表明:
1) 使用SVM可以准确预测管材弯曲内侧起皱,使用交叉验证的方法优化网络参数可以有效提高预测的准确性,预测准确率达到95%以上。
2) RBF神经网络可以较为准确地预测弯曲外壁的减薄与回弹角度。预测与实验的差距在10%以内。
该方法对于管材数控弯曲工艺的制定可以起到良好的指导作用。
参考文献
| [1] | TANG N C. Plastic-deformation analysis in tube bending[J].Internal Journal Pressure Vessels and Piping, 2000, 77(12): 751–759.DOI:10.1016/S0308-0161(00)00061-2 |
| [2] | 林艳, 杨合, 李恒, 等. 薄壁管数控弯曲过程中失稳起皱的主要影响因素[J].航空学报, 2003, 24(5): 456–461.LIN Y, YANG H, LI H, et al. Influences of forming parameters on wrinkling in NC thin-walled tube bending[J].Acta Aeronautica et Astronautica Sinica, 2003, 24(5): 456–461.(in Chinese) |
| [3] | LI H, YANG H, ZHAN M, et al. The interactive effects of wrinkling and other defects in thin-walled tube NC bending process[J].Journal of Materials Processing Technology, 2007, 187-188: 502–507.DOI:10.1016/j.jmatprotec.2006.11.100 |
| [4] | LI H, YANG H, ZHAN M, et al. Role of mandrel in NC precision bending process of thin-walled tube[J].International Journal of Machine Tools & Manufacture, 2007, 47(7-8): 1164–1175. |
| [5] | LI H, YANG H, ZHAN M. A study on plastic wrinkling in thin-walled tube bending via an energy-based wrinkling prediction model[J].Modelling and Simulation in Materials Science and Engineering, 2009, 17(3): 035007.DOI:10.1088/0965-0393/17/3/035007 |
| [6] | ZHAN M, YANG H, HUANG L, et al. Springback analysis of numerical control bending of thin-walled tube using numerical-analytic method[J].Journal of Materials Processing Technology, 2006, 177(1-3): 197–201.DOI:10.1016/j.jmatprotec.2006.03.183 |
| [7] | JIANG Z Q, YANG H, ZHAN M, et al. Coupling effects of material properties and the bending angle on the springback angle of a titanium alloy tube during numerically controlled bending[J].Materials & Design, 2010, 31(4): 2001–2010. |
| [8] | SHARAD G, NANDEDKAR V M. Springback in sheet metal u bending-fea and neural network approach[J].Procedia Materials Science, 2014, 6: 835–839.DOI:10.1016/j.mspro.2014.07.100 |
| [9] | PANDEY A K, DUBEY A K. Fuzzy expert system for prediction of kerf qualities in pulsed laser cutting of titanium alloy sheet[J].Machining Science and Technology, 2013, 17(4): 545–574.DOI:10.1080/10910344.2013.806182 |
| [10] | YAN J, YANG H, ZHAN M, et al. Forming limits under multi-index constraints in NC bending of aluminum alloy thin-walled tubes with large diameters[J].Science China Technological Sciences, 2010, 53(2): 326–342.DOI:10.1007/s11431-009-0331-x |
| [11] | HE Y, JING Y, MEI Z, et al. 3D numerical study on wrinkling characteristics in NC bending of aluminum alloy thin-walled tubes with large diameters under multi-die constraints[J].Computational Materials Science, 2009, 45(4): 1052–1067.DOI:10.1016/j.commatsci.2009.01.010 |
| [12] | PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks[J].Neural Computation, 1991, 3(2): 246–257.DOI:10.1162/neco.1991.3.2.246 |
| [13] | KAMI A, DARIANI B M. Prediction of wrinkling in thin-walled tube push-bending process using artificial neural network and finite element method[J].Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture, 2011, 225(10): 1801–1812.DOI:10.1177/0954405411404300 |
| [14] | LI Y.LIBSVM-FarutoUltimate Version:A Toolbox with Implements for Support Vector Machines Based on Libsvm[EB/OL].2009.[2014-8-31].https://github.com/faruto/Libsvm-FarutoUltimate-Version |
| [15] | CHANG C C, LIN C J. Libsvm:A library for support vector machines[J].ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 27. |
