目前机载告警设备的威胁评估方式只是与预先装订好的数据库进行快速数据比对,判定威胁等级,无法应对没有先验信息的信号样式,且辐射源威胁等级评估还有亟待解决的问题:情报数据与先验信息有限,而且先验信息的准确度与完备性有待考究,尤其是高威胁目标的信号特征与脉冲参数难以获得;电磁环境日益复杂,空间中电磁信号已达每秒百万量级,信号样式复杂多变,机载资源有限,难以保证准确快速的排序;对多维脉冲描述字进行决策时,数据维数的增多必将导致计算量的激增与实时性的下降;装备能力有限,致使参数的测量精度受限甚至出现错误。上述客观因素严重制约着辐射源威胁高速准确地评估,因此要求评估算法必须具有极强的实时性、良好的通用性与适当的容错性。
为解决辐射源威胁等级排序的短板,诸多****进行了深入的研究并取得丰硕的成果。文献[2-3]结合计算机网络和专家知识库集成技术,提出集群目标威胁评估的新方案;文献[4]采用模糊认知图的方式,通过构建模糊结构,建立复杂系统模型,实现对空中目标威胁等级进行评估;文献[5-6]采用基于直觉模糊集理论,构建威胁评估模型,实现对目标威胁程度的判定。上述方案在一定条件下均具有良好的处理能力与应用前景,但专家系统或模糊灰色处理等方案会由于决策者具有不同的知识结构、经验集成和个人偏好,导致不同专家给定的最终参考方案差距较大,主观因素影响严重,且某些参数一旦设定就难以改变,不适宜动态更新,限制评估结果的准确性。文献[7-8]提出基于神经网络的威胁评估方法,通过监督学习的方式,准确地完成对空战目标威胁评估;文献[9-10]采用支持向量机(SVM)的方式,根据有限的样本信息在模型的复杂性和学习能力之间寻找最佳折中,利用其特有的推广能力实现对于目标威胁等级的判定。两者具备良好的泛化能力与容错性,但神经网络与SVM内部运算属于黑盒处理,需要大量的先验信息作为训练样本,同时神经网络与SVM需要调用大量的系统资源,当输入矢量维数过多和训练样本过大时,计算复杂度及空间复杂性会大大增加,导致收敛速度慢,致使算法的效率大打折扣,难以满足现代空战对于实时性的要求。
针对上述方案的局限与对算法特性的需求,本文采用粗糙集-信息熵的方法实现对辐射源进行威胁评估。粗糙集方法通过处理大数据量、处理不确定数据、消除冗余信息等步骤,约简训练数据,寻找最小属性集,得到有效的决策规则[11-13]。粗糙集理论作为一种处理不精确、不一致、不完整等各种不完备的信息有效工具,一方面得益于它的数学基础成熟、不需要先验知识;另一方面在于它的易用性,且粗糙集在进行离散化处理时对数据有一定的容错性。然而经典粗糙集无法处理没有决策值的信息系统。因此本文将信息熵理论[14-15]与粗糙集相结合,通过计算熵值确定信息量最大的属性来代替决策属性,拓展粗糙集理论的适用范围,实现对于辐射源的威胁等级排序。
1 辐射源威胁评估处理流程 基于粗糙集-信息熵的威胁评估处理流程如图 1所示。
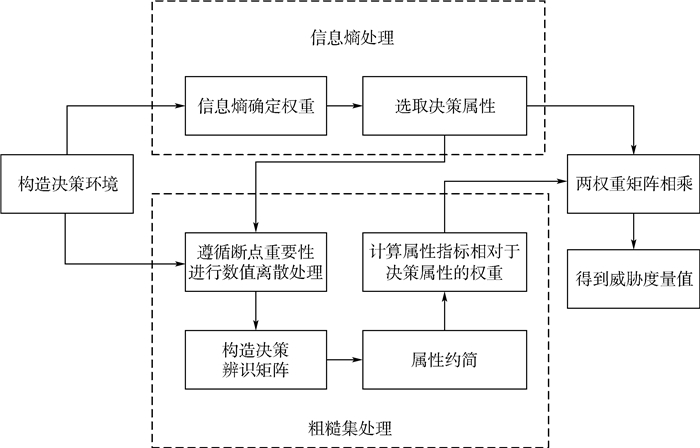 |
| 图 1 威胁评估处理流程 Fig. 1 Processing flow of threat evaluating |
| 图选项 |
机载电子对抗设备将测得脉冲描述字输入威胁评估流程,首先按照粗糙集理论构造决策环境,将形成的信息表中数据进行双路并行处理:一路采用信息熵的处理方式,确定每个属性的权重,并确定代替的决策属性;另一路基于粗糙集理论,将数据遵循断点重要性的方法进行离散,构建决策辨识矩阵,采用析取合取运算进行属性约简,再计算属性指标相对于决策属性的权重。将两路输出的权重矩阵相乘,即可得到衡量每个辐射源的威胁度量值,进行排序后即可实现威胁评估。
2 评估处理模型 Step 1 构建决策环境。
定义1[16] 称{U,A,F,d}为决策信息系统,其中U={x1,x2,…,xn}为对象集,U中的每个元素xi(i≤n)称为一个对象。A={a1,a2,…,am}为属性集,A中的每个元素al(l≤m)称为一个属性。F={fl:U→Vl(l≤m)}为U与A之间的关系集,其中Vl为al(l≤m)的值域。d:U→Vd为决策,Vd取有限值。每个属性子集a?A决定了一个不可区分的关系ind(A):
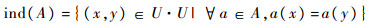 | (1) |
关系ind(a)(a?A)构成了U的划分,用U/ind(a)表示。
定义2[17] 称{U,A,F,d}为一个信息系统,对于任意B?A,记
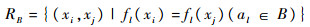 | (2) |
RB则是U上的等价关系,记
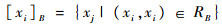 | (3) |
则U/RB={[xi]B|xi∈U}是U上的划分。同理:
 | (4) |
通过式(1),可以先将数据进行整理,形成一个原始的对象与属性之间的初始数据表。
Step 2 基于信息熵计算权重向量。
此处采用基于信息熵的多属性决策方法,计算得到各个属性的权重,具体流程如下:
1) 通过对象集U上m个决策对象对n个决策的属性评价,可以得到特征值矩阵,特征值矩阵用λ表示:
 | (5) |
简要判定属性是效益型还是成本型,计算得到规范化的属性优度指标矩阵R=(rij)m×n。
效益型就是指其值越大,目标函数函数越大,计算公式如下:
 | (6) |
成本型就是指其值越大,目标函数函数越小,计算公式如下:
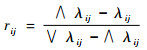 | (7) |
式中:“∧”表示合取运算;“∨”表示析取运算。
2) 对矩阵R=(rij)m×n进行列归一化,得到
 | (8) |
式中:
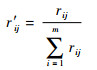 | (9) |
3) 计算属性aj输出的信息熵:
 | (10) |
3) 计算属性权重向量
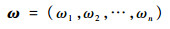 | (11) |
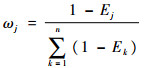 | (12) |
采用上述步骤即可以计算得出多属性决策表属性的权重,其中ωj为aj的权重。
Step 3 选定代替决策值。
将上述的结果中权重的最大值选出来,由于本问题中没有涉及决策,根据粗糙集理论,选定权重最大值的属性为代替决策值,同时也得到各个属性的权重系数。
本模型关于信息熵处理过程到此为止,接下来转入利用粗糙集的处理步骤。
Step 4 将属性值离散化。
对于属性进行离散化的方法很多,本模型采用属性重要性的离散化方法,具体的过程如下所示:
1) 选择初始种群,初始化初始种群pop(G),G=1。
2) 首先定义B对于F近似分类的质量为
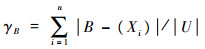 | (13) |
式中:F为决策属性集d导出的分类。条件属性子集B在条件属性集A中的重要性定义为
 | (14) |
计算各个个体的适应度fitness(i)及适应度的和sum(G)。
3) 选择操作:采用轮盘赌选择法(roulette wheel selection),每一轮产生一个[0, 1]均匀随机数,选择累计概率与该随机数最接近的个体作为下一代的个体,得到下一代种群pop(G+1)。杂交操作:采用单点杂交,产生随机数,确定要杂交的次数,要参与杂交的父辈个体,随机选取杂交点,然后对杂交点后的部分子串进行交换,即产生下一代个体。变异操作:随机选择要变异的个体,及要变异的断点,若为0,则变异为1,为1则变异为0。
4) 对所有个体进行统计,删除重复的个体。
5) 如满足结束条件:sum(G)/total(G)>1-ε,则结束;否则,G=G+1,返回步骤2)。其中,ε为给定的小正数。采用上述方法处理后得到离散化的数据。
Step 5 构造决策辨识集进行属性约简[18]。
根据粗糙集的决策辨识集,设{U,A,F,d}为决策信息系统,记
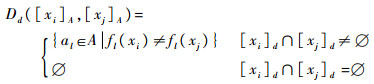 | (15) |
称Dd([xi]A,[xj]A)为[xi]A与[xj]A的决策辨识集,称Dd为决策信息系统的决策辨识矩阵,从而得到系统的决策辨识矩阵为
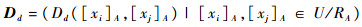 | (16) |
根据粗糙集系统的决策约简集的定义,设{U,A,F,d}为决策信息系统,当且仅当对于任意的Dd([xi]A,[xj]A)≠?,有
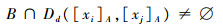 | (17) |
则B为决策协调集。若B的任何真子集均不为决策协调集时,则称B为决策约简集。即可以保留系统决策不变的约简属性集,属性约简后可以降低系统的冗余度。对以上决策表进行约简,得到系统的核心属性,并将离散化后的数据进行属性约简得到约简后的决策表。
Step 6 计算在属性指标下相对于决策属性的权重表。
通过计算方案及对于每个属性的分类。定义:
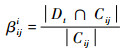 | (18) |
称为决策属性的第t个等价类与每一个条件属性的等价类间的等价近似度,取maxβiji,记为对象在决策属性中的局部权重。
利用式(18),得到各个属性在属性指标下相对于决策属性的权重表。最后得到量化辐射源威胁能力的指标为
 | (19) |
最后将衡量指标进行排序得到辐射源的威胁程度的排序,即可得到对于辐射源的威胁排序。
3 辐射源威胁评估决策系统 本文选取文献[19]中5个辐射源的雷达脉冲描述字作为威胁等级排序的仿真验证条件,构建已知方案集,即初始信息表,并形成条件属性:
对象集:U={x1,x2,x3,x4,x5}
指标(属性)集:A={a,b,c,d,e}
式中:a为载频周期(RF),MHz;b为脉冲重复间隔(PRI),μs;c为脉冲宽度(PW),μs;d为到达方位角(AOA),(°);e为脉冲幅度(PA),dB。
具体数据如表 1所示。
表 1 原始各个辐射源的脉冲描述字 Table 1 Original data of each radiator’s PDWs
| 对象 | 属性 | ||||
| a | b | c | d | e | |
| x1 | 9 500 | 3 | 1.2 | 11 | 10 |
| x2 | 9 800 | 11.4 | 0.29 | 2 | 12 |
| x3 | 9 000 | 3.1 | 1.1 | 30 | 6 |
| x4 | 1 500 | 100 | 1.1 | 15 | 11 |
| x5 | 10 000 | 3 | 0.5 | 45 | 5 |
表选项
根据雷达信号的特征与用途初步判定每种脉冲描述字为成本型或效益型属性。
对于执行空战任务的战机而言,除却雷达导引头,威胁等级最高的辐射源即为机载火控雷达,机载火控雷达的一大明显特点是载频绝大部分处于X波段,载频相较于其他用途的雷达而言要大,因而判定载频为效益型;PRI的倒数为脉冲重复频率(PRF),为了精确测量目标信息,机载火控雷达常采用高重频(HPRF)模式,实现高精度测量目标参数,为武器系统实施火力打击构建火控解算条件,因此PRI为成本型;PW越窄,指向性越强,对目标信息测量的精准度就越高,更有助于构建火力打击条件,并有可能形成脉冲压缩处理,即PW为成本型;AOA越小,敌方辐射源与我方战机的迎头性越强,致使我方战机越难以规避敌方武器系统的攻击,威胁程度越大,AOA即为成本型属性;PA越大,侦收到敌方信号的能量越强,与本机的距离越近,威胁程度越高,因此将PA判定为效益型。
4 仿真验证 按照图 1所示的流程并结合第3节构建的模型,对初始方案集进行处理。首先利用式(5)求取出表 1的特征值矩阵,根据第3节对辐射源参数定性类型的界定,并结合式(6)~式(9)对得到的特征值矩阵进行列归一化处理,得到归一化决策矩阵,如表 2所示。
表 2 归一化决策矩阵 Table 2 Decision matrix after normalizing
| 对象 | 属性 | ||||
| a | b | c | d | e | |
| x1 | 0.238 0 | 0.000 2 | 0.000 2 | 0 | 0 |
| x2 | 0.245 8 | 0.112 6 | 0.112 6 | 0.054 0 | 0.054 3 |
| x3 | 0.225 5 | 0.208 4 | 0.208 4 | 0.343 9 | 0.362 0 |
| x4 | 0.040 1 | 0.322 3 | 0.322 3 | 0.018 2 | 0.080 8 |
| x5 | 0.250 6 | 0.356 5 | 0.356 5 | 0.583 9 | 0.503 0 |
表选项
计算得到属性a、b、c、d、e的信息熵,如表 3所示。
表 3 5个属性的信息熵 Table 3 Information entropy of five attributes
| 属性 | a | b | c | d | e |
| 信息熵 | 0.214 3 | 0.716 1 | 0.928 5 | 0.705 2 | 0.917 6 |
表选项
属性a、b、c、d、e的属性权重向量如表 4所示。
表 4 5个属性的权重向量 Table 4 Weight vector of five attributes
| 属性 | a | b | c | d | e |
| 权重 | 0.517 5 | 0.187 0 | 0.047 1 | 0.194 2 | 0.054 3 |
表选项
从表 4的权重向量中可以看出a的权重最大,虽然对于雷达自身而言,载频并不携带信号信息,但对于侦察方可以根据其载频的特性初步判定该辐射源为机载火控雷达。在实际应用中,同等条件下RF有助于直接判定辐射源类型,符合实际侦察的情况。结合上述模型,可以将载频信息看成是粗糙集理论中决策表的决策属性D。将各个参量离散化后,构建完备的信息决策表,如表 5所示。
表 5 离散化后辐射源的脉冲描述字 Table 5 Each radiator’s PDWs after discreting
| 对象 | 属性 | ||||
| b | c | d | e | D | |
| x1 | 1 | 4 | 1 | 3 | 4 |
| x2 | 1 | 1 | 1 | 4 | 4 |
| x3 | 1 | 4 | 3 | 1 | 4 |
| x4 | 4 | 4 | 2 | 4 | 1 |
| x5 | 1 | 1 | 4 | 1 | 4 |
表选项
得到决策辨识矩阵,如表 6所示。
表 6 决策辨识矩阵 Table 6 Decision discernibility matrix
| 对象 | x1 | x2 | x3 | x4 | x5 |
| x1 | ? | ? | ? | bde | ? |
| x2 | ? | ? | ? | bcd | ? |
| x3 | ? | ? | ? | bde | ? |
| x4 | bde | bcd | bde | ? | bcde |
| x5 | ? | ? | ? | bcde | ? |
表选项
得到系统的决策核心属性为:b,d;相对必要属性为:c,e;没有不必要属性,从而不需要进行属性约简。
得到方案集对于属性的分类为
U/b={x1,x2,x3,x5},{x4}
U/c={x1,x3,x4},{x2,x5}
U/d={x1,x2},{x3},{x4},{x5}
U/e={x1},{x2,x4},{x3,x5}
U/D={x1,x2,x3,x5},{x4}
基于粗糙集多属性决策的排序法得到每个方案在每一个指标下相对于决策属性的权重如表 7所示。
表 7 每个指标相对于决策属性的权重值 Table 7 Weight of each attribute relative to decision property
| 对象 | 属性 | ||||
| b | c | d | e | D | |
| x1 | 1 | 0.67 | 1 | 1 | 1 |
| x2 | 1 | 1 | 1 | 0.5 | 1 |
| x3 | 1 | 0.67 | 1 | 1 | 1 |
| x4 | 1 | 0.67 | 1 | 0.5 | 1 |
| x5 | 1 | 1 | 1 | 1 | 1 |
表选项
最终得到各个辐射源的威胁度量值Q,如表 8所示。
表 8 各个辐射源的威胁度量值Q Table 8 Threat metric value Q of each radiator
| 对象 | x1 | x2 | x3 | x4 | x5 |
| Q值 | 0.984 5 | 0.972 9 | 0.984 5 | 0.957 3 | 1.000 0 |
表选项
对Q值进行排序,得到的威胁状态的排序为
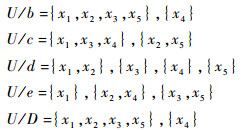 |
由原始数据也可以看出:x5辐射源的PW窄,PRI低,符合制导雷达的特征,威胁等级为最高,x1和x3辐射源的PW较窄,PRI较低,有可能处于单目标跟踪(STT)或者边跟踪边扫描(TWS)状态测定我机状态信息,用以引导攻击,威胁等级较高;x2由于PRI较大,难以实现对我方战机参数的精确测量,无法构成火控解算条件,但我方侦测到其功率较大,距离我机较近,威胁等级较次,有可能采用以精度换取探测范围的搜索状态;x4的信号特征与远程警戒或机载预警雷达相似,实现对我方的远程粗略探测,从而引导飞机布防,威胁等级不高。由此可见,本文的仿真验证结果与实际威胁等级相吻合,可以实现较好的判定辐射源的威胁状况。
5 结 论 1) 构建的数学模型实现了对于辐射源威胁程度的有效评估。采用基于粗糙集理论的方法,利用原始数据特征,有效地规避了由于主观因素产生的arrow不可能性定理,并减少了对于先验信息的需求。
2) 本模型可以通过计算得到辐射源威胁度量值,定量地体现出辐射源威胁程度,根据辐射源威胁程度的量化值进行排序,过程简单易于操作,结果直观准确,且具有良好的实时性与可行性。
3) 由于电磁环境的复杂性与实际装备的限制,可能导致侦察到的脉冲描述字存在错误,或者部分参数丢失的情况,而粗糙集本身具有一定的容错性,适宜实际威胁排序的需求。
4) 本文提出的方法拓展了粗糙集的应用范围,可以在未知决策属性时实现对于对象的排序,使粗糙集理论进一步完善。仿真过程完全依照流程处理,不需人为干预,所得结果与实际的情况相符,佐证了方法的正确性。本文方法具有良好的时效性与通用性,且方法易于实现,对推进威胁等级排序的理论研究与工程实践具有借鉴意义。
参考文献
| [1] | 姜宁, 胡维礼, 孙翱. 辐射源威胁等级判定的模糊多属性方法[J].兵工学报, 2004, 25(1): 56–59.JIANG N, HU W L, SUN A. Fuzzy multiattribute method of emitter threatening grade evaluation[J].Acta Armamentarii, 2004, 25(1): 56–59.(in Chinese) |
| [2] | 黄大荣, 郭安学, 李云生, 等. 基于专家知识属性重要度的集群目标威胁评估方法[J].兵工学报, 2009, 30(10): 1357–1362.HUANG D R, GUO A X, LI Y S, et al. An object-group threat assessment method based on attribute significance of multi-field expert systems[J].Acta Armamentarii, 2009, 30(10): 1357–1362.(in Chinese) |
| [3] | 张媛, 刘文彪, 张立民. 基于主客观综合赋权的CGF态势评估建模研究[J].系统工程与电子技术, 2013, 35(1): 85–90.ZHANG Y, LIU W B, ZHANG L M. Situation assessment modeling for CGF based on the subject and objective integrated weight[J].Systems Engineering and Electronics, 2013, 35(1): 85–90.(in Chinese) |
| [4] | CHEN J, YU G H, GAO X G. Cooperative threat assessment of multi-aircrafts based on synthetic fuzzy cognitive map[J].Shanghai Jiao Tong University(Science), 2012, 17(2): 228–232.DOI:10.1007/s12204-012-1257-1 |
| [5] | 潘红华, 王建明, 朱森, 等. 目标威胁判断的模糊模式识别模型[J].兵工学报, 2004, 25(5): 576–580.PAN H H, WANG J M, ZHU S, et al. A fuzzy pattern recognition model for the threat evaluation of targets[J].Acta Armamentarii, 2004, 25(5): 576–580.(in Chinese) |
| [6] | XU Y J, WANG Y C, MIU X D. Multi-attribute decision making method for air target threat evaluation based on intuitionistic fuzzy sets[J].Journal of Systems Engineering and Electronics, 2012, 23(6): 891–897.DOI:10.1109/JSEE.2012.00109 |
| [7] | 陈洁钰, 姚佩阳, 王勃, 等. 基于结构熵和IGSO-BP算法的动态威胁评估[J].系统工程与电子技术, 2015, 37(5): 1076–1083.CHEN J Y, YAO P Y, WANG B, et al. Dynamic threat assessment based on structure entropy and IGSO-BP algorithm[J].Journal of Systems Engineering and Electronics, 2015, 37(5): 1076–1083.(in Chinese) |
| [8] | 王改革, 郭立红, 段红, 等. 基于萤火虫算法优化BP神经网络的目标威胁估计[J].吉林大学学报(工学报), 2013, 43(4): 1064–1069.WANG G G, GUO L H, DUAN H, et al. Target threat assessment using glowworm swarm optimization and BP neural network[J].Journal of Jilin University(Engineering and Technology Edition), 2013, 43(4): 1064–1069.(in Chinese) |
| [9] | 郭辉, 徐浩军, 刘凌. 基于回归型支持向量机的空战目标威胁评估[J].北京航空航天大学学报, 2010, 36(1): 123–126.GUO H, XU H J, LIU L. Target threat assessment of air combat based on support vector machines for regression[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(1): 123–126.(in Chinese) |
| [10] | 李姜, 郭立红. 基于改进支持向量机的目标威胁估计[J].光学精密工程, 2014, 22(5): 1354–1362.LI J, GUO L H. Target threat assessment using improved SVM[J].Optics and Precision Engineering, 2014, 22(5): 1354–1362.DOI:10.3788/OPE.(in Chinese) |
| [11] | FENG Z Q, LIU C G, HUANG H. Knowledge modeling based on interval-valued fuzzy rough set and similarity inference:Prediction of welding distortion[J].Journal of Zhejiang University-Science C (Computers & Electronics), 2014, 15(8): 636–650. |
| [12] | WANG J, PENG J X, LIU O. Density-based rough set model for hesitant node clustering in overlapping community detection[J].Journal of Systems Engineering and Electronics, 2014, 25(6): 1089–1097.DOI:10.1109/JSEE.2014.00125 |
| [13] | 李俊, 孟涛, 张立新, 等. 基于粗糙集规则提取的导弹武器质量性能评估方法研究[J].兵工学报, 2013, 34(12): 1529–1535.LI J, MENG T, ZHANG L X, et al. Research on evaluation method for quality and performance of missile weapon based on rough set rule extraction[J].Acta Armamentarii, 2013, 34(12): 1529–1535.(in Chinese) |
| [14] | 樊冰, 曾瑛, 唐良瑞. 基于信息熵的电力通信网脆弱性评价方法[J].电子与信息学报, 2014, 36(9): 2138–2144.FAN B, ZENG Y, TANG L R. Vulnerability assessment of power communication network based on information entropy[J].Journal of Electronics & Information Technology, 2014, 36(9): 2138–2144.(in Chinese) |
| [15] | 王展, 颜云辉, 焦学勇. 基于灰色理论的迷彩伪装多指标综合评价[J].兵工学报, 2013, 34(10): 1250–1257.WANG Z, YAN Y H, JIAO X Y. Multi-index comprehensive evaluation of camouflage based on gray theory[J].Acta Armamentarii, 2013, 34(10): 1250–1257.(in Chinese) |
| [16] | 索中英, 程嗣怡, 袁修久, 等. 优势决策信息系统规则获取方法及应用[J].兵工学报, 2015, 36(3): 539–545.SUO Z Y, CHENG S Y, YUAN X J, et al. Rule acquisition method and application of dominance decision-making information system[J].Acta Armamentarii, 2015, 36(3): 539–545.(in Chinese) |
| [17] | 文莹, 肖明清, 王邑, 等. 基于信息熵属性约简的航空发动机故障诊断[J].仪器仪表学报, 2012, 33(8): 1773–1778.WEN Y, XIAO M Q, WANG Y, et al. Aero-engine fault diagnosis based on information entropy attribute reduction[J].Chinese Journal of Scientific Instrument, 2012, 33(8): 1773–1778.(in Chinese) |
| [18] | 张文修, 仇国芳. 基于粗糙集的不确定决策[M].北京: 清华大学出版社, 2006: 26-27.ZHANG W X, QIU G F. Uncertain decision making based on rough sets[M].Beijing: Tsinghua University Press, 2006: 26-27.(in Chinese) |
| [19] | 王睿甲, 王星, 程嗣怡, 等. 基于脉冲样本图的机载RWR/ESM辐射源威胁评估[J].电光与控制, 2015, 22(6): 1–8.WANG R J, WANG X, CHENG S Y, et al. Airborne RWR/ESM threaten assessment of radiation source based on the pulse sequence pattern[J].Electronics Optics & Control, 2015, 22(6): 1–8.(in Chinese) |
