然而对于GNSS信号质量监测及GNSS射频信号模拟器测试等应用,为了高精度地测量信号本身的特性而抑制背景噪声的影响,测量接收机处理的是有用信号功率远高于噪声功率的强信号。强信号条件保证了接收机能够尽可能逼真地复现出有用信号的各种特征、精确地估计/测量出描述信号特性的所有参数[8]。这种强信号条件下接收机前端处理对有用信号产生的损耗更不容忽视,造成的信号功率损耗会对相关损耗、复用效率、调制平衡度、载噪比等多个指标的测量产生影响[9-11],且其影响很容易超过热噪声的影响。对于强信号条件下接收机前端处理引起的有用信号相关损耗,目前还没有适用的解析模型及仿真结果见诸报道。
在GNSS信号中广泛应用的二进制相位移位键控(BPSK)调制和二进制偏移载波(BOC)调制都是直接在单频载波上进行180°相移键控,因此调制后的信号具有包络恒定、时域基本脉冲波形为正弦函数的特点。以此为前提,本文研究了前端BSQ处理造成的信号相关损耗。首先,推导了不考虑量化作用时由滤波和采样引起的损耗;然后,通过仿真分析得到了强信号条件下使量化器量化误差最小/量化信噪比最高的最佳量化间隔,并推导了不考虑前端滤波作用时由量化和采样引起的损耗;最后,对于BSQ共同作用时的损耗,由于很难求出解析解,因此使用蒙特卡罗模拟方法仿真了GPS L1 C/A信号在不同带宽和量化比特数下的信号归一化相关功率,并探讨了基于仿真结果拟合得到相关损耗经验模型的方法。
1 分析模型 1.1 接收机模型 GNSS接收机的处理模型可以简化为图 1所示的框图[12]。在强信号条件下,由高增益天线接收的卫星信号(对于信号质量监测应用)或是直接送入测量接收机射频端口的强信号(对于射频信号模拟器的测试应用)经过射频前端信号调理电路(如滤波、放大、下变频等处理)后到达抗混叠滤波器。本文着重分析BSQ处理引起的信号功率损耗,而不考虑抗混叠滤波器之前的射频处理损耗。输入滤波器的信号为r(t),抗混叠限带滤波后的信号r(t)经过采样(设采样频率为fS)和量化,成为时间和幅度都离散的数字信号rq(t)。最后rq(t)和本地理想信号做相关,得到相关值Z,相关功率值即为Z2。以下通过推导Z2的解析式和对Z2进行蒙特卡罗仿真两种方法来研究BSQ引起的信号相关损耗。
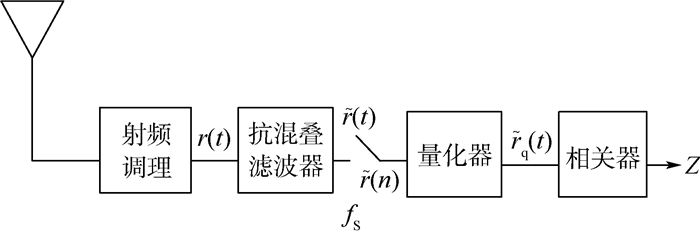 |
| 图 1 GNSS接收机信号处理模型[12] Fig. 1 GNSS receiver signal processing model[12] |
| 图选项 |
1.2 信号模型 对于正常的弱信号条件下的BSQ损耗,采用等效基带模型往往可以简化分析过程[3-4]。但是在强信号条件下,不同量化比特数对载波解调结果的影响显著、不可忽略;若仍将BPSK和BOC信号等效到基带来分析,则由于等效后的基带信号幅值波动范围很小,信号电平可以认为只能取正负两个电平值,因此多比特量化的效果和1比特量化没有明显区别,不符合实际情况。因此,不失一般性,本文从中频信号的角度展开研究。输入的导航信号r(t)可以表示为
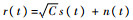
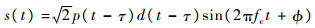 | (1) |
式中:p(t)为伪码序列或者调制了BOC副载波的伪码序列;d(t)为导航电文数据;τ为基带信号的延迟时间;fc为载波频率;Φ为初始载波相位。
以下在分析有用信号功率损耗的时候,可以舍去输入信号r(t)中的噪声项,即
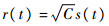 | (2) |
2 理论分析与仿真 2.1 不考虑量化作用时的信号损耗 设抗混叠滤波器的冲击响应为h(t),则输入信号通过滤波器后可以表示为
 | (3) |
滤波后的信号经采样得到
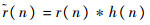 | (4) |
在高比特数量化时,可以认为量化器对输入信号的量化作用没有失真,r(n)直接与本地理想信号sI(t)的采样信号sI(n)进行相关运算。sI(n)可以表示为
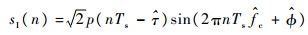 | (5) |
式中:Ts为采样周期;
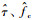
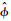
r(n)与sI(n)的相关值
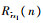
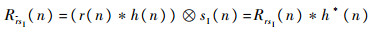 | (6) |
式中:h*(n)表示h(n)的共轭。
因此,相关值Z可以表示为
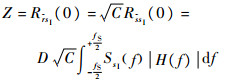 | (7) |
式中:D为调制的数据位;
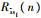
这里需注意的是,对于线性相移特性的滤波器,式(7)即为相关器输出的理论值。对于非线性相移特性的滤波器,由于受到信号失真的影响,接收机稳态跟踪下实际参与鉴相器运算的相关值与滤波器群时延特性和相关器间距有关[13-14],与式(7)得出的值有一定出入,其计算较为复杂,也超出了本文的讨论范围。
相关器输出的信号功率为Z2,则相关损耗为
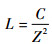 | (8) |
将式(7)代入式(8),得到不考虑量化作用时的信号相关损耗为
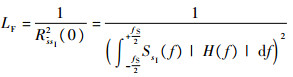 | (9) |
实际接收机收到的卫星信号并非如式(1)所示的理想信号,例如卫星上的滤波器将信号限制在发射带宽以内,设卫星上产生的理想信号经过传输函数为Hc(f)的信道(包括卫星发射链路滤波器、星地链路传输特性及接收天线传输特性)到达接收机滤波器,则这一部分信道造成的信号相关损耗为
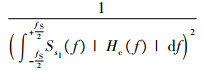 | (10) |
因此,LF可以重新表示为
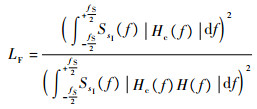 | (11) |
2.2 不考虑滤波作用时的信号损耗 量化是一个非线性、不可逆的一个过程,对于图 2所示的均匀量化器,横轴x表示量化器输入值,纵轴y表示量化器输出值,Q为量化间隔。用V表示量化器的最大量化电平,量化电平数为N,则量化间隔可以表示为
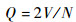 | (12) |
在接收机对于同一输入信号的前端处理过程中,采用不同的前端滤波器带宽会导致不同的量化误差。这里首先不考虑前端滤波的影响(滤波器带宽足够宽)分析量化器对于强信号的处理特性。
BPSK和BOC信号的时域波形是在正弦波上进行180°相位调制,由于量化器的幅度对称性,量化损耗对输入信号的符号不敏感,因此可以用正弦波替代BPSK和BOC信号进行分析。以3比特量化为例,采用图 2所示的量化器,输入幅度归一化的正弦信号sin(t)、量化器输出信号q(t)和量化误差如图 3所示,其中T为周期数。
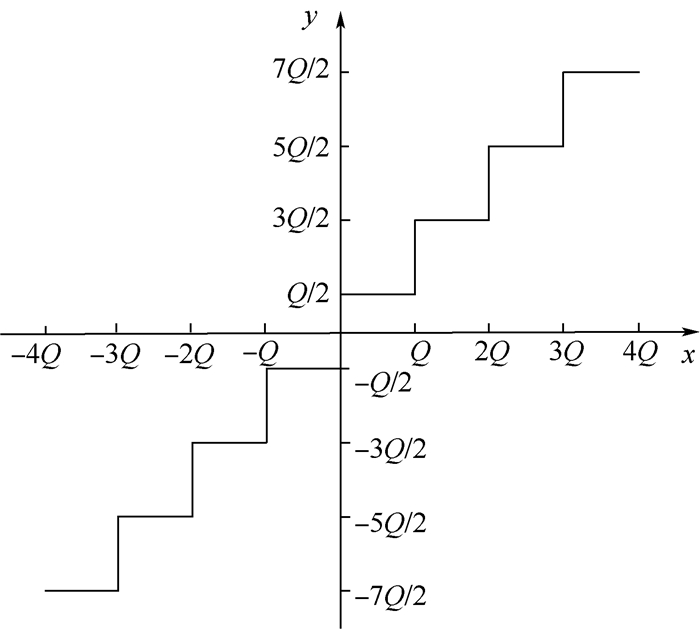 |
| 图 2 均匀量化器输入输出特性曲线 Fig. 2 Input-output characteristic curve of a uniform quantizer |
| 图选项 |
 |
| 图 3 3比特量化 Fig. 3 3 bit quantization |
| 图选项 |
由图 3可知,由于正弦曲线的非线性变化,量化误差在正弦信号的波峰附近与过零点附近的变化特性有着明显差异。适当调节V值,可以在量化比特数一定的情况下,使量化误差功率最小。即采用式(13)计算使量化误差功率σq2最小的量化器最佳V值[15]。
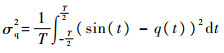 | (13) |
通过仿真可得正弦信号sin(t)在各量化比特数N下的最佳V值和相应的量化信噪比(SQNR)如表 1所示。从表中可以发现,随着N的增加,V趋近于1, 且每增加一个量化比特数,SQNR增加约6 dB。由表 1中的V值和式(12)可以得到最佳量化间隔值。
表 1 最佳V值 Table 1 Optimal V
| N | V | SQNR/dB |
| 1 | 1.273 1 | 7.221 6 |
| 2 | 1.138 2 | 13.776 5 |
| 3 | 1.071 2 | 20.003 0 |
| 4 | 1.037 0 | 26.077 2 |
| 5 | 1.019 0 | 32.085 8 |
| 6 | 1.009 9 | 38.071 0 |
| 7 | 1.005 2 | 44.051 7 |
| 8 | 1.002 5 | 50.034 9 |
| 9 | 1.001 2 | 56.020 6 |
| 10 | 1.000 7 | 62.076 1 |
表选项
采样和量化分别是对时间和幅度的离散,可以对这两个过程交换顺序进行分析。对于无滤波的强信号来说,量化器输入信号的载波为图 3中正弦信号sin(t)形式,量化器输出为q(t)形式。
对周期信号q(t)进行傅里叶级数展开:
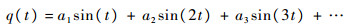 | (14) |
式中:
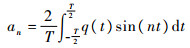 | (15) |
因此,强信号r(t)采样量化后可以表示为
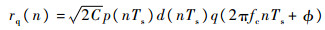 | (16) |
与本地理想信号相关之后,得到相关值:
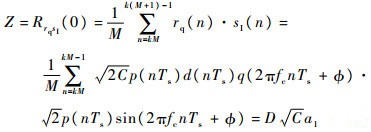 | (17) |
式中:M为第k个相关周期的相关点数;a1为式(14)中傅里叶展开式第一项的系数。
将式(17)代入式(8), 得到不考虑滤波作用时的损耗为
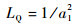 | (18) |
对于不同量化比特数,取最佳V值时,将q(t)进行傅里叶级数展开后,得到a1的取值如表 2所示。
表 2 最佳V值时a1的取值 Table 2 a1 for each optimal V
| N | V | a 1 |
| 1 | 1.273 1 | 0.810 48 |
| 2 | 1.138 2 | 0.958 12 |
| 3 | 1.071 2 | 0.989 98 |
| 4 | 1.037 0 | 0.997 56 |
| 5 | 1.019 0 | 0.999 36 |
| 6 | 1.009 9 | 0.999 86 |
| 7 | 1.005 2 | 0.999 98 |
| 8 | 1.002 5 | 0.999 99 |
| 9 | 1.001 2 | 0.999 99 |
| 10 | 1.000 7 | 1 |
表选项
2.3 BSQ共同作用时的损耗 一般情况下,接收机前端滤波器带宽并非无限大,量化比特数也是有限的,当BSQ共同作用时,情况比较复杂。滤波器的带限效应会使信号在码片翻转处产生振铃效应,同时信号的幅度过冲会使量化器过载。过冲的幅度随着前端带宽的增大而减小,最后趋于一个固定值,这即是吉布斯现象。
由式(11)和式(18)的表达式可以看出,在采样率大于奈奎斯特频率时,采样对于信号功率没有损耗,因此仅需分析量化和滤波作用产生的损耗。采用蒙特卡罗模拟方法,可以从统计的角度观察二者共同作用的效果。本文采用自研的数字中频信号软件模拟器和软件接收机作为闭环测试系统仿真了GPS L1 C/A信号在不同带宽和量化比特数下输出的归一化相关功率值,结果如表 3所示。仿真中模拟器输出信号未加噪声,滤波器采用基于hamming窗的46阶有限长单位冲激响应(FIR)滤波器,量化器V值仍采用表 1的值;信号中频为12.36 MHz,采样率为50 MHz。需说明的一点是,能够使接收机正常工作的不同中频和采样率配置并不影响表 3的结果。
表 3 相关器输出信号归一化功率值 Table 3 Normalized power of output signal of correlator
| N | 带宽/MHz | 无滤波 | ||||
| 2 | 4 | 6 | 8 | 10 | ||
| 1 | 0.526 6 | 0.583 4 | 0.611 9 | 0.623 0 | 0.625 4 | 0.656 0 |
| 2 | 0.647 2 | 0.756 9 | 0.818 3 | 0.846 9 | 0.856 5 | 0.919 2 |
| 3 | 0.691 5 | 0.810 6 | 0.877 2 | 0.909 7 | 0.916 6 | 0.978 1 |
| 4 | 0.710 0 | 0.831 5 | 0.897 7 | 0.923 5 | 0.934 8 | 0.995 7 |
| 5 | 0.718 7 | 0.839 0 | 0.903 8 | 0.930 8 | 0.939 7 | 0.998 8 |
| 6 | 0.722 4 | 0.842 7 | 0.906 6 | 0.933 0 | 0.942 2 | 0.998 5 |
| 7 | 0.724 4 | 0.844 8 | 0.908 0 | 0.933 8 | 0.943 5 | 0.998 5 |
| 无量化 | 0.764 3 | 0.869 1 | 0.924 7 | 0.947 7 | 0.954 9 | 0.999 0 |
表选项
对于表 3中无滤波和无量化情况下的理论值可以通过式(7)和式(17)中的Z值计算Z2得到。其理论值和仿真结果的对比如表 4和表 5所示。
表 4 无量化时相关功率的理论值与仿真值 Table 4 Theoretical and simulated correlation power without quantization
| 带宽/MHz | 相关功率 | |
| 理论值 | 仿真值 | |
| 2 | 0.765 3 | 0.764 3 |
| 4 | 0.870 2 | 0.869 1 |
| 6 | 0.925 9 | 0.924 7 |
| 8 | 0.949 0 | 0.947 7 |
| 10 | 0.956 4 | 0.954 9 |
表选项
表 5 无滤波时相关功率的理论值与仿真值 Table 5 Theoretical and simulated correlation power without band-limiting
| N | 相关功率 | |
| 理论值 | 仿真值 | |
| 1 | 0.656 9 | 0.656 0 |
| 2 | 0.918 0 | 0.919 2 |
| 3 | 0.980 1 | 0.978 1 |
| 4 | 0.995 1 | 0.995 7 |
| 5 | 0.998 7 | 0.998 8 |
| 6 | 0.999 7 | 0.998 5 |
| 7 | 1 | 0.998 5 |
表选项
表 3给出了强信号条件下接收机输出归一化功率的参考,其倒数即为相应的损耗值。表 3表明,随着量化比特数和带宽的增加,相关器输出信号功率增加,但增加的速度越来越缓慢。7比特量化和无量化时功率有微小差异,这是因为按照表 1取V值的情况下,量化器过载使功率产生的额外损耗逐渐占据主导地位。从表 4和表 5可以看出,无量化/无滤波时得到的仿真结果很好地符合理论值,式(7)和式(17)的估计精度达到了0.2%,从而验证了理论分析的正确性。
为了简化分析,人们希望得到关于BSQ共同作用时信号损耗的解析表达式从而无需进行具体的仿真即可对损耗的大小做出评估。如文献[5]所言,在传统分析弱信号条件下前端处理损耗时,往往将量化损耗和滤波损耗相乘得到二者共同作用损耗的估计值[1, 7],这会造成估计损耗比实际损耗值小。强信号条件下也是如此,由于滤波器对信号时域波形的改变,在量化器和滤波器共同作用的时候,并不能简单地用无量化和无滤波时的信号损耗理论值相乘得到二者共同作用的损耗。通过对大量仿真结果的分析发现,将量化损耗和滤波损耗相乘后再乘以一个与滤波器相关的修正项Lm可以得到相对精确的估计结果。此时相关器输出的归一化功率可以表示为
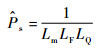 | (19) |
Lm和具体的滤波器类型及参数有关,可表示为
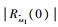
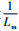
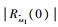
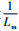
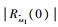
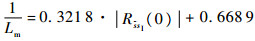 | (20) |
将式(9)、式(18)、式(20)代入式(19),并用式(19)对表 3中的相应带宽和量化比特数的功率估计时,其估计的相对误差如表 6所示。由结果可知,式(19)对相关器输出的信号功率估计具有较高的估计精度,仅在1比特量化且带宽较窄时估计的误差较大。究其原因,首先,1比特量化器仅判断输入信号的符号,此时滤波器对输出功率的影响减弱,造成根据式(19)估计的相关功率过低;其次,滤波器带宽较窄时,信号过冲和振荡引起的量化过载更严重,造成根据式(19)估计的相关功率偏高。
表 6 式(19)的估计误差 Table 6 Estimation error of equation (19)
| N | 带宽/MHz | ||||
| 2 | 4 | 6 | 8 | 10 | |
| 1 | -0.092 6 | -0.050 4 | -0.034 3 | -0.016 9 | -0.011 9 |
| 2 | 0.031 6 | 0.022 7 | 0.009 0 | 0.010 5 | 0.008 2 |
| 3 | 0.030 9 | 0.019 6 | 0.004 9 | 0.004 4 | 0.005 8 |
| 4 | 0.019 4 | 0.009 2 | -0.002 9 | 0.004 5 | 0.001 3 |
| 5 | 0.010 7 | 0.003 8 | -0.006 0 | 0.000 3 | -0.000 2 |
| 6 | 0.006 5 | 0.000 4 | -0.008 1 | -0.001 0 | -0.001 8 |
| 7 | 0.004 0 | -0.001 7 | -0.009 4 | -0.001 6 | -0.002 9 |
表选项
当量化滤波共同作用时,GPS L1 C/A信号相关损耗的估计式可以表示为
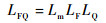 | (21) |
尽管上述仿真结果是基于GPS L1 C/A BPSK(1)信号得到的,但是由于BPSK和BOC信号都是在正弦载波上进行180°相位调制,接收机前端对其信号功率损耗有相同的作用机制,因而式(21)适用于所有BPSK(n)和BOC(m, n)信号。
另外,本节的仿真虽然选用了46阶hamming窗FIR滤波器,但式(21)所表示的分析方法对于其他类型的滤波器上也是适用的。通过仿真方法确认Lm后,即可定量地分析量化滤波过程带来的信号相关损耗。
3 结论 本文针对高精度GNSS信号质量监测和射频信号模拟器测试的应用需求,选择接收机BSQ输入及相关器输出为参考点,研究了强信号条件下接收机带限滤波、采样、量化过程造成的信号相关损耗。
1) 通过理论分析,分别给出了无滤波作用时和无量化作用时,相关损耗的解析表达式,并通过仿真结果验证了理论分析的正确性。
2) 对于滤波、采样和量化共同作用的情况,使用蒙特卡罗模拟方法仿真了不同滤波器带宽和量化比特数下GPS接收机相关器输出的归一化功率参考值,并探讨了根据仿真结果拟合得到相关损耗计算公式的方法,可以作为简化定量分析的手段。
参考文献
| [1] | BETZ J W.Bandlimiting, sampling, and quantization for modernized spreading modulations in white noise[C]//Proceedings of the Institute of Navigation National Technical Meeting.Manassas, VA:ION, 2008:981-991. |
| [2] | VAN DIERENDONCK A J.GPS Receivers, Chapter 8.Global positioning system:Theory and applications, Vol.I[M].PARKINSON B W, SPILKER J J.Reston:AIAA, 1996:329-407. |
| [3] | HEGARTY C J. Analytical model for GNSS receiver implementation losses[J].Navigation:Journal of the Institute of Navigation, 2011, 58(1): 29–44. |
| [4] | HEGARTY C J, CERRUTI A P.Results from an analytical model for GNSS receiver implementation losses[C]//Proceedings of the 23rd International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2010:2820-2834. |
| [5] | CURRAN J, BORIO D, MURPHY C C.Front-end filtering and quantisation effects on GNSS signal processing[C]//Proceedings of the 20091st International Conference on Wireless Communication, Vehicular Technology, Information Theory and Aerospace and Electronic Systems Technology, Wireless VITAE 2009.Piscataway, NJ:IEEE Press, 2009:227-231. |
| [6] | CURRAN J, BORIO D, LACHAPELLE G, et al. Reducing front-end bandwidth may improve digital GNSS receiver performance[J].IEEE Transactions on Signal Processing, 2010, 58(4): 2399–2404.DOI:10.1109/TSP.2009.2037860 |
| [7] | BETZ J W, SHNIDMAN N R.Receiver processing losses with bandlimiting and one-bit quantization[C]//Proceedings of the Institute of Navigation ION-GNSS-2007.Manassas, VA:ION, 2007:1244-1256. |
| [8] | KOU Y H, SUI J T, CHEN Y B, et al.Test of pseudorange accuracy in GNSS RF constellation simulator[C]//Proceedings of the 25th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2012:161-173. |
| [9] | SOELLNER M, KURZHALS C, HECHENBLAIKNER G, et al.GNSS offline signal quality assessment[C]//Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2008:909-920. |
| [10] | BUTMAN S, TIMOR U. Interplex-An efficient multichannel PSK/PM telemetry system[J].IEEE Transactions on Communications, 1972, 20(3): 415–419.DOI:10.1109/TCOM.1972.1091213 |
| [11] | PARTRIDGE M D, DAFESH P A.Code power measurement methodology for GPS block ⅡR-M and ⅡF on-orbit test procedures[C]//Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2001:2764-2772. |
| [12] | 谢刚. GPS原理与接收机设计[M].北京: 电子工业出版社, 2009: 237-241.XIE G. Principles of GPS and receiver design[M].Beijing: Publishing House of Electronics Industry, Beijing, 2009: 237-241.(in Chinese) |
| [13] | RAPISARDA M, ANGELETTI P, CASINI E.A simulation framework for the assessment of navigation payload non-idealities[C]//2nd Workshop on GNSS Signals & Signal Processing-GNSS SIGNALS.Noordwijk:ESTEC, 2007:24-25. |
| [14] | SOELLNER M, KOHL R, LUETKE W, et al.The impact of linear and non-linear signal distortions on Galileo code tracking accuracy[C]//Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation.Manassas, VA:ION, 2002:1270-1285. |
| [15] | PROAKIS J, MANNLAKIS M. Digital signal processing:Principles, algorithms and applications[M].4th edEnglewood Cliffs, NJ: Prentice Hall, 2006: 24-25. |
