近年来,翼尖涡不稳定特性及控制是流体力学研究的热点问题。Crow等[2, 3]最早对反向旋转的飞机尾涡系统进行了系统的研究,提出了长波不稳定性的观点。他们认为若仅依靠黏性耗散,旋涡强度不会发生显著衰减;而在外界扰动的作用下,涡管会发生失稳变形,随着涡管向下游发展,其变形幅度逐渐变大,最终2根相邻涡管对接、破裂并形成涡环,涡强迅速减小,即:涡对经历了“稳定阶段—不稳定线性放大阶段—非线性发展阶段”,最终形成小尺度湍流并被黏性耗散掉。基于Crow等的研究,Widnall等[4, 5]提出了另一种不稳定模态,即短波不稳定性,其波长远小于长波不稳定性,通常由一个涡对另一个涡的应力作用触发而产生,表现为涡核的微幅振荡。Leweke和Williamson[6]的研究表明,工程实际中,反向旋转涡对的空间形态通常表现为长波和短波不稳定2种模态的相互耦合。
不稳定模态通常表现出特定的时间尺度特征。传统的展向脉冲射流[7]、活动元件振荡[8]和合成射流[1]等翼尖涡控制技术,主要是通过在机翼翼尖附近施加周期性扰动,在特定频率和强度下,翼尖涡涡核的空间位置、涡核半径和涡量峰值等会发生显著变化。为保证施加的外部扰动与翼尖涡的不稳定模态发生作用,需要明确知道原始流场中涡对的不稳定时间尺度,即不稳定模态频率。
基于上述原因,本文主要通过定量化流动显示技术研究翼尖涡在低雷诺数下的不稳定特性。基于翼尖涡流场灰度信息,首先采用模式识别方法追踪涡核中心位置的时间演化;其次使用动力学模态分解(Dynamic Mode Decomposition,DMD)方法直接从流动显示灰度场中提取涡核的振荡频率信息,并与模式识别方法进行对比验证。本文工作将为后续翼尖涡不稳定演化的研究提供必备的研究手段。
1 实验技术和数据后处理方法1.1 实验技术实验在北京航空航天大学低速回流式水洞中进行,该水洞实验段长12 m,横截面为1.2 m×1 m的长方形。水洞自由来流速度可在0~50 cm/s的范围内无级调节,实验段湍流度不超过0.8%。该水洞进行过大量条带稳定性方面的实验研究,流场品质满足旋涡稳定性实验要求[9]。实验模型为三维椭圆机翼,如图 1所示,机翼截面为低雷诺数翼型E387,展长b=6 cm,翼根弦长c=3.5 cm。机翼模型由3D打印制作,模型表面进行了抛光处理。实验装置示意图如图 2所示,其中x、y和z分别代表流向、法向和展向方向。以机翼模型根弦长后缘作为坐标原点。模型通过连接杆固连在攻角装置上,机翼攻角可在-20°~20°范围内调整。
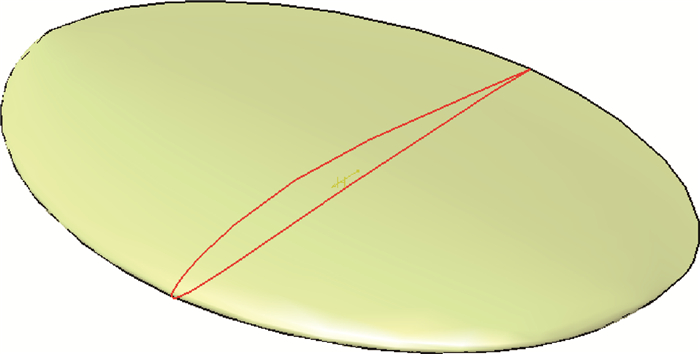 |
| 图 1 椭圆机翼模型 Fig. 1 Elliptical wing model |
| 图选项 |
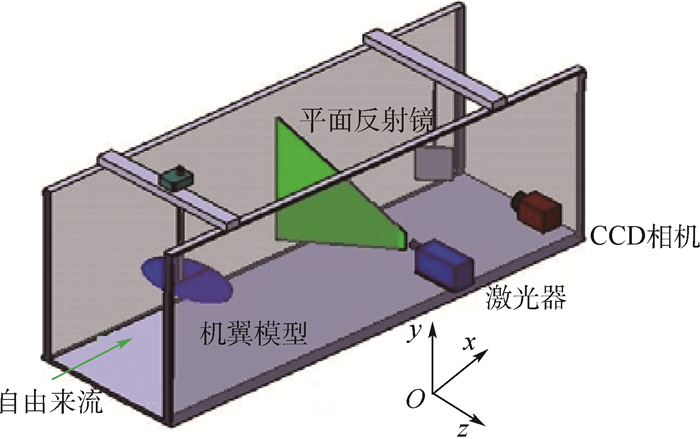 |
| 图 2 实验装置示意图 Fig. 2 Schematic of experimental setup |
| 图选项 |
传统的流动显示方法,例如染色液方法[10],需要在模型表面开孔,或者引入导管,不可避免地会对流场引入额外的扰动。为避免外界扰动对旋涡稳定性的影响,本实验使用了染色剂表面涂层方法来定性显示翼尖涡涡核的形态,具体方法是:将少量罗丹明染料和芦荟胶混合均匀,然后均匀涂抹于机翼模型翼尖处;模型置于水洞中后,胶状混合物逐渐溶解于水,染料被释放到周围流体中。由于旋涡的卷携作用,染料被逐渐卷入涡核中心,从而显示出涡核附近的结构。需要说明的是,表面涂层非常薄,厚度小于0.1 mm,在低雷诺数条件下涂层并不影响机翼表面的流动。涂层可稳定持续释放荧光染料超过20 min,足以保证实验图像的采集。
流动显示的照明光源为半导体激光器,提供波长为532 nm的连续激光,输出能量为8 W,通过透镜组产生厚度约为1 mm的平面片光,垂直来流方向照亮实验段横截面。片光下游60 cm处竖直安装一个45°倾斜的光学平面反射镜。分辨率为2 456像素×2 058像素的CCD相机(相机型号IMPERX B2520)通过平面反射镜反射记录激光片光照亮的流动图像,相机配备45 mm尼康定焦镜头。图像采样频率为14 Hz。根据不同来流速度,曝光时间间隔Δt在2~10 ms范围内调整。相机拍摄的物理平面的视野范围为9 cm×12 cm(y-z平面),图像空间分辨率约为21像素/mm。
图 3为采用上述流动显示方法得到的垂直于旋涡轴线的翼尖涡涡对图像。从图中可以看出,荧光染料逐渐卷入旋涡中心,轨迹清晰,涡核中心为高浓度的染料,涡对中间区域为机翼后缘脱落的剪切层,翼尖涡保持层流状态。
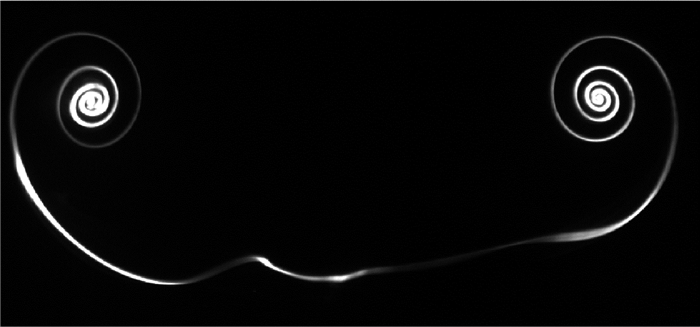 |
| 图 3 反向旋转翼尖涡对流动显示 Fig. 3 Flow visualization of counter-rotating wing-tip vortex pair |
| 图选项 |
研究类似翼尖涡这种拉格朗日流动结构,通常有2种观测方法:一种是拖曳实验;另一种是在固定截面定点观测。相比拖曳实验,定点观测有以下3点优势:①可针对涡对运动进行固定站位的长时间统计观测;②可避免拖曳实验中拖车启动停止对流场的扰动;③由于涡对的诱导作用,翼尖涡卷起后会以速度w=Γ/2πb0(Γ为翼尖涡环量,b0为涡核中心间距)下沉,进行拖曳实验需要保证足够的视野范围,这对实验观测设备提出很高的要求。当前实验采用定点观测方法对垂直于流向的翼尖涡切面进行长时间观测统计。在固定流向站位观测时,涡对的平均法向高度并不会改变,由于涡对自身的不稳定性,涡对仅会在平均的涡核中心空间位置附近波动。观测平面布置在距离机翼后缘50 cm处,总共进行了4个攻角(2°,4°,6°,8°)、2个流速(5 cm/s,10 cm/s)的实验观测,基于翼根弦长和自由来流速度的特征雷诺数Re≈1 750,3 500。
1.2 模式识别技术模式识别技术是辨识并追踪流动相干结构的一种常用数据后处理方法,主要的应用包括边界层中展向涡识别[11]和圆柱尾迹中卡门涡街的追踪[12]等。
模式识别技术通常针对某一类物理场数据,例如速度场、涡量场及灰度场数据。首先需要定义或者构建数学模型对需要识别的流动结构做初始估计,然后基于互相关计算在相邻2帧数据之间进行匹配分析,由此可以得到流动结构的空间位置。
本文基于流动显示的翼尖涡灰度场数据,利用模式识别技术连续追踪翼尖涡涡核中心在不同时刻的空间位置,具体操作如下:首先,在第1帧图像上,选定大小为100像素×100像素并包含翼尖涡涡核中心的矩形区域作为初始模型,如图 4中小正方形框包含的区域;然后,在下一帧图像中进行互相关匹配,找到初始模型在下一帧图像上的空间位置,以此类推,通过在连续2帧图像间进行匹配,可以得到翼尖涡涡核区域在不同时刻的空间位置;最后,通过计算涡核区域灰度值权重中心,可以得到涡核中心的空间位置坐标,如图 4中“+”所示。需要说明的是,为了节省计算时间,根据翼尖涡振荡的幅值,人工设定一更大的区域作为互相关计算区域,如图中点划线正方形框所示,而不是在整个图像上进行互相关匹配。由于涡对的形态随时间变化相对比较稳定,相邻2帧之间无量纲化的互相关系数均大于0.9,基于灰度场的涡核中心识别方法被证明是可行的。
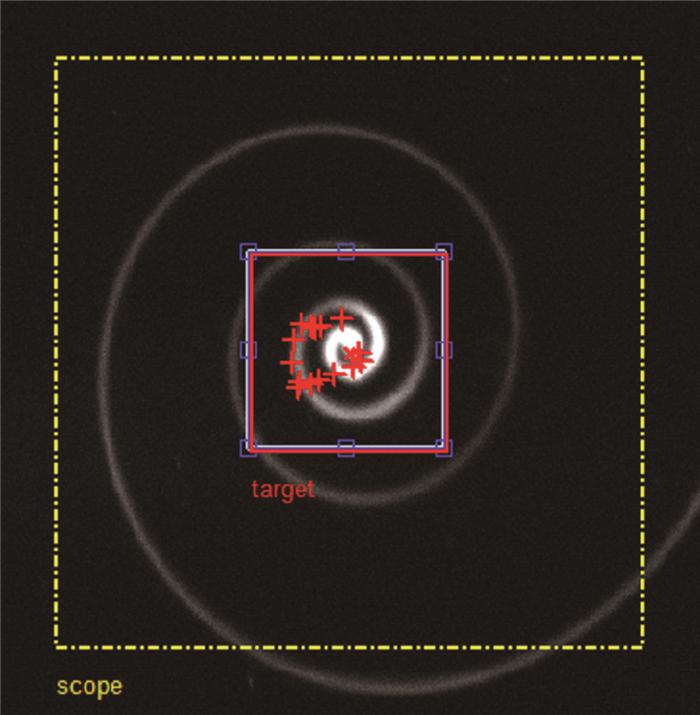 |
| 图 4 模式识别技术追踪翼尖涡涡核中心 Fig. 4 Illustration of pattern recognition technique for tracking wing-tip vortex core center |
| 图选项 |
1.3 DMD技术DMD技术是Schmid等[13, 14]最近提出的一种针对流体动力学系统的模态分解技术。DMD技术基于瞬时流场数据,能够分离、提取复杂流场中暗含的动力学信息而无需知道流动控制方程[15],这对于理解复杂流动机理提供了极大的便利。
以速度场为例简单介绍DMD原理。更多有关DMD分解原理可参见文献[14, 15]。DMD技术通过一系列矩阵运算将时空变化的速度项u(x,t)分解成2个独立项,其中一项与时间变化有关,即时间系数项(ai(t)),另外一项与空间分布(φi(x))有关,即

DMD方法通过时空解耦,将流场分解为不同的空间模态以及时间系数,每一模态对应的时间项暗含模态频率、增长(衰减)率以及能量信息,因此,DMD可以定量地刻画流场中存在的不同尺度流动结构的增长/衰减及频率特性。
DMD方法已被大量应用到复杂流场的定量分析中,如Gurney襟翼尾迹涡脱落频率测量[15]、高速列车尾流频谱分析[16]和边界层旁路转捩扰动分析[17]等。本文中,将DMD技术应用到翼尖涡图像的灰度场数据中,提取翼尖涡涡核振荡的频率信息。
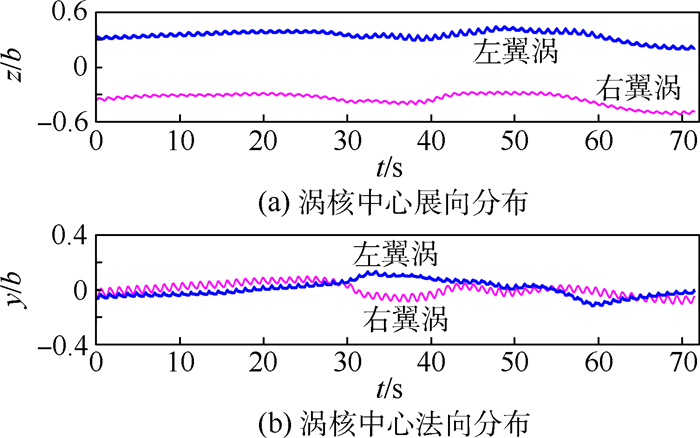
2 实验结果与讨论2.1 基于模式识别的不稳定频率辨识采用1.1节介绍的流动显示方法,对垂直于流向的翼尖涡截面图像进行连续纪录,纪录时长为72 s,采集的总的图像序列为1 000帧,图 3为一个典型的翼尖涡对图像。基于翼尖涡灰度图像序列,采用模式识别技术提取涡核中心在y-z平面的空间位置。图 5(a)、图 5(b)给出了攻角α=8°、自由来流速度V∞=5 cm/s工况下,左右涡核中心在展向和法向方向的空间位置随时间的变化过程(纵坐标的长度单位采用机翼展长无量纲化)。从图中可以看出,有2种明显的不稳定波动,即长波不稳定和短波不稳定,同时存在于翼尖涡的运动模态中。Breitsamter[1]按照不稳定波长来划分不稳定模态,长波:λ/b0>2π,短波:π/2>λ/b0>π/4,λ为波长。高频的涡核振荡属于短波不稳定性,低频长周期的涡对摆动属于长波不稳定性。与Leweke和Williamson[6]类似,当前实验中同样观测到长波与短波不稳定模态的耦合(如图 5所示),高频的涡核振荡耦合在低频涡对摆动中。相比于短波,长波的波动振幅明显更大,振幅大约为0.1b。在展向方向(z方向),左右涡对的长波摆动近似呈反对称;而在法向方向(y方向)则呈近似对称。翼尖涡涡核中心平均间距为0.72b。理论计算给出的椭圆机翼翼尖涡涡心间距为d/b=π/4[3](d为涡对间距),与实验测量结果存在一定差异,实验测量结果略小于理论值。
 |
| 图 5 翼尖涡涡核中心空间位置分布 Fig. 5 Spatial position distribution of wing-tip vortex core center |
| 图选项 |
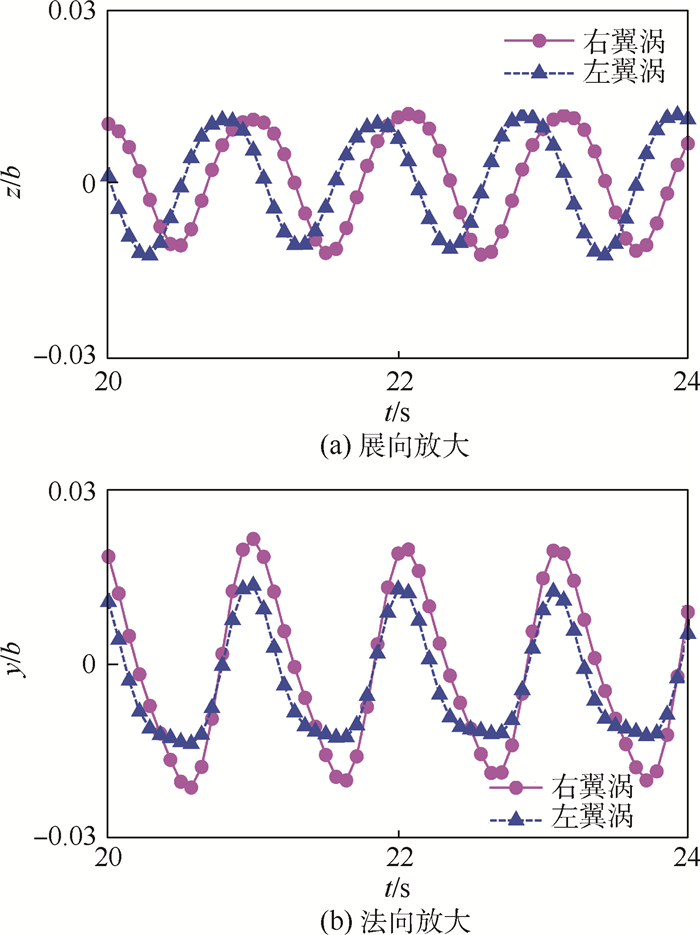
当前实验重点关注短波不稳定特性。通过计算每一瞬时涡核中心展向间距dz和法向间距dy,在原有数据点上减去展向和法向半间距,剔除掉长波的影响,得到短波不稳定模态下涡核中心的空间位置分布,如图 6所示,短波的振幅最大不超过机翼展长的4%。图 7给出了涡核中心短波振荡的放大图。在展向方向,如图 7(a)所示,涡核中心存在约π/2的相位差;而在法向方向,如图 7(b)所示,涡核中心几乎同相位。
 |
| 图 6 翼尖涡涡核中心短波不稳定性空间位置分布 Fig. 6 Spatial position distribution of wing-tip vortex core center for short-wave instability |
| 图选项 |
 |
| 图 7 翼尖涡涡核中心短波不稳定性放大图 Fig. 7 Zoom-in view for short-wave instability of wing-tip vortex core center |
| 图选项 |
从图 6、图 7可以看出,左右翼尖涡涡核中心振幅并不完全对称,且振幅随时间发生变化。这样的非对称性在实验观测中普遍存在。通常来讲,对于这种类似机翼翼尖涡的稳定性实验,测量的主要误差来源有以下3个方面:自由来流中的扰动、机翼支撑装置的扰动及机翼后缘分离剪切层的扰动,这样的误差在当前实验中不可避免。尽管如此,实验并未观测到转捩等现象,翼尖涡保持良好的层流状态,而且上述的非对称性并不影响涡核振荡频率和相位的测量。
对短波模式下翼尖涡涡核中心空间位置进行谱分析,可得涡核中心短波振荡的不稳定频率。图 8(a)、图 8(b)分别给出了左右翼尖涡展向和法向短波不稳定性的能谱特性。如图 8所示,展向方向上,左右翼尖涡振荡的特征频率均为0.952 Hz;法向方向为0.966 Hz。此外,均出现能量集中的高次谐波。
 |
| 图 8 涡核中心空间位置坐标能谱 Fig. 8 Energy spectrum of spatial displacement of vortex core center |
| 图选项 |
2.2 基于DMD的不稳定频率辨识2.1节通过模式识别技术追踪每一时刻翼尖涡涡核中心的空间位置,然后分离出短波不稳定模态,进而进行快速傅里叶变换(FFT),得到的翼尖涡特征频率精确,是一种单点的局部分析方法,但是实现起来比较复杂。相比于单点分析方法,DMD技术是一种全局特征辨识与分离方法。本文将DMD技术直接应用到灰度图像的分析上。DMD技术将瞬时场数据分解为不同的模态,并且可以得到不同模态的频谱特性。图 9给出了相同工况下翼尖涡涡核中心振荡的DMD能谱特性。横坐标fi代表某一模态的特征频率,纵坐标||ai||是该模态时间系数的范数,代表这一模态所具有的能量。如图 9所示,能量峰值所对应的主频为f1=0.924 Hz,即涡核振荡的短波频率。其他的高频能量峰值对应2倍频和3倍频等高阶谐波。
 |
| 图 9 DMD能谱 Fig. 9 DMD energy spectrum |
| 图选项 |
对比图 8和图 9,DMD得到的主频与单点谱分析得到的主频存在一定误差,误差的主要来源为本实验的图像采集频率过低。在对实验数据进行DMD分解之前,Pan等[18]对DMD算法进行了系统的误差分析,研究结果表明,DMD对数据分解的精度依赖于输入的数据质量,在一定的范围内,数据的采集频率越高,误差越小。对于当前实验,由于CCD相机采集频率所限,本实验最大采样频率为14 Hz,但是DMD分解得到的频率已经非常接近单点分析的结果,相对误差最大不超过5%。
2.3 翼尖涡不稳定频率的影响规律采用上述单点谱分析方法和DMD技术,分别计算了4个攻角(2°,4°,6°,8°)、2个自由来流速度(V∞=5,10 cm/s)下翼尖涡涡核振荡的无量纲频率,表 1和图 10分别给出了2种方法的计算结果(单点谱分析方法给出的是左右翼尖涡法向无量纲频率),结果表明无量纲频率随雷诺数增大而增大;随机翼攻角增大而减小,且近似呈线性减小。
表 1 翼尖涡涡核振荡无量纲频率 Table 1 Non-dimensional frequency of wing-tip vortex core oscillation
| 攻角/(°) | V∞=5 cm/s | V∞=10 cm/s | ||
| 单点谱分析 | DMD分析 | 单点谱分析 | DMD分析 | |
| 2 | 1.708 | 1.747 | 2.020 | 2.033 |
| 4 | 1.516 | 1.579 | 1.944 | 1.932 |
| 6 | 1.313 | 1.310 | 1.793 | 1.747 |
| 8 | 1.159 | 1.109 | 1.658 | 1.663 |
表选项
 |
| 图 10 翼尖涡涡核中心振荡无量纲频率对比 Fig. 10 Comparison of non-dimensional frequency of wing-tip vortex core oscillation |
| 图选项 |
3 结 论本文通过水洞实验,采用流动显示技术对垂直于流向的翼尖涡截面流场进行了观测,研究了翼尖涡涡对的不稳定频率特性;分别采用模式识别方法和动力学模态分解技术提取了涡核中心振荡的特征频率。研究结果表明:
1) 在低雷诺数下,翼尖涡涡对的不稳定运动通常表现出短波与长波2种模态,高频的涡核振荡耦合在低频涡对摆动中。
2) 在当前的实验条件下,产生了层流翼尖涡对,通过模式识别方法识别出涡核中心进而得到涡核不稳定振荡的频率。将动力学模态分解技术应用于流动显示图像,也可提取出不稳定频率信息,与单点分析方法相比,DMD方法具有更强的适用性,且精度有保证。
3) 从现有的8个实验工况来看,涡核振荡的无量纲频率随机翼攻角增大而减小,随雷诺数增大而增大。
参考文献
| [1] | BREITSAMTER C. Wake vortex characteristics of transport aircraft[J].Progress in Aerospace Sciences,2011,47(2):89-134. |
| Click to display the text | |
| [2] | CROW S C. Stability theory for a pair of trailing vortices[J].AIAA Journal,1970,8(12):2172-2179. |
| Click to display the text | |
| [3] | CROW S C, BATE E R.Lifespan of trailing vortices in a turbulent atmosphere[J].Journal of Aircraft,1976,13(7):476-482. |
| Click to display the text | |
| [4] | WIDNALL S E, BLISS D,TSAI C Y.Instability of short-waves on a vortex ring[J].Journal of Fluid Mechanics,1974,66(Part 1):35-47. |
| Click to display the text | |
| [5] | WIDNALL S E, BLISS D,ZALAY A.Theoretical and experimental study of the stability of a vortex pair[M]//Aircraft wake turbulence and its detection.Boston:Springer,1971:305-338. |
| Click to display the text | |
| [6] | LEWEKE T, WILLIAMSON C H K.Experiments on long-wavelength instability and reconnection of a vortex pair[J].Physics of Fluids,2011,23(2):465-474. |
| Click to display the text | |
| [7] | HEYES A L, SMITH D A R.Spatial perturbation of a wing-tip vortex using pulsed span-wise jets[J].Experiments in Fluids,2004,37(1):120-127. |
| Click to display the text | |
| [8] | BREITSAMTER C, ALLEN A.Transport aircraft wake influenced by oscillating winglet flaps[J].Journal of Aircraft,2009,46(1):175-188. |
| Click to display the text | |
| [9] | GUO H, BORODULIN V I,KACHANOV Y S,et al.Nature of sweep and ejection events in transitional and turbulent boundary layers[J].Journal of Turbulence,2010(11):N34. |
| Click to display the text | |
| [10] | HU Y,WANG J J. Dual leading-edge vortex structure for flow over a simplified butterfly model[J].Experiments in Fluids,2011,50(5):1285-1292. |
| Click to display the text | |
| [11] | SCARANO F, BENOCCI C,RIETHMULLER M L.Pattern recognition analysis of the turbulent flow past a backward facing step[J].Physics of Fluids,1999,11(12):3808-3818. |
| Click to display the text | |
| [12] | GIRALT F, FERRÉ J A.Structure and flow patterns in turbulent wakes[J].Physics of Fluids A:Fluid Dynamics,1993,5(7): 1783-1789. |
| Click to display the text | |
| [13] | SCHMID P J,SESTERHENN J. Dynamic mode decomposition of numerical and experimental data[J].Journal of Fluid Mechanics,2010,656(10): 5-28. |
| Click to display the text | |
| [14] | SCHMID P J. Application of the dynamic mode decomposition to experimental data[J].Experiments in Fluids,2011,50(4):1123-1130. |
| Click to display the text | |
| [15] | PAN C,YU D, WANG J.Dynamical mode decomposition of Gurney flap wake flow[J].Theoretical and Applied Mechanics Letters,2011,1(1):012002. |
| Click to display the text | |
| [16] | MULD T W, EFRAIMSSON G,HENNINGSON D S.Flow structures around a high-speed train extracted using proper orthogonal decomposition and dynamic mode decomposition[J].Computers & Fluids,2012,57(4):87-97. |
| Click to display the text | |
| [17] | HE G S, PAN C,WANG J J.Dynamics of vortical structures in cylinder/wall interaction with moderate gap ratio[J].Journal of Fluids and Structures,2013,43(7):100-109. |
| Click to display the text | |
| [18] | PAN C, XUE D,WANG J J.On the accuracy of dynamic mode decomposition in estimating in stability of wave packet[J].Experiment in Fluids,2015,56(8):1-15. |
| Click to display the text |
