近些年,随着计算流体动力学(Computational Fluid Dynamics,CFD)的进步,气流场的研究也愈加地全面。2002年,Polsky[2]对LHA两栖攻击舰空气尾流进行了计算,证明了CFD方法对于计算气流场的可行性。2007年,赵维义和王占勇[3]应用粒子图像测速技术获得了舰船空气尾流场特征,验证了上层建筑对飞行甲板上方区域的流场影响较大。2013年,郜冶和刘长猛[4]研究了风向变化产生的航母甲板涡结构特征。
而与此同时,对于气流场计算结果的分析评估还处于初级阶段。在舰船评估方法的方面,目前应用较多的是针对总体方案评估方法,其中的赋权方法都基本使用了层次分析法(Analytic Hierarchy Process,AHP),而排序方法有文献[5]提出的基于改进优劣解距离法(Technique for Order Preference by Similarity to an Ideal Solution,TOPSIS)的舰船总体方案群决策方法、文献[6]提出的基于面积和斜率灰色关联度的舰船方案群决策方法、文献[7]提出的基于相对熵排序的舰船总体方案评价方法等。这些方法都适用于舰船总体方案的评估,而对于气流场这种专家主观成分多、赋权结果一致性检验困难、打分结果模糊性大的评估对象并不适合。
本文提出一种能够全面、综合评价大型水面舰船气流场的方法,从而对不同大型水面舰船方案在气流场方面做出优劣判断。本文在对不同舰船方案气流场进行CFD计算的基础上,针对气流场特征以及其影响对象舰载机的作业特点,建立评价气流场的指标体系,基于群决策特征根法(Group Eigenvalue Method,GEM)和决策熵理论给出各级指标的权重,使用改进模糊(ELECTRE,Elimination et Choise Translating Reality)法对不同舰船方案在气流场方面进行排序,从而建立多专家群决策的大型水面舰船气流场综合评估模型,得到对不同方案气流场方面的优劣判断,为今后气流场的总体研究与评价提供指导信息和理论依据。
1 气流场评估指标体系 舰船的气流场评估研究是一个大信息量、多目标的复杂的系统问题,几何空间巨大,涉及的物理量众多,如果考察所有涉及的物理量,不仅会耗费大量成本,而且也不尽科学。对于气流场的研究,应该紧紧围绕气流场的主要服务对象——固定翼舰载机来展开,以气流场对舰载机作业的影响为中心,建立气流场评估指标体系。
大型水面舰船在进行舰载机起降作业时,分为起飞和降落2种状态。在起飞状态时,由于舰载机在开始启动的一段时间里处于加速阶段,其与空气的相对速度较小,气流场对其的影响较小,所以在气流场评估时不考察这一阶段,而应考察舰载机在甲板上加速起飞的后半程以及舰载机离舰后的这一范围的气流场数据。其中,空气与舰载机的相对风速直接影响舰载机的升力和操纵性;侧风风速会使舰载机产生侧滑、横滚运动,对舰载机的安全起飞有负面影响;流场压力的变化以及涡量分布对舰载机的飞行稳定性有一定影响。所以,在评估起飞状态时的气流场采用相对风速、侧风风速、压力分布、涡量分布这4项底层指标进行评估[8-9]。需要注意的是,一般的大型水面舰船有多条起飞跑道,本文考察的是舰艏的2条起飞跑道,从右舷到左舷依次标注为1号、2号起飞跑道。
在降落状态时,舰载机沿最后进场方向,即五边(final)进近,越过最低决断高度(minimum decision attitude)后保持飞行状态下降直至尾钩勾住阻拦索制动后完成降落,在这个过程中舰船气流场主要在舰载机越过最低决断高度后、尾钩勾住阻拦索前对舰载机有较大影响,所以在气流场评估时应考察这一范围的气流场数据。其中,空气与舰载机的相对风速直接影响舰载机的升力和操纵性,过低的相对风速容易使低速飞行的舰载机陷入失速状态;侧风风速会对舰载机产生侧滑、横滚运动,对舰载机的安全降落有负面影响;下洗速度会使舰载机在最后进近过程中掉高,对舰载机的安全降落有负面影响;涡量分布对舰载机的飞行稳定性有一定影响;流线的变化对舰载机的飞行稳定性有直接影响,如果流线变化剧烈,可能使舰载机的飞行状态发生突变,对降落产生不利影响。所以,在评估降落状态时的气流场采用相对风速、侧风风速、下洗速度、涡量分布和流线变化这5项底层指标进行评估[8]。
在5项的指标中,相对风速、侧风风速、下洗速度是定量指标,即可以由CFD计算直接得出客观数值,直接进行比较评估;压力分布、涡量分布、流线变化是定性指标,即不能直接由CFD计算得出客观数值,需要专家根据CFD计算得出的压力云图、涡量云图、流线图进行主观评判打分后再进行比较评估。气流场的评估范围如图 1所示。综上,气流场评估指标体系如图 2所示。同时对指标进行编号(如B1、C1),便于之后的说明与计算。
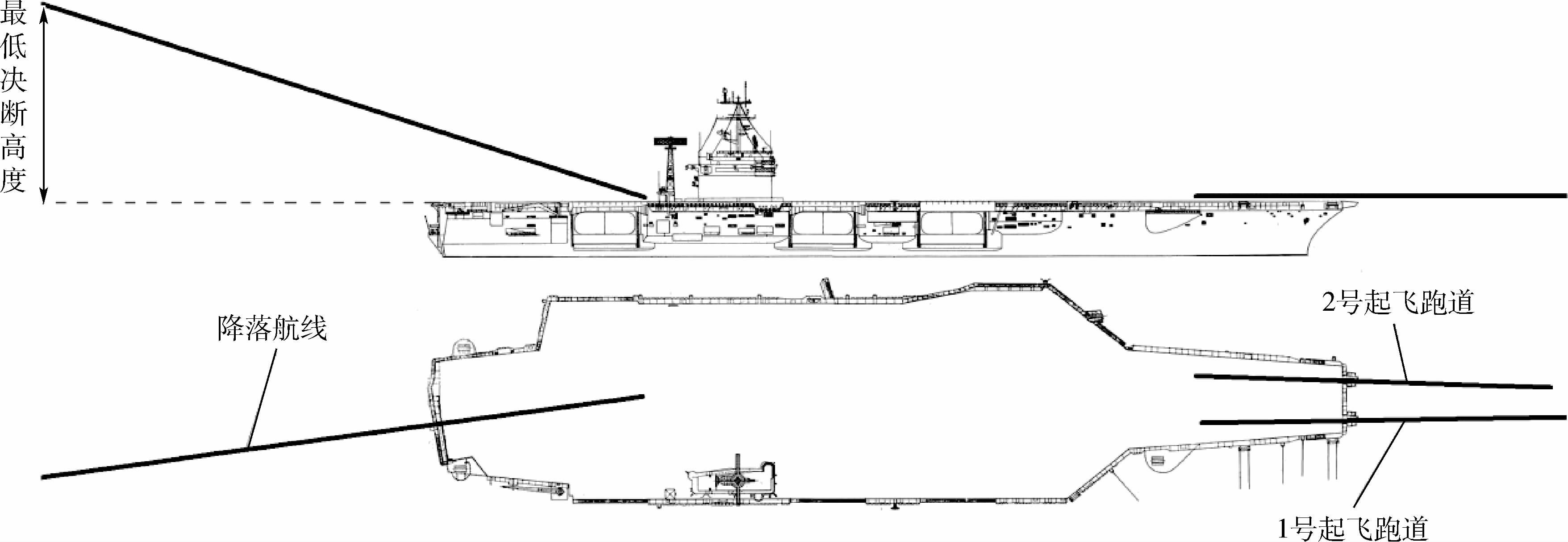 |
| 图 1 气流场评估范围示意图 Fig. 1 Schematic diagram of evaluation area of airflow field |
| 图选项 |
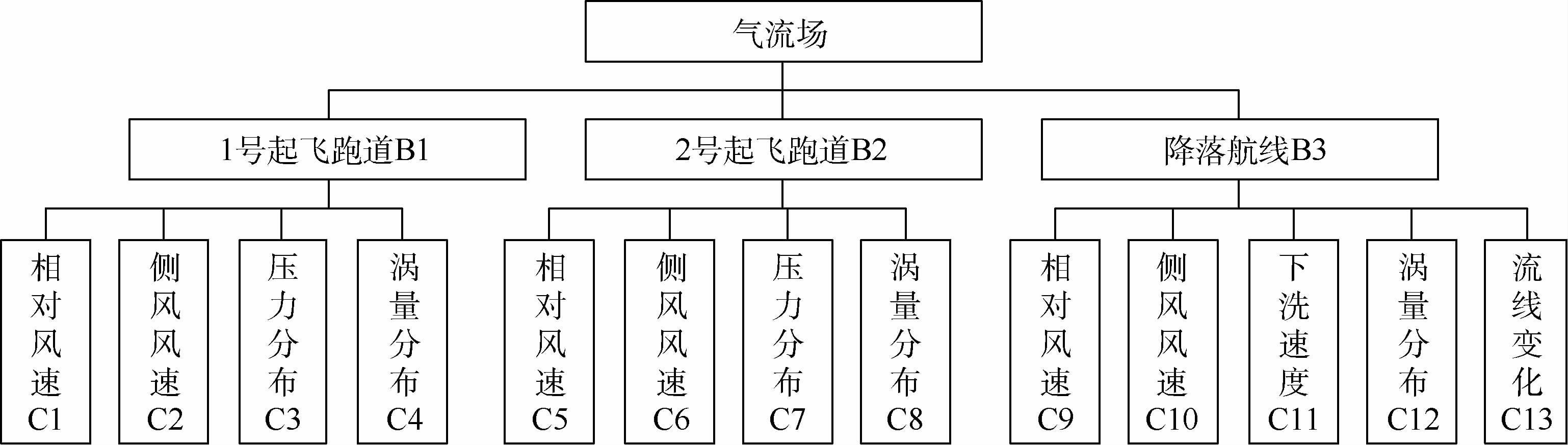 |
| 图 2 气流场评估指标体系 Fig. 2 Evaluation index system of airflow field |
| 图选项 |
2 基于GEM与决策熵的赋权方法 由于指标体系中各个分量对于总体的重要性各异,所以必须对各个分量赋予权重,以计量各个分量的重要性,并用于之后的排序计算。
目前在舰船总体评估计算中,赋权方法一般采用层次分析法,并以C.R.为判据进行一致性检验[5, 9]。在应用实践中,由于专家的意见各异,特别是像本文针对的大型水面舰船气流场评估这种研究处于起步阶段的赋权,专家很难达成趋于统一的意见,群赋权的一致性很难保证。并且一般用0.1作为一致性检验C.R.的临界值是相当粗略的,很难说有什么客观标准和意义,在理论上讲,把C.R.作为一致性检验是有缺陷的[10]。
针对这一问题,本文采用基于GEM和决策熵理论的赋权方法,将一致性与可靠性进行科学量化,让决策者可以直观地控制赋权结果的可靠性,特别针对大型水面舰船气流场评估的赋权,可以在量化可靠性的基础上得到可以接受的赋权结果。
2.1 基于GEM的群赋权计算法 假定有由S1,S2,…,Sm组成的m个专家群组决策系统G,对n个指标B1,B2,…,Bn进行赋权,第i个专家Si对第j个被赋权对象Bj的权重值记为xij∈[0,1](i=1,2,…,m;j=1,2,…,n)。xij的值越大,目标Bj的权重越高,在所有指标中的重要性越高。Si及其群组G的赋权结果组成n维列向量xi和m×n阶矩阵x为
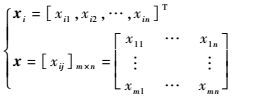 | (1) |
$\sum\limits_{a=1}^{n}{{{x}_{ia}}=1}$为专家群组在一次赋权过程中所做的结论,代表各自对被赋权项的赋权值。
专家的赋权水平不仅取决于他的专业水平、经验、知识面和综合能力,而且与赋权时的精神状态、情绪和偏好密切相关。所以,现实中赋权可靠性达到最大值1的专家是不存在的。因此,假设一个赋权最准、最公正,即赋权水平最高的专家叫做理想专家S*,他的评分向量为
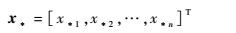 |
由于人们总是聘请水平较高的专家参与,所以人们现实地定义理想专家为对被赋权项的认识与专家群体G有最高一致性的专家,即S*的赋权结论与G的完全一致,与专家个体间的差异最小。因此,理想专家S*的赋权结果x*就是要求出的这个群赋权事件中专家群体的赋权结果。而求在群赋权事件中的x*可以通过求解方程
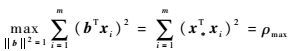
因此,求得矩阵F=xTx的特征向量x*,之后将其中的各元素进行归一化处理后,就可以得到在这个群赋权事件中各个指标所得出的对应的权重[11] 。
2.2 基于决策熵的群赋权可靠性分析方法 在群赋权事件中,由于专家及其群组在进行赋权时存在赋权水平差异,所以需要对于整体的赋权结果进行可靠性检验,而使用基于决策熵理论的可靠性模型可以很好地验证整体赋权的可靠性[12]。
将各已知因素单位化
 | (2) |
式中:

再以Ni=[Ni1,Ni2,…,Nin]表示按专家Si(i=1,2,…,m)的赋权大小排序的被赋权目标B1,B2,…,Bn的大小名次。
则专家Si的赋权水平向量为
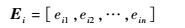 | (3) |
式中:eij=1-N*j-Nij-d*j-dij,i=1,2,…,m,j=1,2,…,n。
由此可以计算出专家Si赋权结果的不准确性的度量——决策熵Hi。Hi等于Si的赋权水平向量各分量的广义熵之和,即
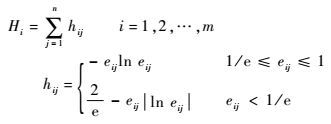 | (4) |
而群组G的整体赋权水平测度函数为
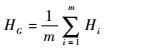 | (5) |
式中:HG为群组决策熵,简称群组熵。
而通过决策熵值和可靠性的关系,就可以得出个体和群组在这个群赋权事件中的可靠性。
2.3 基于GEM和决策熵理论的赋权方法流程 在群赋权事件中,由于个体专家的赋权水平问题,仅仅通过使用GEM计算有时得不到令人满意的整体赋权结果,这时就需要进行修正。通过对个体和群组在这个群赋权事件中的可靠性分析,可以对群赋权结果进行修正和优化,从而得到令人满意的结果。基于GEM和决策熵理论的赋权方法流程图如图 3所示。
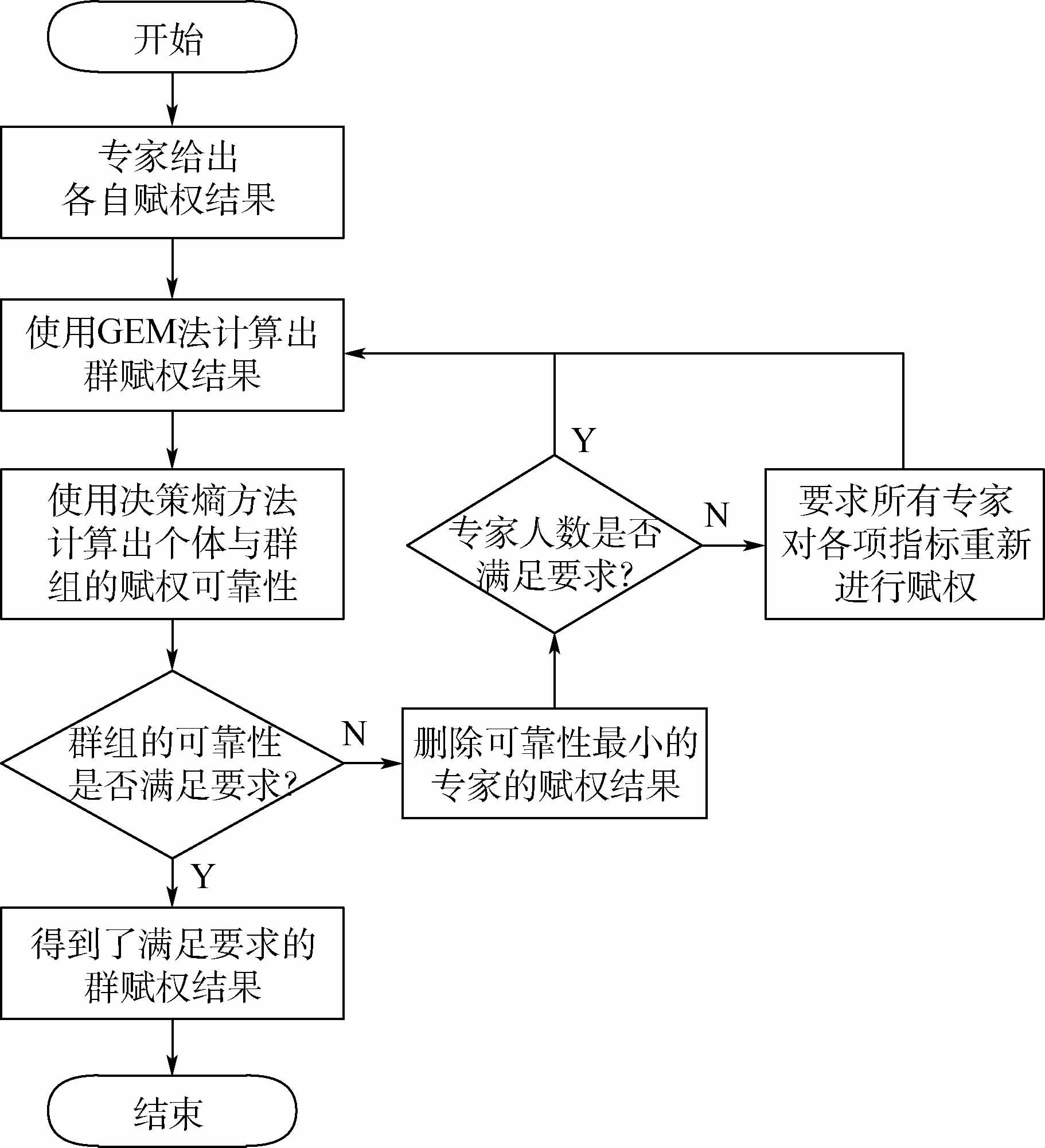 |
| 图 3 基于GEM和决策熵理论的赋权方法流程图 Fig. 3 Flowchart of weighting method based on GEM andtheory of decision entropy |
| 图选项 |
3 基于改进ELECTRE法的排序方法 3.1 基本原理 ELECTRE是由Roy等在20世纪60年代提出的求解多属性决策问题的常见方法之一,这种方法使用简便,广泛应用于决策问题[13]。
ELECTRE法实质上是一种消除与选择转化算法,即先淘汰部分备选方案,使决策者可把全部备选方案排列成序,从而选出最合理的方案。
传统ELECTRE法缺点在于不能直接处理不确定信息,在解决复杂的现实决策问题方面还有局限性。目前采用的模糊ELECTRE法用来计算全定性指标,并不能很好处理定性、定量混合指标体系。在本文中,对已有ELECTRE法进行改进,将其拓展到模糊环境下,同时将定性、定量指标一同处理,其中不确定信息以三角模糊数形式给出,确定信息以特殊三角模糊数形式给出,这样可在专家评价定性指标时给予更多的自由空间而不仅局限于传统的优良评价,同时结合定量指标计算,可更好地解决航母气流场评价这种有较多定性指标的模糊多属性群决策问题[14-15]。
3.2 计算步骤 第1步 每位专家给出对所有方案与指标的模糊评价矩阵,即
 |
其中:A1,A2,…,An为n个被排序的方案;C1,C2,…,Cm为方案中用于分析比较的m个独立指标;k为专家的编号,总共有K个专家参与评价。对于定量指标,评价结果直接使用实际数值,用特殊三角模糊数,即q=(a,a,a)表示;对于定性指标,需要专家进行主观评判,专家对指标的评价$\tilde{x}$ijk使用三角模糊数表示,即$\tilde{x}$ijk=xijlk,xijmk,xijrk,xijlk、xijrk和xijmk分别为专家认为的最低值、最高值和最有可能的值,3个值都在[0,1]上表示。
第2步 构造模糊群决策矩阵,令
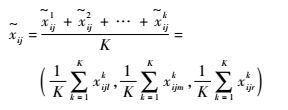 | (6) |
这样可以得到模糊群决策矩阵$\tilde{X}$,即
 | (7) |
第3步 将矩阵$\tilde{X}$规范化为$\tilde{R}$=(${{\widetilde{r}}_{ij}}$)m×n。
这里,将所有的指标值进行横向比较,将原有的有量纲数都化为数值在0到1之间的无量纲数,这个无量纲数即为对该指标的评价值,以便式(8)对不同指标之间的比较计算。
 | (8) |
第4步 进行模糊和谐性检验,令
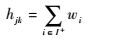 | (9) |
式中:hjk为和谐性指数;I+={i|$\tilde{r}$ji>$\tilde{r}$ki},i=1,2,…,n;wi为各指标的权重值,三角模糊数之间使用RS准则进行比较。由此构造出方案之间的和谐性指数矩阵:
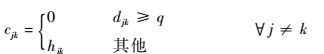 |
第5步 进行模糊非和谐性检验,令
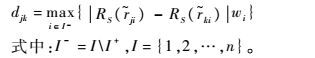 | (10) |
式中:I-=I\I+,I={1,2,…,n}。
第6步 建立一致性比较矩阵,令
 | (11) |
式中:
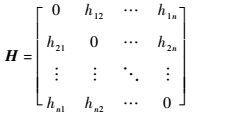 |
这里q为否决门槛值,cjk体现了在总体上Aj级别高于Ak的程度。以此为判据,可以衡量个方案的优劣,进而确定各方案的次序关系。
4 应用实例 现通过赋权与排序方法对3个大型水面舰船气流场方案进行评估。3个设计方案包括了核动力弹射起飞方案、常规动力弹射起飞方案以及常规动力滑跃起飞方案,以验证评估模型的广泛适用性。在指标体系中涉及的定量指标数值如表 1所示。将3个方案的设置为典型工况,即迎风30°、40 kn风速,按照已有的CFD方法对3种方案进行数值计算[16-17],计算结果如图 4~图 6所示,分别给出了3种方案的合速度Vm云图、侧风风速Vy云图、涡量Ω云图和流线图。
表 1 各方案定量指标计算结果 Table 1 Calculation results of quantitative index ineach plan
| 指标 | 方案1 | 方案2 | 方案3 |
| C1 | 20.6 | 16.5 | 17.0 |
| C2 | 2.92 | 4.27 | 2.29 |
| C5 | 19.3 | 14.8 | 15.2 |
| C6 | 0.68 | 1.52 | 0.49 |
| C9 | 13.9 | 15.1 | 14.4 |
| C10 | 5.33 | 5.82 | 2.51 |
| C11 | 0.14 | 1.39 | 0.06 |
表选项
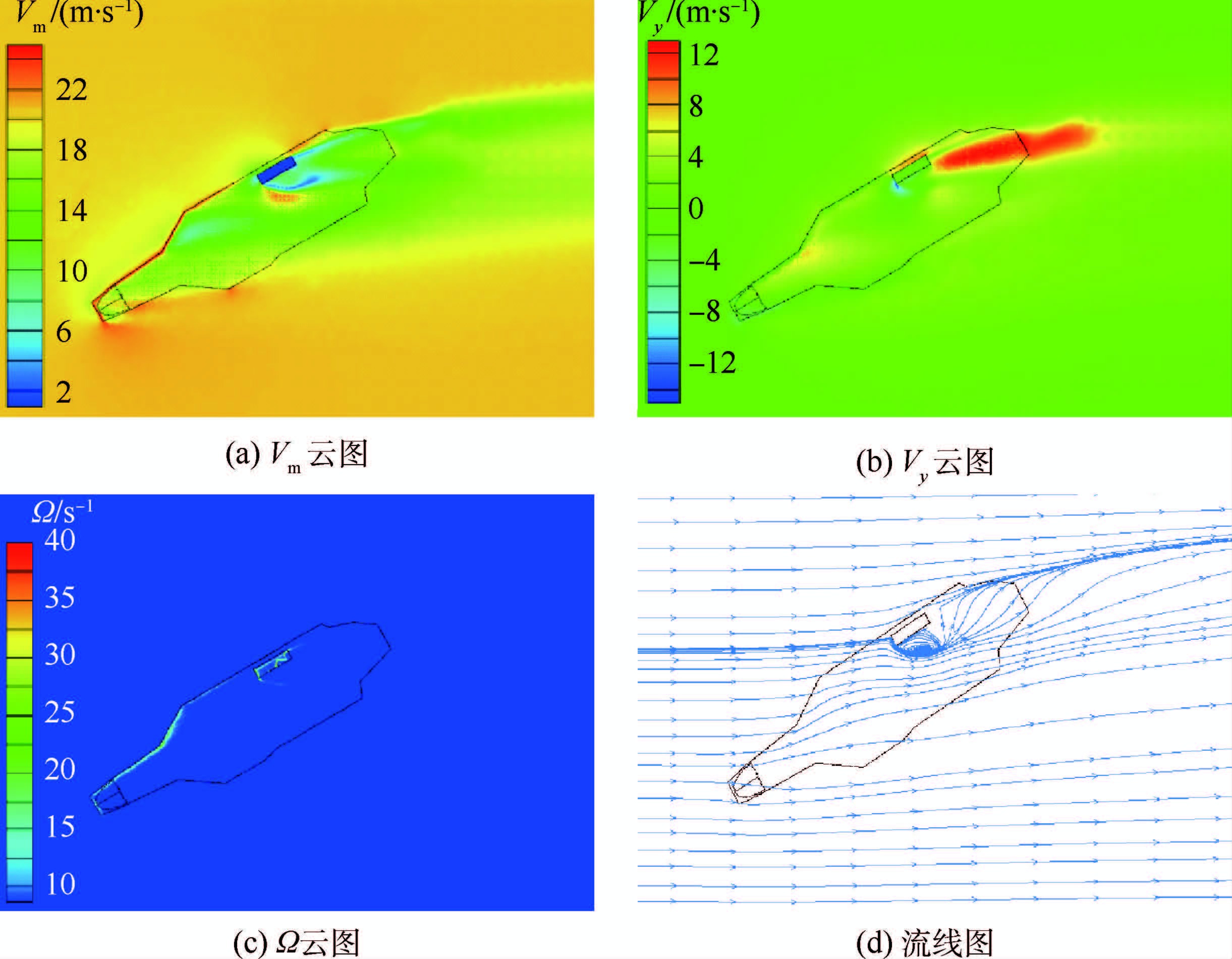 |
| 图 4 方案1的Vm、Vy和 Ω云图及流线图 Fig. 4 Contours of Vm,Vy and Ω and streamline diagram in plan 1 |
| 图选项 |
 |
| 图 5 方案2的Vm、Vy和 Ω云图及流线图 Fig. 5 Contours of Vm,Vy and Ω and streamline diagram in plan 2 |
| 图选项 |
 |
| 图 6 方案3的Vm、Vy和 Ω云图及流线图 Fig. 6 Contours of Vm,Vy and Ω and streamline diagram in plan 3 |
| 图选项 |
首先邀请5位专家对指标体系的各层、各部分进行赋权,同时设定可以接受的群决策可靠性为60%,需要有半数以上的有效赋权。以3个一级指标B1、B2、B3为例,专家的赋权结果见表 2。
表 2 一级指标的专家赋权结果 Table 2 Results of weighting for indexes in the firstclass by experts
| 专家编号 | B1 | B2 | B3 |
| 专家1 | 0.30 | 0.30 | 0.40 |
| 专家2 | 0.33 | 0.33 | 0.34 |
| 专家3 | 0.35 | 0.35 | 0.30 |
| 专家4 | 0.40 | 0.30 | 0.30 |
| 专家5 | 0.33 | 0.33 | 0.34 |
表选项
由此得
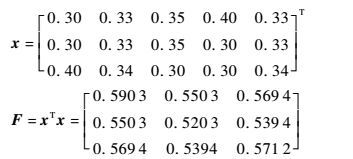 |
求得F的特征向量并经过标准化后得到群赋权结果x*=(0.334 5,0.334 5,0.311 1),再经过式(2)~式(5)计算得群组决策熵HG=0.806 1,查表得群赋权可靠性为65%,符合要求。所以3个一级指标B1、B2、B3的权重为0.334 5、0.334 5、0.311 1。
同理,计算底层权重,经过标准化处理后得到的底层权重如表 3所示。
表 3 底层权重结果 Table 3 Results of weighting for indexes inthe second class
| 指标 | 权重 |
| C1 | 0.118 1 |
| C2 | 0.093 8 |
| C3 | 0.073 4 |
| C4 | 0.049 1 |
| C5 | 0.118 1 |
| C6 | 0.093 8 |
| C7 | 0.073 4 |
| C8 | 0.049 1 |
| C9 | 0.056 2 |
| C10 | 0.091 5 |
| C11 | 0.068 3 |
| C12 | 0.035 6 |
| C13 | 0.059 5 |
表选项
5位专家对定性指标主观评判在按照式(6)处理后得到群体三角模糊数评判值,见表 4。
表 4 群体的三角模糊数评判值 Table 4 Group evaluation value of triangularfuzzy number
| 指标 | 方案1 | 方案2 | 方案3 |
| C3 | (0.68,0.80,0.88) | (0.56,0.68,0.74) | (0.66,0.76,0.86) |
| C4 | (0.58,0.68,0.78) | (0.46,0.56,0.66) | (0.62,0.74,0.80) |
| C7 | (0.76,0.84,0.88) | (0.62,0.74,0.82) | (0.72,0.80,0.86) |
| C8 | (0.76,0.86,0.96) | (0.54,0.66,0.70) | (0.74,0.82,0.90) |
| C12 | (0.60,0.72,0.82) | (0.50,0.62,0.72) | (0.60,0.70,0.82) |
| C13 | (0.44,0.58,0.64) | (0.66,0.74,0.84) | (0.38,0.54,0.62) |
表选项
加上定量指标的数值,按照式(7)共同构成群模糊决策矩阵$\tilde{X}$:
 |
接着由式(8)得到规范化的群决策矩阵,再代入各指标的权重值,根据式(9)和式(10)分别进行和谐性检验和非和谐性检验,取否决门槛值q=0.5,最终由式(11)可以得到一致性比较矩阵C:
 |
根据矩阵C得到的方案的优先次序为:方案1优于方案3优于方案2,可见方案1在气流场方面为最优方案。
5 结 论 本文针对大型水面舰船气流场评估问题:
1) 以气流场对舰载机作业的影响为中心,建立了气流场评估指标体系。
2) 分析之前方案评估所用方法对气流场评估的适用性的基础上,提出了基于GEM和决策熵理论的赋权方法。
3) 基于改进模糊ELECTRE法的方案排序方法,提出了舰船气流场方案排序方法。
4) 建立了一套完善的大型水面舰船气流场评估体系,并通过对3种不同的大型水面舰船设计方案的气流场进行CFD计算并经过完整的评估计算,验证了所提出的评估体系的可行性,证明了所提出的评估模型具有广泛的适用性。
在实际应用中,提出的评估模型可进行一定程度上的简化和调整,如对群决策可靠性的取值范围、否决门槛值参数等,使其满足实际应用要求。
参考文献
| [1] | 贺少华, 刘东岳, 谭大力, 等. 载机舰船气流场相关研究综述[J].舰船科学技术, 2014, 36(2): 1–7.HE S H, LIU D Y, TAN D L, et al. A review of researches on ship airwakes[J].Ship Science and Tchonology, 2014, 36(2): 1–7.(in Chinese) |
| [2] | POLSKY S A.A computational study of unsteady ship air-wake:AIAA-2002-1022[R].Reston:AIAA,2002.http://cn.bing.com/academic/profile?id=2025749486&encoded=0&v=paper_preview&mkt=zh-cn |
| [3] | 赵维义, 王占勇. 舰船空气尾流场对直升机着舰的影响研究[J].海军航空工程学院学报, 2007, 22(7): 435–438.ZHAO W Y, WANG Z Y. Research on the effect of warship air-wake on helicopter landing on shipboard[J].Journal of Naval Aeronautical Engineering Institute, 2007, 22(7): 435–438.(in Chinese) |
| [4] | 郜冶, 刘长猛. 护卫舰气流场数值计算研究[J].哈尔滨工程大学学报, 2013, 34(5): 599–603.GAO Y, LIU C M. Numerical calculation of frigate ship airwake[J].Journal of Harbin Engineering University, 2013, 34(5): 599–603.(in Chinese) |
| [5] | 黄胜, 郭海鹏, 侯远杭, 等. 基于改进TOPSIS法的舰船总体方案群决策方法[J].上海交通大学学报, 2014, 48(1): 92–97.HUANG S, GUO H P, HOU Y H, et al. Group decision-making method of warship based on improved TOPSIS[J].Journal of Shanghai Jiao Tong University, 2014, 48(1): 92–97.(in Chinese) |
| [6] | 黄胜, 郭海鹏, 王超. 基于面积和斜率灰色关联度的舰船方案群决策方法[J].船舶工程, 2014, 36(1): 100–103.HUANG S, GUO H P, WANG C. Group decision-making of warship scheme based on area and slope grey degree[J].Ship Engineering, 2014, 36(1): 100–103.(in Chinese) |
| [7] | 侯远杭, 黄胜, 胡玉龙, 等. 基于相对熵排序的舰船总体方案评价方法[J].上海交通大学学报, 2012, 46(8): 1218–1222.HOU Y H, HUANG S, HU Y L, et al. Evaluation of warship based on relative entropy method[J].Journal of Shanghai Jiao Tong University, 2012, 46(8): 1218–1222.(in Chinese) |
| [8] | POLSKY S A,NAYLOR S.CVN airwake modeling and Integration:Initial steps in the creation and implementation of a virtual burble for F-18 carrier landing simulations:AIAA-2005-6298[R].Reston:AIAA,2005. |
| [9] | 廖全蜜, 黄胜, 王宇, 等. 基于改进TOPSIS法的舰船通道人机效能研究[J].西南交通大学学报, 2015, 50(3): 536–542.LIAO Q M, HUANG S, WANG Y, et al. Research of human performance in warship passageway based on improved TOPSIS method[J].Journal of Southwest Jiaotong University, 2015, 50(3): 536–542.(in Chinese) |
| [10] | 李学全, 李松仁, 韩旭里. AHP理论与方法研究:一致性检验与权重计算[J].系统工程学报, 1997, 12(2): 111–117.LI X Q, LI S R, HAN X L. Study of AHP theory and method:Test of consistency and calculation of weight vector[J].Journal of Systems Engineering, 1997, 12(2): 111–117.(in Chinese) |
| [11] | 邱菀华, 刘美芳. 管理决策及其应用[M].北京: 机械工业出版社, 2012: 131-137.QIU W H, LIU M F. Managerial decision making and its application[M].Beijing: China Machine Press, 2012: 131-137.(in Chinese) |
| [12] | 马俊, 邱菀华, 张浩. 招投标决策模型及其应用[J].北京航空航天大学学报, 2000, 26(4): 470–472.MA J, QIU W H, ZHANG H. The bidding decision model and its application[J].Journal of Beijing University of Acronautics and Astronautics, 2000, 26(4): 470–472.(in Chinese) |
| [13] | 张吉军. 模糊层次分析法(FAHP)[J].模糊系统与数学, 2002, 14(2): 80–88.ZHANG J J. Fuzzy analytical hierarchy process(FAHP)[J].Fuzzy Systems and Mathematics, 2002, 14(2): 80–88.(in Chinese) |
| [14] | 高璟, 张强. 基于ELECTRE方法的模糊多属性群决策[J].数学实践与认识, 2009, 39(9): 21–27.GAO J, ZHANG Q. Extensions of the ELECTRE for group decision-making under fuzzy environment[J].Mathematics in Practice and Theory, 2009, 39(9): 21–27.(in Chinese) |
| [15] | XU Z, CHEN J. An interactive method for fuzzy multiple attribute group decision making[J].Journal of Information Science, 2007, 177(1): 248–263.DOI:10.1016/j.ins.2006.03.001 |
| [16] | 陆超, 姜治芳, 王涛. 利用缩比模型CFD数值模拟计算舰面空气流场相似准则数的影响探讨[J].中国舰船研究, 2008, 3(6): 45–48.LU C, JIANG Z F, WANG T. Discussion on comparability of scaled models for CFD numerical simulation for ship airwake[J].Chinese Journal of Ship Research, 2008, 3(6): 45–48.(in Chinese) |
| [17] | REDDY K, TOFFOLETTO R, JONES K. Numerical simulation of ship airwake[J].Computer & Fluids, 2000, 29(4): 451–465. |
