本文以装备设计、试验过程中必须进行的FMECA[5]分析为基础,结合模糊数学的思想,考虑故障模式对任务的影响程度,提出任务可靠性定性与定量相结合的综合评价方法。
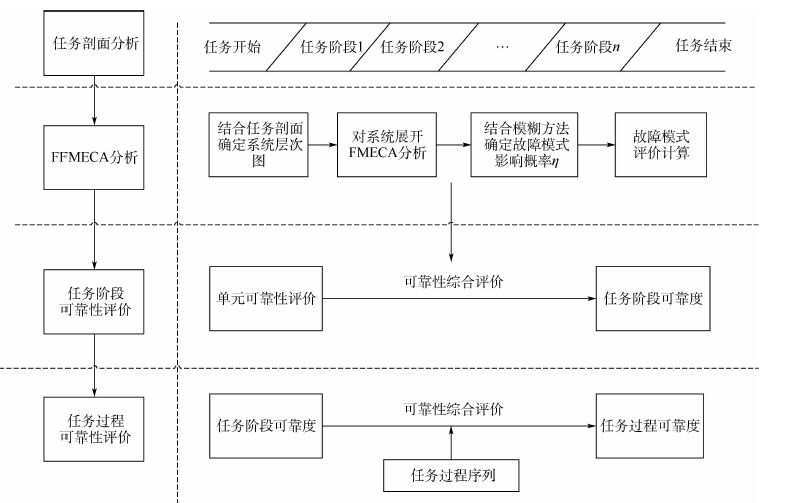
1 基于模糊的任务可靠性评价方法 按照装备可靠性设计研制流程,FMECA分析是必须进行的一个工作项目[6]。FMECA分析是分析系统中每一产品所有可能产生的故障模式及其对系统造成的所有可能影响,并按照每一故障模式的严重程度及其发生概率予以分类的一种归纳方法。本文在FMECA的基础上,引入模糊数学[7-8]的思想,对其进行适当改进,将其应用到任务可靠性的评价中。基于FFEMCA分析的任务可靠性评价如图 1所示。
由图 1可知,基于FFMECA分析的任务可靠性评价方法包括如下4个步骤:
1) 任务剖面分析:通过对任务的分析研究,建立任务剖面,描述产品在完成规定任务这段时间内所经历的事件和环境的时序。并在此基础上建立产品的任务可靠性模型,为任务可靠性评价提供基础。
2) FFMECA分析:对参与任务剖面的各个系统设备进行FFMECA分析。首先进行FMECA分析,在此基础上,进行故障模式影响概率η的计算,确定各故障模式在不同严酷度类别下的占比。在故障模式试验数据的基础上,对各故障模式进行可靠性评价。
3) 任务阶段可靠性评价:完成各单元或各故障模式的可靠性评价后,按照建立的任务阶段可靠性数学模型完成任务阶段的可靠性评价。
4) 任务过程可靠性评价:利用文献[9]中评价方法或蒙特卡罗仿真技术对任务阶段进行可靠性综合后得到任务成功概率。
 |
| 图 1 基于FFMECA分析的任务可靠性评价方法 Fig. 1 Mission reliability assessment method based on FFMECA |
| 图选项 |
1.1 任务剖面分析 任务剖面分析按照国军标进行[10],并给出任务可靠性模型,此处不详细叙述。
1.2 FFMECA分析 在没有关于故障模式影响概率η详细统计数据的情况下,基于传统FMECA分析方法,引入模糊数学思想,可计算故障模式影响概率。下面介绍计算故障模式影响概率的具体方法。
1.2.1 确定评价因素、评价等级 由审视严酷度的一般性的定义[11]可以知道,评价(识别)一个故障模式任务影响的程度归属于哪一等级,通常考虑其最终影响后果的4种损失程度(因素):人身安全、产品功能、经济损失和系统损伤(根据FMECA所分析的系统不同,考虑的因素也会有所变动)。故评价(识别)一个故障模式严酷度的因素(特征)集可为
U={人身安全(u1),产品功能(u2),经济损失(u3),系统损伤(u4)}
易知,评价一个故障模式的评语集(待识别经典模糊集)即为严酷度各等级:
V={Ⅰ类(v1),Ⅱ类(v2),Ⅲ类(v3),Ⅳ类(v4)}
1.2.2 构造模糊评价矩阵 构造一个评价矩阵,可以从获得各单因素评价向量 r i出发,之后通过整合就可以得到评价矩阵 R [12]。
获得损失程度ui的评价向量 r i,即确定从损失程度ui角度考虑该故障模式对严酷度各等级的隶属度:
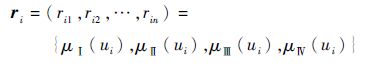 |
获得单因素评价向量的方法为:首先建立故障模式各因素对严酷度各等级的隶属度函数,隶属度函数一般选取梯形分布[13]。隶属度函数的变量为专家按照一定的标准做出的评分值。之后,制作专家打分表,通过专家评价给分,专家根据每一具体的评价对象的每一项指标,根据专家的经验和看法按照一定的标准规则打分,再通过对调查表统计,得到各因素对应等级的评分值,将评分值代入到严酷度的隶属度函数中即可得到各因素对应各等级的隶属度,从而得到各因素的评价向量 r i[14]。各因素整合即得模糊评价矩阵:
 | (1) |
式中:μⅠ(u1)为从因素u1考虑,该故障模式对Ⅰ类严酷度的隶属程度;μⅡ(u2)为从因素u2考虑,该故障模式对Ⅱ类严酷度的隶属程度;以此类推。
1.2.3 获得各因素的权重 各因素的权重代表了工程技术人员或专家****评审人员对各因素ui(i=1,2,3,4)的重视程度[15]。
层次分析法作为数学加权的一种,是通过专家调查法获得基础数据,然后根据数学方法进行科学合理地运算得出权重。专家的经验可能掺杂着一定的主观性,但因数学方法严格的逻辑性可以对数据进行“修复”处理,以尽量剔除主观成分,符合客观现实。因此,本文采用层次分析法获得权重。可以通过表 1调查得出各因素的相对重要性。
表 1 因素重要等级判断值 Table 1 Important level judgment of factor value
| 因素ui,uj相比较的重要程度等级 | fuj(ui) | fui(uj) |
| ui与uj“同等重要” | 1 | 1 |
| ui比uj“稍微重要” | 3 | 1 |
| ui比uj“明显重要” | 5 | 1 |
| ui比uj“强烈重要” | 7 | 1 |
| ui比uj“绝对重要” | 9 | 1 |
| 注:若重要性介于各等级之间则取2,4,6,8中之一。 | ||
表选项
令pij=fuj(ui)/fui(uj)(i,j=1,2,…,m),由此可以构造判断矩阵为(这里同样设为4个因素,下同):
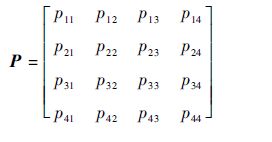 | (2) |
显然,pii=1,pij=1/pji。根据判断矩阵求解权重向量的数学方法有很多,鉴于可以利用计算机辅助运算,采用如下方法:计算它的最大特征值λmax及其所对应的特征向量 ξ = x1 x2 x3 x4 ,如果有必要可以再对此特征向量做归一化处理,即得权重向量 A =[a1 a2 a3 a4],ai为因素ui的重要程度系数(i=1,2,3,4)。
判断矩阵需经过一致性检验。在构造满足一致性的矩阵时常常是很难的,尤其是在判断矩阵的阶数n>2时更难以把握。判断矩阵的一致性条件允许有偏差,但偏离应有一个度。举例来说,一个出现诸如“A比B重要,B比C重要,C又比A重要”之类的明显不符合常理的判断矩阵,是令人难以置信的。因此,在利用判断矩阵计算权重向量之前,必须判读其一致性偏差是否在可接受的范围内。一致性检验的数学实现是计算一致性比率(consistent ratio):
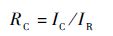 | (3) |
式中:IC为一致性指标(consistent index),IC=(λmax-n)/(n-1);IR为随机一致性指标(random consistent index)均值,是关于矩阵阶数的变量,可以通过查表 2获得。
表 2 IR值 Table 2 Value of IR
| 阶数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| IR | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 |
表选项
当RC<0.1时,认为判断矩阵一致性标准是可以接受的;否则,该矩阵应做适当地修正并重新计算以达到要求。
为降低个人主观因素带来的偏差,这里也可采用统计方法进行适当修正。设通过多人调查获得n个判断矩阵,经过计算获得n个权重向量( A 1,A 2,…,A n),可以通过求其平均值作为修正后的最终权重:
 | (4) |
1.2.4 建立评价模型,进行模糊评价(识别) 模糊评价矩阵 R 中的不同行反映了被评价的故障模式从不同角度对各严酷度等级的隶属程度。用模糊权重向量对各行进行综合,就得到从故障模式整体来看对各严酷度等级的隶属程度——模糊综合评价结果向量,即
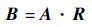 | (5) |
式中: B 为模糊评价结果向量。
B =(b1,b2,b3,b4)中,bj表示了被评价故障
模式具有严酷度等级vj的程度。如果
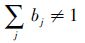
将影响任务完成的Ⅰ、Ⅱ类严酷度占比相加,即得到η:
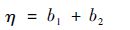 | (6) |
1.2.5 故障模式可靠性评价 传统FMECA的定量分析中,危害性矩阵分析是以失效率λ为基础,求取故障模式危害度Cm和产品危害度Cr,这两个定量指标是以任务时间内故障模式的发生次数来度量的[11]。武器装备系统是机电一体化的高科技产品,当中包含成败型产品、寿命型产品和非寿命型产品,不同类型的产品服从的数学分布不同,指数型产品的失效率是不变的,分析此类产品可以应用传统的危害性矩阵分析法。其他诸如威布尔分布、正态分布和二项分布等,失效率不是恒定的,用传统方法进行危害性分析是有局限性的。
例如,机械产品由于其试验成本较高,很难甚至无法在相对短的时间内通过大量的试验来获得足够的失效数据,因此,机械产品更多地采用了理论分析方法来评价其可靠性,大多采用“载荷-强度干涉模型”;对于武器装备系统中某些成败型产品,例如地雷中的机械单元和爆炸单元等,其在执行任务过程中是瞬发型的,且只有成功和失败两个状态,不能用失效率等时变可靠度参数对其进行考察评价,而应该用时不变可靠度参数如不可靠度或故障概率来考察。
综上,在FMECA分析的基础上,对故障模式的评价应针对故障模式的特点,灵活采用不同的分布类型进行可靠度的评价,所以,本文对FMECA分析表进行更改(见表 3),以适应任务可靠性定性与定量的评价。
表 3 FFMECA分析表 Table 3 Analytical statement of FFMECA
| 代码 | 产品或功能 标志 | 功能 | 故障 模式 | 故障 原因 | 任务阶段 与工作方式 | 故障影响 | 故障模式 发生概率F | 故障模式 影响概率η | 备注 | ||
| 局部影响 | 高一层次影响 | 最终影响 | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 注:1~9栏与传统FMECA方法相同;10栏填写得出的故障模式的失效概率,无论产品的失效分布服从哪一个类型,都以可靠性指标不可靠度或可靠度来度量;11栏为故障模式影响概率,指假定某故障模式已发生时,其最终影响导致某严酷度等级的条件概率,此值按照第1.2.4节方法进行计算获得。 | |||||||||||
表选项
不同类型产品的故障模式可按表 4进行评价。
表 4 故障模式评价方法 Table 4 Assessment method of failure mode
| 序号 | 产品类型 | 数据采集要求 | 评价方法 |
| 1 | 机械产品 | 特征量如推力、 应力等 | 应力强度干涉模 型、非概率方法 |
| 2 | 机电产品 | 累积试验时间、 故障模式发生数 | 威布尔方法 |
| 3 | 电子产品 | 累积试验时间、 故障模式发生数 | 指数型方法 |
| 4 | 火工品 | 子样数、故障 模式发生数 | 二项分布方法 |
表选项
1.3 任务阶段可靠性评价 单元在任务过程中出现m种故障模式,各种故障模式之间相互独立,第i种故障模式出现的概率为pi,造成任务无法完成的故障模式影响概率为ηi,则第i种故障模式出现且造成单元故障的概率为ηipi,第i种故障模式不影响单元完成任务的概率为1-ηipi,单元正常工作,意味着所有m种故障模式都不影响单元完成任务,将第i个单元故障看成该单元所有故障模式的串联。所以考虑相互独立的不同故障模式影响时,单元任务可靠度Rj为
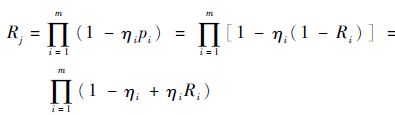 | (7) |
式中:Ri=1-pi为第i种故障模式不出现的概率;j为第j个单元。
任务阶段的可靠度可用RK表示,K为第K任务阶段,其表达式可按照任务阶段内单元的串并联关系写出。
2 可撒布地雷任务可靠性评价 以可撒布地雷任务过程中攻击目标阶段为例进行分析。
2.1 任务剖面分析 本文讨论的可撒布地雷从弹仓打开后开始执行任务,因此任务剖面主要由扶起阶段、攻击目标阶段、自毁阶段和自失能阶段组成。弹仓打开后,经过支腿扶起,直至90 s时进入待发状态,扶起阶段结束。从90 s至272 h这段时间内,是攻击目标阶段。如果目标出现,检测信号、点火、攻击目标,完成攻击任务。如果目标未出现,地雷进入自毁阶段。如果自毁未完成,进入自失能阶段。详细的任务剖面如图 2所示。
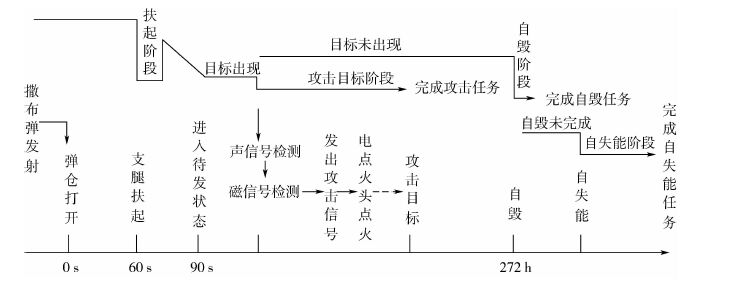 |
| 图 2 可撒布地雷任务剖面 Fig. 2 Mission profile of scatterable landmines |
| 图选项 |
2.2 FFMECA分析 将可撒布地雷的任务过程分为主要的4个阶段:扶起阶段、攻击目标阶段、自毁阶段和自失能阶段。可撒布地雷系统包含成败型单元(如雷管、电点火头)、电子产品单元(如引信电路)和机械产品单元(如机械保险机构等)。下面只以攻击目标阶段为例进行任务阶段的FFMECA分析,见表 5。各故障模式的发生概率可根据表 4的评价方法进行计算,课题项目涉密,表中所列计算结果并非真实 数据,只为方法叙述过程提供基础。故障模式影响概率ηi按照第1.2节的方法进行计算,最后获得评价向量,可以根据对严酷度等级的定义来确定ηi,一般Ⅰ、Ⅱ类严酷度等级会影响任务完成,可以取这两类严酷度值的和作为ηi的值,计算结果见表 6。结合正常研制过程,对故障模式进行数据采集(器件失效率),进行故障模式的可靠性评价,并得到攻击目标阶段故障模式的可靠度结果。
表 5 可撒布地雷攻击目标阶段FFMECA分析 Table 5 FFMECA of scatterable landmines in attack mission stage
| 代码 | 产品或功能 标志 | 功能 | 故障 模式 | 故障 原因 | 任务阶段与 工作方式 | 故障影响 | 故障模式 发生概率F | 故障模式 影响概率η | 备注 | ||
| 局部影响 | 高一层次影响 | 最终影响 | |||||||||
| 1 | 虚焊 | 环境原因 | 攻击目标阶段 | 电路短路、断路 | 引信非正常工作 | 地雷失效 | 0.000 2 | 0.78 | 无 | ||
| 2 | 电池漏碱,容量下降 | 腐蚀 | 攻击目标阶段 | 引信电路不能启动 | 引信不能正常工作 | 地雷失效 | 0.000 4 | 0.84 | 无 | ||
| 3 | 引信电路 | 接收、处理信号,输出点火脉冲 | 点火电容不能充电 | 器件失效 | 攻击目标阶段 | 电容失效 | 引信点火电路不能发火 | 地雷失效 | 0.000 4 | 1 | 无 |
| 4 | 晶振失效 | 振动冲击过载 | 攻击目标阶段 | 电路不能工作 | 引信失效 | 地雷失效 | 0.000 7 | 1 | 无 | ||
| 5 | 电点火头失效 | 生产原因 | 攻击目标阶段 | 不能引爆雷管 | 无法正常起爆 | 不能毁伤目标 | 0.000 3 | 1 | 无 | ||
| 6 | 传爆序列 | 传递雷管能量,放大输出,可靠起爆 | 电点火头串火 | 与滑块间隙过大 | 攻击目标阶段 | 不能引爆雷管 | 无法正常起爆 | 不能毁伤目标 | 0.000 12 | 0.85 | 无 |
| 7 | 威力不足 | 药型罩同心度不好 | 攻击目标阶段 | 爆炸后成型不好 | 爆破效果差 | 不能有效炸毁目标 | 0.000 21 | 0.82 | 无 | ||
表选项
表 6 各因素损失程度的评分标准 Table 6 Scoring criteria of various factors’ loss degree
| 评判指标 | 0.8~1.0 | 0.6~0.8 | 0.4~0.6 | 0.4以下 |
| 人员损失 | 造成人员伤亡 | 引起人员严重伤害 | 人员轻度伤害 | 没有造成人员的伤害 |
| 经济损失 | 完全毁坏 | 系统严重受损 | 系统或器材的轻度损坏 | 没有造成系统或器材的损害 |
| 战斗战备损失 | 完全无法执行任务 | 任务失败 | 导致任务延误或降级 | 导致非计划的维修 |
| 国际国内影响 | 造成国外和国内轰动性影响 | 影响非常大 | 一般性影响 | 不大 |
表选项
2.2.1 确定评价因素、评价等级 可撒布地雷的评价因素可选取为
U={人身安全(u1),产品功能(u2),经济损失(u3),系统损伤(u4)}
评价等级为
V={Ⅰ类(v1),Ⅱ类(v2),Ⅲ类(v3),Ⅳ类(v4)}
2.2.2 构造模糊评价矩阵 评分标准按照表 6进行,针对某一故障模式对多名专家进行评分调查,取评分均值代入隶属度函数,隶属度函数采用梯形分布,此处不详细叙述。以引信电路中的虚焊为例进行调查,将调查结果代入隶属度函数得到模糊评价矩阵:
 | (8) |
2.2.3 确定因素权重 按照第1.2.3节方法获得4个因素的综合权重向量为
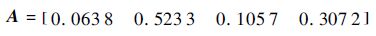 | (9) |
2.2.4 建立评价模型,确定η 模糊结果向量为
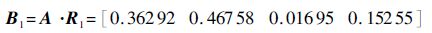 | (10) |
取严酷度Ⅰ类、Ⅱ类对应的值,取两位有效数字,得到
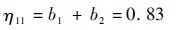 | (11) |
其他故障模式中,直接导致单元丧失功能的,η取1;不能确定的故障模式,可按上述方法求得η。
2.3 攻击目标阶段可靠性评价 表 5为攻击目标阶段的FFMECA分析,可以建立攻击目标阶段的可靠性数学模型为
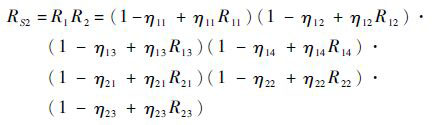 | (12) |
代入η,得
 | (13) |
采用文献[7]中的方法进行攻击目标阶段的任务可靠性评定,结果为0.997 8。
当不考虑故障模式影响概率时,任务时间为272 h,用Relax软件进行任务可靠度计算,得到其在置信度为90的情况下结果为0.996 9。
3 结 论 1) 本文提出了基于FFMECA分析的任务可靠性评价方法,此方法基于模糊数学思想,综合专业人员对故障模式的严酷度评价结果,定量给出故障模式严酷度的隶属度,实现了故障模式严酷度的定量评价。
2) 通过对故障模式严酷度隶属度函数的归一化处理,定义了故障模式出现产生各种严酷度后果的概率值。成功地解决了统计参数不够完整的情况下难以评价故障模式影响概率的工程实际难题。利用相关定性与定量信息,考虑故障模式的影响程度进行任务可靠性的评价,更加符合工程实际情况。
3) 运用研究方法对可撒布地雷的任务过程进行可靠性评价。此方法紧密结合任务剖面,针对可撒布地雷的特点进行了任务阶段的划分。完成了可撒布地雷任务可靠性的定性与定量的综合评价。形成了武器装备任务可靠性评价流程,对可靠性评价方法的工程应用具有一定的指导意义。
参考文献
| [1] | 苟仲秋, 李兴乾, 于潇. 基于RPA的交会对接任务可靠性评估[J].航天器工程, 2012, 21(2): 73–78.GOU Z Q, LI X Q, YU X. PRA-based reliability assessment approach in space rendezvous and docking[J].Spacecraft Engineering, 2012, 21(2): 73–78.(in Chinese) |
| [2] | 金星, 张明亮, 王军, 等. 大型复杂系统可靠性评定的近似计算方法[J].装备指挥技术学院学报, 2004, 15(5): 53–57.JIN X, ZHANG M L, WANG J, et al. An approximate method of reliability evaluation for large-scale complicated system[J].Journal of the Academy of Equipment Command & Technology, 2004, 15(5): 53–57.(in Chinese) |
| [3] | 周源泉, 翁朝曦. 可靠性评定[M].北京: 科学出版社, 1990: 198-216.ZHOU Y Q, WENG C X. Reliability assessment[M].Beijing: Science Press, 1990: 198-216.(in Chinese) |
| [4] | 丁定浩. 复杂系统进行快速的可靠性预计和设计[J].电子产品可靠性与环境试验, 2014, 32(5): 1–6.DING D H. Quick reliability prediction and design of complex system[J].Electronic Product Reliability and Environment Testing, 2014, 32(5): 1–6.(in Chinese) |
| [5] | O'DELL S W,WILSON N H M.Optimal real time control strategies for rail transit operations during disruptions[M]//WILSON N H M.Computer-aided scheduling.Berlin: Springer-Verlag,1999:299-323. |
| [6] | 贡金鑫, 赵国藩. 国外结构可靠性理论的应用与发展[J].土木工程学报, 2005, 38(2): 1–7.GONG J X, ZHAO G F. Applications and developments of structural reliability theory abroad[J].China Civil Engineering Journal, 2005, 38(2): 1–7.(in Chinese) |
| [7] | 崔文彬, 吴桂涛, 孙培廷, 等. 基于FMEA 和模糊综合评判的船舶安全评估[J].哈尔滨工程大学学报, 2007, 28(3): 263–267.CUI W B, WU G T, SUN P T, et al. Ship safety assessment based on FMEA and fuzzy comprehensive evaluation methods[J].Journal of Harbin Engineering University, 2007, 28(3): 263–267.(in Chinese) |
| [8] | 周源泉. 可靠性基础知识讲座:第九讲可靠性评定[J].强度与环境, 1990(4): 54–65.ZHOU Y Q. Lectures of basic reliability knowledge: Lecture 9 Reliability assessment[J].Strength and Environment, 1990(4): 54–65.(in Chinese) |
| [9] | 金星, 洪延姬. 系统可靠性评定方法[M].北京: 国防工业出版社, 2005: 231-237.JIN X, HONG Y J. Assessment methods of system reliability[M].Beijing: National Defense Industry Press, 2005: 231-237.(in Chinese) |
| [10] | 中国人民解放军总装备部.故障模式、影响及危害性分析指南:GJB/Z 1391-2006[S].北京:总装备部军标出版发行部,2006:9-17.General Armament Department of the PLA.Guide to failure mode,effects and critically analysis:GJB/Z 1391-2006[S].Beijing: Military Standard Publishing and Distribution Department of General Equipment Department,2006:9-17(in Chinese). |
| [11] | 庹奎, 胡启国, 谢国宾. 基于ANSYS的连杆结构强度混合可靠性分析[J].组合机床与自动化加工技术, 2014(6): 113–117.TUO K, HU Q G, XIE G B. Hybrid reliability analysis for structural of the connecting rod based on ANSYS[J].Modular Machine Tool & Automatic Manufacturing Technique, 2014(6): 113–117.(in Chinese) |
| [12] | 周凌, 章家保, 李艳辉, 等. 考虑结构多失效模式的电动舵机系统可靠性预计[J].电光与控制, 2014, 21(11): 69–72.ZHOU L, ZHANG J B, LI Y H, et al. System reliability prediction of electromechanical actuator under structure multi-failure mode[J].Electronics Optics & Control, 2014, 21(11): 69–72.(in Chinese) |
| [13] | 严焕斌, 吴兆华. 随机振动载荷下混装组件焊点的可靠性分析[J].机械工程与自动化, 2014(6): 142–144.YAN H B, WU Z H. Reliability analysis of mixed component solders under random vibration load[J].Mechanical Engineering & Automation, 2014(6): 142–144.(in Chinese) |
| [14] | 汤巍, 景博, 黄以锋. 小子样变总体下的Bayes测试性验证方法[J].系统工程与电子技术, 2014, 36(12): 2566–2570.TANG W, JING B, HUANG Y F. Testability verification method based on Bayes theory under small sample and varying population circumstance[J].Systems Engineering and Electronics, 2014, 36(12): 2566–2570.(in Chinese) |
| [15] | 刘震宇, 马小兵, 洪东跑, 等. 基于飞行剖面的作战飞机任务可靠性评估方法[J].北京航空航天大学学报, 2012, 38(1): 59–63.LIU Z Y, MA X B, HONG D P, et al. Mission reliability assessment for battle-plane based on flight profile[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(1): 59–63.(in Chinese) |
