1 CEEMDAN核心理论 本节介绍EMD和CEEMDAN的基本概念。但出于逻辑上的清晰,首先简要介绍希尔伯特变换[15],以说明CEEMDAN算法的必要性。
1.1 希尔伯特变换 对于任意实信号x(t),其希尔伯特变换为
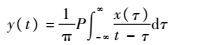 | (1) |
式中:P为柯西主分量。结合y(t),可获得实信号的解析形式:
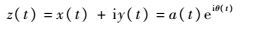 | (2) |
式中:
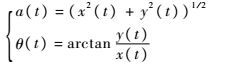 | (3) |
a(t)为瞬时幅度,而θ(t)为瞬时相位。则瞬时频率为
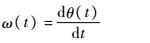 | (4) |
希尔伯特变换是分析单成分信号的高效工具。然而由于真实信号往往是多成分的,希尔伯特变换获得的瞬时频率对其来说往往没有物理意义[16],这一点极大地限制了希尔伯特谱分析的应用范围。为解决这一问题,可采用类EMD算法,如CEEMDAN。
1.2 EMD和CEEMDAN EMD的主要思想是将一信号x(t)分解为一系列本征模态函数(IMF),再使用希尔伯特变换分析IMF。IMF必须满足两个条件:①在全局特性上看,极值点数和过零点数相差不能超过1;②在局部特性上看,各处由局部极大值点定义的包络线和局部极小值定义的包络线的均值都为0。
EMD的局部特性可能导致单个IMF产生不同幅度的震荡,或者多个IMF产生相似幅度的震荡。当不需要这种现象出现或者不同IMF需要相似幅度的时候,这就成为所谓的“模式混淆”问题。CEEMDAN使用噪声协助类方法来解决该问题。算法具体表述如下:令Ek(·)为产生第k个IMF的算子,且令w(i)为零均值单位方差白噪声的一个实现,接着:
步骤1?对i= 1,2,…,I使用EMD分解x(i)=x+β0w(i),并定义第一CEEMDAN IMF为${{\tilde{d}}_{1}}=\frac{1}{I}\sum\limits_{i=1}^{k}{d_{1}^{\left( i \right)}}={{\bar{d}}_{1}}$。
步骤2?计算第一残差:r1=x-${{\tilde{d}}_{1}}$。
步骤3?使用EMD获得r1+β1E1(w(i)),i=1,2,…,I的第一IMF,定义第二CEEMDAN IMF为:${{\tilde{d}}_{2}}=\frac{1}{I}\sum\limits_{i=1}^{k}{{{E}_{1}}\left( {{r}_{1}}+{{\beta }_{1}}{{E}_{1}}\left( {{w}^{\left( i \right)}} \right) \right)d_{1}^{\left( i \right)}}$。
步骤4?对k = 2,3,…,K计算第k残差:rk=r(k-1)-$\tilde{d}$k。
步骤5?使用EMD获得rk+βkEk(w(i)),i=1,2,…,I的第一IMF,定义第(k+1)CEEMDAN IMF为${{\tilde{d}}_{\left( k+1 \right)}}=\frac{1}{I}\sum\limits_{i=1}^{I}{{{E}_{1}}\left( {{r}_{k}}+{{\beta }_{k}}{{E}_{k}}\left( {{w}^{\left( i \right)}} \right) \right)d_{1}^{\left( i \right)}}$。
步骤6?对下一个k回到步骤4。
重复步骤4~步骤6直至获取的残差不能被EMD继续分解。系数βk=εkstd(rk)允许在每一次迭代中选择信噪比(SNR),其中:std(·)为标准偏差算子。
2 基于CEEMDAN的雷达信号重构和脉内细微特征向量提取 下面提出本文的特征提取方法。本文首先验证CEEMDAN对雷达信号数据的挖掘能力,并利用雷达信号的IMF成分重构信号,同时测试该信号重构算法的抑噪性能,以考查其在真实噪声环境下的重构效果。最后,基于该重构算法提取了3种脉内特征构成新的特征空间。该特征空间的识别效能将在下一节进行实验验证与分析。
假设x(t)为接收到的某部雷达辐射的待识别雷达信号,且$\tilde{d}$k,k = 1,2,…,K为CEEMDAN算法计算出的x(t)的IMF。根据1.2节,x(t)可以被表示为
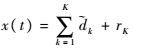 | (5) |
将希尔伯特变换施于每个IMF,而该信号可表示为
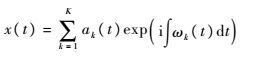 | (6) |
等式(6)使得幅度(或者能量)可以被表达为时间和频率的函数。
雷达信号为了抗干扰和功能需要,通常包含复杂的调制,并且为典型的多成分非线性非平稳随机过程。为此,这里采用两种现代雷达系统常用的发射调制样式进行分析,即线性调频(LFM)和二相频移键控(BPSK)。
2.1 基于CEEMDAN的信号重构 首先对以上提到的两种调制波形施以CEEMDAN,析取的IMF在图 1中给出。结果表明,可以在一个雷达信号中分解出多达10个成分,这充分说明雷达信号中存在过多的信号成分,亦即是说在每一瞬间存在过多的瞬时频率值;同时可以看出,信号的主要成分集中在IMF4~IMF7之间,因此本文使用这些成分重构被噪声污染的信号,亦即取其和信号为重构信号。
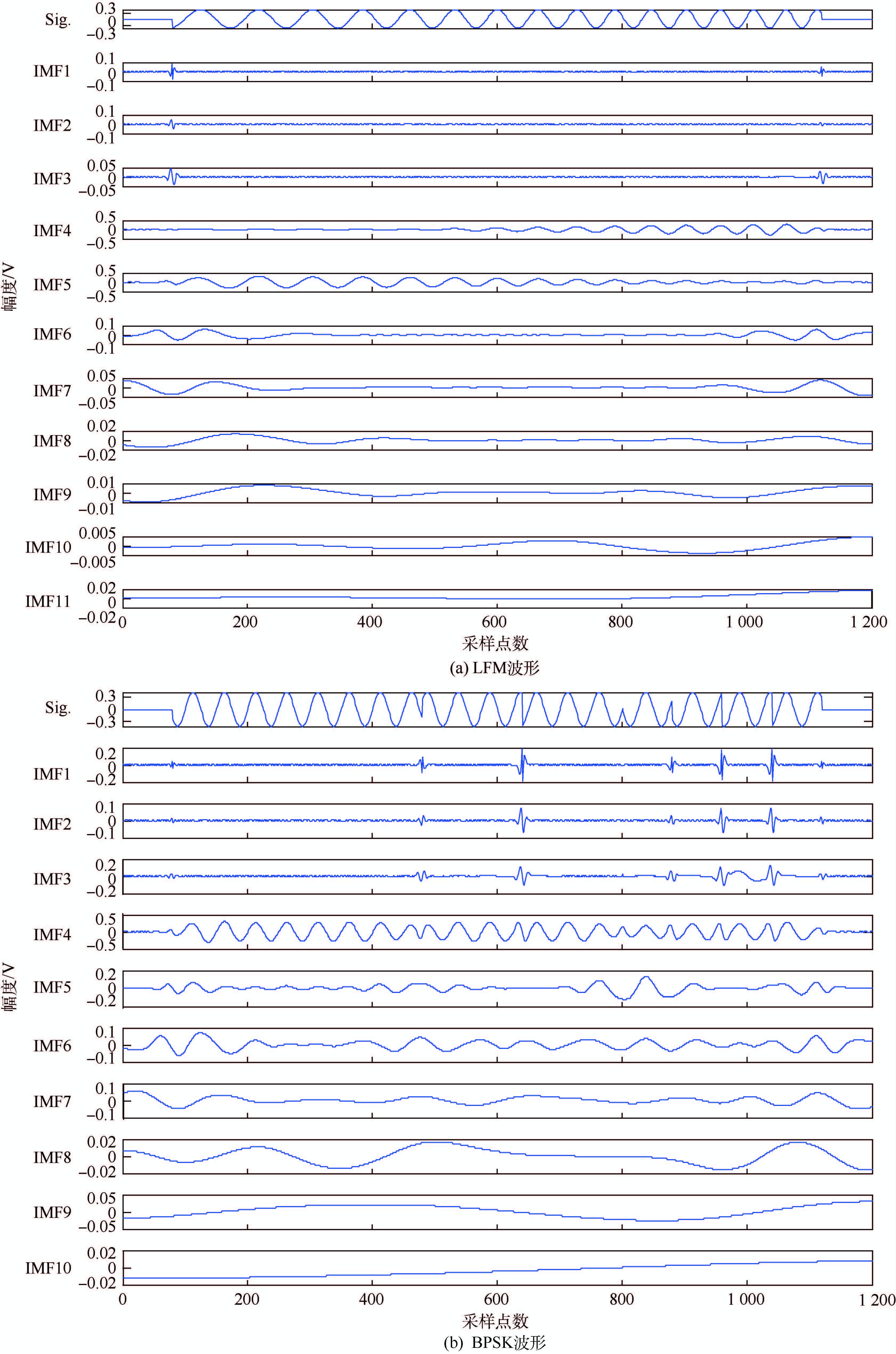 |
| 图 1 两种波形的CEEMDAN分解 Fig. 1 CEEMDAN decomposition of two waveforms |
| 图选项 |
事实上,ECM接收机收到的真实雷达信号不可能是上文讨论的纯净信号,而往往是噪声污染过的。因为CEEMDAN是基于噪声协助的类EMD方法,算法中使用的独立同分布噪声集在集合平均计算中彼此抵消,在本节实验中表现出了对信号加性噪声较好的压制作用。本文采用了信噪比分别为10 dB和20 dB的信号,对每种信号施加CEEMDAN(协助噪声标准差为0.05 V)并提取IMF4~IMF7对信号进行重构,进行1 000次蒙特卡罗实验。结果表明对于10 dB信噪比LFM和BPSK雷达信号,污染信号样本和纯净信号之间均方误差平均值分别为0.316 3 V和0.315 3 V,而重构信号和纯净信号之间均方误差平均值为0.100 7 V和0.108 7 V;而对于20 dB信噪比信号,该均方误差平均值在重构之前为0.098 9 V和0.097 1 V,重构之后则为0.042 5 V和0.051 8 V。从图 2中可以看到,本文信号重构方法的去噪性能非常好,说明该重构方法有效地捕捉了带噪信号空间中的信号主要成分。
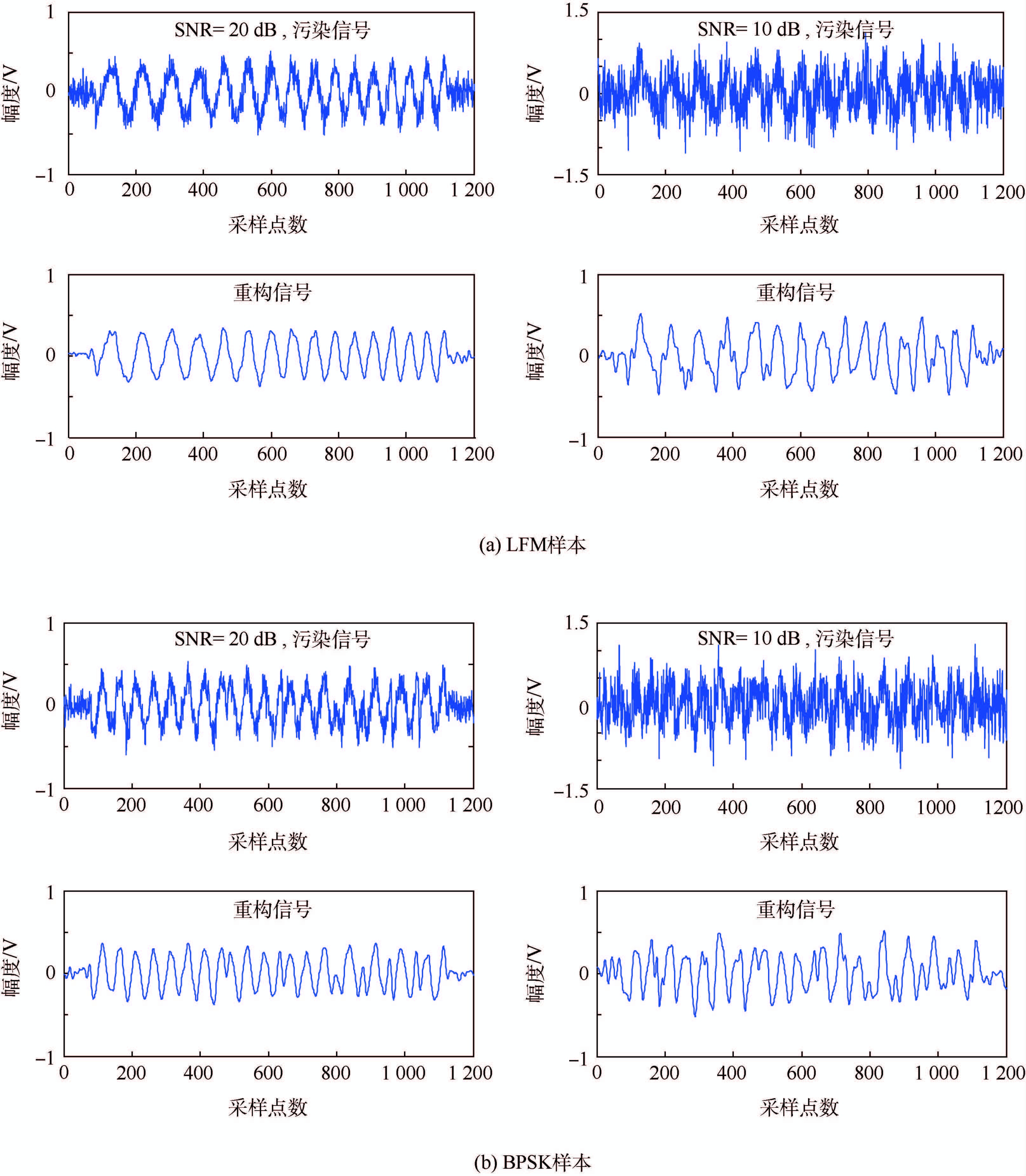 |
| 图 2 对两种波形样本的抑噪效果 Fig. 2 De-noising effect on two kinds of waveform samples |
| 图选项 |
2.2 特征向量和特征空间构建 据2.1节,雷达信号的主要信息可以通过其重构信号表达,由于IMF是单一成分信号,可以对其施加希尔伯特变换提取其瞬时特征,如式(1)~式(4),因此与原始雷达信号不同,重构信号在保留了其主要信息的同时,是可以进行希尔伯特变换的,因此就可提取出基于其时频分布的信号特征。基于重构信号,本文提出3种信号特征,并构成特征向量和特征空间。
1) 首要成分相似比
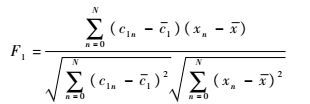 | (7) |
式中:N为采样点数;x为雷达信号;c1为信号首要IMF成分,本文中为IMF4;xn和c1n分别为x和c1的采样后形式;F1描述c1与x的相似程度。
2) 首要成分带宽
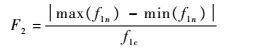 | (8) |
 | (9) |
式中:f1n为首要IMF成分的瞬时频率;f1c为其平均值,即首要IMF成分的中心频率;F2描述c1的频域跨度。
3) 成分瞬时频率方差
 | (10) |
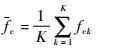 | (11) |
式中:K为用于重构信号的IMF成分个数;fck为第k成分中心频率;F3描述用于重构信号的各IMF之间的频域差异。
事实上,基于重构信号可以提取的特征数目是无穷的,然而从计算成本角度考虑,特别是航空应用条件下的空间限制和计算实时性要求,本文只提出3种特征以刻画雷达脉内细微特征。其中,由于用于重构信号的各IMF之中,首要成分c1又居其主干,因此F1及F2的计算只涉及信号首要成分,以进一步降低算法时间和空间复杂度;而F3则从全局角度考察重构信号,以提供更丰富的信号细节。总的来讲,本文提出特征的考量在于在保留特征向量充足信息量和降低算法时空复杂度之间达到均衡。
则本文提出的特征向量可表示为F=[F1,F2,F3],选用合适的分类器,雷达信号就可以被有效识别。本文特征提取方法的计算流程详见图 3伪代码,并将在第3节进行验证。
 |
| 图 3 本文雷达辐射源识别特征提取方法计算流程伪代码 Fig. 3 Computational pseudocode of proposed featureextraction method for radar emitter identification |
| 图选项 |
3 实验与结果分析 为验证本文算法,本节进行基于MATLAB(R2014a)的仿真。本节模拟了位于同一方位的6部雷达,即脉冲到达方位(DOA)认为全部相同。发射信号的调制形式与彼此略有不同,见表 1。
表 1 仿真辐射源信号的调制参数 Table 1 Signal modulation parameters of simulated emitters
| 辐射源 | 调制参数 | ||||
| 载频f0/GHz | 脉冲宽度T/μs | 脉冲幅度A/V | 调频斜率α/(GHz·μs-1) | 相位编码函数$\varphi $i | |
| E1 | 2.1 | 10.4 | 0.32 | 0.10 | |
| E2 | 1.9 | 10.3 | 0.33 | 0.15 | |
| E3 | 2.0 | 10.2 | 0.31 | 0.20 | |
| E4 | 1.8 | 10.3 | 0.30 | [1111100110101] | |
| E5 | 1.9 | 10.5 | 0.32 | [11100010010] | |
| E6 | 2.2 | 10.4 | 0.31 | [1110010] | |
表选项
由表 1可见,前3种信号为LFM信号,后3种为BPSK信号。6种信号在载频f0、脉冲宽度T和脉冲幅度A上基本一致,但3种LFM信号在调频斜率α相互区分,而BPSK信号在相位编码函数$\varphi $i上相互区分。这样设计实验调制参数的原因在于充分模拟待识别信号PDW高度重叠的情况。为验证本文算法的实用性,将不同能量的白噪声叠加在表 1所述信号上,并附加大小不同的相移,产生信噪比0~20 dB、相位在-π/2~π/2 的样本信号。表 1中每种信号产生500个样本,也即共有3 000个样本。所有样本在图 4(a)所示的PDW特征空间中以不同颜色的点表示,每种信号对应一种颜色。从中可以看出,任何一种信号都无法在PDW特征空间中与其他辐射源信号区分开。实际上PDW中尚有其他参数,但出于图形表示的明晰性,不失一般性地予以略去。接下来将全部样本在归一化的本文特征空间中绘出,如图 4(b)所示。可以看出,除了部分信号类别的边缘略有接触,各个辐射源信号样本点都是可以清晰区分的。这证明本文特征空间对于雷达脉内细微特征能够良好地捕捉,对复杂体制雷达信号识别是可用的。
 |
| 图 4 两种特征空间中的信号样本对比 Fig. 4 Comparison of signal samples in two feature space |
| 图选项 |
尔后随机选取1 000个样本训练SVM分类器,余下的2 000个样本用来测试该分类器。作为与本文算法的对比,同时用Pu的方法和CWT方法提取雷达信号特征,如文献[9-10],采用的分类器同样为SVM。3种算法的识别精度见表 2。
表 2 在变化信噪比下的3种方法仿真结果 Table 2 Simulation results of three methods under changing SNR
| 方法 | 精度/% | |||||
| SNR=0 dB | SNR=4 dB | SNR=8 dB | SNR=12 dB | SNR=16 dB | SNR=20 dB | |
| Pu的方法 | 68.9 | 77.2 | 85.1 | 91.2 | 97.3 | 97.6 |
| CWT方法 | 80.1 | 85.4 | 90.5 | 94.1 | 98.2 | 98.5 |
| 本文方法 | 90.7 | 92.8 | 94.1 | 96.3 | 99.6 | 100 |
表选项
从表 2中可见,在信噪比高达20 dB时,3种方法的识别精度都相当高,但2种对照算法的精度随着信噪比下降均有大幅下滑,而本文算法在各种信噪比条件下仍保持很高的识别精度。0 dB信噪比时,CWT方法的识别精度下降到80.1%,Pu的方法精度为68.9%,这对于电子战来说已经相当低,但本文方法仍有90%以上的识别精度,这是由于本文方法的高效抑噪性能。此外,应注意到CWT和Pu的方法的识别精度上限分别在98.5%和97.6%左右,说明该两种算法仍未完全利用雷达信号的细微脉内特性,在特征空间中的各类样本对于SVM是线性不可分的,也即SVM算法无法给出没有错误的分离超平面;而本文方法的精度在信噪比为20 dB时已经达到100%,说明本文方法给出的特征在提取脉内细微特征方面较之两种对照方法性能更优。
4 结 论 脉内特征是雷达信号特征提取的重要研究方向,然而目前大部分脉内特征提取方法仍不能在非平稳非线性信号上取得足够好的效果,而此类信号恰恰构成了实际环境中雷达信号的主体。本文提出一种基于CEEMDAN的雷达辐射源识别脉内细微特征提取算法,仿真实验表明:
1) CEEMDAN可以准确提取出构成常见雷达调制信号的IMF成分,且部分成分可用于重构雷达信号。
2) 由于CEEMDAN在非平稳非线性信号处理上的优势,本文信号重构方法具有足够好的抑噪性能以在低信噪比条件下工作。
3) 本文特征空间可以充分区分PDW高度重叠的雷达信号样本,同时本文方法较之该领域主流方法具有更好的雷达辐射源识别精度。
4) 类EMD方法在雷达辐射源识别信号特征提取领域有较大的应用空间,为进一步探索类EMD方法在该领域的应用打下了基础。
由于类EMD方法属于经验方法,目前缺少相应的数学支撑,使得本文无法在数学层面上进行论证,这也是类EMD雷达信号处理仍需解决的课题。
参考文献
| [1] | MONTAZER G, KHOSHNIAT H, FATHI V. Improvement of RBF neural networks using fuzzy-OSD algorithm in an online radar pulse classification system[J].Applied Soft Computing, 2013, 13(9): 3831–3838.DOI:10.1016/j.asoc.2013.04.021 |
| [2] | JIANG H,PANG Z,TANG P,et al.Intrapulse modulation recognition based on pulse description words[C]//Proceedings of the 2013 6th International Congress on Image and Signal Processing.Piscataway,NJ:IEEE Press,2013,3:1367-1371. |
| [3] | MATUSZEWSKI J,PARADOWSKI L.The knowledge based approach for emitter identification[C]//Proceedings of the 12th International Conference on Microware & Radar,MIKON '98.Piscataway,NJ:IEEE Press,1998,3:810-814. |
| [4] | 刘海军, 柳征, 姜文利, 等. 基于联合参数建模的雷达辐射源识别方法[J].宇航学报, 2011, 32(1): 142–149.LIU H J, LIU Z, JIANG W L, et al. A joint-parameter modeling based radar emitter identification method[J].Journal of Astronautics, 2011, 32(1): 142–149.(in Chinese) |
| [5] | 关一夫, 张国毅. 一种基于隐马尔科夫模型的雷达辐射源识别方法[J].火力与指挥控制, 2015, 40(10): 98–103.GUAN Y F, ZHANG G Y. A radar emitter recognition algorithm based on hidden markov models[J].Fire Control & Command Control, 2015, 40(10): 98–103.(in Chinese) |
| [6] | XIAO W,WU H,YANG C.Support vector machine radar emitter identification algorithm based on AP clustering[C]//Proceedings of the 2013 International Conference on Quality,Reliability,Risk maintenance,and Safety Engineering (QR2MSE).Piscataway,NJ:IEEE Press,2013:2062-2064. |
| [7] | SINGH A, RAO K. Digital receiver-based electronic intelligence system configuration for the detection and identification of intrapulse modulated radar signals[J].Defence Science Journal, 2014, 64(2): 152–158.DOI:10.14429/dsj |
| [8] | KAWALEC A,OWCZAREK R.Radar emitter recognition using intrapulse data[C]//Proceedings of the 15th International Conference on Microwaves,Radar and Wireless Communications,2004,MIKON-2004.Piscataway,NJ:IEEE Press,2004,2:435-438. |
| [9] | PU Y W,JIN W D,ZHU M,et al.Classification of radar emitter signal based on cascade feature extraction and hierarchical decision technique[C]//Proceedings of the 8th International Conference on Signal Processing.Piscataway,NJ:IEEE Press,2006. |
| [10] | ZHU B, JIN W D. Feature analysis of advanced radar emitter signals based on continuous wavelet transform[J].Applied Mechanics and Materials, 2013, 246-247: 1125–1129. |
| [11] | PENG Z, TSE P, CHU F. A comparison study of improved Hilbert-Huang transform and wavelet transform:Application to fault diagnosis for rolling bearing[J].Mechanical Systems and Signal Processing, 2005, 19(5): 974–988.DOI:10.1016/j.ymssp.2004.01.006 |
| [12] | TORRES M,COLOMINAS M,SCHOLOTTHAUER G,et al.A complete ensemble empirical mode decomposition with adaptive noise[C]//Proceedings of the 2011 IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway,NJ:IEEE Press,2011:4144-4147. |
| [13] | HUANG N E,SHEN Z,LONG S,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[C]//Proceedings of the Royal Society of London A:Mathematical,Physical and Engineering Sciences.London:The Royal Society,1998,454(1971):903-995. |
| [14] | WU Z H, HUANG N E. Ensemble empirical mode decomposition:A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1): 1–41.DOI:10.1142/S1793536909000047 |
| [15] | HAHN S L. Hilbert transforms in signal processing[M].Norwood: Artech House on Demand, 1996: 1-55. |
| [16] | HUANG N E.Computing instantaneous frequency by normalizing Hilbert transform:US,6901353[P].2005-05-31. |
