目前研究姿态控制/角动量管理(Attitude Control/Momentum Management,ACMM)的成果较多,但大部分是在轨道系下进行的。Wie等[1]利用重力梯度力矩和陀螺耦合力矩来平衡姿态,假设惯量积为零且姿态偏差为小量,将俯仰轴与滚动/偏航轴解耦,并且引入滤波变量采用线性二次型(Linear Quadratic Regulators,LQR)算法求解控制器,但该算法在姿态角偏差较大时并不适用。Parlos和Sunkel[2-4]针对大角度偏差的情况采用自适应控制算法,但该算法所设计出的控制器较为复杂,实现起来有一定难度。
Harduvel[5]采用三轴耦合的模型,引入滤波状态量抑制常值、1倍和2倍于轨道频率的扰动对系统的影响,在轨道系下设计了线性化的ACMM控制器,该控制器采用传统的LQR算法,即通过选取权重矩阵Q和代价矩阵R解出反馈增益矩阵,这也是目前国际空间站采用的ACMM算法。该算法的不足之处在于:所得到的三轴耦合状态空间方程达到了24维,要想选出合适的Q矩阵使得系统有较好的暂态和稳态性能并不是一件容易的事情,且线性化系统不适用于大角度偏差的情况。为了适应系统大角度偏差,朱孟萍等[6-7]分别采用基于参数辨识的自适应算法和非线性最优控制算法对轨道系下ACMM进行了仿真验证,取得了较好的效果,但其采用θ-D[8]算法求解状态相关黎卡提方程得到的是次优解。
在极点配置理论方面,针对LQR算法在求解高维状态方程时遇到Q矩阵选取困难的问题,Shieh等[9-10]提出了带极点配置的LQR算法,该算法能够将极点配置到与虚轴夹角为±45°或±30°的扇形范围内,同时为了保证闭环系统具有一定的鲁棒性,该算法可以在虚轴左侧指定一条平行于虚轴的直线,然后将极点移动到该直线的左侧[11-12]。这种设计方法的优越性在于:极点配置并不是通过指定每一个极点位置来实现的,而是指定一个扇形区域,将闭环系统配置到该区域内,实现起来较为简单。Sunkel等[13-14]建立了轨道系下ACMM模型,同时利用该算法求解出控制器,但在建立模型时并没有抑制扰动对姿态的影响,导致其姿态角的周期性波动较大。
对于惯性系下的ACMM,张军等[15]采用与文献[5]相似的方法验证了惯性系下的角动量管理的可行性,但该算法也存在选取Q矩阵困难的问题,同时没有验证系统的可控性,在俯仰轴方向只要存在常值扰动即有可能导致系统失控,即在俯仰轴方向系统没有鲁棒性。
本文对惯性系下ACMM问题进行分析,考虑到惯性系下气动力矩绕俯仰轴一周基本不积累,故将其作为外部扰动处理,仅采用引力梯度力矩来平衡姿态。由于角动量反馈控制对挠性附件具有较强的鲁棒性[16],并且柔性构件的固有频率一般在0.1Hz以上,远大于轨道频率,因此在控制器设计时忽略太阳帆板挠性模态的影响。同时分析了在俯仰轴方向角动量管理的不可行性,将俯仰轴与滚动/偏航轴解耦,将扰动项引入方程以抑制其对姿态的影响。采用带极点配置的LQR算法[9-10, 17]求解出反馈增益矩阵,该算法根据给出的代价矩阵R、稳定裕度以及阻尼角, 通过迭代算法将系统闭环极点配置到指定的区域。
1 惯性系ACMM模型 定义轨道系fo(Ooxoyozo),原点在系统质心,z轴在轨道平面内指向地心,x轴正向指向空间站飞行方向,y轴按右手定则确定;惯性系fi(Oixiyizi),其是一种中间坐标系,在t0时刻与轨道系重合;本体系fb(Obxbybzb),姿态角为零时与惯性系重合。
忽略柔性构件,惯性系下空间站刚体部分姿态动力学方程为
 | (1) |
式中:

CMG动力学方程为
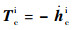 | (2) |
式中:
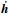
引力梯度力矩在近圆轨道下为
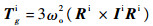 | (3) |
式中:ωo为轨道角速度;Ri为惯性系下地心到卫星的单位矢量;Ii为惯性系下本体转动惯量,即
 |
由坐标系定义可知,在t0时刻轨道系与惯性系重合,则在t时刻轨道系与惯性系之间的旋转角度即为轨道系绕yo轴转到惯性系的角度υio=ωo(t-t0),于是轨道系到惯性系的坐标转换矩阵可表示为
 | (4) |
显然,地心到卫星的单位矢量在惯性系下的分量与轨道系下分量关系为
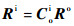 | (5) |
式中:Ro=00-1T为轨道系下地心到卫星的单位矢量。
结合式(3)~式(5),惯性系下引力梯度力矩为
 | (6) |
采用3-1-2旋转顺序的欧拉角表示本体系到惯性系的旋转角度θib=[φ υ ψ]T,在小角度偏差时,从本体系到惯性系的转换矩阵近似为
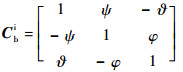 | (7) |
定义本体系下航天器本体的惯量阵为
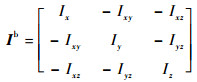 | (8) |
忽略高阶项,根据2阶张量之间的转换关系Ib=CibIiCbi,得到本体系与惯性系下空间站转动惯量之间的近似关系为
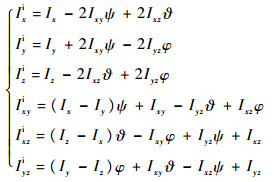 | (9) |
将式(9)代入式(6)得到本体系下转动惯量表示的惯性系下引力梯度力矩表达式为
 | (10) |
式中:
 |
显然,引力梯度力矩被分为两部分:姿态相关项和姿态无关项。当本体系坐标轴与惯性系主轴重合时,惯量积为零,此时引力梯度力矩只有周期性的成分,而不会引起CMG角动量积累,因此惯性系下角动量管理就是通过姿态偏置来消除引力梯度力矩及其他扰动引起的常值积累。
惯性系下空间站角动量为
 | (11) |
式中:ωibi为本体系到惯性系的绝对角速度在惯性系下的分量,其与姿态角速度之间的关系为(
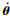
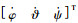
 | (12) |
对式(11)保留1阶项,得到线性化的姿态运动学方程为
 | (13) |
将式(10)代入式(1), 再联合式(2)和式(13), 得到线性化的ACMM模型。将此模型写成状态方程的形式如下:
 | (14) |
式中:E为3×3的单位矩阵。
2 ACMM状态方程分析 从引力梯度力矩表达式(10)可以看出,在姿态零偏置时,滚动/俯仰、俯仰/偏航方向的惯量积会导致CMG积累。因此在姿态平衡处,滚动/俯仰、偏航/俯仰轴的主惯量差产生控制力矩补偿滚动/俯仰、偏航/俯仰惯量积以及其他扰动带来的常值力矩。系统达到稳定姿态时,其姿态偏置可以通过引力梯度力矩及其他干扰力矩大致估算出:
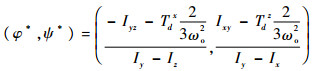 | (15) |
式中:φ*和ψ*分别为滚动轴和偏航轴平衡姿态角;Tdx为扰动力矩Tdi在惯性系x轴方向的常值分量;Tdz为扰动力矩Tdi在惯性系z轴方向的常值分量。
下面对俯仰轴方向是否能进行角动量管理进行理论分析。空间站可以进行角动量管理的必要条件是需要存在额外力矩来平衡扰动。重新观察式(10)可以发现,在滚动/偏航方向上都存在与姿态相关的引力梯度力矩,通过姿态机动就可以调节引力梯度力矩来抵消扰动力矩对系统的影响,从而避免滚动/偏航方向的CMG角动量积累。但在俯仰轴方向上并不存在与姿态相关的引力梯度力矩,说明俯仰轴方向上没有额外力矩来平衡可能存在的常值扰动,即俯仰轴方向扰动力矩产生的角动量只能通过CMG吸收。需要强调的是,这并不是近似线性化产生的结果,在用惯性系下转动惯量表示引力梯度力矩的式(6)中,并没有进行近似处理,但可以看出俯仰轴方向也只存在2倍于轨道频率的扰动力矩。
下面从可控性的角度来分析俯仰轴不能角动量管理对系统的影响。显然系统状态方程式(14)中至少有3个极点“0”,利用PBH判据来判断极点“0”的可控性,可以发现无论其他参数如何,式(14)的可控性指数均小于8,这就说明至少存在1个极点“0”是不可控的。结合本节分析可知,在俯仰轴方向上存在不可控状态量,即姿态角和CMG动量不能同时约束,只要在俯仰轴方向上存在常值扰动,就会导致姿态角发散或者CMG角动量积累,换句话说在俯仰轴方向不具备鲁棒性。在实际工程应用中,这是不能接受的。
考虑到ACMM首先是要能够控制姿态,并保证一定的姿态精度。为了解决上述问题,将俯仰轴与滚动/偏航轴解耦,不再约束俯仰轴方向的CMG角动量,因此去除状态方程中俯仰轴方向的CMG角动量,这样在俯仰轴方向上的姿态控制就不再考虑CMG角动量是否积累,滚动/偏航轴方向则保持不变。同时考虑到大气扰动主要是1倍于轨道频率,而从式(10)可以看出引力梯度力矩主要为2倍于轨道频率,为了让周期性扰动通过CMG吸收,而常值扰动通过姿态偏置来抵消,根据内模原理将系统状态方程扩维,引入滤波状态量:f=[f0Tf11Tf12Tf21Tf22T]T,f0用于抑制常值扰动,f11、f12用于抑制1倍于轨道频率的扰动,f21、f22用于抑制2倍于轨道频率的扰动,把常值、1倍和2倍于轨道频率的扰动引入状态方程中,得到最终的滚动/偏航轴状态方程及控制方程如下:
 | (16) |
 | (17) |
式中:
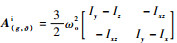
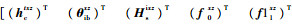
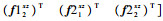
相应的,在俯仰轴方向上状态方程及控制器为
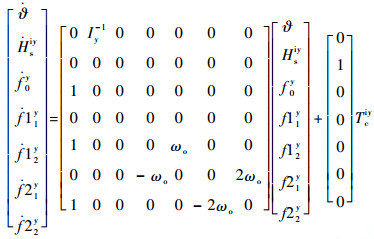 | (18) |
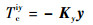 | (19) |
式中:Tciy为Tci在俯仰轴方向上的分量;y=
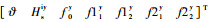
3 带极点配置的LQR算法 3.1 极点配置算法基本理论 本文采用的极点配置算法是Shieh等[9-10]提出的,该算法通过给定的阻尼角、稳定裕度以及系统的代价矩阵R,通过迭代自动将极点配置到指定的扇形区域,该扇形区域与虚轴的夹角可以为30°~90°,为实现该算法,现介绍相关定理和引理如下。
考虑线性时不变连续时间系统:
 | (20) |
设LQR代价函数为
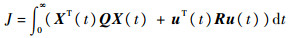 | (21) |
式中:A和B分别为状态转移矩阵和控制输入矩阵;权重矩阵Q和代价矩阵R分别为Rn×n的半正定矩阵和Rm×m的正定矩阵。
最小化式(21)性能指标的反馈控制律为
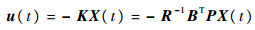 | (22) |
式中:K=-R-1BTP为m×n反馈增益;P为n×n非对称阵,满足黎卡提方程:
 | (23) |
引理1[9] ????记(A, B)为等式(20)描述的系统的可控对,取h≥0表示系统的稳定裕度,则闭环系统A-BR-1BTP所有的特征值将位于-h垂线的左侧,其中矩阵P是下列方程的解:
 | (24) |
引理2[17]????记{λi-}ni=1-表示矩阵A在虚轴上和纯左半平面的特征子集,{λi+}ni=1+表示在纯右半平面上的特征子集,则有:
1) 最优闭环系统的特征值集合:
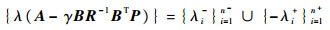 | (25) |
当γ=1且矩阵P满足Q=0时的黎卡提方程式(23)。
2) 记(λi-)ni=1-为特征值{λi-}ni=1-对应的特征向量,那么黎卡提方程的最大解半正定P满足:Pζi-=0, i=1, 2,…。而对应特征值集合{λ(A-BR-1BTP)}保持不变。另外的n+个特征值在纯左半平面上,其中γ>0.5。
引理3[17]????对于给定矩阵A∈Rn×n,定义2个相关矩阵A-∈Rn×n和A+∈Rn×n,并且有
 | (26) |
式中:所有参数同引理2。从引理2还可知,闭环系统A-BR-1BTP所有特征值λi-、-λi+都是当Q=0时的黎卡提方程式(23)的解,从而有
 | (27) |
式中:tr(·)为矩阵的迹。
引理4[17]????若(A, B)可控,则(-A2, B)、(A3, B)也是可控的。
引理5[9] ????考虑在复平面左半平面内的一个扇形区域:其边界与负实轴夹角为±45°/±30°直线包络而成。假定系统矩阵A为渐近稳定,其所有特征值分布在左半平面内,可分成扇形区域内、外2个特征值子集。定义保角映射

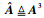
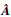
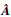
定理1[10] ????设稳定的系统矩阵A有特征值{λi-}i=1n-位于引理5所示的扇形区域内。而{λi+}i=1n+位于扇形区域外,考虑以下2个黎卡提方程:
 | (28) |
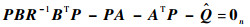 | (29) |
则对于闭环系统为
 | (30) |
其特征值除{λi-}i=1n-外,至少还会有一个实特征值或一对共轭复特征值位于扇形区域内,对于常增益系数γ满足:
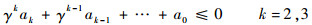 | (31) |
式中:
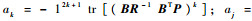

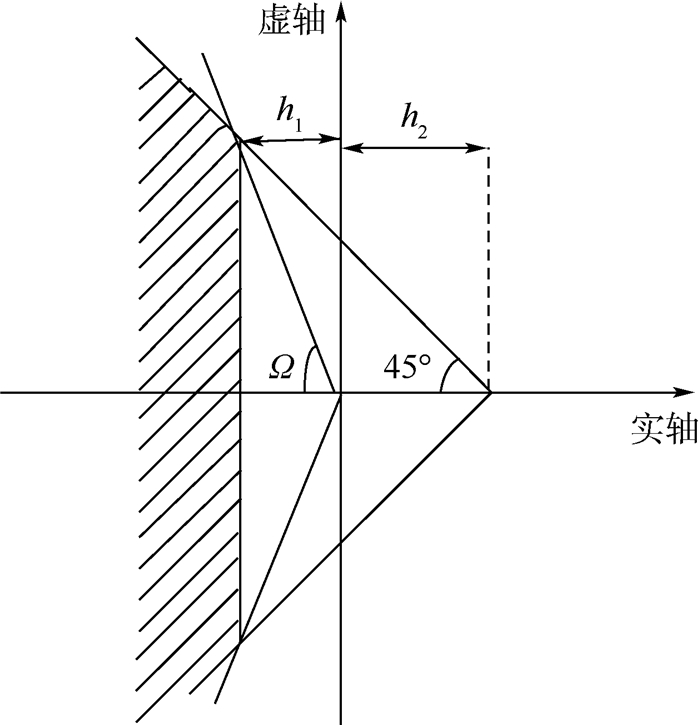
3.2 空间站ACMM控制器求解流程 从引理1~引理5可以看出,通过迭代算法可以将系统闭环极点配置到±45°或±30°以内。通常闭环极点在±45°左右时系统具有较短的调节时间,超调量也不会很大。为了使控制器求解有更大的灵活性,现做如图 1和图 2所示改进,即先根据引理1将极点配置到所需稳定裕度的左边,再根据所需要的角度Ω将虚轴向右移动h2,此时得到的极点将可以大致配置在30°~90°内。
 |
| 图 1 极点配置到45°~90°内 Fig. 1 Pole placement within region of 45°-90° |
| 图选项 |
 |
| 图 2 极点配置到30°~45°内 Fig. 2 Pole placement within region of 30°-45° |
| 图选项 |
具体算法实现简述如下:
1) 对于状态方程
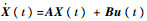
 | (32) |
解出半正定矩阵P0,则当前闭环系统为A1=A-BR-1BTP0,此时闭环系统所有极点在-h1左侧,记i=1。
2) 判断系统所需的阻尼角,若为30°~45°(见图 2),转步骤3);若为45°~90°(见图 1),转步骤7)。
3) 对于给定的阻尼角Ω,将复平面的虚轴向右移动:
 | (33) |
得到新的状态矩阵A1=A1-E·h2。
4) 解方程:
 | (34) |
解出半正定矩阵


5) 解方程:
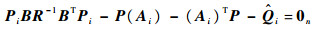 | (35) |
解出半正定矩阵Pi,对于新的闭环系统
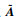
 | (36) |
式中:
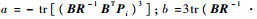

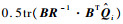
6) i=i+1;转步骤4)。
7) 对于给定的阻尼角Ω,将复平面的虚轴向右移动:
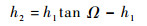 | (37) |
得到新的状态矩阵A1=A1-E·h2。
8) 解方程:
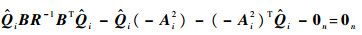 | (38) |
解出半正定矩阵


9) 解方程:
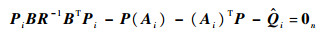 | (39) |
解出半正定矩阵Pi,对于新的闭环系统
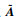
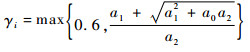 | (40) |
式中:
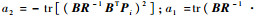

10) i=i+1, 转步骤8)。
11) 算法完成计算,最终系统增益矩阵为
 | (41) |
将u=-Kx代入到系统状态方程,则闭环系统所有的极点都会移动到指定的区域。
分别给出系统俯仰轴与滚动/偏航轴的性能指标,然后将状态方程代入到上述算法即可求解出相应的ACMM控制器。
4 仿真验证 本文针对“T”字构型的空间站进行仿真验证,仿真中动力学模型采用带挠性附件的中心刚体模型,执行机构只采用CMG。考虑到CMG角动量测量较为精确,其测量误差不会影响到控制器的稳定性。另外,由于平衡姿态并非本体系与惯性系重合,不失一般性,取初始姿态角和姿态角速度为零,系统干扰力矩如表 1所示。本体系下转动惯量为
表 1 其他干扰力矩Tdi Table 1 Other disturbance torque Tdi
| 干扰力矩 | 表达式 |
| Tdx | 0.002+0.3sin(ωot)+0.1sin(2ωot) |
| Tdy | 0.0001+sin(ωot)+0.2sin(2ωot) |
| Tdz | 0.0003+0.5sin(ωot)+0.2sin(2ωot) |
表选项
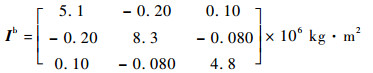 |
空间站的运行轨道为400km的近圆轨道,故轨道角速度近似取ωo=0.0011rad/s。
从状态方程式(16)和式(18)可以看出,扩维后的方程在滚动/偏航方向上常值扰动通过姿态偏置吸收,避免了CMG角动量的积累,周期性的扰动通过CMG吸收;而在俯仰轴方向常值扰动、1倍和2倍于轨道频率的扰动均由CMG吸收。从式(15)估算出稳态时平衡姿态角为
 | (42) |
在俯仰轴方向和滚动/偏航轴方向代价矩阵R均取单位矩阵。为了使系统有一定的鲁棒性,同时又有比较快的响应速度,仿真时在俯仰轴方向稳定裕度取0.2ωo,阻尼角取45°。在滚动/偏航方向由于需要约束CMG角动量,如果阻尼角取太小,会使得反馈增益阵过大,从而导致暂态时CMG输出力矩较大,因此在滚动/偏航方向上稳定裕度取0.25ωo,阻尼角取60°,用第3节算法求解出闭环极点如表 2所示,闭环反馈增益矩阵如表 3所示。为了更加直观地显示闭环极点的位置,现在复平面上表示出,如图 3和图 4所示。
表 2 闭环极点(-ωo) Table 2 Closed-loop pole (-ωo>)
| 滚动/偏航轴 | 俯仰轴 | |
| -3.828+3.298i | -3.828-3.298i | -5.846+5.411i |
| -3.828+3.298i | -3.828-3.298i | -5.846-5.411i |
| -1.534+0i | -1.482+0i | -1.544+1.073i |
| -1.034+0i | -0.9816+0i | -1.544-1.073i |
| -0.8038+0.9690i | -0.8038-0.9690i | -0.4000+0i |
| -0.8038+0.9690i | -0.8038-0.9690i | -0.4000+2.609×10-5i |
| -0.5000+9.820×10-7i | -0.5000-9.820×10-7i | -0.4000-2.609×10-5i |
| -0.5000+5.610×10-7i | -0.5000-5.610×10-7i | |
表选项
表 3 反馈增益矩阵(转置) Table 3 Feedback gain matrix(transpose)
| 滚动/偏航轴 | 俯仰轴 | |
| 0.028902 | 0.00034304 | 1168.1 |
| 0.00043344 | 0.029133 | 0.017578 |
| 470.01 | 5.3047 | 0.039637 |
| 5.6011 | 440.64 | -1.1645 |
| 0.042975 | 0.00028788 | 0.085026 |
| 0.00037828 | 0.043173 | 0.43774 |
| 4.5677×10-6 | 3.0982×10-8 | 3.0593 |
| 4.4604×10-8 | 4.5902×10-6 | |
| -0.12140 | -0.0053014 | |
| -0.0051838 | -0.11601 | |
| 0.29737 | -0.0039060 | |
| -0.0033021 | 0.27472 | |
| 0.24296 | -0.010226 | |
| -0.0092752 | 0.22053 | |
| 0.67539 | 0.0097575 | |
| 0.010057 | 0.63436 | |
表选项
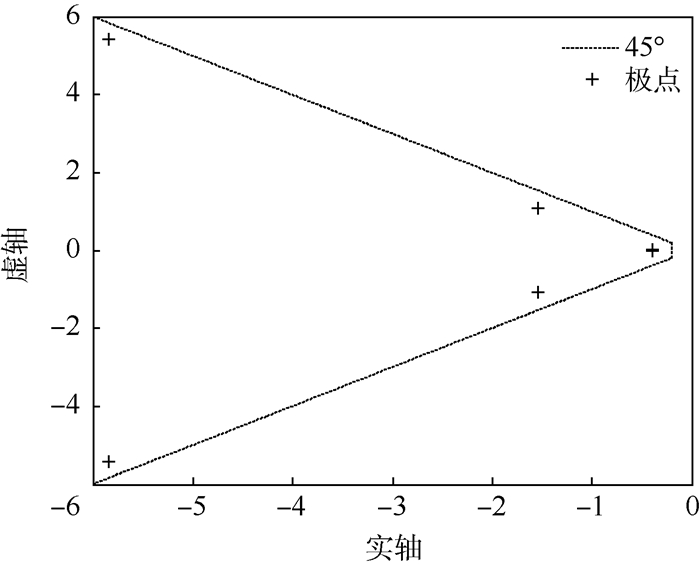 |
| 图 3 俯仰轴闭环极点 Fig. 3 Closed-loop pole in pitch axis |
| 图选项 |
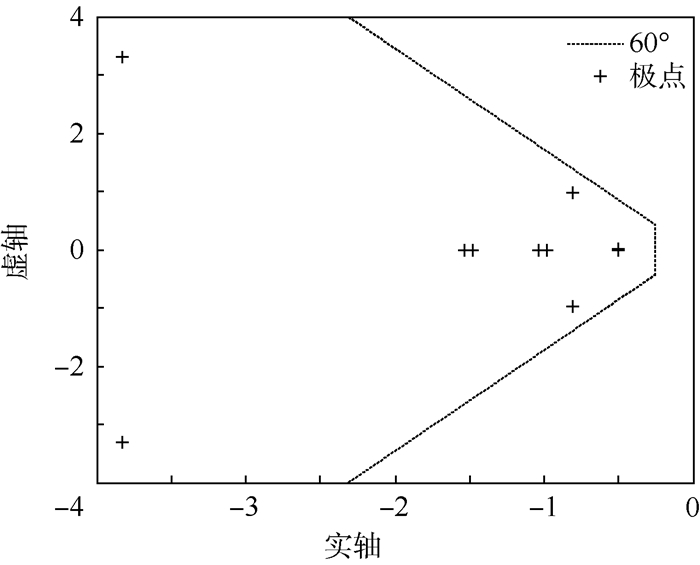 |
| 图 4 滚动/偏航轴闭环极点 Fig. 4 Closed-loop pole in roll/yaw axis |
| 图选项 |
从图 3中可以清楚看出,在俯仰轴方向,所有极点均被配置到了离虚轴0.2ωo~6ωo的地方,同时闭环极点都在±45°以内,说明在俯仰轴方向会有较短的调节时间和较小的超调量;从图 4可以看出,在滚动/偏航轴方向所有极点均在±60°内,保证了较小的超调量,且都在离虚轴0.25ωo~4ωo内,保证了较短的调节时间,也避免了出现暂态CMG输出力矩较大的情况。系统角动量管理仿真结果如图 5~图 8所示。
 |
| 图 5 姿态角 Fig. 5 Attitude angle |
| 图选项 |
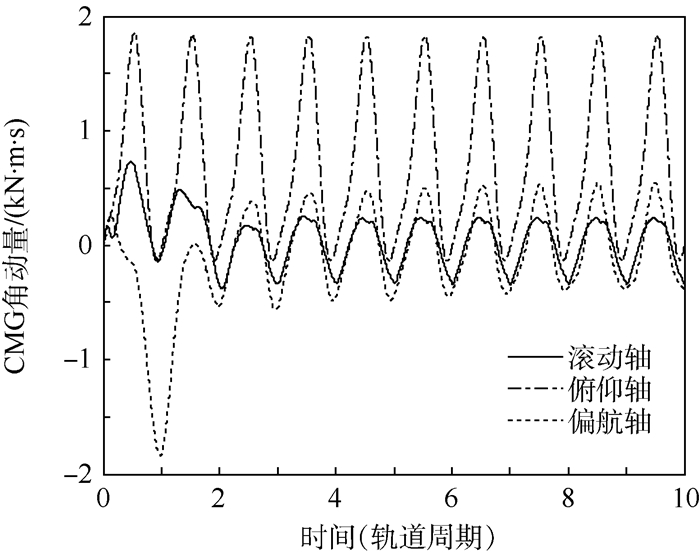 |
| 图 6 CMG角动量 Fig. 6 CMG angular momentum |
| 图选项 |
 |
| 图 7 引力梯度力矩产生的角动量 Fig. 7 Angular momentum caused by gravity-gradient torque |
| 图选项 |
 |
| 图 8 其他干扰力矩引起的角动量积累 Fig. 8 Accumulation of angular momentum caused by other disturbance torques |
| 图选项 |
从图 5可以看出,3个轨道周期后系统基本达到稳定状态,俯仰轴基本没有偏差,周期性的波动幅值也很小;滚动轴最终稳定在-1.4°左右,偏航轴最终稳定在3.6°左右,这与式(42)估计结果相符。由于在状态方程中引入了滤波变量,抑制了1倍、2倍于轨道频率的扰动对姿态的影响,稳定时的姿态角仅有一些幅值较小的高频波动。
结合图 5~图 8可以看到,CMG的角动量周期性波动但基本不积累,抵消掉了周期性的扰动对姿态的影响。同时在滚动/偏航方向引力梯度力矩几乎没有周期性扰动,而只存在常值偏置,正是因为滚动/偏航方向的姿态偏置才抵消掉了滚动/偏航方向的常值扰动以及俯仰/偏航、俯仰/滚动轴之间的惯量积。俯仰方向的引力梯度力矩引起的角动量周期性波动比较大,这主要通过俯仰方向的CMG来吸收。对于其他干扰力矩来说,滚动/偏航方向的少量的常值项积累通过滚动/偏航方向的姿态机动来与重力梯度力矩相抵消,而俯仰方向几乎没有常值积累,但周期性扰动比较大。总体来说控制器的设计达到了目的。
5 结论 本文综合分析了惯性系下空间站利用引力梯度力矩平衡姿态的可行性,经过理论分析及仿真验证表明:
1) 提出了一种较为实用的惯性系下角动量管理控制器求解算法,在设计空间站构型时,为了保证平衡姿态角较小,需要增大俯仰轴与滚动/偏航轴方向转动惯量差,同时应尽量减少惯量积。
2) 基于极点配置的LQR算法具有较好的通用性,特别适合于高维的状态方程,利用计算机求解有较大优势。
3) 仿真结果说明,尽管俯仰轴方向没有额外力矩来平衡姿态,但在俯仰轴方向常值扰动较小CMG角动量积累较慢,并不需要经常卸载。
为了使本文算法更好地满足实际需求,还需要进一步探索存在不确定性参数时的ACMM问题。
参考文献
| [1] | WIE B, BYUN K, WARREN V, et al. New approach to attitude/momentum control for the space station[J].Journal of Guidance, Control, and Dynamices, 1988, 12(5): 714–722. |
| [2] | PARLOS A G, SUNKEL J W.Adaptive stability and control for space station/orbiter berthing operations:AIAA-1992-4480[R].Reston:AIAA, 1992. |
| [3] | PARLOS A G, SUNKEL J W. Adaptive control and momentum management for large-angle spacecraft maneuvers[J].Journal of Guidance, Control, and Dynamices, 1992, 15(4): 1018–1028.DOI:10.2514/3.20937 |
| [4] | PARLOS A G, SUNKEL J W.Attitude control/momentum management of the space station freedom for large angle torque-equilibrium-attitude configurations:AIAA-1990-3352[R].Reston:AIAA, 1990. |
| [5] | HARDUVEL J T. Continuous momentum management of earth-orbited spacecraft[J].Journal of Guidance, Control, and Dynamices, 1992, 15(6): 1417–1426.DOI:10.2514/3.11405 |
| [6] | 朱孟萍, 徐世杰, 陈新龙, 等. 基于参数辨识的大型航天器自适应角动量管理[J].空间控制技术与应用, 2014, 40(3): 47–52.ZHU M P, XU S J, CHEN X L, et al. Adaptive momentum management of large spacecraft based on parameter identification[J].Aerospace Control and Application, 2014, 40(3): 47–52.(in Chinese) |
| [7] | ZHU M P, XU S J. Stability-based SDRE controller for spacecraft momentum management[J].Acta Astronautica, 2013, 89: 71–82.DOI:10.1016/j.actaastro.2013.03.026 |
| [8] | XIN M, BALAKRSHNAN S N.A new method for suboptimal control of a class of nonlinear systems[C]//41st IEEE Conference on Decision and Control. Piscataway, NJ:IEEE Press, 2002:2756-2761. |
| [9] | SHIEH S L, DIB M H, GANESAN S. Linear quadratic regulators with eigenvalue placement in a specified region[J].Automatica, 1988, 24(6): 819–823.DOI:10.1016/0005-1098(88)90058-1 |
| [10] | SHIEH S L, DIB M H, GANESAN S. Continuous-time quadratic regulators and pseudo-continuous-time quadratic regulators with pole placement in a specific region[J].IEEE Proceedings D-Control Theory and Applications, 1987, 134(5): 338–346.DOI:10.1049/ip-d.1987.0056 |
| [11] | SHIEH S L, DIB M H, GANESAN S. Linear quadratic regulators with eigenvalue placement in a vertical strip[J].IEEE Transaction on Automatic Control, 1986, 31(3): 241–243.DOI:10.1109/TAC.1986.1104233 |
| [12] | KOSHKOUEI A J, ZINDOBER A S I. Comment on "linear quadratic regulators with eigenvalue placement in a vertical strip"[J].IEEE Transactions on Automatic Control, 1999, 44(7): 1417–1419.DOI:10.1109/9.774113 |
| [13] | SUNKEL J W, SHIEH L S, ZHANG J L. Digital redesign of an optimal momentum mangement controller for the space station[J].Journal of Guidance, Control, and Dynamices, 1991, 14(4): 712–723.DOI:10.2514/3.20704 |
| [14] | SUNKEL J W, SHIEH L S. Multistage design of an optimal momentum management controller for the space station[J].Journal of Guidance, Control, and Dynamices, 1991, 14(3): 492–502.DOI:10.2514/3.20668 |
| [15] | 张军, 马艳红, 何英姿. 空间站组合体惯性系内角动量管理控制[J].空间控制技术与应用, 2010, 36(6): 1–5.ZHANG J, MA Y H, HE Y Z. Momentum management control of space station complex in intertial reference[J].Aerospace Control and Application, 2010, 36(6): 1–5.(in Chinese) |
| [16] | 张洪华, 吴宏鑫, 陈义庆. 挠性卫星姿态的角动量反馈控制[J].宇航学报, 2002, 23(3): 8–12.ZHANG H H, WU H X, CHENG Y Q. Angular momentum feedback control for flexible spacecraft[J].Journal of Astronautics, 2002, 23(3): 8–12.(in Chinese) |
| [17] | KAWASAKI N, SHIMEMURA E. Determining quadratic weighting matrices to locate poles in a specified region[J].Automatica, 1983, 19(5): 557–560.DOI:10.1016/0005-1098(83)90011-0 |
