直升机飞行动力学建模是分析全机配平特性的基础,且气动干扰建模是直升机飞行动力学模型和全机配平特性分析的核心内容之一。基于准定常假设,早期飞行动力学模型中的旋翼气动力忽略尾迹对诱导入流和非定常气动载荷的影响[7],因而主要用于直升机全机配平和稳定性分析。随着直升机对飞行品质的要求提高,建立包括旋翼入流动态特性的高阶直升机飞行动力学模型得到逐步发展[8-10],旋翼气动力模型普遍采用线性非均匀非定常入流模型、高阶动态入流模型以及二维翼型非定常气动力模型,并根据静态吹风数据或经验公式体现旋翼对机身和平尾的气动干扰作用。相比早期直升机飞行动力学模型,计算精度得到改善,但仍然未能准确考虑旋翼畸变尾迹对平尾气动和操纵特性的影响。为此,通过自由尾迹模型模拟旋翼畸变尾迹,得到更真实的桨盘诱导速度分布,并计算机身和平尾处诱导速度,而后通过经验模型或风洞试验数据间接考虑旋翼/机身/平尾气动干扰,建立精度更高的直升机飞行动力学模型[11-13],但仍未很好体现旋翼尾迹与平尾的非定常气动干扰对全机配平特性和操纵特性的影响,因而难于准确捕捉直升机低速前飞状态下的操纵量突增和显著的机体“抬头”现象[11]。
为更准确分析旋翼尾迹与平尾气动干扰对直升机全机配平特性的影响,直升机飞行动力学模型需嵌入旋翼/平尾气动干扰模型。旋翼/平尾气动干扰模型主要采用相对简单的旋翼尾迹模型。通过采用势流理论和升力面方法预测靠近平尾的旋翼桨尖涡强度和平尾非定常载荷[14]。由于预定尾迹难于准确得到不同飞行状态下的旋翼尾迹,因此分析精度较低。通过采用平面尾迹模型分析高速前飞状态的平尾载荷[15],然而平面尾迹难于准确得到低速状态的畸变尾迹,因此难于准确分析旋翼与平尾的气动干扰特性。基于Eulerian体系的涡量输运法(Vorticity Transport Method,VTM)可用于分析旋翼流场和旋翼/机身气动干扰[16],但基于Eulerian体系而存在非物理耗散,因而该方法仍然存在旋翼尾迹耗散问题,且基于升力面模型而难于体现旋翼尾迹对平面表面的非线性影响。基于Eulerian体系的计算流体力学(Computational Fluid Dynamics,CFD)能较准确分析旋翼流场[17],但数值耗散较大,计算资源需求仍然较多,且计算得到的旋翼尾迹耗散较快[18],因此在分析旋翼尾迹与平尾的气动干扰方面仍需发展。
基于Lagrangian体系定义涡量场,并求解Navier-Stokes方程,黏性涡粒子法可较好地分析旋翼尾迹的非定常特性,并于近年成功用于分析旋翼流场[19-20]。耦合非定常面元,黏性涡粒子法[21]能较准确捕捉旋翼尾迹的非定常特性,并能较准确体现旋翼干扰下的平尾和尾桨气动载荷[22-23]。为更准确分析旋翼尾迹与平尾的非定常气动干扰对直升机全机配平特性的影响,本文将基于非定常面元/黏性涡粒子法,通过在平尾面元中增加由旋翼和平尾尾迹时变干扰产生的非定常压力项,建立旋翼/平尾气动干扰模型,直接计算平尾非线性气动载荷,并嵌入直升机飞行动力学模型,耦合基于GA/LM混合优化的直升机全机配平方法,构建基于旋翼/平尾气动干扰的直升机全机配平特性分析方法。通过计算UH-60A直升机的旋翼操纵量和机体姿态,并与UH-60A、OH-6A、EH-101试验结果对比,分析旋翼/平尾气动干扰对全机配平特性的影响,并分析平尾构型对直升机全机配平特性的影响规律。
1 计算方法 1.1 旋翼/平尾气动干扰模型 1) 非定常面元/黏性涡粒子法
在桨叶和平尾的表面附近和尾流区之外,可假设流场无黏、无旋、不可压,由此旋翼流场势函数φv由旋翼桨叶、平尾和尾迹涡面上的汇σs和偶极子μd组成[21]。
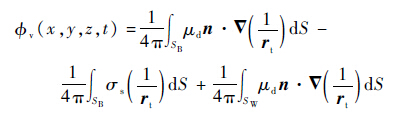 | (1) |
式中:SB和SW分别为旋翼或平尾等物面和尾迹涡面;n为旋翼或平尾的外法线单位矢量;rt=(x,y,z)为时变位置矢量。
由相对于旋翼或平尾表面的法向速度为零和旋翼或平尾对流体扰动在无限远处为零条件可得
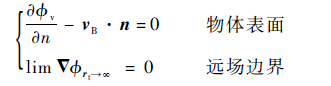 | (2) |
式中:vB为表面速度矢量。
由物面Neumann边界条件、桨叶和平尾后缘Kutta条件,可将式(2)的边界条件转为代数方程,由此求得桨叶和平尾的汇σs和偶极子μd分布。
旋翼和平尾的涡量场可由Navier-Stokes方程描述[19-22]。基于Lagrangian体系定义涡量场,得到黏性涡粒子控制方程:
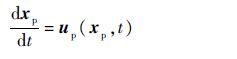 | (3a) |
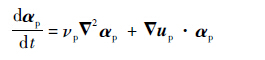 | (3b) |
式中:xp为涡粒子的位置矢量;αp为涡粒子的涡矢量;νp为流体运动黏性系数;up为涡粒子速度矢量。式(3a)体现涡量的输运效应;式(3b)体现涡量的耗散和拉伸效应,可采用粒子强度交换法计算旋翼尾迹涡量耗散效应νp▽2αp;通过采用直接求解法计算由速度梯度产生的旋翼尾迹涡量拉伸和旋转效应▽up·αp。
基于涡量等效原则,将桨叶和平尾尾随偶极子面元转为由等效面涡γ和线涡μl积分的涡粒子[21],并基于Neumann条件计算得到面元/黏性涡粒子法。基于此方法,通过非定常面元模拟旋翼和平尾气动载荷,黏性涡粒子法模拟旋翼和平尾的畸变尾迹特性,得到随前飞速度变化的平尾气动载荷[22]。
2) 平尾气动模型
前飞状态下,由于旋翼桨尖涡贴近并穿过平尾表面,因此对平尾气动载荷产生较显著的影响。在旋翼尾迹黏性涡粒子法的黏性效应求解中,对于无物面边界的旋翼涡量场,对称粒子强度交换法的涡量守恒,即∑dαp/dt=0,但低速飞行时,平尾将浸润在旋翼涡量场中,旋翼桨尖涡贴近平尾表面,受到平尾边界的剪截作用,从而导致部分旋翼涡量穿过平尾上下表面边界而丢失,由此改变旋翼尾迹干扰下的平尾非定常气动载荷。为此本文基于镜面映射方式确保旋翼尾迹涡量守恒(见图 1)。图 1中涡粒子i在平尾表面附近的部分涡量进入平尾内部。假设涡粒子i的涡强为均匀分布,则进入平尾内部的涡强可由涡粒子涡量与体积VACB之积求得。通过平尾表面涡量镜像映射方式,该涡强也等于镜像涡量与体积VADB之积,因此平尾镜面映射方式可确保旋翼涡量守恒,则镜面映射后的涡粒子涡量可表示为
 |
| 图 1 涡粒子涡量镜像映射 Fig. 1 Mirror-mapping of vortex particle vorticity |
| 图选项 |
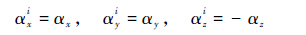 | (4) |
式中:αx和αy分别为涡粒子i的涡量在平尾表面x和y方向的分量;αz为涡粒子i的涡量在平尾表面的法线分量;αxi和αyi分别为镜面涡粒子i′的涡量在平尾表面x和y方向的分量;αzi为镜面涡粒子i′的涡量在平尾表面的法线分量。
由于旋翼尾迹在靠近平尾表面时存在速度变化,且受到旋翼尾迹几何的时变影响,平尾表面压力发生变化,由此产生时变非线性的平尾气动载荷。基于非定常伯努利方程,采用流场速度势和平尾表面速度计算平尾表面的压力分布。为更准确体现由旋翼尾迹速度和几何的时变特性对平尾表面非定常压力的影响,本文在计算平尾气动载荷过程中增加由旋翼和平尾尾迹产生的非定常压力项以及由旋翼桨叶时变气动载荷诱发的非定常压力项,由此平尾表面无量纲压力系数为
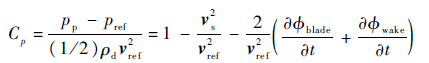 | (5) |
式中:vs、pp、pref、vref、ρd、φblade和φwake分别为平尾表面的空气速度、当地压力、参考压力、参考速度、空气密度、桨叶产生的速度势和尾迹产生的速度势。
旋翼桨叶的时变诱导影响可基于速度势的微分直接求解得到
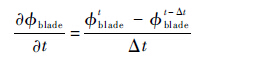 | (6) |
旋翼和平尾尾迹产生的非定常压力项可通过计算尾迹对平尾表面面元的诱导速度和尾迹自身速度之积得到,即
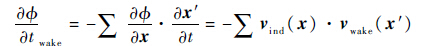 | (7) |
式中:vind为尾迹对平尾表面面元的诱导速度;vwake为尾迹自身速度。
基于此,旋翼尾迹干扰下的平尾非定常气动载荷可表示为
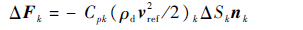 | (8) |
式中:ΔFk为表面面元气动力;ΔSk为面元面积;Cpk为面元压力系数;nk为面元外法线矢量。
1.2 直升机全机配平模型 直升机全机配平建模是直升机空气动力学、飞行力学及旋翼结构动力学的基础,在机体姿态响应计算和稳定性分析方面均发挥重要作用。直升机全机配平的基础是飞行动力学模型,目前国内外已对全机飞行动力学建模做了较深入的研究[7-13]。基于直升机旋翼、机身、平尾及尾桨等典型气动力部件的动力学方程和运动方程,建立直升机全机动力学方程[24]为
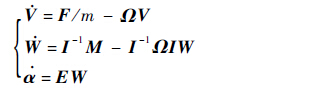 | (9) |
式中:m为全机质量;V=(u,v,w)T为线速度;W=(p,q,r)T为角速度;F为各部件合力;M为外力矩;I为全机惯性矩阵;Ω为叉乘向量算子;α=(φ,θ,ψ)T为欧拉角;E为角速度至欧拉角速度的转换矩阵。
全机配平点定义为状态量导数为常数或零,同时操作输入为固定值。对于直升机稳定飞行状态,、、和为零(a为一阶谐波形式的挥舞运动向量),及V、W、a均为定值,由此直升机全机飞行动力学方程可表示为状态方程,即
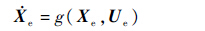 | (10) |
式中:e表示平衡状态;Xe=[Ve,We,αe,ae]T为配平状态量;Ue=(θ0,θ1c,θ1s,θT0)eT为配平操纵量。
基于状态方程式(10),直升机非线性方程组可表示为
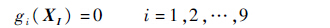 | (11) |
为此,构造目标函数:
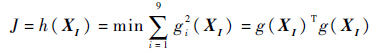 | (12) |
当J=0时,XI为式(11)的精确解,从而将直升机全机配平转变为优化问题,也即寻找XI使J最小。针对直升机稳定飞行状态,以UH-60A直升机为例,旋翼总距范围为[9.9°,25.9°],纵向周期变距范围为[-8.0°,8.0°],横向周期变距范围为[-12.5°,16.3°],尾桨总距范围为[4.5°,36.5°],旋翼挥舞角范围为[-6°,25°],俯仰角和滚转角范围为[-90°,90°],从而构建得到配平解空间的约束条件。根据笔者建立的基于GA/LM混合优化方法[24]实现全局直升机全机配平解搜索,采用遗传算法(Genetic Algorithm,GA)搜索全局较优配平解,而后将较优解定义为Levenberg-Marquardt(LM)优化方法的初值,利用此方法的快速收敛特性搜索物理最优配平真解,从而得到直升机全机配平操纵量。
1.3 耦合方法 常规直升机全机配平模型主要通过计算旋翼下洗流或尾迹诱导速度,而后基于二维翼型气动特性间接考虑旋翼对平尾气动干扰,但未充分体现旋翼尾迹对平尾非定常气动干扰产生的非线性气动载荷影响。为此,本文将第1.1节的非定常面元/黏性涡粒子法嵌入第1.2节的直升机飞行动力学模型中,根据式(8)计算旋翼尾迹干扰下的平尾非定常气动载荷,代入直升机动力学模型式(11),以体现直升机低速前飞状态下,旋翼/平尾气动干扰对直升机全机配平特性的影响。首先基于旋翼诱导入流和二维翼型气动特性的GA/LM混合优化全机配平方法计算直升机初始操纵量,而后采用非定常面元/黏性涡粒子法计算旋翼非定常气动载荷和平尾非定常气动载荷,随后将旋翼和平尾非定常气动载荷代入直升机飞行动力学方程,通过基于GA/LM混合优化的直升机全机配平方法重新计算直升机的操纵量和机体姿态,并根据解空间约束和优化条件得到最终操纵量和机体姿态。计算流程如图 2所示。
 |
| 图 2 直升机全机配平流程图 Fig. 2 Flowchart of whole helicopter trim |
| 图选项 |
1.4 方法验证 为验证本文方法的准确性,计算UH-60A各飞行速度操纵量,并与飞行测试数据[25]对比验证。计算得到UH-60A旋翼操纵量和机体姿态变化特性如图 3所示,其中旋翼总距θ0、纵向周期变距θ1c、横向周期变距θ1s以及尾桨总距θT0均为桨根值,θpitch为俯仰角,θroll为滚转角。从图 3中可以看出,本文计算得到的旋翼操纵量和机体俯仰角与UH-60A试飞测量值总体吻合较好,由此表明本文方法的可行性。各前飞状态,旋翼纵向操纵量与试飞测量值吻合较好,机体姿态与试飞测试略有误差,由于暂未直接计算旋翼与机身、旋翼与尾桨之间干扰产生的非定常气动载荷,因而机体俯仰角与试飞测量值略有误差。
 |
| 图 3 旋翼操纵量和机体姿态的变化 Fig. 3 Variation of rotor control and fuselage attitude |
| 图选项 |
2 旋翼/平尾气动干扰对全机配平特性的影响 为分析旋翼/平尾气动干扰对直升机全机配平特性的影响,采用本文耦合旋翼/平尾气动干扰(Rotor/Empennage aerodynamic Interaction,REI)模型的全机配平方法和通过诱导速度考虑旋翼/平尾气动干扰的常规全机配平方法[24]分别计算UH-60A固定低平尾下的旋翼操纵量和机体姿态(见图 4),并与OH-6A和EH-101试验结果对比。
 |
| 图 4 旋翼/平尾气动干扰下的旋翼操纵量和机体姿态 Fig. 4 Rotor control and fuselage attitude under rotor/empennage aerodynamic interaction |
| 图选项 |
由于难于获得OH-6A和EH-101试验的详细测试数据,因此本节将主要对比计算结果与试验结果的特性趋势。
在悬停到小速度前飞的过渡阶段,由于平尾气动效率较低,旋翼尾迹/平尾干扰较弱,即使直接考虑旋翼对平尾的非定常影响,平尾气动载荷也较小,因此本文方法计算的旋翼纵向操纵量和机体俯仰角与基于诱导速度的常规全机配平方法计算结果基本相同。低速阶段,由于旋翼尾迹/平尾气动干扰显著,旋翼尾迹贴近平尾表面移动,使得平尾气动载荷迅速增加,并随旋翼尾迹的远离又快速减小,因此采用本文方法计算得到的旋翼纵向操纵量和机体俯仰角显著增加,形成典型的“抬头”现象,并与UH-60A[2]、OH-6A试验[3]中所出现的纵向操纵量突增(见图 5(a))、EH-101飞行试验[4]中所出现的机体俯仰角快速增加相吻合(见图 5(b))。受旋翼/平尾非定常气动干扰的影响,旋翼纵向操纵量和机体俯仰角分别增加240%和295%,纵向操纵量大于中等速前飞(200km/h)的纵向操纵量,增量约为21.2%,且机体俯仰角高达10°。而基于诱导速度的常规全机配平方法计算的旋翼纵向操纵量和机体俯仰角未明显增加,并未出现UH-60A、OH-6A、EH-101飞行测试中出现的纵向操纵量和机体俯仰角突增现象[2-4],因此通过诱导速度间接考虑旋翼/平尾气动干扰的全机配平难于准确反映低速状态旋翼/平尾气动干扰对旋翼纵向操纵量和机体姿态特性的影响。中等速度和高速前飞状态下,旋翼尾迹离开平尾上表面,旋翼与平尾气动干扰强度较弱,平尾气动载荷变化较小,因此直接计算旋翼/平尾非定常气动干扰后得到的旋翼纵向操纵量和机体俯仰角与基于诱导速度的计算结果相似。因此,通过直接计算旋翼尾迹干扰下的平尾非定常气动载荷,本文方法更准确体现旋翼/平尾气动干扰对直升机全机配平特性影响,并更准确分析直升机低速纵向操纵量和机体俯仰突增特性。
 |
| 图 5 OH-6A旋翼纵向操纵量和EH-101机体俯仰角 Fig. 5 Rotor longitudinal control of OH-6A and fuselage pitch angle of EH-101 |
| 图选项 |
3 平尾构型对直升机全机配平特性的影响 直升机[26]平尾构型定义如图 6所示。
 |
| 图 6 直升机平尾位置 Fig. 6 Empennage’s position of helicopters |
| 图选项 |
3.1 平尾垂向位置 根据图 6的平尾构型定义,保持平尾的纵向位置不变,将平尾高度分别调整为-0.328R、-0.24R、0.05R,得到低、中、高平尾。采用本文方法计算得到低、中、高平尾的旋翼操纵量和机体姿态随前飞速度变化,如图 7所示。
 |
| 图 7 低、中、高平尾的旋翼操纵量和机体姿态 Fig. 7 Rotor control and fuselage attitude for low-, middle- and high-set empennage |
| 图选项 |
过渡阶段,由于旋翼尾迹与平尾干扰较弱,3种平尾向下载荷基本相同,因此旋翼纵向操纵量和机体俯仰角均相似。低速阶段,由于旋翼尾迹与低、中置平尾干扰显著,旋翼尾迹贴近低、中平尾表面,低、中置平尾向下气动载荷较大,因而旋翼纵向操纵量和机体俯仰角突增量较大。相比于低平尾,旋翼尾迹的干扰作用减弱,气动载荷减小,中平尾旋翼纵向操纵量和机体俯仰角明显减小,约为低平尾的58.6%和56.5%。由于旋翼尾迹远离高平尾下表面,旋翼尾迹/高平尾干扰较弱,因此高平尾旋翼纵向操纵量和机体俯仰角缓慢增加。中高速阶段,旋翼尾迹逐步远离低、中置平尾上表面,旋翼尾迹/平尾干扰较弱,气动载荷较小,因此中、低平尾旋翼纵向操纵量和机体俯仰角突增量较小,而旋翼尾迹逐步靠近高平尾,并贴近高平尾表面,旋翼尾迹/高平尾气动干扰仍然明显,气动载荷较大,因此高平尾旋翼纵向操纵量和机体俯仰角均出现一定突增,但幅度较弱。
3.2 平尾纵向位置 保持高度不变,将平尾纵向位置分别调整为0.9R、1.18R、1.3R,得到前、中、后置平尾,对应的旋翼操纵量和机体俯仰角变化如图 8所示。
 |
| 图 8 前、中、后置平尾的旋翼操纵量和机体姿态 Fig. 8 Rotor control and fuselage attitude for forward-, middle- and backward-set empennage |
| 图选项 |
前、中、后置平尾的旋翼操纵量和机体俯仰角随前飞速度的变化特性基本相似。过渡阶段到低速阶段,旋翼尾迹均靠近平尾表面,形成较明显的旋翼/平尾干扰,平尾气动载荷突增较大,因此3种平尾构型的旋翼纵向操纵量和机体俯仰角均出现突增。但旋翼/前置平尾干扰对应的前飞速度较小,气动载荷较小,在平尾非线性气动载荷和力臂均减小的双重作用下,前置平尾的旋翼纵向操纵量和机体俯仰角突增量较小,约为中置平尾的54.7%和60.0%,机体俯仰角得到抑制。相比中置平尾,后置平尾的旋翼纵向操纵量和机体俯仰角突增峰值对应的前进比后移,推迟机体抬头的出现,但突增减小量较小,机体俯仰角并未得到有效抑制。
3.3 左右单边平尾 将平尾展长减半,得到左、右单边平尾。右旋直升机采用左、右单边平尾的旋翼操纵量和机体姿态角随前飞速度变化如图 9所示。
 |
| 图 9 单边平尾的旋翼操纵量和机体姿态 Fig. 9 Rotor control and fuselage attitude of half-set empennage |
| 图选项 |
单边平尾的旋翼纵向操纵量和机体俯仰角随前飞速度的变化特性与对称平尾相似。过渡阶段,旋翼尾迹远离平尾下表面,旋翼/平尾干扰较弱,左、右单边平尾向下载荷基本相同,因此左、右单边平尾旋翼纵向操纵量和机体俯仰角基本相同。低速阶段,受到后行桨距角增加,尾迹涡量强度增加,旋翼尾迹/左平尾干扰较强,左平尾向下载荷大于右平尾,因此左平尾旋翼纵向操纵量和机体俯仰角大于右平尾。中高速阶段,为保证旋翼横向力矩平衡,后行边桨距增加,前行边桨距减小,后行边桨尖涡强度更大,旋翼尾迹/左平尾干扰较强,高置左单边平尾向下载荷大于右单边平尾,因此左单边平尾旋翼纵向操纵量和机体俯仰角大于右单边平尾,右平尾有利于抑制旋翼/平尾气动干扰产生的旋翼纵向操纵量和机体俯仰角突增。
4 结 论 1) 耦合旋翼/平尾气动干扰模型和GA/LM混合优化全机配平方法,建立旋翼/平尾气动干扰作用下的全机配平特性分析方法,相比于由诱导速度考虑旋翼/平尾干扰的常规全机配平方法,本文方法更准确体现旋翼/平尾气动干扰对直升机全机配平特性的影响,更准确分析直升机低速纵向操纵量和机体俯仰角突增特性。
2) 直升机低速阶段的纵向操纵量和机体俯仰角突增主要由旋翼/平尾气动干扰产生的平尾载荷变化所致,旋翼/平尾气动干扰对旋翼纵向操纵量和机体俯仰姿态特性影响显著。
3) 受旋翼尾迹较强的干扰,低平尾直升机低速阶段纵向操纵量和机体抬头显著,高平尾直升机则较弱,但对应速度转移至中等速度。
4) 相比于后置平尾,前置平尾直升机低速纵向操纵量和机体俯仰角显著减弱,但速度区间增加。
5) 受旋翼后行桨叶桨尖涡强度较大的影响,右旋直升机右单边平尾有利于减小纵向操纵量和机体俯仰角。
参考文献
| [1] | LEISHMAN J G. Principles of helicopter aerodynamics[M].2nd ed.New York: Cambridge University Press, 2006: 658-682. |
| [2] | LEONI R D. Black hawk:The story of a world class helicopter[M].Reston: AIAA, 2007: 88-102. |
| [3] | PROUTY R W,AMER K B.The YAH-64 empennage and tail rotor-a technical history[C]//38th American Helicopter Society Annual Forum.Fairfax,VA:AHS,1982:247-261. |
| [4] | MAIN B J,MUSSI F.EH101-development status report[C]//Proceedings of the 16th European Rotorcraft Forum.Glasgow:ERF,1990:Ⅲ.2.1.1-12. |
| [5] | EGLIN P.Aerodynamic design of the NH90 helicopter stabilizer[C]//Proceedings of the 23rd European Rotorcraft Forum.Glasgow:ERF,1997:68.1-68.10. |
| [6] | 朱宇, 张宏林, 刘莉. 直升机低速飞行特性试验分析[J].航空工程进展, 2012, 3(4): 433–437.ZHU Y, ZHANG H L, LIU L. Flight test research on helicopter low speed flight characteristics[J].Advances in Aeronautical Science and Engineering, 2012, 3(4): 433–437.(in Chinese) |
| [7] | TALBOT P D,TINLING B E,DECKER W A,et al.A mathematical model of a single main rotor helicopter for piloted simulation:NASA TM-84281[R].Moffett Field:NASA,1982. |
| [8] | HE C,LEWIS W D.A parametric study of real time mathematical modeling incorporating dynamic wake and elastic blades[C]//Proceedings of the 48th Annual Forum of the American Helicopter Society.Fairfax,VA:AHS,1992:1181-1196. |
| [9] | 陈仁良.直升机飞行动力学数学建模及机动性研究[D].南京:南京航空航天大学,1998:25-56.CHEN R L.Helicopter flight dynamics mathematical modeling and maneuvering research[D].Nanjing:Nanjing University of Aeronautics and Astronautics,1998:25-56(in Chinese). |
| [10] | 曹义华. 直升机机动飞行旋翼的气动力模拟[J].航空学报, 1999, 20(1): 39–42.CAO Y H. Modeling the aerodynamic force of a maneuvering helicopter rotor[J].Acta Aeronautica et Astronautica Sinica, 1999, 20(1): 39–42.(in Chinese) |
| [11] | THEODORE C R.Helicopter flight dynamics simulation with refined aerodynamic modeling[D].College Park,Maryland:University of Maryland,2000:35-105. |
| [12] | SPOLDI S,RUCKEL P.High fidelity helicopter simulation using free wake,lifting line tail,and blade element tail rotor models[C]//Proceedings of the 59th Annual Forum of the American Helicopter Society.Fairfax,VA:AHS,2003:92-99. |
| [13] | 李攀.旋翼非定常自由尾迹及高置信度直升机飞行力学建模研究[D].南京:南京航空航天大学,2010:14-58.LI P.Rotor unsteady free-vortex wake model and investigation on high-fidelity modeling of helicopter flight dynamics[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2010:14-58(in Chinese). |
| [14] | GANGWANI S T. Calculation of rotor wake induced empennage airloads[J].Journal of the American Helicopter Society, 1983, 28(2): 37–46.DOI:10.4050/JAHS.28.37 |
| [15] | CURTISS H C,QUACKENBUSH T R.The influence of the rotor wake on rotorcraft stability and control[C]//15th European Rotorcraft Forum.Glasgow:ERF,1989:70.1-70.24. |
| [16] | FLETCHER T M,BROWN R E.Main rotor-empennage interaction and its effects on helicopter flight dynamics[C]//Proceedings of the American Helicopter Society 63rd Annual Forum.Fairfax,VA:AHS,2007:1-11. |
| [17] | WANG B, ZHAO Q J, XU G H, et al. Numerical analysis on noise of rotor with unconventional blade tips based on CFD/Kirchhoff method[J].Chinese Journal of Aeronautics, 2013, 26(3): 572–582.DOI:10.1016/j.cja.2013.04.045 |
| [18] | KOMERATH N M, SMITH M J, TUNG C. A review of rotor wake physics and modeling[J].Journal of the American Helicopter Society, 2011, 56(2): 022006–1.DOI:10.4050/JAHS.56.022006 |
| [19] | HE C J, ZHAO J G. Modeling rotor wake dynamics with viscous vortex particle method[J].AIAA Journal, 2009, 47(4): 902–915.DOI:10.2514/1.36466 |
| [20] | 魏鹏, 史勇杰, 徐国华, 等. 基于粘性涡模型的旋翼流场数值方法研究[J].航空学报, 2011, 33(5): 771–780.WEI P, SHI Y J, XU G H, et al. Numerical method for simulating rotor flow field based upon viscous vortex model[J].Acta Aeronautica et Astronautica Sinica, 2011, 33(5): 771–780.(in Chinese) |
| [21] | TAN J F, WANG H W. Simulating unsteady aerodynamics of helicopter rotor with panel/viscous vortex particle method[J].Aerospace Science and Technology, 2013, 30(1): 255–268.DOI:10.1016/j.ast.2013.08.010 |
| [22] | 谭剑锋, 王浩文, 吴超, 等. 基于非定常面元/黏性涡粒子混合法的旋翼/平尾非定常气动干扰研究[J].航空学报, 2014, 35(3): 643–656.TAN J F, WANG H W, WU C, et al. Rotor/empennage unsteady aerodynamic interaction with unsteady panel/viscous vortex particle hybrid method[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(3): 643–656.(in Chinese) |
| [23] | 谭剑锋. 直升机旋翼对尾桨非定常气动载荷的影响[J].航空学报, 2015, 36(10): 3228–3240.TAN J F. Influence of helicopter rotor on tail rotor unsteady aerodynamic loads[J].Acta Aeronauica et Astronautica Sinica, 2015, 36(10): 3228–3240.(in Chinese) |
| [24] | 吴超, 谭剑锋, 王浩文, 等. 基于GA/LM混合优化的直升机全机配平算法[J].飞行力学, 2014, 32(1): 5–19.WU C, TAN J F, WANG H W, et al. Optimal trim for helicopter based on GA and LM hybrid algorithm[J].Flight Dynamics, 2014, 32(1): 5–19.(in Chinese) |
| [25] | CROSS J,BRILLA J,KUFELD R,et al.The modern rotor aerodynamic limits survey:A report and data survey:NASA TM-4446[R].Moffett Field:NASA,1993. |
| [26] | 倪先平. 直升机手册[M].北京: 航空工业出版社, 2003: 65-68.NI X P. Manual of helicopter[M].Beijing: Aviation Industry Press, 2003: 65-68.(in Chinese) |
