有效的热传感器位置分布方法可以在使用有限数量热传感器的情况下,估计芯片的所有热点温度。Long等[3]提出了一种基于网格的插值技术,用于确定最优的热传感器位置。Memik等[4]提出了一种优化的热传感器位置分布算法,可以在热点温度估计方面获得较高的精度。对于均匀间隔放置的热传感器,采用虚拟插值方法确定最优的传感器位置;对于非均匀间隔放置的热传感器,在二维k-均值聚类(k-means clustering)算法的基础上,加入热点的温度信息,构造出三维“距离”,并进一步引入感知因子,使得优化的传感器位置向温度较高的方向移动。文献[4]的目的是最大化热点温度估计精度,并不考虑全局监控问题,因而根据该方法获得热传感器的位置分布后,进行热分布重构得到的平均温度误差较大。Reda等[5]使用启发式迭代方法将热传感器数量分配问题近似为一个非确定性多项式困难问题(Non-deterministic Polynomial hard,NP-hard),并提出了一种新颖的软测量技术,该技术结合实际热传感器温度读数对没有放置传感器的位置温度进行估计,进一步提高了热点温度估计精度。Li等[6]针对热传感器位置分布优化问题,提出了3种简单、有效的热传感器位置分布策略;针对热传感器数量分配问题,提出了一种静态热传感器数量分配技术,能够使用相对较少数量的热传感器监控所有热点温度。
总体而言,目前已有的局部监控相关研究成果尚未有考虑热传感器噪声因素的影响,使其实用性受到了一定的限制。本文在考虑热传感器噪声因素影响下,提出了一种基于模拟退火算法(simulated annealing)的热传感器优化位置分布方法,能够在很大程度上减小噪声的影响,降低热点的误警率和提高热分布重构的性能,对动态热管理的温度监控具有很大的实用意义。
1 热图像降维 主成分分析(Principal Component Analysis,PCA)[7]是一种常用的数据分析方法,其通过线性变换将原始数据表示为一组各维度线性无关的组合,可用于提取数据的主要特征分量,已在信号处理、数据压缩、人脸识别等领域相对成熟。
由于在计算机处理过程中任何连续的变量必须离散化,因此,将整个芯片区域中连续的温度信号离散化为L×W的网格表述,L和W分别为离散热图像的长和宽。假设温度t[x,y]为定义在(x,y)坐标上的离散温度,0≤x≤L-1,0≤y≤W-1。通过提取热图像的列来获得向量化的热图像w[i],其中0≤i≤N-1,N=LW。提取公式为
 | (1) |
式中:$\left\lfloor {} \right\rfloor $表示取下整函数;mod为求余计算。
假定有M幅热图像,得到向量化热图像集合{wj}j=0M-1,第j幅热图像的均值为${\mu _j} = {1 \over N}\sum\limits_{i = 1}^N {{w_j}} $。因此,零均值向量集合为$\varphi $={wj-μj}j=0M-1,计算协方差矩阵C=E[$\varphi $ $\varphi $T],E为数学期望;$\varphi $T为$\varphi $的转置矩阵,利用公式CΦi=λiΦi,求矩阵C的特征值λi和对应的特征向量Φi。通过上述步骤后可得到PCA处理的结果Ω,其定义为
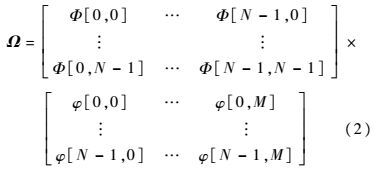 | (2) |
将协方差矩阵C的特征值从小到大排列:λ0≥λ1≥…≥λN-1≥0,按照特征值所占的能量比例来选取前面K(K<N)个特征向量:
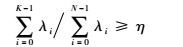 | (3) |
通常取η=90%~99%。在满足均方差最小的条件下,选取所占能量比最大的K个特征值所对应的{Φi}i=0K-1为最佳近似正交向量子空间。降维后近似的热图像集合{$\hat w$j}j=0M-1可表示为
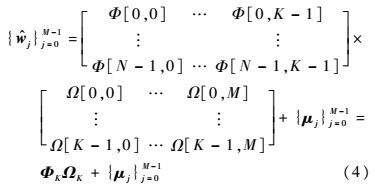 | (4) |
这样,每幅热图像都可以投影到ΦK的子空间中,用来表示热图像的主要特征信息。
2 优化热传感器放置技术 2.1 传感器位置分布理论 假定在坐标{(xn,yn)}n=1P上放P个传感器,根据式(1)可得向量化的传感器位置{di}i=1P,由式(4)得传感器测量矩阵{wjS} j = 0M-1为
 | (5) |
从ΦK中取出对应的P行得到P×K维传感矩阵$\tilde \Phi $K,由于{μj}j=0M-1每行具有相同值,则可以取{μj}j=0M-1中任意P行组成P×M维均值矩阵{μSj}j=0M-1。
通常传感器的读数易于受到多种噪声的影响,因此,加入噪声因素,式(5)可以修正为
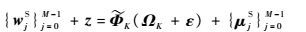 | (6) |
式中:z为噪声项;ε为在降维过程中产生近似误差项ε={$\hat w$j}j=0M-1-{wj}j=0M-1。
令λS={wjS}j=0M-1-{μSj}j=0M-1,可以将式(6)变为
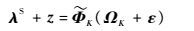 | (7) |
分析式(6),可以推出:
 | (8) |
式中:||2||为二范数;Cond2( )为矩阵二范数条件数。
根据式(8)可知,条件数表示矩阵计算对于误差的敏感性。因此,在给定噪声的基础上,提高热重构的稳定性和精度必须使$\tilde \Phi $K的条件数最小。这个结论可以用来确定传感器的最优位置:在矩阵ΦK中挑选P行得到具有最小条件数的传感矩阵$\tilde \Phi $K,其相应的行所在位置即为传感器的最优位置,这是一个NP-hard问题。
2.2 模拟退火算法放置传感器方法 现代进化算法主要包括模拟退火算法、遗传算法和蚁群算法等,它们有一个共同的目标——求解NP-hard组合优化问题的全局最优解。为此,本文采用基于模拟退火算法进行启发式搜索获得最小条件数的传感矩阵$\tilde \Phi $K。
模拟退火算法[8]是一种通用概率算法,相对于其他最优化算法,大量实践表明模拟退火算法非常适合求解组合优化问题,在参数合适的情况下基本上可以100%得到全局最优解,在一定程度上可以解决NP-hard问题。在本节中,提出一种基于模拟退火算法的热传感器优化位置分布方法。在ΦK中选择P行得到有最小的条件数的满秩矩阵$\tilde \Phi $K。算法可以描述为:
1) 设置退火时间表,包括初始温度T、终止温度Tstop、衰减参数α和马尔科夫链长度LM。
2) 从ΦK矩阵N行中随机挑选2组P(P≥K)行得到传感器位置向量{di}i=1P和{dic}i=1P,形成传感矩阵$\tilde \Phi $K和$\tilde \Phi $Kc。如果rank($\tilde \Phi $K)=K和rank($\tilde \Phi $cK)=K,分别计算$\tilde \Phi $K和$\tilde \Phi $Kc的条件数,条件数小的为最佳解X而另一个为当前解Xc。
3) 初步搜索步骤如下:
① 生成一个随机整数补偿量{mi}i=1P,并且令
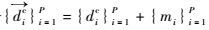
② 计算$\overrightarrow{\tilde{\Phi }_{K}^{c}}$的条件数作为新解$\overrightarrow {{X^c}} $。
③ 如果$\overrightarrow {{X^c}} $<X,令X=$\overrightarrow {{X^c}} $,$\tilde \Phi $K=$\overrightarrow{\tilde{\Phi }_{K}^{c}}$并且{$\overrightarrow{d_{i}^{c}}$}i=1iP={dc}i=1P。
④ 在[0,1]内产生一个均匀分布的随机数θ,并根据Metropolis准则,计算可接受概率为
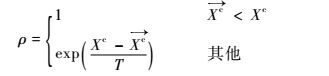 | (9) |
如果θ<ρ,接受一个新解。设定Xc=$\overrightarrow {{X^c}} $,令{dic}i=1P={$\overrightarrow{d_{i}^{c}}$}i=1P。
⑤ 重复执行步骤①~④,直到搜索步骤的数目等于LM。
4) 如果T>Tstop,设定T=αT并跳至步骤3)。
5) 如果rank($\tilde \Phi $K)=K,储存$\tilde \Phi $K作为最佳传感矩阵,并将{di}i=1P作为最优传感器位置向量,否则跳转至步骤2)。
值得注意的是,在确定传感器最优位置分布时,需要计算ΦK中所有P个可能子矩阵的条件数,计算量大概是N!。模拟退火算法在搜索过程中需要精确调整接受退化结果的条件才可能取得较优解,在无法得到实际问题精确最优解的情况下,无论从存储空间还是计算效率考虑,其都不失为一种优越的近似方法,特别是对解大规模NP-hard问题更是如此。遗传算法的主要缺点在于,一方面其局部搜索能力相对较差,尤其是在优化后期搜索效率较低,增加了优化时间消耗;另一方面,该算法需要对问题进行编码,在求解结束时还需要对问题解码,同时交叉率与变异率以及全体规模等参数的选择对算法性能影响很大,而合适值的选择通常对经验要求较高。对于结构复杂的组合优化问题,搜索空间大,不合适参数的选择会让优化陷入“早熟”。而蚁群算法是一个建模方案复杂的算法,具有非常高的时间复杂度。因此,本文选择模拟退火算法用于求解传感器的最优位置问题。
3 算法性能验证 3.1 含噪热图像重构技术 给定的M幅热图像的向量化集合{wj}j=0M-1,根据式(5)可以得到的传感矩阵$\tilde \Phi $K,在此基础上,采用模拟退火算法计算出P个含噪传感器的优化位置分布{di}i=1P。如果P≥K并且rank($\tilde \Phi $K)=K,重构图像向量集合{wj}j=0M-1可以表示为[9]
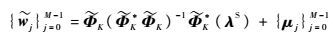 | (10) |
3.2 仿真平台的搭建 为了验证上述算法的有效性,本文采用仿真工具链[10]来模拟一个基于Alpha 21264架构的16核处理器[11]的热特性分布。通过微处理器性能仿真软件SimpleScalar[12]在该芯片架构上仿真SPEC2006[13]标准测试程序,并通过Wattch infrastructure[14]来计算模块的功耗,最后由热特性仿真软件Hotspot[15]计算出处理器的温度分布。
3.3 实验结果 实验中所有程序均在物理内存为8 GB、主频为4 GHz的Intel Skylake四核处理器上由MATLAB编写完成。这里给出以下性能指标:
1) 平均重构误差。考虑设定M幅原始温度图像T={Tj}j=0M-1,平均重构误差定义为
 | (11) |
2) 最大重构误差。其定义为
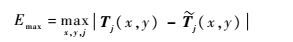 | (12) |
3) 均方误差。其表达式为
 | (13) |
4) 误警率。误警热点的定义包含2种情况:①热点的实际温度达到或超过门限温度,而传感器对相应热点的温度估计值低于门限温度;②热点的实际温度没有达到门限温度,而传感器对相应热点的温度估计值达到或超过门限温度。其公式为
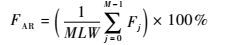 | (14) |
式中:Fj为Tj的误警热点数量。
3.4 传感器分布性能比较 为了验证本文方法的有效性,分别作了3组实验进行比较。随机从SPEC2006所有29个应用程序产生的热图像中选择M=22个样本图像,每幅热图像N=1 024,离散为L=W=32。第1组实验中,在放置不同数量传感器的条件下,分别对4种传感器放置的方法(本文算法、贪婪算法[9]、随机放置方法和均匀放置方法)所得到传感矩阵$\tilde \Phi $K的条件数进行比较。其结果如图 1所示,可以观察到,相对于其他方法,本文算法能够获得传感矩阵的最小条件数。
 |
| 图 1 传感矩阵条件数对比 Fig. 1 Comparison of sensing matrix condition number |
| 图选项 |
热重构技术可以近似复原整个芯片温度,主要应用于动态热管理中实现全局监控。为了验证本文算法的热重构性能,第2组实验中在噪声标准差为5%的情况下,采用EigenMaps[9]热重构方法进行重构实验。根据式(10)执行10 000次模拟获得性能指标数据,如表 1所示。对于上述4种不同传感器分布方法的热重构性能,分别从平均重构误差、最大重构误差、均方误差和信噪比等方面进行比较。图 2~图 5的实验结果证明了本文算法在热重构方面的优越性能。
表 1 噪声标准差为5%时,热重构性能比较 Table 1 Comparison of thermal reconstruction performance with noise standard deviation of 5%
| 方法 | 传感器数量 | 平均重构误差/℃ | 最大重构误差/℃ | 均方误差/℃ | 信噪比/dB | 误警率/% |
| EigenMaps+本文算法 | 4 | 2.39 | 12.74 | 9.73 | 0.65 | 18.85 |
| 9 | 1.21 | 6.29 | 2.48 | 6.58 | 9.79 | |
| 16 | 1.13 | 5.96 | 2.15 | 7.18 | 9.06 | |
| 25 | 0.84 | 4.50 | 1.19 | 9.76 | 6.52 | |
| EigenMaps+贪婪算法 | 4 | 2.77 | 17.27 | 14.31 | -0.94 | 20.55 |
| 9 | 1.81 | 11.36 | 5.97 | 2.83 | 14.19 | |
| 16 | 1.40 | 7.96 | 3.39 | 5.24 | 11.46 | |
| 25 | 1.07 | 6.11 | 1.99 | 7.53 | 8.77 | |
| EigenMaps+随机放置方法 | 4 | 3.76 | 26.31 | 29.07 | -3.95 | 24.29 |
| 9 | 2.54 | 13.28 | 11.70 | -0.05 | 19.66 | |
| 16 | 1.43 | 8.46 | 3.72 | 4.83 | 11.47 | |
| 25 | 0.95 | 5.76 | 1.59 | 8.52 | 7.32 | |
| EigenMaps+均匀放置方法 | 4 | 3.74 | 23.33 | 26.19 | -3.57 | 24.93 |
| 9 | 2.06 | 11.79 | 7.47 | 1.83 | 16.38 | |
| 16 | 1.22 | 7.62 | 2.63 | 6.36 | 9.94 | |
| 25 | 1.15 | 6.67 | 2.31 | 6.90 | 9.05 |
表选项
 |
| 图 2 最大重构误差对比 Fig. 2 Comparison of maximum reconstruction error |
| 图选项 |
 |
| 图 3 平均重构误差对比 Fig. 3 Comparison of average reconstruction error |
| 图选项 |
 |
| 图 4 均方误差对比 Fig. 4 Comparison of mean square error |
| 图选项 |
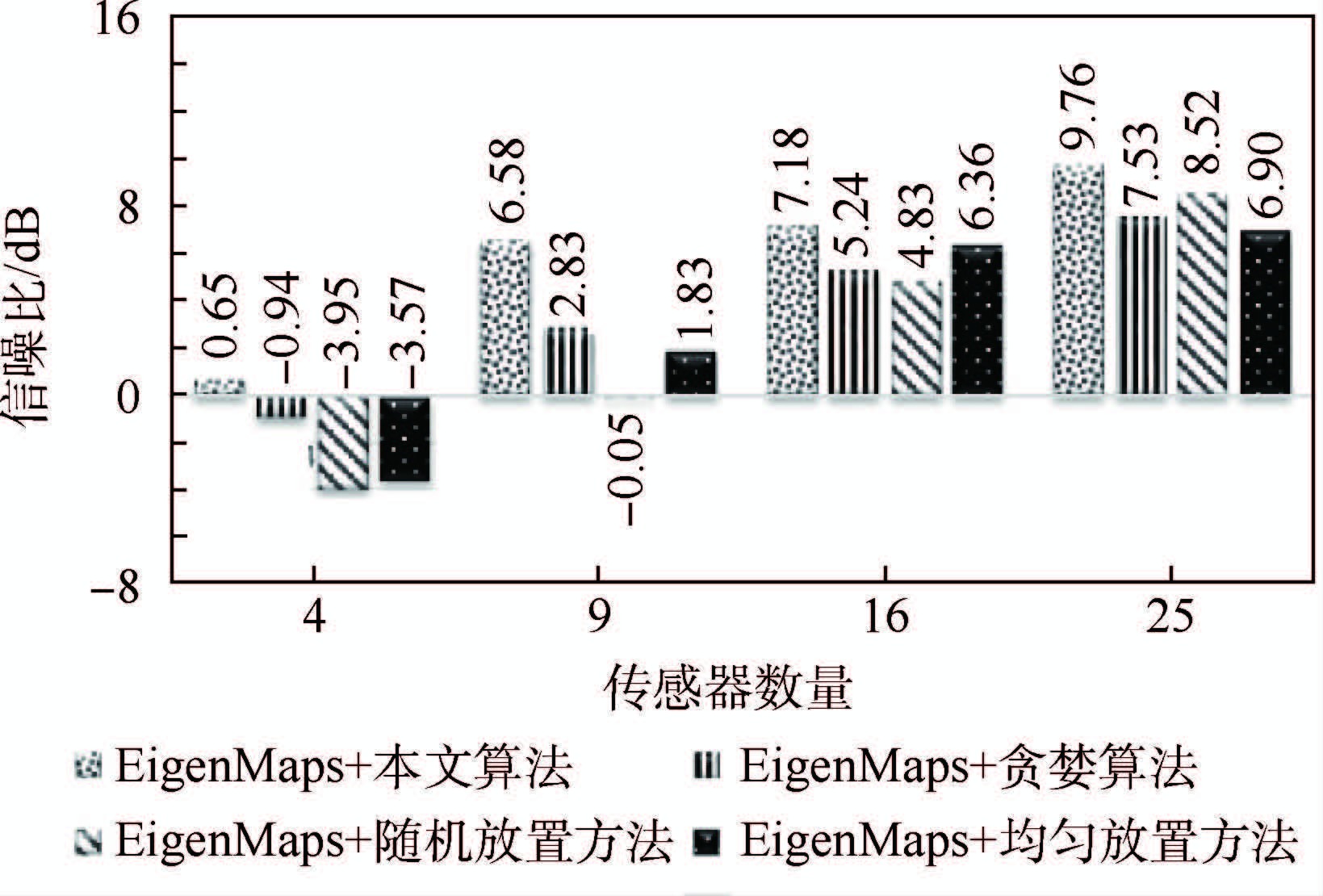 |
| 图 5 信噪比对比 Fig. 5 Comparison of SNR |
| 图选项 |
由于实际芯片中传感器不可避免地伴随有多种噪声,这无论给局部监控还是全局监控都带来了热点误警率的增加,在一定程度上会加剧错误的预警和不必要的响应,使动态热管理的可靠性受到影响。第3组实验中,在噪声标准差为5%的情况下,比较4种传感器分布方法在误警率方面的性能,如图 6所示。实验结果证实,当传感器读数受到噪声影响时,本文算法可以显著减少误警率,能够有效运用在动态热管理中实现精确的热监控。
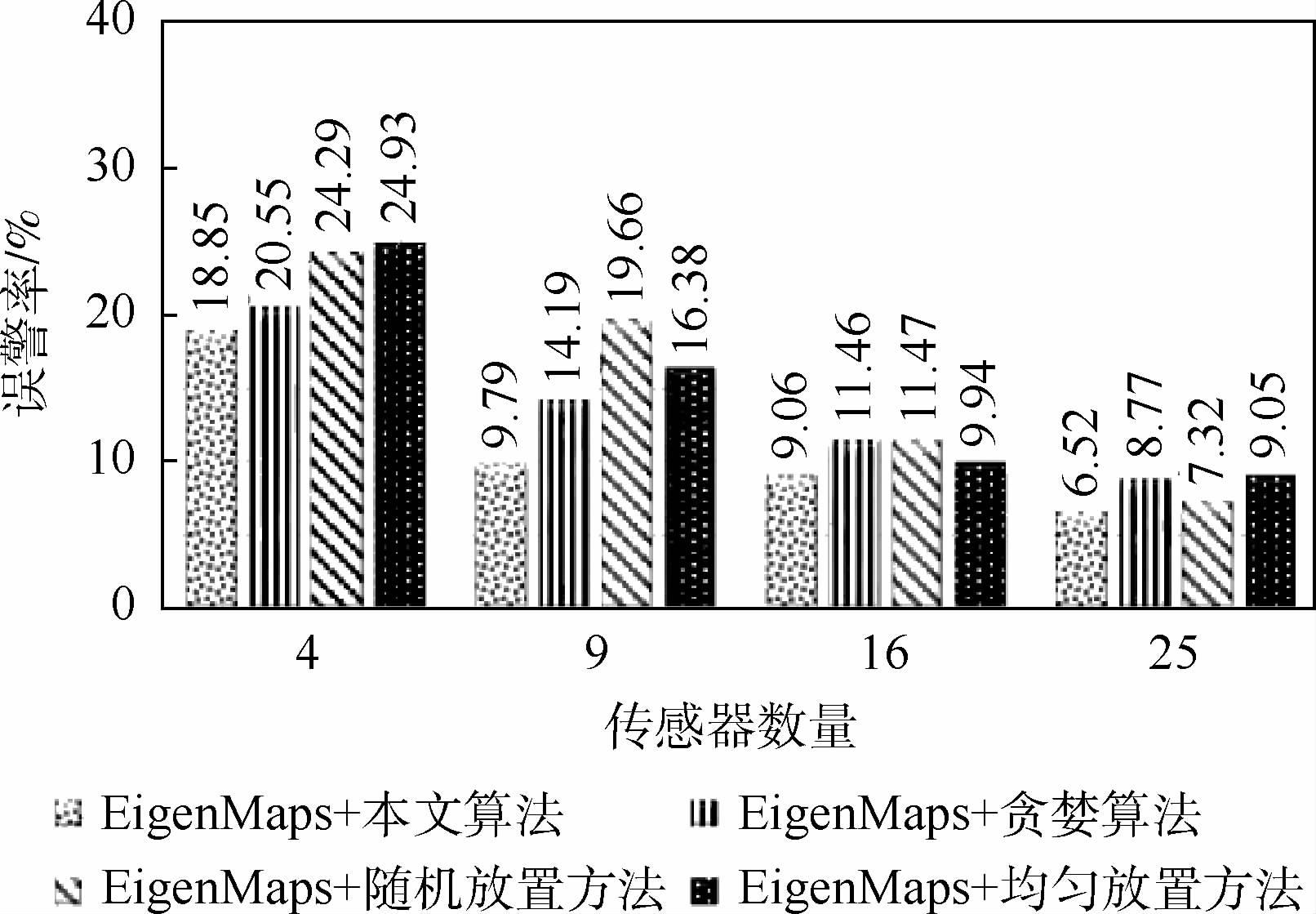 |
| 图 6 误警率对比 Fig. 6 Comparison of false alarm rate |
| 图选项 |
4 结 论 本文提出微处理器中考虑噪声因素的热传感器位置分布优化方法。
1) 在均方误差最小的原则下,对原始热图像样本矩阵进行降维近似处理,并结合矩阵扰动分析建立了含噪热传感器位置分布理论。
2) 使用基于模拟退火算法寻找最优传感器位置。
3) 实验结果证明,本文算法比现有的贪婪算法在热重构误差、信噪比和误警率等性能方面有了一定提高,能够有效运用在动态热管理中实现精确的热监控。
在今后的工作中,会对遗传算法和蚁群算法的性能进行详细比较,并结合其他现代优化算法做进一步的优化和完善。
参考文献
| [1] | SHI B, ZHANG Y, SRIVA A, et al. Dynamic thermal management under soft thermal constraints[J].IEEE Transactions on VLSI Systems, 2013, 21(11): 2045–2054.DOI:10.1109/TVLSI.2012.2227854 |
| [2] | ZHANG Y, SRIVA A. Accurate temperature estimation using noisy thermal sensors for Gaussian and non-Gaussian cases[J].IEEE Transactions on Very Large Scale Integration Systems, 2011, 19(9): 1617–1626.DOI:10.1109/TVLSI.2010.2051567 |
| [3] | LONG J, MEMIK S O, MEMIK G, et al. Thermal monitoring mechanisms for chip multiprocessors[J].ACM Transactions on Architecture and Code Optimization, 2008, 5(2): 9. |
| [4] | MEMIK S O, MUKHERJ R, LONG J, et al. Optimizing thermal sensor allocation for microprocessors[J].IEEE Transactions on Computer-Aided Design of Integrated Circuits, 2008, 27(3): 516–527.DOI:10.1109/TCAD.2008.915538 |
| [5] | REDA S, COCHRAN R, NOWROZ A N. Improved thermal tracking for processors using hard and soft sensor allocation techniques[J].IEEE Transactions on Computers, 2011, 60(6): 841–851.DOI:10.1109/TC.2011.45 |
| [6] | LI X, RONG M, LIU T, et al. Inverse distance weighting method based on a dynamic voronoi diagram for thermal reconstruction with limited sensor data on multiprocessors[J].IEICE Transactions on Electronics, 2011, 94(8): 1295–1301. |
| [7] | KOTTAIMALAI R,RAJASEKARAN M P,SEVAM V,et al.EEG signal classification using principal component analysis with neural network in brain computer interface applications[C]//2013 IEEE International Conference on Emerging Trends in Computing,Communication and Nanotechnology (ICECCN).Piscataway,NJ:IEEE Press,2013:227-231. |
| [8] | KEIKHA M M.Improved simulated annealing using momentum terms[C]//2011 Second International Conference on Intelligent Systems,Modelling and Simulation (ISMS).Piscataway,NJ:IEEE Press,2011:44-48. |
| [9] | RANIERI J,VINCENZI A,CHEBIRA A,et al.‘EigenMaps':Algorithms for optimal thermal maps extraction and sensor placement on multicore processors[C]//Proceedings of the 49th Annual Design Automation Conference.Piscataway,NJ:IEEE Press,2012:636-641. |
| [10] | LI X, RONG M, WANG R, et al. Reducing the number of sensors under hotspot temperature error bound for microprocessors based on dual clustering[J].IET Circuits,Devices & Systems, 2013, 7(4): 211–220. |
| [11] | MANIATAKOS M, MICHAEL M K, MAKRIS Y, et al. Multiple-bit upset protection in microprocessor memory arrays using vulnerability-based parity optimization and interleaving[J].IEEE Transactions on VLSI Systems, 2015, 23(11): 2447–2460.DOI:10.1109/TVLSI.2014.2365032 |
| [12] | BAZZAZ M, SALEHI M, EJLAI A, et al. An accurate instruction-level energy estimation model and tool for embedded systems[J].IEEE Transactions on Instrumentation and Measurement, 2013, 62(7): 1927–1934.DOI:10.1109/TIM.2013.2248288 |
| [13] | ZOU Q,YUE J,SEGEE B,et al.Temporal characterization of SPEC CPU2006 workloads analysis and synthesis[C]//2012 IEEE 31st International Performance Computing and Communications Conference(IPCCC).Piscataway,NJ:IEEE Press,2012:11-20. |
| [14] | BROOKS D,TIWARI V,MARTONOSI M.Wattch:A framework for architectural-level power analysis and optimizations[C]//Proceedings of the 27th International Symposium on Computer Architecture.Piscataway,NJ:IEEE Press,2000:83-94. |
| [15] | HUANG W, GHOSH S, VEKYSAMY S, et al. HotSpot:A compact thermal modeling methodology for early-stage VLSI design[J].IEEE Transactions on VLSI Systems, 2006, 14(5): 501–513.DOI:10.1109/TVLSI.2006.876103 |
