近年来随着低温物理学科的发展,超流体陀螺开始进入人们的视线[3-4],由美国加州大学Packard提出的基于交流约瑟夫森效应的双弱连接超流体陀螺[5],在精度、体积、温度要求和受噪声影响等方面具有巨大的优势。理论上基于物质波干涉的超流体干涉仪的角速度检测灵敏度比基于光子干涉的光纤陀螺灵敏度高将近10个数量级[6]。
目前超流体陀螺的研究尚停留在机理推导和初步实验阶段[7],特别是在超流体陀螺高精度大量程设计和控制系统设计方面,还存在很多问题需要深入研究。
文献[8]对双弱连接超流体陀螺干涉仪进行了原理推导和相关实验,从薄膜幅值中提取出地球自转角速度分量,从而提出将其发展为新型陀螺的构想;文献[9-10]的研究表明,超流体陀螺可高灵敏、高精度感知角速度,其可检测角速度范围有限,但未提出可行的量程扩展方案;文献[11-12]提出热像移辅助方法来扩大超流体陀螺的量程,但未考虑系统惯性延迟的问题,从而不可避免地制约超流体陀螺的敏感精度和动态特性。文献[13]虽然考虑了一阶惯性滞后,为热像移辅助回路设计了简单可行的比例(P)控制器,但系统的动态性能和控制精度有待进一步提高。此外,关于模糊控制系统优化设计方面,文献[14]提出采用粒子群算法来优化模糊控制规则,算法简单且计算方便,但容易陷入局部最优,导致结果不理想。文献[15]提出使用BP神经网络优化模糊隶属函数,该优化算法具有自适应自学习的能力,但其优化结果对训练样本依赖大且学习过程较复杂,工程应用较难实现。
为了克服以上问题,本文在分析超流体陀螺幅值-角速度工作曲线特点的基础上,从工程应用角度出发,旨在实现陀螺量程范围的扩展。考虑了热相位与温升延时关系的基础上,设计并优化了基于热相位补偿实现陀螺量程范围的扩展方案。在幅值锁定模糊控制系统中,引入重叠因子的概念,实现隶属函数左半宽度的间接编码,在提高遗传优化效率的同时确保了相邻隶属不会没有重叠或者重叠部分太多的情况,实现了超流体陀螺薄膜幅值快速且稳定地锁定在期望值,在保证测量精度的同时提高了陀螺系统的量程范围。
1 超流体陀螺的敏感原理 超流体陀螺如图 1所示,由加热电阻、干涉腔、弱连接和薄膜振动幅值输出模块组成。超流体陀螺工作时,通过加热铜镍合金电阻丝使弱连接两侧形成一定的化学势差,干涉腔内的液氦Ⅱ在该化学势差的作用下,在布满由孔径70 nm,间隔3 μm的若干微孔组成的弱连接处发生约瑟夫森效应,形成超流体物质波。当外界有微小角速度输入时,超流体陀螺能以极高的灵敏度敏感并通过物质波干涉效应引起超流体陀螺的薄膜产生振动位移,使得薄膜的幅值被输入角速度调制。通过高精度的超导量子干涉仪对薄膜振动检测并记录下来,结合幅值-角速度解算关系便可求解出相应的角速度,实现角速度的敏感。
 |
| 图 1 超流体陀螺示意图 Fig. 1 Schematic diagram of superfluid gyroscope |
| 图选项 |
热驱动装置通过加热铜镍合金的电阻丝来改变干涉腔内的温度和压力,使弱连接两端形成一定的驱动势能[7]:
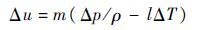 | (1) |
式中:Δu为化学势差; m和ρ分别为超流体液氦Ⅱ的原子质量和密度;l为液氦Ⅱ超流体熵密度;ΔT和Δp分别为热驱动装置控制弱连接两端温差和压差。
在驱动势能的作用下,超流体流经2个弱连接,并在双弱连接的微孔处分别形成临界流量幅值为Ic、相位为ΔΦ0和ΔΦ1的物质波。考虑双弱连接的结构完全对称相同,则流经2个弱连接的对称微孔的流量也相同,管道内的总流量为[7]
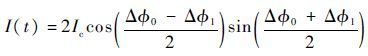 | (2) |
由于超流体物质波的Sagnac效应,当外部以角速度ω旋转时,在超流体陀螺干涉回路中会形成与角速度量相对应的Sagnac相位差:
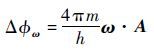 | (3) |
式中:h为普朗克常数;A为感应面积的矢量。在超流体陀螺工作回路中,两弱连接的相位差和外部转动引起的相位差满足
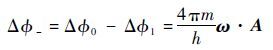 | (4) |
在热驱动势能作用下超流体陀螺开始工作,超流体陀螺环路中相位变化和驱动势差的关系满足约瑟夫森效应原理[7]
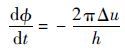 | (5) |
进一步对式(5)沿着双弱连接干涉腔积分得到环路内总的超流体相位为
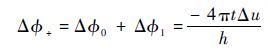 | (6) |
考虑弱连接所含孔数为N,将式(4)、式(6)代入式(2),可得干涉腔内总的超流体流量为[13]
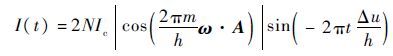 | (7) |
在超流体流量作用下,薄膜内腔的体积发生变化,驱动薄膜发生位移变化,弹性薄膜的位移和超流体流量的关系为
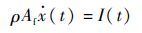 | (8) |
式中:Af为弹性薄膜的面积。对超流体陀螺质量流量进行积分得到薄膜的位移:
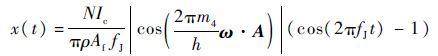 | (9) |
式中:fJ为约瑟夫森振荡频率;m4为氦4原子质量。
通过位移传感器实时检测薄膜的位移,结合式(3)、式(7)~式(9)便可解算出外部转动的角速度。
2 幅值锁定量程扩展方案 外部转动引起的相位,对弱连接处产生的超流体流量振动信号的振幅进行了调制。由式(9)得到薄膜振动幅值为
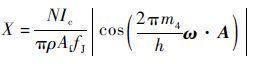 | (10) |
定义F=2m4ω·A/h为角速度引起的旋转通量,得到角速度引起的相位变化量πF和薄膜振动幅值的超流体陀螺工作曲线如图 2所示。
 |
| 图 2 超流体陀螺工作曲线 Fig. 2 Superfluid gyroscope working curve |
| 图选项 |
从图 2可以看出角速度引起的相位变化和薄膜振动幅值之间呈周期变化关系。通过幅值检测得到薄膜的振动幅值,当角速度输入引起的相位变化超过区间(0,π/2)时,由幅值解算得到相位变化量只是πF的余量πF-nπ/2,并非真实的相位变化量πF。只有当πF在(0,π/2)的区间内,幅值和角速度才是单值对应关系,可直接解算角速度ω=F·h/2m4A。综上分析,基于双弱连接的超流体陀螺实现角速度检测的工作区间仅为(0,π/2),直接限制了陀螺的量程范围。
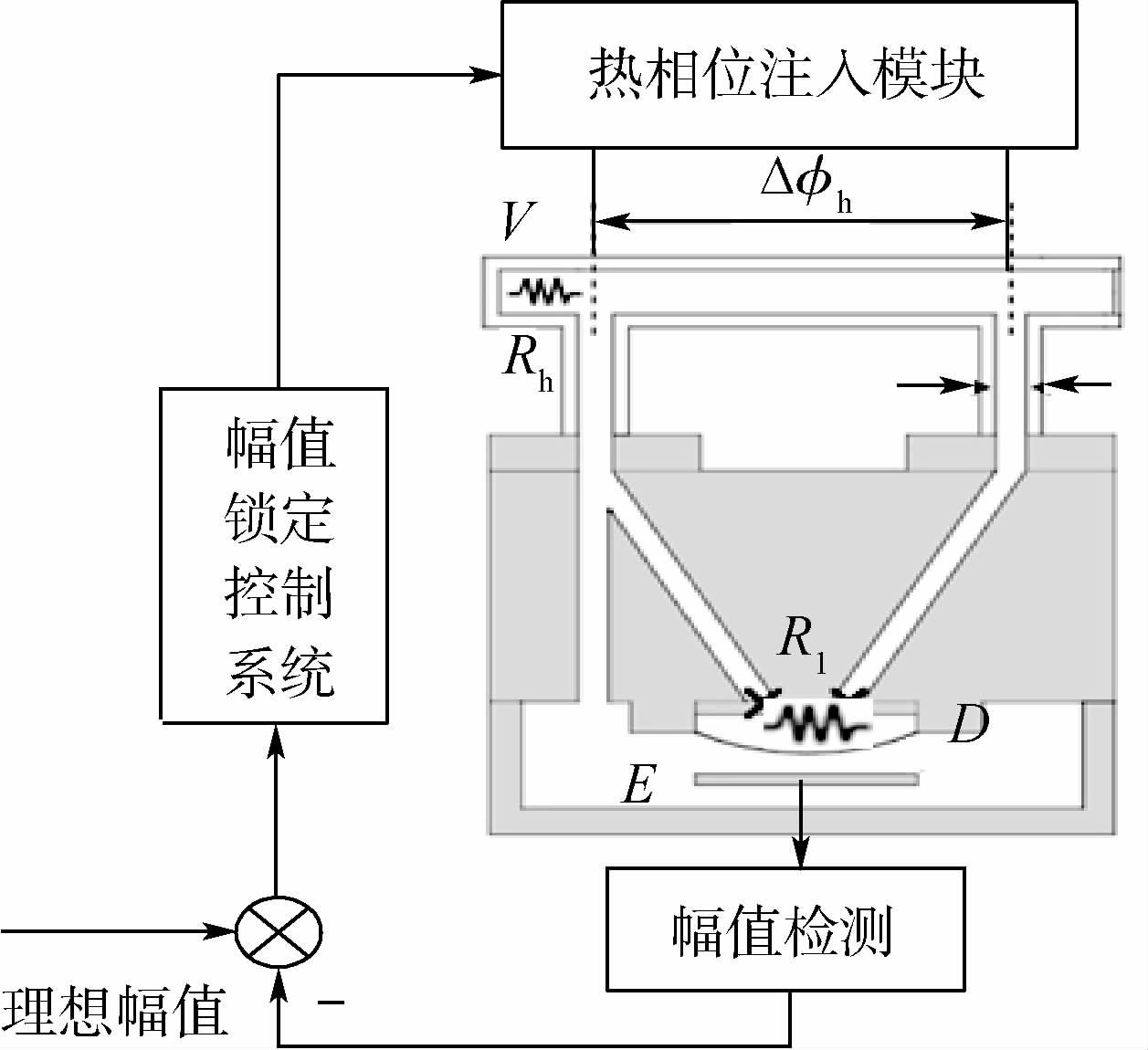
为此,设计如图 3所示的幅值锁定量程扩展方案,通过加热电阻,使得热相位注入模块开始启动。当外界角速度引起相位变化πF时,通过热相位注入ΔΦh来抵消这种相位变化,将陀螺继续维持在某一固定相位处,则对应的薄膜振动幅值也将维持在恒定位置。
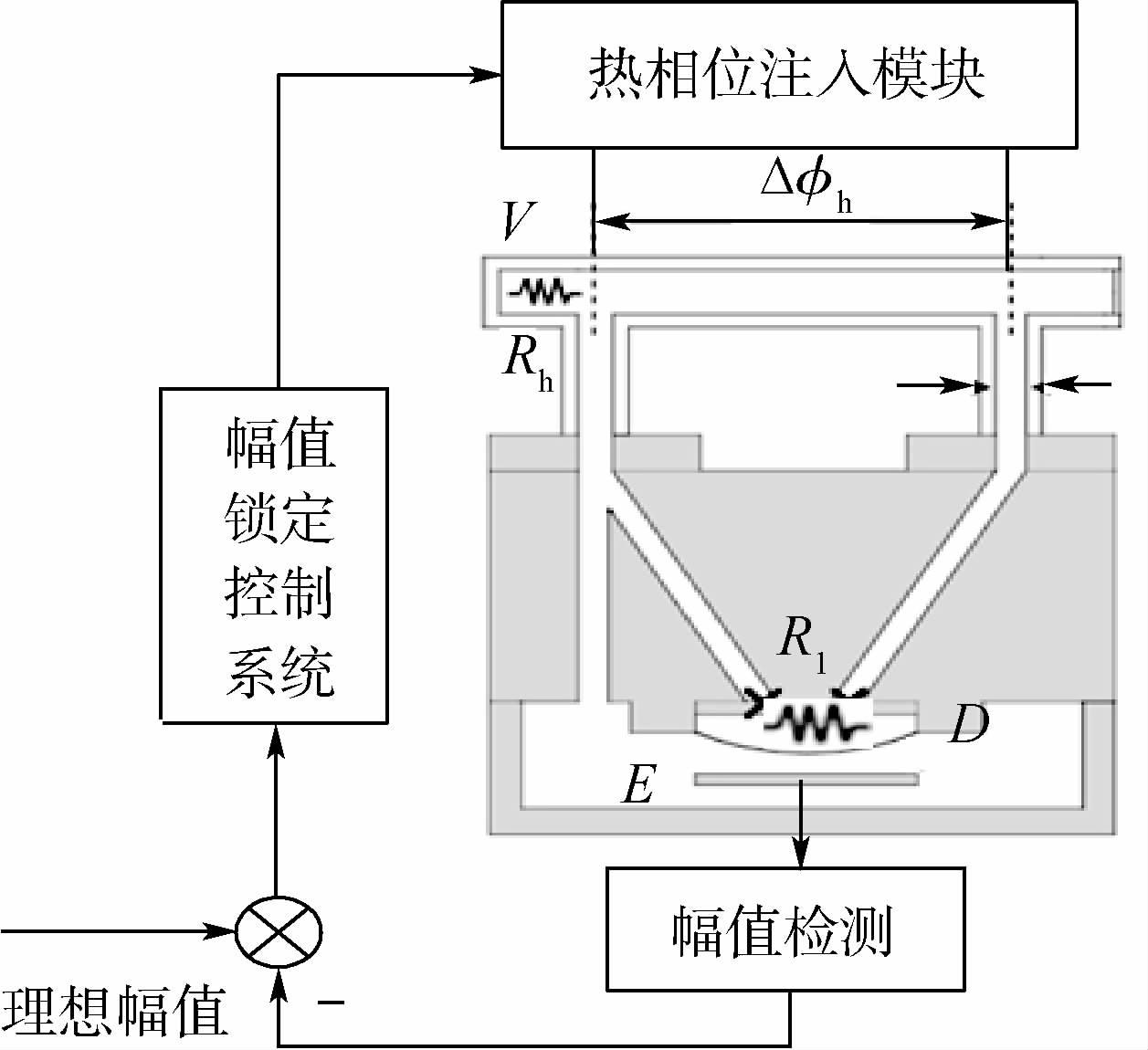 |
| 图 3 幅值锁定量程扩展方案图 Fig. 3 Amplitude-locking range extension scheme |
| 图选项 |
理论上陀螺的量程可以通过注入补偿实现无限的扩展。工作点相位可在区间(0,π/2)内取值,此处选取π/4作为系统的工作锁定相位。热相位补偿量为ΔΦh,则工作中满足
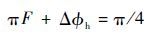 | (11) |
此时可直接反解得到外部转动角速度为
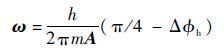 | (12) |
考虑在长度为L、半径为R的管道内,流体的流速υ与管路压力的变化Δp的关系[7]
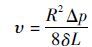 | (13) |
式中: δ为普通流体的黏度。
又Δp与管内温度的变化ΔT的关系为
 | (14) |
式中: k为温度差与压力差的相关系数。
由质量守恒定律对环内的流体有
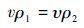 | (15) |
式中:v为超流体的流速;ρ1为超流部分的密度;ρ2为常流部分的密度。
将式(13)和式(14)代入式(15)得超流体流速:
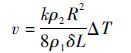 | (16) |
超流体的相位差ΔΦ与超流体的流速v满足
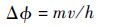 | (17) |
将式(16) 代入式(17),最终得到注入的热相位与环内的温度关系为
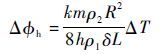 | (18) |
3 超流体陀螺幅值锁定优化设计 3.1 幅值锁定系统设计 由式(18)可知,注入的热相位与腔内的温度变化成正比例关系,而腔内温度变化主要是通过加热电阻实现,由于加热电阻的温升过程一般近似为一阶惯性环节1/(1+Ts),其中T为与结构相关的时间常数,s为复变量,所以热相位注入必然存在延迟影响。又由式(12)可知,角速度解算依赖于注入的热相位,热相位注入不及时将导致超流体的幅值不能精准地锁定在目标位置,直接影响超流体陀螺的角速度解算精度。
考虑陀螺包含位移检测的积分环节,整体陀螺系统是一个非线性时变系统,为此设计具有高动态的实时补偿的幅值锁定控制系统,使得热相位能实时补偿角速度输入引起的相位变化,从而维持薄膜的幅值始终锁定在固定值处。设计如图 4所示的模糊自适应PID幅值锁定控制系统。
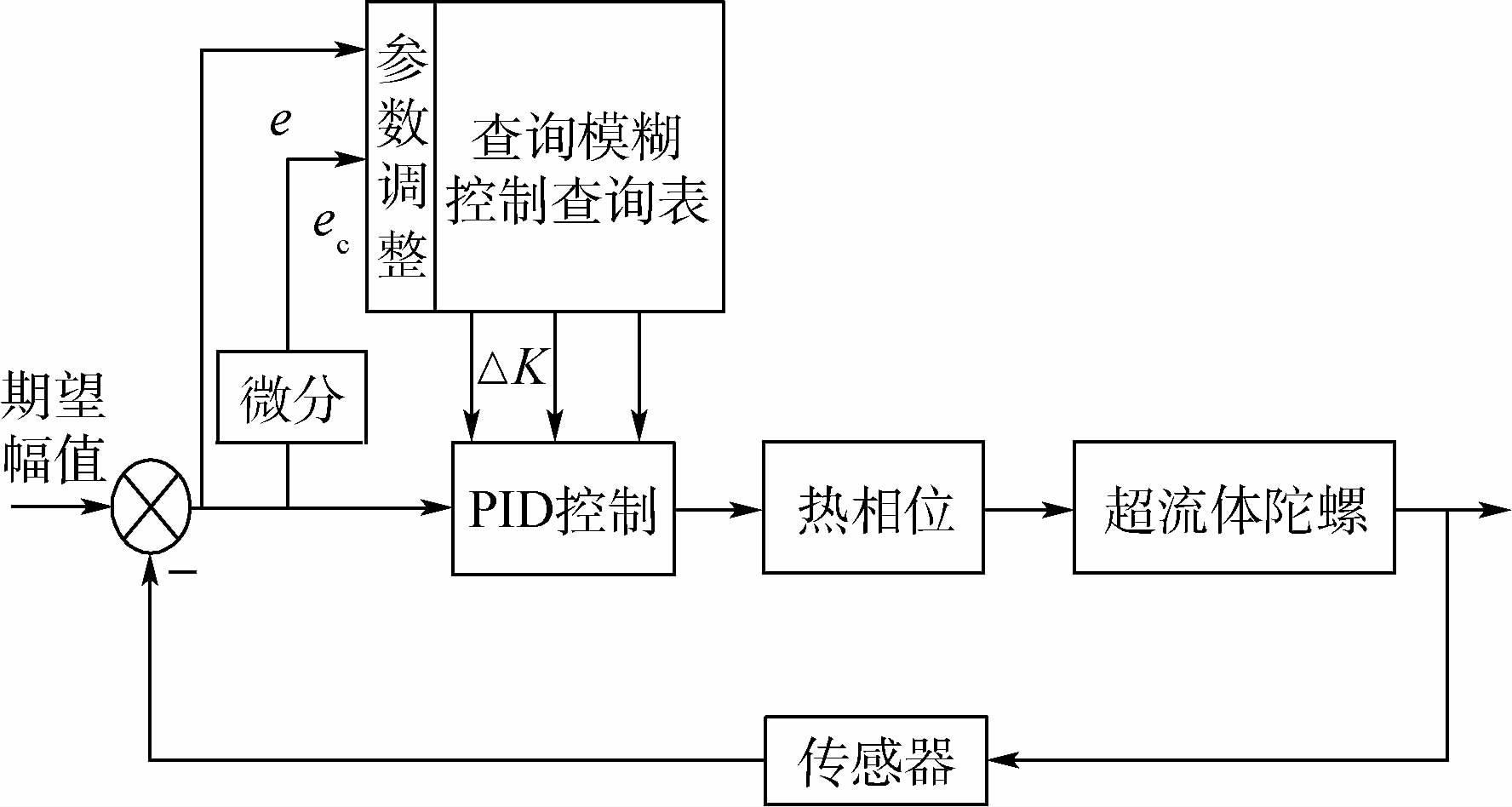 |
| 图 4 幅值锁定控制系统示意图 Fig. 4 Schematic diagram of amplitude-lockingcontrol system |
| 图选项 |
图 4中e、ec分别表示期望薄膜幅值与实际薄膜的幅值差和幅值差的变化率。通过实时检测e和ec,将检测量通过量化处理得到E、EC,经过模糊推理得出不同时刻E、EC对应的PID输出比例、积分、微分的模糊量参数Kp、Ki和Kd。经过解模糊得到对应的模糊自适应PID参数实际修正ΔK(kp,ki,kd);结合PID初始参数K(kp0,ki0,kd0),最终模糊自适应PID控制器的控制参数为K′(kp′,ki′,kd′):
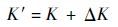 | (19) |
式中:kp0、ki0和kd0分别为PID控制器的初始比例、积分、微分参数;kp、 ki和 kd分别为比例、积分、微分参数修正值;kp′、ki′和kd′分别为模糊自适应PID控制器的比例、积分、微分参数。
则模糊自适应PID输出的实际控制量为
 | (20) |
3.2 引入重叠因子的优化设计 模糊控制器虽然具有鲁棒性强、无需被控对象精确建模等优点[16],但在参数选取方面大多还是依赖工作经验,人为性和主观性强[17]。遗传算法对所求解的优化问题没有太多的数学要求,有良好的进化特性,寻优过程不依赖问题的内在性质,可处理任意形式的目标函数[18]。
输入输出在论域的隶属函数分布通常为如图 5所示的典型等腰三角形隶属函数[19]。图 5中:O1、O2、O3、O4、O5、O6、O7分别为隶属函数NL(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PL(正大)的中心点;d1、d2、d3、d4、d5、d6分别为各隶属函数的中心点到右边界点的宽度,称为隶属函数的右半宽度;a1、a2、a3、a4、a5、a6为相邻隶属函数交点的纵坐标,即重叠因子。
 |
| 图 5 输入输出隶属函数分布 Fig. 5 Input-output membership function distribution |
| 图选项 |
对PS和PM隶属函数分析,其分布如图 6所示。
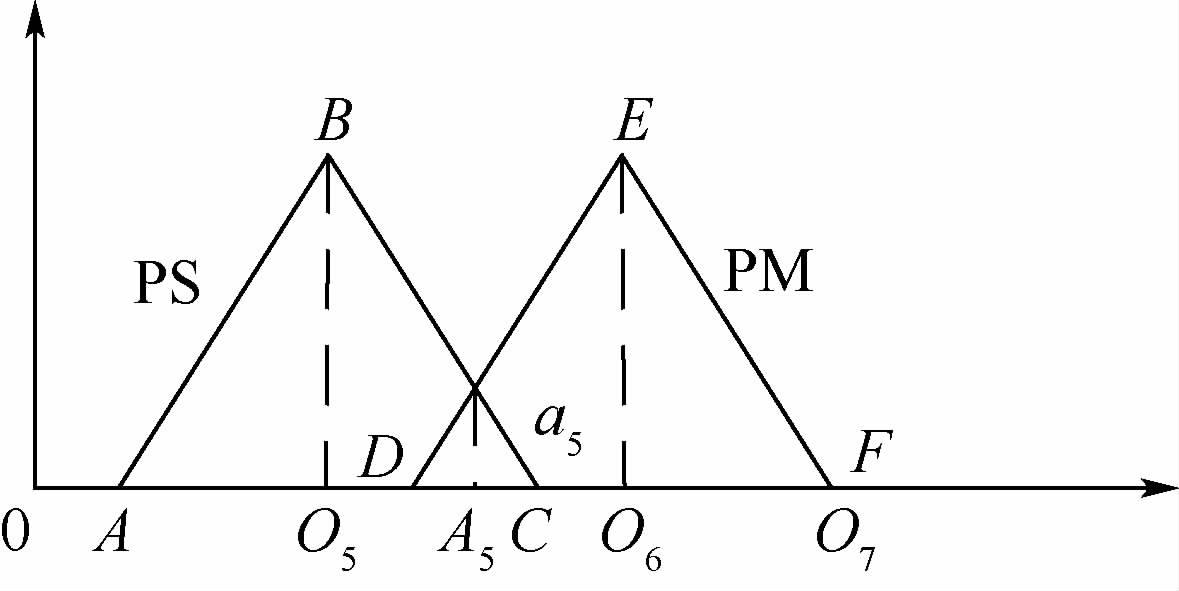 |
| 图 6 PS和PM的隶属函数分布 Fig. 6 PS and PM membership function distribution |
| 图选项 |
三角形隶属函数由中心、左半宽度和右半宽度共同决定。考虑遗传优化中,可能会出现相邻模糊隶属函数没有交集或者重叠部分太多导致优化求解速率下降或者出现无用解集。在此引入重叠因子的概念,即相邻隶属函数的交点的纵坐标定义为重叠因子。直接对三角形的右半宽度进行编码,而对于其左半宽度则是通过引进重叠因子来间接编码,同时设定重叠因子在合理的区间[0.2 0.6]。
由三角形相似定理有在△BCO5中
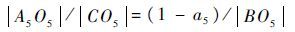 | (21) |
则A5O5=d5(1-a5),其中d5表示PS隶属函数的右半宽度。在△DEO7中,A5O6=dl(1-a5),其中dl表示PS隶属函数的左半宽度。
又由于
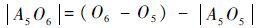 | (22) |
综合式(21)、式(22)得到隶属函数的左半宽度
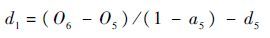 | (23) |
这样通过引入重叠因子,结合隶属函数右半半宽度便实现了隶属函数左半宽度的间接表达。对于本文设计的模糊推理系统,包含2个输入E、EC,3个输出Kp、Ki、Kd,需要编码的有6个相应的右半宽度、6个重叠因子和7个中心,根据每个参数的范围(Umin,Umax),依据式(24)再对M取整,便实现了将区间上的实数m转变为10位二进制码。
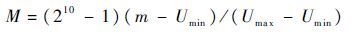 | (24) |
优化过程中首先将每个参数优化成二进制串,再串联成为一个染色体,通过对该染色体进行遗传操作直到求得最优解G(G为使代价函数值取最小时对应的解值)。随后通过拆分染色体得到对应最优参数,按照式(25)进行解码,将得到的数G转化为区间(Umin,Umax)上的实数
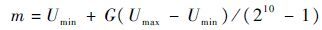 | (25) |
适应度函数f的设计需避免寻优开始较早出现过大的适应度值,而湮灭其他个体[18]。防止控制能量过大,目标函数中加入控制输入项,同时综合考虑薄膜幅值锁定系统的动态性能和超调,将惩罚函数融于优化指标,设计参数代价函数为
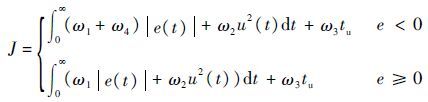 | (26) |
式中:ω1、ω2、ω3和ω4为权值,ω4$\gg $ω1;e(t)和u(t)分别为误差和控制器输出;tu为上升时间。
根据适应度函数f=1/J,个体i被选中的概率正比于个体的适应度值。个体的复制概率和其适应度值成比例,即
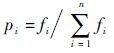 | (27) |
式中:n为群体大小;fi为第i个个体的适应度。
间接编码隶属函数左半宽度后,通过遗传寻优的实现过程是通过模糊推理系统计算出在参数范围内取不同值时,超流体陀螺薄膜幅值的实际输出幅值和此时对应的指标值,从种群中选择复制群体,同时保留每一代的最优个体,完成交叉和变异操作,形成下一代新个体,重复操作,在进化代数范围内,综合考虑系统动态性和超调性的代价函数,得到模糊自适应PID控制器最优参数。
4 仿真验证 采用间接编码三角形隶属函数左半宽度的遗传优化算法,首先初始化输入输出隶属函数为等腰三角形隶属函数,且相邻两三角形隶属函数的交点垂直坐标均为0.5,即重叠因子为0.5;接着初始化遗传算法的参数;最后利用模糊推理系统计算出此时系统的实际输出,计算对应的最优指标。样本个数为30个,交叉、变异概率分别为0.93、0.05,取ω1=0.92,ω2=0.98,ω3=2.5,ω4=100。超流体陀螺弱连接的微孔数目为4 225个,工作温度为2.175 K时,根据二流体模型,此时超流体密度为3 kg/m3,普通液氦Ⅱ的密度为143 kg/m3,超流体流过弱连接的临界流量为5.2×10-12 kg/s,弹性薄膜的面积为0.5×10-4 m2,发生约瑟夫森振荡的频率为1 000 Hz,相位锁定值设为π/4,注入热相位上限为500π。
为了验证本文对超流体陀螺系统优化设计的有效性和可行性,在MATLAB/Simulink环境中,基于重叠因子编码后,经遗传寻优得到优化前后输入隶属函数参数表(表 1)及优化前后输出隶属函数参数表(表 2);图 7为经过间接编码隶属函数左半宽度后,优化得到的最终输入-输出Kp、Ki、Kd模糊推理特性曲面。
表 1 优化前后输入隶属函数参数 Table 1 Original and optimized input membership function parameters
| 隶属函数 | 优化前E(EC) | 优化后 | |
| E | EE | ||
| NL | [-6 -6 -4] | [-6 -6 -3.922] | [-6 -6 -4.048] |
| NM | [-6 -4 -2] | [-5.46 -3.48 -1.857] | [-5.8 -3.8 -2.016] |
| NS | [-4 -2 0] | [-3.41 -1.476 -0.146] | [-3.44 -1.698 0] |
| ZO | [-2 0 2] | [-0.9365 -0.126 0.832] | [-0.968 -0.095 2 1.349] |
| PS | [0 2 4] | [0.254 1.127 3.41] | [0.349 2 1.603 3.946] |
| PM | [2 4 6] | [1.73 3.476 5.32] | [1.921 3.4 6] |
| PL | [4 6 6] | [3.81 6 6] | [4.27 6 6] |
表选项
表 2 优化前后输出隶属函数参数 Table 2 Original and optimized output membership function parameters
| 隶属函数 | 优化前KK、KK、KK | 优化后 | ||
| KK | KK | KK | ||
| NL | [-0.6 -0.6 -0.4] | [-0.6 -0.6 -0.395] | [-0.6 -0.6 -0.440 2] | [-0.6 -0.6 -0.395 2] |
| NM | [-0.6 -0.4 -0.2] | [-0.6 -0.45 -0.2] | [-0.547 -0.357 1 -0.183] | [-0.544 4 -0.375 -0.176] |
| NS | [-0.4 -0.2 0] | [-0.36 -0.2 0] | [-0.403 -0.169 8 -0.003 17] | [-0.36 -0.17 -0.017 46] |
| ZO | [-0.2 0 0.2] | [-0.08 0 0.12] | [-0.074 6 0 0.144 4] | [-0.106 3 0.003 17 0.132] |
| PS | [0 0.2 0.4] | [0 0.128 6 0.29] | [0.030 2 0.163 5 0.38] | [0.033 33 0.16 0.367] |
| PM | [0.2 0.4 0.6] | [0.144 0.306 3 0.6] | [0.22 0.354 0.6] | [0.22 0.392 1 0.6] |
| PL | [0.4 0.6 0.6] | [0.369 8 0.6 0.6] | [0.433 3 0.6 0.6] | [0.395 2 0.6 0.6] |
表选项
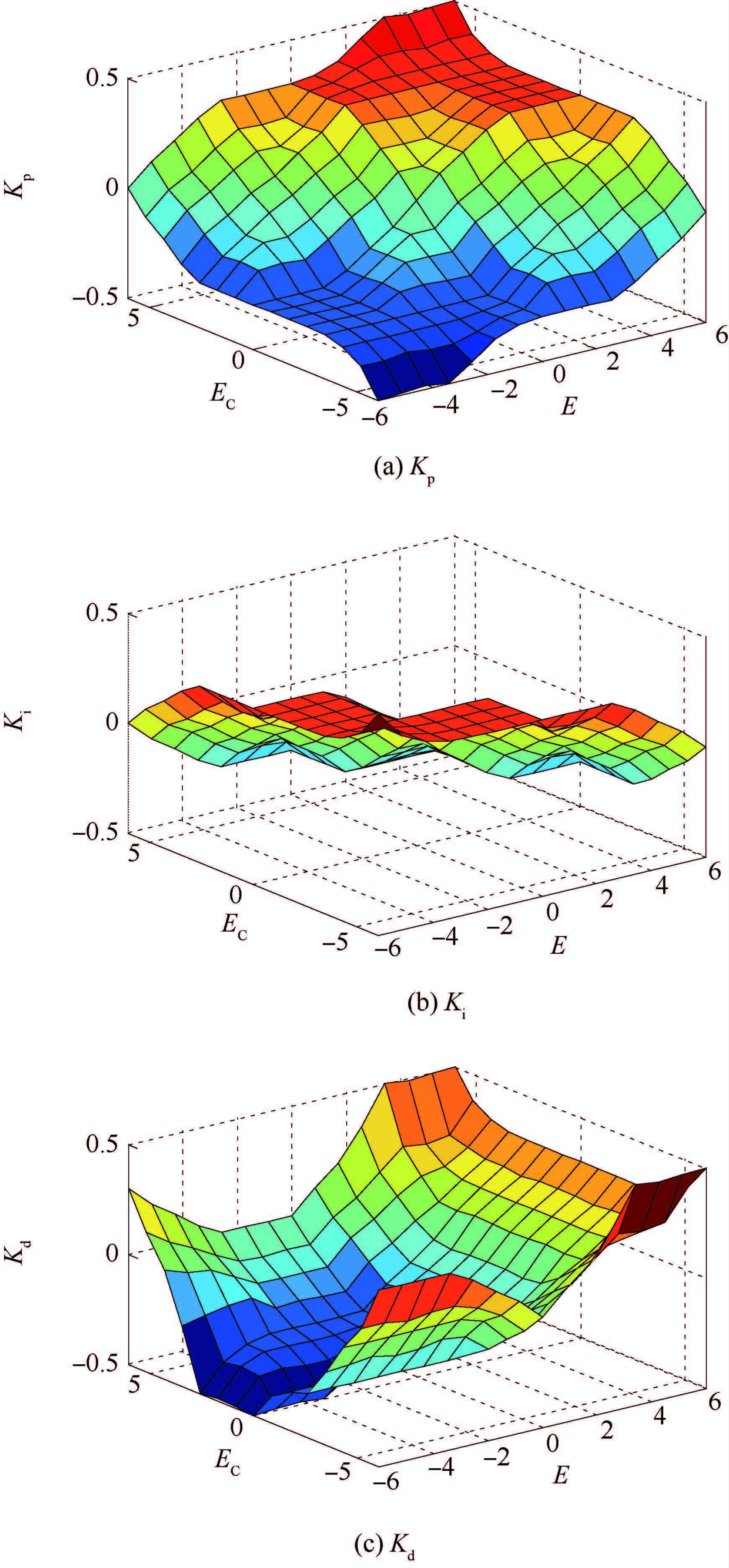 |
| 图 7 输入-输出Kp、Ki、Kd推理特性曲面 Fig. 7 Input-output reasoning feature surface of Kp,Ki and Kd |
| 图选项 |
从优化前后的输入输出隶属函数参数可以看出,优化后的隶属函数分布不再是简单的均匀三角形分布。隶属函数的形状在误差较小的论域,对应的坡度较陡,此时系统具有较好的灵敏度;在误差较大的论域,对应的隶属函数形状较缓,此时系统的隶属函数分辨率较低,控制特性较平缓,利于系统的稳定性。通过引入重叠因子间接编码三角形隶属函数,克服了优化结果可能存在相邻隶属函数无交点或重叠太多等无效解的情况,提高了优化效率。
通过模糊推理特性曲面可以直观分析出控制系统输入输出特性,曲面上某一点的三轴坐标表征着相应的控制参数。其中水平坐标对应不同的E、EC值;竖直坐标对应不同E、EC取值时,模糊推理系统的输出控制量Kp、Ki、Kd,推理特性曲面较为平滑,表征控制较为理想。
代价函数J的优化过程如图 8所示,随着优化代数逐渐增大,代价函数值逐渐减小,最终趋于稳定的较小值,此时对应参数解是最优的。
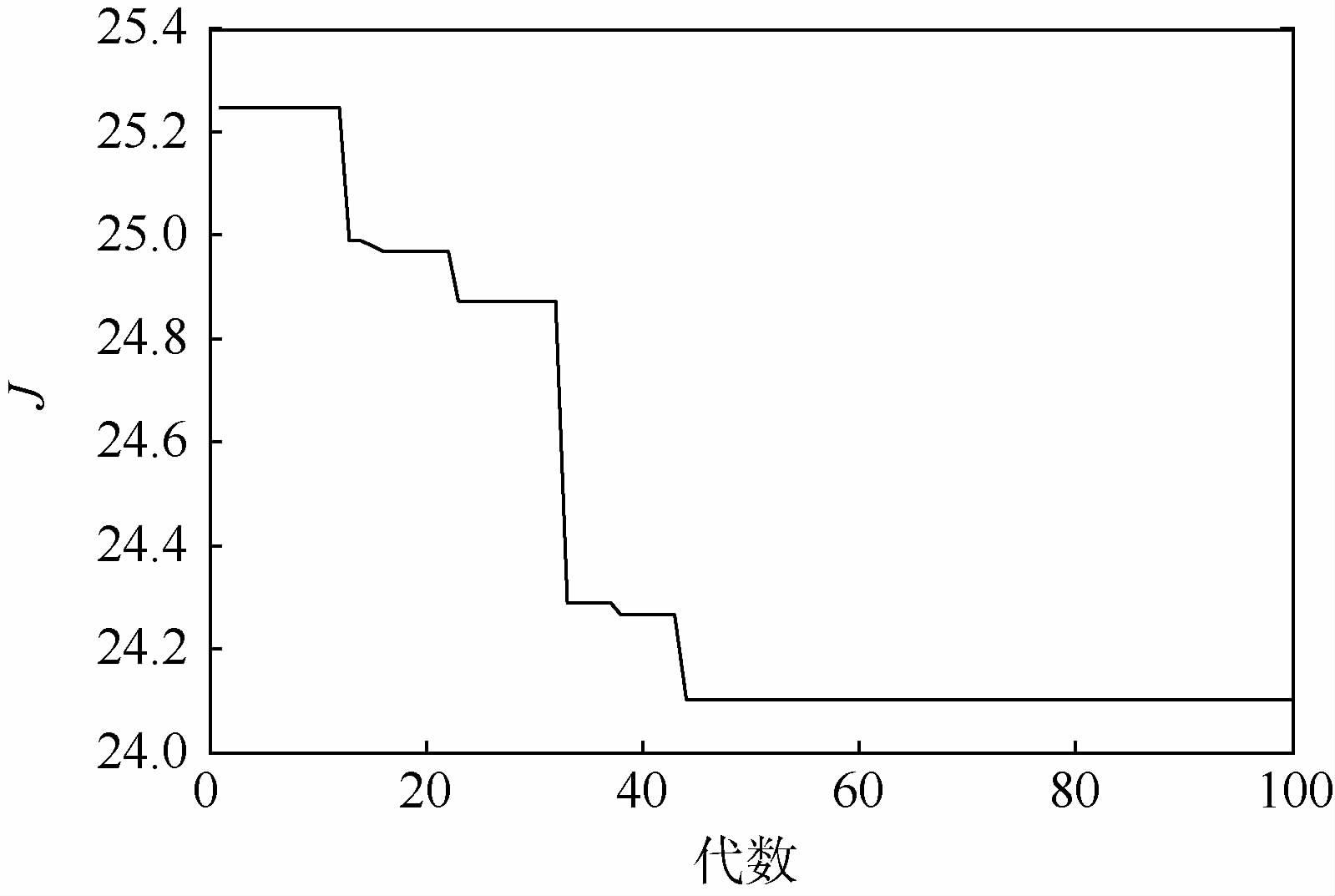 |
| 图 8 代价函数J的优化过程 Fig. 8 Optimization process of cost function J |
| 图选项 |
将优化后的参数作为幅值锁定系统控制参数,图 9为传统P控制和本文方法下超流体陀螺系统的薄膜幅值锁定对比情况。传统P控制下薄膜幅值在期望幅值73 nm附近波动,波动幅值约为100 nm,由于热相位注入延迟的影响,导致薄膜幅值始终不能很好地锁定在期望值;经过遗传优化的模糊控制下,由局部放大图可知,陀螺系统在0.17 s时,薄膜幅值已经能很好地锁定在理想值,且能长时间地工作在锁定幅值处,没有明显的幅值波动。
 |
| 图 9 薄膜幅值锁定对比图 Fig. 9 Film amplitude-locking contrast diagram |
| 图选项 |
图 10为传统P控制和本文方法下超流体陀螺系统的幅值锁定误差对比情况。从局部放大图可知,传统P控制下系统始终有较大的锁定误差,陀螺系统在0.17 s时的锁定误差比本文方法下的误差高将近23倍。在0.17 s之后,系统幅值波动始终在13.7%左右,这是由于温升延迟和控制欠佳共同造成的;而经过遗传优化模糊控制下的陀螺系统在0.17 s后,相对期望值的幅值波动约为0.3%,这个误差对角速度解算的影响已经很小了,可实现较高精度的角速度测量。
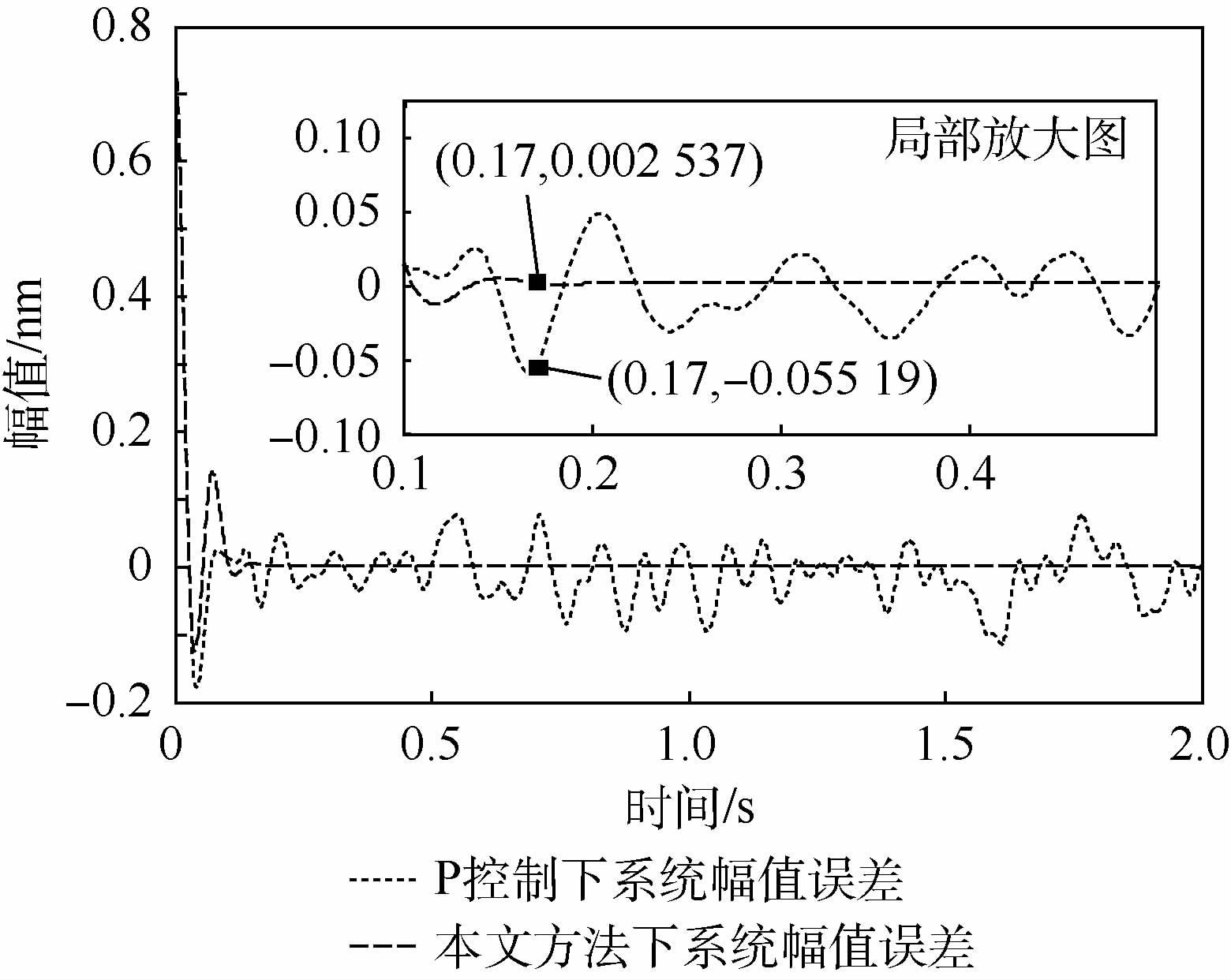 |
| 图 10 薄膜幅值锁定误差对比图 Fig. 10 Film amplitude-locking error contrast diagram |
| 图选项 |
综上所述,通过引入重叠因子间接编码的隶属函数,经过遗传寻优,使得隶属函数的形状根据误差论域的大小而自适应地进行调整,避免了单一均匀隶属形状选取盲目性。同时遗传优化模糊控制改善了超流体陀螺系统的动态响应性能,使系统达到稳定的时间大大提高。克服了由于加热电阻升温延迟对陀螺系统的影响,使得薄膜的幅值尽快且良好地锁定在期望薄膜幅值,提高了陀螺系统的敏感精度。
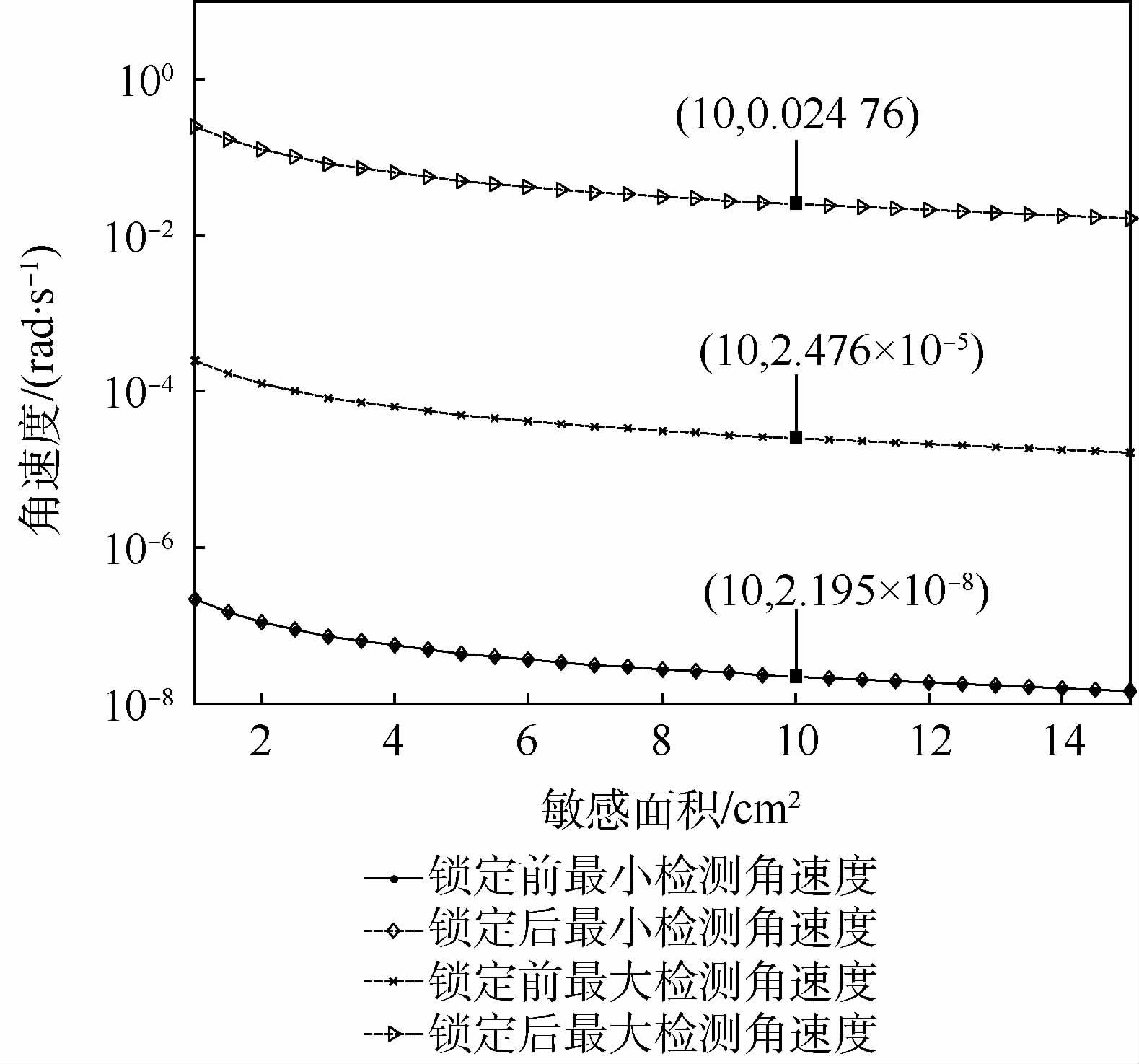
图 11为未施加锁定控制和施加锁定控制后超流体陀螺的角速度测量对比情况。
 |
| 图 11 角速度测量对比图 Fig. 11 Angular velocity measurement contrast diagram |
| 图选项 |
从图 11可以看出,幅值锁定控制前后的陀螺最小检测角速度曲线重合,可见幅值锁定控制方法并不改变陀螺的最小检测角速度。
外界角速度输入时,薄膜幅值将被调制,当调制量恰与测量元件能检测最小薄膜位移的精度相等时,对应的角速度值为陀螺的最小检测角速度。受限于目前检测薄膜幅值的超导量子干涉仪检测精度仅为10-15 m,在敏感面积10 cm2时超流体陀螺的最小检测角速度为2.195×10-8 rad/s。此外随着敏感面积的增大,陀螺的最大检测角速度变小,限制超流体陀螺使用的关键是如何扩展其角速度测量量程上限,陀螺做的越小,其敏感面积就越小,对应可实现的检测角速度越大。 在敏感面积为10 cm2的情况下,幅值锁定前后的最大检测角速度由2.476×10-5 rad/s增大到2.476×10-2 rad/s,可见幅值锁定控制较好地实现了陀螺的量程扩展。
5 结 论 热驱动型双弱连接超流体陀螺利于物质波的干涉效应可实现极高灵敏度的角速度检测,然而目前其角速度检测范围仅为10-8~10-5 rad/s,本文对此引入幅值锁定概念进行了量程扩展方案的研究,得到以下结论:
1) 基于重叠因子优化的幅值锁定控制系统可实现较好的薄膜幅值锁定效果,在较短调节时间内将幅值波动控制在0.3%左右,可实现较高精度的角速度测量。
2) 幅值锁定控制方案实现了超流体陀螺角速度检测范围的扩展。使用超导量子干涉仪检测薄膜位移时,在相同敏感面积下,最大检测角速度提高了3个数量级,最小检测角速度不变。为实现陀螺的更大量程范围,在施加幅值锁定控制的同时,可使用更高分辨率的检测器件,且陀螺面积也应该做得越小越好。
参考文献
| [1] | FANG J C, SUN J J, XU Y L, et al. A new structure of permanent magnet biased axial hybrid magnetic bearing[J].IEEE Transactions on Magnetics, 2009, 45(12): 5319–5325.DOI:10.1109/TMAG.2009.2024687 |
| [2] | HAN B C, HU G, FANG J C. Optimization design of magnetic suspended gyroscope rotor[J].Optics and Precision Engineering, 2006, 14(4): 662–666. |
| [3] | KAPALE K T,DIDOMENICO L D,LEE H.Quantum interferometric sensors[C]//Proceedings of SPIE -The International Society for Optical Engineering,V 6603,2007,Noise and Fluctuations in Photonics,Quantum Optics,and Communications.Bellingham,WA:SPIE,2007.http://cn.bing.com/academic/profile?id=2126394146&encoded=0&v=paper_preview&mkt=zh-cn |
| [4] | HODBY E, HOPKINS S A. Experimental observation of a superfluid gyroscope in dilute Bose-Einstein condensate[J].Physics Review Letters, 2003, 91(9): 090403.DOI:10.1103/PhysRevLett.91.090403 |
| [5] | PACKARD R. The role of the Josephson-Anderson equation in superfluid helium[J].Reviews of Modern Physics, 1998, 70(2): 641–651.DOI:10.1103/RevModPhys.70.641 |
| [6] | HOSKINSON E.Superfluid 4He weak links[D].Berkeley:University of California,2005:5-9. |
| [7] | GOLOVASHKIN A I, ZHERIKHINA L N, TSKHOVREBOV A M, et al. Ordinary SQUID interferometers and superfluid helium matter wave interferometers:The role of quantum fluctuations[J].Journal of Experimental and Theoretical Physics, 2010, 111(2): 332–339.DOI:10.1134/S1063776110080285 |
| [8] | HAKONEN A P, VAROQUAUX E. Detection of the rotation of the earth with a superfluid gyrometer[J].Physical Review Letters, 1997, 78(19): 3602–3605.DOI:10.1103/PhysRevLett.78.3602 |
| [9] | PACKARD R E. Principles of superfluid helium gyroscopes[J].Physical Review B, 1992, 46(6): 3540–3549.DOI:10.1103/PhysRevB.46.3540 |
| [10] | HOSKINSON E, PACKARD R. Thermally driven Josephson oscillations in superfluid 4He[J].Physical Review Letters, 2005, 94(15): 155303.DOI:10.1103/PhysRevLett.94.155303 |
| [11] | SATO Y, ADITYA J, PACKARD R. Flux locking a superfluid interferometer[J].Applied Physics Letters, 2007, 91(7): 1–3. |
| [12] | SATO Y.Experiments using 4He weak link[D].Berkeley:University of California,2007:51-58. |
| [13] | 谢征.基于物质波干涉效应的新型低温超流体陀螺关键技术研究[D].南京:南京航空航天大学,2012:121-125.XIE Z.Research on the key techniques for new cryogenic superfluid gyroscope based on matter wave interference effect[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2012:121-125(in Chinese).http://epub.cnki.net/kns/detail/detail.aspx?QueryID=0&CurRec=1&FileName=1014005318.nh&DbName=CDFD1214&DbCode=CDFD&pr= |
| [14] | STIMAC G, BRAUT S, ZIGULI R. Comparative analysis of PSO algorithms for PID controller tuning[J].Chinese Journal of Mechanical Engineering, 2014, 27(5): 928–936.DOI:10.3901/CJME.2014.0527.302 |
| [15] | YANG Y Q, WANG G J. Parameters optimization of polygonal fuzzy neural networks based on GA-BP hybrid algorithm[J].International Journal of Machine Learning and Cybernetics, 2014, 5(5): 815–822.DOI:10.1007/s13042-013-0224-y |
| [16] | SONG S J, MOON Y J, LEE D H, et al. Comparative study of fuzzy PID control algorithms for enhanced position control in laparoscopic surgery robot[J].Journal of Medical and Biological Engineering, 2015, 35(1): 33–44. |
| [17] | ESFANDYARI M, FANAEI M A, ZOHREIE A. Adaptive fuzzy tuning of PID controllers[J].Neural Computing and Applications, 2013, 23(1): 19–28. |
| [18] | ZHANG N N, GUO Y B. Control strategy for hybrid electric vehicle based on fuzzy logic[J].International Journal of Automotive Technology, 2012(112): 563–571. |
| [19] | HAN J Q. From PID to active disturbance rejection control[J].IEEE Transactions on Industrial Electronics, 2009, 56(3): 900–906.DOI:10.1109/TIE.2008.2011621 |
