惯导系统动基座传递对准的过程就是在高精度主惯导的辅助条件下,利用主、子惯导系统导航参数或测量信息的差值作为观测量,对主、子惯导系统间的失准角、速度误差、位置误差等导航参数误差及惯性元件误差进行估计,并根据估计结果对子惯导系统进行高精度对准,从而达到提高子惯导导航精度的目的[2]。
目前,针对惯导系统动基座传递对准技术的研究主要集中在匹配算法的应用和改进[3]、运载体弹性形变及杆臂效应的影响分析与补偿[4-6]、时间延时效应的分析与补偿[6-8]、对准精度的评估[9]与非线性滤波算法研究[10]等方面。而系统可观测性分析作为对系统状态可估计能力的描述,是Kalman滤波收敛的前提条件[11-12],同样也引起了广泛研究[13-14]。
然而,由于动基座条件下传递对准系统是非线性的、时变的,虽然理论上可通过检查Grammian矩阵的秩来判断其可观测性,但计算量较大,且只能通过数值分析的方法对系统的性质进行研究,在实际应用中十分不便[11]。传统的可观测性分析方法通常用线性化模型代替原系统非线性模型,利用分段定常系统(Piece-Wise Constant System,PWCS)理论[15-16],通过求解系统可观测性矩阵的秩或奇异值判断系统的可观测性。这种方法虽然大大简化了非线性时变对准模型的可观测性分析,但存在以下问题[17]:①当系统的维数较高或分段过多时,工作量较大;②经过线性化与分段定常两次近似后得到的系统模型与原始的系统模型之间存在一定的误差;③不能充分揭示系统可观测性与载体运动状态之间的联系和内在机理。
针对上述问题,本文从惯导系统动基座传递对准原始的非线性模型出发,根据可观测性的基本定义对系统状态变量进行了分析,给出了系统可观测性的充分条件,深刻地揭示出系统可观测性同载体运动状态的内在联系。该方法避免了由于线性化过程而引入的模型误差,且无需经过复杂的数值计算过程,极大地减小了计算量,并为合理规划载体的机动方案提供了理论依据。
1 系统模型建立 在惯导系统动基座传递对准过程中,存在主、子两套惯导系统,为便于说明问题,同时避免发生混淆,对坐标系及部分相关符号进行了定义。定义主惯导体坐标系为a系;子惯导体坐标系为b系;采用当地地理坐标系(即北-天-东坐标系)作为导航坐标系,记为n系,并记子惯导计算机建立的数字平台坐标系为n′系;定义惯性坐标系i系,并与初始时刻的地面坐标系e系和导航坐标系n系重合。考虑惯性器件的测量误差,子惯导系统的运动学方程可表示为[18]
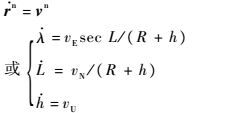 | (1) |
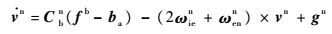 | (2) |
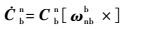 | (3) |
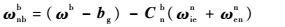 | (4) |
式中:rn为惯性测量单元(Inertial Measurement Unit,IMU)在n系下的位置;λ、L和h分别为经度、纬度和高程;R为地球平均半径;vn=$\left[ \begin{matrix} {{v}_{N}} & {{v}_{U}} & {{v}_{E}} \\\end{matrix} \right]$T为IMU在n系下的地速(下标N、U、E分别代表速度的北向、天向和东向分量);Cbn为子惯导体坐标系b系到其导航坐标系n系的坐标转换矩阵,也即子惯导系统输出的姿态矩阵;ωien=$\left[ \begin{matrix} {{w}_{ie}}\cos L & {{w}_{ie}}\sin L & 0 \\\end{matrix} \right]$T为在n系下表示的地球自转角速度;ωnbb为弹体相对导航系的转动角速度在子惯导体坐标系下的投影;ωenn=$\left[ \begin{matrix} {{v}_{E}} & {{v}_{E}}\tan L & {{v}_{N}} \\\end{matrix} \right]$T/(R+h)为导航坐标系n系相对于地面坐标系e系的转动角速度在n系下的投影; f b为加速度计测量的比力;ωb为陀螺仪测量的弹体相对于惯性空间的转动角速度;gn为在n系表示的当地重力加速度;×表示矢量积运算;[a×]表示为向量a的反对称矩阵;ba、bg分别为加速度计零偏和陀螺漂移,本文将其视为随机常数,即
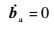 | (5) |
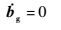 | (6) |
由于主、子惯导安装位置不同,杆臂的影响导致主、子惯导输出的位置、速度存在如下关系:
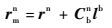 | (7) |
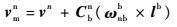 | (8) |
式中:rmn和vmn分别为主惯导系统输出的载体在导航系下的位置和地速。
在不考虑载体变形及弹体弹性形变的前提下,主、子惯导间的安装关系不会发生改变,杆臂矢量可视为常值,即
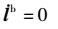 | (9) |
式(1)~式(9)构成了惯导系统动基座传递对准模型,其状态量包括子惯导所在弹体的位置、速度、姿态以及子惯导的惯性器件误差(加速度计零偏和陀螺漂移)和杆臂矢量,系统观测量则包括主惯导实时输出的精确的位置、速度和姿态信息以及子惯导加速度计和陀螺仪的测量输出。
2 可观测性分析 根据文献[19]中关于系统可观测性定义可知,若系统可观,则意味着根据系统的输出和输入信息即可唯一确定系统的初始状态量。因此,系统的可观测性分析问题可转化为判断系统状态量是否存在唯一解的问题。与此同时,通过对状态量解的分析,可以看出载体机动方式对状态量可观测性的影响,进而可获得满足系统可观测的充分条件。
利用改进方法,本节将对系统的状态量逐一进行分析,并给出系统可观测的充分条件,为进一步设计载体的运动轨迹提供理论指导。
1) 加速度计零偏的可观测性
假设载体作直线运动,且姿态不发生变化,即ωnbb=0,$\dot{C}$bn=0,则式(8)可写为
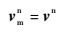 | (10) |
即主、子惯导速度相等,不受杆臂影响。
对式(10)两端求导,并代入式(2),有
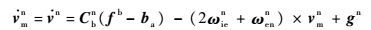 | (11) |
由式(11)可解得
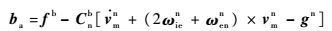 | (12) |
式中:f b由子惯导加速度计测量获得,ωien和ωenn可通过主惯导输出的位置及速度信息计算获得,而gn在位置矢量已知后,即为已知(由杆臂造成的位置误差较小,可忽略不计)。故式(11)等号右端除Cnb外,各项均为已知。因此,令
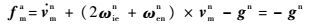 | (13) |
即载体加速度为0,便可唯一确定ba,故加速度计零偏是可观测的。
2) 陀螺漂移的可观测性
已知在直线运动状态下,ωnbb=0,则式(4)可改写为
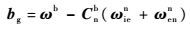 | (14) |
对式(11)两端求导,并根据式(5),可得
 | (15) |
整理得
 | (16) |
式中:f b、ωien、ωenn和gn各项已知,故其导数也均为已知量。
由文献[20-21]可知,若存在两个不相等的时刻t1、t2,满足$\dot{f}$ b(t1)和$\dot{f}$ b(t2)线性不相关,则可确定该运动状态下的姿态矩阵Cbn。
将已知的Cbn代入式(14),即可确定bg,即陀螺漂移是可观测的。注意,此条件同样可满足加速度计零偏可观测。
3) 姿态的可观测性
直线运动状态下,式(11)成立,其中Cbn项满足
 | (17) |
式中:Φn(t0,t)和Φb(t0,t)分别为n系和b系从t0到t时刻的姿态转移矩阵,可由主惯导输出信息及子惯导补偿后的陀螺测量数据计算得到,为已知量。将式(17)代入式(11),进一步整理可得
 | (18) |
式中:除Cbn(t0)外,各项皆为已知。注意到ΦbT(t0,t)(f b-ba)为子惯导真实比力在其初始时刻体坐标系下的投影,记
 | (19) |
因此,若存在f b(0)(t3)和f b(0)(t4)且t3≠t4,使这两个时刻的f b(0)(t)线性不相关,则Cbn(t0)可被唯一地确定[20-21],进而任意时刻的姿态都是已知的,即姿态是可观测的。
4) 安装误差角的可观测性
除子惯导惯性器件误差及杆臂影响外,安装误差同样是导致主、子惯导输出不一致的因素之一。定义ψa为弹体的安装误差角,即
 | (20) |
已知载体姿态矩阵Can可由主惯导精确提供,故Cbn已知后,安装误差矩阵Cba=(Can)T·Cbn即为已知。由定义式(20),可解得
 | (21) |
由此可唯一确定ψa,即安装误差角是可观测的。
5) 速度的可观测性
在直线运动假设下,对式(11)进行积分,得
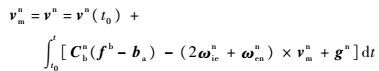 | (22) |
由式(22)可解得速度初值
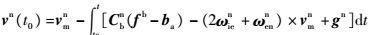 | (23) |
则任意时刻速度都可确定,速度可观。
6) 杆臂的可观测性
将式(8)改写为
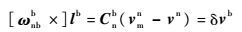 | (24) |
式中:除lb外各项均为已知。注意到矩阵[ωnbb×]的秩为2,因此若存在时刻t5≠t6,满足ωnbb(t5)与ωnbb(t6)线性不相关,则有
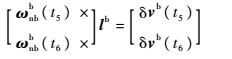 | (25) |
由于
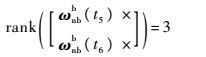 | (26) |
lb有唯一解。
因此,需载体作曲线运动,且存在两个不同的时刻满足ωnbb线性不相关,则可满足杆臂可观测。
综上所述,对于惯性导航动基座传递对准系统,有如下结论。
结论1 载体作直线运动,姿态不发生变化,即ωnbb=0,$\dot{C}$bn=0,且载体加速度为0,则加速度计的零偏是可观测的。
结论2 载体作直线运动,姿态不发生变化,即ωnbb=0,$\dot{C}$bn=0,且存在两个时刻t1≠t2,满足比力导数 b(t1)和 b(t2)线性不相关,则陀螺的常值漂移是可观测的。
结论3 载体作直线运动,姿态不发生变化,即ωnbb=0,$\dot{C}$bn=0,且存在两个时刻t3≠t4,满足f b(0)(t3)和f b(0)(t4)线性不相关,则子惯导姿态、速度和安装误差角是可观测的。
结论4 载体作曲线运动,姿态发生变化,且存在两个时刻t5≠t6,满足ωnbb(t5)与ωnbb(t6)线性不相关,则杆臂矢量是可观测的。
3 仿真验证 为了对可观测性分析的结论进行验证,本节用MATLAB进行了数值仿真。以导航参数误差为状态变量,同时将惯性器件(加速度计及陀螺仪)测量误差的常值项和子惯导的安装误差增广为状态变量,构成传递对准的状态方程组,采用“速度+姿态”的匹配模式[2],利用扩展Kalman滤波器(EKF)对系统的状态变量进行估计,并通过滤波效果判断各状态变量的可观测性。
3.1 仿真参数设计 仿真的基本参数设置为:惯导系统的数据更新频率为100 Hz;杆臂向量设置为lb=$\left[ \begin{matrix} 1 & 4 & 2 \\\end{matrix} \right]$T(m),仿真时间为60 s。
子惯导系统的基本参数设置为:安装误差为ψa=$\left[ \begin{matrix} 1 & 3 & 2 \\\end{matrix} \right]$T(°),加速度计零偏为ba=$\left[ \begin{matrix} 0.01 & 0.01 & 0.01 \\\end{matrix} \right]$T (m/s2),陀螺漂移为bg=$\left[ \begin{matrix} 0.005 & 0.005 & 0.005 \\\end{matrix} \right]$T((°)/s)。为达到较好的仿真效果,惯性器件的测量噪声设置为0。此外,在对准开始时,子惯导系统状态量的初值由主惯导赋予。
滤波器误差状态的初值均取为0,滤波周期为0.01 s,其余参数根据系统进行设置,采用4阶龙格-库塔积分算法。
3.2 载体机动方案规划 由第2节推导得出的结论可知,系统各状态变量可观测性的确定具有一定的先后顺序:①加速度计零偏;②陀螺漂移;③子惯导姿态;④子惯导的速度和安装误差角;⑤杆臂。因此,载体的机动方案也应依据前述的4个条件分段设计。
由结论1,载体静止或作匀速直线运动,即可满足加速度计零偏可观测。
根据结论2,若载体作直线运动,则比力的变化将始终沿着载体前进的方向,无法满足线性不相关的要求。因此,在直线行驶的末端,载体的运动轨迹必须发生变化,依靠转弯瞬间的侧向加速度来实现不同时刻比力导数 b(t)的线性不相关。但这样的机动只能使结论2中的条件在很短的时间段内得到满足,难以达到满意的估计效果。为得到较好的仿真结果,以验证理论的正确性,不妨假设载体在变加速直线运动的同时进行上升、下降或侧向平移等机动,且过程中保持姿态不发生变化,则载体在机动前后的比力导数是线性不相关的,即满足结论2中陀螺漂移可观测的要求。
在结论3中,只要求存在两个不同的时刻使f b(0)(t)线性不相关。此处需要注意的是,比力矢量等于惯性加速度与重力加速度之差,因此只要a(t)不恒定,即载体作变加速直线运动,便可满足要求,使子惯导的姿态、速度及安装误差角可观测。由此可见,载体第3段的机动方案包含于第2段中,因此无需再额外进行特定的机动。
依据结论4的要求,载体作曲线运动,若行进过程中存在俯仰、偏航或滚转3种姿态运动中的任意两种或全部,即可满足不同时刻ωnbb(t)线性不相关的要求,使杆臂可观测。
由上述分析,对载体的机动方案进行如下设计。
机动段1:0~10 s,载体静止不动。
机动段2:10~40 s,载体沿纵轴作变加速直线运动,25~40 s,载体作变加速的升降运动。
机动段3:40~60 s,载体同时进行滚转运动和俯仰运动。
载体比力和角速度的具体变化情况分别如图 1和图 2所示。
 |
| 图 1 载体的比力 Fig. 1 Specific force of vehicle |
| 图选项 |
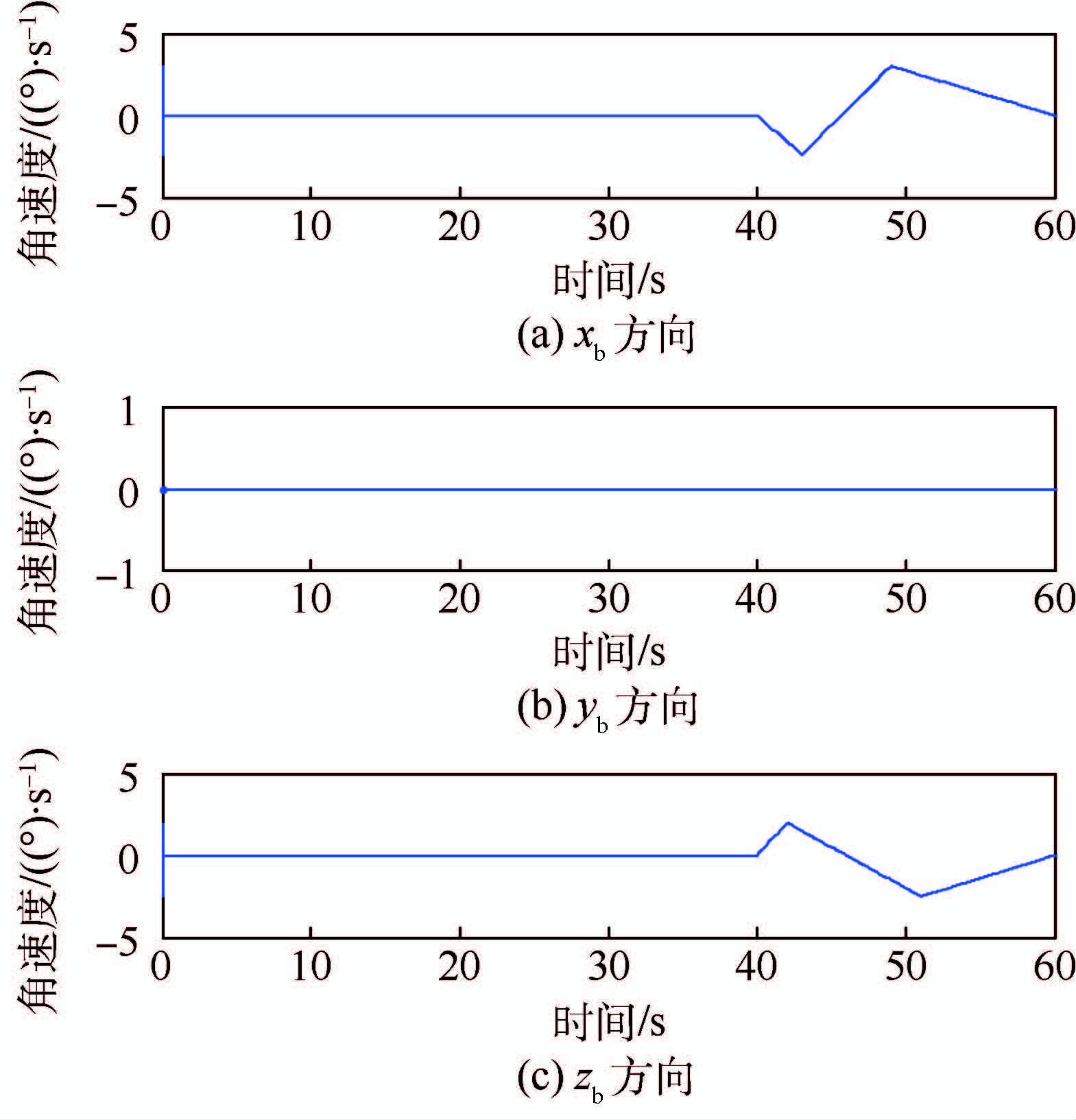 |
| 图 2 载体的角速度 Fig. 2 Angular velocity of vehicle |
| 图选项 |
3.3 仿真结果 图 3给出了子惯导加速度计零偏的估值曲线。在0~10 s之间,载体保持静止,满足结论1中的条件,加速度计零偏自仿真开始即迅速收敛,趋于真值。
 |
| 图 3 加速度计零偏估计结果 Fig. 3 Estimation results of accelerometer bias |
| 图选项 |
图 4给出了子惯导陀螺漂移的估值曲线。由图 1可见,在25 s之前,比力仅沿xb轴方向变化,不能唯一确定陀螺漂移,zb轴方向上的陀螺漂移始终未收敛至真值。而在25 s之后,yb轴方向上的比力也开始发生变化,满足${\dot{f}}$ b线性不相关的条件,根据结论2,此时陀螺完全可观。因此,曲线开始向真值收敛。
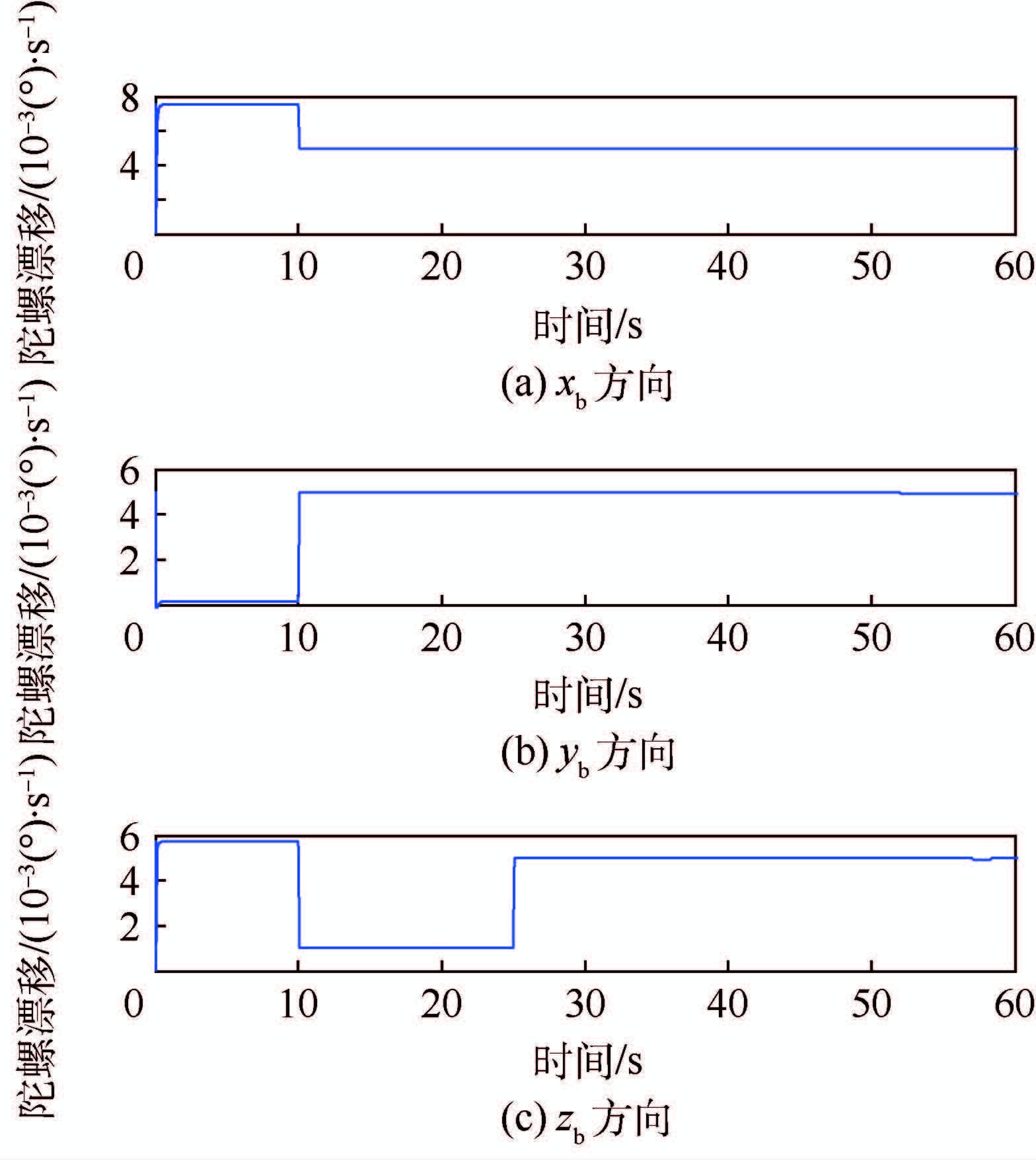 |
| 图 4 陀螺漂移估计结果 Fig. 4 Estimation results of gyro drift |
| 图选项 |
图 5给出了子惯导安装误差角的估值曲线。由于使安装误差角可观测的载体机动条件同陀螺漂移相同,同样,其估值曲线在25 s后开始向真值收敛,仿真结果与结论3一致。
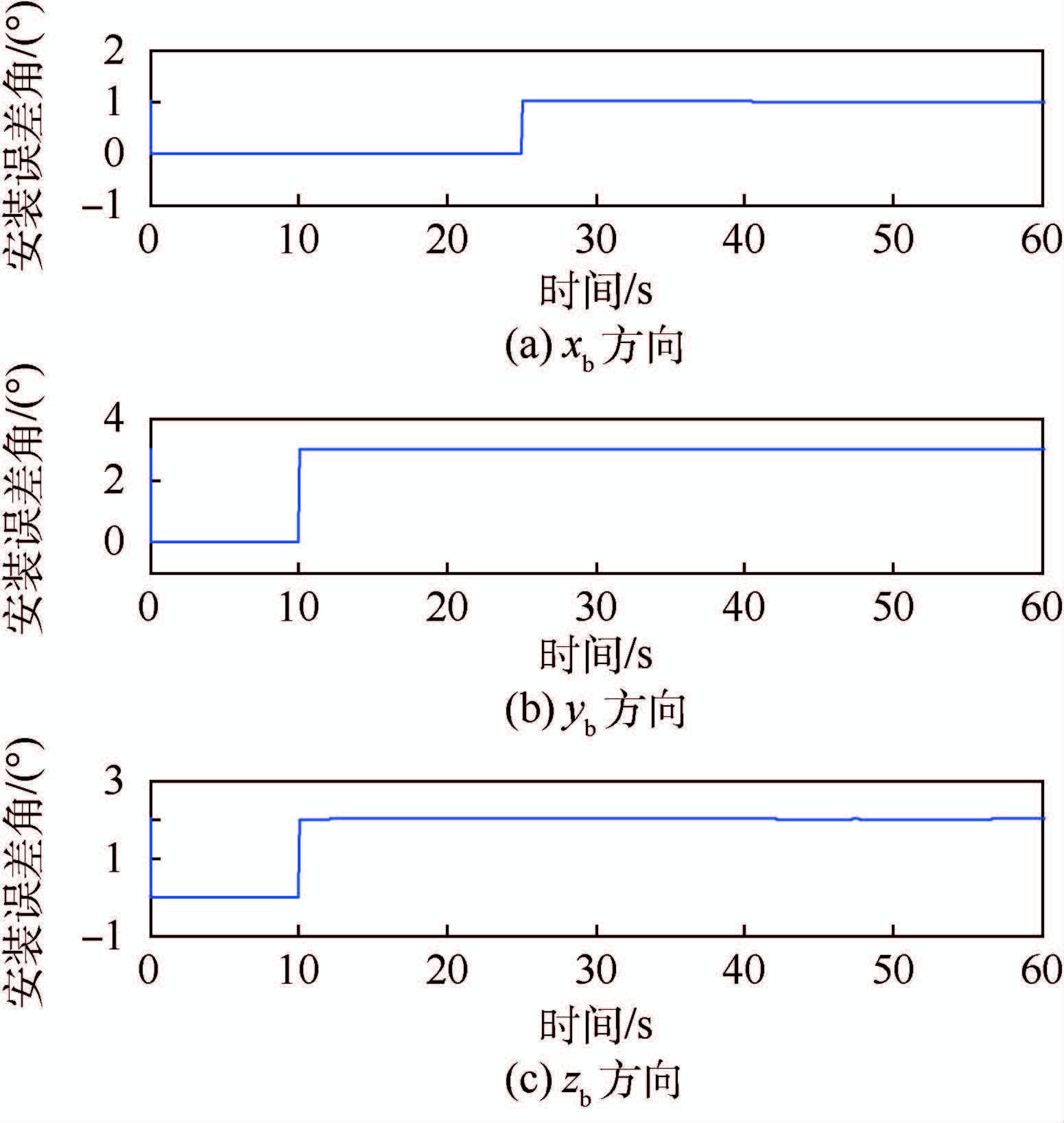 |
| 图 5 安装误差角估计结果 Fig. 5 Estimation results of fix error angle |
| 图选项 |
图 6给出了杆臂的估值曲线。对比图 2可以看出,在40 s前,载体未进行任何姿态运动,杆臂在各方向上的估值基本保持在初值附近。而在40 s后,载体在滚转和俯仰方向的姿态同时发生变化,满足ωnbb线性不相关的条件,此时杆臂可观,估值曲线开始向真值收敛,仿真结果与结论4相符。
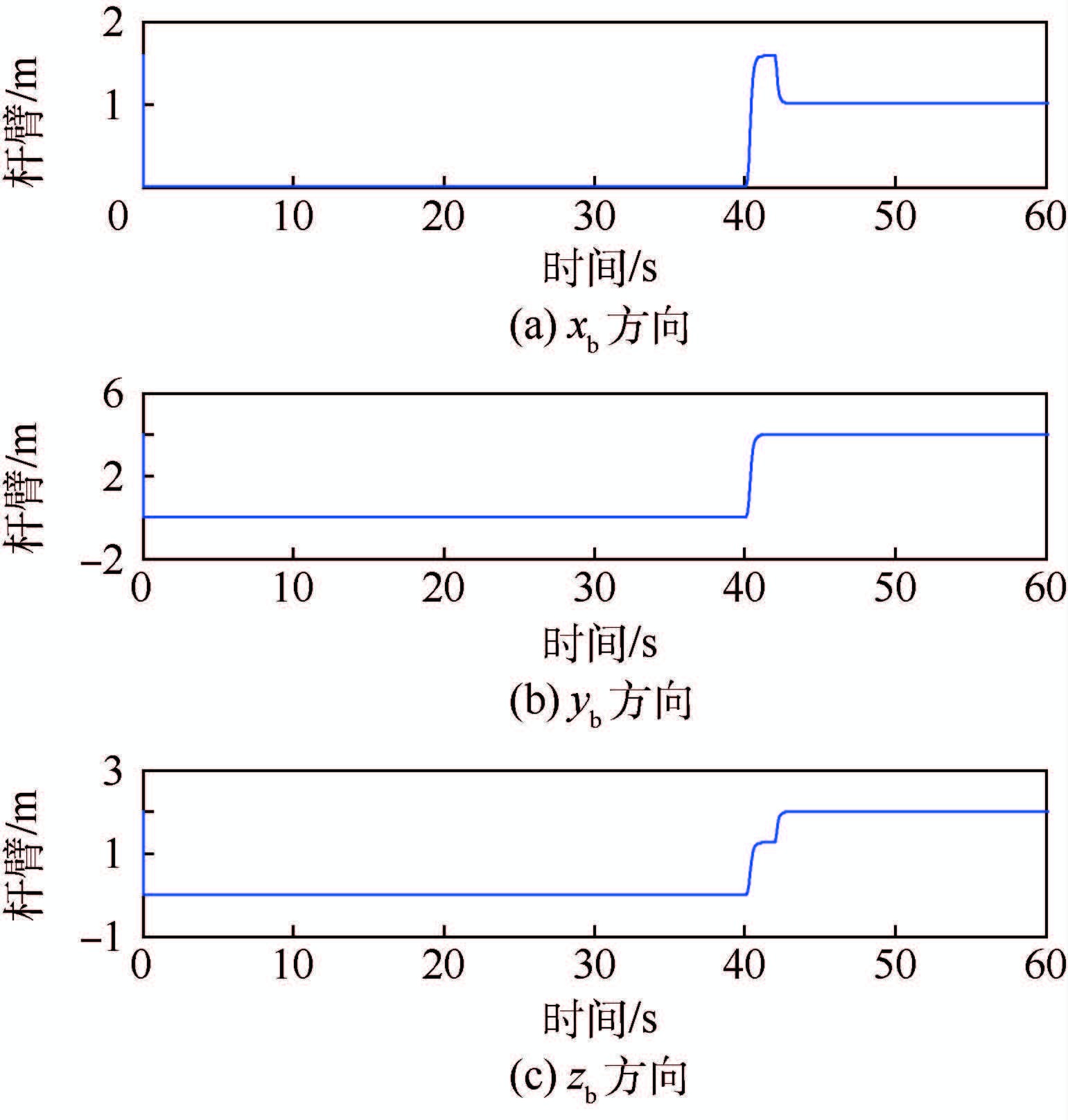 |
| 图 6 杆臂估计结果 Fig. 6 Estimation results of lever arm |
| 图选项 |
上述仿真结果与第2节中的理论分析一致,充分验证了理论分析的正确性,也直观地反映了载体机动状态对系统状态可观测性的影响。
4 结 论 本文针对惯性导航系统传递对准过程中的可观测性问题,提出了从基本定义出发的非线性可观测性分析方法,解决了传统方法存在的模型误差不可避免、计算量较大、物理意义不明确等问题。
1) 根据理论分析的结果对载体的机动策略进行了规划,通过EKF仿真验证了理论分析的正确性,分析过程直观、简洁,且结论更加准确、清晰。
2) 系统可观测性的条件较易满足,只需载体先后进行不同方向上的变加速直线运动及姿态运动即可,且变加速直线运动可以增强系统惯性器件零偏、安装误差角及姿态的可观测性,而姿态运动则有助于对杆臂矢量的估计。
3) 全面、深刻地揭示了系统状态估计同载体机动之间的联系,为载体运动轨迹的规划和滤波器的设计提供了理论指导,同时也为惯性导航系统高精度传递对准奠定了基础。
参考文献
| [1] | KAIN J E,CLOUTIER J R.Rapid transfer alignment for tactical weapon application:AIAA-1989-3581[R].Reston:AIAA,1989:1290-1300. |
| [2] | 高伟, 奔粤阳, 李倩. 捷联惯性导航系统初始对准技术[M].北京: 国防工业出版社, 2014: 124.GAO W, BEN Y Y, LI Q. Initial alignment for strapdown inertial navigation system[M].Beijing: National Defense Industry Press, 2014: 124.(in Chinese) |
| [3] | 韩英宏, 陈万春. 新型快速传递对准方法[J].北京航空航天大学学报, 2012, 38(2): 149–152.HAN Y H, CHEN W C. New method for rapid transfer alignment[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 149–152.(in Chinese) |
| [4] | 解春明, 赵剡, 王纪南. 传递对准中机翼弹性变形建模与滤波处理[J].北京航空航天大学学报, 2010, 36(8): 931–935.XIE C M, ZHAO Y, WANG J N. Modeling of wing flexure and filtering solution in transfer alignment[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8): 931–935.(in Chinese) |
| [5] | 高伟, 张亚, 孙骞, 等. 传递对准中杆臂效应的误差分析与补偿[J].仪器仪表学报, 2013, 34(3): 559–565.GAO W, ZHANG Y, SUN Q, et al. Error analysis and compensation for lever-arm effect in transfer alignment[J].Chinese Journal of Scientific Instrument, 2013, 34(3): 559–565.(in Chinese) |
| [6] | LYOU J, LIM Y C. Transfer alignment considering measurement time delay and ship body flexure[J].Journal of Mechanical Science and Technology, 2009, 23: 195–203.DOI:10.1007/s12206-008-0821-y |
| [7] | 刘红光, 陈志刚, 陈刚. 基准信息时间延迟对速度匹配传递对准性能的影响分析[J].中国惯性技术学报, 2012, 20(5): 544–551.LIU H G, CHEN Z G, CHEN G. Time-delay's effect on velocity matching transfer alignment[J].Journal of Chinese Inertial Technology, 2012, 20(5): 544–551.(in Chinese) |
| [8] | 陈雨, 赵剡, 李群生, 等. 快速传递对准中主惯导信息滞后补偿方法[J].中国惯性技术学报, 2013, 21(5): 576–580.CHEN Y, ZHAO Y, LI Q S, et al. Compensation method for master inertial navigation system information delay in rapid transfer alignment[J].Journal of Chinese Inertial Technology, 2013, 21(5): 576–580.(in Chinese) |
| [9] | 江云, 鲁浩, 位晓峰. 弹载捷联惯导系统空中传递对准精度评估[J].弹箭与制导学报, 2012, 32(1): 21–26.JIANG Y, LU H, WEI X F. Accuracy estimation for missile-borne strapdown inertial navigation systems during in-flight transfer alignment[J].Journal of Projectiles,Rockets,Missiles and Guidance, 2012, 32(1): 21–26.(in Chinese) |
| [10] | 解春明, 赵剡, 邓俊云. 一种改进的自适应平方根传递对准滤波算法[J].系统工程与电子技术, 2011, 33(3): 622–626.XIE C M, ZHAO Y, DENG J Y. Improved adaptive square root filtering algorithm for transfer alignment[J].Systems Engineering and Electronics, 2011, 33(3): 622–626.(in Chinese) |
| [11] | HAM F M, BAR-ITZHACK I Y. Observability,eigenvalues,and Kalman filtering[J].IEEE Transaction on Aerospace and Electronic Systems, 1983, 19(2): 269–273. |
| [12] | KRELNDLER E, SARACHIK B E. On the concepts of controllability and observability of linear systems[J].IEEE Transactions on Automatic Control, 1964, AC-9(2): 129–136. |
| [13] | 房建成, 周锐, 祝世平. 捷联惯导系统动基座对准的可观测性分析[J].北京航空航天大学学报, 1999, 25(6): 714–719.FANG J C, ZHOU R, ZHU S P. Observability analysis of strapdown inertial navigation system on moving base[J].Journal of Beijing University of Aeronautics and Astronautics, 1999, 25(6): 714–719.(in Chinese) |
| [14] | 秦峰, 战兴群, 湛雷, 等. 机载武器传递对准可观测性分析[J].北京航空航天大学学报, 2012, 38(9): 1134–1138.QIN F, ZHAN X Q, ZHAN L, et al. Observability analysis of transfer alignment of airborne weapons[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(9): 1134–1138.(in Chinese) |
| [15] | GOSHEN-MESKIN D, BAR-ITZHACK I Y. Observability analysis of piece-wise constant systems-part I:Theory[J].IEEE Transaction on Aerospace and Electronic Systems, 1992, 28(4): 1056–1067.DOI:10.1109/7.165367 |
| [16] | GOSHEN-MESKIN D, BAR-ITZHACK I Y. Observability analysis of piece-wise constant systems-part Ⅱ:Application to inertial navigation in-flight alignment[J].IEEE Transaction on Aerospace and Electronic Systems, 1992, 28(4): 1068–1075.DOI:10.1109/7.165368 |
| [17] | 汤勇刚.载波相位时间差分/捷联惯导组合导航方法研究[D].长沙:国防科技大学,2007:9-11.TANG Y G.Research on time-differenced carrier phase/SINS integrated navigation approach[D].Changsha:National University of Defense Technology,2007:9-11(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-2008098447.htm |
| [18] | WEI M, SCHWARZ K P. A strapdown inertial algorithm using an earth-fixed cartesian frame[J].Journal of Institute of Navigation, 1990, 37(2): 153–167.DOI:10.1002/navi.1990.37.issue-2 |
| [19] | CHEN C T. Linear system theory and design[M].3rd edNew York: Oxford University Pres, 1999. |
| [20] | BLACK H D. A passive system for determining the attitude of a satellite[J].AIAA Journal of Guidance,Control,and Dynamics, 1964, 2(7): 1350–1351. |
| [21] | SHUSTER M D, OH S D. Three-axis attitude determination from vector observations[J].AIAA Journal of Guidance,Control,and Dynamics, 1981, 4(1): 70–77.DOI:10.2514/3.19717 |
