对EIDI系统的研究,可分为电动力学研究、结构动力学研究和应用试验研究等方向。在结构动力学方面,主要研究系统结构对脉冲力的动力响应特性,如加速度、应变等。在脉冲力作用下,蒙皮的真实响应是沿三维空间分布且随时间变化的。Bernhart和Gien[6]采用Love-Timoshenko运动关系式建立了闭合的状态方程组。该方法考虑了横向剪切力的合成以及纵向惯性对于结构的影响,能够以较高精度预估蒙皮的响应能力。然而,真实的EIDI系统具有极为复杂的边界条件,其中绝大多数无法利用此方法直接获得精确解。因此该方法仅具有理论分析的价值,无法处理实际问题。
随着计算机技术的不断发展,采用有限元方法仿真求解结构动力学问题已成为当前的主要研究手段。Zumwalt[7]率先对铝质矩形平板在电脉冲作用下的结构响应展开研究,获得了线圈附近法向脉冲力的分布形式;此外,计算了铝板受上述脉冲力作用下的动态响应(应力和加速度随时间的变化),与实验情况进行对比,计算得到的正加速度峰值比实验值小12%,应力最大值比实验值小5%。
Gien[8]采用有限元模型研究理想半圆柱前缘结构在脉冲力作用下的结构变形。为了验证模型的正确性,首先在简单边界条件下对比模型结果与闭合状态方程的精确解。结果显示,对于正加速度的峰值二者误差约为7%,负加速度峰值误差约为4%,从而验证了模型的正确性。在此基础上,对半圆柱试验结果与该有限元方法的计算结果进行对比,发现计算与试验的误差约为7%。
Khatkhate等[3]采用MSC/NASTRAN有限元软件,对铝质蒙皮和积冰层建立模型,重点研究了冰层与蒙皮之间的剪切应力。同时,将计算结果与NASA Lewis研究中心开展的一系列针对EIDI系统的冰风洞试验结果进行对比,验证了该方法可用来预测除冰区域。Scavuzzo和Chu[9]在此基础上进行了改进,考虑了蒙皮振动时的阻尼现象。他们的计算结果显示,蒙皮与冰层之间的剪切应力在线圈附近较大,从脉冲位置处沿弦向迅速衰减。
Labeas等[10]在前人研究基础上,利用ANSYS有限元仿真软件对EIDI系统的除冰过程进行了仿真研究,分析了冰层厚度、线圈位置、线圈数、脉冲振幅和前缘曲率半径对除冰效果的影响。
国内李清英等[11-12]搭建了包括电路系统、除冰实验机架与结除冰环境实验舱的EIDI系统实验台,完成了脉冲放电电路的性能测试,同时也完成了振动实验如加速度、位移、模态实验,进行了EIDI实验。张文杰等[13]研究了冰层失效的范围,运用动力学分析了冰-铝板界面之间的应力状态。
本文采用线圈和金属平板组成的电脉冲系统作为EIDI结构动力学模型的研究对象,使用商业有限元软件MSC/NASTRAN,对实验对象进行固有特性(模态与频率)与时域响应分析,并利用实验数据进行对比和验证,最后重点研究了基于模型的EIDI系统结构动力学特性,蒙皮表面应变与位移随时间变化的规律及最大应变和位移在空间的分布规律。
1 研究方法 1.1 有限元建模 本文选用一块长方形铝板作为飞机蒙皮的简化计算/实验模型,如图 1所示,铝板长300 mm、宽200 mm、厚度2.5 mm。4个边角及长边中点位置共有6个直径为10 mm的固定圆孔,实验中通过螺栓固定。
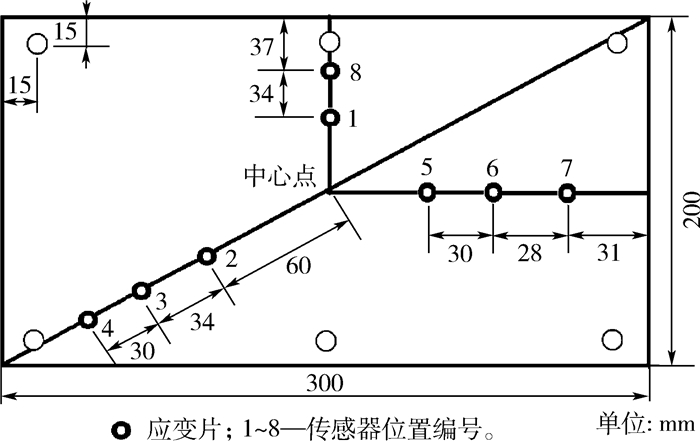 |
| 图 1 机翼蒙皮简化模型 Fig. 1 Simplified model of wing skin |
| 图选项 |
利用同轴双圆环电流电磁理论建立了EIDI电动力学数学模型,数值求解获得脉冲载荷在时间域和空间域上的分布。脉冲力F和通电线圈电流I随放电时间t变化的示例见图 2(a); 不同时刻,脉冲力F(r)沿线圈半径方向r分布见图 2(b)(r0为线圈半径),本文所使用的EIDI电动力学数学模型详见文献[14]。
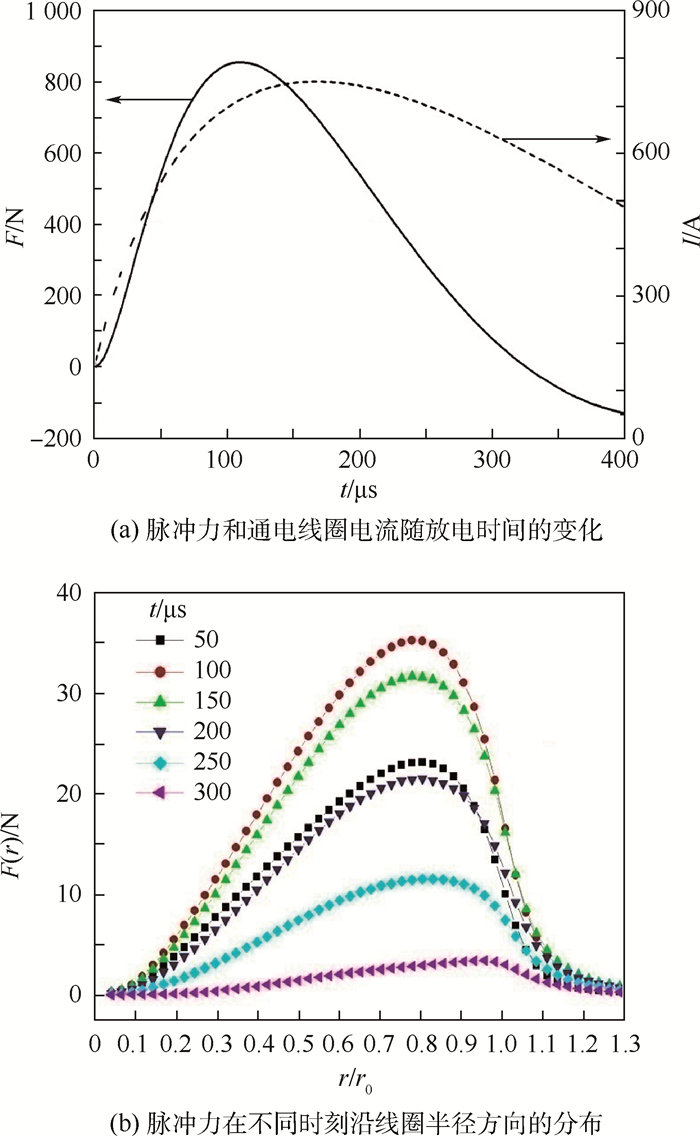 |
| 图 2 脉冲载荷的时空的分布 Fig. 2 Impulse load distribution in space and time |
| 图选项 |
将图 2分析获得的脉冲载荷的作用区域简化为一个受力中心点与平板中心同轴的圆形。受力区域的直径为63.5 mm,在整个受力区内,沿半径方向等间距划分为10个同心的圆环。假定在每一个圆环内,所受的力是平均作用在各圆环面积上的。在有限元模拟中,以压强方式进行载荷加载。
本文有限元建模采用平面模型。4个边角处的圆孔相对于整个平板的尺寸不可忽略,因此有限元建模时必须保留其存在。为了方便载荷加载,在平板的中心建立了10个同心圆环。在网格划分的时候,将圆环之间共用的结点重合。模型材料为硬铝,弹性模量为70 GPa,泊松比为0.33,密度为2 700 kg/m3。通过与实验数据的对比,将结构阻尼系数设置为0.1。模型的约束方式和载荷加载区域如图 3所示。考虑到实际物理模型是通过埋螺帽固定平板的4个圆孔,在有限元模型中,约束方式是固定圆孔边上的结点的x、y、z 3个方向的位移Ux、Uy、Uz。
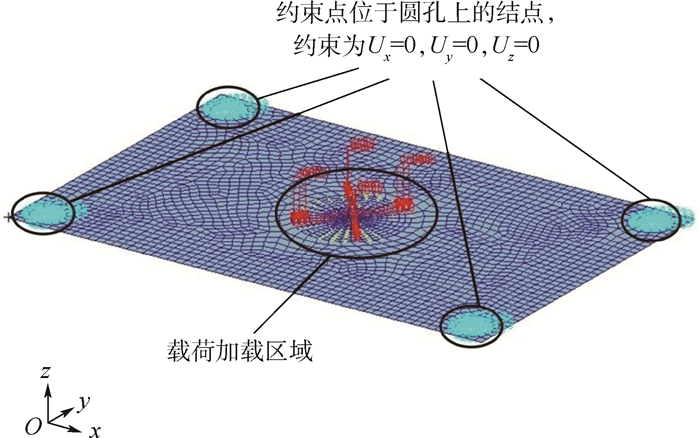 |
| 图 3 模型的约束方式和载荷加载区域 Fig. 3 Model constraint condition and load adding region |
| 图选项 |
1.2 实验方法与设备 为验证有限元计算的可靠性,本文还在已有EIDI实验台[15]上开展了铝板结构响应的实验测量,测量内容包括铝板表面应变与位移。实验件与计算模型相同,电脉冲发生装置的充电电压实验在600~800 V范围内可调,充电电容在200~400 μF范围内可调,铝板与线圈间距为2.5 mm。在图 1所标示的1~8号测点位置粘贴应变片。EIDI实验台与应变测量系统见图 4。位移测量采用激光非接触测试系统。
 |
| 图 4 EIDI实验台与应变测量系统 Fig. 4 EIDI experimental platform and strain measurement system |
| 图选项 |
2 结果与分析 2.1 模态分析 为了了解模型的振动以哪阶模态为主,首先对有限元模型进行模态分析,得出模型的固有频率。表 1给出了模型的固有频率。
表 1 不同模态阶数下模型的固有频率 Table 1 Natural frequency under different modes order
| 模态阶数 | 固有频率/Hz |
| 1 | 141.23 |
| 2 | 231.31 |
| 3 | 356.15 |
| 4 | 403.56 |
| 5 | 561.62 |
| 6 | 568.82 |
| 7 | 584.74 |
| 8 | 909.04 |
| 9 | 940.82 |
| 10 | 976.91 |
| 11 | 1 241.5 |
| 12 | 1 596.4 |
表选项
采用模态叠加法对模型进行瞬态响应分析,得出中心点的位移如图 5(a)所示。最大位移为1.619 mm,发生在时间t=2.39×10-3 s。图 5(b)给出了中心点位移数据的频谱分析。可以看出,中心点的位移主要以149.92 Hz以及599.7 Hz的振动为主。对比模型的固有频率可知,模型受到冲击载荷作用下,主要以第1阶模态和第7阶模态振动为主。
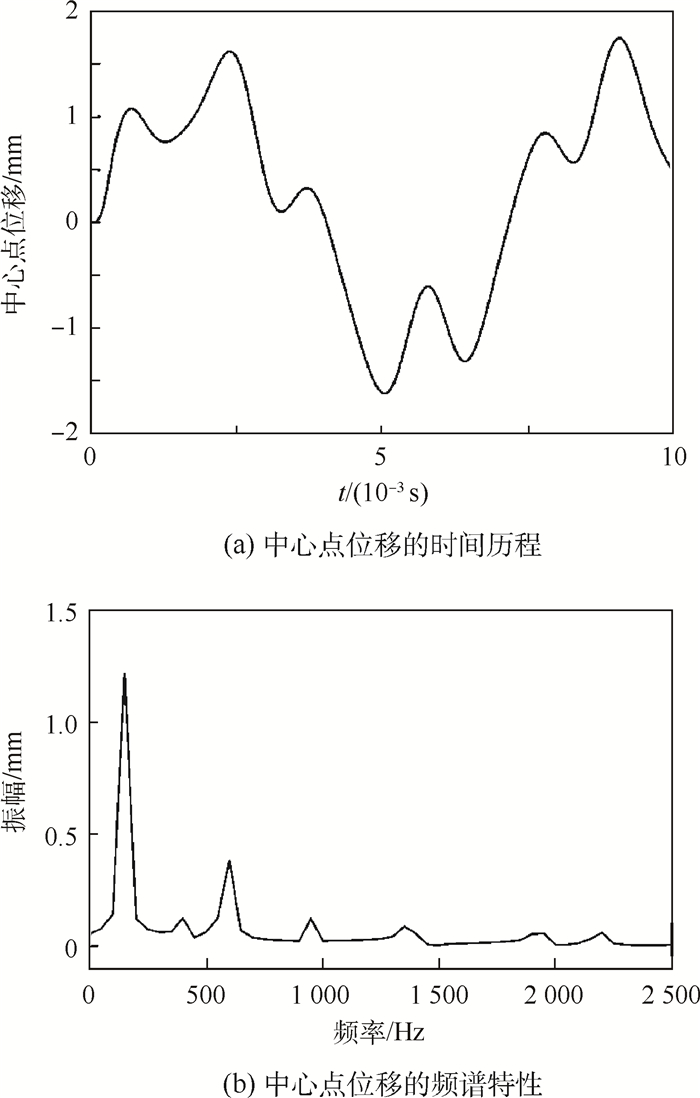 |
| 图 5 模型中心点的瞬态响应 Fig. 5 Transient response of model centroid |
| 图选项 |
2.2 实验验证 根据仿真模型,可求解获得蒙皮表面任意位置处在整个脉冲过程中的应变ε。为了验证仿真结果的正确性,将其与实验测量的结果进行对比。图 6对比了图 1中5号测点处实验测量与有限元仿真所获得的应变的时间历程。如图 6所示,在实验参数范围内,仿真模型能够准确预测出应变峰值及达到峰值的时间。在峰值之后的过程中,仿真结果与实验数据的变化趋势基本相同。但仿真分析的数值普遍低于实验,其原因可能是有限元模型中结构振动的阻尼特性设置偏大,导致蒙皮在经过第1次振动后,振动幅度快速降低。
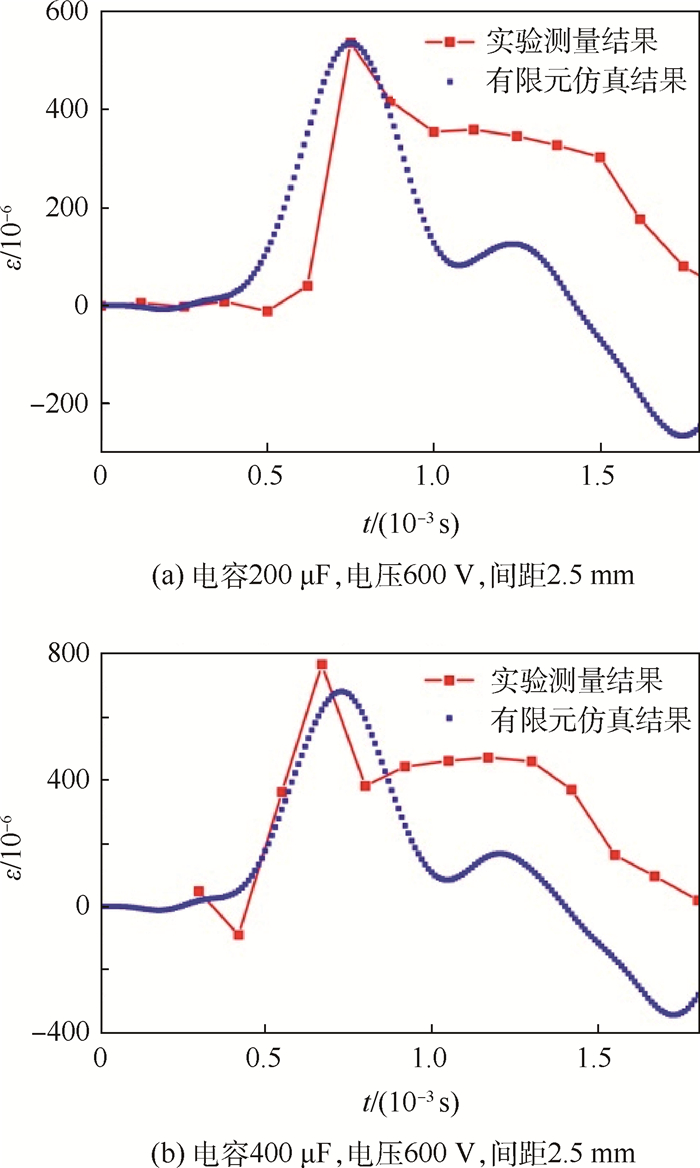 |
| 图 6 5号测点处应变的时间历程 Fig. 6 Time histories of strain on No.5 station |
| 图选项 |
此外,还将模型中心点处沿外法线方向的位移进行了对比验证,如图 7所示。仿真结果和实验数据的中心点位移时间历程几乎相同,尤其是峰值(或谷值)出现的时刻以及幅值能够较好的匹配。综上,仿真模型的计算结果与实验测量结果在应变率与法向位移两方面均能较好吻合,由此验证了本文有限元仿真的可靠性。
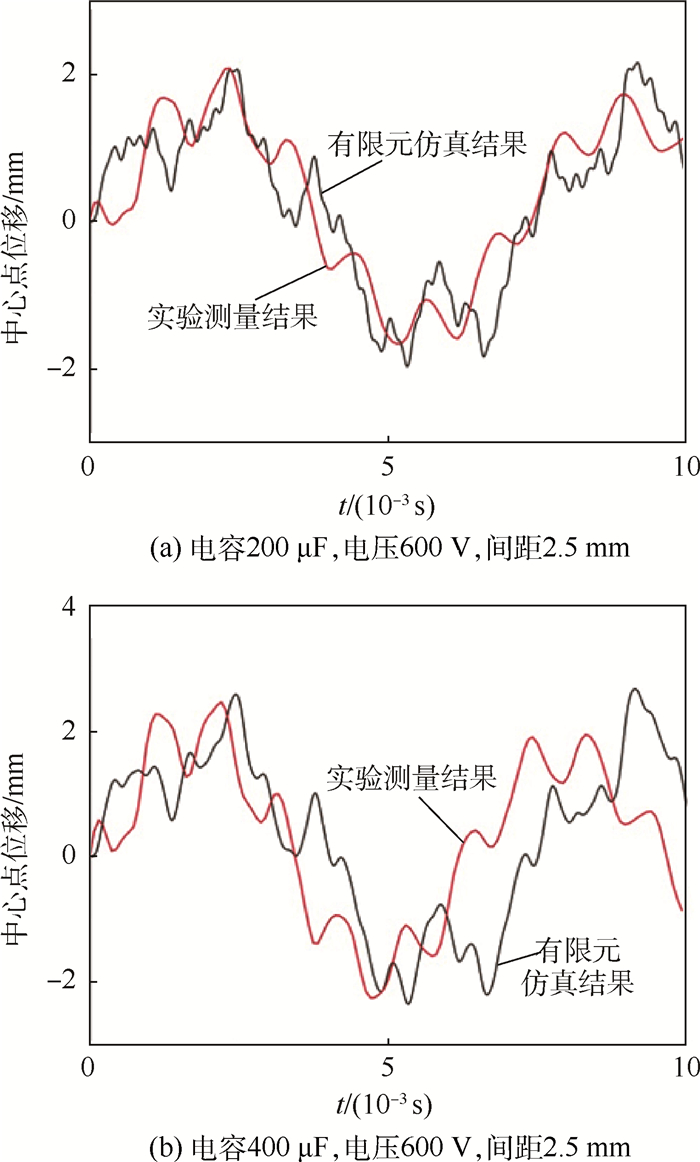 |
| 图 7 模型中心点位移的时间历程 Fig. 7 Time histories of displacement of model centroid |
| 图选项 |
2.3 最大应变和位移的空间分布 最大位移(或应变),是指在一个电脉冲信号周期内蒙皮表明所达到的最大变化值zmax。该参数是一个与时间无关的物理量,仅取决于位置点坐标(x, y),即zmax=f(x, y),便于理解蒙皮表面的结构变形特性。
图 8给出用有限元仿真得到的最大位移和最大应变在蒙皮表面的分布(EIDI系统参数:电容200 μF、电压600 V、间距2.5 mm)。此工况下,脉冲力的最大值为730 N。如图 8所示,最大位移的分布特性近似“马鞍型”。此外,在线圈对应位置处的应变较大,且沿半径方向逐步递减,而在长边处应变再次增大。这是由边界条件决定的:4个顶点固定的约束条件,决定了在较长的边界上将会产生较大的变形。在图 8(b)中,4个固定点附近的应变远大于平板其他位置。如果不考虑这些固定点,则线圈对应位置处、靠近y轴与蒙皮交汇处、靠近x轴与蒙皮交汇处的地方,应变较大。
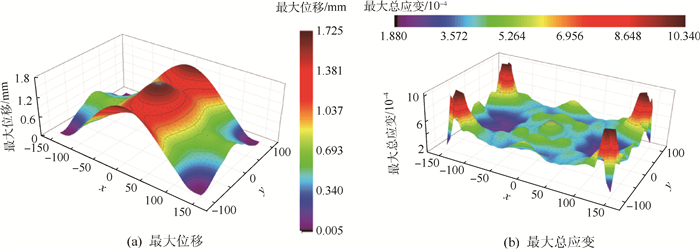 |
| 图 8 蒙皮表面在1个电脉冲周期内的最大响应(EIDI系统参数:电容200 μF、电压600 V、间距2.5 mm) Fig. 8 Maximum skin response within one electro-impulse period (EIDI system parameters: capacitance equals to 200 μF, voltage equals to 600 V, spacing equals to 2.5 mm) |
| 图选项 |
进一步的仿真结果表明,增大EIDI系统参数至电容400 μF、电压700 V,脉冲力的峰值将增大至1 800 N。此工况下,最大应变、最大位移的数值(如图 9所示)均大于图 8所示工况,最大位移(见图 9(a))在蒙皮表面的分布规律与图 8(a)无异。但线圈对应位置处的最大应变明显高于其他位置的结果,甚至高于固定螺栓位置。导致这一结果的原因,主要是脉冲力的绝对值改变了蒙皮表面的振动特性,此外,脉冲力的作用时间也发现了显著改变。在该工况下,蒙皮的结构变形量得到显著提升,有利于除冰效果;另一方面,固定位置处的变形量反而减小,避免了疲劳损伤。
 |
| 图 9 蒙皮表面在1个电脉冲周期内的最大响应(EIDI系统参数:电容400 μF、电压700 V、间距2.5 mm) Fig. 9 Maximum skin response within one electro-impulse period(EIDI system parameters: capacitance equals to 400 μF, voltage equals to 700 V, spacing equals to 2.5 mm) |
| 图选项 |
3 结论 本文基于有限元分析软件MSC/NASTRAN,建立了一套针对典型平板-线圈结构的EIDI系统结构动力学仿真模型。模型计算的应变和位移结果与实验测量数据吻合较好,模型的正确性得以验证。
根据有限元仿真结果,提出了最大应变和最大位移的概念,分析了这2个参数在蒙皮表面的分布规律和特性:
1)本文给定的边界条件下,最大位移的分布特性近似“马鞍型”。此外,在线圈对应位置处的应较大,且沿半径方向逐步递减,而在长边处应变再次增大。
2)电容和电压由200 μF和600 V提升至400 μF和700V后,脉冲力峰值增大,且振动特性发生变化。一方面使得结构变形量显著提升,另一方面削弱了固定位置处的应变。
本文研究结果为后续除冰准则关系的建立提供了数据支撑。
参考文献
| [1] | 钟长生, 洪冠新. 飞机翼面结冰对飞行特性影响的研究[J].航空科学技术, 2004(3): 32–34.ZHONG C S, HONG G X. Review about effects of lifting surface icing on aircraft flight characteristics[J].Aeronautical Science & Technology, 2004(3): 32–34.(in Chinese) |
| [2] | LYNCH F T, KHODADOUST A. Effects of ice accretions on aircraft aerodynamics[J].Progress in Aerospace Sciences, 2001, 37(8): 669–767.DOI:10.1016/S0376-0421(01)00018-5 |
| [3] | KHATKHATE A A, SCAVUZZO R J, CHU M L.A finite element study of the EIDI system[C]//Proceedings of the 26th AIAA Aerospace Sciences Meeting.Reston:AIAA, 1988:1-8. |
| [4] | THOMAS S K, CASSONI R P, MACARTHUR C D. Aircraft anti-icing and de-icing techniques and modeling[J].Journal of Aircraft, 1996, 33(5): 841–854.DOI:10.2514/3.47027 |
| [5] | 周莉, 徐浩军, 龚胜科. 飞机结冰特性及防除冰技术研究[J].中国安全科学学报, 2010, 20(6): 105–110.ZHOU L, XU H J, GONG S K. Research of aircraft icing characteristics and anti-icing and de-icing technology[J].China Safety Science Journal, 2010, 20(6): 105–110.(in Chinese) |
| [6] | BERNHART W D, GIEN P H.A structural dynamics investigation related to EIDI applications:AIAA-1986-0550[R].Reston:AIAA, 1986. |
| [7] | ZUMWALT G W.Analysis and tests for design of an electro-impulse de-icing system:NASA/CR-1987-174919[R].Washington, D.C.:NASA, 1987. |
| [8] | GIEN P H. Free vibration and transient analysis of a semi-cylinder subjected to electro-impulse de-icing forces[M].Wichita, Kansas: Wichita State University, 1985: 19-37. |
| [9] | SCAVUZZO R J, CHU M L. Finite element studies of the electro impulse de-icing system[J].Journal of Aircraft, 1990, 27(9): 757–763.DOI:10.2514/3.45935 |
| [10] | LABEAS G N, DIAMANTAKOS I D, SUNARIC M M. Simulation of the electroimpulse de-icing process of aircraft wings[J].Journal of Aircraft, 2006, 43(6): 1876–1885.DOI:10.2514/1.21321 |
| [11] | 李清英, 朱春玲, 白天. 电脉冲除冰系统的除冰实验与数值模拟[J].航空动力学报, 2012, 27(2): 350–356.LI Q Y, ZHU C L, BAI T. De-icing experiment and numerical simulation of the electro-impulse de-icing system[J].Journal of Aerospace Power, 2012, 27(2): 350–356.(in Chinese) |
| [12] | 李清英, 朱春玲, 白天. 电脉冲除冰系统激励简化与影响因素[J].航空学报, 2012, 25(8): 1384–1393.LI Q Y, ZHU C L, BAI T. Simplification of de-icing excitation and influential factors of the electro-impulse de-icing system[J].Acta Aeronautica et Astronautica Sinica, 2012, 25(8): 1384–1393.(in Chinese) |
| [13] | 张文杰, 董文俊, 王斌团. 电脉冲除冰仿真冰层松脱准则研究[J].计算机工程与应用, 2012, 48(3): 232–233.ZHANG W J, DONG W J, WANG B T. Study on de-icing criterion of electro-impulse de-icing simulation[J].Computer Engineering and Applications, 2012, 48(3): 232–233.(in Chinese) |
| [14] | 李广超, 何江, 林贵平. 电脉冲除冰(EIDI)系统电动力学模型分析[J].航空动力学报, 2011, 26(1): 54–59.LI G C, HE J, LIN G P. Research of electrodynamics in electro-impulse de-icing (EIDI) system[J].Journal of Aerospace Power, 2011, 26(1): 54–59.(in Chinese) |
| [15] | 李广超, 何江, 林贵平. 电脉冲除冰(EIDI)技术研究[J].航空动力学报, 2011, 26(8): 1718–1735.LI G C, HE J, LIN G P. Electro-impulse de-icing(EIDI) technology study[J].Journal of Aerospace Power, 2011, 26(8): 1718–1735.(in Chinese) |
