目前跳跃机器人的腿部结构形式主要有3种:串联结构、并联/混联结构和简化结构。哺乳动物或昆虫的腿都是由大腿(腿节)、小腿(胫节)和足(跗节)组成,因此腿部结构是典型的多自由度串联机构。为实现仿生特性,许多跳跃机器人的腿部结构都采用了近似仿生式的设计原则。例如模仿狗的后肢而研制的跳跃机器人Kenken[5-6]和跳跃机器人Mowgli[7]的腿部结构都是由大腿杆、小腿杆和足部连杆三部分组成,是典型的仿生串联结构。除了仿生跳跃机器人外,仿生串联腿的结构设计还应用在部分多足步行机器人上,例如,仿生多足机器人KOLT[8-10]、BigDog[11]、仿猎豹机器人[12]的腿部结构形式也都是仿生串联结构。串联腿能够较好模拟生物的运动形态,再现生物的运动特征,但是当机器人运动的速度较快、且自身质量较大时,串联腿的刚度和运动精度都有所下降,限制了机器人的运动功能。相对于串联机构,并联机构具有刚度大、承载能力强、误差小及精度高等一系列优点[13],因此也被用于机器人腿部的结构设计。例如,燕山大学研制的四足/两足可重组步行机器人[14]和密西根州立大学研制的连续跳跃机器人[15]都具有并联的腿部结构形式。同时,为兼备串联机构和并联机构的优点,上海交通大学还对3种混联腿进行了分析比较,并将该机构用于多足步行机器人的研制[16]。然而,并联/混联腿的结构形式复杂,增加了机器人的自身重量及控制的难度。除了上述两种腿部结构形式外,部分科研机构还对诸如“C型腿”这样的简化腿部结构进行了研究,其通过材料的柔性变形进行储能和缓冲,也具有较好的缓冲效果[17-18]。
上述科研单位虽然对仿生机器人的腿部结构进行了研究,但研究内容多集中在跳跃机器人的起跳过程及多足步行机器人的行走减震,并未针对腿部结构在着陆缓冲过程中所起到的作用进行详细的分析,且没有对不同缓冲腿的性能进行分析比较。为了实现仿生蝗虫跳跃机器人腿部运动灵活、储能效率高的特点,在原有仿生式腿部结构的基础上,设计了一种新型缓冲腿,并对缓冲性能进行了详细的分析。结果表明,相对于原有仿生串联缓冲腿,新型缓冲腿具有更好的缓冲性能和储能能力,这为仿生蝗虫跳跃机器人进一步的研制提供了的基础。
1 缓冲腿结构设计 蝗虫着陆瞬间如图 1所示,蝗虫的前腿和中腿先着地,然后向下缓冲直到速度为零。在缓冲过程中,蝗虫腿部起到了重要的缓冲作用,因此有必要对仿生跳跃机器人腿部结构进行详细的设计和分析,从而实现仿生机器人良好的缓冲性能。
 |
| 图 1 蝗虫着陆示意图 Fig. 1 Schematic diagram of locust landing |
| 图选项 |
蝗虫腿部结构如图 2所示,其可简化认为是由腿节、胫节和跗节组成,相邻两部分通过关节相连接。蝗虫腿部主要通过肌肉的收缩来实现能量的吸收,其肌肉主要集中在腿节与躯干之间及胫节与腿节之间。
 |
| 图 2 蝗虫腿部结构示意图 Fig. 2 Schematic diagram of locust's leg structure |
| 图选项 |
根据仿生设计思路,常见的仿生串联缓冲腿如图 3所示,其与蝗虫腿部结构近似相同。其中,躯干与腿节之间可简化为一个胡克铰,胫节和腿节之间可视为一个转动副,胫节和跗节之间同样可简化为一个转动副。为模拟缓冲过程中腿部肌肉的储能过程,弹簧1和弹簧2分别用来模拟腿部肌肉,限制腿部髋关节和膝关节的运动,从而实现储能及缓冲效果[19]。为在不改变腿部灵活性的基础上实现更大的储能能力,在原有仿生串联缓冲腿的基础上增加了辅助缓冲的可伸缩分支,该分支的一端通过胡克铰U2与躯干在D点相连接,另一端通过铰链R3与胫节在F点相连接,分支可伸缩部分通过弹簧3限制其相对运动。其中胡克铰U1和U2竖直方向的轴线重合,具体结构如图 4所示。由于蝗虫前4条腿结构参数相差不大,因此可认为仿生蝗虫机器人的前腿和中腿完全相同。
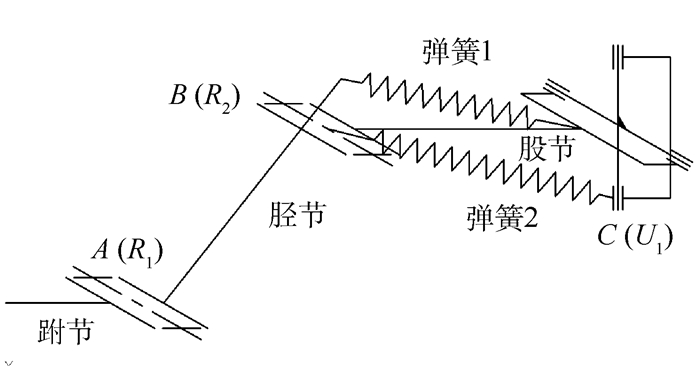 |
| 图 3 仿生串联缓冲腿结构示意图 Fig. 3 Structural diagram of bionic series buffering leg |
| 图选项 |
 |
| 图 4 新型缓冲腿结构示意图 Fig. 4 Structural diagram of new buffering leg |
| 图选项 |
固定坐标系的原点与转动副R1中心重合,z0轴与转动副轴线重合,y0轴竖直向上,x0轴方向可通过右手定则得到。各个运动关节的坐标系如图 4所示,其坐标原点分别位于各个关节中心处。在初始状态下,各坐标系的轴线方向与固定坐标系相同。记胫节连杆AB长度为l1,连杆BC长度为l2,连接点AF的长度为l3,弹簧1与连杆AB的连接点到B点距离为l4,弹簧2在躯干连接点到C点距离为l5,CD距离为l6,DE距离为l7。
2 力学性能分析 2.1 运动学分析 通过对新型缓冲腿进行运动学分析,可求出蝗虫在缓冲过程中的关节角度及弹簧力的大小,为力学性能分析提供依据。
为了分析新型缓冲腿是否改变了原有仿生串联缓冲腿的灵活性,首先需要对其自由度进行分析。对于原有仿生串联缓冲腿,其自由度数目为4,结构限制了机器人躯干部分绕x0轴方向的转动和沿z0轴方向的移动。而对于辅助分支DF,其运动旋量可表示为
 | (1) |
该运动旋量的反旋量可表示为
 | (2) |
从式(2)中可以看出,辅助分支DF对躯干的约束运动与原有仿生串联缓冲腿对躯干的约束相同,仍然是限制了机器人躯干部分绕x0轴方向的转动和沿z0轴方向的移动。因此该辅助分支为冗余约束,对腿部结构的自由度没有影响,新型缓冲腿的设计保证了腿部结构具有较好的灵活性。此外,根据文献[1]可知,无论是机器人前4条腿同时着地或者6条腿同时着地,机器人的躯干只能沿y0轴方向进行运动,躯干的自由度为1。因此,本文仅考虑向下的缓冲运动,不考虑水平方向的速度变化。
由于辅助分支对结构自由度没有影响,因此首先对不包含辅助分支的腿部结构进行运动学分析。由于CD杆在地面上的投影点O是固定不变的,根据位置关系建立闭环ABCO的矢量方程为
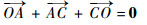 | (3) |
此时转动副R1、R2及胡克铰U1的转动角度可根据文献[19]求得。
在求得R1、R2和U1各个关节转角后,在△FBD中,便可求得辅助分支移动副的移动距离,可表示为
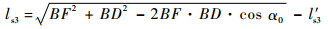 | (4) |
式中:l′s3为弹簧, 3的初始长度; α0为BF与BD之间的夹角。由此便完成了对新型缓冲腿的运动学分析。
2.2 支撑力分析 通过对腿部结构进行受力分析,可求得地面对新型缓冲腿的支撑力,由此作为判断缓冲性能的主要参数之一。
记连杆AB为连杆1,连杆BC为连杆2,躯干为连杆3。对于第i连杆,力和力矩平衡方程为
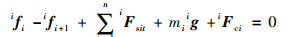 | (5) |
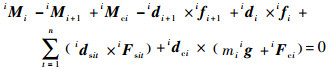 | (6) |
式中:ifi和ifi+1分别为第i-1连杆和第i+1连杆对第i连杆的作用力;iMi和iMi+1分别为第i-1连杆和第i+1连杆对第i连杆的作用力矩;iFci和iMci分别为惯性力和惯性力矩; iFsit为连杆所受到的弹簧力; mi为第i连杆的质量;ig为重力加速度在第i连杆坐标系下的表示; idi+1、 idci、 idi、和 idsit为力的位置矢量; 上标i表示该作用力所处坐标系。
根据实验可知,蝗虫腿的质量相对于身体质量较小,因此在分析中忽略腿的质量,将质量集中在躯干部分。此时,对式(5)和式(6)进行简化可得
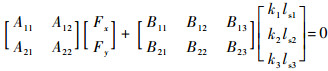 | (7) |
式中:
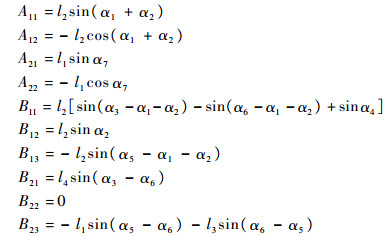 |
其中:lsi (i=1, 2, 3)为各个弹簧的变形量; ki(i=1, 2, 3)为弹簧刚度系数;α1为弹簧2与水平方向的夹角; α2为弹簧2与连杆BC的夹角; α3为弹簧1与水平方向的夹角; α4为弹簧1与连杆BC的夹角; α5为弹簧3与水平方向的夹角; α6为连杆AB与水平方向的夹角。αi可由运动学分析求得。地面对新型缓冲腿的支撑力沿x方向和y方向的分力可由式(7)得到。根据上述分析,便可求出缓冲过程中地面对腿部结构的支撑力。
2.3 等效动力学分析 仿生蝗虫机器人的缓冲过程是依靠腿部弹簧的变形进行储能。由于仿生蝗虫机器人着陆时多足同时着地(根据实验观测,前4足同时着地的情况较为常见),且每条腿的自由度数目及弹簧数目较多,因此对整个缓冲过程的描述较为复杂,缓冲过程可表示为一个复杂的微分方程。为更方便地对缓冲过程的力学性能及缓冲时间进行描述,考虑到缓冲过程中机器人躯干只有一个自由度,只能沿竖直方向运动,因此缓冲过程可简化为一个振动系统[19]。由式(7)可知,躯干所受到的恢复力是非线性的,可近似拟合为多项式函数,因此缓冲过程可等效为非线性振动系统,如图 5所示。若该多项式函数不是奇函数时,振动系统的振幅是非对称的,考虑到机器人缓冲运动主要为第1个周期时的向下缓冲运动,当振幅不对称时,无法准确地进行等效分析。因此恢复力可简化为一个奇函数:Fr=-e1x-e2x3,其中e1和e2为恢复力系数。
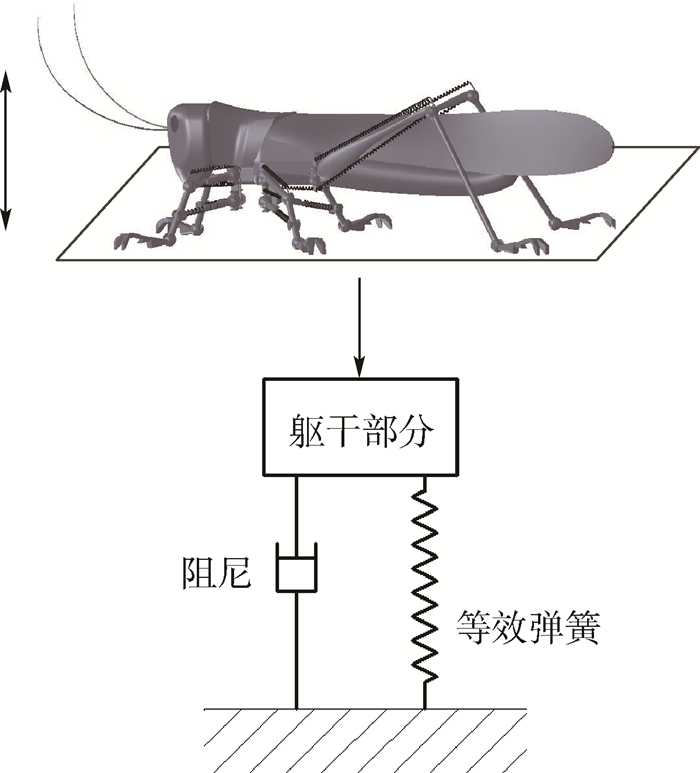 |
| 图 5 等效振动模型 Fig. 5 Equivalent vibration model |
| 图选项 |
根据上述分析,此时振动方程可表示为
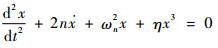 | (8) |
式中:ωn2=e1/m3,ωn为弹簧振动频率; η=e2/m3,m3为机器人的质量; 2n=r/m3,r为阻尼系数。在实际计算中为简便起见,令阻尼系数为0,根据里茨-伽辽金法[20],可以方便地求解出第1个周期中振动方程的解及振动频率为
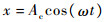 | (9) |
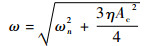 | (10) |
式中:Ac为振幅。记弹簧处于平衡位置时的变形量为δ,此时仿生蝗虫机器人从着陆初始点到缓冲速度为零所用的时间可表示为
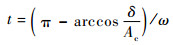 | (11) |
根据上述分析,可以方便地对蝗虫从着陆瞬间到向下缓冲直到速度为零的过程进行描述,且可以求解出缓冲的时间。
3 结构参数分析与优化 为了对蝗虫腿的缓冲性能进行分析,首先需要对结构参数进行优化,使得缓冲腿的综合性能处于最佳状态。根据式(11)可知,当着陆速度一定时,缓冲时间变化较小,因此不再进行考虑。
3.1 缓冲性能描述 根据仿生蝗虫跳跃机器人的运动过程,缓冲性能主要包括两个方面:
1) 地面支撑力。在缓冲的过程中,地面的支撑力幅值应该尽可能地小,且整个周期变化平稳,即变化的幅值和单位缓冲距离下的变化率都应在合理范围内,否则如果机器人瞬间受到较大的地面作用力,会严重影响机器人的性能。
2) 储能能力。储能能力主要分为两点:一是总储能量W,二是单位缓冲距离下的储能能力Wu。对于前者,机器人的总储能量越大,机器人所能容纳的初始速度越大,但相反的,此时机器人所受到的单位缓冲距离下的地面支撑力也越大。因此,应该综合考虑W和地面支撑力之间的关系,使得二者都在合理范围内。对于后者,如果随着缓冲距离的增大,Wu也越大,则说明该结构的储能能力更强。
3.2 结构参数分析 新型缓冲腿的结构参数主要包括各个连杆长度li (i=1, 2, …, 7)和弹簧刚度系数ki (i=1, 2, 3)。由于结构的限制,l6和l7的变化范围较小,因此将其设定为固定值。为分析方便,令连杆AB和连杆BC的总长度L (L=l1+l2)不变,则此时结构参数可表示为
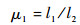 | (12) |
同样的,对于辅助分支在胫节连杆上的位置,结构参数可表示为
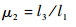 | (13) |
为了保证缓冲过程中的安全性,令仿生蝗虫机器人在着陆时前腿和中腿同时着地,且缓冲距离为最大缓冲高度一半时,机器人速度为零,此时3个弹簧刚度系数之间存在耦合关系,可表示为
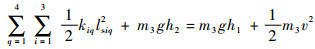 | (14) |
式中:h1为缓冲前的高度; h2为缓冲后的高度; v为初始速度; q为着陆腿的数量。根据上述分析,可变结构参数包括μ1、μ2、l4、l5以及弹簧刚度系数ki(i=1, 2)。此外,新型缓冲腿的不变结构参数如表 1所示。其中,l0为CD杆在地面上的投影点O到A点的距离。表 1中参数均为采用高速摄像机对蝗虫多次着陆缓冲过程进行观测和记录后所测量得到的平均值,以反应蝗虫的着陆特性。
表 1 不变结构参数 Table 1 Invariant structural parameters
| 参数 | m3/g | L/mm | l6/mm | l7/mm | v/(m·s-1) | h1/mm | l0/mm |
| 数值 | 2.1 | 14.5 | 3 | 5 | 0.8 | 10 | 10 |
表选项
另外,在上述可变参数中,还需要考虑两个问题:①参数对缓冲性能的影响是否明显;②参数对缓冲性能的影响趋势是否相同。若改变参数值,缓冲性能无明显变化,则该参数不再进行考虑。而若所有参数对缓冲性能影响好坏的影响趋势一致,则没有优化的必要性。以弹簧刚度系数为例,取μ1=1.4,μ2=0.35,l4=1.5 mm,l5=1.5 mm,k1、k2的变化范围为[800,1 200] N/m。此时弹簧刚度系数与缓冲性能的关系如图 6~图 8所示。从图中可以看出,弹簧刚度系数对缓冲性能有较为明显的影响且影响趋势不同,对于沿x方向的支撑力和能量吸收量W,弹簧刚度系数越大越好,而对于沿y方向的支撑力,弹簧刚度系数越小越好,这也说明了参数优化的必要性。经过分析可知,上述结构参数都能够较大幅度地影响缓冲性能且影响趋势不同,因此都在优化的考虑范围内。
 |
| 图 6 k1、k2与地面支撑力沿x方向分力之间的关系 Fig. 6 Relationship among k1, k2 and ground supporting force along x axis |
| 图选项 |
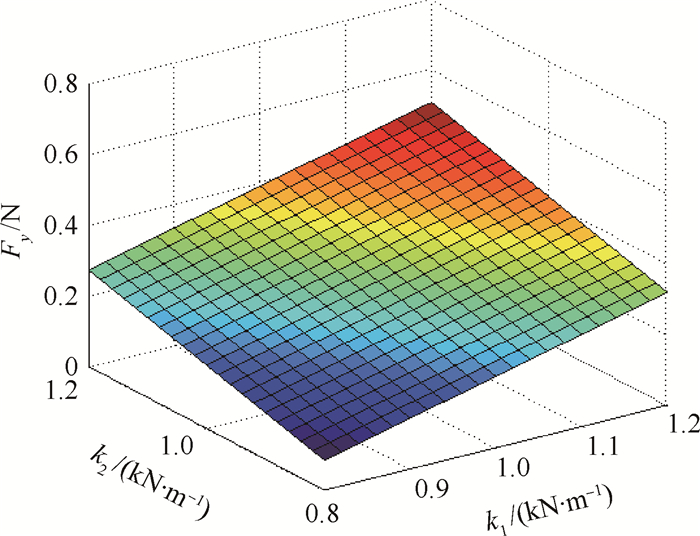 |
| 图 7 k1、k2与地面支撑力沿y方向分力之间的关系 Fig. 7 Relationship among k1, k2 and ground supporting force along y axis |
| 图选项 |
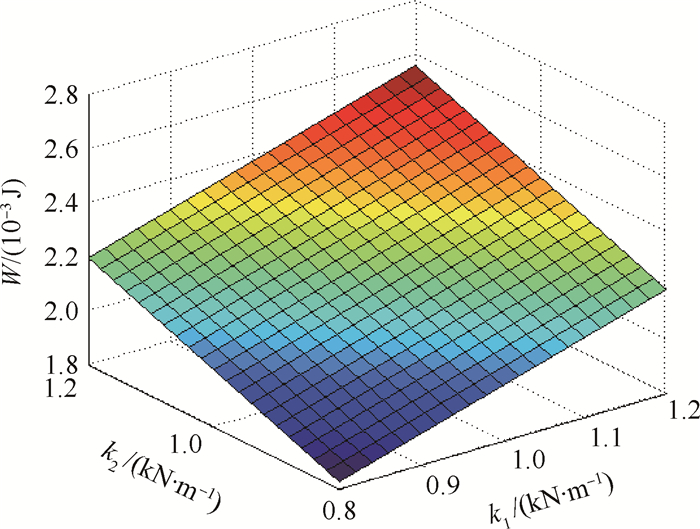 |
| 图 8 k1、k2与能量吸收量之间的关系 Fig. 8 Relationship among k1, k2 and energy absorption |
| 图选项 |
3.3 结构参数优化 在确定了优化参数后,需要进一步确定优化的目标函数。根据3.1节缓冲性能的描述,优化的目标函数可确定为
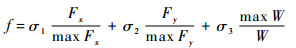 | (15) |
式中:为了进行无量纲处理,缓冲性能参数分别除以各自的最大值。σi (i=1, 2, 3)为比例系数,σ1+σ2+σ3=1。当σ1取较大值时,可使得Fx更接近最小值;当σ2取较大值时,可使得Fy更接近最小值;当σ3取较大值时,可使腿部结构吸收的总能量W更接近最大值。
此外,还需要进一步确定优化参数的约束条件。根据实际情况,约束条件如表 2所示。
表 2 结构参数的约束条件 Table 2 Constraint condition of structural parameters
| 参数 | μ1 | μ2 | l4/mm | l5/mm | k1/(N·m-1) | k2/(N·m-1) |
| 数值 | [0.6, 1.4] | [0.2, 0.5] | [0.5, 1.5] | [0.5, 1.5] | [0, 4 000] | [0, 4 000] |
表选项
4 缓冲性能分析 在优化过程中,σ1=σ2=σ3=1/3。为了防止弹簧刚度系数的差值过大而对结构的稳定性和寿命产生影响,令弹簧刚度系数之间的比值上限为5。根据结构参数优化的结果,μ1=0.8,μ2=0.35,l4=1.5 mm,l5=1.5 mm,k1=424 N/m,k2=2 110 N/m。根据式(14)计算可得k3=426.5 N/m。为了能更好地说明新型缓冲腿的缓冲性能,可将新型缓冲腿与原有仿生串联缓冲腿的性能进行比较。对于原有仿生串联缓冲腿(如图 3所示),其主要结构参数与函数优化过程可根据第3节同样的方法求得。对于原有仿生串联缓冲腿优化后的结果为:μ1=1.4,l4=1.5 mm,l5=1.5 mm,k1=1 640 N/m,k2=329.3 N/m。根据求得的结果,地面对缓冲腿的支撑力沿x0轴方向和y0轴方向的变化规律如图 9所示。图中,Model 1表示本文设计的新型缓冲腿,Model 2表示在不增加辅助分支的情况下的原有仿生串联缓冲腿。从图中可以看出,新型缓冲腿所受到的沿x0轴方向的作用力幅值大幅减小,幅值比为0.422 7 N/0.773 6 N=0.546 4,减小了45.36%;而沿y0轴方向的作用力幅值略有增大,幅值比为0.490 5 N /0.488 4 N=1.004 3,增大了0.43%。地面对缓冲腿合力的大小如图 10所示,新型缓冲腿的合力最大值为0.647 5 N,原有仿生串联缓冲腿的合力最大值为0.866 9 N。这说明了新型缓冲腿受到地面的作用力更小,而沿x0轴方向和y0轴方向的分力也都在合理范围内,因此力学性能更好。
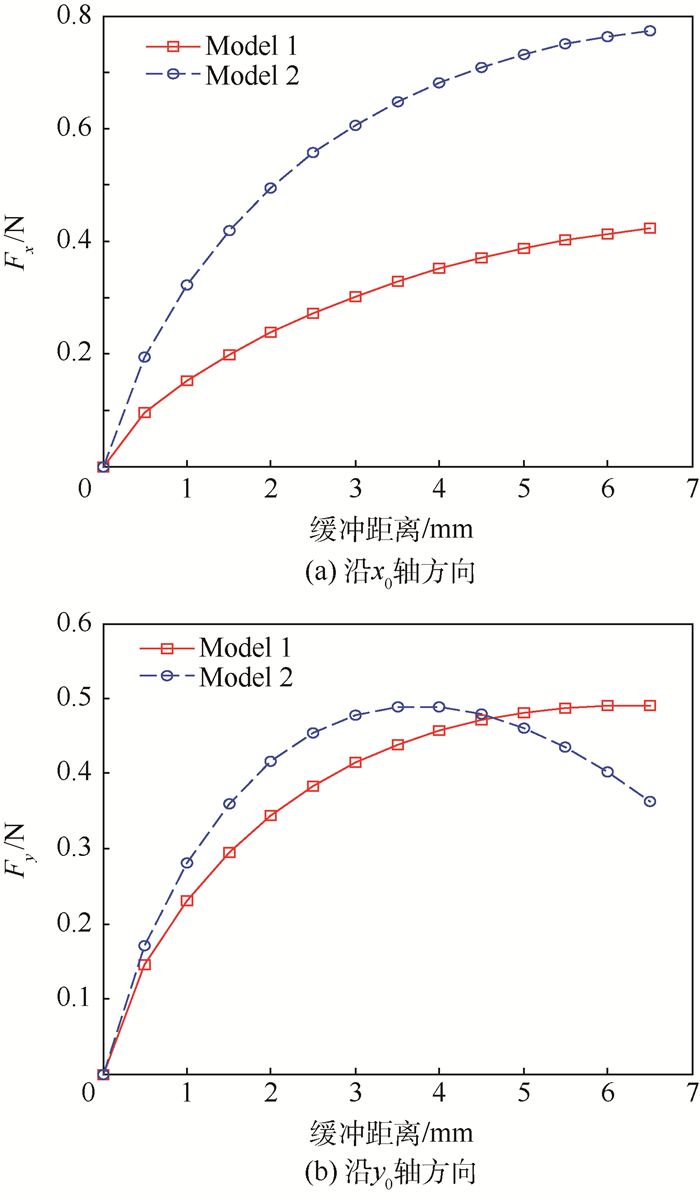 |
| 图 9 地面支撑力沿x0轴和y0轴方向的分力 Fig. 9 Ground supporting force along x0 and y0 axis |
| 图选项 |
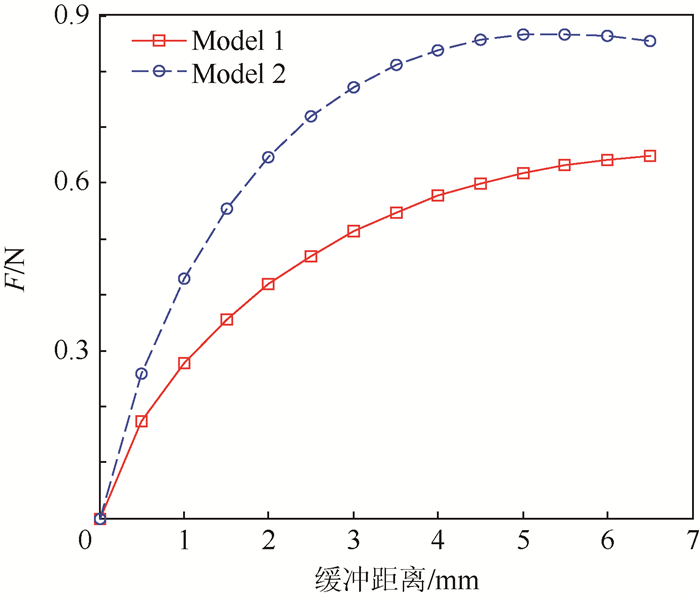 |
| 图 10 地面支撑力的合力 Fig. 10 Resultant force of ground supporting force |
| 图选项 |
新型缓冲腿能量变化规律如图 11和图 12所示。其中,图 11表示总的吸能量,根据设计原则,在缓冲距离为最大缓冲距离的一半时,吸收的能量相等。而当缓冲距离继续增大,当h2=0.5 mm时,新型缓冲腿吸收的能量明显较原有仿生串联缓冲腿吸收的能量大,幅值比为3.593×10-3 J/2.669×10-3 J=1.346 2,增大了34.6%。图 12表示单位缓冲距离的吸能量,从图中可以看出,随着缓冲距离的增大,单位缓冲距离的吸能量远大于原有仿生串联缓冲腿的吸能量。这说明新型缓冲腿具有较好的能量吸收能力。
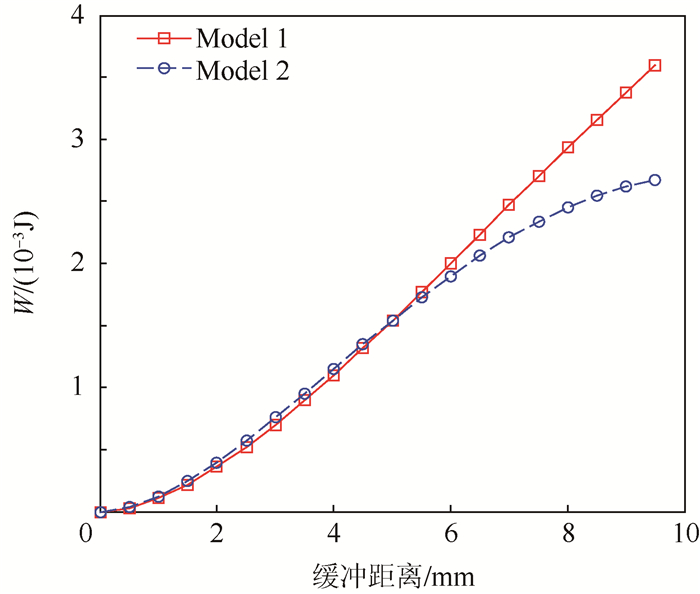 |
| 图 11 缓冲腿吸收的总能量W Fig. 11 Total energy W absorbed by buffering leg |
| 图选项 |
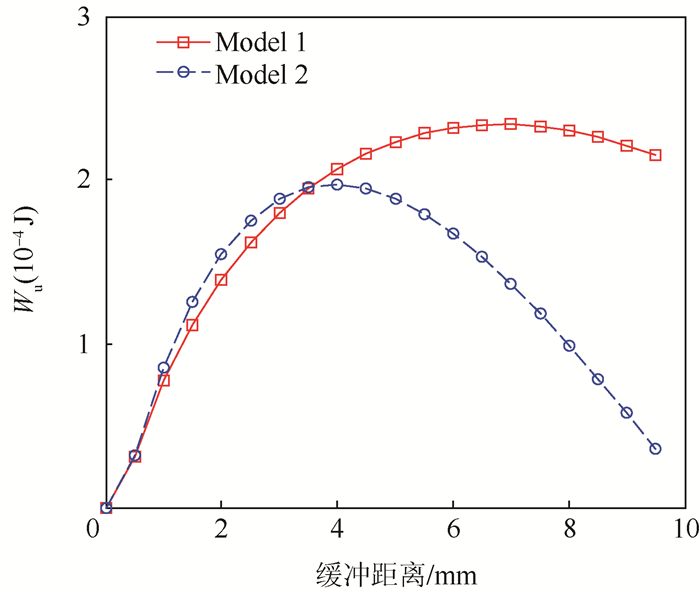 |
| 图 12 单位缓冲距离吸收的能量Wu Fig. 12 Energy Wu absorbed with unit buffer distance |
| 图选项 |
5 结论 1) 在新型缓冲腿作用下,仿生蝗虫机器人的缓冲过程可等效为一个非线性振动系统,通过对该系统进行分析,可详细描述机器人的缓冲运动。
2) 新型缓冲腿的结构参数对缓冲性能的影响各不相同,可根据性能评价原则对参数进行优化分析,使得缓冲腿综合性能处于最佳状态。
3) 相对于原有仿生串联缓冲腿,在运动灵活性方面,新型缓冲腿结构的灵活性没有发生变化;在力学性能方面,地面对新型缓冲腿沿x0方向的作用力幅值减小了45.36%,沿y0方向的作用力幅值增大了0.43%,合力的幅值减少了25.3%,综合力学性能有了较大幅度的提高;在储能能力方面,最大储能量提高了34.6%,且单位缓冲距离下具有更大的储能能力。这表明新型缓冲腿具有更好的缓冲性能。
参考文献
| [1] | 陈殿生, 张自强, 陈科位. 仿生蝗虫机构着陆缓冲过程中的能量分配[J].机械工程学报, 2015, 51(13): 196–202.CHEN D S, ZHANG Z Q, CHEN K W. Energy allocation in landing buffering process for biomimetic locust mechanism[J].Journal of Mechanical Engineering, 2015, 51(13): 196–202.DOI:10.3901/JME.2015.13.196(in Chinese) |
| [2] | ZHANG J, SONG G, LI Y, et al. A bio-inspired jumping robot:Modeling, simulation, design, and experimental results[J].Mechatronics, 2013, 23(8): 1123–1140.DOI:10.1016/j.mechatronics.2013.09.005 |
| [3] | CHEN D S, YIN J M, CHEN K W, et al. Biomechanical and dynamic mechanism of locust take-off[J].Acta Mechanica Sinica, 2014, 30(5): 762–774.DOI:10.1007/s10409-014-0065-2 |
| [4] | CHEN D S, YIN J M, CHEN K W, et al. Prototype design and experimental study on locust air-posture righting[J].Journal of Bionic Engineering, 2014, 11(3): 459–468.DOI:10.1016/S1672-6529(14)60058-5 |
| [5] | HYON S H, EMURA T, MITA T. Dynamics-based control of a one-legged hopping robot[J].Proceedings of the Institution of Mechanical Engineers, Part I:Journal of Systems and Control Engineering, 2003, 217(2): 83–98.DOI:10.1177/095965180321700203 |
| [6] | HYON S H, MITA T.Development of a biologically inspired hopping robot-"Kenken"[C]//Proceeding of the IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2002, 4:3984-3991. |
| [7] | NIIYAMA R, NAGAKUBO A, KUNIYOSHI Y.Mowgli:A bipedal jumping and landing robot with an artificial musculoskeletal system[C]//Proceeding of the IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2007:2546-2551. |
| [8] | ESTREMERA J, WALDRON K J. Thrust control, stabilization and energetics of a quadruped running robot[J].The International Journal of Robotics Research, 2008, 27(10): 1135–1151.DOI:10.1177/0278364908097063 |
| [9] | NICHOL J G, SINGH S P N, WALDRON K J, et al. System design of a quadrupedal galloping machine[J].The International Journal of Robotics Research, 2004, 23(10-11): 1013–1027.DOI:10.1177/0278364904047391 |
| [10] | PALMER L R, ORIN D E, MARHEFKA D W, et al.Intelligent control of an experimental articulated leg for a galloping machine[C]//Proceeding of IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2003, 3:3821-3827. |
| [11] | WOODEN D, MALCHANO M, BLANKESPOOR K, et al.Autonomous navigation for BigDog[C]//Proceeding of IEEE International Conference on Robotics and Automation (ICRA).Piscataway, NJ:IEEE Press, 2010:4736-4741. |
| [12] | SEOK S, WANG A, CHUAH M Y, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT Cheetah robot[J].IEEE/ASME Transactions on Mechatronics, 2014, 20(3): 1117–1129. |
| [13] | 陈学生, 陈在礼, 孔民秀, 等. 并联机器人研究的进展与现状[J].机器人, 2002, 24(5): 464–470.CHEN X S, CHEN Z L, KONG X M, et al. Recent development and current status of stewart platform research[J].Robot, 2002, 24(5): 464–470.(in Chinese) |
| [14] | 王洪波, 齐政彦, 胡正伟, 等. 并联腿机构在四足/两足可重组步行机器人中的应用[J].机械工程学报, 2009, 45(8): 24–30.WANG H B, QI Z Y, HU Z W, et al. Application of parallel leg mechanisms in quadruped/biped reconfigurable walking robot[J].Journal of Mechanical Engineering, 2009, 45(8): 24–30.DOI:10.3901/JME.2009.08.024(in Chinese) |
| [15] | ZHAO J, XI N, GAO B, et al.Development of a controllable and continuous jumping robot[C]//Proceedings of the 2011 IEEE International Conference on Robotics and Automation, ICRA 2011.Piscataway, NJ:IEEE Press, 2011:4614-4619. |
| [16] | 田兴华, 高峰, 陈先宝, 等. 四足仿生机器人混联腿构型设计及比较[J].机械工程学报, 2013, 49(6): 81–88.TIAN X H, GAO F, CHEN X B, et al. Mechanism design and comparison for quadruped robot with parallel-serial leg[J].Journal of Mechanical Engineering, 2013, 49(6): 81–88.DOI:10.3901/JME.2013.06.081(in Chinese) |
| [17] | LIU G H, LIN H Y, LIN H Y, et al. A bio-inspired hopping kangaroo robot with an active tail[J].Journal of Bionic Engineering, 2014, 11(4): 541–555.DOI:10.1016/S1672-6529(14)60066-4 |
| [18] | CHOU Y C, HUANG K J, YU W S, et al. Model-based development of leaping in a hexapod robot[J].IEEE Transactions on Robotics, 2015, 31(1): 40–54.DOI:10.1109/TRO.2014.2376141 |
| [19] | CHEN D S, ZHANG Z Q, CHEN K W. Dynamic model and performance analysis of landing buffer for bionic locust mechanism[J].Acta Mechanica Sinica, 2016, 32(3): 551–565.DOI:10.1007/s10409-015-0523-5 |
| [20] | 周纪卿, 朱因远. 非线性振动[M].西安: 西安交通大学出版社, 1998: 140-143.ZHOU J Q, ZHU Y Y. Nonlinear vibration[M].Xi'an: Xi'an Jiaotong University Press, 1998: 140-143.(in Chinese) |
