在数字直扩系统中，PN码相位的测量精度直接决定了扩频同步或测距的精度。扩频同步多采用码跟踪环的方法^[1-3]，须要迭代循环，运算量较大。现有众多PN码相位精确测量方法的测量精度均依赖于采样频率，而采样频率的增加会成倍数增加处理的运算量和复杂度。因此，最常使用的方法是借助于内插或拟合思想实现超采样率级的PN码相位精确测量。
文献[4-6]分别使用最大的3个相关值进行两点线性内插、三角内插或者抛物线内插以提高相位测量精度，但该类内插方法提高PN码相位的测量精度的效果不明显，测量精度提高较小。文献[7]提出了使用分段相关来提高系统的抗频偏能力，但是该方法没有考虑如何提高同步精度。文献[8]利用相关峰两侧的数据作直线拟合实现精确同步，虽然精度高，但如文献[9]指出相关曲线的非理想特性对于伪码同步精度影响较大，因此该方法难以满足工程需求。
文献[10-16]提出了采用最小二乘拟合的方法提高PN码相位测量精度，相对于内插类方法该方法实现简单，同步精度高。文献[10]最早提出用最小二乘(LS)法提高测量精度，但该方法测量范围较小，仅适合于PN码相位误差在一个采样点以内的测量区域。文献[11]在文献[10]的基础上进行改进，利用延迟锁相环(DLL)S型鉴相曲线中间部分的线性特点，采用最小二乘法，得到精确PN序列相位值。但该方法要求先进行DLL跟踪，保证粗同步误差在一个采样点偏差以内，而DLL跟踪过程又较为复杂，如果不跟踪，在粗同步误差较大时，该方法不再适用。文献[12]提出一种有效抵抗频偏的基于最小二乘法的测相方案，具有精度高的优点，但该方法仍受制于应用范围太小。文献[13]引入了多速率处理，提高了相位测量精度，但该方法的内插处理增加了运算量，而且应用范围有限。文献[14]对拟合的鉴相曲线所得数据进行滑动筛选，并利用一组最优数据估计同步位置。文献[15]采用迭代方法降低了对粗同步的要求。文献[14-15]虽然使用范围较大，但都需要迭代循环处理，增加了相位测量时间。文献[16]利用正交三角(QR)分解和奇异值分解的整体最小二乘法拟合出鉴相曲线，可以得到优于基于普通最小二乘法的同步测量精度和稳定性。但整体最小二乘法需要矩阵QR分解和奇异值分解，运算量太大。
因此，本文提出一种宽范围粗同步误差下的最小二乘精确相位测量方法。该方法利用早迟码相位估计器鉴相曲线最大值和最小值之间的数据样点进行最小二乘线性拟合完成相位测量，可实现粗同步误差在半个码元宽度范围内PN码相位的精确测量。
1 最小二乘法 理想条件下PN序列相关值为

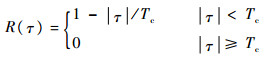(1)

式中：τ为相位差；T_c为码元宽度。
如图 1所示，当相位差为τ时，理想条件下PN序列鉴相曲线如实线所示，t为相位，黑点表示离散样点。实线左右两边的虚线分别代表着相位延迟正负半个码元的鉴相曲线，也呈现与实线相似的线性特征。

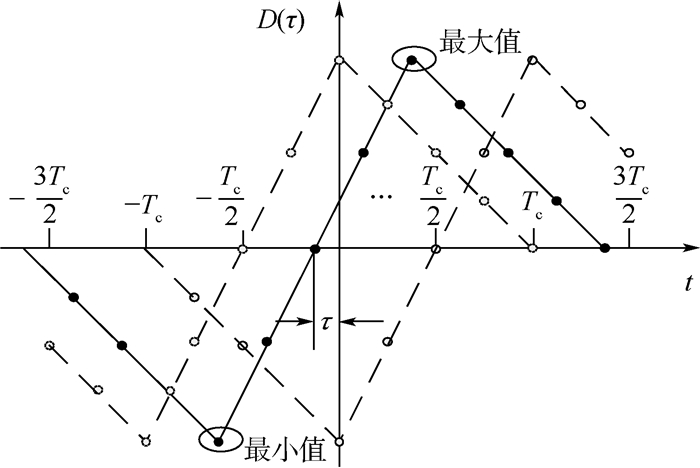图 1 鉴相曲线示意图 Fig. 1 Diagrammatic sketch of phase discrimination curve

图选项

文献[11]指出，鉴相曲线的中间部分具有线性特征，在误差平方和最小准则下，基于最小二乘法测量PN码相位的方法，基于拟合直线的方法化离散为连续，能够获得分数倍采样周期的测量精度的相位差τ。
以实线为例，鉴相曲线为

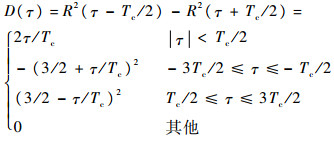(2)

文献[10]中指出利用图 1中鉴相曲线的线性部分，基于最小二乘直线拟合实现高精准度的相位测量。计算过程如下。
设鉴相值坐标为(x_i, y_i)，i=1, 2, …, K，K为参与拟合的点数。建立拟合直线，则误差的平方和为

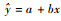
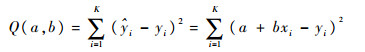(3)

根据最小二乘法，取a、b使Q(a, b)最小，即

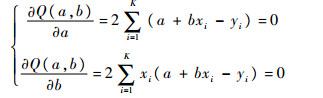(4)

解式(4)，得

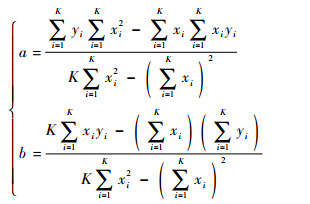(5)

因此，PN序列相位差为

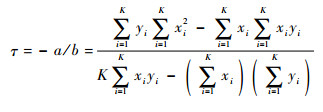(6)

2 累加最小二乘法 在粗同步完成后，相位差在区间(-T_c/2, T_c/2)，鉴相曲线如图 1中实线所示。而图 1中实线左右两边的虚线是鉴相曲线分别左右平移了T_c/2个单元。可以看出，虚线依然具有线性特征。因此，可以利用鉴相曲线的中间部分，以曲线的最大值和最小值为临界点，进行线性拟合。
非相干早迟码相位估计器原理图如图 2所示。图 2(a)中，r(kT_s)为下变频后的基带信号，k为采样点位置，T_s为采样时间，将其分别超前和滞后N路，N为采样率，共须要2N+1路鉴相器单元。经过鉴相器单元，得到鉴相值D(kT_s)。图 2(b)为鉴相器单元，将延迟后的信号分别与超前和滞后半个码元宽度的PN序列作匹配相关处理后，取超前减滞后功率差D(kT_s)，然后用最小二乘法拟合得到精确相位τ。

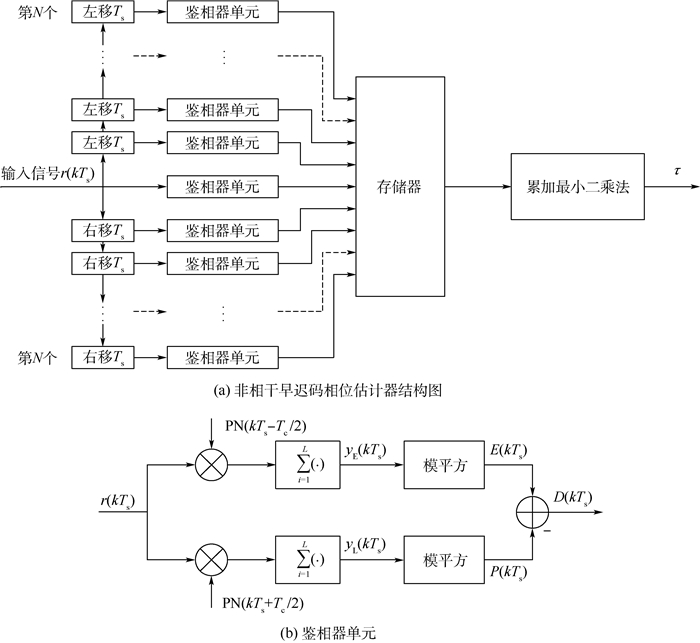L—PN序列长度；yE(kTs)，yL(kTs)—相关后的超前和滞后信号；E(kTs)—超前支路信号模平方；P(kTs)—滞后支路信号模平方。 图 2 非相干早迟码相位估计器原理图 Fig. 2 Schematic diagram of non-coherent early-later code delaying phase estimator

图选项

接收到的信号为

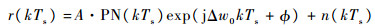(7)

式中：A为接收信号的幅度；PN(kT_s)为采样后的伪随机码；Δw₀为归一化数字频偏；?为载波初始相位；n(kT_s)为噪声项，服从均值为0、方差为σ²的高斯分布。
理想鉴相曲线由3段直线组成，区分3段曲线的拐点为曲线的最大值和最小值，因此可以使用最大值和最小值将曲线分为3段，利用中间段的线性部分进行参数特征的提取。假设频偏较小，不足以影响检测相关峰的出现，累加最小二乘法实现步骤如下所示。
步骤1??求出鉴相曲线，以矩阵的形式存储这些样点，记为Y，Y为M阶×(2N+1)阶的矩阵，M为非相干累加次数。
步骤2??将矩阵Y的每列相加，得到向量Z，取出Z的最大值和最小值所在位置，分别记为z_max和z_min。
步骤3??取区间(z_min, z_max)之间的K个点，且K≤2N-1，K为不定长；利用最小二乘法进行线性拟合，然后计算相位差τ。
因此，PN码相位差为

(8)

3 方法有效性分析 接收到的信号r(kT_s)经过滑动相关累加后得到两路信号y_E(kT_s)和y_L(kT_s)，表达式为

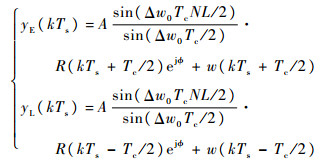(9)

式中：R(kT_s-T_c/2)和R(kT_s+T_c/2)分别为超前和滞后的相关累加值；w(kT_s+T_c/2)和w(kT_s-T_c/2)为n(kT_s)相关累加后的噪声信号，服从N(0, 2NLσ²)。因此y_E(kT_s)和y_L(kT_s)服从的分布为

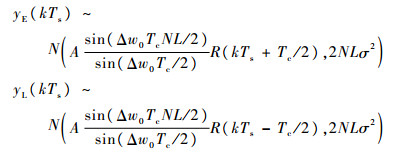E(kT_s)服从自由度为2M的非中心χ²分布，非中心参数的均值为

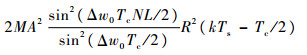信道为加性高斯白噪声(AWGN)信道，累加后判决量z的概率密度函数为

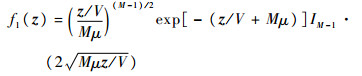其中：I_M-1(·)为M-1阶贝塞尔函数；V=2NLσ²；μ=M₁²/V，M₁²=N²L²A²D²(kT_s)。
由于f₁分布含有贝赛尔函数，考虑到z分布的自由度比较高，根据中心极限定理，可将其近似为高斯分布。则y_E的概率密度分布为

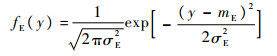(10)

式中：

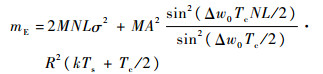(11)

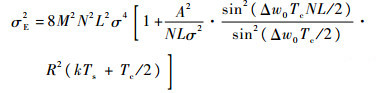(12)

同理可得，y_L的概率密度分布为

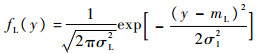(13)

式中：

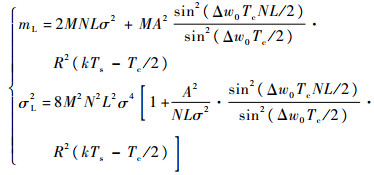(14)

因此，D(kT_s)=E(kT_s)-P(kT_s)服从N(μ_D, σ_D²)，均值和方差分别为

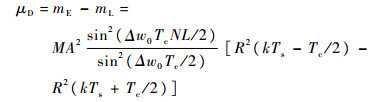(15)

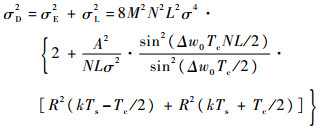(16)

由式(15)可知，在鉴相曲线中间段μ_D呈线性特征，因此可以使用线性拟合方式估计相位差τ，表明本文提出方法的有效性。
4 仿真分析 为了验证提出方法的性能，选取生成多项式为x⁴+x+1，长度为31的m序列为例，采样率取8，归一化频偏为0，仿真1 000次，对比本文方法与文献[5, 11]方法。
4.1 不同初始相位测量精度仿真 信噪比(SNR)为0 dB，不累加，即累加次数为1，设置m序列初始相位为0~4T_s。如表 1所示，文献[5]在0~4T_s时的相位测量均方根值约为1，在小于1个采样点时文献[11]的均方根值较小，但超出一个采样点时，测量误差迅速增大，大于2个采样点时超过1。而提出的方法在初始相位在0~4T_s时，均方根误差基本没有增加，大约为1/4采样点。因此，提出方法的均方根误差远小于文献[5]的，在偏差较小时与文献[11]的均方根误差接近，但当偏差增大时，提出的方法均方根误差基本没有增加，而文献[11]增大很多。因此，本文方法在信噪比恒定情况下可以得到更为稳定且准确的相位差估计，具有更宽的适用范围和适用性。
表 1 不同初始相位均方根误差 Table 1 Root mean square error in different initial phases

测量方法	初始相位
	0	1Ts	2Ts	3Ts	4Ts
文献[5]方法	1.016	1.022	1.045	1.069	1.074
文献[11]方法	0.220	0.321	0.481	2.591	17.691
本文方法	0.220	0.220	0.226	0.232	0.238

表选项






4.2 不同信噪比相位测量精度仿真 设置信噪比为从-10 dB至10 dB，累加次数为1，步长为3 dB。图 3表明，文献[5]的均方根误差相比提出的方法增大很多。当偏差较小时，提出方法与文献[11]的抗噪声能力接近，但当相位偏差增大时，文献[11]的均方根误差急剧增大。而提出的方法在信噪比变化时，误差变化不明显。因此，提出的方法受信噪比影响较小，具有很好的抗噪声能力。

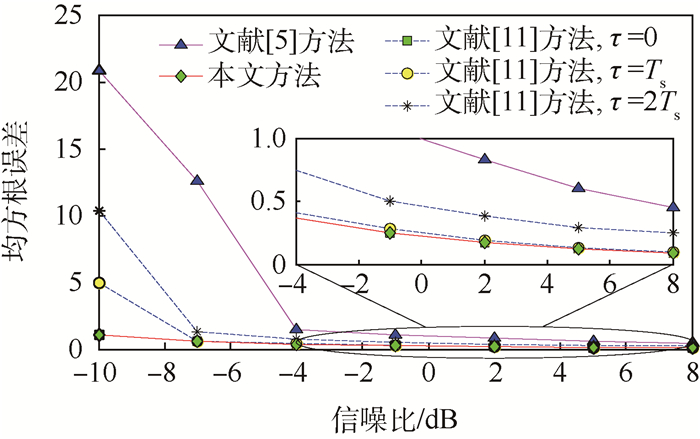图 3 不同信噪比下的均方根误差 Fig. 3 Root mean square error at different SNRs

图选项

4.3 不同累加次数相位测量精度仿真 分别累加1、2、4、8和16次，对比不同累加次数(M)的均方根误差，如图 4所示。从图 4可以看出，累加次数越多，相位测量的均方根误差越小，但随着累加也会出现平台效应，均方根误差趋于稳定。而且累加次数的增加会增加信号的长度和处理时间，因此设计时常对累加次数和运算量折衷考虑。

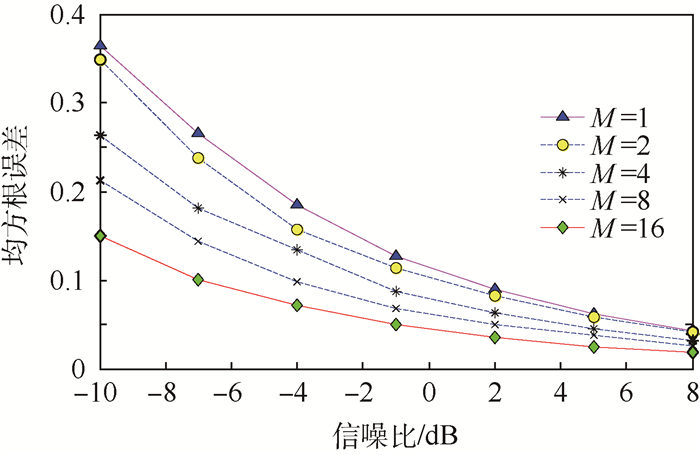图 4 不同累加次数下的均方根误差 Fig. 4 Root mean square error at different accumulative times

图选项

5 结论 本文给出了一种非相干鉴相结构，在该结构基础上提出基于累加最小二乘法的PN序列相位精确测量方法，经实验验证表明：
1)?在不累加的情况下，在初始相位小于半个码元宽度条件下，方法相比于其他现有的最小二乘法，运算量基本相同，可获得更高的相位测量精度，达到分数级的测量精度；而且抗噪声能力更强。
2)?在累加的情况下，相位测量精度更佳，而且累加次数越多，精度越高。
为使本文的方法在更广的环境下应用，仍需改进该方法使其在多径或存在人为干扰的复杂电磁环境下正常使用。

参考文献

[1]	沈锋, 李伟东, 李强. 基于I/Q支路相干积分观测滤波的GPS接收机信号跟踪方法[J].电子与信息学报, 2015, 31(1): 37–42.SHEN F, LI W D, LI Q. GPS receiver signal tracking method based on I/Q branch coherent integration measurements filter[J].Journal of Electronics & Information Technology, 2015, 31(1): 37–42.(in Chinese)
[2]	程俊仁, 刘光斌, 姚志成, 等. 一种鲁棒GNSS矢量跟踪环[J].航空学报, 2014, 35(11): 3106–3114.CHENG J R, LIU G B, YAO Z C, et al. A robust GNSS vector tracking loop[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 3106–3114.(in Chinese)
[3]	刘晗超, 简伟, 侯建文. 再生伪码测距中的码跟踪环实现[J].时间频率学报, 2014, 37(2): 104–110.LIU H C, JIAN W, HOU J W. A realization of code tracking loop in PN code ranging[J].Journal of Time and Frequency, 2014, 37(2): 104–110.(in Chinese)
[4]	KRASNR R, NORMAN F.GPS receiver and method for processing GPS signals:United States, Patent 6725159[P].2004-04-20.
[5]	FRANCESCO B, GAETANO G. A fast time-delay estimator of PN signals[J].IEEE Transactions on Communications, 2011, 59(8): 2057–2062.DOI:10.1109/TCOMM.2011.051311.100025
[6]	龚国辉, 李思昆. 提高DSSS信号PN码相位测量精度的三点二次插值法[J].通信学报, 2007, 28(2): 130–133.GONG G H, LI S K. Improving DSSS signal PN code phase measurement precision by 3-point quadratic interpolation[J].Journal on Communications, 2007, 28(2): 130–133.(in Chinese)
[7]	王磊, 徐大专. 一种抗频偏的时间精同步方法及性能分析[J].电子与信息学报, 2011, 33(2): 300–303.WANG L, XU D Z. An anti frequency offset fine time synchronization method and its performance analysis[J].Journal of Electronics & Information Technology, 2011, 33(2): 300–303.(in Chinese)
[8]	李柏渝, 陈雷, 李彩华, 等. 通道非理想特性对导航接收机伪码测距零值的影响分析[J].电子与信息学报, 2011, 33(9): 2138–2143.LI B Y, CHEN L, LI C H, et al. The impact non-ideal-front-end characteristic on PN zero value measurement of navigation receivers[J].Journal of Electronics & Information Technology, 2011, 33(9): 2138–2143.(in Chinese)
[9]	罗海军, 彭卫东, 李明阳, 等. 基于分段直线拟合的伪随机码相位测量法[J].计算机测量与控制, 2015, 23(3): 727–730.LUO H J, PENG W D, LI M Y, et al. Method of phase measurement of PN codes based on piecewise linear fitting[J].Computer Measurement & Control, 2015, 23(3): 727–730.(in Chinese)
[10]	胡修林, 张俊, 杨灵. 直接序列扩频通信系统中PN码相位的精确测量方法[J].电讯技术, 2005(4): 128–131.HU X L, ZHANG J, YANG L. A method for accurately measuring the phase of PN code in DSSS systems[J].Telecommunication Technology, 2005(4): 128–131.(in Chinese)
[11]	胡修林, 曾臻, 张俊, 等. 直扩系统伪码精同步及FPGA实现[J].华中科技大学学报(自然科学版), 2005, 33(6): 44–46.HU X L, ZENG Z, ZHANG J, et al. Synchronization of pseudorandom code and its implementation on FPGA in DSSS[J].Journal of Huazhong University of Science & Technology (Nature Science Edition), 2005, 33(6): 44–46.(in Chinese)
[12]	王徐华, 柏鹏, 李明阳, 等. 基于最小二乘法的高动态条件下抗频偏的精确同步方法[J].电子与信息学报, 2012, 34(11): 2755–2760.WANG X H, BAI P, LI M Y, et al. Anti-frequency offset method for precision synchronization on highly dynamic condition based on the least squares[J].Journal of Electronics & Information Technology, 2012, 34(11): 2755–2760.(in Chinese)
[13]	王徐华, 柏鹏, 李寰宇, 等. 基于多速率内插和最小二乘法的精确同步方法[J].计算机应用研究, 2012, 29(10): 3922–3925.WANG X H, BAI P, LI H Y, et al. Precise synchronization approach based on multi-rate interpolation and least squares method[J].Application Research of Computers, 2012, 29(10): 3922–3925.(in Chinese)
[14]	王徐华, 柏鹏, 李明阳, 等. 一种基于滑动最小二乘法的精确同步方法[J].重庆邮电大学学报(自然科学版), 2013, 25(5): 599–604.WANG X H, BAI P, LI M Y, et al. A precise synchronization method based on slipping least square algorithm[J].Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2013, 25(5): 599–604.(in Chinese)
[15]	李明阳, 柏鹏, 王徐华, 等. 一种基于迭代最小二乘法的精确同步方法[J].电子与信息学报, 2013, 35(4): 832–837.LI M Y, BAI P, WANG X H, et al. A precise synchronization method based on iterative least square algorithm[J].Journal of Electronics & Information Technology, 2013, 35(4): 832–837.(in Chinese)
[16]	罗海军, 彭卫东. 整体最小二乘法在精同步中的应用[J].计算机测量与控制, 2014, 22(7): 2291–2294.LUO H J, PENG W D. Application of total least squares in precise synchronization[J].Computer Measurement & Control, 2014, 22(7): 2291–2294.(in Chinese)