工程中常使用比例-积分-微分(PID)控制器进行高度控制,在无扰动情况下可以实现无静差控制,但在扰动情况下,控制精度往往难以达到要求,为此国内外****在高精度高度控制上展开了大量研究。文献[2]针对无人机的高精度着陆控制采用了L1自适应控制,仿真结果表明误差满足精度要求,但如何选取最优的反馈回路低通滤波器难度较大。文献[3]采用模糊增益调度控制在紊流等扰动存在的情况下,提升了轨迹跟踪性能,但规则库的设计对经验要求较高。文献[4]构造非线性干扰观测器对建模误差和外在干扰进行观测,并在此基础上设计滑模控制器,虽可实现较高的控制精度,但存在控制抖振问题。文献[5]对俯仰角控制应用自抗扰控制器,取得了较好的控制效果,但并未给出有效的参数设计方法。
韩京清[6-7]提出的自抗扰控制方法具有鲁棒性强,可控范围大,算法简单,工程易实现等优点。本文基于线性自抗扰控制(LADRC) ,以无人机高度通道为研究对象,对定高控制策略、控制结构和控制器参数优化设计展开研究,实现高精度高度控制。
1 线性自抗扰控制器理论 自抗扰控制是针对观测系统的“干扰总和”,并加以补偿的一种控制方法。其利用扩张状态观测器(ESO)观测出系统的未建模动态、非线性动态特性以及外部扰动来进行闭环系统的控制补偿。
虽然传统自抗扰方法具有高精度、高反馈效率等方面的优势,但其选取的参数过多,参数整定比较繁琐,且在工程上难以进行稳定性等指标分析。为此,高志强等[8-9]提出了LADRC方法,控制器参数较少,且具有明确的物理含义,十分便于理论分析和工程应用。LADRC结构如图 1所示。
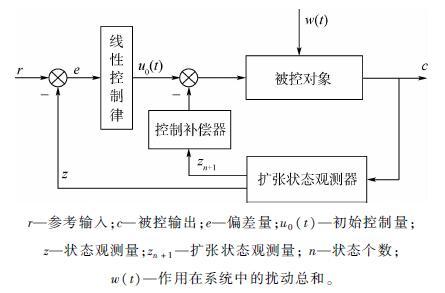 |
| r—参考输入;c—被控输出;e—偏差量;u0(t)—初始控制量;z—状态观测量;zn+1—扩张状态观测量; n—状态个数;w(t)—作用在系统中的扰动总和。 图 1 LADRC结构 Fig. 1 Structure of LADRC |
| 图选项 |
设带有未知扰动的不确定对象为
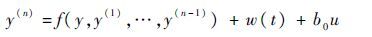 | (1) |
式中:u和y分别为系统输入和输出;b0为已知常数。取状态变量[x1,x2,…,xn]T=[y,y(1),…,y(n-1)]T,令a(t)=f+w(t),它包含了系统模型和外扰的总和,称之为系统的扩张状态变量。令b(t)=% $\dot a$(t),可得到系统的扩张状态方程为
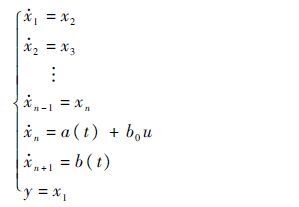 | (2) |
构造式(1)系统的线性ESO为
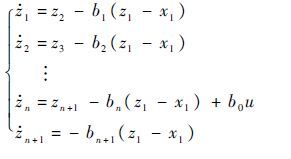 | (3) |
式中:b1,b2,…,bn+1为(s+ω)n+1展开后从第2项开始的各项系数,ω的选取可根据系统带宽的要求确定或在线整定。ESO可以以一定速度跟踪系统的各个状态,且观测出的扩张状态值即为作用在系统上的扰动总和,即
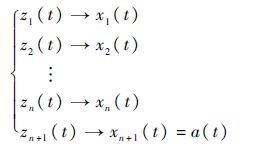 | (4) |
自抗扰控制器的本质就是利用ESO观测系统的内部和外部扰动。将观测出的扰动总和引入到控制量中进行补偿,即可抑制扰动对系统输出带来的影响,从而提高控制器的控制性能。
2 无人机纵向控制器结构 无人机纵向高度控制通道的常规操纵面主要有升降舵和油门。本文对纵向的高度和速度控制采用俯仰高度/油门空速控制策略,即通过升降舵控制内环俯仰角实现外环高度控制,通过油门控制空速。
将纵向控制通道划分为高度控制通道和速度控制通道,其中高度通道采用内外环控制结构,分为内环俯仰角控制通道和外环高度控制通道。反馈高度H,俯仰角$\vartheta $和空速V,分别在3个通道构造LADRC控制器,LADRC利用ESO观测出纵向内环俯仰角通道、外环高度通道和空速通道中存在的扰动,将扰动量引入控制量中进行补偿,达到提高控制精度的效果。无人机纵向通道控制结构如图 2所示,本文为了便于分析设计,反馈控制律均取为线性形式。
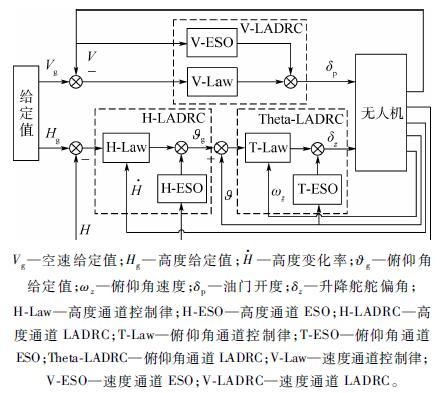 |
| Vg—空速给定值;Hg—高度给定值;$\dot{H}$—高度变化率;∂g—俯仰角给定值;ωz—俯仰角速度;δp—油门开度;δz—升降舵舵偏角;H-Law—高度通道控制律;H-ESO—高度通道ESO;H-LADRC—高度通道LADRC;T-Law—俯仰角通道控制律;T-ESO—俯仰角通道ESO;Theta-LADRC—俯仰角通道LADRC;V-Law—速度通道控制律;V-ESO—速度通道ESO;V-LADRC—速度通道LADRC。 图 2 无人机纵向通道控制结构 Fig. 2 Control structure of UAV longitudinal channel |
| 图选项 |
2.1 内环俯仰角控制器 无人机的姿态运动可用关于俯仰角的二阶微分方程来描述,从纵向运动方程中提取出$\vartheta $和ωz的相关项,引入二阶LADRC控制器,实现对纵向俯仰角的姿态控制。
首先引入三阶线性ESO,观测纵向内环可能存在的扰动总和,ESO表达式为
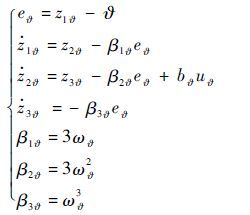 | (5) |
式中: e$\vartheta $为俯仰角跟踪误差;z1$\vartheta $和z2$\vartheta $分别为观测得到的俯仰角和俯仰角速度;z3$\vartheta $为俯仰角通道观测到的总扰动;b$\vartheta $为升降舵舵偏角对俯仰角的控制比例系数;u$\vartheta $为实际升降舵舵偏角;β1$\vartheta $、β2$\vartheta $和β3$\vartheta $为俯仰角通道ESO系数,取决于待整定观测器参数ω$\vartheta $。
根据俯仰角给定值与实际值的偏差,以及俯仰角速度,设计线性误差反馈律,得到初始控制量u0$\vartheta $,再将ESO观测的扰动z3$\vartheta $引入到控制中进行补偿,最终得到实际控制量u$\vartheta $。
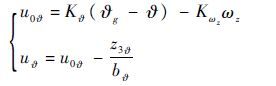 | (6) |
b$\vartheta $可根据无人机气动参数和飞行状态确定具体数值。优化控制器参数K$\vartheta $、Kωz和ω$\vartheta $就可以获得满意的俯仰角观测效果和控制效果。
2.2 外环高度控制器 无人机纵向外环高度运动可用以高度H为输出,俯仰角$\vartheta $为输入的一阶微分方程描述,将迎角α看作扰动量,引入一阶LADRC控制器,实现高度控制。
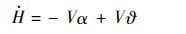 | (7) |
对此一阶系统引入二阶线性ESO观测纵向外环可能存在的扰动总和,引入线性误差反馈控制律实现外环高度控制,具体形式为
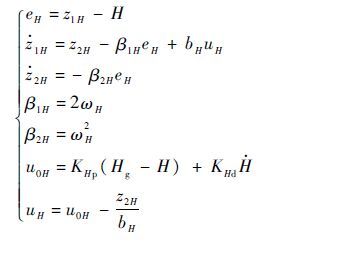 | (8) |
式中:eH为高度跟踪误差;u0H为高度通道初始控制量;z1H为观测得到的航迹高度;z2H为高度通道观测出的总扰动;uH为实际俯仰角给定值;β1H和β2H为高度通道ESO系数,取决于待整定观测器参数ωH;bH=V为无人机当前飞行空速。优化控制器参数KHp、KHd和ωH可以获得满意的高度观测效果和控制效果。
2.3 空速控制器 无人机的空速通道同外环高度通道类似,可用以空速V为输出,油门δp为输入的一阶微分方程来描述,将其余项均看作扰动量f,引入一阶LADRC控制器,实现空速控制。
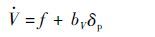 | (9) |
式中:bV=cos(α*+φp)/m可根据无人机气动参数和飞行状态确定具体数值,φp为发动机安装角,m为无人机质量,α*为配平迎角。对此一阶系统引入二阶线性ESO观测速度通道可能存在的扰动总和,引入线性误差反馈控制律实现速度闭环控制,具体形式为
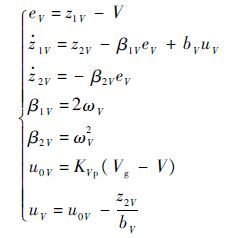 | (10) |
式中:eV为速度跟踪误差;bV为油门对空速的控制比例系数;z1V为观测得到的空速;z2V为速度通道观测出的总扰动;uV为实际油门控制量;β1V和β2V为高度通道ESO系数,取决于待整定观测器参数ωV。优化控制器参数KVp和ωV可以获得满意的速度观测效果和控制效果。
3 复杂气流扰动分析 飞行过程中存在的复杂气流扰动主要有大气紊流和离散突风2种[10],控制律能否有效地减小复杂气流扰动带来的影响,是实现高精度控制的关键,因此对这2种扰动特性进行研究分析,使控制参数设计具有针对性,减小控制器参数设计的保守性。
对大气紊流(德莱顿模型)和离散突风(1-cos模型)[11]进行频谱分析,大气紊流的功率谱密度X(ω)、Y(ω)和Z(ω)如图 3所示,离散突风的功率谱密度如图 4所示,ω为频率。
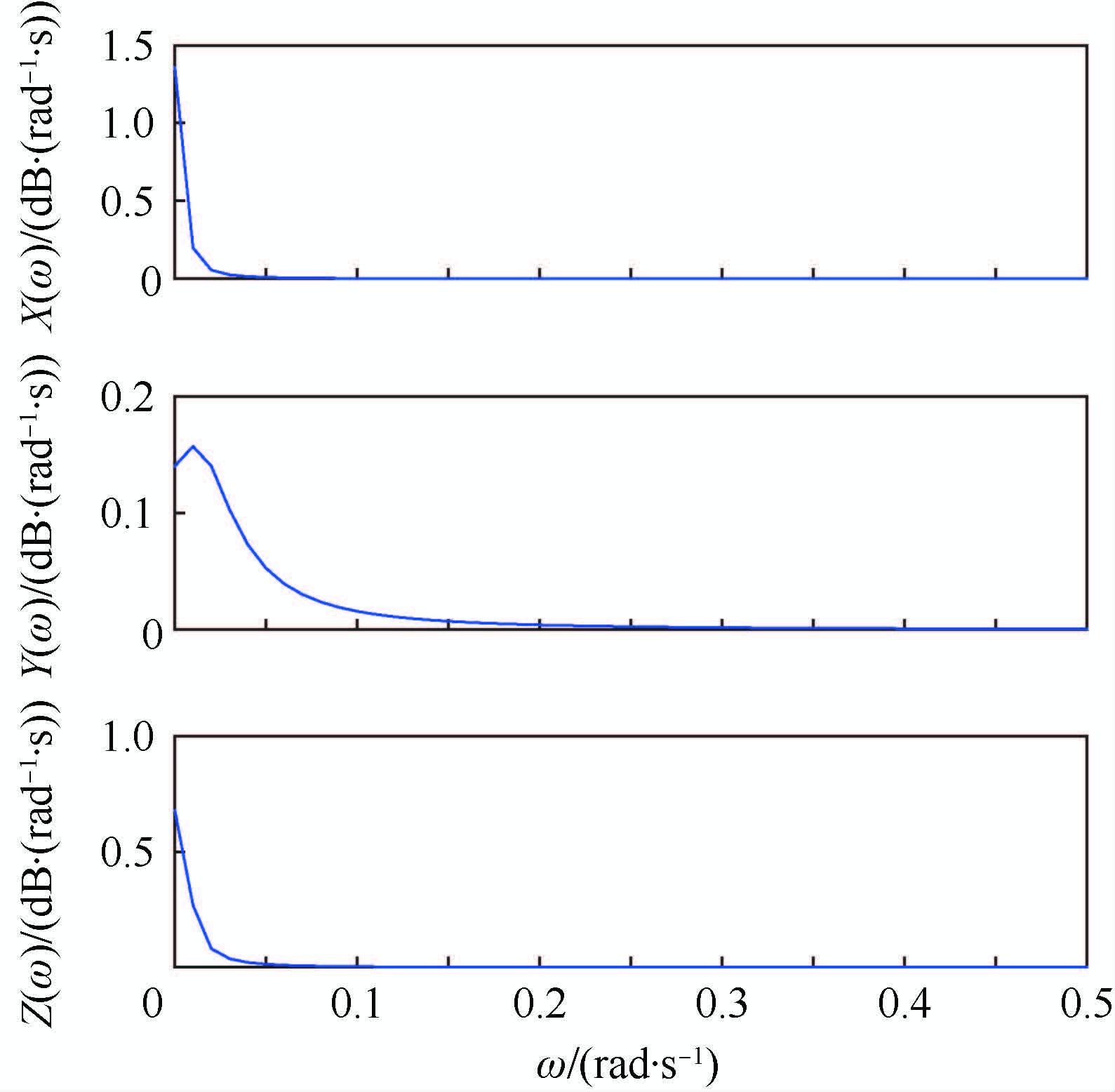 |
| 图 3 大气紊流(德莱顿模型)功率谱密度 Fig. 3 Power spectrum density of wind turbulence (Dryden model) |
| 图选项 |
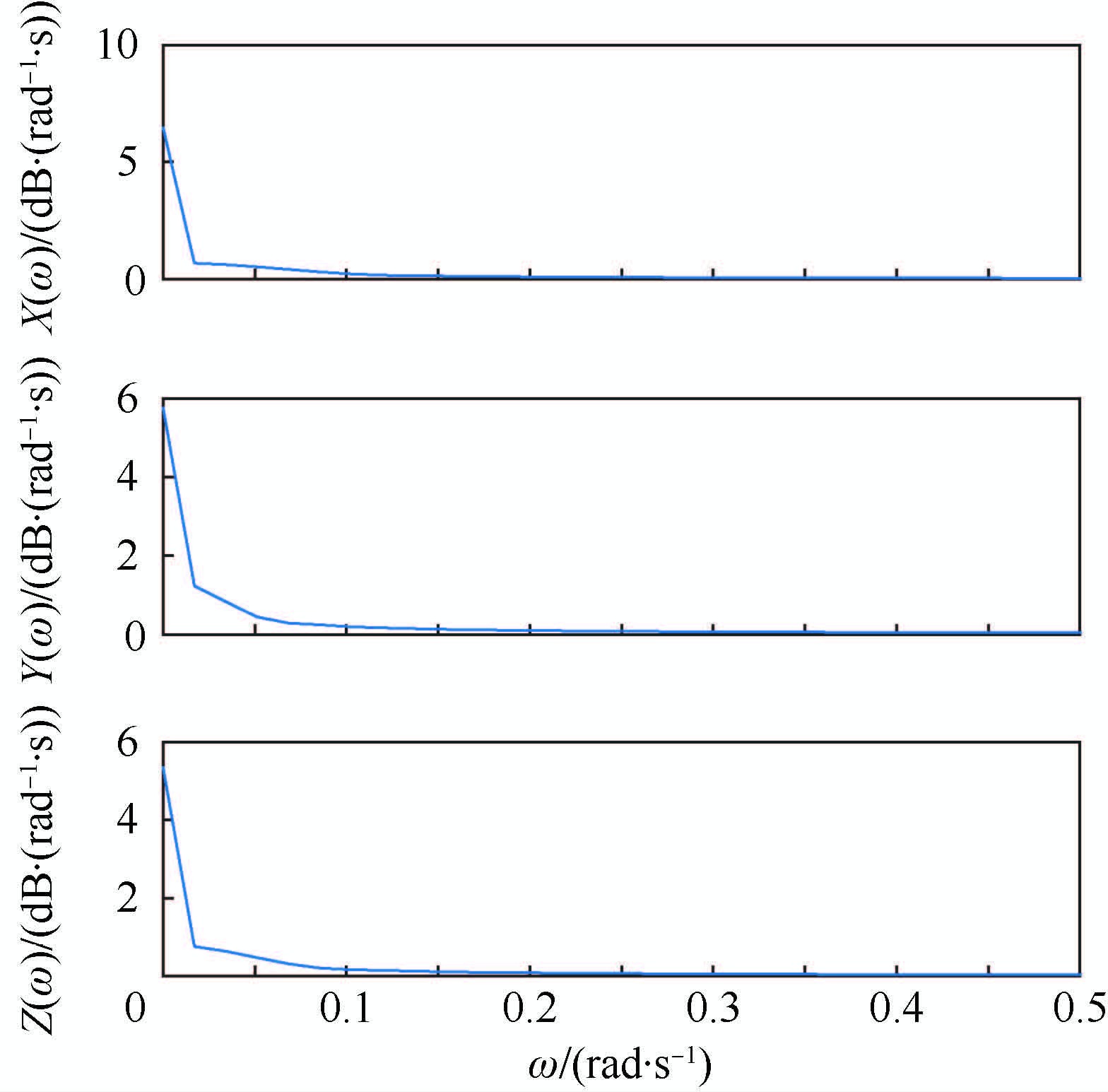 |
| 图 4 离散突风(1-cos模型)功率谱密度 Fig. 4 Power spectrum density of discrete wind gust (1-cos model) |
| 图选项 |
从图 3和图 4中可以看出,无论是大气紊流还是离散突风,其主要成分频率均在区间[0~0.2]rad/s之内。设计时应重点考虑频率在此区间内的大气扰动带来的影响,从而减小设计的保守性。
4 复杂气流扰动下无人机线性模型 文献[12]中对在非平静大气中固定翼飞机的运动方程进行了比较详细的分析。大气扰动的作用实际上就是改变了飞行器上的相对气流,从而改变了飞行器所受到的气动力。根据分析与计算,可以得到在复杂气流扰动下的纵向运动方程为
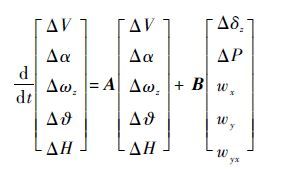 | (11) |
式中:A和B的定义如下,其余各变量具体意义参见文献[12]。由于小型无人机在飞行过程中可以看作质点,因此方程的输入量紊流梯度量wyx可认为是零。在此线性化模型的基础上,可以对复杂扰动对无人机纵向飞行状态的影响进行定量分析,从而为控制器参数优化设计提供抗扰性方面的优化准则。
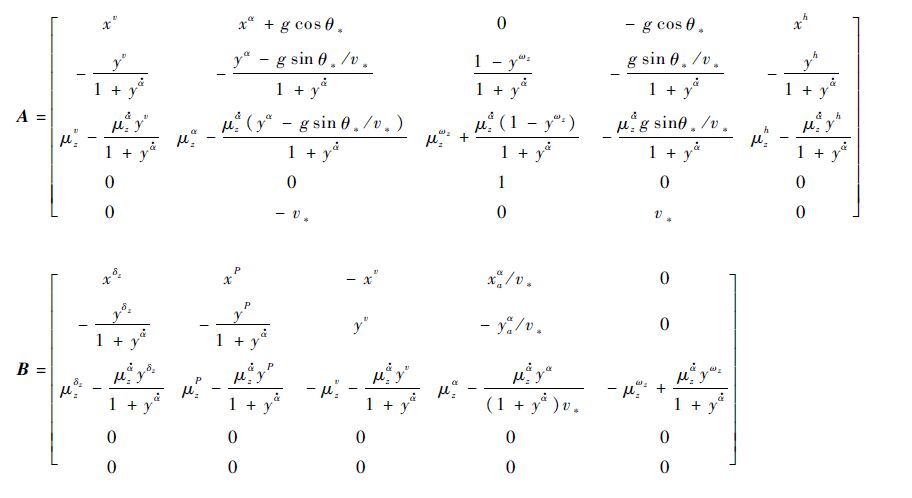 |
5 控制器参数优化设计 在本文中,基于LADRC的无人机纵向高度控制器共有8个待整定参数,如果通过人工试凑的方法来确定,不仅工作量比较大,而且并不一定能保证找到最优的参数。利用粒子群优化算法(PSO)进行控制器参数的寻优设计,可以提高设计效率和控制性能。粒子群优化算法[13-15]是由Eberhart和Kennedy在对鸟群捕食行为进行研究的基础上,提出的一种新型进化算法,其具有实现容易、精度高和收敛快等优点,在解决实际问题中展示出了优越性。
采用粒子群优化算法进行参数寻优设计,其关键是给出目标适应度函数。根据经典控制理论,控制律以大气扰动为输入、航迹高度为输出的闭环放大倍数在区间[0~0.2]rad/s上越小,则其对相应频率区间扰动的抗扰能力越强,控制器的控制精度也就越高。为了兼顾控制器的快速性和稳态性能,以高度阶跃响应的上升时间tr=7 s,无稳态误差等指标安排过渡过程,要求幅值裕度GM≥10 dB,相角裕度PM≥45°,构建粒子群优化算法适应度函数。
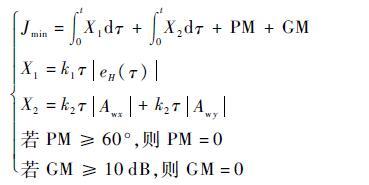 | (12) |
式中:Jmin为目标函数;t为时间;τ为积分步长;Awx和Awy分别为区间[0~0.2]rad/s上的误差闭环放大倍数;k1、k2根据各项的重要程度进行选取,在本文中取k1=1,k2=2。
在该适应度函数中,第1项$\int_0^t {{X_1}d\tau } $的物理意义在于保证高度响应与给定过渡过程间具有最小的跟踪误差;第2项$\int_0^t {{X_2}d\tau } $的物理意义在于使特定频率范围的风干扰到高度输出的闭环放大倍数最小,提高对风干扰的抑制能力;最后两项PM+GM用以兼顾控制器的稳定裕度,相当于设立“惩罚”机制,若稳定裕度不满足幅值裕度GM≥10 dB,相角裕度PM≥60°,则在适应度计算结果中会直接叠加上响应的稳定裕度数值,从而排除不满足所要求稳定裕度的控制器参数。
设定粒子群优化算法的最大迭代次数为100,粒子群种群大小为40,变量维数为8,惯性因子w=0.9,学习因子c1=2,社会因子c2=2,约束因子r1=r2=1。适应度变化曲线如图 5所示。
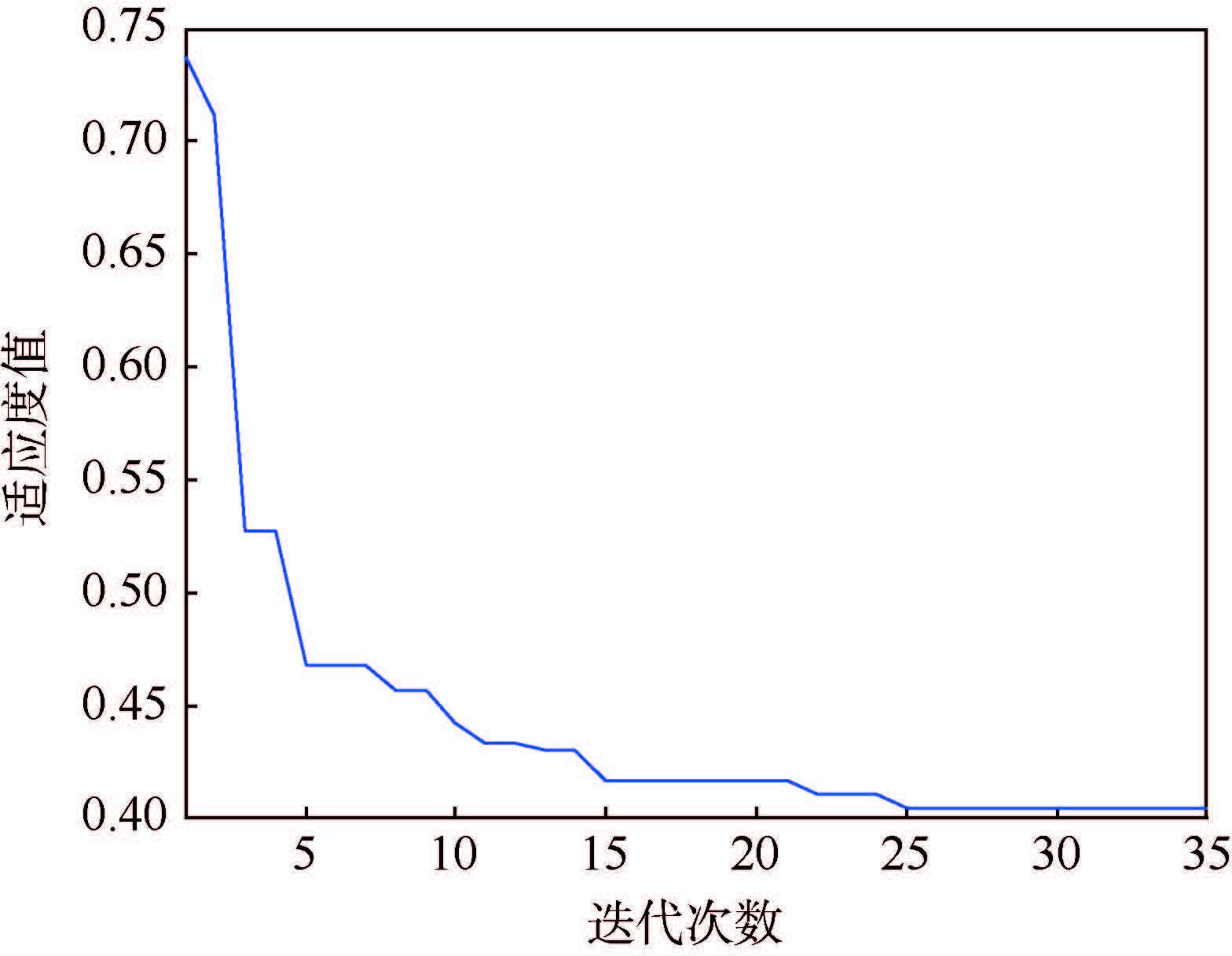 |
| 图 5 适应度变化曲线 Fig. 5 Changing curve of fitness |
| 图选项 |
从图 5中可以看出,算法在第25次迭代时收敛到最优值,最终得到的控制器参数为ωH=1.12,ω$\vartheta $=1.27,ωV=3.8,KHp=3.34,KHd=6.76,KVp=0.32,K$\vartheta $=1.39,Kωz=0.82,LADRC的高度阶跃响应曲线和伯德图分别如图 6和图 7所示。
从图 7中可以看出高度阶跃响应无超调,上升时间tr≈7 s,幅值裕度GM≈10.7 dB,相角裕度PM≈60.4°,完全满足指标要求。
采用C语言与MATLAB语言混合编程,用C语言实现MATLAB中耗时较长的插值函数,降低仿真过程中无人机全量模型的解算时间,从而缩短粒子群优化算法参数优化设计的仿真时间。经过多次仿真,结果表明该算法均可快速收敛,且在配置为Core i7处理器,3G内存,32位Windows 7操作系统的电脑下,控制器参数优化设计的平均时间消耗约为40 min,完全可以满足参数离线设计的要求。
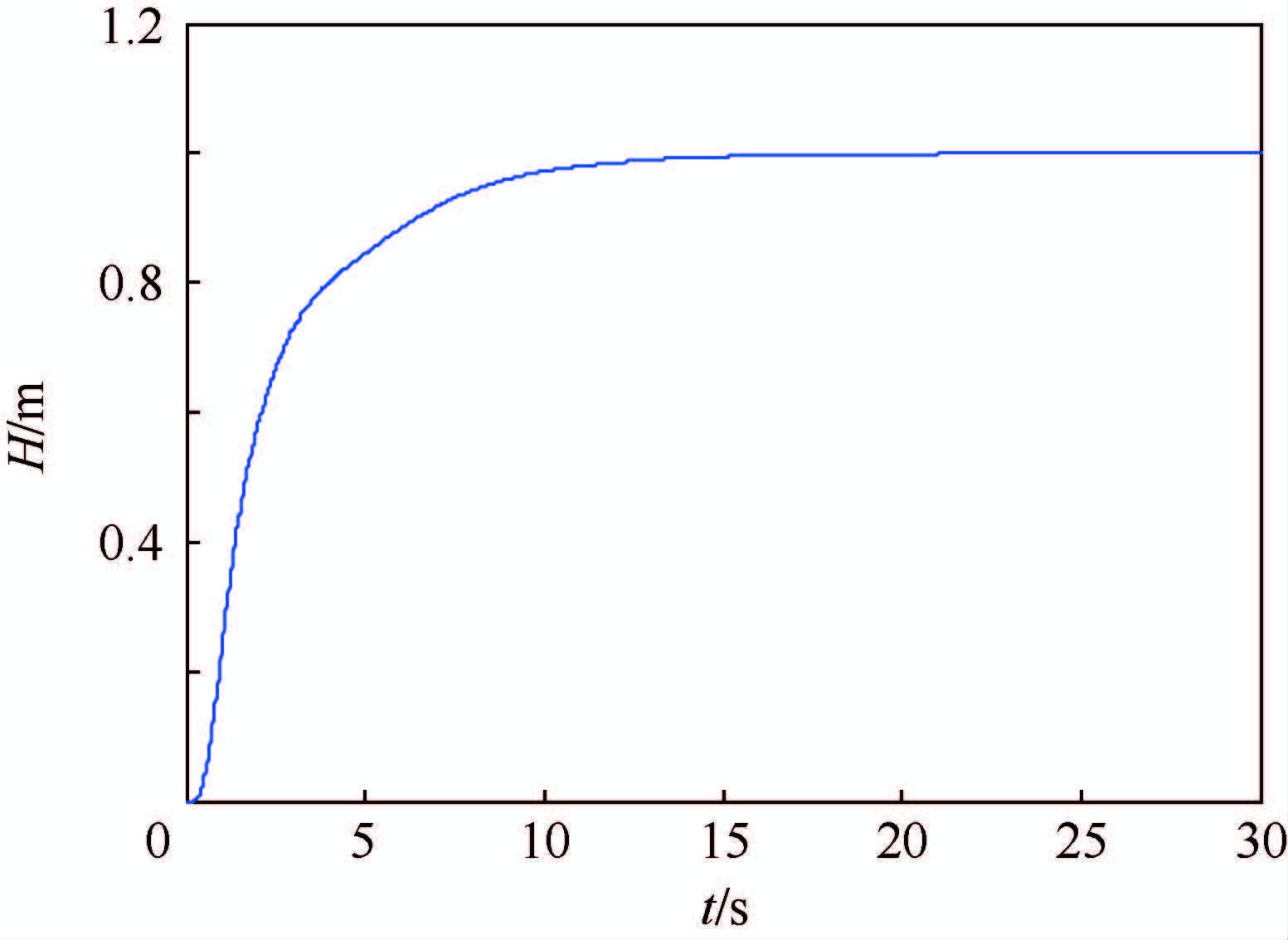 |
| 图 6 LADRC高度阶跃响应曲线 Fig. 6 Height step response curve of LADRC |
| 图选项 |
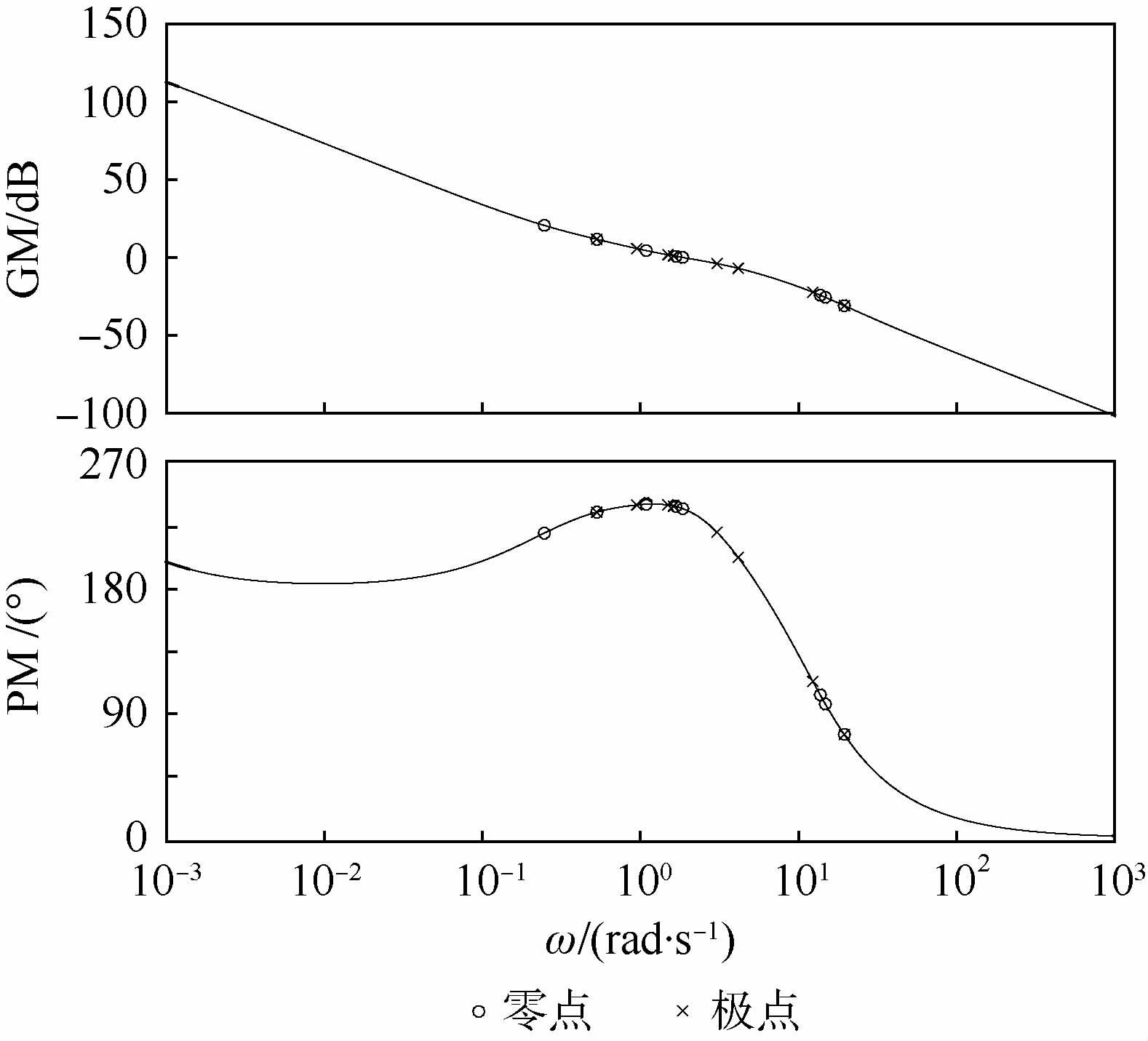 |
| 图 7 LADRC伯德图 Fig. 7 Bode diagram of LADRC |
| 图选项 |
6 仿真分析 在第2节控制器的基础上,分别从ESO观测扰动效果、在复杂气流扰动作用下的LADRC效果和气动参数摄动下的LADRC效果3个方面,验证LADRC的控制性能。
6.1 ESO观测扰动效果仿真结果分析 在俯仰角内回路、高度外回路和速度回路中分别对俯仰角加速度、高度和空速上叠加扰动量w(t)=0.5sin(0.5t),LADRC中相应ESO的观测效果如图 8所示,$\vartheta $″为俯仰角加速度。
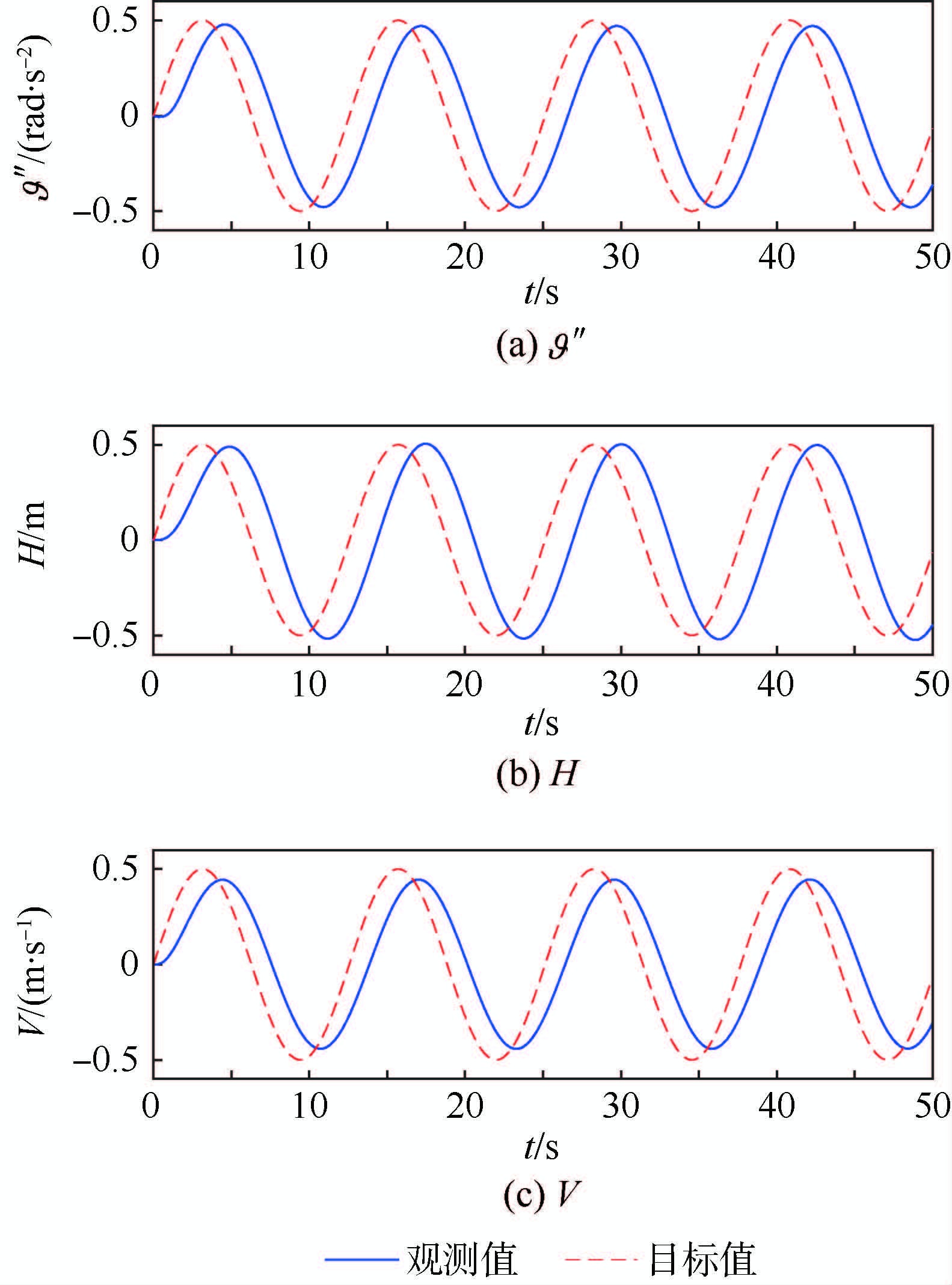 |
| 图 8 ESO观测结果 Fig. 8 Observed results of ESO |
| 图选项 |
由图 8可知,3个回路的ESO扰动跟踪整体效果较好,其中扰动幅值观测值和实际值基本相同,相位观测值与实际值间的偏差均在可接受的范围内。良好的ESO对干扰的观测跟踪效果,为LADRC抵抗扰动实现高精度控制奠定了基础。
6.2 复杂气流扰动仿真结果分析 为了说明在复杂气流扰动作用下LADRC的控制性能,分别引入离散突风和大气紊流2种风扰动,在H=8 m,V=25 m/s状态下,将LADRC的高度控制效果与PID的高度控制效果进行对比,其中PID控制器在无风干扰情况下的单位阶跃高度控制响应与LADRC基本相同。
在离散突风(半波长1-cos模型)干扰仿真中,在0 s给定8~ 9 m的高度阶跃指令,2种控制以相似的动态过程将无人机控制在9 m高度。在20 s后分别引入幅值为4 m/s的离散垂直突风扰动和离散顺向突风扰动,无人机相关运动情况如图 9和图 10所示,升降舵和油门响应以及各LADRC的控制补偿量如图 11和图 12所示。图中:Δ$\vartheta $g为高度通道补偿量,其实际为对俯仰角给定值的补偿;Δδz为俯仰角通道补偿量,其实际为对升降舵舵偏角的补偿量;Δδp为速度通道补偿量,其实际为对油门的补偿量。
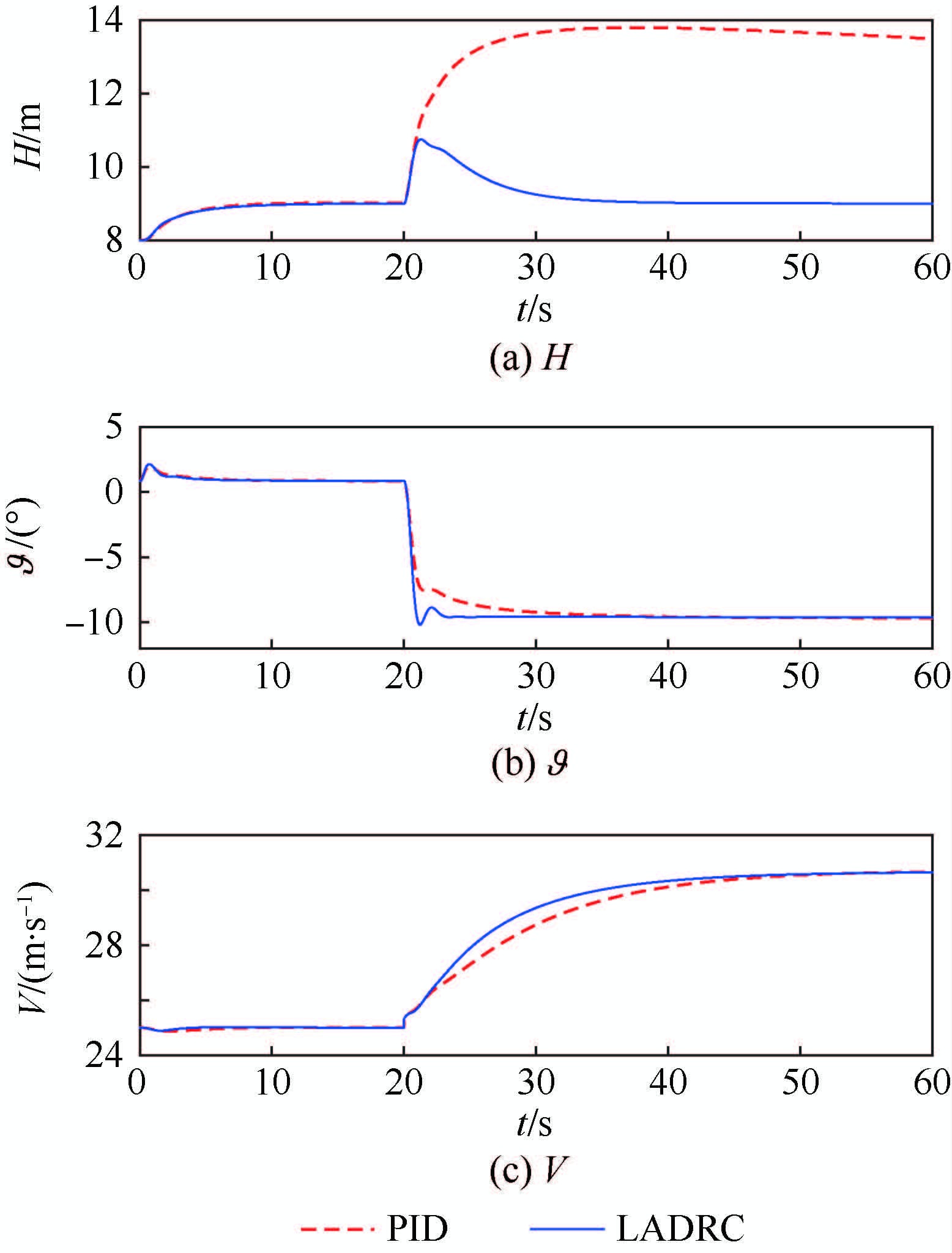 |
| 图 9 离散垂直突风下高度控制仿真结果 Fig. 9 Simulation results of height control underdiscrete vertical wind gust condition |
| 图选项 |
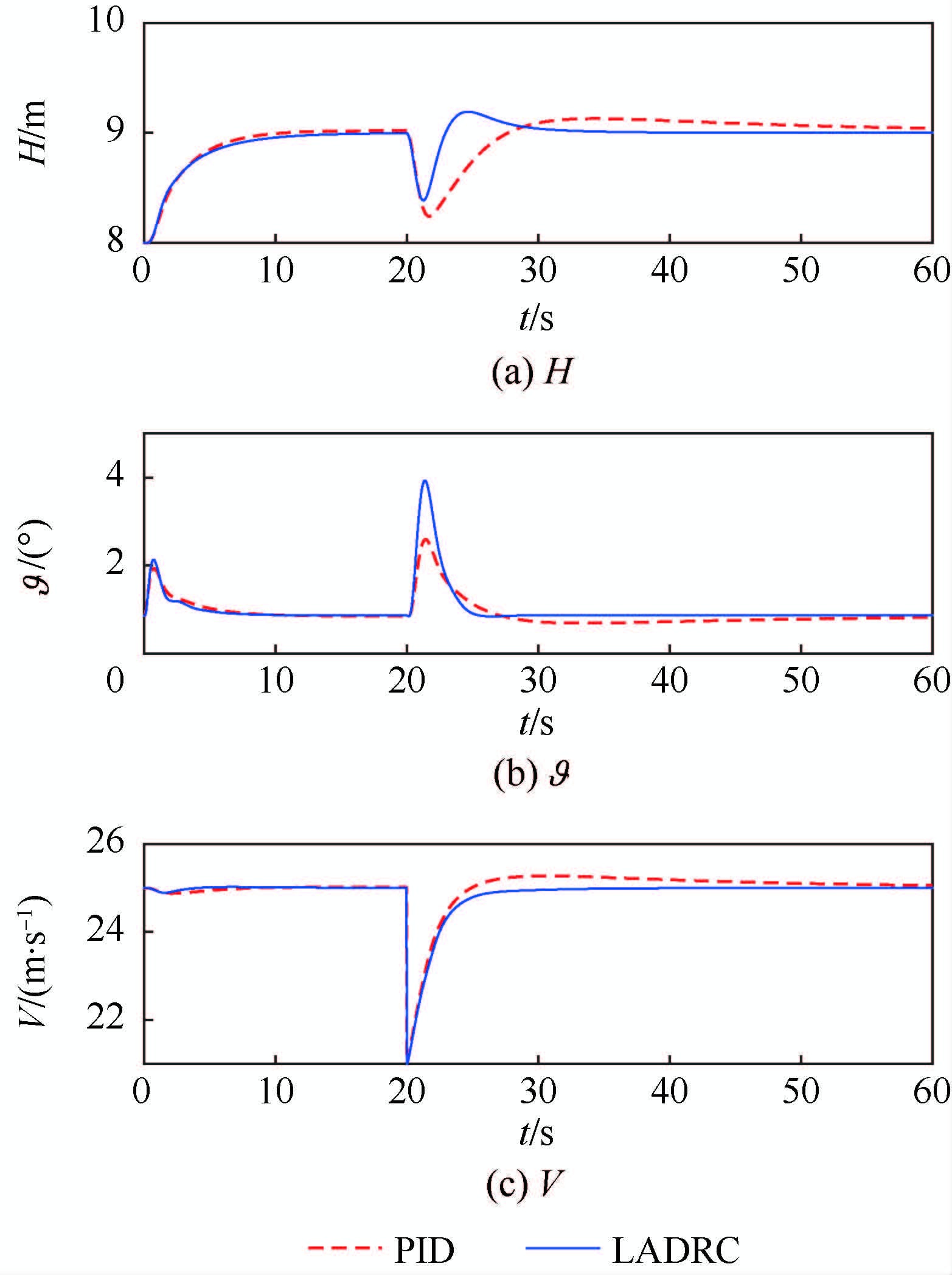 |
| 图 10 离散顺向突风下高度控制仿真结果 Fig. 10 Simulation results of height control underdiscrete forward wind gust condition |
| 图选项 |
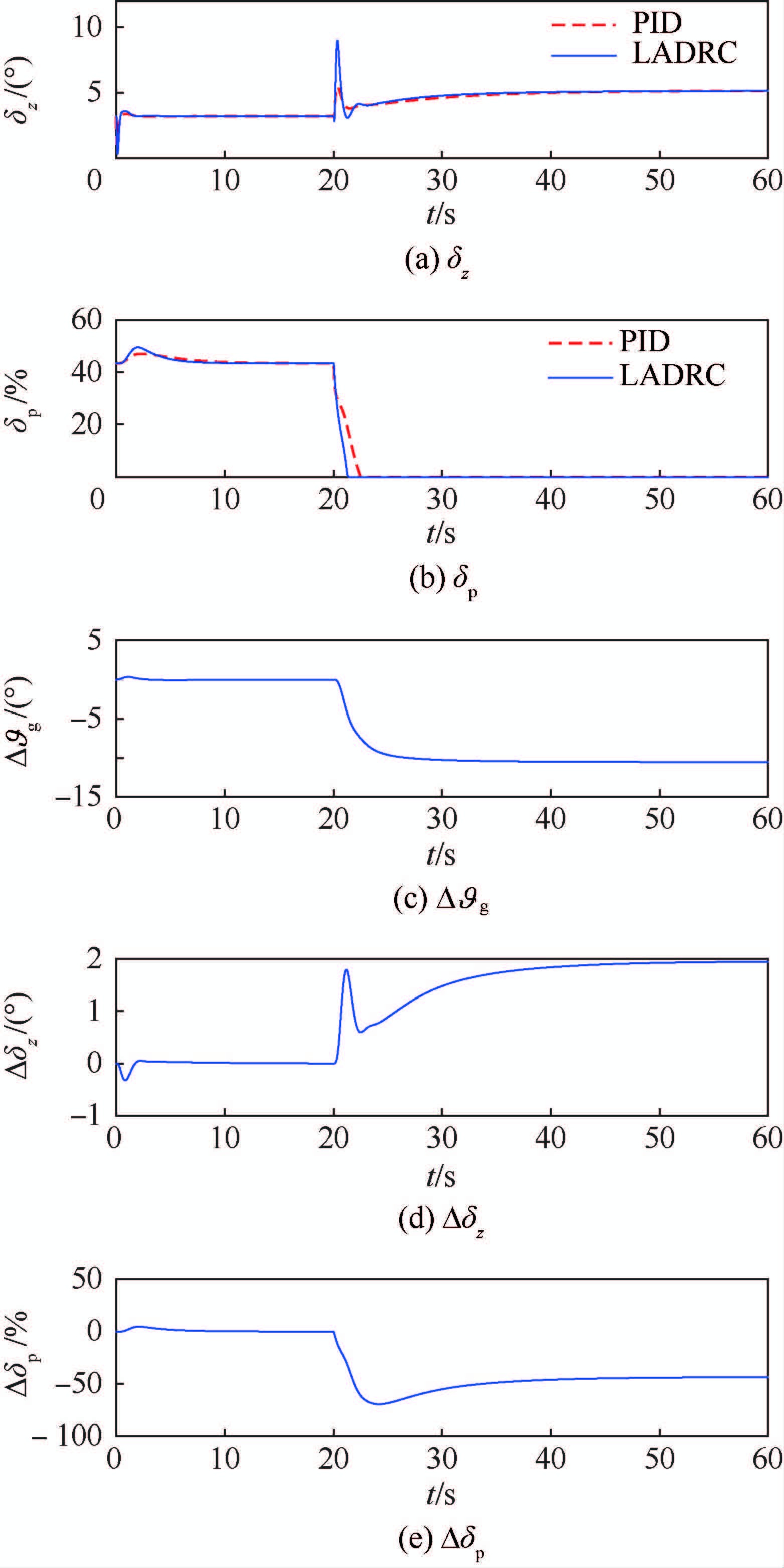 |
| 图 11 离散垂直突风下控制量与补偿量仿真结果 Fig. 11 Simulation results of control and compensatingquantities under discrete vertical wind gust condition |
| 图选项 |
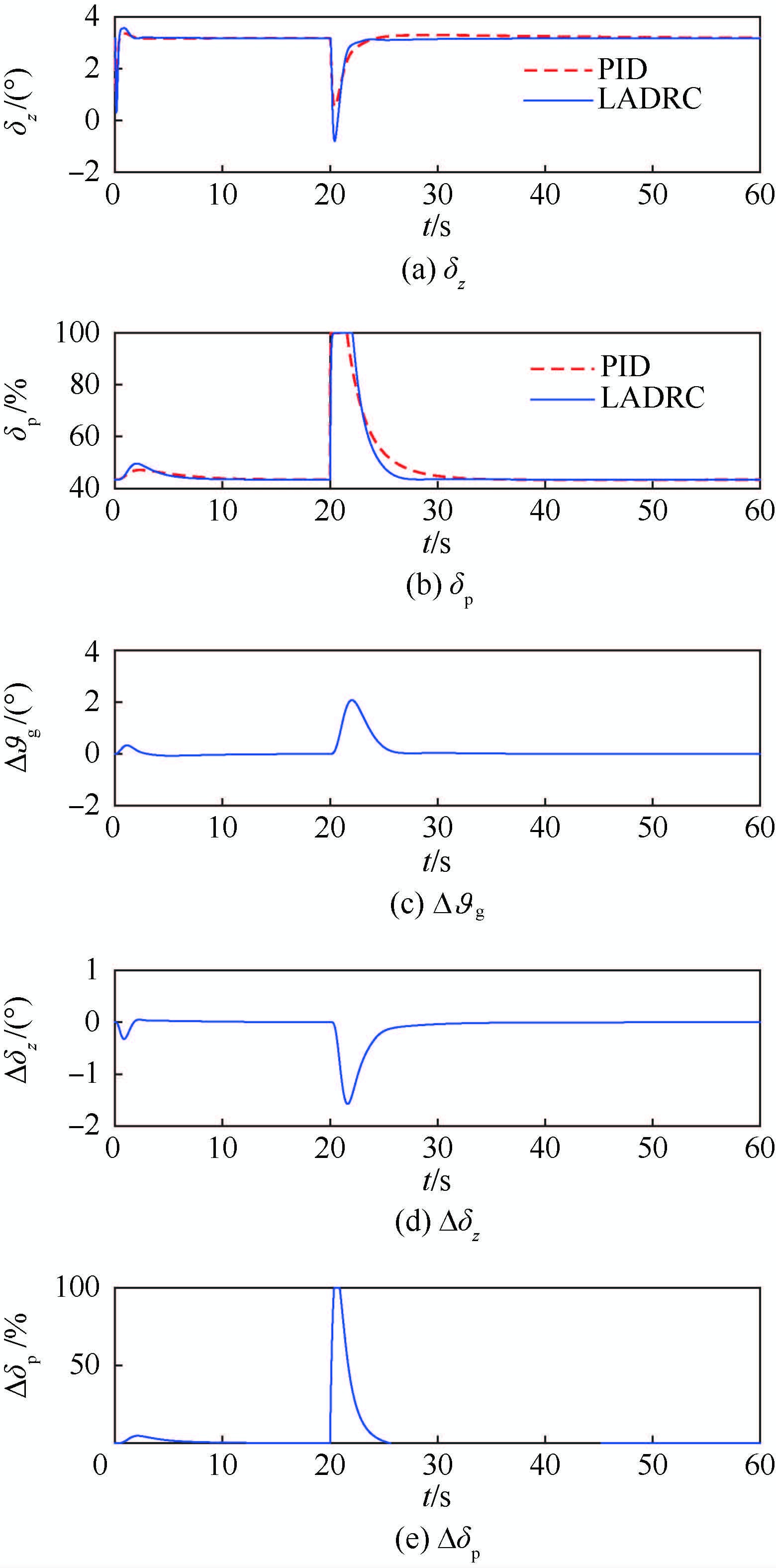 |
| 图 12 离散顺向突风下控制量与补偿量仿真结果 Fig. 12 Simulation results of control and compensatingquantities under discrete forward wind gust condition |
| 图选项 |
从图 12仿真结果中可看出LADRC的控制性能无论在受扰幅度或恢复基准值的快速性上,都明显优于PID控制器。以顺向突风为例,对仿真结果进行分析。
若无人机在飞行过程中受到顺向离散突风扰动,无人机空速减小导致升力减小,航迹高度降低,为了保持给定空速和高度,升降舵将上偏使飞机抬头,油门增加使空速增大。对于LADRC控制器,由于各通道ESO对扰动的观测作用,俯仰角给定值、升降舵舵偏角和油门会在控制中叠加补偿量,PID控制器相比,相应控制量均较大,因此高度和空速均可以更快恢复到基准值,从而提高控制律对风扰动的抑制作用,增强了抗干扰能力。垂直突风结果分析与此类似,此处不再赘述。
在大气紊流(德莱顿模型)干扰仿真中,假定无人机在H=8 m,V=25 m/s状态下作定高平飞,引入大气紊流扰动,升降舵和油门控制量以及各控制通道补偿量如图 13所示,PID控制器和LADRC的高度、俯仰角和空速控制效果对比如图 14所示。
 |
| 图 13 大气紊流作用下控制量与补偿量仿真结果 Fig. 13 Simulation results of control and compensatingquantities under wind turbulence condition |
| 图选项 |
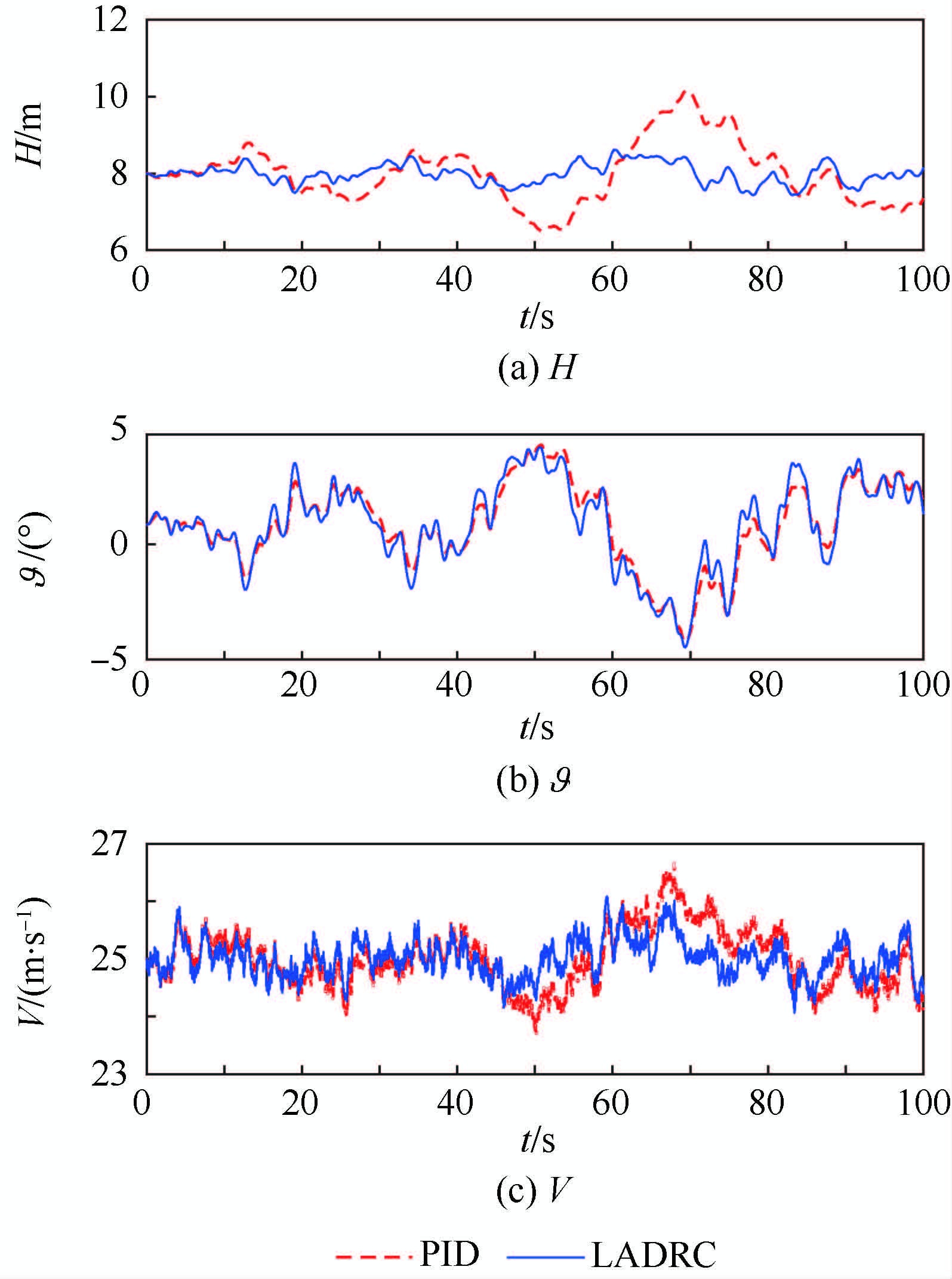 |
| 图 14 大气紊流作用下高度控制仿真结果 Fig. 14 Simulation results of height control underwind turbulence condition |
| 图选项 |
从图 13中可以看出LADRC下航迹高度和空速在大气紊流扰动作用下的波动幅度明显小于PID控制器,实现了高精度高度控制,其本质同上述分析相同,由ESO观测风扰动,并在控制中引入控制补偿以减小风扰动的影响。
6.3 气动参数摄动仿真结果分析 对于低速小型无人机而言,气动参数的不确定性对控制器的控制性能也有着较大的影响。为了说明气动参数摄动下LADRC的控制性能,引入气动参数摄动,将升力对迎角的导数Cyα和升降舵舵效mzδz减小40%,俯仰力矩对迎角的导数mzα增大40%,PID控制与LADRC下的高度阶跃响应结果对比如图 15所示。
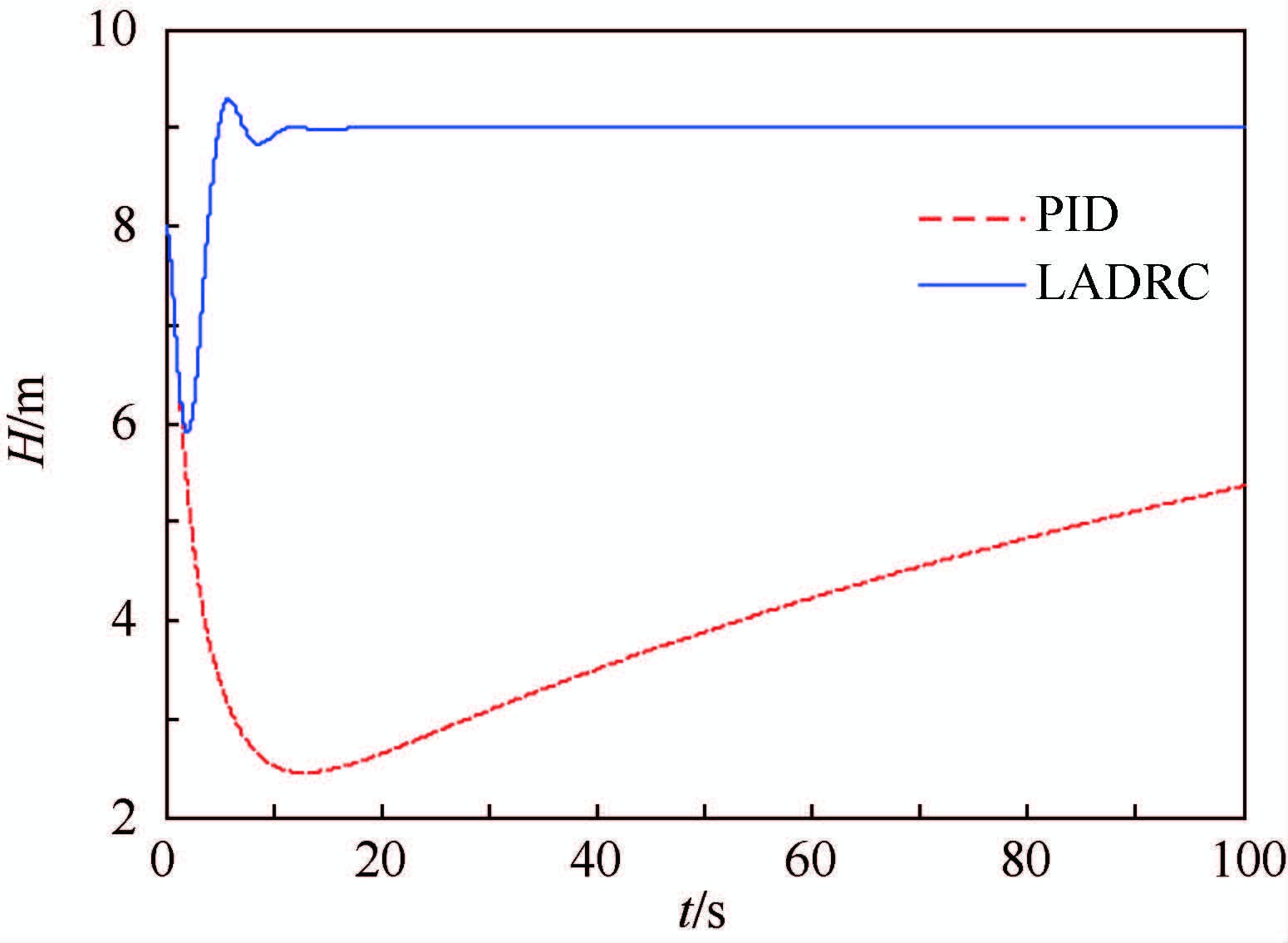 |
| 图 15 气动参数摄动仿真结果 Fig. 15 Simulation results of aerodynamicparameter perturbation |
| 图选项 |
从图 15仿真结果可以看出,PID控制器高度响应需要很长的时间才能达到给定值,而LADRC则可以很快达到给定值,LADRC较PID控制在存在气动参数摄动的情况下具有更好的控制效果。其本质是将气动参数摄动归结为系统的内部扰动,通过ESO估计出这一部分扰动,在控制量中叠加补偿,减小气动参数摄动的影响。
7 结 论 本文基于LADRC理论,实现了存在复杂气流扰动和气动参数摄动情况下的高精度高度控制,主要结论如下:
1) 在控制律设计过程中考虑风干扰的功率谱分布,可以减小控制器设计的保守性。
2) 仿真结果表明在复杂气流扰动情况下,与PID控制器相比较,LADRC具有更好的高度控制精度和抗干扰性能。
本文以 “天钩”方式回收为背景,对其他应用场合的相关控制也具有参考价值。
参考文献
| [1] | 孙林峰, 马晓平, 吴佳凯. 无人机绳钩回收仿真研究[J].科学技术与工程, 2012, 12(7): 1572–1575.SUN L F, MA X P, WU J K. Simulation research of rope-hook recovery of unmanned aerial vehicle[J].Science Technology and Engineering, 2012, 12(7): 1572–1575.(in Chinese) |
| [2] | DONG I Y,JUNG Y D,SUNG W C.A guidance and control law design for precision automatic take-off and landing of fixed-wing UAVs:AIAA-2012-4674[R].Reston:AIAA,2012. |
| [3] | CHEOLKEUN H. Gain-scheduled directional guidance controller design using a genetic algorithm for automatic precision landing[J].International Journal of Control Automation and Systems, 2010, 8(1): 107–117.DOI:10.1007/s12555-010-0114-y |
| [4] | 张建宏, 张平. 无人机自主精确着陆控制律设计及仿真研究[J].系统仿真学报, 2009, 21(3): 743–748.ZHANG J H, ZHANG P. Autonomous precise landing control law for UAV[J].Journal of System Simulation, 2009, 21(3): 743–748.(in Chinese) |
| [5] | 熊治国, 孙秀霞, 胡孟权, 等. 自抗扰控制器的飞机纵向运动控制律设计[J].电机与控制学报, 2006, 10(4): 420–430.XIONG Z G, SUN X X, HU M Q, et al. Control law design of aircraft longitudinal movement based on active disturbances rejection controller[J].Electric Machines and Control, 2006, 10(4): 420–430.(in Chinese) |
| [6] | 韩京清. 控制理论-模型论还是控制论[J].系统科学与数学, 1998, 9(4): 328–335.HAN J Q. Control theory-model or control[J].Journal of System Science and Mathmetic, 1998, 9(4): 328–335.(in Chinese) |
| [7] | 韩京清. 自抗扰控制技术-估计补偿不确定因素的控制技术[M].北京: 国防工业出版社, 2009: 255-261.HAN J Q. Active disturbance rejection control-control technique for estimating and compensating uncertain factor[M].Beijing: National Defense Industry Press, 2009: 255-261.(in Chinese) |
| [8] | GAO Z Q.Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the American Control Conference.Piscataway,NJ:IEEE Press,2003:4989-4996. |
| [9] | GAO Z Q,HU S H,JIANG F J.A novel motion control design approach based on active disturbance rejection[C]//Proceedings of the 40th IEEE Conference on Decision and Control.Piscataway,NJ:IEEE Press,2001:1547-1552. |
| [10] | 肖业伦, 金长江. 大气扰动中的飞行原理[M].北京: 国防工业出版社, 1993: 11-14.XIAO Y L, JIN C J. Flight principles in wind disturbances[M].Beijing: National Defense Industry Press, 1993: 11-14.(in Chinese) |
| [11] | ROBINSON P A, REID L D. Modeling of turbulence and downbursts for flight simulators[J].Journal of Aircraft, 1990, 27(8): 700–707.DOI:10.2514/3.25343 |
| [12] | 肖业伦. 飞行器运动方程[M].北京: 航空工业出版社, 1987: 93-94.XIAO Y L. Motion equations of aerial vehicles[M].Beijing: Aeronautics Industry Press, 1987: 93-94.(in Chinese) |
| [13] | SHI Y H. Particle swarm optimization[J].IEEE Connections, 2004, 2(1): 8–13. |
| [14] | JACA F S, ALBERT A G. A study of global optimizaition using particle swarms[J].Journal of Global Optimization, 2005, 31(1): 93–108.DOI:10.1007/s10898-003-6454-x |
| [15] | CHATTERJEE S P. Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[J].Computers & Operations Research, 2006, 33(3): 859–871. |
