行星齿轮系统因其结构紧凑、功率密度高及自对中性能好等多种优点被各型直升机广泛采用,是直升机主减速器的主要部件,其可靠性在直升机传动系统各部件中占据首要位置。自20世纪70年代澳大利亚海军尝试用振动信号分析主齿轮箱的健康状况以来,国内外大量****集中于研究齿轮故障与齿轮传动的动力学特性的故障诊断,通过建立齿轮传动的非线性动力学模型[4],研究断齿、齿侧间隙和负载对传动动态特性的影响[5-7]及在齿轮箱上加装振动传感器进行故障特征提取[3, 8-9]等方法取得了一些卓有成效的研究成果。而行星架的疲劳裂纹故障一直没能引起人们足够关注,直到2002年美军在两架UH-60A黑鹰直升机的主减速器行星架上发现疲劳裂纹[10],导致一批黑鹰直升机停飞,并由此启动了一系列针对此类故障的研究[5, 11-13],但至今鲜有相关研究文献报道此类问题研究取得长足进展。
行星架疲劳裂纹故障的发生、发展的初期具渐进性和隐蔽性的特点。因为行星架安装在主减速器机匣中,例行的常规检查手段不易触及。另外主减速器的机载工况复杂,行星架裂纹故障信号极易被淹没在上、下游旋转部件的噪声中,并且较短的行星架疲劳裂纹并不造成传动系统性能的显著降低,使得现有的现场技术手段很难有效检测和发现行星架裂纹故障。文献[10]中显示,美军资助了大量的以UH-60A黑鹰直升机主减速器的82 mm裂纹行星架为基础的现场试验和实验室研究以后得出结论:“目前尚无有效手段能够在机载低扭矩条件下检测到(行星架)裂纹故障,或者机载测试环境的低扭矩值不足以暴露(行星架)裂纹故障信号。”然而,由于金属疲劳裂纹的扩展在疲劳破坏累积效应下,存在裂纹失稳扩展阶段,在疲劳裂纹扩展的末段会急速断裂,使得构件迅速失效[14]。因此,准确预测行星架疲劳裂纹的发生、发展,预测裂纹故障状态下行星架的剩余使用寿命,在疲劳裂纹故障发展到恶劣程度、传动系统失控之前,预警直升机操控人员采取处置措施,显得极为重要。
针对疲劳机理和规律的研究兴起于20世纪中叶[14]。在过去的几十年里,疲劳寿命预测技术也有了长足的发展。精确的疲劳寿命预测受多种随机因素影响,依赖大量样本统计数据作为基础[15]。目前工程应用中,有很多研究者采用随机模型进行剩余寿命估计[16-19],然而统计学方法并不真正关心疲劳机理和裂纹的发生、发展过程,往往关注于母体而失去个体。疲劳和断裂力学理论因其在定量描述疲劳机理和断裂过程方面的巨大优势,被大量****广泛用于定量地计算疲劳寿命、指导产品设计和疲劳寿命预测,也取得了较为显著的成果[20-24]。
本文在深入研究行星架疲劳裂纹故障机理的基础上,分析行星架裂纹发生和发展规律,基于线弹性断裂力学理论,依据裂纹扩展过程中的对数线性规律,提出将行星架疲劳裂纹扩展过程离散化,联合Miner准则和Paris公式,将疲劳裂纹扩展损伤过程累积,得到行星架的寿命预测数据。并采用ANSYS Workbench对疲劳过程进行仿真,对比验证了方法的有效性。
1 行星架疲劳裂纹故障 1.1 故障特点及状态划分 某型直升机主减速器中单级行星齿轮系统结构与传动关系如图 1所示。该行星系统由1个绕中心旋转的太阳齿轮、1个绕中心旋转的行星架、5个通过轴承(图中不可见)安装在行星架立柱上的行星齿轮和1个固定在减速器机壳上的内齿圈组成。太阳齿轮旋转提供系统输入,驱动行星齿轮绕安装立柱自转,同时推动行星架绕中心转动,行星架通过轮毂内花键输出扭矩,花键联接直升机主旋翼轴,提供直升机飞行所需升力。行星架是行星齿轮系统健康工作的核心部件,结构上由向上的内置花键轮毂、盘面和向下的5个立柱组成。考虑减重目的,立柱结构上采用通孔设计,同时,盘面上另有等间距分布的5个减重孔。
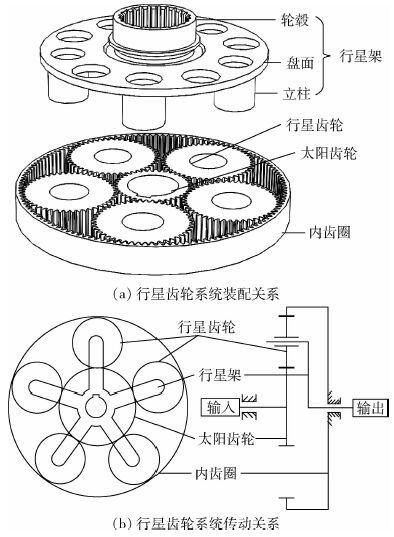 |
| 图 1 直升机主减速器行星轮系 Fig. 1 Planetary gear train of a helicopter main transmission |
| 图选项 |
行星架盘面疲劳裂纹故障形式具有以下特点:
1) 起始:裂纹起始于立柱根部与盘面下表面相接位置,亦即结构的应力集中位置。
2) 扩展:裂纹萌生后向两端扩展,短裂纹阶段,裂纹扩展主要朝向行星架盘面外缘,直至外缘撕裂,然后向内直达轮毂根部。
3) 走向:裂纹走向沿立柱外缘和轮毂外缘公切线方向,约成直线。
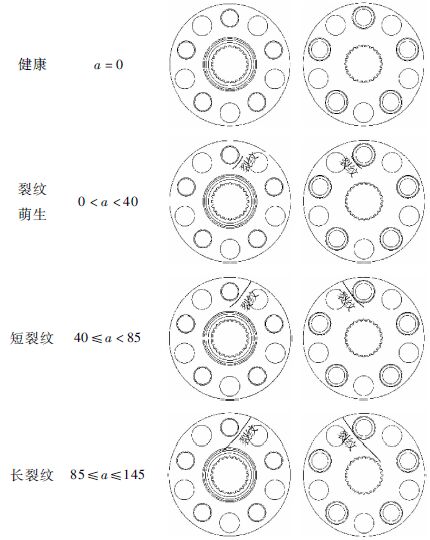
本文根据裂纹故障的发生、发展情况,将行星架裂纹故障划分为4个状态(含健康无裂纹),如表 1所示, a为裂纹长度。
在行星架健康(无裂纹)和裂纹萌生、短裂纹、长裂纹共4个状态下,其裂纹局部结构内应力的情况也有极大的不同:
1) 健康(无裂纹)状态下,由于结构和动力学环境造成的应力集中主要位于行星齿轮安装立柱与行星架盘面相接处,即便排除(材料缺陷、构件加工工艺缺陷、装配误差等)随机因素影响,应力集中部位的周期加载,极易使得疲劳裂纹在相应位置产生。
表 1 行星架裂纹故障状态 Table 1 Crack fault state of a planetary carrier plate
| 状态 | a/mm | 顶视 | 底视 |
 | |||
表选项
2) 裂纹萌生阶段,行星架盘体底面产生表面裂纹,但尚未完全穿透厚度方向,裂纹尖端局部有多个应力集中点(不少于2个),疲劳损伤累积使得裂纹一方面洞穿盘面,一方面向外缘扩展。
3) 短裂纹阶段,裂纹贯穿行星架盘体厚度方向,形成穿透裂纹,裂纹的两个尖端中,朝向外缘的尖端局部承受较大的应力集中,疲劳裂纹沿立柱外缘切向,向盘面外缘扩展,直至盘面外缘破裂。
4) 长裂纹阶段,裂纹局部应力集中指向盘面内部,疲劳裂纹沿立柱外缘和轮毂外缘公切线方向扩展,直至轮毂根部,行星架失效。
1.2 裂纹尖端局部应力载荷谱 排除材料各向异性、材料内部缺陷、构件加工工艺缺陷及装配误差等随机因素影响,行星架疲劳裂纹故障受结构应力集中和局部应力的循环加载而造成的损伤累积影响最大。在本文中,做如下假设:
1) 无论行星架故障程度,均保持其输出功率不变,亦即行星架输出扭矩不变。
2) 行星架上5个立柱受均等载荷。
在上述假设前提下,本文利用有限元软件ANSYS Workbench(Version 15.0) 对裂纹故障的行星架进行了裂纹尖端应力仿真(裂纹尖端,以下简称裂尖,是指行星架盘面下表面裂纹扩展活动的最前端,如图 2中所示),软件仿真条件如表 2所示,得到应力(σ)曲线如图 3所示。
 |
| 图 2 裂纹尖端示意图 Fig. 2 Schematic diagram of crack tip |
| 图选项 |
表 2 裂纹尖端应力软件仿真条件 Table 2 Software simulation conditions of crack-tip stress
| 项目 | 仿真条件 |
| 网格单元尺寸/mm | 5 |
| 网格划分方式 | Tetrahedrons |
| 材料 | Structural Steel |
| 固定支撑 | 花键槽 |
| 扭矩 | 100% |
| 载荷力 | 作用于各立柱外表面,大小按扭矩值折算 |
| 等价应力类型 | Equivalent(von-Mises) Stress |
表选项
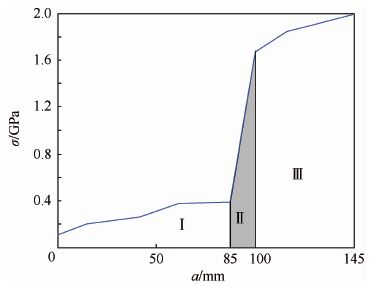 |
| 图 3 裂纹扩展过程中裂纹尖端应力仿真曲线 Fig. 3 Crack-tip stress simulation curves in crack propagation process |
| 图选项 |
由图 3可知,在行星架疲劳裂纹扩展过程中,裂尖应力有突然跃升的现象,裂纹长度85 mm和100 mm处存在两个较为明显的奇异点,原因在于:①短裂纹阶段(40 mm≤a<85 mm)下表面有两个裂尖(本文中该段应力曲线取值向外的那个裂尖),此时裂纹扩展方向朝外,向盘面外缘发展。在裂纹长度为85 mm时,行星架盘面外缘破裂,下表面裂纹扩展活动转为朝里,向轮毂根部发展,仿真发现此时裂尖应力值有大幅增长,裂尖应力曲线出现第1个奇异点。②裂纹长度为100 mm时,裂纹向里扩展至轮毂根部退刀槽区域,盘面厚度变薄,裂纹扩展加速,但裂尖应力值增长速度变缓,裂尖曲线在100 mm前后的斜率不一致,曲线出现第2个奇异点。本文中依据应力曲线走势,取85 mm和100 mm做为分界点,将行星架疲劳裂纹扩展过程划分Ⅰ、Ⅱ、Ⅲ共3个阶段。
另外需要说明的是,研究[25-26]发现,裂尖存在较高的应力梯度且尖端处应力与应变具有1/r奇异性,r为有限元网格单元长度,通过把裂尖附近二阶单元的中间节点沿裂尖方向移至靠近裂尖1/4分点处,就可以使裂尖附近应力场达到奇异性。裂尖奇异单元如图 4所示。本文中,围绕裂尖的第1行单元采用奇异单元划分网格,余下部分采用常规单元进行划分,取第2行单元中点应力值为计算依据,以保障求解精度。
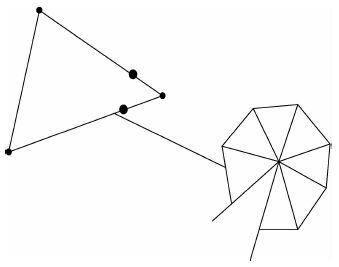 |
| 图 4 裂纹尖端奇异单元 Fig. 4 Singularity elements around crack-tip |
| 图选项 |
2 裂纹扩展寿命预测理论 2.1 线性累积损伤与Miner准则 疲劳寿命被定义为在循环加载下,产生疲劳破坏的应力循环次数或应变循环数。Miner准则是目前应用最为广泛的疲劳累积损伤准则。Miner准则定义的疲劳损伤是均匀、等效的,其疲劳损伤积累与应力循环次数成线性关系[27]。在某一等幅疲劳应力Si作用下(i为等幅应力的加载序数,对应的等幅疲劳寿命为Ni,由S-N曲线确定),在每一应力循环里,材料吸收的净功Δω相等,当这些被材料吸收的净功累积达到临界值W时,疲劳破坏发生。即
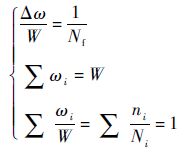 | (1) |
式中:ni为构件在恒幅应力水平Si作用下的循环次数,由载荷谱给出;ωi为在Si作用下产生的净功;Nf为材料失效寿命。图 5给出试件在应力S1作用下进行疲劳试验到A点,经历应力S2作用下进行疲劳试验到B点,其累积损伤效应可在OF上直接相加。
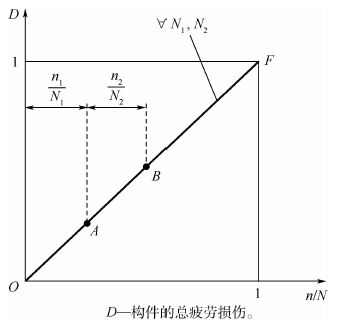 |
| 图 5 Miner准则中疲劳损伤的累积方式 Fig. 5 Fatigue damage cumulative approach in Miner rule |
| 图选项 |
Miner准则原理简单,计算方便,但用于裂纹扩展的寿命预测时,它的难点在于如何确定裂纹在各应力水平下的裂纹扩展速率,并因而影响预测的精度。
2.2 疲劳裂纹扩展速率与Paris公式 疲劳裂纹扩展速率da/dN是在疲劳载荷作用下,裂纹长度a随循环次数N的变化率,反映裂纹扩展的快慢。lg(da/dN)-lg ΔK曲线可以分为低、中、高速率3个区,如图 6所示。图中:ΔK为应力强度因子幅值,是疲劳裂纹扩展的主要控制参量;ΔKth为反映疲劳裂纹是否扩展的一个重要的材料参数,称为疲劳裂纹扩展的门槛应力强度因子幅度, 是da/dN-ΔK曲线的下限;R为应力比,是循环最小应力Smin和最大应力Smax的比值;KC为材料断裂时的应力强度因子,又称材料的断裂韧性。
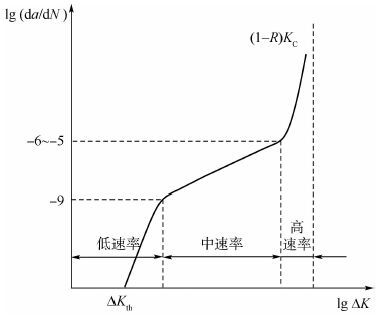 |
| 图 6 裂纹扩展速率与ΔK的关系 Fig. 6 Relationship between crack growth rate and ΔK |
| 图选项 |
大量研究表明,中速率区内da/dN-ΔK有良好的对数线性关系[14, 21, 23]。利用这一关系进行裂纹扩展寿命预测,是疲劳裂纹断裂研究的重点。对于中速率区的稳定裂纹扩展,da/dN-ΔK间的关系可以表达为
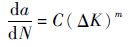 | (2) |
式(2) 就是著名的Paris公式[28],C、m为材料常数,是描述材料疲劳裂纹扩展性能的基本参数,由实验确定。
应力强度因子幅值为
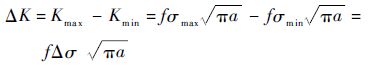 | (3) |
式中:Kmax为应力强度因子的最大值;Kmin为应力强度因子的最小值;σmax为裂尖承受应力的最大值;σmin为裂尖承受应力的最小值;Δσ为裂尖承受应力变程;f为几何修正系数,是裂纹长度a和其他几何尺寸的函数,可以由手册查得[29]。
将式(3) 代入式(2) ,有
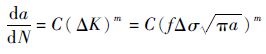 | (4) |
对式(4) 求积分,有
 | (5) |
式中:af为破坏发生时裂纹长度;a0为起始裂纹长度。
将实际应力Δσ改写为名义应力变程ΔS=Smax-Smin,同时,注意应力幅Sa=ΔS/2=(Smax-Smin)/2,式(5) 可得
 | (6) |
式中:Cl为材料的疲劳寿命参数。
可见,在中速率区稳定裂纹扩展阶段,疲劳寿命完全由裂纹扩展所贡献,由Paris公式推出了Sa-N曲线公式,式(2) 和式(6) 的指数m相同,为预测疲劳裂纹扩展寿命提供了理论依据。
2.3 Miner准则联合Paris公式的损伤累积裂纹扩展理论 假设尺寸为a0的初始裂纹,在应力水平ΔS1、ΔS2、ΔS3作用下分别经历N1、N2、N3次循环后扩展到定义破坏尺寸af。若在ΔS1作用下循环n1次,裂纹尺寸从a0扩展到a1,由式(6) 可得
 | (7) |
式中:
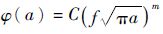
在ΔS1作用下,裂纹尺寸从a0扩展到af,有
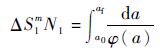 | (8) |
ΔS1作用下应力循环比为
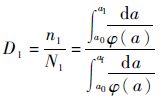 | (9) |
式中:N1为在ΔS1作用下一直扩展到破坏的裂纹扩展寿命。然后在ΔS2作用下循环n2次,裂纹尺寸从a1扩展到a2,得到ΔS2作用下应力循环比为
 | (10) |
同样地,若在ΔS3作用下循环n3次,裂纹尺寸从a2扩展到a3(a3=af),得到ΔS3作用下应力循环比为
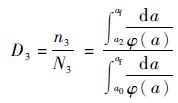 | (11) |
总损伤为
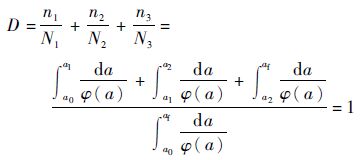 | (12) |
依据Miner准则,各应力水平下的应力循环比累积到1时,失效发生。
3 基于过程离散化的行星架疲劳裂纹扩展寿命预测 3.1 分阶段等分应力谱折线 由于行星架裂纹过程中力学结构变化快、影响裂纹扩展速率的因素多,裂纹萌生以后扩展至构件失效阶段的疲劳寿命计算是行星架整寿命计算过程中的难点。本文基于da/dN-ΔK的对数线性关系,提出等分应力谱折线的方法,将连续的裂纹扩展过程离散化处理,并联合Miner准则和Pairs公式,计算了行星架疲劳裂纹的扩展寿命。
本文中将裂纹扩展阶段Ⅰ、Ⅱ、Ⅲ的应力谱折线等分为若干小段(如图 7所示),依据Paris公式积分计算小段区间疲劳裂纹扩展损伤值;取每小段折线区间中点应力值作为该区间当量应力均值,按照Miner准则累积各小段区间疲劳裂纹扩展寿命,得到行星架疲劳裂纹扩展寿命数据。
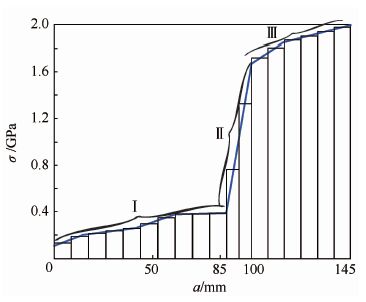 |
| 图 7 分阶段等分应力谱折线 Fig. 7 Aliquots of phased stress polyline |
| 图选项 |
其数学计算过程如下:
裂纹扩展速率函数为
 | (13) |
第i小段裂纹扩展损伤为
 | (14) |
Ⅰ/Ⅱ/Ⅲ阶段裂纹扩展损伤为
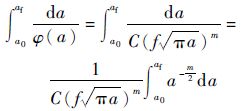 | (15) |
因此,第i小段的应力循环比为
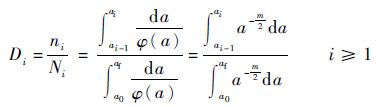 | (16) |
式(16) 及以后的计算中,C和f因同时出现在分式的分子和分母中而相互抵消。
可得,第i小段应力ΔSi施加的循环数为
 | (17) |
将各小段循环数累加,可得行星架疲劳裂纹扩展寿命为
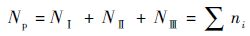 | (18) |
3.2 行星架疲劳裂纹扩展寿命计算 行星架疲劳裂纹扩展寿命计算过程中用到的材料S-N曲线如图 8所示,其方程为
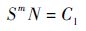 | (19) |
式中:m=1.5;Cl=8×1018。
行星架疲劳裂纹扩展寿命计算结果见表 3。
 |
| 图 8 材料的S-N曲线 Fig. 8 S-N curve of adopted material |
| 图选项 |
表 3 行星架疲劳裂纹扩展寿命 Table 3 Planetary carrier plate fatigue crack propagation life
| 阶段 | 序号 | a/mm | S/(108Pa) | N/(106周) | ni/(104周) | D/% |
| Ⅰ | 1 | 0 | 1.100 | 6.938 | 390.2 | 56.23 |
| 2 | 8.50 | 1.378 | 4.948 | 52.65 | 10.64 | |
| 3 | 17.00 | 1.656 | 3.756 | 26.79 | 7.13 | |
| 4 | 25.50 | 1.933 | 2.976 | 16.42 | 5.52 | |
| 5 | 34.00 | 2.211 | 2.433 | 11.10 | 4.56 | |
| 6 | 42.50 | 2.489 | 2.037 | 7.988 | 3.92 | |
| 7 | 51.00 | 2.767 | 1.738 | 6.010 | 3.46 | |
| 8 | 59.50 | 3.045 | 1.505 | 4.674 | 3.10 | |
| 9 | 68.00 | 3.323 | 1.321 | 3.733 | 2.83 | |
| 10 | 76.50 | 3.601 | 1.171 | 3.043 | 2.60 | |
| 小计 | 522.6 | 100.00 | ||||
| Ⅱ | 11 | 85.00 | 3.876 | 1.049 | 22.03 | 21.01 |
| 12 | 88.00 | 6.435 | 0.490 1 | 10.03 | 20.47 | |
| 13 | 91.00 | 8.994 | 0.296 6 | 5.925 | 19.98 | |
| 14 | 94.00 | 11.55 | 0.203 7 | 3.973 | 19.50 | |
| 15 | 97.00 | 14.11 | 0.150 9 | 2.877 | 19.06 | |
| 小计 | 44.84 | 100.00 | ||||
| Ⅲ | 16 | 100.00 | 16.67 | 0.117 5 | 3.261 | 27.75 |
| 17 | 111.25 | 17.48 | 0.109 5 | 2.816 | 25.72 | |
| 18 | 122.50 | 18.28 | 0.102 3 | 2.456 | 24.00 | |
| 19 | 133.75 | 19.09 | 0.095 93 | 2.161 | 22.53 | |
| 20 | 145.00 | |||||
| 小计 | 19.71 | 100.00 | ||||
| 合计 | 587.1 |
表选项
如表 3中所示,各小段应力循环次数ni逆向累加,得到任意裂纹长度下的行星架剩余使用寿命。
本文基于过程离散化方法,联合Miner准则和Paris公式,计算得到行星架疲劳裂纹故障从启裂到扩展失效的整寿命数值为5.871×106周。
4 仿真与对比验证 目前应用广泛的商用有限元软件ANSYS Workbench含有疲劳模块,允许用户采用基于应力理论的方法,解决构件高周疲劳问题。ANSYS Workbench疲劳模块基于比例载荷、恒定振幅的应力载荷,可以较为精确地预测构件裂纹萌生寿命,但在预测裂纹扩展寿命方面受到诸多局限。
本文中,在ANSYS Workbench(Version 15.0) 软件环境下,把裂纹扩展视为不断启裂的过程,同样将裂纹扩展过程离散化处理,并采用多段裂纹萌生寿命累加逼近行星架疲劳裂纹扩展寿命,得到仿真曲线,并与本文中数值计算结果进行对比,ANSYS Workbench软件仿真条件如表 4所示,得到剩余使用寿命(NR)计算值与仿真值对比如图 9所示。
表 4 疲劳寿命软件仿真条件 Table 4 Software simulation conditions of fatigue life
| 项 | 值 |
| 网格单元尺寸/mm | 5 |
| 网格划分方式 | Tetrahedrons |
| 材料 | Structural Steel |
| S-N曲线 | S1.5N=8×1018 |
| 疲劳强度因子(Kf) | 0.8 |
| 固定支撑 | 花键槽 |
| 扭矩 | 100% |
| 载荷形式 | Zero-based |
| 平均应力理论 | Mean Stress Curves |
表选项
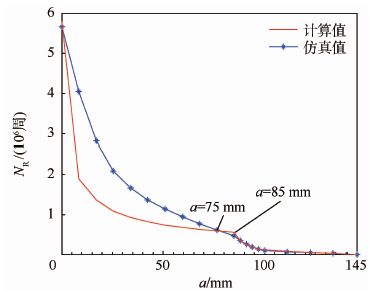 |
| 图 9 剩余使用寿命计算值与仿真值对比 Fig. 9 Comparison between calculated and simulated values of remaining service life |
| 图选项 |
图 9显示了裂纹故障状态下行星架剩余使用寿命随疲劳裂纹长度的变化曲线。在图 9中对本文所提出方法的数学计算值和ANSYS Workbench软件仿真值进行了对比。从图 9中可以看出,两条曲线在75 mm处有交点,在75 mm及以下裂纹长度时,ANSYS Workbench软件计算得到的剩余寿命数值,较本文中的方法偏安全,两者数值相差最大处,软件预测值超出本文计算值53%。ANSYS Workbench软件预测曲线相对平滑,看不到明显分界点,而本文采用方法的预测曲线中,仍能明显看到阶段Ⅰ和阶段Ⅱ的分界点。
由图 9的计算值曲线可以看出,剩余寿命曲线的切线斜率有两个迅猛变化阶段。第1个阶段出现在疲劳裂纹长度0<a≤40 mm即裂纹萌生阶段,微小裂纹的出现也使得构件剩余寿命急剧降低。第2个阶段出现在85 mm≤a≤100 mm,行星架盘面边缘破裂,剩余寿命在短时间内迅速降低。当a>100 mm时,结构失稳严重,行星架几乎不再具有剩余寿命。计算值曲线的变化与行星架疲劳裂纹扩展过程吻合程度高,能够反映行星架疲劳裂纹故障至失效的整个过程。
5 结论 线弹性断裂力学理论认为,裂尖附近的应力场是由应力强度因子K控制的,故裂纹在疲劳载荷作用下的扩展应当能够利用应力强度因子K进行定量的描述。基于此,本文提出将行星架疲劳裂纹扩展过程载荷谱离散化处理并联合Miner准则和Paris公式的方法,定量估计行星架疲劳裂纹扩展寿命,主要结论如下:
1) 本文提出的线弹性断裂力学方法计算得出的疲劳裂纹剩余,使用寿命曲线,相比较ANSYS Workbench 仿真曲线,与行星架疲劳裂纹扩展过程吻合程度高,能够反映行星架疲劳裂纹故障发生至构件失效的整个过程。
2) 本文基于线弹性断裂理论的方法,摆脱了传统的基于随机模型的疲劳寿命预测理论对于大量的构件疲劳寿命采样数据的依赖,因而经济性较好。
3) 本文中的计算未计入材料缺陷、加工工艺缺陷、装配误差等随机因素影响,文中的行星架疲劳裂纹状态下剩余使用寿命对于行星架的疲劳寿命确定具有参考价值。计入随机因素影响的多样本疲劳裂纹数据,理论上仍应服从威布尔分布。
致谢
衷心感谢许金泉教授对本文的付出和悉心指导。
参考文献
| [1] | HARRIS F D,KASPER E F,ISELER L E. US civil rotorcraft accidents,1963 through 1997:NASA/TM-2000-209597[R].California:Administration NASA,2000.http://cn.bing.com/academic/profile?id=2088799539&encoded=0&v=paper_preview&mkt=zh-cn |
| [2] | 侯胜利. 直9B型机故障研究[J].直升机技术, 2002(2): 40–42.HOU S L. Fault research of Z-9B helicopter[J].Helicopter Technique, 2002(2): 40–42.(in Chinese) |
| [3] | SAMUEL P D, PINES D J. A review of vibration-based techniques for helicopter transmission diagnostics[J].Journal of Sound and Vibration, 2005, 282(1-2): 475–508.DOI:10.1016/j.jsv.2004.02.058 |
| [4] | BOTMAN M. Epicyclic gear vibrations[J].Journal of Manufacturing Science and Engineering, 1976, 98(3): 811–815. |
| [5] | BOTMAN M. Vibration measurements on planetary gears of aircraft turbine engines[J].Journal of Aircraft, 1980, 17(5): 351–357.DOI:10.2514/3.57912 |
| [6] | KAHRAMAN A. Planetary gear train dynamics[J].Journal of Mechanical Design, 1994, 116(3): 713–720.DOI:10.1115/1.2919441 |
| [7] | WU B,SAXENA A,KHAWAJA T S,et al.An approach to fault diagnosis of helicopter planetary gears[C]//Procceedings of IEEE Autotestcon 2004.Piscataway,NJ: IEEE Press,2004:475-481. |
| [8] | YUKSEL C, KAHRAMAN A. Dynamic tooth loads of planetary gear sets having tooth profile wear[J].Mechanism and Machine Theory, 2004, 39(7): 695–715.DOI:10.1016/j.mechmachtheory.2004.03.001 |
| [9] | BLUNT D M, KELLER J A. Detection of a fatigue crack in a UH-60A planet gear carrier using vibration analysis[J].Mechanical Systems and Signal Processing, 2006, 20(8): 2095–2111.DOI:10.1016/j.ymssp.2006.05.010 |
| [10] | PATRICK R,ORCHARD M E,ZHANG B,et al.An integrated approach to helicopter planetary gear fault diagnosis and failure prognosis[C]// Procceedings of IEEE Autotestcon 2007.Piscataway,NJ:IEEE Press,2007:547-552. |
| [11] | PATRICK-ALDACO R.A model based framework for fault diagnosis and prognosis of dynamical systems with an application to helicopter transmissions[D].Geogia:Georgia Institute of Technology,2007:280. |
| [12] | ORCHARD M E, VACHTSEVANOS G J. A particle-filtering approach for on-line fault diagnosis and failure prognosis[J].Transactions of the Institute of Measurement and Control, 2009, 31(3-4): 221–246.DOI:10.1177/0142331208092026 |
| [13] | 陈传尧. 疲劳与断裂[M].武汉: 华中科技大学出版社, 2002: 147-157.CHEN C Y. Fatigue and fracture[M].Wuhan: Huazhong University of Science and Technology Press, 2002: 147-157.(in Chinese) |
| [14] | 高镇同. 疲劳可靠性[M].北京: 北京航空航天大学出版社, 2000: 1-24.GAO Z T. Fatigue reliability[M].Beijing: Beihang University Press, 2000: 1-24.(in Chinese) |
| [15] | 司小胜, 胡昌华, 张琪, 等. 不确定退化测量数据下的剩余寿命估计[J].电子学报, 2015, 43(1): 30–35.SI X S, HU C H, ZHANG Q, et al. Estimating remaining useful life under uncertain degradation measurements[J].Acta Electronica Sinica, 2015, 43(1): 30–35.(in Chinese) |
| [16] | 孙磊, 贾云献, 蔡丽影, 等. 基于 EM-KF 算法的直升机主减速器剩余寿命预测方法[J].航空动力学报, 2015, 30(2): 431–437.SUN L, JIA Y X, CAI L Y, et al. Remaining useful life estimation method of helicopter's main retarder based on EM-KF algorithm[J].Journal of Aerospace Power, 2015, 30(2): 431–437.(in Chinese) |
| [17] | SIKORSKA J, HODKIEWICZ M, MA L. Prognostic modelling options for remaining useful life estimation by industry[J].Mechanical Systems and Signal Processing, 2011, 25(5): 1803–1836.DOI:10.1016/j.ymssp.2010.11.018 |
| [18] | GEBRAEEL N Z, LAWLEY M A, LI R, et al. Residual-life distributions from component degradation signals:A Bayesian approach[J].ⅡE Transactions, 2005, 37(6): 543–557. |
| [19] | MOHANTY J, VERMA B, RAY P. Prediction of fatigue crack growth and residual life using an exponential model:Part I (constant amplitude loading)[J].International Journal of Fatigue, 2009, 31(3): 418–424.DOI:10.1016/j.ijfatigue.2008.07.015 |
| [20] | 张国胜, 张志强, 刘艳芳, 等. 42CrMo 钢疲劳裂纹扩展剩余寿命评估[J].中国测试, 2014, 40(6): 127–131.ZHANG G S, ZHANG Z Q, LIU Y F, et al. Residual life evaluation of fatigue crack growth of 42CrMo steel[J].China Measurement & Test, 2014, 40(6): 127–131.(in Chinese) |
| [21] | 吴金亮, 汪中厚, 李刚. 斜齿圆柱齿轮裂纹扩展特性及剩余寿命研究[J].机械传动, 2014, 38(12): 1–4.WU J L, WANG Z H, LI G. Study on the crack propagation characteristic and remaining life of helical gear[J].Journal of Mechanical Transmission, 2014, 38(12): 1–4.(in Chinese) |
| [22] | YUAN R, LI H, HUANG H Z, et al. A nonlinear fatigue damage accumulation model considering strength degradation and its applications to fatigue reliability analysis[J].International Journal of Damage Mechanics, 2014, 24(5): 646–662. |
| [23] | ZARRIN-GHALAMI T, FATEMI A. Cumulative fatigue damage and life prediction of elastomeric components[J].Fatigue & Fracture of Engineering Materials & Structures, 2013, 36(3): 270–279. |
| [24] | DATTOMA V, GIANCANE S, NOBILE R, et al. Fatigue life prediction under variable loading based on a new non-linear continuum damage mechanics model[J].International Journal of Fatigue, 2006, 28(2): 89–95.DOI:10.1016/j.ijfatigue.2005.05.001 |
| [25] | FEHL B D, TRUMAN K Z. An evaluation of fracture mechanics quarter-point displacement techniques used for computing stress intensity factors[J].Engineering Structures, 1999, 21(5): 406–415.DOI:10.1016/S0141-0296(97)00221-6 |
| [26] | 王锋.三维应力强度因子分析及干涉预应力影响研究[D].西安:西北工业大学,2007.WANG F.Three-dimensional stress intensity factor analysis and research on the impact of interference prestressed[D].Xi'an:Northwestern Polytechnical University,2007(in Chinese).http://cdmd.cnki.com.cn/article/cdmd-10699-2007057083.htm |
| [27] | MANSON S. Interfaces between fatigue,creep,and fracture[J].International Journal of Fracture Mechanics, 1966, 2(1): 327–363.DOI:10.1007/BF00698478 |
| [28] | PARIS P, ERDOGAN F. A critical analysis of crack propagation laws[J].Journal of Fluids Engineering, 1963, 85(4): 528–533. |
| [29] | 中国航空研究院.应力强度因子手册[M].北京:科学出版社,1981:174-187.Chinese Aeronautical Establishement.Stress intensity factor manual[M].Beijing:Science Press,1981:174-187(in Chinese). |
