文献[7]针对具有未知随机时延的飞行器故障检测问题,通过泰勒公式将随机时延进行近似处理,在此基础上设计了故障检测滤波器。文献[8-9]将存在数据传输阻塞的无人机编队系统建模为离散马尔可夫跳变系统,基于几何方法和H∞滤波方法设计了故障检测与隔离算法。文献[10]研究了一类混合结构的故障检测问题,分别针对连续状态和离散状态设计了故障检测与隔离算法,并将该算法应用在四旋翼无人飞行器编队控制中。文献[11]针对二阶动态执行机构故障,综合多模型和自适应重构方法研究了飞行控制系统跟踪补偿控制问题。文献[7-11]研究了故障检测滤波器与容错控制器的设计方法,但对于故障信号的特性如故障频率等描述比较宽泛,而实际研究中,故障信号通常只存在于某一个特定频率段。
有限频域故障是指故障频率在一定范围内的故障[12], 针对有限频域故障的研究已经取得了很多成果[13-16],文献[14]和文献[15]分别研究了线性时变离散系统和含有丢包问题的马尔可夫跳变系统有限频域故障检测问题,通过选取综合性能指标保证故障检测滤波器对故障的检测性能。文献[16]中网络控制系统的故障常常发生在一定频段范围内,通过引入加权函数描述故障的有限频域特性,进而设计故障检测滤波器,但是加权函数会增加系统设计的复杂度,而且对于故障频段的描述也不准确。目前对于有限频域问题的研究主要集中在故障检测问题方面,关于网络控制系统有限频域故障检测与容错控制问题的研究尚未见诸文献。
本文针对网络环境下飞行器的有限频域故障,设计了故障检测和容错控制系统。首先设计了面向有限频域故障的故障检测滤波器,将在线获得的故障残差信号反馈至容错控制单元。进一步设计了包含状态反馈和残差反馈2部分的主动容错控制器。在无故障情况下,状态反馈部分起主要作用,保证系统稳定并满足一定性能指标;在有限频域故障发生情况下残差反馈部分补充状态反馈,使得系统在稳定的前提下对故障信号和外部干扰具有一定的鲁棒性。
1 系统描述及建模 网络控制系统由被控对象、传感器、故障检测滤波器、容错控制器和执行机构组成,结构图如图 1所示。
 |
| A/D—连续/离散转换器; D/A—离散/连续转化器; f (t),d (t)-L2范数有界的故障信号和外界干扰信号; |
| 图选项 |
设网络控制系统模型为
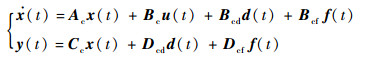 | (1) |
式中:u (t) 为控制输入;矩阵Ac、Bc、Bcd、Bcf、Cc、Dcd和Dcf为适维已知矩阵。不失一般性,设系统稳定并且可观,对飞行器网络控制系统作如下假设。
假设1??系统时变时延τk小于一个采样周期。
假设2??受益于网络控制系统内部的信号调度与监测机制,忽略系统中的丢包。
由于系统中时延的存在,会导致控制输入的更新出现滞后,即
 | (2) |
式中:T为采样周期。
由上述分析可知,系统式 (1) 经采样离散化后可以表达为
 | (3) |
式中:d (k) 和f (k) 分别为第k个采样周期的干扰和故障;A=eAcT;B0 (τk)=∫0T-τkeActBcdt;Bd=∫0TeAct·Bcddt;Bf=∫0TeActBcfdt;B1 (τk)=∫T-τkTeActBcdt;C=Cc;Dd=Dcd;Df=Dcf。
定义Δu (k)=u (k-1)-u (k),B=B0 (τk)+B1 (τk),则式 (3) 可以重新写为
 | (4) |
由于τk∈[0, T) 是一个未知时变的量,因此B1 (τk) 也是未知时变的,采用一阶泰勒公式对未知项B1 (τk) Δu (k) 近似解耦[17]:
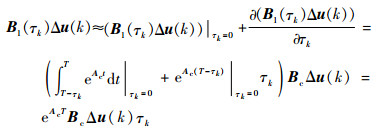 |
定义Bτ=eAcTBc,τu, k=Δukτk,则式 (4) 转化为
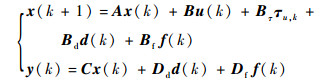 | (5) |
根据以上模型构造式 (6) 的基于观测器的故障检测滤波器作为残差产生系统:
 | (6) |
式中:? (k) 为y (k) 的估计;L为待求的滤波器参数。
为了实现故障检测,选择如式 (7) 所示的残差评估函数和阈值:
 | (7) |
式中:J (k) 为残差评估函数; Jth为阈值;‖?‖2,E表示向量二范数。
综上所述,利用式 (8) 所示的逻辑进行故障检测。
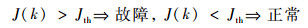 | (8) |
由于残差信号中含有丰富的故障信息,因此利用残差信号对故障进行补偿。设计形如式 (9) 的主动容错控制器:
 | (9) |
式中:K和H为待设计的反馈增益矩阵。
定义滤波器观测误差

 | (10) |
式中:
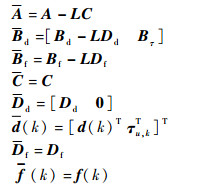 |
由式 (10) 可以看出残差信号受故障f (k) 和扰动d (k) 的影响。为了保证系统在给定频域内系统的故障检测性能,给出如下定义。
定义1??对于给定频域ω1≤ω≤ω2,传递函数向量G (z) 此频域内的H_范数为‖G (z)‖-[-ω1, ω2]=inf σmin (G (jω)), ?ω1≤ω≤ω2,σmin为最小奇异值。
残差信号应在对干扰信号鲁棒的前提下尽量对故障信号敏感。因此滤波器参数L的设计目标是使残差系统式 (10) 在d (k)=0,f (k)=0时渐近稳定且对于给定的α > 0,β > 0,以下性能指标成立:
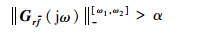 | (11) |
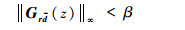 | (12) |
式中:Grf (jω) 为f (k) 与r (k) 之间的传递函数;Grd (jω) 为d-(k) 与r (k) 之间的传递函数。
综合式 (5)、式 (6) 和式 (9) 可得到如下闭环控制系统:
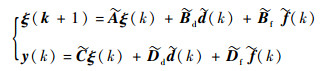 | (13) |
式中:
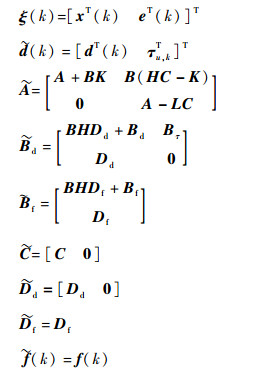 |
容错控制的目的是保证系统在干扰和故障的影响下稳定,且输出尽量平稳。基于以上分析,本文的主动容错控制问题可以描述为:在完成滤波器参数L设计的基础上,设计反馈增益矩阵K和H,使得闭环系统 (13) 渐近稳定,且在零初始条件下分别满足如下控制性能指标:
 | (14) |
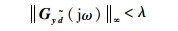 | (15) |
式中:γ和λ为给定常量;
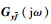
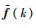
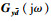

2 故障检测滤波器设计 首先给出有限频域内KYP (Kalman-Yakubovich-Popov) 引理。
引理1[13]??给定线性离散系统:
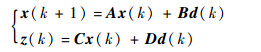 | (16) |
其传递函数为Gzd (ejω)=C (ejωI-A)-1B+D。对于频率范围ω1≤ω≤ω2和对称矩阵Π,以下2个说法等价:
1) 不等式 (17) 成立
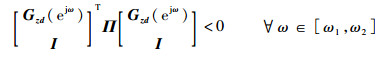 | (17) |
2) 存在适维自共轭矩阵Q > 0、P,使得式 (18) 成立。
 | (18) |
式中:
 |
在上述分析基础上,定理1给出了故障检测滤波器存在的充分条件。
定理1??对形如式 (5) 的飞行器网络控制系统,给定标量α > l0,β > 0,频率范围ω∈[ω1, ω2],存在形如式 (6) 的故障检测滤波器,使得残差系统 (式 (10)) 在d (k)=0,f (k)=0情况下渐近稳定,且满足性能指标式 (11) 和式 (12)。当且仅当存在Hermitian矩阵Q > 0、W > 0和P,实数矩阵X满足如下线性矩阵不等式 (Linear Matrix Inequality, LMI):
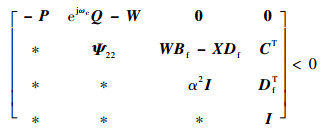 | (19) |
 | (20) |
式中:*代表矩阵的对称部分。
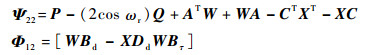 |
则故障检测滤波器参数矩阵L=W-1X。
证明??若残差系统式 (10) 满足性能指标式 (11),即
 | (21) |
取
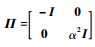
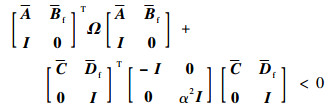 | (22) |
将式 (22) 重写为
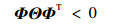 | (23) |
式中:
 |
令Ψ=Φ⊥=[-IA Bf]T。根据project引理[14],若存在Hermitian矩阵W > 0使得
 | (24) |
式中:Ξ=[0 I 0],则式 (23) 成立。经过矩阵变换,式 (24) 等价于
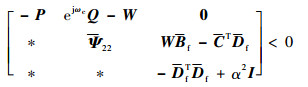 | (25) |
式中:
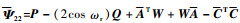
令X=WL并应用Schur补引理,式 (25) 变换为式 (19)。因此当LMI式 (19) 成立,性能指标式 (11) 满足。
下面证明若式 (20) 成立,则指标式 (12) 满足且系统渐近稳定。令

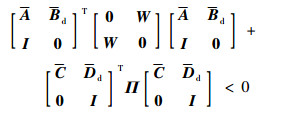 | (26) |
经过矩阵变换式 (26) 变换为
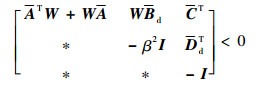 | (27) |
令X=WL, 式 (27) 可变换为式 (20),即当式 (20) 成立,性能指标 (式 (12)) 满足。又知当式 (27) 成立,易得ATW+WA < 0,则残差系统式 (10) 渐近稳定。
综上所述,当LMI (式 (19) 和式 (20)) 成立时,残差系统式 (10) 渐近稳定且满足性能指标式 (11) 和式 (12)。?????????证毕
在不等式 (19) 和式 (20) 中,可以将α作为优化变量来提高故障检测系统的灵敏度,即求解如式 (28) 所示的凸优化问题。
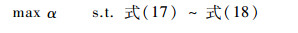 | (28) |
3 主动容错控制器设计 本节将给出主动容错控制器存在的充分条件,以及反馈控制增益矩阵K和H的求解方法。
定理2??给定标量γ > 0、λ > 0, 闭环系统式 (13) 渐近稳定且满足性能指标式 (14) 和式 (15),当且仅当存在Hermitian矩阵

 | (29) |
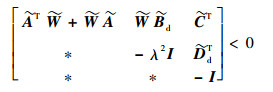 | (30) |
证明??分别取
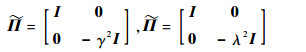 |
按照定理1的证明方法,应用引理1可得当式 (29) 和式 (30) 成立,闭环系统式 (13) 渐近稳定且满足性能指标式 (14) 和式 (15)。??????????证毕
下面给出反馈增益矩阵的求解方法。
引理2[18]??假设B列满秩,总存在正交矩阵U∈Rn×n和V∈Rm×m使得
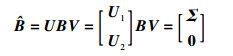 | (31) |
式中:U1∈Rm×n;U2∈R(n-m)×n;Σ=diag (σ1, σ2, …, σm) 为B的非零奇异值。
引理3[19]??对于列满秩矩阵B∈Rn×m,如果矩阵X1有如下结构:
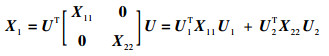 | (32) |
式中:X11∈Rm×m > 0,X22∈R(n-m)×(n-m) > 0,则一定存在一个非奇异矩阵
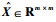
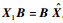
定理3??考虑闭环系统式 (13),给定标量γ > 0、λ > 0, 闭环系统式 (13) 渐近稳定且满足性能指标式 (14) 和式 (15),当且仅当存在Hermitian矩阵P1, P2, Q1 > 0, Q2 > 0, W1 > 0, W2 > 0,适当维数矩阵M,N,满足线性矩阵不等式 (33) 和式 (34)。
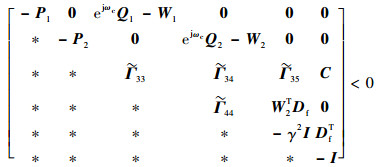 | (33) |
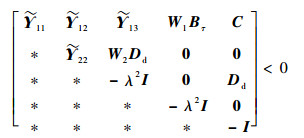 | (34) |
式中:
 |
形如式 (9) 的主动容错控制反馈增益矩阵可以通过式 (35)~式 (36) 求得。
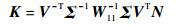 | (35) |
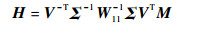 | (36) |
证明??将
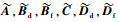
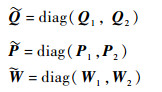 |
得到
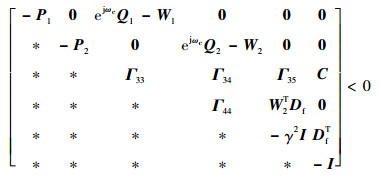 | (37) |
 | (38) |
式中:
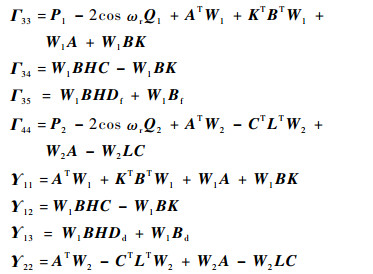 |
设B列满秩,根据引理2可知一定存在正交矩阵U和V,使得B作如下分解:
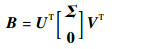 | (39) |
根据引理3若B列满秩,存在一个非奇异矩阵?,使得W1B=B?,将式 (39) 代入,可得
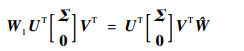 | (40) |
令W1=UT1W11U1+UT2W22U2,代入式 (40),可得
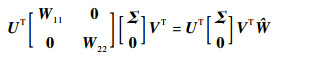 | (40) |
得到
 | (42) |
令
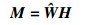 | (43) |
 | (44) |
将式 (42)~式 (44) 和W1B=B?代入式 (37) 和式 (38) 可得式 (33) 和式 (34)。?????????证毕
将γ、λ分别作为提高残差信号对故障信号和干扰信号鲁棒性的优化变量,则主动容错控制器参数K和H通过求解如下凸优化问题得到:
 | (45) |
式中:c1和c2为选择的优化比例因子。
4 数值仿真 本节验证所提故障检测滤波器和残差反馈容错控制器设计方法的有效性。以HiMAT飞行器[20]纵向短周期运动模型为例,将某一设计点以升降舵作为输入进行线性化,得到该设计点处的连续系统模型:
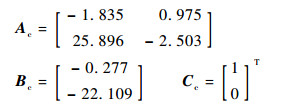 |
设采样周期为1 ms,取扰动和故障分布阵为
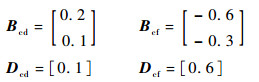 |
根据定理1,求解LMIs (式 (19) 和式 (20)) 和优化问题式 (28) 可得滤波器参数L和对应的αmax为
 | (46) |
假设τk为在[0, T) 间均匀分布的随机变量,干扰信号d (k) 为均值为0,幅值小于0.05的随机信号。
取故障的频率范围已知为ω∈[0.1, 10]rad/s,假设故障f (t) 为已知频率为π/4的正弦函数,即
 |
为验证本文方法对有限频域范围内故障的检测效果,分别应用本文有限频域方法和全频域方法对上述故障进行检测,故障检测仿真结果如图 2和图 3所示。由图 2可以看出采用本文方法获得的残差能够更好地反映系统故障。
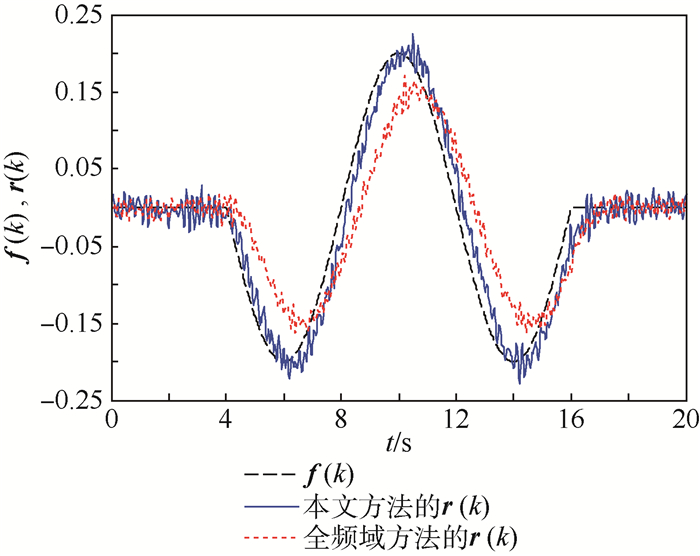 |
| 图 2 残差信号对比 Fig. 2 Comparison of residual signals |
| 图选项 |
 |
| 图 3 残差评估函数对比 Fig. 3 Comparison of residual evaluation functions |
| 图选项 |
残差评估函数如图 3所示,应用全频域方法当t=4.239 s时,J (k)=0.149 > Jth,检测时间Td=0.239 s;应用本文有限频域方法当t=4.157 s可以看出应用本文方法下故障检测速度更快。
为进一步验证本文所提方法的有效性,在选定频率段ω∈[0.1, 10]rad/s内,分别采用本文所提方法和全频域方法,对不同频率故障进行多次仿真,故障检测结果如表 1所示,可以看出设计的滤波器对已知频率范围内的故障检测效果更好。
表 1 不同频率故障检测时长 Table 1 Duration of fault detection under different frequency
| 故障频率/(rad·s-1) | 检测时长/s | |
| 本文方法 | 全频域方法 | |
| 0.1 | 0.178 | 0.241 |
| 1.0 | 0.143 | 0.238 |
| 4.0 | 0.126 | 0.235 |
| 10.0 | 0.175 | 0.232 |
表选项
根据定理3求解LMIs (式 (33) 和式 (34)) 并代入式 (35) 和式 (36),选取优化比例因子c1=5c2,可得容错控制器参数K=[1.641-6.622],H=[-0.623],相应的γ=0.3931和λ=1.454。
将上述控制器参数代入闭环系统进行仿真,同样为验证本文方法对有限频域范围内故障的补偿效果,应用全频域方法求解一组控制器参数进行仿真对比,飞行器迎角α变化如图 4所示。
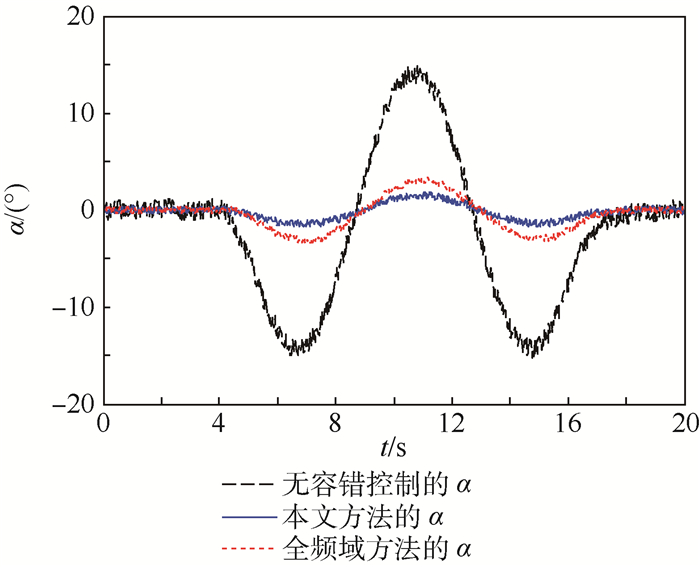 |
| 图 4 被控输出对比 Fig. 4 Comparison of controlled outputs |
| 图选项 |
从图 4中仿真结果可以归纳得出:发生有限频域内正弦故障后,在全频域方法设计的主动容错控制器作用下飞行器迎角浮动∣Δα∣ < 3.5°,在本文方法设计的残差反馈主动容错控制器作用下飞行器迎角浮动∣Δα∣ < 2.1°,说明本文方法设计的控制器参数对于一定频率范围内的故障鲁棒性更强,同样对不同频率故障进行多次仿真,迎角输出变化幅值如表 2,可以看出设计的主动容错控制器对已知频率范围内的故障容错效果更好。
表 2 不同频率下控制输出结果 Table 2 Control output results under different frequency
| 故障频率/(rad·s-1) | ∣Δαmax∣/(°) | |
| 本文方法 | 全频域方法 | |
| 0.1 | 2.6 | 3.5 |
| 1.0 | 2.0 | 3.4 |
| 4.0 | 1.8 | 3.4 |
| 10.0 | 2.5 | 3.3 |
表选项
5 结论 本文在存在随机短时延的情况,针对有限频域内的故障,设计了故障检测滤波器和基于残差反馈的主动容错控制器。通过对飞行器的仿真表明:
1) 对于特定频率段的故障信号,相比于传统方法,采用本文提出的算法,可以有效缩短检测时长。
2) 采用基于残差反馈的主动容错控制器,可以对故障进行有效的补偿,而且对于有限频段的故障信号,能够获得更好的控制性能。
3) 提出的方法对于系统中普遍存在的干扰和时延具有一定的鲁棒性,在存在时延和外界干扰的情况下仍然能实现故障检测和容错控制,并且具有良好的性能。
综上所述,所提方法能够有效抑制外界干扰和未知时延对系统的影响。对于飞行器发生的有限频域内故障具有良好的检测性能和容错控制效果。
参考文献
| [1] | XU L J, WANG Q, LI W, et al. Stability analysis and stabilisation of full-envelope networked flight control systems:Switched system approach[J].IET Control Theory & Applications, 2012, 6(2): 286–296. |
| [2] | DONG W, SHI P, WANG W, et al. Non-fragile H∞ control for switched stochastic delay systems with application to water quality process[J].International Journal of Robust and Nonlinear Control, 2014, 24(11): 1677–1693. |
| [3] | LIAN J, MU C, SHI P. Asynchronous H∞ filtering for switched stochastic systems with time-varying delay[J].Information Sciences, 2013, 224: 200–212.DOI:10.1016/j.ins.2012.10.009 |
| [4] | 董全超. 线性时滞系统鲁棒H∞故障估计与主动容错控制[D]. 济南: 山东大学, 2010.DONG Q C.Robust H∞ fault estimation and active fault tolerant control for linear time-delay system[D].Jinan:Shandong University, 2010(in Chinese). |
| [5] | WANG Y Q, YE H, WANG G Z. Residual generation and evaluation of networked control systems subject to random packet dropout[J].Automatica, 2009, 45(10): 2427–2434.DOI:10.1016/j.automatica.2009.06.031 |
| [6] | GAO Z W. Fault estimation and fault-tolerant control for discrete time dynamic systems[J].IEEE Transactions on Industrial Electronics, 2015, 62(6): 3874–3884. |
| [7] | 马奥家, 董朝阳, 王青. 飞行器网络控制系统故障检测与时域优化[J].北京航空航天大学学报, 2014, 40(3): 407–412.MA A J, DONG C Y, WANG Q. Fault detection and time domain of flight networked control system[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(3): 407–412.(in Chinese) |
| [8] | MESKIN N, KHORASANI K. Fault detection and isolation of discrete-time Markovian jump linear systems with application to a network of multi-agent systems having imperfect communication channels[J].Automatica, 2009, 45(9): 2032–2040.DOI:10.1016/j.automatica.2009.04.020 |
| [9] | MESKIN N, KHORASANI K. Actuator fault detection and isolation for a network of unmanned vehicles[J].IEEE Transactions on Automatic Control, 2009, 54(4): 835–840. |
| [10] | MESKIN N, KHORASANI K, RABBATH C A. A hybrid fault detection and isolation strategy for a network of unmanned vehicles in presence of large environmental disturbances[J].IEEE Transactions on Control Systems Technology, 2010, 18(6): 1422–1429. |
| [11] | GUO Y Y, JIANG B. Mulitiple model-based adaptive reconfiguration control for actuator fault[J].Acta Automatica Sinica, 2009, 35(11): 1452–1458. |
| [12] | DONG Q C, ZHONG M Y, DING S X. Active fault tolerant control for a class of linear time-delay systems in finite frequency domain[J].International Journal of System Science, 2012, 43(3): 543–551. |
| [13] | IWASAKI T, HARE S. Generalized KYP lemma:Unified frequency domain inequalities with design applications[J].IEEE Transactions on Automatic Control, 2005, 50(1): 41–59. |
| [14] | WANG H, YANG G H. A finite frequency domain approach fault detection for linear discrete-time systems[J].International Journal of Control, 2008, 81(7): 1162–1171.DOI:10.1080/00207170701691513 |
| [15] | LONG Y, YANG G H. Fault detection in finite frequency domain for networked control systems with missing measurements[J].Journal of the Franklin Institute, 2013, 350(9): 2605–2626.DOI:10.1016/j.jfranklin.2013.01.015 |
| [16] | DU D S, JIANG B, SHI P. Fault detection for discrete time switched systems with intermittent measurements[J].International Journal of Control, 2012, 85(1): 78–87.DOI:10.1080/00207179.2011.639087 |
| [17] | 王永强, 叶昊, 王桂增. 网络化控制系统故障检测技术最新进展[J].控制理论与应用, 2009, 26(4): 400–409.WANG Y Q, YE H, WANG G Z. Recent development of fault detection techniques for networked control systems[J].Control Theory and Applications, 2009, 26(4): 400–409.(in Chinese) |
| [18] | FENG J, WANG S Q, ZHAO Q. Closed-loop design of fault detection for networked non-linear systems with mixed delays and packet losses[J].IET Control Theory & Applications, 2013, 7(6): 858–868. |
| [19] | LIU Y R, WANG Z D, LIANG J L, et al. Synchronization and state estimation for discrete time complex networks with distributed delays[J].IEEE Transactions on System, Man, and Cybernetics Part B:Cybernetics, 2008, 38(5): 1314–1325.DOI:10.1109/TSMCB.2008.925745 |
| [20] | HOU Y Z, DONG C Y, WANG Q. Stability analysis of switched linear systems with locally overlapped switching law[J].Journal of Guidance, Control and Dynamics, 2010, 33(2): 396–403.DOI:10.2514/1.45795 |
