关于GNSS海洋反射信号的模拟还处于起步阶段,相关的文献很少。文献[12]给出了P2EPS模拟器的结构,该系统最后输出的是延迟多普勒映射 (DDM) 结果,还不能直接用于GNSS-R模拟器。文献[13]对SAVERS模拟器进行了描述,利用ZV模型提取出DDM模块的参数,但也不能用于生成反射信号。文献[14]介绍了一种GNSS-R模拟器的设计和关键技术,但只是进行了简略的描述,并没有具体的实现模型。本文对复杂的海洋反射信号用近似拟合的方法进行简化,利用ZV模型建立起海面反射信号时延和功率的模型,从而实现海洋反射信号的模拟。
1 海洋反射信号模型建立 GNSS海洋反射信号是由不同海面散射单元散射的信号共同作用的结果,如图 1所示。由于海面的粗糙特性,反射信号总体表现为信号幅度的衰减和不同反射面元信号的叠加,同时相对于直射信号,不同的反射面元反射后的信号有着不同的时间延迟和多普勒频移。在机载高度下一般不需要考虑多普勒频移对散射信号功率的影响。因此,如果不考虑多普勒频移对反射信号功率的影响,可认为反射信号的多普勒频率与直射信号的多普勒频率相同。此时,只需要建立反射信号时延和功率之间相对于直射信号的模型即可实现对GNSS海洋反射信号的模拟。
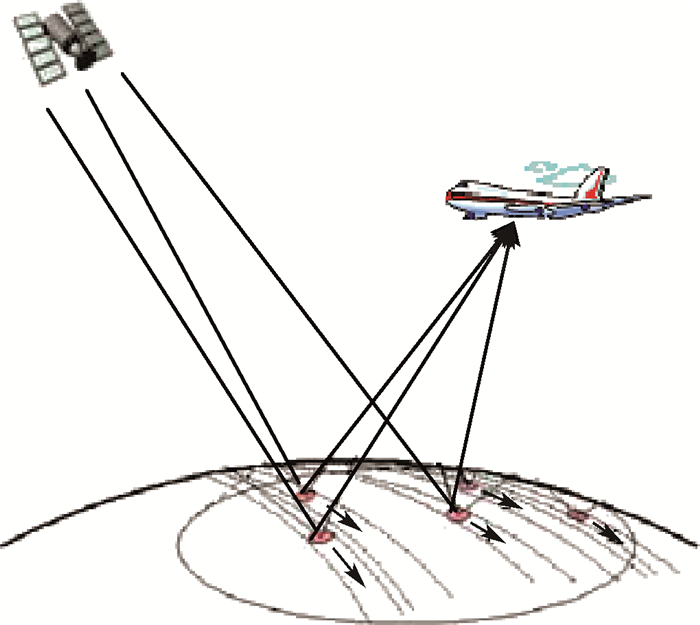 |
| 图 1 海洋反射信号示意图 Fig. 1 Schematic diagram of ocean reflection signal |
| 图选项 |
海洋反射信号模拟的大致流程如图 2所示。首先通过ZV模型求得时延一维相关功率曲线,并以直射信号作归一化处理。然后对海洋反射信号进行近似,用拟合的方法建立反射信号时延和功率的模型。接下来估算反射信号与直射信号之间的时延,从而得到模拟反射信号所需的时延、多普勒频率、功率3个参数。最后,对模拟的反射信号进行相关处理的仿真验证。
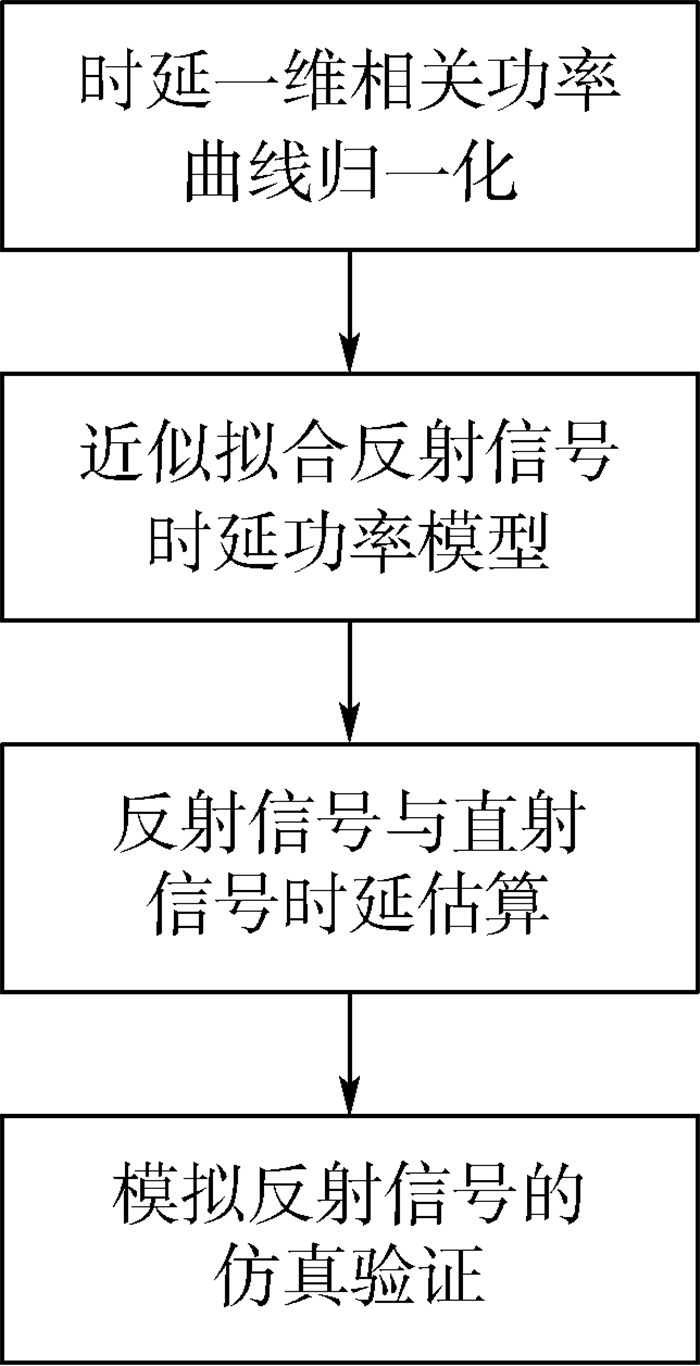 |
| 图 2 海洋反射信号模拟的大致流程 Fig. 2 General procedure of ocean reflection signal simulation |
| 图选项 |
1.1 时延一维相关功率曲线归一化 在利用GPS海面散射信号进行海面风场遥感的研究中,Zavorotny和Voronovich[15]在双基雷达方程的基础上利用Kirchhoff近似的几何光学方法建立了GPS海面散射信号的相关功率模型。模型的形式如下:
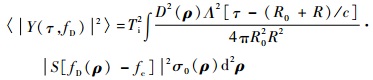 | (1) |
式中:Y为相关函数;τ为时延;fD为多普勒频移;fc为镜面反射点处的多普勒频率;c为光速;Ti为相干积分时间;D为接收机天线的增益;Λ为GPS伪随机码的自相关函数;S为多普勒滤波函数;σ0为粗糙海面的标准化散射截面;ρ为镜像反射点到平均海面上某一点的向量;R0和R分别为GPS卫星和接收机到ρ端点的距离。
为了表达结果的相对值,通常将数值计算的反射功率归一化,归一化因子可以取直射信号的功率或者总的反射功率。若以直接信号作归一化处理,表示为
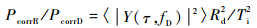 | (2) |
式中:PcorrR为反射通道的相关功率;PcorrD为直射通道的相关功率;Rd为GPS卫星到接收机的距离。
1.2 近似拟合反射信号时延功率模型 根据扩频通信原理,接收机经过相关处理后,信号无失真通过,功率不变[16]。由于接收机反射通道与直射通道之间存在的天线和器件特性不一致, 会出现功率差异。可设反射信号与直射信号的功率比和接收机输出的相关功率比满足:
 | (3) |
式中:PR为反射信号的功率;PD为直射信号的功率;G为接收机的反射信号与直射信号的增益差。如果直射信号和反射信号在接收和处理时的增益相等,则两者相关功率比就等于接收时的两者信号功率比。
由于海面粗糙度的影响,在反射面相对于所采用的GNSS信号载波波长粗糙时,海洋反射面可以看作是大量独立反射元的集合,而散射信号可以看着每个反射元反射的信号的叠加,每个信号具有不同的时延。为了便于区分,称每个反射元反射的信号为反射信号,接收机接收到的反射信号为海面反射信号。那么,海面反射信号是许多条具有不同时延反射信号的叠加。在模拟的过程中,海面反射信号可近似为由等时延间隔的少量条反射信号叠加而成。海面反射信号相关函数为等时延间隔信号相关结果的叠加,如图 3所示。
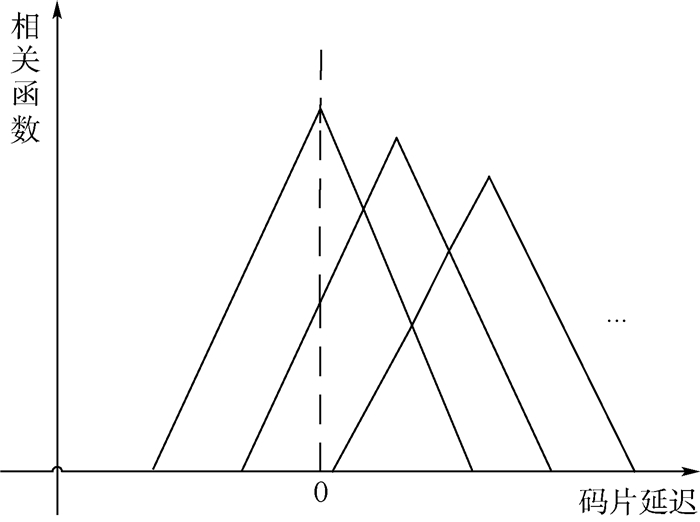 |
| 图 3 等时延信号相关结果示意图 Fig. 3 Schematic diagram of correlation result of equal delay signals |
| 图选项 |
经过叠加后,海面反射信号相关函数的波形如图 4所示。不同时延信号的叠加使得反射信号相关结果峰值后移,拖尾增长。
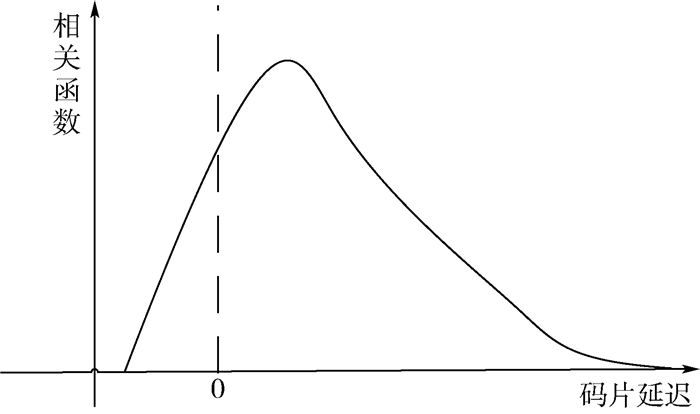 |
| 图 4 海面反射信号相关函数波形 Fig. 4 Correlation function waveform of sea surface reflection signal |
| 图选项 |
在理论上,海面反射信号的相关函数波形可由ZV模型中的时延一维相关功率曲线得到。然后,再由相关函数的数据来建立反射信号的时延功率模型,则构成逆向问题。而曲线拟合是逆向工程中的核心问题和主要方法。
由于相关函数波形是等时延信号相关结果的叠加,因此采用数值迭代优化的拟合方法。假设相关函数的数据由等时延间隔的n条反射信号相关结果叠加而成,以镜面反射点信号为第1条反射信号,每条反射信号的幅值不同,用三角形的自相关函数的叠加来迭代拟合出各路反射信号的幅值。拟合的函数表达式为
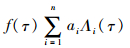 | (4) |
式中:f(τ) 为τ时的海面反射信号相关值;Λi(τ) 为τ时的第i条反射信号自相关值;ai为第i条反射信号的幅值,为拟合要得到的结果。
这样拟合出的结果中可能有负值,只能大体上反映出反射信号幅值的变化趋势,因此还需要对迭代拟合得到的数据进行第2次拟合。从镜面反射点信号开始,不同反射信号的强度随着信号时延的增加是逐渐衰减的。因此,第2次拟合的函数采用双指数衰减的数学模型,其表达式为
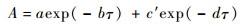 | (5) |
式中:A为信号的幅值;a、b、c′和d为待定系数;τ=0为镜面反射信号的时延。
1.3 反射信号与直射信号时延估算 在反射信号的应用中,一般采用镜面反射点处的反射信号作为参考。镜点反射信号相对于导航卫星发射信号的路径延迟可表示为
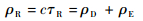 | (6) |
式中:τR为反射信号相对于发射点的时间延迟;ρD为直射信号相对于发射点的路径延迟;ρE为反射信号相对于直射信号的路径延迟。
在信号模拟的过程中,直射信号相对于发射点的路径延迟是已知的,所以只需计算反射信号相对于直射信号的路径延迟便可得到反射信号的时延。利用反射事件的几何关系[17]可以获取反射信号相对于直射信号的时延值为
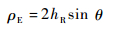 | (7) |
式中:hR为接收机平台相对基准水平面的高度;θ为反射信号对应卫星的仰角。
1.4 模拟反射信号的仿真验证 为了验证模拟的GPS海面反射信号,需对模拟的海面反射信号进行相关处理。图 5为反射信号的处理结构。对于直射信号的处理过程与普通的软件接收机类似,经过捕获、跟踪后,求得导航卫星位置、接收机位置。导航卫星和接收机的位置信息用于计算镜面反射点的时间延迟,此延迟可求解本地反射信号的伪码。本地反射信号的载波可直接利用从直射信号中恢复的载波生成。海面反射信号是多路反射信号叠加后的信号,将其与本地载波混频后,再与各路本地伪码进行相关后,即可得到反射信号相关功率的波形。
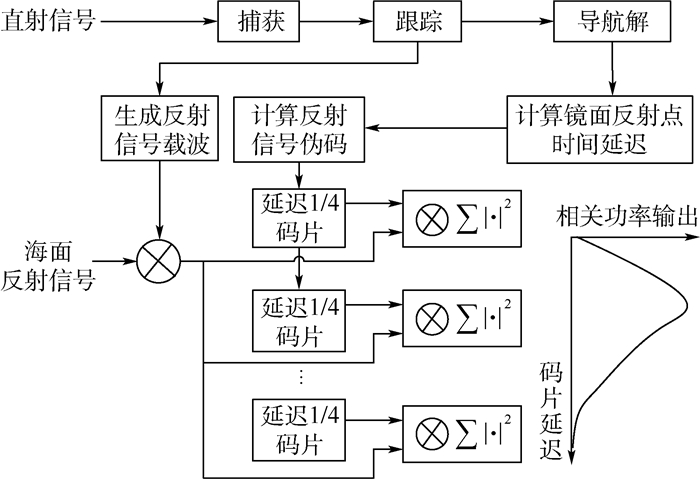 |
| 图 5 反射信号处理结构 Fig. 5 Reflection signal processing structure |
| 图选项 |
2 仿真结果 为了实现GPS海面散射信号幅值的拟合,需要先对相关功率波形进行数值仿真。仿真参数设置为:接收机高度为5 km,GPS卫星仰角为60°,风速为5 m/s,风向与入射面的夹角为0°。在不考虑噪声的情况下,仿真得到的时延一维相关功率曲线如图 6所示。
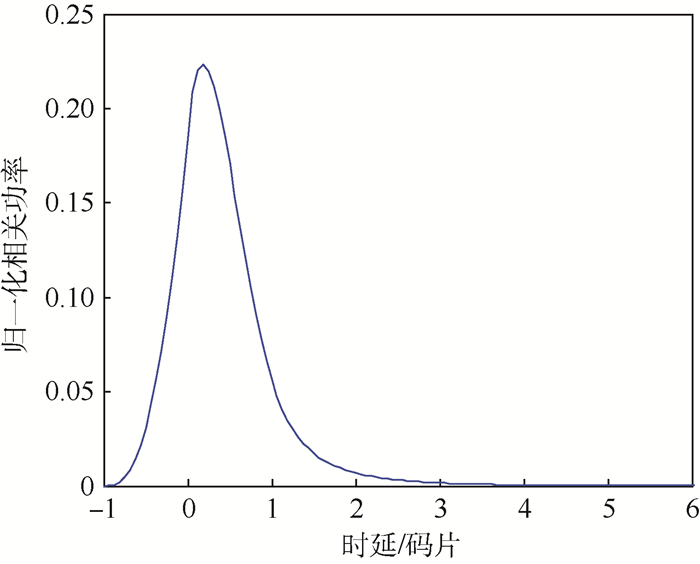 |
| 图 6 时延一维相关功率曲线 Fig. 6 Curve of delay one-dimensional correlation power |
| 图选项 |
从时延一维相关功率曲线可知,海面粗糙度导致的信号码延迟主要在[-1, 4]个码片的范围内。因此,在拟合时选用这个范围内的数据即可,并且对相关功率曲线的数据开方得到拟合所需的数据。在迭代拟合中,假设每条反射信号时延间隔1/4个码片,共有16路反射信号组成,采用最小二乘法进行迭代拟合,最小二乘拟合曲线如图 7所示。
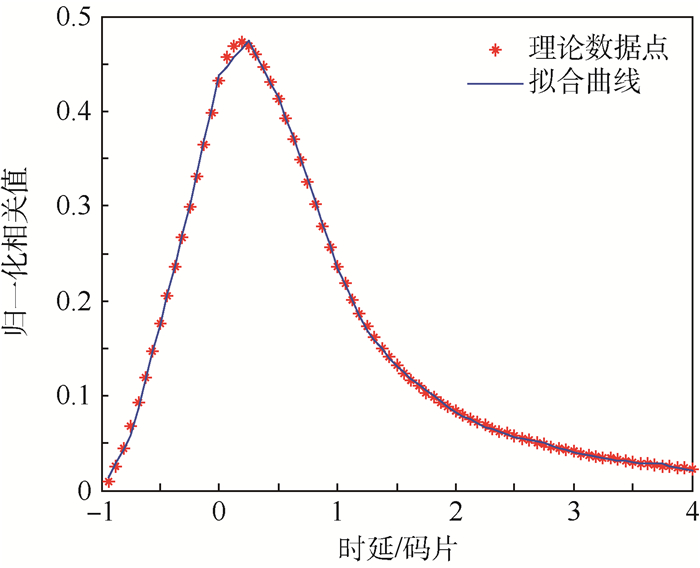 |
| 图 7 最小二乘数据拟合的比较 Fig. 7 Comparison of least square data fitting |
| 图选项 |
从图 7可以看出,最小二乘拟合能较好地对相关函数曲线进行近似,相关系数达到0.999 8。最小二乘法拟合得到的数据是如图 8中星形线的值。这些数据只能大体反映出反射信号幅值的趋势,而且有一些值是负值,不符合实际情况,因此还需要对这些数据进行再次拟合。采用式 (5) 进行非线性的数据拟合,第2次数据拟合的结果为图 8中的圆形线。第2次拟合可得到双指数函数的系数是:a=0.239 7,b=1.951 3,c′=0.013 0,d=0.037 1。
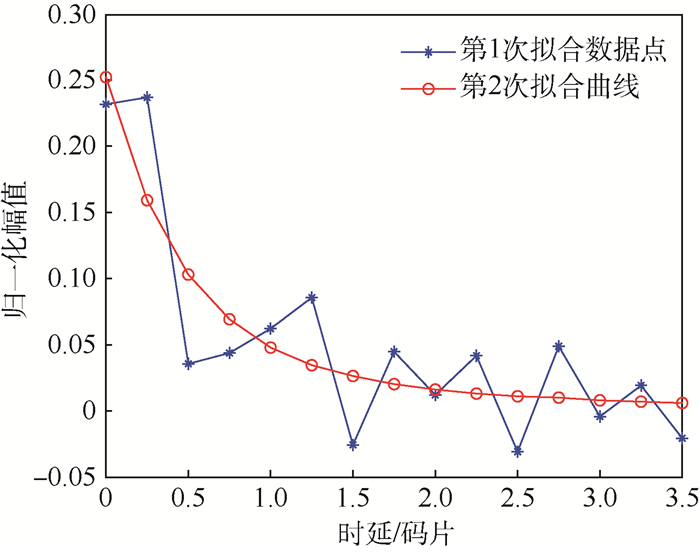 |
| 图 8 第2次数据拟合的比较 Fig. 8 Comparison of the second data fitting |
| 图选项 |
在信号模拟中,假设直射信号的时延为0码片,多普勒为-273 Hz,功率为-158.5 dBW。根据式 (7) 可以得到镜点反射信号相对于直射信号的延迟为29.56码片。根据式 (5) 可以得到相应时延信号的归一化幅值,然后根据直射信号的功率可以计算得到相应的反射信号功率。接收机的高度是5 km,忽略多普勒频移对海面反射信号功率的影响。则每条反射信号的多普勒频率与直射信号的多普勒频率相同。这样,可以得到各条反射信号的时延、多普勒频率和功率参数。16条反射信号的主要参数如表 1所示,其中第1条信号为镜点反射信号。
表 1 16路反射信号的主要参数 Table 1 Main parameters of 16 reflection signals
| 信号序数 | 时延/码片 | 多普勒频率/Hz | 功率/dBW |
| 1 | 29.56 | -273 | -170.45 |
| 2 | 29.56+0.25 | -273 | -174.42 |
| 3 | 29.56+0.50 | -273 | -178.23 |
| 4 | 29.56+0.75 | -273 | -181.84 |
| 5 | 29.56+1.00 | -273 | -185.13 |
| 6 | 29.56+1.25 | -273 | -188.05 |
| 7 | 29.56+1.50 | -273 | -190.51 |
| 8 | 29.56+1.75 | -273 | -192.44 |
| 9 | 29.56+2.00 | -273 | -193.94 |
| 10 | 29.56+2.25 | -273 | -195.04 |
| 11 | 29.56+2.50 | -273 | -195.76 |
| 12 | 29.56+2.75 | -273 | -196.29 |
| 13 | 29.56+3.00 | -273 | -196.70 |
| 14 | 29.56+3.25 | -273 | -196.99 |
| 15 | 29.56+3.50 | -273 | -197.14 |
| 16 | 29.56+3.75 | -273 | -197.29 |
表选项
按照图 5中的结构图,对16条反射信号组成的海面反射信号进行相关处理。在仿真过程中,设本地伪码共有64个相关器,相互间隔为1/4码片。按照表 1中的顺序分别用不同数目的模拟信号叠加成反射信号,进行相关处理。经过多次仿真后,结果表明, 用前14条模拟信号叠加的反射信号进行相关处理后,相关功率曲线和ZV模型理论曲线近似程度最高,相关系数为0.994 4,如图 9所示。
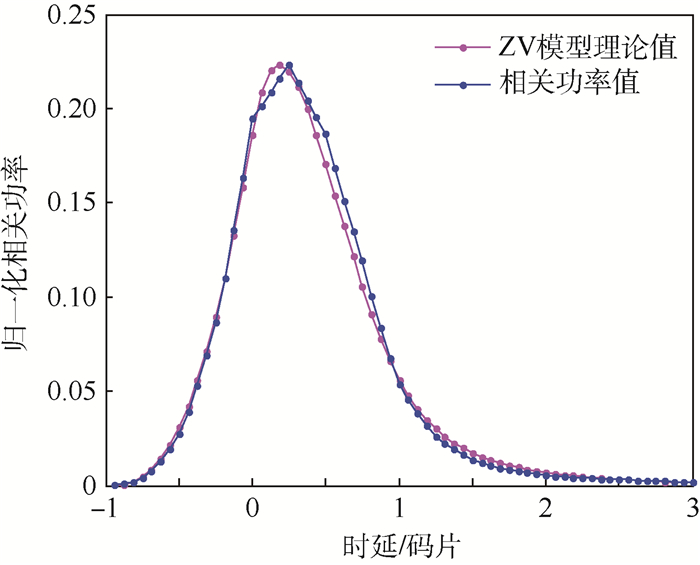 |
| 图 9 反射信号处理结果 Fig. 9 Results of reflection signal processing |
| 图选项 |
3 结论 1) 根据海洋反射信号的散射原理,将海面反射信号近似为由等时延间隔的少量条反射信号叠加而成是合理可行的。
2) 根据逆向工程中常用的曲线拟合法,利用最小二乘拟合法和非线性拟合法的2次拟合可较快速地、较准确地得到反射信号时延和功率的参量值。
3) 用该方法模拟的海洋反射信号被相关处理后,与理论值相比,相关系数优于0.99。因此,该方法在GNSS反射信号模拟器的研制中具有较强的实用性。
参考文献
| [1] | GARRISON J L, KATZBERG S J. The application of reflected GPS signals to ocean remote sensing[J].Remote Sensing of Environment, 2000, 73(2): 175–187.DOI:10.1016/S0034-4257(00)00092-4 |
| [2] | 张益强. 基于反射信号的海洋微波遥感技术[D]. 北京: 北京航空航天大学, 2008.ZHANG Y Q.Microwave remote sensing of ocean using GNSS reflection signal[D].Beijing:Beihang University, 2008(in Chinese). |
| [3] | MARTIN-NEIRA M, CAPARRINI M, FDNT-ROSSELLO J, et al. The PARIS concept:An experimental demonstration of sea surface altimetry using GPS reflected signals[J].IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 142–150.DOI:10.1109/36.898676 |
| [4] | LOWE S T, KORGER P Y, FRANKLIN G, et al. A delay/Doppler-mapping receiver system for GPS-reflection remote sensing[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(5): 1150–1164.DOI:10.1109/TGRS.2002.1010901 |
| [5] | YOU H, GARRISON J L, HECKLER G, et al. The autocorrelation of waveforms generated from ocean-scattered GPS signals[J].IEEE Geoscience and Remote Sensing Letters, 2006, 3(1): 78–82.DOI:10.1109/LGRS.2005.856704 |
| [6] | CARDELLACH E, RUFFINI G, PINO D, et al. Mediterranean balloon experiment:Ocean wind speed sensing from the stratosphere, using GPS reflections[J].Remote Sensing of Environment, 2003, 88(3): 351–362.DOI:10.1016/S0034-4257(03)00176-7 |
| [7] | LI W Q, YANG D K, ZHANG B. Real-time processing of reflected GNSS signal for remote sensing:System and experiments[J].The Journal of Navigation, 2011, 64(S1): 127–140.DOI:10.1017/S0373463311000403 |
| [8] | 白伟华. GNSS-R海洋遥感技术研究[D]. 北京: 中国科学院研究生院, 2008.BAI W H.Study of the GNSS-R ocean remote sensing technique[D].Beijing:Graduate University of Chinese Academy of Sciences, 2008(in Chinese). |
| [9] | 李峰辉, 王烁, 段维波. 基于数字波束形成的GNSS-R海洋反射接收机系统[C]//第五届中国卫星导航学术年会. 北京: 中国卫星导航学术年会组委会, 2014.LI F H, WANG S, DUAN W B.A GNSS-R ocean reflection receiver system based on digital beamforming[C]//The 5th China Satellite Navigation Conference.Beijing:China Satellite Navigation Scientific Committee, 2014(in Chinese). |
| [10] | 李世光, 杨军. 卫星导航信号模拟器现状与发展趋势[J].现代电子技术, 2015, 38(7): 131–134.LI S G, YANG J. Current status and developing trend satellite navigation signal simulator[J].Modern Electronic Technique, 2015, 38(7): 131–134.(in Chinese) |
| [11] | SAVIN A A, KRAT N M.A test equipment for the navigation receivers of space vehicles[C]//2015 International Siberian Conference on Control and Communications.Piscataway, NJ:IEEE Press, 2015:1-4. |
| [12] | PARK H, CAMPS A, PASCUAL D, et al.Improvement of the PAU/PARIS end-to-end performance simulator (P2EPS) in preparation for upcoming GNSS-R missions[C]//2013 IEEE International Geoscience and Remote Sensing Symposium (IGARSS).Piscataway, NJ:IEEE Press, 2013:362-365. |
| [13] | PIERDICCA N, GUERRIERO L, GIUSTO R, et al. SAVERS:A simulator of GNSS reflections from bare and vegetated soils[J].IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(10): 6542–6554.DOI:10.1109/TGRS.2013.2297572 |
| [14] | 王晔, 孟斌, 李潇, 等. 一种GPS海洋反射信号测试系统[C]//第三届中国卫星导航学术年会. 北京: 中国卫星导航学术年会组委会, 2012.WANG Y, MENG B, LI X, et al.A GNSS-R testing system based on GPS signal generator[C]//The 3rd China Satellite Navigation Conference.Beijing:China Satellite Navigation Scientific Committee, 2012(in Chinese). |
| [15] | ZAVOROTNY V, VORONOVICH A. Scattering of GPS signals from the ocean with wind remote sensing application[J].IEEE TGRS, 2000, 38(2): 951–964. |
| [16] | 田日才. 扩频通信[M].北京: 清华大学出版社, 2007: 21-26.TIAN R C. Spread spectrum communication[M].Beijing: Tsinghua University Press, 2007: 21-26.(in Chinese) |
| [17] | 杨尧. GNSS-R有效波高反演算法研究与实现[D]. 北京: 北京航空航天大学, 2013.YANG Y.The study and implement of significant wave height retrieval methods using GNSS-R[D].Beijing:Beihang University, 2013(in Chinese). |
