信道选择和功率控制是抗干扰的重要方法[2-3],选择可用性高的信道进行信息传输,是一种避免干扰、保证通信畅通、提高频谱利用率的方法,多用于认知无线电网络、无线传感器网络以及自适应跳频系统等通信系统中[4-6], 功率控制在移动通信中应用较多[7],是无人机数据链避免干扰的重要手段[8]。信道选择经常需要与功率控制配合使用,然而信道选择、功率控制往往是分离的2个过程,算法复杂,时间长,例如目前常用信道参数和机器学习理论结合的方法[9-10]选择信道,这种方法通常将信道质量划分等级,信道参数与信道质量等级构成映射,只能得到信道可用性判别,还需要额外的功率控制算法估计发送功率大小。
本文针对以上问题,考虑无人机数据链工作环境,提出了结合相关向量回归 (Relevance Vector Regression,RVR) 的无人机数据链信道选择和功率控制的方法,将信道选择和功率控制合为一个过程,快速计算出保证通信质量的最小化发送功率,并选择质量优的信道。通过实际地理环境仿真实验证明了本文方法能够准确预测最小化的发送功率,选择合适的信道,减少信道检测次数,以低功率达到明显的抗干扰效果,具有很高的可行性。
1 无人机数据链可靠性影响因素 1.1 外部干扰 外部干扰主要考虑白高斯噪声、单音干扰、脉冲干扰、随机二元码干扰。在具有干扰的信道质量评估时,信噪比 (Signal Noise Ratio,SNR)、干扰功率、干扰中心频率和带宽都是影响误码率 (Bit Error Rate,BER) 的因素。本文将干扰功率转换为干扰噪声比 (Interference-to-Noise Ratio, INR),干扰中心频率转换为干扰中心频率相对于信号中心频率的偏移程度,计算公式为
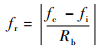 | (1) |
式中:fc为无人机信号中心频率;fi为干扰信号中心频率;Rb为无人机信号码元速率。
图 1是具有不同的中心频率和带宽的随机二元码干扰在不同干扰噪声比情况下产生的误码率仿真,其中无人机信号是扩频系数为31的扩频信号,带宽为1 MHz,中心频率为1 440 MHz,B为带宽。
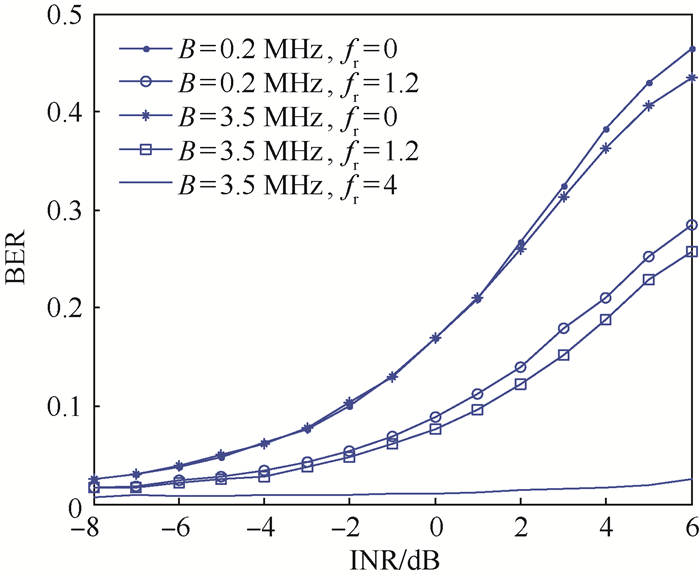 |
| 图 1 随机二元码干扰BER仿真 Fig. 1 BER simulation of random binary code interference |
| 图选项 |
1.2 复杂地理环境 复杂的地理环境,不规则的地形使接收端信号包含直射、反射和散射路径信号,导致严重的多径衰落,误码率增加,通信质量下降明显[11]。因此本文考虑复杂地理环境对通信质量的影响使用Longley-Rice模型计算路径损耗,Longley-Rice模型综合了包括地形参数在内的多个衰落影响因素,具有高稳定性[12],适用于0.02~40 GHz的频段、1~2 000 km的传输距离,符合无人机的飞行情况。
2 信道选择和功率控制方法 本文的信道选择与功率控制方法示意图如图 2所示。首先选择待检测信道,获得干扰频率、带宽、功率和噪声功率等参数,对于已知干扰源的情况,可以直接获取干扰参数,对于电磁干扰未知的情况,则需要通过频谱感知[13]和干扰认知获取干扰参数,然后把这些干扰参数和系统要求的BER输入SNR预测模型,得到相应的最小化SNR,与噪声功率相乘得到接收端所需要的最小接收功率,再加上路径损耗,得到地面基站需要发送功率的最小值pmin。SNR预测模型是信道选择和功率控制的基础,具体建立方法在第3节中详细描述。理论上信号功率越大误码率越低,抗干扰能力越强,但是功率过大不仅增大能量开销,也会干扰其他通信系统,pmin是信道满足误码率要求的发送端最小发送功率,当切换信道时,应将发送功率调整至相应信道的pmin,在保证无人机数据链通信质量的同时尽可能使用低发射功率。因此把pmin作为衡量信道质量好坏的标准,pmin越大信道质量越差,地面控制站对比pmin和发送功率门限值pth,若pmin≤pth,则认为该信道可用,然后进行频谱决策,即选择该信道,设置发送功率为pmin,进行信号传输,否则,选择与当前检测信道相关性低的候选信道作为预测下一待测信道,重复以上过程直至选出可用信道,如此即可实现信道选择与功率控制。
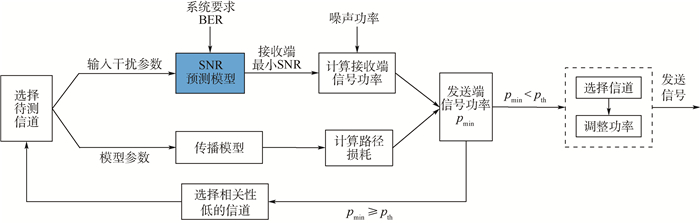 |
| 图 2 无人机数据链信道选择与功率控制方法示意图 Fig. 2 Schematic of a channel selection and power control method for UAV data link |
| 图选项 |
本文利用信道相关性选择待测信道是为了减少信道检测次数。对于无人机信道选择来说,信道检测进行信道质量好坏的预测,具体通过预测pmin实现,这会带来一定的时间开销,特别是当候选信道数目多或大部分候选信道质量差的时候,考虑到在实际的通信环境中,信道相关性普遍存在,引入信道相关性,若预测pmin大于阈值,则选择与当前信道相关系数低的信道作为下一信道进行预测或感知,通过该方法降低信道检测次数,降低时间开销。利用信道相关性降低频谱感知次数已被用于无线传感器网络频谱感知中[14],从时间统计的角度给出信道相关系数的计算公式为
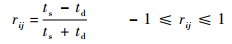 | (2) |
式中:ts为i和j信道同时可用或不可用的时间,称为状态相同;td为i和j信道状态不同的时间。rij越大,信道相关性越大,当判断某信道为不可用时,选择该信道相关系数最低的信道进行下次检测,直到选出可用信道。
3 SNR预测模型的建立 建立SNR预测模型的目的是能根据信道噪声和干扰等信道质量影响因素的变动,预测出满足通信质量要求的SNR,即建立干扰信息、BER和SNR之间的回归关系。目前常用的回归方法有神经网络法、支持向量回归 (Support Vector Regression,SVR) 和RVR等,由于建立信噪比回归模型的样本数有限,因此神经网络法不具优势,SVR在时间序列预测、凸二次规划和复杂工程近似分析等方面具有广泛应用[15],但是SVR受到核函数必须满足Mercer条件限制,回归中需要交叉验证,复杂度会随训练样本数增加而急剧增加[16]。本文选用RVR的方法建立SNR预测模型,RVR适合处理非线性和小样本的问题,RVR比SVR更稀疏,时间开销低。
3.1 RVR模型描述 RVR在模式识别[17]、计算机视觉问题[18]和数据拟合[19]等领域获得成功。RVR模型表达式[16]为
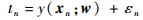 | (3) |
式中:{xn, tn}n=1N为训练数据集,N为训练数据数目;w=[w0, w1, …, wN]T为权向量;εn为方差为σ2的独立高斯噪声;
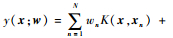
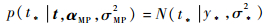 | (4) |
式中:t为目标向量;αMP和σMP2分别为使后验概率p(α, σ2|t) 最大化的超参数向量和协方差值。
RVR预测模型的预测输出计算公式为[16]
 | (5) |
预测方差计算公式为[16]
 | (6) |
式中:μ、Σ分别为权值后验概率分布的均值和协方差,μ=σ-2ΣΦTt,Σ=(σ-2ΦTΦ+A)-1,A=diag (α0, α1, …, αN)。
3.2 预测误差评价 本文采用预测信噪比均方根误差 (RMSE) 和相对百分比误差 (RPE) 作为预测误差评价标准。通常,RPE处于10%以内,认为预测模型较准确。
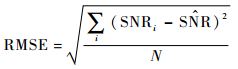 | (7) |
 | (8) |
式中:
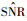
3.3 最小化功率预测过程 图 3是基于RVR的最小化信噪比预测流程图。最小化信噪比预测流程具体实现步骤如下。
 |
| 图 3 SNR预测模型建立流程图 Fig. 3 Flowchart of SNR prediction model establishment |
| 图选项 |
1) 选取数据样本,确定自变量、因变量,数据处理,进行归一化处理,在特征向量数目多时,需要进行特征向量降维处理。
在回归模型中,把干扰信息,即干扰比、干扰中心频率、干扰带宽以及BER作为自变量,SNR作为因变量。数据处理和归一化的目的是提高模型预测的准确程度,数据处理主要是把BER转换为dB形式,根据式 (1) 把干扰中心频率转换为相比于信号中心频率的偏移程度。建模前需要对所有训练数据和预测数据进行归一化处理,归一化公式为
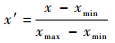 | (9) |
式中:x′为x归一化后的数据;x为原始数据;xmin和xmax分别为原始数据的最小、最大值。
干扰情况复杂时,特征向量维度增加,为了避免模型训练以及测试时间开销增大,提高适应性,应当在第一步数据处理时进行特征向量降维处理。常用的特征提取方法有主成分分析法 (Primary Components Analysis, PCA)[20]、因子分析法和线性判别分析法等,其中主成分分析最典型。本文采用主成分分析法降维。
2) 选择核函数类型,初始化模型参数σ2和α,设置最大迭代次数。
3) 进入RVR训练器,计算权重w、均值μ和协方差Σ等参数,按照
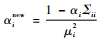

4) 判断迭代次数是否大于预设值或误差小于阈值,如果是即终止训练。
5) 保留最能体现模型特征的相关向量 (Relevance Vector,RV)。
6) 利用预测数据进行拟合预测,使用式 (5) 计算预测结果,使用式 (6) 计算预测方差。
7) 使用式 (7) 和式 (8) 评价预测准确度。
3.4 基于RVR的最小化功率预测举例 举例说明无人机数据链受到2个干扰源影响情况下最小化SNR预测模型建立过程。无人机信号是带宽为1 MHz,扩频系数为31的扩频信号,信噪比取值5~16 dB, 2个干扰源产生随机二元码干扰信号,干扰噪声功率比分别为INR1与INR2,取值-8~8 dB, 干扰带宽分别为B1取值范围0.1~1 MHz,B2取值范围2~4 MHz,中心频率偏移均为0~5,仿真得到BER,共获得样本数5 267组,INR1、INR2、中心频率偏移、B1、B2和BER作为自变量,SNR作为因变量,随机选取3 584组作为训练数据,进行建模,选取1 683组作为测试数据,用于评价模型预测准确度。
本节采用RVR常用的核函数有高斯核函数、多项式核函数和Laplace核函数进行训练,同时给出SVR的训练结果,进行性能比较。
表 1是分别采用不同核函数RVR和SVR得到的训练结果,RVs和SVs分别为相关向量和支持向量的数目。总体来说,RVR预测SNR的均方根误差小于SVR,除了采用Laplace核函数外,相关向量数小于支持向量数目,相关向量回归机更稀疏,回归性能更好。对于RVR而言,高斯核函数是使用最广泛的核函数,虽然预测误差略大于多项式回归机,其相关向量最少,预测时间更少,多项式核函数阶数越多训练结果越准确,但是训练时间也更长,所以本文采用高斯核函数RVR算法预测信噪比。
表 1 RVR和SVR训练结果 Table 1 Training results of RVR and SVR
| 训练结果 | RVR | SVR | ||||
| 高斯 | 5阶多项式 | Laplace | RBF | 多项式 | ||
| RVs,SVs | 71 | 73 | 3 564 | 604 | 1 404 | |
| RMSE | 0.023 1 | 0.020 3 | 0.062 6 | 0.074 | 0.58 | |
| RPE/% | 0.198 | 0.180 | 0.325 | 0.887 | 5.17 | |
表选项
2个干扰特征向量共7维,采用主成分分析法对训练数据特征向量分别降维至4、5和6。表 2是降维后的训练结果,降维至5和6时RPE值均小于5%,模型预测结果较准确,能用于抗干扰,维度为4时,预测误差过大,预测模型不准确,因此,对于本例输入向量可降至5维。文中2个干扰相互独立,在干扰情况复杂时,干扰间可能具有相关性,降维效果会更明显。
表 2 采用PCA降维后RVR训练结果 Table 2 Training results of RVR after dimensionality reduction using PCA
| 训练结果 | RVR (高斯核函数) | ||
| 特征向量为6维 | 特征向量为5维 | 特征向量为4维 | |
| RMSE | 0.301 | 0.302 | 6.479 |
| RPE/% | 4.30 | 4.56 | 24.65 |
表选项
4 性能分析 本节从信道质量评估标准的合理性、误码率性能和信道检测评估次数3个角度分析本文信道选择与功率控制方法的性能。使用3.4节中的高斯核RVR方法建立SNR预测模型,路径损耗采用自由空间传播模型,无人机与地面控制基站相距5 km,系统要求BER为0.01。令无人机信道1~5带宽均为2 MHz,通信频率来源于无人驾驶航空器使用频率,分别为843、1 439、1 441、1 443、2 420 MHz。假设无人机数据链受到2个干扰源干扰,一个是带宽为3.5 MHz,针对信道3的干扰,中心频率为1 441 MHz,另一个是带宽为0.2 MHz,针对信道2的干扰,中心频率为1 439 MHz,INR1取值[-6:0.5:6] dB,INR2取值[6:-0.5:-6] dB,各信道噪声功率相等,均为-82.5 dBm。
1) 信道质量评估标准的合理性分析
常用的信道质量评估法是通过发送探测序列获知接收信号强度、信号干扰噪声比 (Signal to Interference and Noise Ratio,SINR) 或BER等参数来评判信道质量好坏、是否可用,以BER为标准的信道评估最准确,SINR标准使用最广泛,图 4是采用本文方法设定BER=0.01时,获得的各信道最小发送功率。
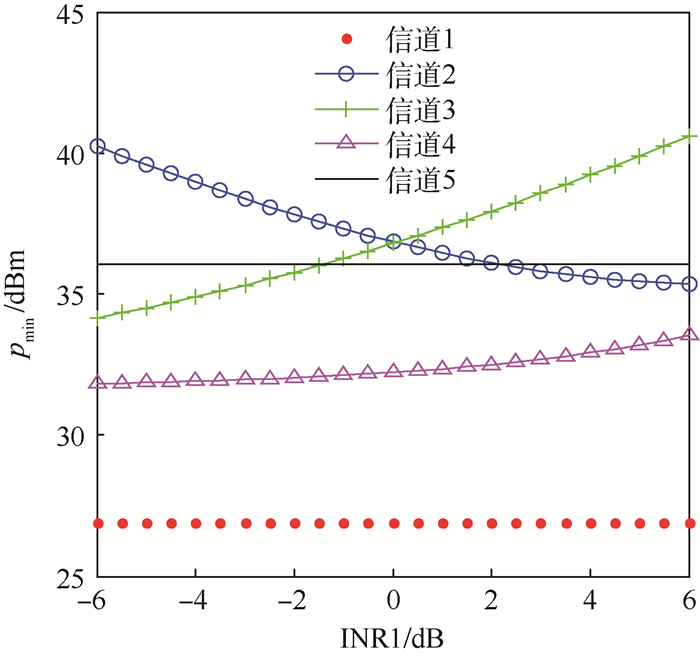 |
| 图 4 各信道预测发送功率最小值pmin Fig. 4 Minimum predicted transmit power pmin for every channel |
| 图选项 |
表 3是本文基于预测发送功率pmin的信道评估方案和基于BER、SINR信道评估准则的信道质量排序情况,采用BER和SINR标准时,发送功率为36 dBm。本文方法以信道最小发送功率pmin为标准判断信道质量优劣,比常用的SINR标准更接近信道质量真实情况,因此只要判断信道质量优劣的功率阈值pth设置合理,根据pmin判断信道质量的方法可靠。
表 3 不同标准下的信道质量排序 Table 3 Channel quality ranking based on different criteria
| INR1/dB | pmin标准 | SINR标准 | BER标准 |
| -6~-2.5 | 1-4-3-5-2 | 1-4-3-5-2 | 1-4-3-5-2 |
| -2.5~-1.5 | 1-4-3-5-2 | 1-4-3-2-5 | 1-4-3-5-2 |
| -1.5~0 | 1-4-5-3-2 | 1-4-3-2-5 | 1-4-5-3-2 |
| 0~0.5 | 1-4-5-2-3 | 1-4-3-2-5 | 1-4-5-2-3 |
| 0.5~2 | 1-4-5-2-3 | 1-4-2-3-5 | 1-4-5-2-3 |
| 2~3.5 | 1-4-2-5-3 | 1-4-2-3-5 | 1-4-2-5-3 |
| 3.5~6 | 1-4-2-5-3 | 1-4-2-5-3 | 1-4-2-5-3 |
表选项
2) 误码率性能
误码率性能可以直接反映无人机数据链抗干扰效果。图 5是使用本文抗干扰策略得到的BER与系统要求BER=0.01的误差,统计了分别采用RVR和SVR模型各信道的误码率与系统要求误码率相比的平均相对百分比误差。由图 5可知使用RVR和SVR得到的BER与0.01都很逼近,除了信道5外,采用RVR模型比SVR模型得到的误码率RPE小,RVR的RPE值都在2%以内,优势明显,说明采用本文提出的信道选择和功率控制方法能够准确预测满足一定BER的最小发送功率pmin,有较好的抗干扰效果。
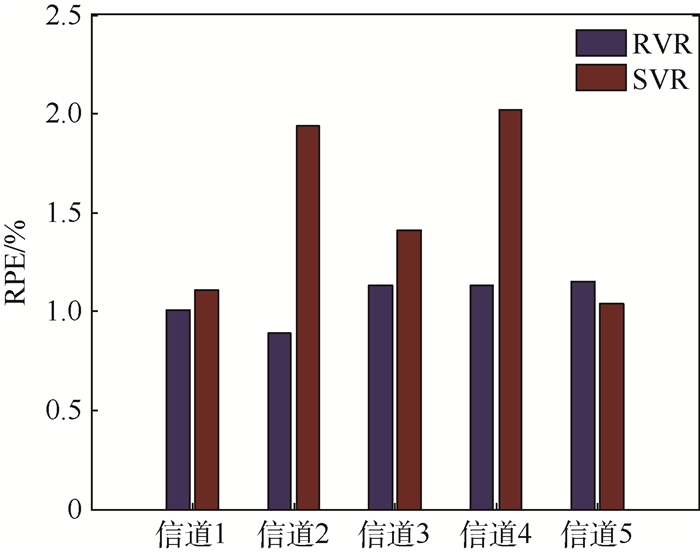 |
| 图 5 各信道误码率的RPE值 Fig. 5 RPE value of BER for every channel |
| 图选项 |
3) 信道检测次数分析
设置功率阈值pth=33 dBm,首先进行信道检测,预测信道最小发送功率pmin<pth,则认为信道质量优,为可用信道,选择该信道通信,否则认为信道质量差,选择相关性低的信道进行下一次检测。分析中认为信道2、信道3、信道5两两间的相关系数为1,与信道1和信道4的相关系数为-1,信道1和信道4的相关系数为1。表 4对比了随机检测法和相关检测法的检测次数,随机检测法是每次从候选信道中随机选择信道进行质量评估,直到检测到可用信道,利用信道相关性的感知评估法随机选择第一条信道,若不可用,则根据信道相关性选择下一条候选信道。
表 4 信道检测次数对比 Table 4 Comparison of channel detected iterations
| 检测方法 | 不考虑信道5 | 考虑信道5 | |||
| 随机检测 | 相关检测 | 随机检测 | 相关检测 | ||
| 检测次数 | 1.67 | 1.5 | 2 | 1.6 | |
表选项
对比是否考虑信道5的2种情况:①不考虑信道5;②考虑信道5并且认为信道5不可用。总体上说,考虑信道相关性的信道检测次数要少于随机选择的情况,可用信道数目越少,待检测信道数目越多,是否利用相关性的信道检测次数差距更大,考虑信道相关性的方案优势更明显。尤其对于需要进行频谱感知和干扰认知获取干扰参数的情况,利用信道相关性检测信道,能够明显降低时间开销。
5 仿真实验 5.1 仿真场景 仿真实验地理环境如图 6所示,图 6(a)是使用谷歌地球获得的地形图,范围约为39.920°N~40.036°N,116.144°E~116.332°E,图 6(b)是对应的高程图。无人机航线由A到B,约为15 km,C为地面基站,实验中采用点对点模式的Longley-Rice模型计算路径损耗,地面基站和干扰源天线高度为100 m,无人机天线高度为1 km。无人机信道1~5与性能分析中信道参数相同。在航线附近有2个随机二元码干扰源Ⅰ1、Ⅰ2, Ⅰ1为带宽为3.5 MHz针对信道3的干扰,中心频率f1为1 441 MHz,由于Ⅰ1是宽带干扰,干扰频带宽,信道2、4与信道3频距近,因此会受到Ⅰ1干扰影响,Ⅰ2带宽为0.2 MHz,针对信道2的干扰,中心频率f2为1 439 MHz。信道噪声功率均为-82.5 dBm。
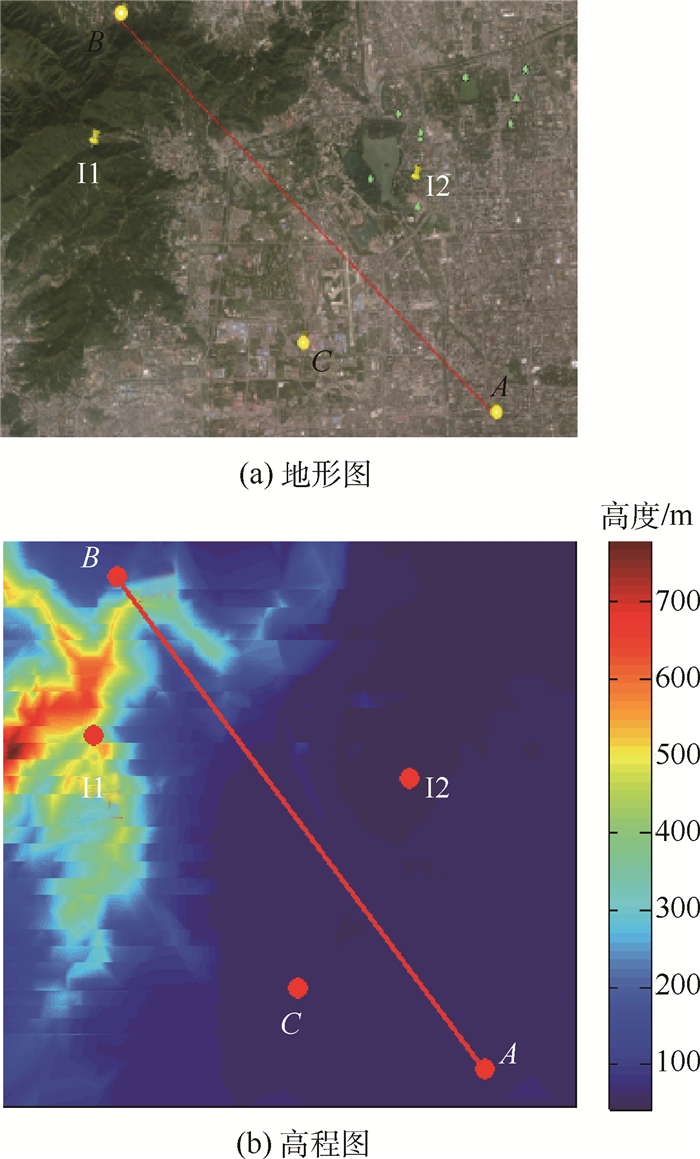 |
| 图 6 仿真实验地理环境 Fig. 6 Geographical environment of simulation experiment |
| 图选项 |
图 7表示飞行路径上各点受到干扰功率大小分布,d为飞行距离。对于干扰源2来说,飞行终点附近有山地阻挡,因此干扰功率衰减大,几乎为0,而干扰源1本身处于山地上,飞行终点处的山体对干扰源1并不造成明显阻挡,因此干扰功率依然较大。
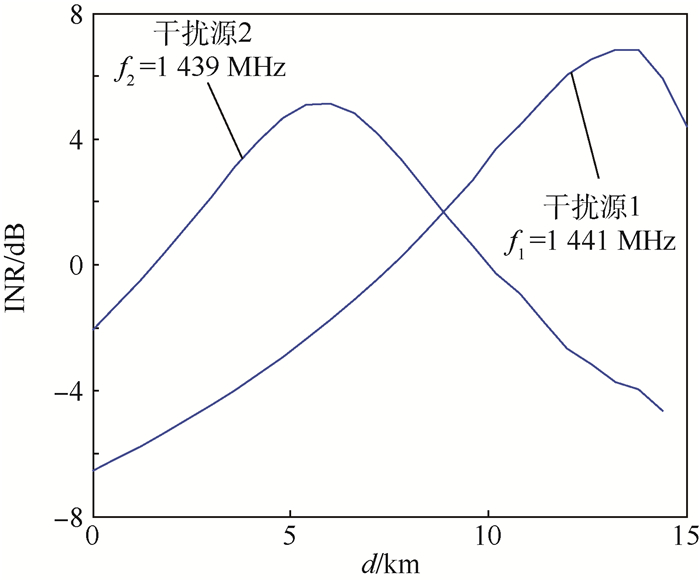 |
| 图 7 干扰功率分布 Fig. 7 Distribution of interference power |
| 图选项 |
5.2 仿真结果及分析 图 8是采用高斯核RVR模型预测得到的各信道在不同位置时的SNR,纵坐标表示保证0.01的误码率,即保证一定通信质量所需要的SNR最小值,理论上,干扰功率越强,信道质量越差,完成通信所需要的最小SNR越大。从图 8中可以看出,信道1和信道5因为和2个干扰源的频距远,几乎不受干扰源影响,仅受噪声影响信号发送功率曲线,因此二者预测信噪比相同且不变。信道3、4受到干扰源Ⅰ1和噪声影响,SNR预测值变化趋势与Ⅰ1功率变化趋势相同,Ⅰ1中心频率相比较于信道4有较大偏移,信道4受到影响小于信道3,所需SNR小于信道3,信道2主要受到窄带干扰源Ⅰ2,但同时受到干扰源Ⅰ1的影响,前半程信道2的SNR预测值变化趋势与Ⅰ2功率变化趋势相仿,后半程Ⅰ2功率变大,使得SNR下降缓和,在终点处Ⅰ2功率几乎为0,主要受Ⅰ1影响,此时与信道4情况类似,因此SNR相同。
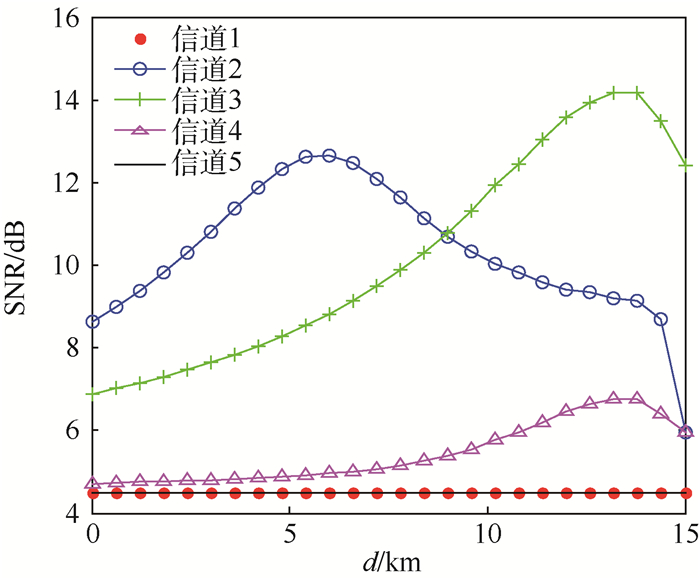 |
| 图 8 各信道预测SNR与飞行距离的关系 Fig. 8 Relationship between predicted SNR and flight distance for every channel |
| 图选项 |
本文将pmin作为衡量信道质量好坏的标准,pmin越大,信道质量越差,pmin越小,信道质量越好。图 9表示各信道在飞行航迹的前14 km所需基站发送功率,由于考虑路径损耗因素,各信道预测发送功率变化趋势与路径损耗变化趋势相关,与SNR变化趋势有较大不同,信道5只受噪声影响,具有较低的预测SNR,但是由于信道5频率较大路径损耗大,所需pmin较大,因此尽管信道5和信道1都不受外部干扰源干扰,且具有相同的预测SNR,选择的最佳信道是信道1而不是信道5,信道2~4频率相差不大,信道质量好坏取决于外部干扰情况。
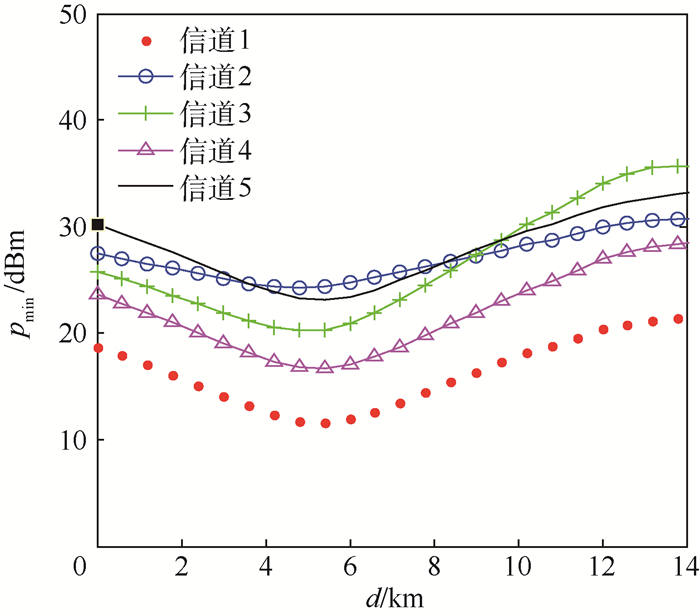 |
| 图 9 各信道pmin与飞行距离的关系 Fig. 9 Relationship between pmin and flight distance for every channel |
| 图选项 |
表 5是从飞行路径上选取的6个点的仿真结果,第6个点表示飞行终点,终点附近山体阻挡,所以pmin较大,各信道采用相应的pmin计算得到的BER都与0.01很接近,认为采用本文提出的无人机抗干扰策略能够控制误码率,有效地抗干扰。按照本文方法,若pth=20 dBm,则在位置1、2、5、6处选择质量优的信道1,平均检测次数是1.8次,而随机检测需要3次,在位置3、4处选择信道1或4,平均检测次数1.6次,而随机检测需要2次。
表 5 信道选择和功率控制方法仿真结果 Table 5 Simulation results of channel selection and power control method
| 信道 | 位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | |||||||||||
| pmin/dBm | BER/dB | pmin/dBm | BER/dB | pmin/dBm | BER/dB | pmin/dBm | BER/dB | pmin/dBm | BER/dB | pmin/dBm | BER/dB | ||||||
| 1 | 18.72 | -1.98 | 15.12 | -1.93 | 11.80 | -1.97 | 13.55 | -1.96 | 17.39 | -1.99 | 20.40 | -2.00 | |||||
| 2 | 27.49 | -1.94 | 25.56 | -1.99 | 24.27 | -1.98 | 25.69 | -2.01 | 27.74 | -2.00 | 29.91 | -2.00 | |||||
| 3 | 25.77 | -2.02 | 22.74 | -1.98 | 20.23 | -2.01 | 23.09 | -2.01 | 28.74 | -2.02 | 34.08 | -1.98 | |||||
| 4 | 23.60 | -1.99 | 20.07 | -2.02 | 16.84 | -2.01 | 18.69 | -2.01 | 23.00 | -2.02 | 26.98 | -2.00 | |||||
| 5 | 30.22 | -1.99 | 26.62 | -2.00 | 23.28 | -1.99 | 24.94 | -2.00 | 28.77 | -1.98 | 31.78 | -1.98 | |||||
| 注:BER取对数,故单位为dB。 | |||||||||||||||||
表选项
6 结论 本文基于相关向量回归模型,提出了一种适用于无人机数据链的信道选择和功率控制方法,通过分析和实验结果证明:
1) 本文方法把信道选择和功率控制联合起来,在复杂的电磁和自然环境中,能够准确选择质量优的信道并确定最小发送功率,以较小的发送功率达到抗干扰和保证通信畅通的目的。
2) 相比常用的SINR信道质量评估方法,本文方法更接近基于BER的信道质量评估结果,对信道质量优劣的判断合理准确。
3) 本文方法在进行信道检测时考虑了信道相关性,检测次数减少,尤其在电磁环境恶劣情况下,能有效降低时间开销。
4) 提出在复杂干扰情况下采用PCA方法对特征向量进行降维,使用适当降维后的特征向量能建立准确的信噪比预测模型。
本文使用PCA方法能够在电磁环境复杂、特征向量多的情况下实现降维,但模型准确度降低,如何保证模型准确率的同时,尽量降低维度,值得进一步研究。
参考文献
| [1] | VACHTSEVANOS G J, VALAVANIS K P.Military and civilian unmanned aircraft[M]//Handbook of unmanned aerial vehicles.Berlin:Springer Netherlands, 2015:93-103. |
| [2] | ⅡDUKAH. Fixed point optimization algorithm and its application to power control in CDMA data networks[J].Mathematical Programming, 2012, 133(1): 227–242. |
| [3] | ZENGEN G, BUESCHING F, POETTNER W B, et al.Adaptive channel selection for interference reduction in wireless sensor networks[C]//Proceedings, ARCS 2015-The 28th International Conference on Architecture of Computing Systems.Nuremberg:VDE, 2015:1-7. |
| [4] | SKOKOWSKI P, MALON K, KELNER J M, et al.Adaptive channels' selection for hierarchical cluster based cognitive radio networks[C]//2014 8th International Conference on Signal Processing and Communication Systems (ICSPCS).Piscataway, NJ:IEEE Press, 2014:1-6. |
| [5] | PAL A, NASIPURI A.A distributed channel selection scheme for multi-channel wireless sensor networks[C]//Proceedings of the thirteenth ACM International Symposium on Mobile Ad Hoc Networking and Computing.New York:ACM, 2012:263-264. |
| [6] | XIAO L, DAI H, NING P. Jamming-resistant collaborative broadcast using uncoordinated frequency hopping[J].IEEE Transactions on Information Forensics and Security, 2012, 7(1): 297–309.DOI:10.1109/TIFS.2011.2165948 |
| [7] | MORIMOTO A, MIKI N, ISHⅡ H, et al.Investigation on transmission power control in heterogeneous network employing cell range expansion for LTE-Advanced uplink[C]//2012 18th European Wireless Conference European Wireless, EW.Nuremberg:VDE, 2012:1-6. |
| [8] | 李思佳, 毛玉泉, 郑秋容, 等. UAV数据链抗干扰的关键技术研究综述[J].计算机应用研究, 2011, 28(6): 2020–2024.LI S J, MAO Y Q, ZHENG Q R, et al. Overview of research on key techniques for anti-jamming of UAV data link[J].Application Research of Computers, 2011, 28(6): 2020–2024.(in Chinese) |
| [9] | BACCOUR N, KOUBAA A, MOTTOLA L, et al. Radio link quality estimation in wireless sensor networks:A survey[J].ACM Transactions on Sensor Networks (TOSN), 2012, 8(4): 34. |
| [10] | WANG Y, MARTONOSI M, PEH L S. Predicting link quality using supervised learning in wireless sensor networks[J].ACM SIGMOBILE Mobile Computing and Communications Review, 2007, 11(3): 71–83.DOI:10.1145/1317425 |
| [11] | 李建东, 郭梯云, 邬国扬. 移动通信[M].4版西安: 西安电子科技大学出版社, 2009: 94-132.LI J D, GUO T Y, WU G Y. Mobile communication[M].4th edXi'an: Xidian University Press, 2009: 94-132.(in Chinese) |
| [12] | PHILLIPS C, SICKER D, GRUNWALD D.The stability of the Longley-Rice irregular terrain model for typical problems:CU-CS-1086-11[R].Boulder:University of Colorado at Boulder, 2011. |
| [13] | VALAVANIS K P, VACHTSEVANOS G J.Handbook of unmanned aerial vehicles[M].[S.l.]:Springer Publishing Company, Incorporated, 2014:749-844. |
| [14] | 崔蓉. 基于序贯决策的无线传感网络频谱感知策略与分配方法[D]. 北京: 北京邮电大学, 2015: 18-29.CUI R.Wireless sensor network spectrum sensing and allocation strategy based on sequential decision[D].Beijing:Beijing University of Posts and Communications, 2015:18-29(in Chinese). |
| [15] | BASAK D, PAL S, PATRANABIS D C. Support vector regression[J].Neural Information Processing-Letters and Reviews, 2007, 11(10): 203–224. |
| [16] | TIPPING M E. Sparse Bayesian learning and the relevance vector machine[J].The Journal of Machine Learning Research, 2001, 1: 211–244. |
| [17] | CAMPS-VALLS G, MARTíNEZ-RAMóN M, ROJO-áLVAREZ J L, et al. Nonlinear system identification with composite relevance vector machines[J].IEEE Signal Processing Letters, 2007, 14(4): 279–282.DOI:10.1109/LSP.2006.885290 |
| [18] | NICOLAOU M A, GUNMES H, PANTIC M. Output-associative RVM regression for dimensional and continuous emotion prediction[J].Image and Vision Computing, 2012, 30(3): 186–196.DOI:10.1016/j.imavis.2011.12.005 |
| [19] | TANTUM S L, SCOTT W R, MORTON K D, et al. Target classification and identification using sparse model representations of frequency-domain electromagnetic induction sensor data[J].IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(5): 2689–2706.DOI:10.1109/TGRS.2012.2215876 |
| [20] | JOLLIFFE I T. Principal component analysis[M].Berlin: Springer, 2002: 41-64. |
