为改善伺服系统的跟踪性能,提高系统的跟踪精度,在工程实践中,常常通过优化系统结构、改进驱动方式、提高检测元件精度等手段来升级系统硬件设施;并通过完善系统模型、加强参数辨识来提升系统建模准确性。在此基础上,为进一步克服内外扰动的影响,科研人员提出了各种控制策略和算法来提高伺服系统的跟踪精度。除了在实际工程中占主导地位的PID及其改进算法[1-4]外,已有的控制策略和算法主要包括内模控制[5-8]、自抗扰控制[9-12]、H∞控制[13-14]、自适应控制[15-17]、扰动观测器补偿[18-21]、滑模控制[22-24]等。
由于滑模控制特殊的调节机制,使其不仅对参数摄动等内部不确定性具有“完全自适应性”[25],而且对外部干扰也具有很强的鲁棒性[26]。因此,滑模控制适用于包含内外扰动的伺服系统。但是,滑模控制也有其自身缺点——抖振。当系统状态变量到达滑模面后,滑模控制器通过不连续函数的高速切换,强制状态轨迹沿着滑模面收敛于平衡点,从而获取很强的鲁棒性,这种高速切换在执行器上表现为一种高频振动。因此,采用滑模控制策略来实现伺服系统高精度跟踪的关键是如何有效削弱抖振的影响。为此,国内外科研人员开展了广泛而深入的研究,并取得了丰硕的成果,特别是高阶滑模[27-29]和自适应增益滑模的提出为削弱抖振开辟了2条不同的道路。
高阶滑模的核心思想是将不连续函数隐藏于滑模变量的高阶导数中,这使得滑模变量的动态调节机制能产生一个连续且尽可能光滑的输出,以抑制抖振的产生,从而获得更高的控制精度。但大部分高阶滑模算法需要计算滑模变量的高阶导数,计算量较大。目前,有2种不需要计算滑模变量的高阶导数的算法较为流行,即Super-Twisting 算法[28, 30]和Sub-Optimal 算法[31]。值得注意的是,根据高阶滑模的定义[32],趋近律[33-34]也是一种二阶滑模算法。以等效原理设计滑模控制器,趋近律同样不需要计算滑模变量的高阶导数。
自适应增益滑模则源于解决一对矛盾:一般情况下,滑模控制器鲁棒性的强弱和滑模变量收敛的快慢都取决于切换函数增益值的大小。为了能有效消除不确定性的影响,并获得更快的响应速度,切换函数的增益值通常应设定较大。然而,滑模控制引起的抖振的幅度与切换函数的增益成正比[35]。从抑制抖振的角度出发,则要求切换函数的增益值越小越好。这就形成了系统响应速度和消抖对增益值要求的矛盾。而消除这对矛盾的关键就是明确系统不确定性的上界,并使切换函数的增益略大于该值。由此,国内外****研究设计了多种切换函数的自适应增益调度算法,从而形成了一系列自适应增益滑模。
自适应增益调度的核心是寻找一种合适的决定增益值增减的判断标准,并以此建立动态调节机制。综合近年来国内外研究成果,自适应增益调度的判断标准可以概括为3类:基于跟踪误差的判断标准[36-37]、基于滑模变量的判断标准[38-46]和基于等效原理的判断标准[35]。其中,前2类标准均有2种调度方式:①增益值直接跟随判断标准发生改变;②首先设定合适的阈值和变化率,当判断标准大于该阈值时,增益值以设定的变化率增加,反之减少。基于等效原理的自适应增益调度是通过判断系统滑动模态是否建立来确定增益值的增减。3类自适应增益调度策略各有所长,其中基于跟踪误差的自适应增益调度实时性最好,基于滑模变量的自适应增益调度往往无需估计系统不确定性的上界,而基于等效原理的自适应增益调度准确性高且物理意义明确。
综上所述,本文结合跟踪误差判断标准的快速性和等效原理判断标准的准确性,提出一种新的自适应增益调度策略,并将其应用于趋近律高阶滑模算法,构成降低系统抖振的双效机制,从而实现系统的高精度位置跟踪。
1 滑模控制的跟踪精度比较分析 1.1 不确定干扰对位置跟踪精度的危害和挑战 考虑如下所示的非线性不确定系统:
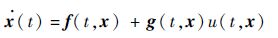 | (1) |
式中:x∈Rn为系统状态向量;u(t,x)∈R为系统控制输入;f(t,x)∈Rn和g(t,x)∈Rn均包含不确定性。
假定设计系统的滑模变量为σ(x),σ(x)∈R,则有
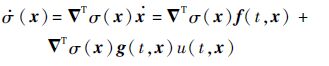 | (2) |
式中:$\nabla $Tσ(x)表示σ(x)梯度的转置。
令
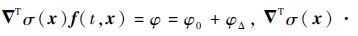
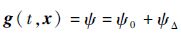
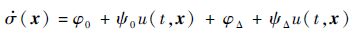 | (3) |
高阶滑模控制的目的就是设计一种控制律,强制σ(x)和(x)在有限时间内趋于零。若设计控制律为
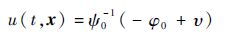 | (4) |
式中:υ为待设计项。
同时令不确定相关项φΔ+ψΔu(t,x)=Φ(t,x),且满足

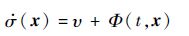 | (5) |
分析式(5)可知,如果系统不存在不确定性,即Φ(t,x)=0,υ仅需设计为简单的线性形式即可使得$\dot{\sigma }\left( x \right)$快速收敛,如υ=-kσ(x),k>0。此时,系统不会出现高频抖振,容易获得较高的跟踪精度。但系统不确定性几乎不可避免。根据滑模控制原理,在设计υ时引入一个高频切换项,如υ=-k1sgn(σ),k1>0,从而获得很强的鲁棒性,则式(5)可表示为
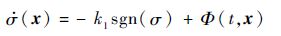 | (6) |
若式(6)的滑动模态能建立,则必须满足到达条件σ(x)$\dot{\sigma }\left( x \right)$<0,即式(7)所示的条件必须满足:
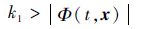 | (7) |
然而在一般情况下,系统的不确定性难以直接测量。因此,k1的值往往被设计得过大。根据等效控制原理[25-26],当系统理想滑动模态建立起来后,满足:
 | (8) |
式中:sgneq(σ)为sgn(σ)的等效值。
如果k1的值选择合理,则系统的抖振幅值取决于扰动的大小;如果k1的值选取过大,则抖振幅值会被人为增加,从而使得执行机构振动幅值增加,最终导致系统的跟踪误差增大。
综上所述,当系统存在扰动时,为使系统稳定而引入的切换函数可以确保系统具有很强的鲁棒性。然而,不合理的切换函数增益会增加系统抖振,从而影响跟踪精度。因此,提高系统滑模控制跟踪精度的关键问题就是寻找合理的切换函数增益。根据滑模控制原理,在系统相轨迹趋向滑模面的阶段,为加快系统收敛速度,k1的值需要设置得较大;而在滑动模态建立后,为提高系统跟踪精度,k1的值应尽量接近于
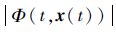
1.2 3类应对不确定性干扰的自适应增益调度策略性能分析 综合近年来的研究成果,根据不同的判断标准,k1的自适应增益调度大致可分为基于跟踪误差、基于滑模变量和基于等效原理3类。为便于比较分析各自性能,本文将这3类自适应调度方法统一表示为相似的结构。
1) 基于跟踪误差的自适应增益调度
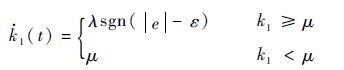 | (9) |
式中:λ>0为增益变化率;e为跟踪误差;ε>0为阈值常数;μ>0为增益最小值。
此类增益调度方式能直常接反应系统的输出状态,增益调度的实时性较好,更适合于输出无超调的系统。但是在跟踪误差振荡收敛过程中,容易使增益值过早地衰减而降低系统的鲁棒性,从而影响系统跟踪精度。
2) 基于滑模变量的自适应增益调度
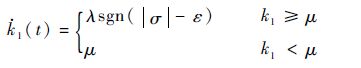 | (10) |
一般情况下,滑模变量是跟踪误差及其代数的组合,如线性组合形式的线性滑模、积分组合形式的积分滑模、指数组合形式的终端滑模等。虽然跟踪误差的非线性信息的引入略微降低了增益调度的实时性,但避免了增益值过早衰减的情况。因此,此类调度使得切换函数的增益值能较好地跟随系统扰动。但是,ε值在一定程度上可以看作是系统滑动模态建立与否的分界线,如何选取该值,即如何通过简单的数值比较来判断系统滑动模态是否建立较为困难。
3) 基于等效原理的自适应增益调度
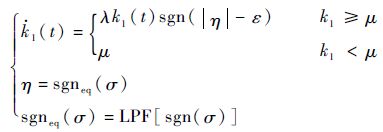 | (11) |
式中:LPF[·]为低通滤波器输出;0<ε<1。
此类增益调度的判断依据是切换函数的等效输出,即切换函数经过低通滤波器后的输出。当系统滑动模态尚未建立时,等效输出的幅值为1。而滑动模态建立后,等效输出小于1[26]。据此,可通过设定一个小于1的阈值来准确调度切换函数的增减。这类判断标准意义明确,调度可靠,能使切换函数有效跟随系统不确定性。但由于低通滤波器的引入,会进一步延缓自适应调度的实时性。特别当滤波常数较大时,影响尤为明显。此外,由于该调度方法采用二次幂速率改变切换函数增益值,变化速度过快,因此需要设定增益值上界。另一方面,为确保控制的鲁棒性,根据式(7)可知,一般情况下增益值应大于系统不确定性的上界。但在工程实际中,系统不确定性的上界是无法有效直接测量或估算的。因此,如何选取式(11)中合适的上界值较为困难。
综合上述3类自适应增益调度策略性能分析可知,一个优良的调度策略应该具备:能有效跟踪系统不确定性、实时性好、意义明确调节简单、无需估算系统不确定性上界等的品质。为此,本文结合误差信息的快速性和等效原理的准确性,构建一种误差为主导的自适应增益调度策略以降低系统抖振,从而提高系统的位置跟踪精度。
2 面向高精度跟踪的误差主导的自适应增益调度及性能分析 2.1 自适应增益调度模型 采用滑模控制策略可以有效地消除伺服系统内外扰动的影响,提升系统的跟踪性能。为进一步降低由滑模控制所带来的系统抖振,加快系统收敛速度,提高系统的跟踪精度,本文提出一种误差主导的切换函数自适应增益调度,如式(12)所示。该增益调度策略有机结合了跟踪误差信息的快速性和等效原理判断的准确性,为高精度滑模控制提供了有效的保障。
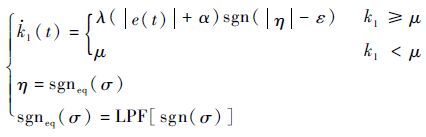 | (12) |
式中:k1>0为切换函数的增益值;λ>0;0<ε<1;μ>0;α>0;LPF[·]为低通滤波器的输出,低通滤波器的传递函数为
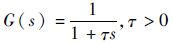
当系统滑动模态已经建立,切换函数的等效输出|η|<1,否则|η|=1。系统通过选取合适的阈值ε和滤波常数τ来判断系统滑动模态是否建立,从而确定增益值的增减性,物理意义明确。此外,增益的变化率由位置跟踪误差主导,构建了一种时变的增益变化率,能有效提高增益调度的实时性。由式(12)的动态调节机制可知,当系统遭遇较大幅值扰动时,跟踪误差|e(t)|将增加,必然引起k1变化率增大,使系统跟踪误差加速收敛到零,获得更快的收敛速度和更强的鲁棒性,最终获得更高的跟踪精度。
2.2 性能分析 由第2.1节分析可知,当系统滑动模态尚未建立之前,只要满足k1(t)>|Φ(t,x)|,系统的滑动模态必然可建立,且在有限长时间内使得式(8)成立。因此,当系统滑动模态建立后,k1(t)最理想的调度结果为
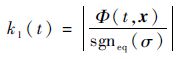
定理1 若系统式(1)的不确定性满足
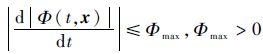
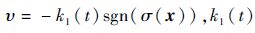
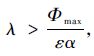
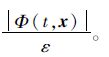
证明 由前述分析可知,当系统滑动模态建立后,有
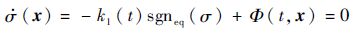
 | (13) |
构建Lyapunov候选函数为
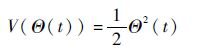 | (14) |
式中:
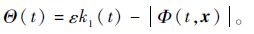
求该Lyapunov候选函数的时间导数,则有
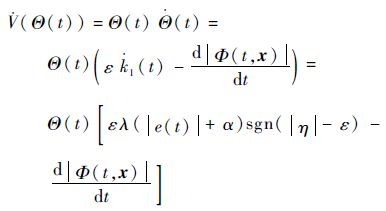 | (15) |
由式(13)可知
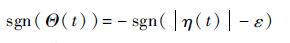 |
联立式(15)可得
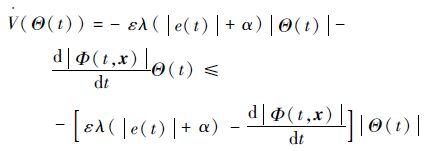 | (16) |
分析式(16)可知,若要保证式(16)的负定性,式(17)必须满足
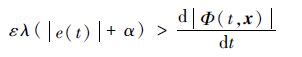 | (17) |
因为ε、α、λ均为正实数,|e(t)|≥0,且
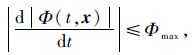
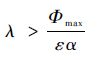 | (18) |
综上可知,当式(18)满足时,可保证Lyapunov候选函数的时间导数的负定性,Θ(t)可在有限时间内收敛到0,即k1(t)可在有限时间内收敛到
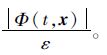
定理1确保在系统滑动模态建立后,k1(t)可有效跟随|Φ(t,x)|。同时,当常数ε设置趋近于1时,k1(t)最终会趋近于|Φ(t,x)|,切换函数增值更小,从而使系统抖振幅值降低,系统的跟踪精度更高。
3 基于误差主导的自适应增益调度滑模控制 3.1 滑模控制律设计 高阶滑模作为一种削弱抖振的有效方法,既能保持系统的鲁棒性,又能提升滑模控制的精度[27, 32]。按照高阶滑模的定义[32],趋近律本质上是一种二阶滑模算法,同样具备高阶滑模算法的性能。本文将误差主导的自适应增益调度与趋近律滑模算法相结合,形成消除系统抖振的双效机制,加快系统收敛速度,在保证系统鲁棒性的前提下降低切换函数增益值,提升系统的跟踪精度。
若系统数学模型为
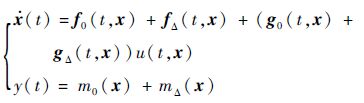 | (19) |
式中:f0(t,x)∈Rn和g0(t,x)∈Rn均为确定项;fΔ(t,x)∈Rn和gΔ(t,x)∈Rn均为有界不确定性项;y(t)∈R为位置输出;m0(x)∈R为确定项;mΔ(x)∈R为有界不确定项。
若参考轨迹为yref(t),系统跟踪误差为
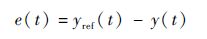 | (20) |
此处将e(t)作为一个新的动态系统,根据系统式(19),跟踪误差的动态调节机制为
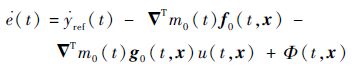 | (21) |
式中:Φ(t,x)为有界不确定项,即
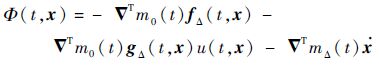 | (22) |
且满足|Φ(t,x)|<Φmax,Φmax>0。滑模控制器的设计目标是寻求一种控制律,能使描述跟踪误差的动态系统式(21)在有限时间内收敛到平衡点。因为在设计系统控制律时只能参考系统的确定信息,所以设计过程均假设Φ(t,x)=0。
设计系统滑模变量为
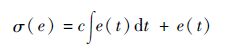 | (23) |
式中:常数c>0。在不考虑系统不确定性的前提下,其时间导数为
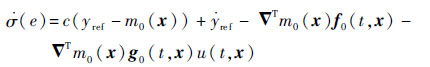 | (24) |
滑模变量的动态调节机制采用如式(25)所示的趋近律的一般形式。
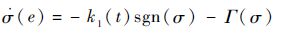 | (25) |
式中:Γ(·)∈R,且满足Γ(0)=0,σ(e)Γ(σ)>0。k1(t)采用式(12)所示的自适应增益调度算法,当$\nabla $Tm0(x)g0(t,x)≠0时,可得系统式(21)的控制律为
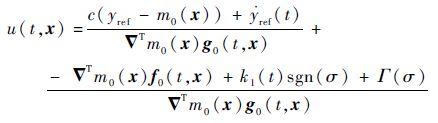 | (26) |
3.2 稳定性分析 若采用式(26)所示的控制律,能使关于跟踪误差的动态系统建立滑动模态,则跟踪误差动态系统就具备渐进稳定性,进而原系统的输出能在有限时间内跟踪上参考轨迹。此特性由定理2给出。
定理 2 系统式(19)的跟踪误差动态特性描述为式(21),若采用式(26)所示的控制律,其中切换函数的增益调度算法为式(12),则关于跟踪误差的动态系统可在有限时间内建立滑动模态,即在有限时间内渐进稳定。
证明 针对跟踪误差动态系统式(21)构建正定的Lyapunov候选函数,如下:
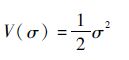 | (27) |
式中:滑模变量σ定义如式(23)。
当考虑系统不确定性时,滑模变量的导数为
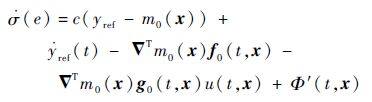 | (28) |
式中:不确定性Φ′(t,x)=Φ(t,x)+cmΔ(x),|Φ′(t,x)|<Φ′max,Φ′max>0。
将设计所得控制律式(26)应用于系统式(21)可得
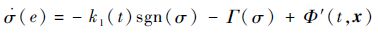 | (29) |
则有Lyapunov候选函数的时间导数为
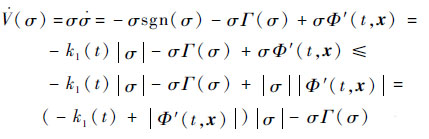 | (30) |
因为σΓ(σ)>0,则当式(31)成立时,可保证Lyapunov候选函数的时间导数为负定。
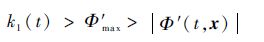 | (31) |
因此,当条件式(31)满足时,跟踪误差动态系统可在有限时间内建立滑动模态。
由式(12)可设k1(t)的初始值为k1(0)≥μ。当系统滑动模态未建立时,|η(t)|=sgneq(σ)=1,则有
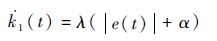 | (32) |
根据式(32)可得
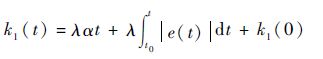 | (33) |
由于需要使得k1(t)>Φ′max成立,则其充分条件为
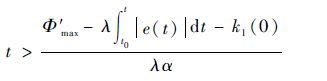 | (34) |
因为k1(0)≥μ且|e(t)|≥0,所以当式(35)成立时,一定可使k1(t)>Φ′max成立。
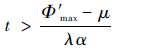 | (35) |
综上可知,采用误差主导的自适应增益调度算法式(12),存在一个最大时间
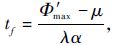
4 仿真与实验结果比较分析 4.1 仿真结果比较分析 为更直观地比较分析第1.2节中所述3类自适应增益调度与本文提出的误差主导增益调度的性能,本节直接将这4类增益调度算法应用于式(5)所示的滑模变量动态调节机制,通过仿真实验对比分析滑模变量的动态响应和不同自适应增益调度的性能。在式(5)中,设定υ=-k1(t)·sgn(σ)-k2σ,即表示滑模变量调节机制采用指数趋近律。设扰动信号Φ(t)为单位阶跃信号,并在第10 s时施加。并设σ的初始值为10,k1(t)初始值为10,仿真时间步长为0.005 s。各算法的参数设置如下:
1) 基于跟踪误差和滑模变量的自适应增益调度:λ=9,ε=0.003,μ=0.001。
2) 基于等效原理的自适应增益调度:λ=3,ε=0.950,μ=0.001,滤波时间常数为0.01 s。
3) 误差主导的自适应增益调度:λ=9,ε=0.950,μ=0.001,α=0.5,滤波时间常数为0.01 s。
不同自适应增益调度算法仿真结果如图 1所示。图中:EB-AG表示基于跟踪误差的自适应增益调度;SV-AG表示基于滑模变量的自适应增益调度;EC-AG表示基于等效原理的自适应增益调度;EG-AG表示误差主导的自适应增益调度。
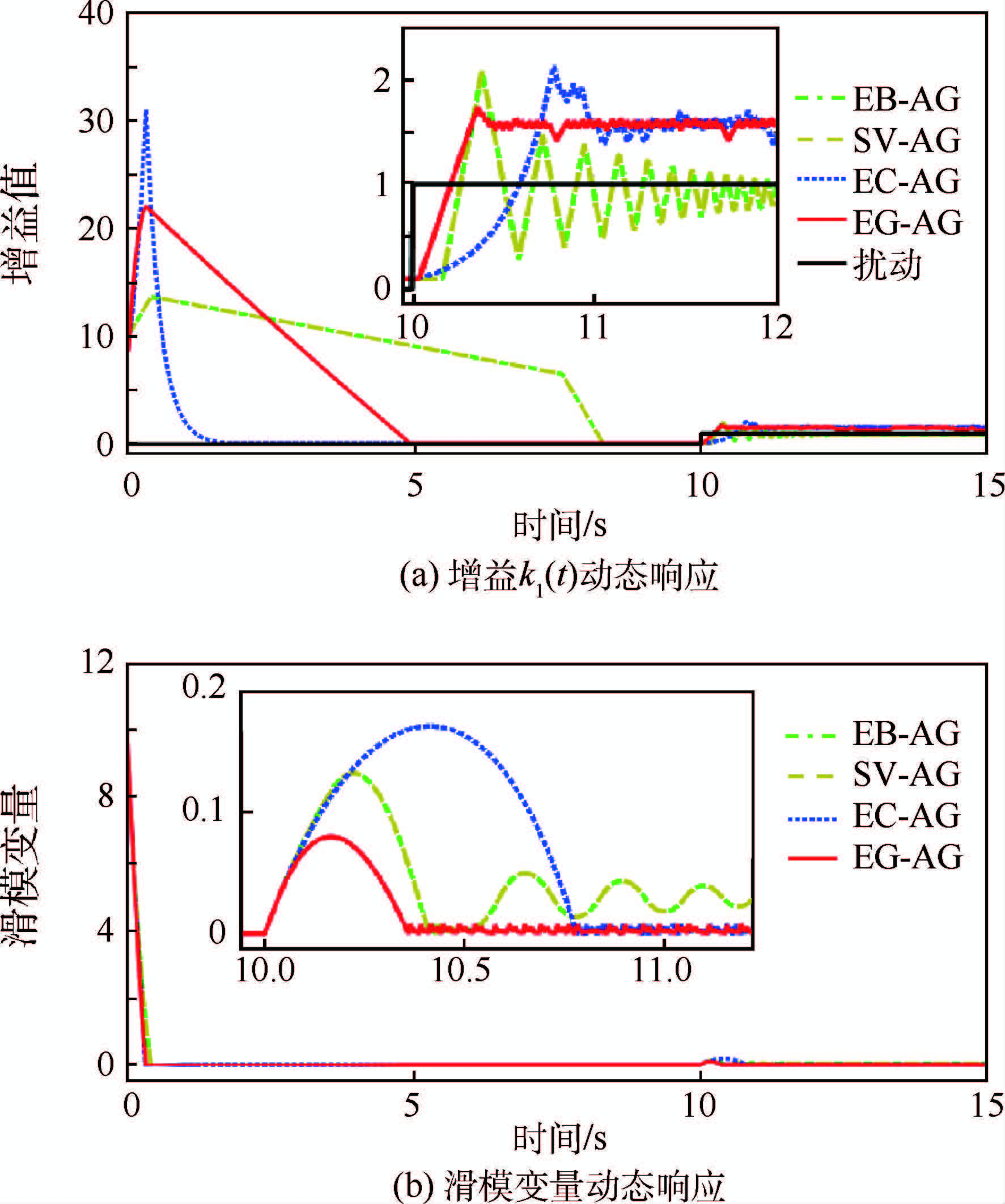 |
| 图 1 不同自适应增益调度算法抗扰对比仿真结果 Fig. 1 Comparative simulation results on resisting disturbance with different adaptive gain schedule algorithms |
| 图选项 |
需要注意的是,由于研究对象为滑模变量,式(5)的输出为滑模变量本身,而系统的参考轨迹为0,则系统的输出误差为滑模变量。因此,基于跟踪误差的自适应增益调度和基于滑模变量的自适应增益调度的判断标准和仿真结果相同。
分析图 1(a)可知,在初始阶段,基于等效原理的增益调度采用幂指数变化率,使得其增益值变化速度最快,在初始阶段使得增益值峰值过高,达到了32;基于跟踪误差和滑模变量的增益调度响应速度最慢,直到9 s左右时才使得切换函数增益值收敛到最小值;而误差主导的增益调度收敛速度适中,增益峰值为22,较为合理。在外部扰动响应阶段,由于低通滤波器的作用,使得基于等效原理的增益调度滞后现象明显;由于收敛过程中滑模变量常常要过零点,使得采用基于跟踪误差和滑模变量的增益调度出现增益值提前衰减,因此,当系统稳定后其增益值往往小于外部扰动;而采用误差主导的自适应增益调度使得增益值响应速度最快,出现的峰值最小,且最后能跟随并略大于外部扰动,更有利于降低系统抖振和增强系统鲁棒性。
由图 1(b)可知,在受到扰动信号干扰时,由于增益调度滞后,采用基于等效原理增益调度的滑模变量收敛到稳定值的时间最长,且峰值高达0.17;采用基于跟踪误差和滑模变量的增益调度,其误差的峰值为0.14,但由于稳定后的增益值小于外部扰动,其稳态误差较大;而采用误差主导自适应增益调度,其误差收敛速度最快,峰值仅为0.07,且稳态误差较小,跟踪精度最高。
综上可知,在同等条件下,相比于其他3类增益调度算法,采用误差主导的自适应增益调度可使系统获得更好的快速性、更强的鲁棒性和更高的跟踪精度。
4.2 实验结果比较分析 直流力矩电机伺服系统是典型的包含内外不确定性的位置跟踪系统,外部扰动主要有摩擦、风扰、热形变等,内部不确定性主要是高阶为建模及参数摄动。为了对比不同自适应增益调度策略对直流力矩电机位置伺服跟踪性能的影响,本文在光电跟踪系统的方位轴子系统上开展了对比实验,实验平台硬件架构如图 2所示。
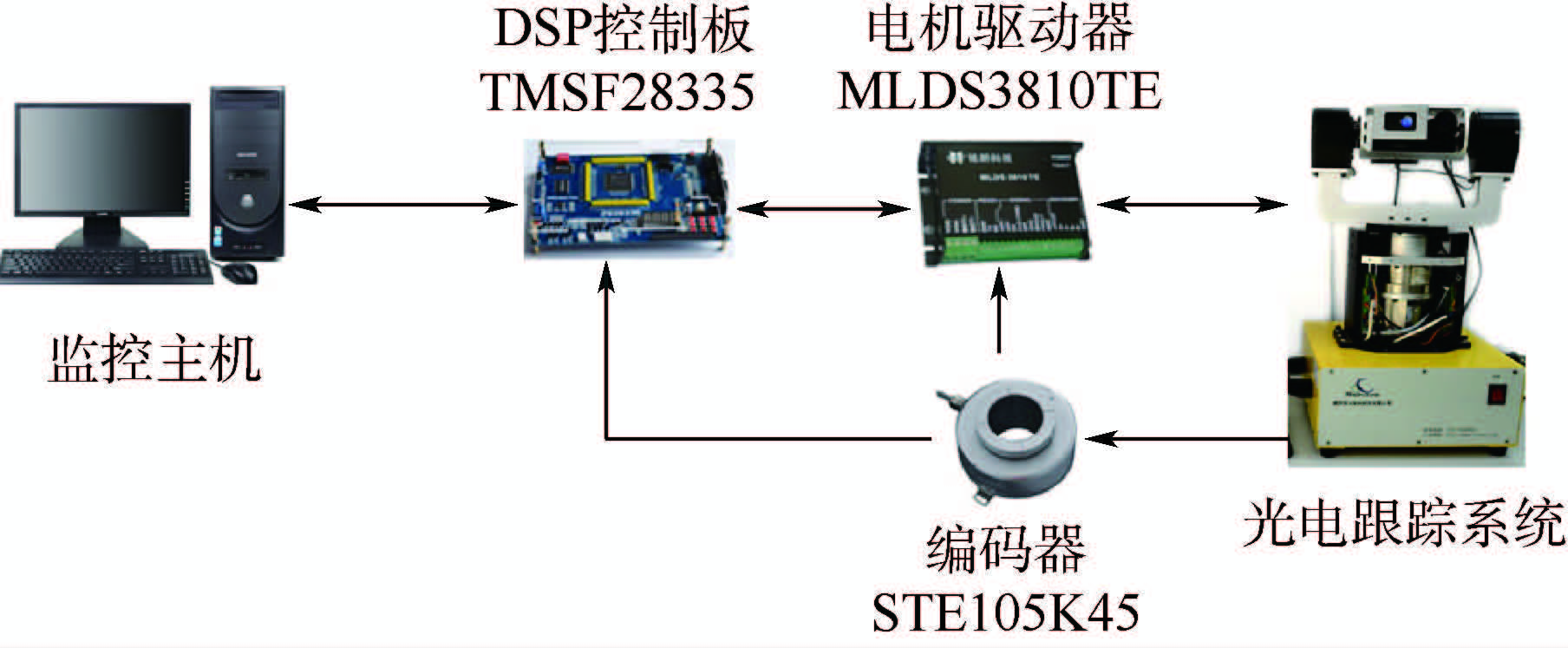 |
| 图 2 光电跟踪实验平台硬件架构 Fig. 2 Hardware architecture of photoelectric trackingexperimental platform |
| 图选项 |
为进一步增强系统的内部不确定性,在伺服系统数学模型中忽略了直流力矩电机的电枢电感和伺服系统的黏性阻尼力矩,从而构成系统未建模不确定性。同时,省略直流电机负载,使其与外部摩擦等一起构成系统的外部扰动,则位置跟踪伺服系统的名义模型为
 | (36) |
式中:θ为位置,();ω为角速度,()/s;J为转动惯量,J=180 kg·m2;R为电枢电阻,Ω;Cm为直流电机力矩常数,Cm=25 N·m/A;Ce为直流电机反电动势常数,Ce=22.28 V/(rad·s-1);u为控制电压,V。
采用指数趋近律滑模算法设计滑模控制器,其中切换函数的增益分别采用第2.2节所述3类增益调度算法和本文提出的误差主导增益调度算法,比较不同增益调度对跟踪性能的影响。主要参数设置如下所示:
1) 跟踪参考轨迹为等效正弦信号45°·sin(0.05π t),DSP工作时间步长为0.001 s,低通滤波器时间常数为0.03 s,切换函数最小增益为0.01。
2) 基于跟踪误差的自适应增益调度:λ=10,ε=0.5。
3) 基于滑模变量的自适应增益调度:λ=10,ε=5。
4) 基于等效原理的自适应增益调度:λ=2,ε=0.95。
5) 误差主导的自适应增益调度:λ=10,ε=0.95,α=1。
直流(DC)力矩电机位置跟踪伺服控制对比实验结果如图 3所示。分析图 3(c)可知,基于跟踪误差的增益调度使得增益值过早衰减而导致增益值普遍较小;基于等效原理的增益调度由于采用幂指数变化率,使得增益值的峰值超过了200;基于滑模变量的增益调度和误差主导增益调度的增益变化率适中,且均未出现较大的增益峰值。
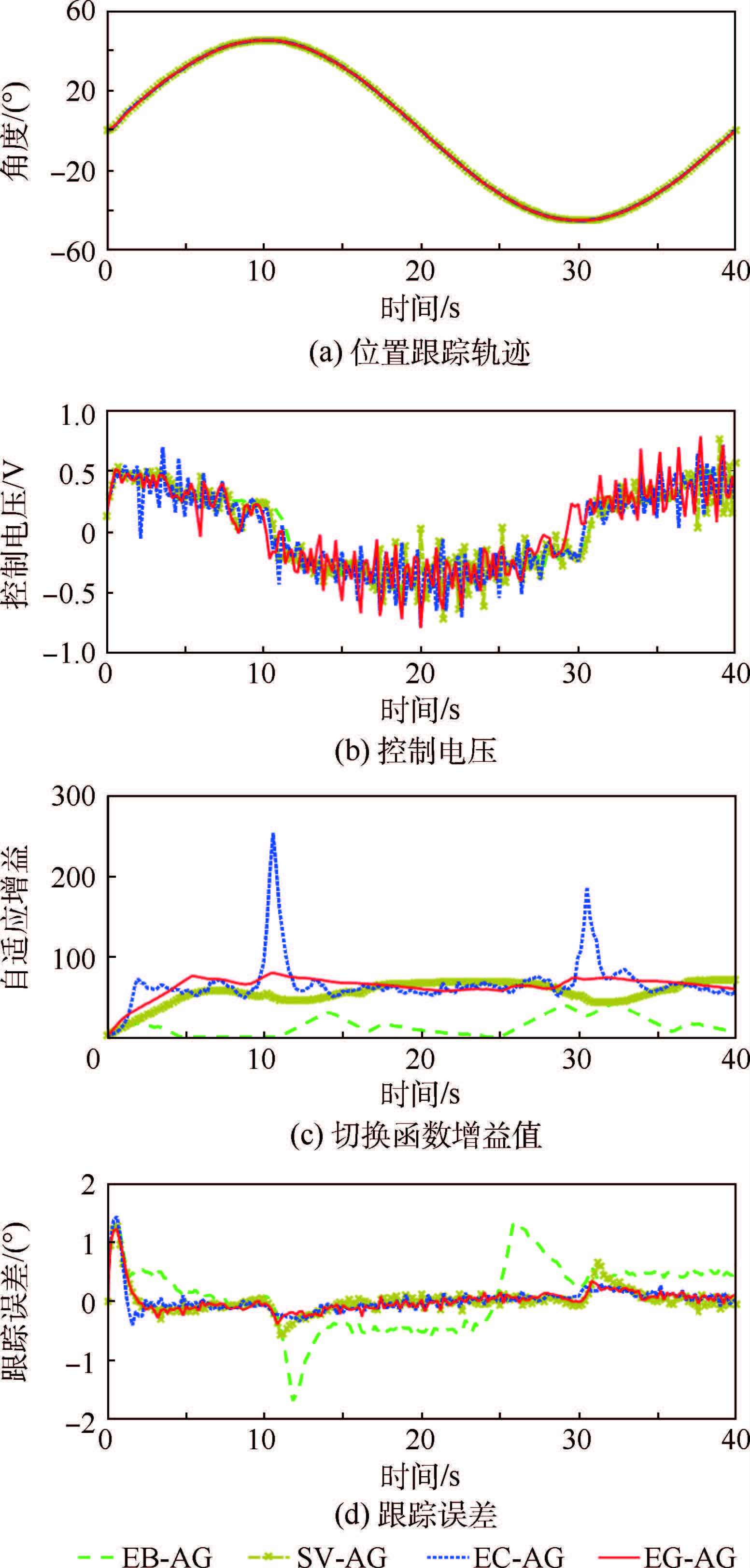 |
| 图 3 直流力矩电机位置跟踪伺服控制对比实验结果 Fig. 3 Comparative experimental results on position trackingservo control of DC torque motor |
| 图选项 |
由图 3(d)可知,由于基于跟踪误差的增益调度产生的增益值过小导致其跟踪误差最大,特别是电机转向时的最大跟踪误差达到1.8°左右;基于滑模变量的增益调度过早衰减情况得到大幅缓解,跟踪精度提升较大,转向时的最大跟踪误差为0.5°左右;基于等效原理的增益调度变化过快,在初始阶段引起较大的超调,最大超调量为0.5°左右;采用误差主导的增益调度较为合理,在初始阶段未出现过大的超调,且跟踪精度最高,在电机转向时的跟踪误差为0.2°左右。
综合实验结果可知,误差主导的自适应增益调度算法能产生较为合理的切换函数增益值,从而提升直流力矩电机伺服系统的跟踪性能,相比另外3类增益调度方式,能获得最高的跟踪精度。
5 结 论 本文针对系统内外不确定性提出的误差主导的自适应增益调度算法在位置跟踪控制系统中具有如下特点:
1) 有机结合了等效原理判断滑动模态建立与否的准确性和跟踪误差信息反映跟踪状态的快速性,能使切换函数的增益值准确快速地跟随系统不确定性的变化。
2) 能加快滑模变量的收敛速度,从而提升系统的响应速度。
3) 与趋近率相结合构成了减小系统抖振的双效机制。能减小系统抖振幅值,在确保系统鲁棒性的同时,提高了滑模控制系统的跟踪精度。
值得注意的是,由于滑模控制策略的固有特点,抖振无法彻底消除。在后期工作中,将开展最小自适应增益算法的理论和实验研究,最大程度上削弱抖振的影响。
参考文献
| [1] | 肖启明, 杨明, 刘可述, 等. PMSM伺服系统速度环PI控制器参数自整定及优化[J].电机与控制学报, 2014, 18(2): 102–108.XIAO Q M, YANG M, LIU K S, et al. Parameters self-tuning and optimization of speed PI controller for PMSM servo system[J].Electric Machines and Control, 2014, 18(2): 102–108.(in Chinese) |
| [2] | 邓昌奇, 廖辉. 基于前馈控制的交流伺服系统精确定位的研究[J].武汉大学学报(工学版), 2013, 46(3): 405–409.DENG C Q, LIAO H. Research on accurate positionting of AC servo system based on feed-forward control[J].Engineering Journal of Wuhan University, 2013, 46(3): 405–409.(in Chinese) |
| [3] | 符慧, 左月飞, 刘闯, 等. 永磁同步电机转速环的一种变结构PI控制器[J].电工技术学报, 2015, 30(12): 237–243.FU H, ZUO Y F, LIU C, et al. A variable structure PI controller for permanent magnetic synchronous motor speed-regulation system[J].Transactions of China Electrotechnical Society, 2015, 30(12): 237–243.(in Chinese) |
| [4] | 左韬, 黄海波, 肖永军. 基于自校正控制的空间光通信精跟踪系统设计[J].仪器仪表学报, 2012, 33(5): 1181–1187.ZUO T, HUANG H B, XIAO Y J. Fine tracking system design of space optical communication based on self-tuning control[J].Chinese Journal of Scientific Instrument, 2012, 33(5): 1181–1187.(in Chinese) |
| [5] | ZHANG Z, YAN P, JIANG H, et al. A discrete time-varying internal model-based approach for high precision tracking of a multi-axis servo gantry[J].ISA Transactions, 2014, 53(5): 1695–1703.DOI:10.1016/j.isatra.2014.04.006 |
| [6] | 闫鹏, 张震, 郭雷, 等. 超精密伺服系统控制与应用[J].控制理论与应用, 2014, 31(10): 1338–1352.YAN P, ZHANG Z, GUO L, et al. Control and application of ultra high precision mechatronics[J].Control Theory & Applications, 2014, 31(10): 1338–1352.(in Chinese) |
| [7] | 夏运霞, 包启亮, 李锦英. 光电跟踪系统视轴稳定的鲁棒内模控制器设计[J].控制与决策, 2013, 28(7): 1117–1121.XIA Y X, BAO Q L, LI J Y. Design of robustness internal model controller for line of sight of photoelectric tracking system[J].Control and Decision, 2013, 28(7): 1117–1121.(in Chinese) |
| [8] | 王秋平, 左玲. 光电跟踪系统双内模控制研究[J].东北电力大学学报, 2014, 34(2): 76–82.WANG Q P, ZUO L. The research of dual internal model control applied to electro-optical tracking systems[J].Journal of Northeast Dianli University, 2014, 34(2): 76–82.(in Chinese) |
| [9] | 高志强. 自抗扰控制思想探究[J].控制理论与应用, 2013, 30(12): 1498–1510.GAO Z Q. On the foundation of active disturbance rejection control[J].Control Theory & Applications, 2013, 30(12): 1498–1510.(in Chinese) |
| [10] | 付永领, 龙满林, 郭栋, 等. 自抗扰控制技术在转台频响伺服中的应用[J].北京航空航天大学学报, 2013, 39(4): 432–437.FU Y L, LONG M L, GUO D, et al. Application of ADRC technology in simulator frequency response servo[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(4): 432–437.(in Chinese) |
| [11] | 叶镭, 夏元清, 付梦印, 等. 无人炮塔炮控系统自抗扰控制[J].控制理论与应用, 2014, 31(11): 1580–1589.YE L, XIA Y Q, FU M Y, et al. Active disturbance rejection control for gun control system of unmanned turret[J].Control Theory & Applications, 2014, 31(11): 1580–1589.(in Chinese) |
| [12] | 陈兴林, 刘川, 武志鹏. 精密运动平台线性自抗扰控制[J].中南大学学报(自然科学版), 2013, 44(8): 3210–3216.CHEN X L, LIU C, WU Z P. Linear active disturbance rejection control used in precision motion platform[J].Journal of Central South University(Science and Technology), 2013, 44(8): 3210–3216.(in Chinese) |
| [13] | 武云丽, 李佳嘉, 曾海波, 等. 带有大型挠性网状天线航天器的鲁棒H∞控制方法[J].控制理论与应用, 2013, 30(3): 365–372.WU Y L, LI J J, ZENG H B, et al. Robust H-infinity control design for spacecrafts with large flexible netted antennas[J].Control Theory & Applications, 2013, 30(3): 365–372.(in Chinese) |
| [14] | 赵欣, 马彩文. 基于混合H2/H∞控制的自适应光学系统设计与仿真[J].光子学报, 2014, 43(12): 1–7.ZHAO X, MA C W. Design and simulation of the adaptive optics system based on mixed H2/H∞ control[J].Acta Photonic Sinica, 2014, 43(12): 1–7.(in Chinese) |
| [15] | 宋康宁, 丛爽, 邓科, 等. 自适应强跟踪卡尔曼滤波在陀螺稳定平台中的应用[J].中国科学技术大学学报, 2015, 45(1): 17–23.SONG K N, CONG S, DENG K, et al. Application of adaptive strong tracking Kalman filter to gyro-stabilized platform[J].Journal of University of Science and Technology of China, 2015, 45(1): 17–23.(in Chinese) |
| [16] | 石勇, 韩崇昭. 自适应UKF算法在目标跟踪中的应用[J].自动化学报, 2011, 37(6): 755–760.SHI Y, HAN C Z. Adaptive UKF method with applications to target tracking[J].Acta Automatica Sinica, 2011, 37(6): 755–760.(in Chinese) |
| [17] | 杨东, 毛耀, 丁科, 等. 模型参考算法在快速反射镜中的应用[J].红外与激光工程, 2013, 42(10): 2790–2796.YANG D, MAO Y, DING K, et al. Application of model reference adaptive algorithm in fast-steering mirrors[J].Infrared and Laser Engineering, 2013, 42(10): 2790–2796.(in Chinese) |
| [18] | GINOYA D, SHENDGE P D, PHADKE S B. Disturbance observer based sliding mode control of nonlinear mismatched uncertain systems[J].Communications in Nonlinear Science and Numerical Simulation, 2015, 26(1-3): 98–107.DOI:10.1016/j.cnsns.2015.02.008 |
| [19] | KIM K S, REW K H. Reduced order disturbance observer for discrete-time linear systems[J].Automatica, 2013, 49(4): 968–975.DOI:10.1016/j.automatica.2013.01.014 |
| [20] | 魏伟, 戴明, 李嘉全, 等. 基于频域的光电稳定平台扰动观测器设计[J].山东大学学报(工学版), 2015, 45(4): 45–50.WEI W, DAI M, LI J Q, et al. Design of the disturbance observer of opto-electronic platform in frequency domain[J].Journal of Shangdong University(Engineering Science), 2015, 45(4): 45–50.(in Chinese) |
| [21] | 任彦, 刘正华, 周锐. 滑模干扰观测器在低速光电跟踪系统中的应用[J].北京航空航天大学学报, 2013, 39(6): 835–841.REN Y, LIU Z H, ZHOU R. Application of low speed opto-electronic tracking systems based on sliding mode disturbance observer[J].Journal of Beijing University of Aeronatutics and Astronautics, 2013, 39(6): 835–841.(in Chinese) |
| [22] | 胡贞, 姜会林, 佟首峰. 滑模控制对激光通信ATP系统跟踪性能的改善[J].北京理工大学学报, 2012, 32(5): 522–526.HU Z, JIANG H L, TONG S F. Improvement of STP system tracking performance of laser communication using sliding mode control[J].Transaction of Beijing Institute of Technology, 2012, 32(5): 522–526.(in Chinese) |
| [23] | 肖海峰, 刘海龙, 贺昱曜, 等. 线性滑模变结构的IPMSM直接转矩控制研究[J].控制工程, 2015, 22(1): 144–150.XIAO H F, LIU H L, HE Y Y, et al. Linear sliding-mode variable structure research of direct torque control for IPMSM[J].Control Engineering of China, 2015, 22(1): 144–150.(in Chinese) |
| [24] | 邹权, 钱林方, 蒋清山. 永磁同步电机伺服系统的自适应模糊滑模控制[J].控制理论与应用, 2015, 32(6): 817–823.ZOU Q, QIAN L F, JIANG Q S. Adaptive fuzzy sliding-mode control for permanent magnet synchronous motor servo system[J].Control Theory & Applications, 2015, 32(6): 817–823.(in Chinese) |
| [25] | 高为炳. 变结构控制理论基础[M].北京: 中国科学技术出版社, 1990.GAO W B. Theory of variable structure control[M].Beijing: Science and Technology of China Press, 1990.(in Chinese) |
| [26] | UTKIN V I. Sliding mode in control and optimizaiton[M].New York: Springer, 1992. |
| [27] | BARTOLINI G,FERRARA A,LEVANT A,et al.On second order sliding mode controllers[M]//YOUNG K D,OZGUNER U.Variable structure systems,sliding mode and nonlinear control.Berlin:Springer,1999:329-350. |
| [28] | DAVILA J, FRIDMAN L, LEVANT A. Second-order sliding-mode observer for mechanical systems[J].IEEE Transactions on Automatic Control, 2005, 50(11): 1785–1789.DOI:10.1109/TAC.2005.858636 |
| [29] | FRIDMAN L,LEVANT A,DAVILA J.High-order sliding-mode observer for linear systems with unknown inputs[C]//Proceedings of 2006 Mediterranean Conference on Control and Automation.Piscataway,NJ:IEEE Press,2006:736-741. |
| [30] | MORENO J A. On strict Lyapunov functions for some non-homogeneous super-twisting algorithms[J].Journal of the Franklin Institute, 2014, 351(4): 1902–1919.DOI:10.1016/j.jfranklin.2013.09.019 |
| [31] | BARTOLINI G, FERRARA A, USAI E. Output tracking control of uncertain nonlinear second-order systems[J].Automatica, 1997, 33(12): 2203–2212.DOI:10.1016/S0005-1098(97)00147-7 |
| [32] | LEVANT A. Sliding order and sliding accuracy in sliding mode control[J].International Journal of Control, 1993, 58(6): 1247–1263.DOI:10.1080/00207179308923053 |
| [33] | 高为炳. 非线性系统的变结构控制[J].自动化学报, 1989, 15(5): 408–416.GAO W B. Variable structure control to nonlinear systems[J].Acta Automatica Sinica, 1989, 15(5): 408–416.(in Chinese) |
| [34] | CHAKRABARTY S, BANDYOPADHYAY B. A generalized reaching law for discrete time sliding mode control[J].Automatica, 2015, 52: 83–86.DOI:10.1016/j.automatica.2014.10.124 |
| [35] | UTKIN V I, POZNYAK A S. Adaptive sliding mode control with application to super-twist algorithm:Equivalent control method[J].Automatica, 2013, 49(1): 39–47.DOI:10.1016/j.automatica.2012.09.008 |
| [36] | ZHONG F L, LI H, ZHONG S M, et al. An SOC estimation approach based on adaptive sliding mode observer and fractional order equivalent circuit model for lithium-ion batteries[J].Communications in Nonlinear Science and Numerical Simulation, 2015, 24(1-3): 127–144.DOI:10.1016/j.cnsns.2014.12.015 |
| [37] | ALWI H, EDWARDS C. An adaptive sliding mode differentiator for actuator oscillatory failure case reconstruction[J].Automatica, 2013, 49(2): 642–651.DOI:10.1016/j.automatica.2012.11.042 |
| [38] | ZHANG M J, LIU X, YIN B J, et al. Adaptive terminal sliding mode based thruster fault tolerant control for underwater vehicle in time varying ocean currents[J].Journal of the Franklin Institute, 2015, 352(11): 4935–4961.DOI:10.1016/j.jfranklin.2015.08.009 |
| [39] | TALEB M, LEVANT A, PLESTAN F. Pneumatic actuator control:Solution based on adaptive twisting and experimentation[J].Control Engineering Practice, 2013, 21(5): 727–736.DOI:10.1016/j.conengprac.2012.06.011 |
| [40] | 丛炳龙, 刘向东, 陈振. 一种改进的自适应滑模控制及其在航天器姿态控制中的应用[J].控制与决策, 2012, 27(10): 1471–1477.CONG B L, LIU X D, CHEN Z. An improved adaptive sliding mode control for spacecraft attitude control[J].Control and Decision, 2012, 27(10): 1471–1477.(in Chinese) |
| [41] | PLESTAN F, SHTESSEL Y, BREGEAULT V, et al. Sliding mode control with gain adaptation-Application to an electropneumatic actuator[J].Control Engineering Practice, 2013, 21(5): 679–688.DOI:10.1016/j.conengprac.2012.04.012 |
| [42] | 谢文博, 付明玉, 施小成. 动力定位船舶自适应滑模无源观测器设计[J].控制理论与应用, 2013, 30(1): 131–137.XIE W B, FU M Y, SHI X C. Adaptive sliding-mode passive observer design for dynamic positioning vessel[J].Control Theory & Applications, 2013, 30(1): 131–137.(in Chinese) |
| [43] | 杨帆, 马大为, 胡健. 防空火箭炮无抖振滑模鲁棒控制策略设计[J].火炮发射与控制学报, 2012(1): 51–56.YANG F, MA D W, HU J. Design of chattering free robustness sliding mode control stratege of antiaircraft rocket launcher[J].Journal of Gun Launch & Control, 2012(1): 51–56.(in Chinese) |
| [44] | 付培华, 陈振, 丛炳龙, 等. 基于反步自适应滑模控制的永磁同步电机位置伺服系统[J].电工技术学报, 2013, 28(9): 288–295.FU P H, CHEN Z, CONG B L, et al. A position servo system of permanent magnet synchronous motor based on back-stepping adaptive sliding mode control[J].Transactions of China Electrotechincal Society, 2013, 28(9): 288–295.(in Chinese) |
| [45] | ASHOKN R, SHTESSEL Y. Control of fuelcell-based electric power system using adaptive sliding mode control and observation techniques[J].Journal of the Franklin Institute, 2015, 352(11): 4911–4934.DOI:10.1016/j.jfranklin.2015.04.010 |
| [46] | 陈强, 南余荣, 邢科新. 基于扩张状态观测器的永磁同步电机混沌系统自适应滑模控制[J].物理学报, 2014, 63(22): 113–120.CHEN Q, NAN Y R, XING K X. Adaptive sliding-mode control of chaotic permanentmagnet synchronous motor system based on extended state abserver[J].Acta Physica Sinica, 2014, 63(22): 113–120.(in Chinese) |
