磁轴承可分为永磁偏置和电磁控制的混合磁轴承,以及偏置、控制均由电磁控制的纯电磁式磁轴承[7]。混合磁轴承靠永磁体产生的磁力承担主要的偏置力,电磁场提供辅助的调节力,但只有电磁力是可控的,导致其控制精度较低。纯电磁式磁轴承的偏置力和控制力均靠电磁场产生,二者均为可控的,因此其控制精度较高。文献[8]提出了一种新型永磁偏置径向磁轴承,该磁轴承通过第二气隙来形成控制磁路,降低了X方向和Y方向磁路的耦合,但该结构磁路相对复杂,给磁轴承的控制带来一定难度。文献[9]提出一种新型的永磁偏置轴向磁轴承,该磁轴承通过偏置磁路与控制磁路共同作用来实现转子的稳定悬浮,但该结构相对复杂,给磁轴承的加工装配带来一定难度。文献[10]提出了一种新颖的主动磁轴承,该磁轴承定子采用爪结构,有效地减小了磁轴承的径向尺寸,但当转子发生偏转时,干扰力矩较大,影响磁轴承的控制精度。文献[11]中的磁悬浮飞轮采用1个轴向磁轴承和2个径向磁轴承实现磁悬浮转子的三自由度悬浮,但当转子偏转时,不能消除干扰力矩的影响。文献[12]中的磁悬浮控制力矩陀螺采用一种Halbach结构的轴向磁轴承,有效地降低了功率损耗,但当其转子发生偏转时,不能避免干扰力矩的出现。文献[13]提出一种径向磁轴承,该磁轴承的永磁磁场和电磁磁场在同一平面,定子由8个磁极构成,在提供相同承载力的前提下减小了轴向尺寸,但由于8个定子磁极的极性不同,增加了转子高速旋转时的涡流损耗,但当转子发生偏转时,会产生较大的干扰力矩,影响磁轴承的控制精度。文献[14]中提出了一种新型异极性永磁偏置径向磁轴承,通过应用于磁悬浮反作用飞轮的设计实例,与传统同级性永磁偏置径向磁轴承比较,验证了新型磁轴承轴向长度短、结构紧凑的特点,但当其转子发生偏移时,产生干扰力矩较大,影响磁轴承控制精度。文献[15]提到一种磁悬浮飞轮用嵌环式永磁偏置径向磁轴承,该磁轴承具有旋转损耗低,磁极轴向短,可灵活设计的优势,但当其转子发生偏转时,干扰力矩较大。文献[16]提到一种新型混合磁轴承,该磁轴承定子磁极采用一体化导磁极板,保证了气隙磁场的均匀、连续性,但当其转子发生偏转时,电磁力产生的干扰力矩较大。文献[17]提出一种新型混合型轴向磁悬浮轴承,该磁轴承具有结构简单紧凑、功耗低的特点,但当其转子发生偏转时,电磁力产生的干扰力矩较大。文献[18]提出一种五自由度锥形磁悬浮轴承,该磁悬浮轴承上电起浮的动态性能良好,能够实现系统的稳定悬浮,但当其转子发生偏转时,电磁力产生的干扰力矩较大。
针对已有磁轴承转子发生偏转时干扰力矩较大的不足,本文提出一种新型的磁悬浮径向球面纯电磁磁轴承设计方法,该磁轴承定、转子均采用球面结构,可有效减小磁轴承的轴向尺寸,当磁轴承产生偏转或偏移时,电磁力会指向转子球心,从而降低定子磁极对转子产生的干扰力矩,提高磁轴承的控制精度。
1 径向球面磁轴承结构及工作原理 径向球面磁轴承主要由定子齿、线圈和转子组成。如图 1所示(图中α为磁轴承相邻2个磁极之间夹角的一半),定子齿上绕制一定匝数的线圈作为定子磁极,共有8个定子磁极。8个定子磁极均为球面结构,且球心重合,共同构成一个球形包络面。球形转子位于定子磁极形成的球形包络面中,转子球心与定子磁极形成的球形包络面球心重合,二者形成的球面气隙为0.35 mm。由于磁轴承采用球形转子,无论球形转子偏转与否,作用在球形包络面上的电磁力始终指向转子球心,不会带来干扰力矩。
 |
| 图 1 径向球面磁轴承结构 Fig. 1 Structure of radial spherical magnetic bearing |
| 图选项 |
假设转子受到扰动沿+X方向产生偏移,高精度电涡流位移传感器[19]检测出转子偏移量,控制器将位移信号变换为控制信号,功率放大器将该控制信号变换为控制电流,通过±X方向的电磁线圈产生控制磁场,作用于转子上产生回复力,直到转子重新回到平衡位置。同理,如果转子受到沿-X、±Y方向的扰动产生偏移时,可以得出类似的结论。
2 径向球面磁轴承建模分析 2.1 等效磁路 根据图 1所示的磁轴承磁路图,运用等效磁路法对磁轴承的磁路进行分析,可以得到径向球场磁轴承的等效磁路图,如图 2所示。Fx11、Fx12、Fx21和Fx22分别为±X方向上、下层定子磁极产生的磁动势,Fy11、Fy12、Fy21和Fy22分别为±Y方向上、下层定子磁极产生的磁动势,单位为安匝数(At);Rx11、Rx12、Rx21和Rx22分别为±Y方向上、下层球壳气隙产生的气隙磁阻,Ry11、Ry12、Ry21和Ry22分别为±Y方向上、下层球壳气隙产生的气隙磁阻,单位为A/Wb。
 |
| 图 2 径向球面磁轴承的等效磁路 Fig. 2 Equivalent magnetic circuit of radial spherical magnetic bearing |
| 图选项 |
根据图 2所示径向磁轴承等效磁路,可以得到径向磁轴承各个气隙内的磁通,Φx1、Φx2分别为±Y方向支路产生的磁通,Φy1、Φy2分别为±Y方向支路产生的磁通,单位为Wb。
2.2 数学模型 根据图 2所示的等效磁路可以建立磁轴承的数学模型,已知径向磁轴承8个球面气隙均为δ;定子铁心极弧面积均为A;真空磁导率为μ0。由此可知球面气隙磁阻为
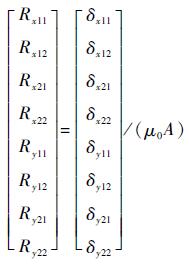 | (1) |
式中:δx11、δx12、δx21和δx22分别为±Y方向上、下层气隙;δy11、δy12、δy21和δy22分别为±Y方向上、下层气隙。
根据式(1)得到的气隙磁阻可得±Y方向支路和±Y方向支路产生的磁通为
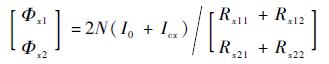 | (2) |
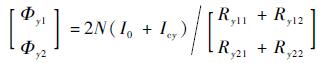 | (3) |
式中:N为单个定子铁心的线圈匝数;I0为径向磁轴承的偏置电流;Icx为磁轴承±Y方向的控制电流;Icy为磁轴承±Y方向的控制电流。
当磁轴承的转子沿±Y方向产生偏移x时,±Y方向的定子磁极均会通入控制电流Icx,-X方向偏置电流I0与控制电流Ic叠加,+X方向偏置电流I0与控制电流Icx相减,电流的改变会导致±Y方向的气隙磁通量发生变化,使-X方向定子磁极产生的电磁力大于+X方向定子产生的电磁力,从而产生回复力Fx,将转子拉回平衡位置。同理,如果转子受到沿-X、+Y或-Y方向的扰动产生偏移时,可以得出类似的结论。
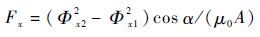 | (4) |
当转子沿+X方向产生x偏移时,将式(1)和式(2)代入到(4)中可得
 | (5) |
式中:Kr=μ0AN2cosα,当x远小于δ,Icx远小于I0时,对式(5)线性化处理可得
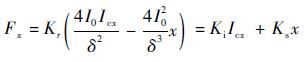 | (6) |
式中:Ki为电流刚度;Ks为位移刚度,如式(7)所示:
 | (7) |
3 结构参数设计 3.1 定子磁极面积和气隙长度的确定 定子磁极面积可由式(8)确定:
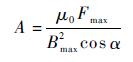 | (8) |
式中:Fmax为最大承载力,根据磁轴承定子转矩产生的陀螺力矩以及重力确定;Bmax为最大磁感应强度。一般软磁材料的饱和磁感应强度为1.5 T,因此设计时取Bmax=0.6~0.8 T。
考虑到磁轴承定子铁心线圈的槽满率以及磁轴承定子、转子铁心的加工精度,气隙δ=0.2~0.5 mm。
3.2 其他尺寸的确定 定子齿内径为
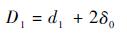 | (9) |
式中:d1为转子外径,根据定子磁极数和陀螺力矩确定;δ0为磁轴承的球壳气隙。
定子齿外径为
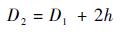 | (10) |
式中:h为定子齿径向长度。
定子磁极宽度为
 | (11) |
式中:lz为定子铁心的周向长度。
单个定子齿的宽度为
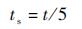 | (12) |
由于磁轴承的定子磁极采用上下2层定子铁心的原因,因此定子磁极宽度被均分为5段。
将最大磁感应强度Bmax、气隙δ和定子齿上的绕组匝数N确定之后,根据式(13),可以将Imax确定。
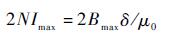 | (13) |
在线圈导线中可能通入最大电流Imax,所以线圈的线径dw要使最大电流不能超过导线的额定电流。已知dw与Imax的关系式为
 | (14) |
式中:ε0为导线截面积与额定电流系数。
根据偏置电流I0与最大电流Imax的如下关系,可以确定偏置电流I0的大小。
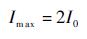 | (15) |
4 设计实例与仿真计算 针对本课题中角动量为15 N·m/s,额定转速为8 000 r/min,转子质量(M)为6 kg的磁悬浮陀螺设计了一种磁悬浮径向球面纯电磁磁轴承,主要参数如表 1所示。
表 1 设计参数表 Table 1 Design parameter table
| 参数 | 数值 |
| D1/mm | 158 |
| D2/mm | 190 |
| h/mm | 16 |
| ll/mm | 70 |
| t/mm | 50 |
| tt/mm | 10 |
| e/mm | 10 |
| d1/mm | 157.3 |
| d2/mm | 100 |
| δ0/mm | 0.35 |
| δ/mm | 0.2 |
| N | 200 |
| dd/mm | 0.25×2 |
| M/kg | 6 |
| Imax/A | 1 |
| I0/A | 0.5 |
| 注:e—定子齿轴向间距;d2—转子内径。 | |
表选项
利用等效磁路法计算磁轴承在起浮状态、偏置状态和悬浮状态下的各个状态量,如表 2所示。
表 2 计算结 Table 2 Calculation results
| 状态 | 起浮状态 | 偏置状态 | 悬浮状态 |
| 气隙磁感应强度/T | 0.4,0.05 | 0.3 | 0.41,0.19 |
| 定子背轭磁感应强度/T | 0.60 | 0.52 | 0.69 |
| 承载力/N | 88 | 201 | 72.6 |
| 控制电流/A | 0.45 | 0 | 0.18 |
| 电流密度/(A·mm-2) | 9.7 | 5.1 | 6.9 |
| 偏移/mm | 0.20 | 0 | 0.01 |
表选项
利用ANSYS商业软件对径向球面磁轴承的定子、转子有限元模型进行网格划分,如图 3所示。
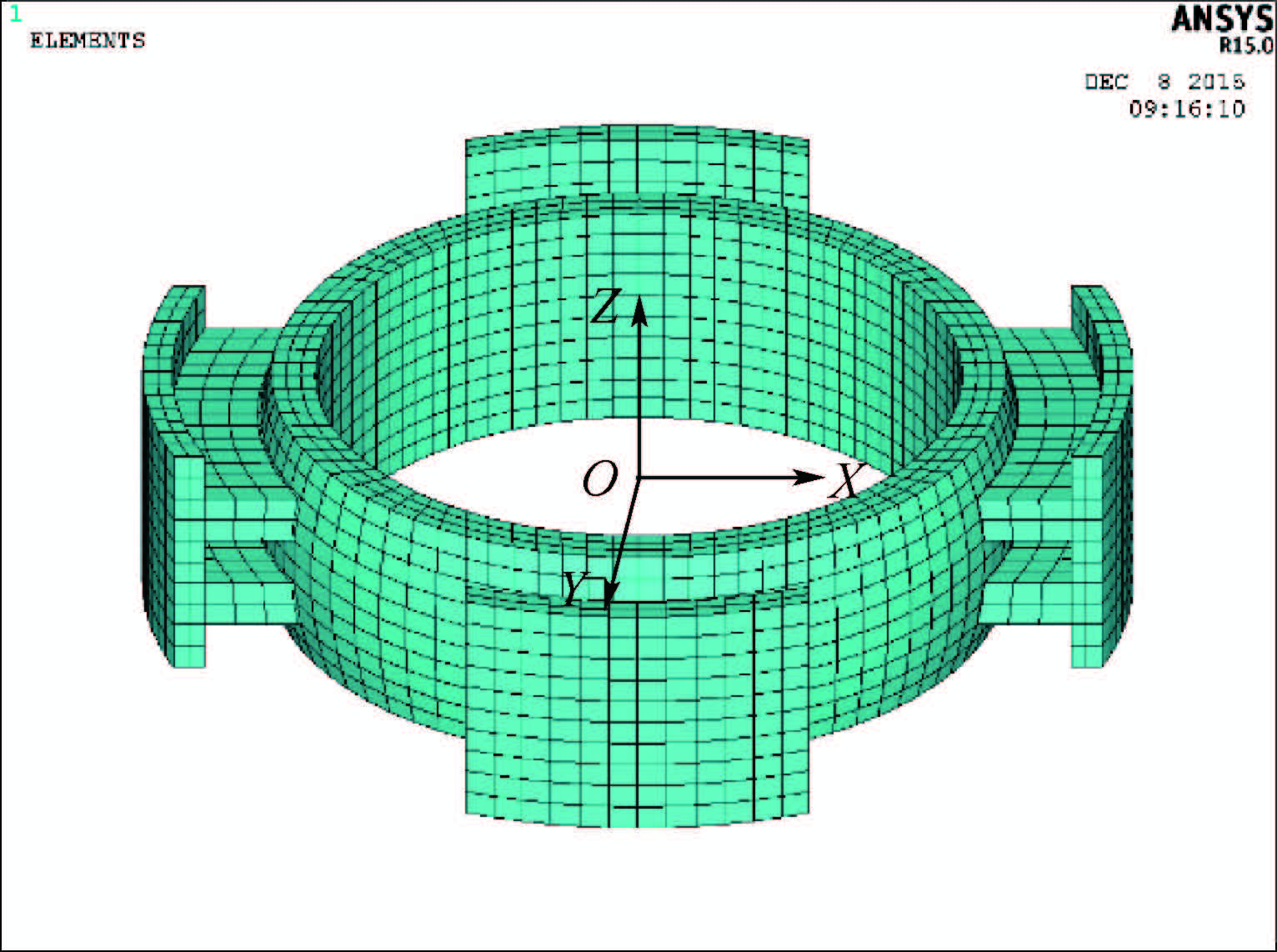 |
| 图 3 径向球面磁轴承定、转子有限元模型 Fig. 3 Finite element model of stator and rotor ofradial spherical magnetic bearing |
| 图选项 |
对图 3所示的径向球面磁轴承定、转子有限元模型进行分析,模拟得到了磁轴承在起浮、偏置和悬浮状态下的磁场强度分布,如图 4所示。
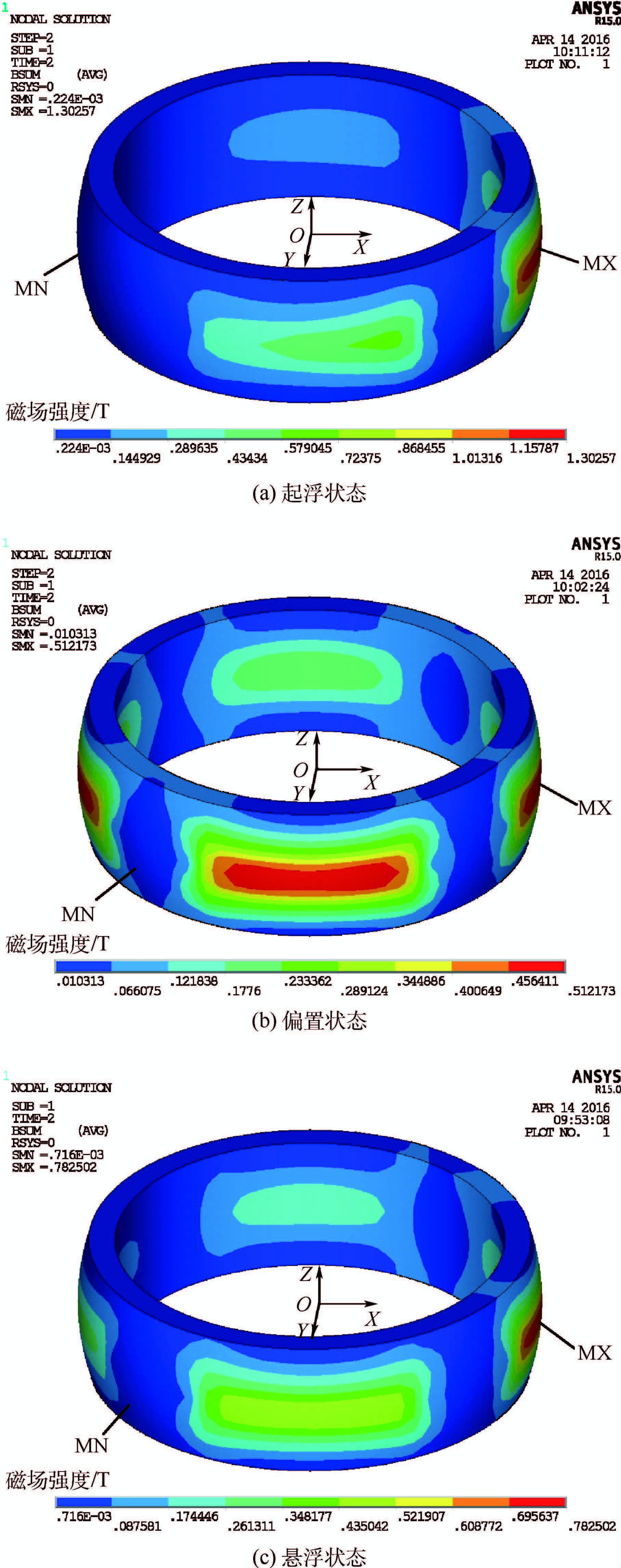 |
| 图 4 径向球面磁轴承3种状态下的磁场强度分布 Fig. 4 Radial spherical magnetic bearing magnetic field intensity distribution under three states |
| 图选项 |
利用等效磁路法和有限元法对磁轴承的位移刚度与电流刚度进行了研究,得到如图 5所示关系曲线。
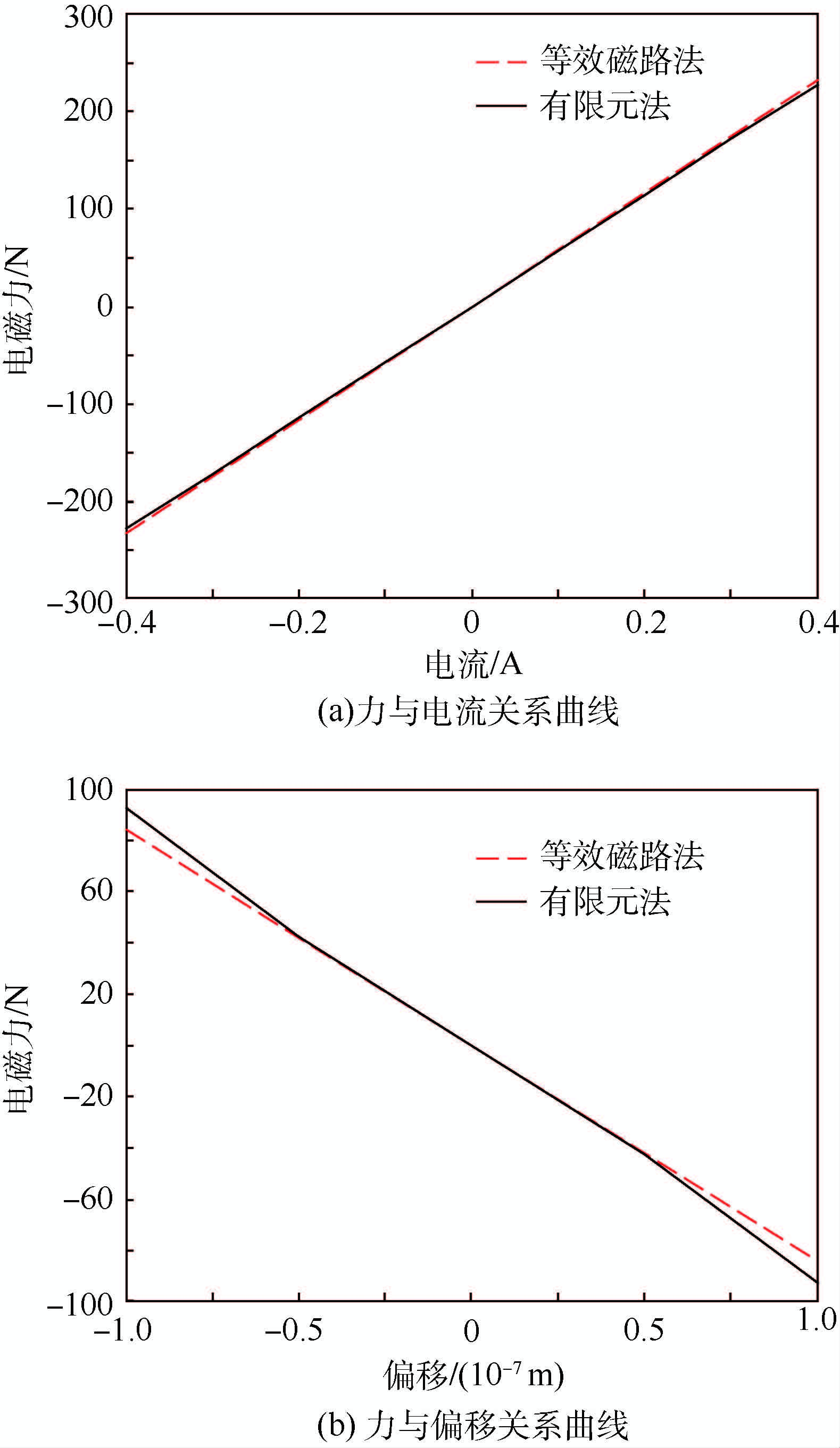 |
| 图 5 径向球面磁轴承设计结果 Fig. 5 Radial spherical magnetic bearing design results |
| 图选项 |
从图 5(a)中可以看出,当电流在-0.3~+0.3 A区间内取值时,等效磁路法和有限元法计算得到的曲线基本吻合,当电流在-0.4~-0.3 A和+0.3~+0.4 A区间内取值时,等效磁路法和有限元法计算得到的曲线有所偏差,当电流取值±0.4 A时,2种方法计算得到的电磁力偏差最大,等效磁路法计算得到的电磁力为232.4 N,有限元法计算得到的电磁力为227.7 N,二者计算结果偏差为2.1%,在误差允许范围内。图 5(b)中,当偏移在(-0.5~+0.5)×10-7 m区间内取值时,等效磁路法和有限元法计算得到的曲线基本吻合,当位移在(-1.0~-0.5)×10-7 m和(+0.5~+1.0)×10-7 m区间内取值时,等效磁路法和有限元法计算得到的曲线有所偏差,当位移取值±1.0×10-7 m时,2种方法计算得到的电磁力偏差最大,等效磁路法计算得到的电磁力为84 N,有限元法计算得到的电磁力为92.6 N,二者计算结果偏差为9.3%,在误差允许范围内。根据图 5可以看出等效磁路法与ANSYS有限元法对于磁轴承的电流刚度与位移刚度的分析结果基本吻合,表明球面磁轴承的有限元分析模型是合理的。
5 球面、柱面磁轴承偏转时力矩分析 球面磁轴承相比于柱面磁轴承的优点在于当转子产生偏转时,球面磁轴承的电磁力指向球心,不会对转子产生干扰力矩,而柱面磁轴承则会产生较大的干扰力矩,影响磁轴承的控制精度。运用有限元法对球面磁轴承和柱面磁轴承进行有限元建模,如图 6所示。
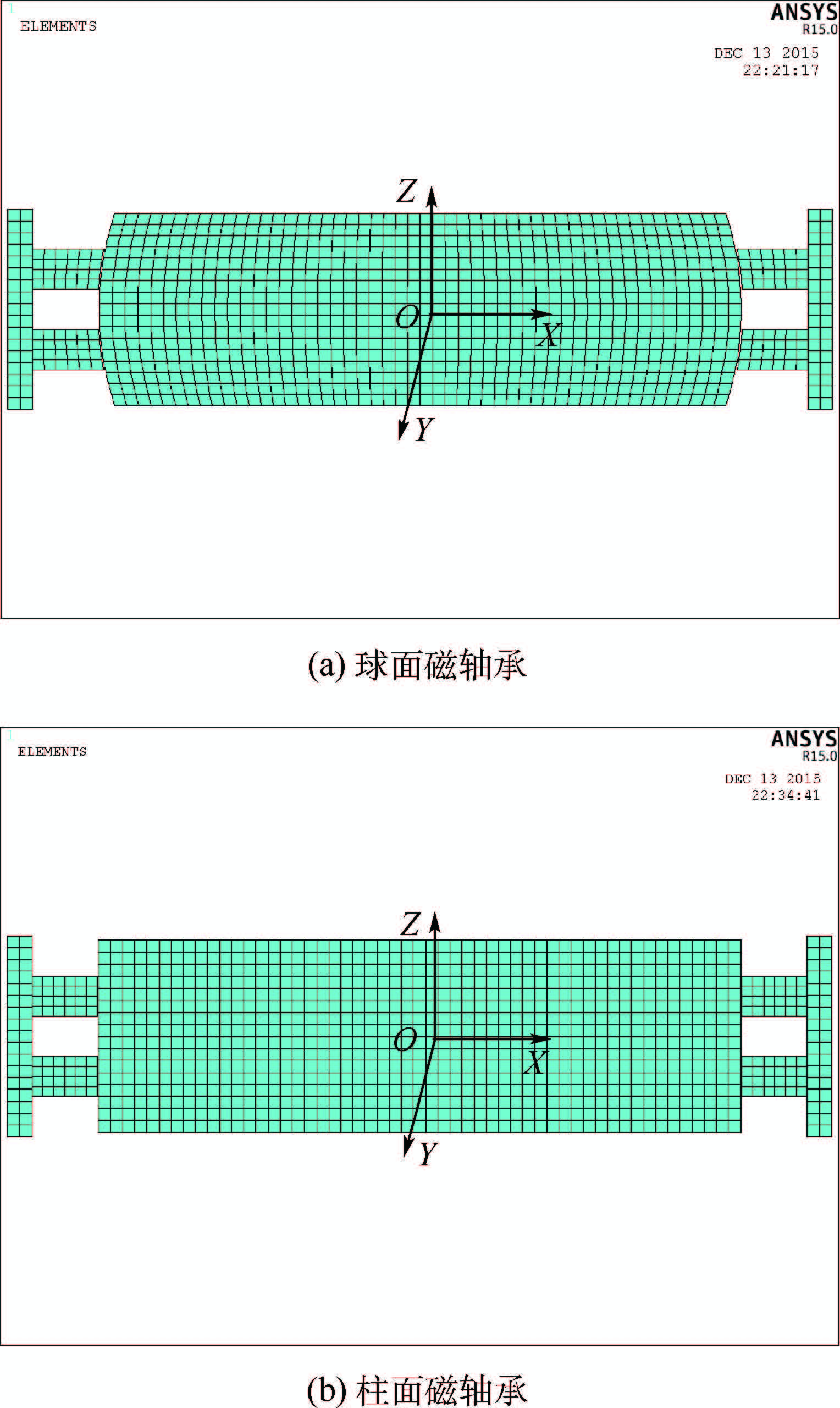 |
| 图 6 球面、柱面磁轴承有限元模型 Fig. 6 Finite element model of spherical and cylindricalmagnetic bearing |
| 图选项 |
基于图 6所示的球面磁轴承和柱面磁轴承的有限元模型,运用有限元法分析球面磁轴承与柱面磁轴承产生偏转时的干扰力矩,如图 7所示。
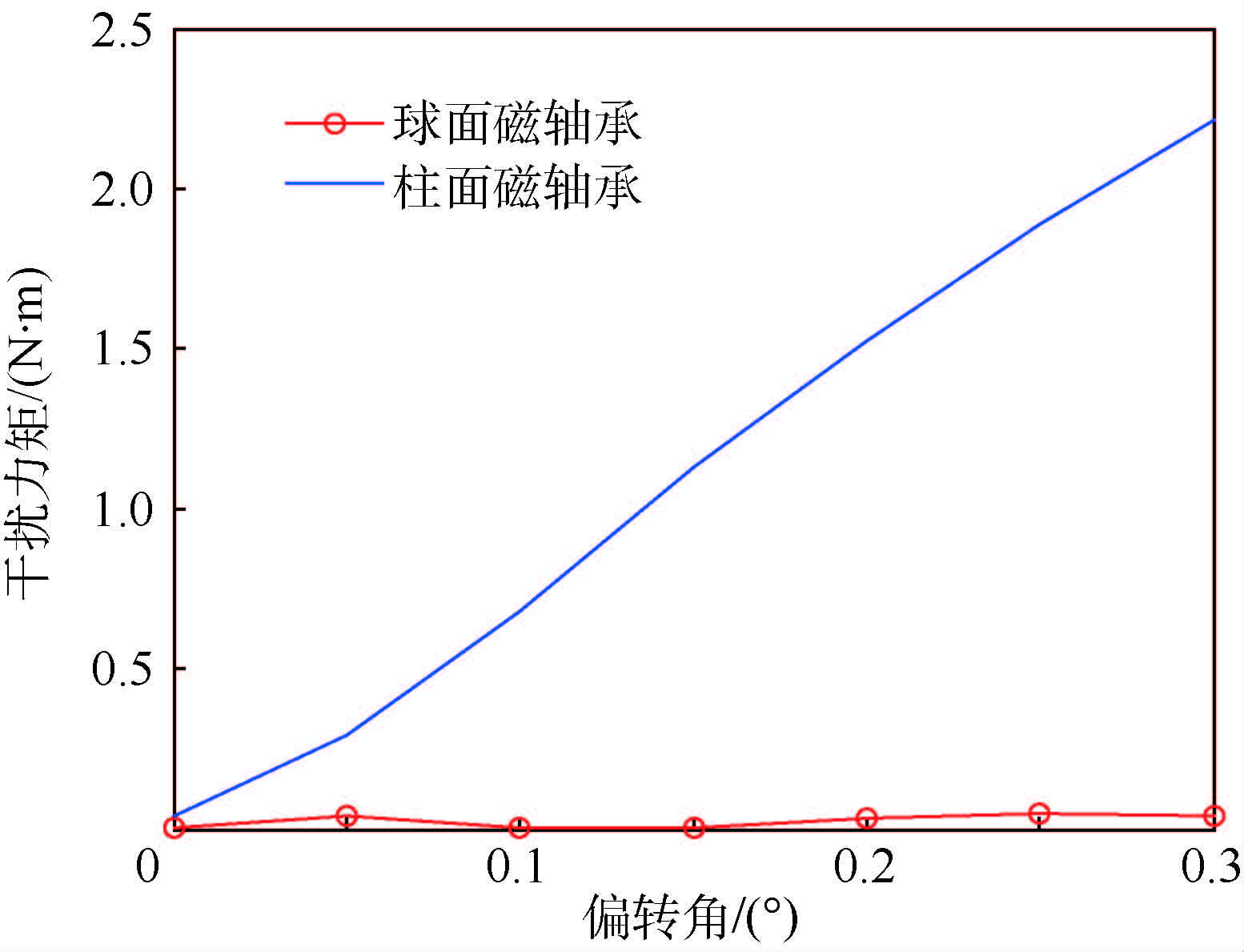 |
| 图 7 球面、柱面磁轴承偏转干扰力矩分析 Fig. 7 Analysis of interference torque of spherical andcylindrical magnetic bearing with deflection |
| 图选项 |
图 7结果表明,当磁轴承发生偏转时,球面磁轴承的干扰力矩要小于柱面磁轴承的干扰力矩,其中,当转子偏转达到最大偏转角0.3°时,柱面磁轴承的干扰力矩为2.2 N·m,球面磁轴承的干扰力矩为0.04 N·m,球面磁轴承的干扰力矩约为柱面磁轴承干扰力矩的1.8%,说明球面磁轴承相对于柱面磁轴承在抗干扰能力方面有很大的优越性,进一步分析球面磁轴承产生X方向和Z方向偏移时的干扰力矩,如图 8所示。
 |
| 图 8 球面磁轴承产生X方向和Z方向偏移时的干扰力矩 Fig. 8 Interference torque of spherical magnetic bearings with X and Z offset |
| 图选项 |
图 8(a)结果表明,当球面磁轴承产生X方向偏移时,电磁力产生的干扰力矩很小,当X方向的偏移为0.175 mm时,磁轴承的干扰力矩达到最大值0.16 N·m,从控制的角度看0.16 N·m仍然很小。图 8(b)中,当球面磁轴承产生Z方向偏移时,电磁力产生的干扰力矩很小,当Z方向的偏移为0.025 mm时,磁轴承的干扰力矩达到最大值0.078 N·m,从控制的角度看0.078 N·m仍然很小。上述有限元分析结果表明,当球面磁轴承产生X方向或者Z方向偏移时干扰力矩都很小,实现磁轴承的控制相对容易,提高了磁轴承的控制精度。
6 结 论 本文提出了一种磁悬浮径向球面纯电磁磁轴承设计方法,可得如下结论:
1) 运用有限元法对比计算球面磁轴承与柱面磁轴承在偏转时所产生的干扰力矩,当转子达到最大偏转角0.3°时,球面磁轴承的干扰力矩为0.04 N·m,柱面磁轴承的干扰力矩为2.2 N·m,球面磁轴承的干扰力矩约为柱面磁轴承干扰力矩的1.8%,表明球面磁轴承相对于柱面磁轴承在抗干扰能力方面有很大的提升。
2) 进一步分析球面磁轴承在X方向或Z方向发生偏移时所产生的电磁干扰力矩,其数值与偏转干扰力矩量级相当,同样表明球面磁轴承的抗干扰能力强于柱面磁轴承。
3) 本文提出的径向球面纯电磁磁轴承无论在偏转或偏移等情形下均具有极低的干扰力矩,可用于磁轴承高精度控制,并为磁悬浮陀螺角速率检测奠定基础。
参考文献
| [1] | ?BABUSKA V,BEATTY S M,BLONK B J,et al.A review of technology developments in flywheel attitude control and energy transmission systems[C]//IEEE Aerospace Conference Proceedings.Piscataway,NJ:IEEE Press,2004,4:2784-2800. |
| [2] | ALEXANDER L, PANAGIOTIS T. A combined application of loop shaping and hinf synthesis to control high-speed fly-wheels[J].IEEE Transactions on Control Systems Technology, 2005, 13(5): 766–777.DOI:10.1109/TCST.2005.847344 |
| [3] | 刘彬, 房建成, 刘刚. 一种磁悬浮陀螺飞轮方案设计与关键技术分析[J].航空学报, 2011, 32(8): 1478–1487.LIU B, FANG J C, LIU G. Design of a magnetically suspended gyrowheel and analysis of key technologies[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(8): 1478–1487.(in Chinese) |
| [4] | 刘迎澍, 黄田. 磁悬浮轴承研究概述[J].机械工程学报, 2000, 36(11): 5–9.LIU Y S, HUANG T. Survey of the research of magnetic bearings[J].Chinese Journal of Mechanical Engineering, 2000, 36(11): 5–9.DOI:10.3901/JME.2000.11.005(in Chinese) |
| [5] | 张鹏波, 张庆荣, 房建成. 高速磁悬浮转子稳定性研究及其在控制力矩陀螺中应用[J].中国惯性技术学报, 2006, 14(3): 47–53.ZHANG P B, ZHANG Q R, FANG J C. Stability of active magnetic bearing for control moment gyroscope[J].Journal of Chinese Inertial Technology, 2006, 14(3): 47–53.(in Chinese) |
| [6] | 王曦, 房建成, 樊亚洪, 等. 磁悬浮飞轮用轴向力偏转永磁偏置轴向磁轴承磁路耦合特性[J].航空学报, 2011, 32(4): 649–663.WANG X, FANG J C, FAN Y H, et al. Magnetic circuit coupling characteristics of axial gimballing magnetic bearing biased with permanent magnet for magnetically suspended flywheel[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(4): 649–663.(in Chinese) |
| [7] | 赵旭升, 邓智泉, 王晓琳, 等. 永磁偏置磁轴承的研究现状及其发展[J].电工技术学报, 2009, 24(9): 9–20.ZHAO X S, DENG Z Q, WANG X L, et al. Research status and development of permanent magnet biased magnetic bearings[J].Teansactions of China Electrotechnical Society, 2009, 24(9): 9–20.(in Chinese) |
| [8] | SUN J J, FANG J C. A novel structure of permanent-magnet-biased radial hybrid magnetic bearing[J].Journal of Magnetism and Magnetic Materials, 2011, 323(2): 202–208.DOI:10.1016/j.jmmm.2010.08.053 |
| [9] | FANG J C, SUN J J, XU Y L, et al. A new structure for permanent-magnet-biased axial hybrid magnetic bearings[J].IEEE Transactions on Magnetics, 2009, 45(12): 5319–5325.DOI:10.1109/TMAG.2009.2024687 |
| [10] | XU S L, FANG J C. A novel conical active magnetic bearing with claw structure[J].IEEE Transactions on Magnetics, 2014, 50(5): 1–8. |
| [11] | HAN B C, ZHENG S Q, WANG X, et al. Integral design and analysis of passive magnetic bearing and active radial magnetic bearing for agile satellite application[J].IEEE Transactions on Magnetics, 2012, 48(6): 1959–1966.DOI:10.1109/TMAG.2011.2180731 |
| [12] | SUN J J, REN Y, FANG J C. Passive axial magnetic bearing with Halbach magnetized array in magnetically suspended control moment gyro application[J].Journal of Magnetism and Magnetic Materials, 2011, 323(15): 2103–2107.DOI:10.1016/j.jmmm.2011.02.020 |
| [13] | 房建成, 孙津济. 一种磁悬浮飞轮用新型永磁偏置径向磁轴承[J].北京航空航天大学学报, 2006, 32(11): 1304–1307.FANG J C, SUN J J. New permanent magnet biased radial magnetic bearing in magnetic suspending flywheel application[J].Journal of Beijing University of Aeronautics and Astronautics, 2006, 32(11): 1304–1307.(in Chinese) |
| [14] | 王曦, 石泳, 樊亚洪, 等. 磁悬浮飞轮用新型异极性永磁偏置径向磁轴承[J].宇航学报, 2014, 35(12): 1457–1464.WANG X, SHI Y, FAN Y H, et al. A new type of heteropolar radial magnetic bearing biased with permanent magnet for magnetically suspended[J].Journal of Astronautics, 2014, 35(12): 1457–1464.(in Chinese) |
| [15] | 王曦, 房建成, 樊亚洪, 等. 磁悬浮飞轮用嵌环式永磁偏置径向磁轴承[J].机械工程学报, 2011, 47(14): 171–183.WANG X, FANG J C, FAN Y H, et al. Thimble permanent magnet biased radial magnetic bearing for magnetically suspended flywheel[J].Journal of Mechanical Engineering, 2011, 47(14): 171–183.DOI:10.3901/JME.2011.14.171(in Chinese) |
| [16] | 侯二永, 刘昆. 混合磁轴承磁场与磁力解析计算[J].机械工程学报, 2012, 48(6): 193–198.HOU E Y, LIU K. Analytical calculation of magnetic field and force for hybrid magnetic bearing[J].Journal of Mechanical Engineering, 2012, 48(6): 193–198.DOI:10.3901/JME.2012.06.193(in Chinese) |
| [17] | 刘程子, 邓智泉, 梅磊, 等. 永磁体位于转子上的混合型轴向磁轴承原理分析与参数设计[J].南京航空航天大学学报, 2012, 44(6): 847–854.LIU C Z, DENG Z Q, MEI L, et al. Principle analysis and parameter design of hybrid axial magnetic bearing with permanent magnet in rotor[J].Journal of Nanjing University of Aeronautics and Astronautics, 2012, 44(6): 847–854.(in Chinese) |
| [18] | 高琳, 徐宗海, 朱凯, 等. 锥形磁悬浮轴承的建模与解耦控制[J].中国电机工程学报, 2013, 33(6): 153–160.GAO L, XU Z H, ZHU K, et al. Modeling and decoupling control of conical magnetic bearings[J].Proceedings of the CSEE, 2013, 33(6): 153–160.(in Chinese) |
| [19] | 王志强, 刘刚, 李红. 磁轴承用电涡流位移传感器串扰产生及抑制方法研究[J].仪器仪表学报, 2010, 31(5): 1035–1040.WANG Z Q, LIU G, LI H. Research on crosstalk noise of eddy current displacement sensor for activemagnetic bearing[J].Chinese Journal of Scientific Instrument, 2010, 31(5): 1035–1040.(in Chinese) |
