目前,发动机常见建模方法有解析法和试验法。解析法(即理论模型法)是根据发动机运行过程中遵循的气动热力学规律建立其数学模型;试验法(即系统辨识法)是基于发动机试验数据进行分析处理从而获得数学模型[3]。试验法对数据采集有较高的要求,所建模型在适用范围上具有一定局限性;而解析法所建模型精度较高,可在全包线内模拟发动机动态与稳态特性,因此被国内外普遍采用[4]。
涡扇发动机因为经济性等优点被民用喷气飞机大量装备,并且在当前极为热门的无人机领域也有着广泛应用。DGEN380是由法国Price Induction公司为小型飞机所设计制造的大涵道比小型涡扇发动机,因体积小、污染少和油耗低等优势被欧美国家用于教学研究,建模并研究其燃油控制规律对于了解小型涡扇发动机性能和控制方案将会带来一定帮助。
本文结合DGEN380发动机特性采用解析法建立其部件级非线性数学模型,利用MATLAB平台对模型进行稳态、动态仿真验证,提出部件共同工作方程组求解过程中常见问题的解决方法,并研究发动机燃油控制规律。
1 发动机结构及建模假设 DGEN380发动机为双转子、分开排气涡扇发动机,核心机采用单级离心式压气机、环形回流式燃烧室和轴流式高压涡轮,低压转子则由高涵道比风扇、齿轮箱(低压转速/风扇转速=3.32)、轴流式低压涡轮组成。采用先进的集成式FADEC控制系统,燃油泵等附件系统均为电驱动且几何不可调。图 1为DGEN380发动机框图。图中:鹅颈为风扇出口至压气机入口的内涵气体通道。
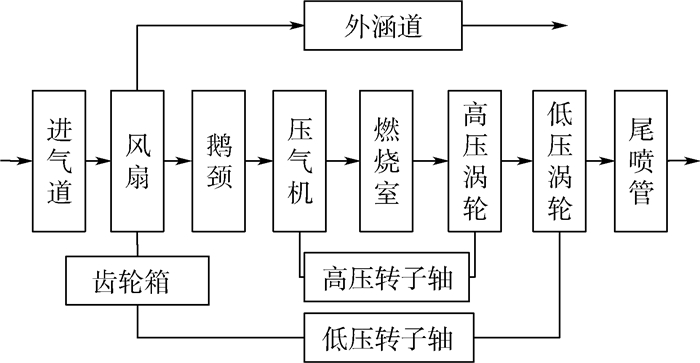 |
| 图 1 DGEN380发动机框图 Fig. 1 Block diagram of DGEN380 engine |
| 图选项 |
因为实体发动机极为复杂,建立与其完全符合的模型难度太高,为简化发动机数学模型推导,特作出如下假设[5]:①忽略燃烧延时及引气流量;②忽略部件热交换以及容积惯性;③气体在外涵道和尾喷管中完全膨胀;④气体绝热指数不随温度变化;⑤高、低压转子转动惯量为常数;⑥鹅颈、外涵道、尾喷管总压恢复系数为常数。
2 发动机气动热力学模型 本文按部件结构顺序,结合发动机本身设计参数以及特性数据,从进气道到尾喷管逐一建立气体流动过程与热力学过程的部件数学模型[6],最后在MATLAB平台上分别将各部件模型公式整合打包为M函数形式。
以压气机为例,按计算顺序排列打包各气动热力学公式后[7],其函数模型最终形式如下:
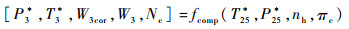 | (1) |
式中:模型输入量T25*和P25*分别为压气机进口总温和总压(即鹅颈出口处总温和总压);nh和πc分别为高压转子转速和压气机增压比;输出量P3*、T3*、W3cor、W3和Nc分别为压气机出口气体总压、总温、换算流量、实际流量和压气机功率。
旋转部件(风扇、压气机和涡轮)建模由于缺少特性数据来构建效率以及流量的插值函数[8],本文使用了读图软件“GetData”,从发动机技术参数文献上扫描特性图后利用该软件读取所需特性数据[9],并以此来绘制可以显示当前部件工作状态的特性图。以压气机为例,图 2为重绘的压气机特性图。图中:方形点为当前工作点。
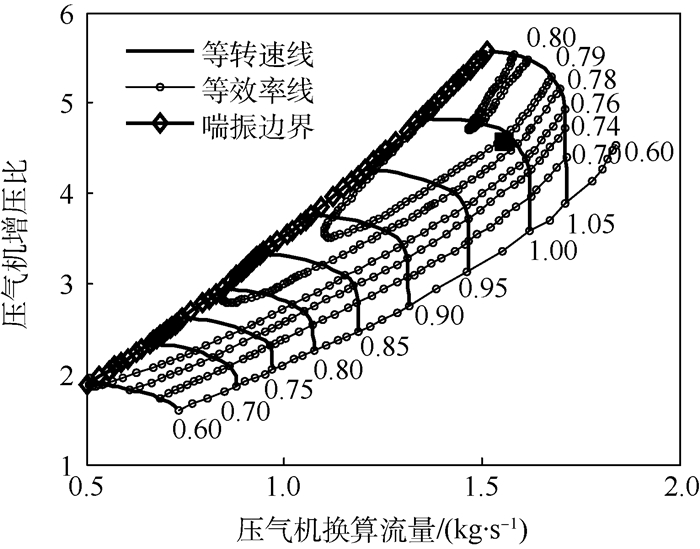 |
| 图 2 压气机特性图 Fig. 2 Figure of compressor characteristics |
| 图选项 |
将各部件模型按结构顺序组合,图 3为发动机气动热力学模型结构框架图。与压气机模型类似,进气道模型fin、风扇模型ffan、外涵道模型fbyp、鹅颈模型fgoo、燃烧室模型fcomb、高压涡轮模型fhpt、低压涡轮模型flpt和尾喷管模型fnoz的输出量分别为:各部件出口气体总温T*、总压P*,实际流量W、换算流量Wcor,排气速度大小V,内、外涵推力大小Fcold、Fhot,部件功率N,涵道比B,数字下标代表各部件出口处横截面编号。从图 3可以看出,按气体流动顺序,后者部件数学模型的输入量均含有前者的输出量。因此,按该顺序将各部件的M函数模型排列组合后,只需要3个自变量(飞行高度H、飞行马赫数Ma和供油量qmf),以及6个状态参数(低压转子转速nl、高压转子转速nh、风扇增压比πf、压气机增压比πc、高压涡轮落压比πhpt和低压涡轮落压比πlpt),即可实现各部件模型的联动运行。图 3中:Nf为风扇功率;Nhpt为高压涡轮功率;Nlpt为低压涡轮功率。
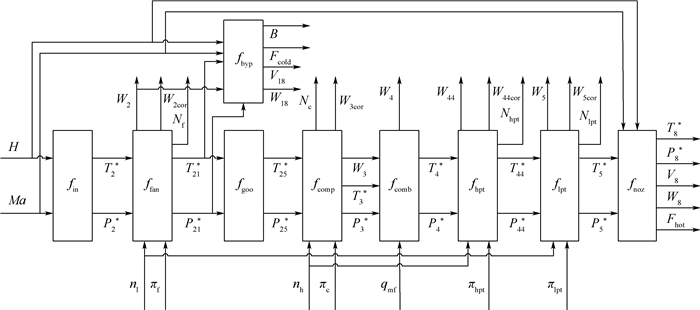 |
| 图 3 发动机气动热力学模型结构框图 Fig. 3 Structure block diagram of engine thermodynamics model |
| 图选项 |
以此打包各部件的M函数模型,获取可用以进行循环计算的发动机临时运行M函数模型:
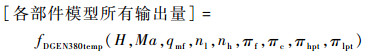 | (2) |
3 稳态仿真及验证 发动机工作状态分为稳态和过渡态2种,根据发动机各部件共同工作的原理,当其处于稳态运行时,各部件之间存在平衡关系,并由此可以列出稳态部件共同工作方程[10]。
1)风扇与内外涵流量平衡方程:
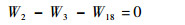 | (3) |
2)燃烧室出口与高压涡轮流量平衡方程:
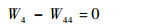 | (4) |
3)高、低压涡轮流量平衡方程:
 | (5) |
4)低压涡轮与尾喷管流量平衡方程:
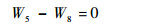 | (6) |
5)高压转子轴功率平衡方程:
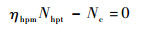 | (7) |
式中:ηhpm为高压转子轴机械效率,本文取常数。
6)低压转子轴功率平衡方程:
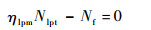 | (8) |
式中:ηlpm为低压转子轴机械效率,本文取常数。
已知H、Ma和qmf时,由建立的发动机临时运行模型将平衡方程式(3)~式(8)中各参量用参数nl、nh、πf、πc、πhpt和πlpt表示,由此可获得一个6维非线性平衡方程组[11]。求解该方程组即可获取发动机当前工作状态参数,并可通过临时运行模型运行获取其他性能参数,从而建立仅需3个输入量即能运行计算的发动机实际稳态工作模型:
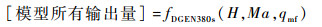 | (9) |
3.1 设计点计算 发动机非线性方程组常用的数值求解方法有Newton-Raphson法、遗传算法、N+1点残量法等。本文选用Newton-Raphson法和遗传算法对发动机设计点进行仿真计算,并对这2种方法进行评估对比,指出二者在计算过程中的常见问题及对应解决方法。
1) Newton-Raphson法在非线性方程组求解过程中因具有较快的收敛速度等优点被广泛采用[12]。将发动机在设计工作条件下(高度3 048 m,马赫数0.338,供油量0.027 6 kg/s)的稳态共同工作方程组去量纲化,使用Newton-Raphson法对其求解,并选取欧几里得范数作为解的误差检验函数。
计算过程为:输入初猜解向量,调用发动机临时运行模型计算当前误差,若满足精度要求则输出当前解,不满足则对解向量扰动后调用临时运行模型计算雅可比矩阵,并根据Newton-Raphson法迭代公式计算修正解向量,循环直至满足精度要求。图 4为Newton-Raphson法误差收敛图,迭代50次后收敛残差为1.4×10-15。
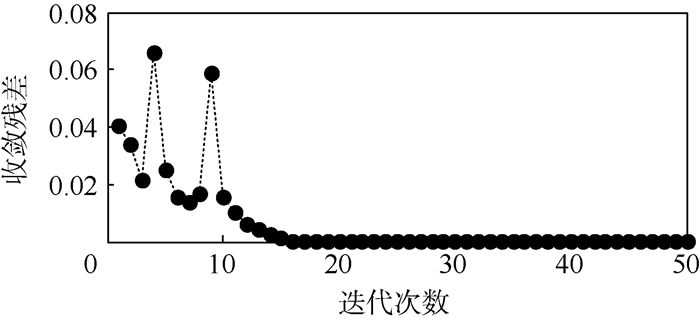 |
| 图 4 Newton-Raphson法误差收敛图 Fig. 4 Error convergence map of Newton-Raphson method |
| 图选项 |
2)遗传算法在理论上具有全局优化性能、适应性强、稳定性高,与Newton-Raphson法相比不需要求导也不具有初值敏感性。对强非线性问题,遗传算法有其独特优势[13]。将方程组去量纲化,选取其欧几里得范数作为目标函数和解的误差检验函数用以衡量种群个体适应度。将非线性方程组求解问题转化为求解目标函数最小值的最优化问题[14],并调用MATLAB遗传算法工具箱进行求解。
计算过程为:根据边界范围生成解向量的初始种群,调用发动机临时运行模型计算各个体目标函数值,若满足精度要求则输出最优解,没有则执行选择、交叉、变异运算生成下一代种群,循环直至满足要求。
针对遗传算法求解速度慢,以及在发动机模型求解时存在的局限性,即在自变量范围内随机生成的种群个体参数在模型计算时不匹配所引发的程序报错和终止问题(例如旋转部件模型的增压比或其他运行参数背离发动机工作点造成后续部件模型无法运行),本文对一般基础模型做出如下改进:当发动机临时运行模型对初始种群个体进行运行计算时,一旦超出部件模型或其他相关工作限制,则直接给出一组模型输出量使当前解的误差值极大,由于采用了比例(轮盘)选择运算,目标函数值大的个体会被更快淘汰,提高了搜索速度,算法则可以流畅地搜索最优解并不断排除无效解。图 5为模型计算流程改进示意图。图中:虚线部分为新增改进步骤。
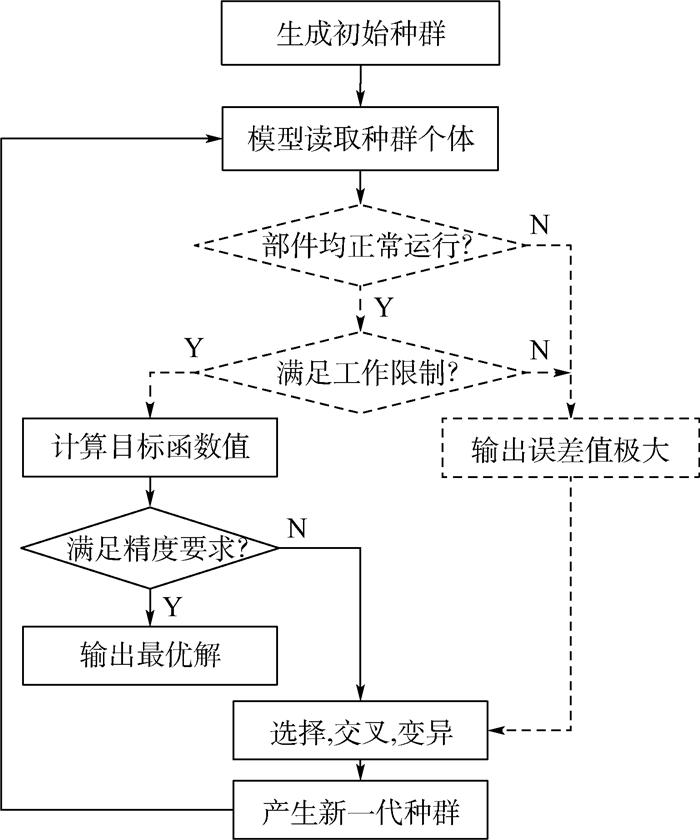 |
| 图 5 模型改进示意图 Fig. 5 Schematic of model improvement |
| 图选项 |
设置种群规模为1 000,单点交叉概率为0.8,变异方式为自适应变异。图 6为遗传算法计算过程误差收敛图。
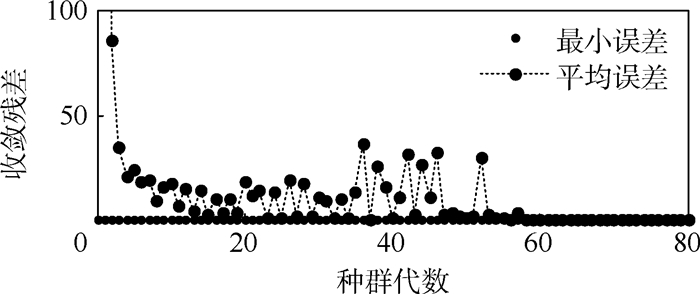 |
| 图 6 遗传算法误差收敛图 Fig. 6 Error convergence map of genetic algorithm |
| 图选项 |
Newton-Raphson法和遗传算法的求解结果见表 1。
表 1 Newton-Raphson法、遗传算法仿真结果 Table 1 Simulation results of Newton-Raphson method and genetic algorithm
| 方法 | nl/ (r·min-1) | nh/ (r·min-1) | πf | πc | πhpt | πlpt |
| Newton-Raphson法 | 42 798 | 50 653 | 1.16 | 4.56 | 2.28 | 1.93 |
| 遗传算法 | 42 919 | 50 712 | 1.17 | 4.56 | 2.30 | 1.92 |
| 实际值 | 42 830 | 50 687 | 1.16 | 4.57 | 2.27 | 1.93 |
表选项
从图 4、图 6和表 1对比可见,Newton-Raphson法具有高收敛速度及精度,但其在求解过程中亦有诸多问题,例如精度不足的初猜值以及不合适的扰动步长会造成迭代不收敛或雅可比矩阵不可逆,以及对靠近限制边界的工作点求解时易出现迭代超出限制造成模型程序报错,对此需要对上述相关参数进行反复调试,此方法对编程技术有一定要求;改进模型后遗传算法在求解最优解时更有针对性,从图 6中可见背离工作点的个体被迅速淘汰,其搜索速度虽不如Newton-Raphson法但也满足需求,此方法适应性强的优点也适合用来进行动态仿真。
3.2 多点仿真验证 采用第3.1节Newton-Raphson法的方式对固定飞行条件(高度3 048 m,马赫数0.338)、不同供油量时的发动机模型进行稳态仿真计算,并将仿真曲线与实际进行对比,图 7为推力和涵道比的变化对比图。
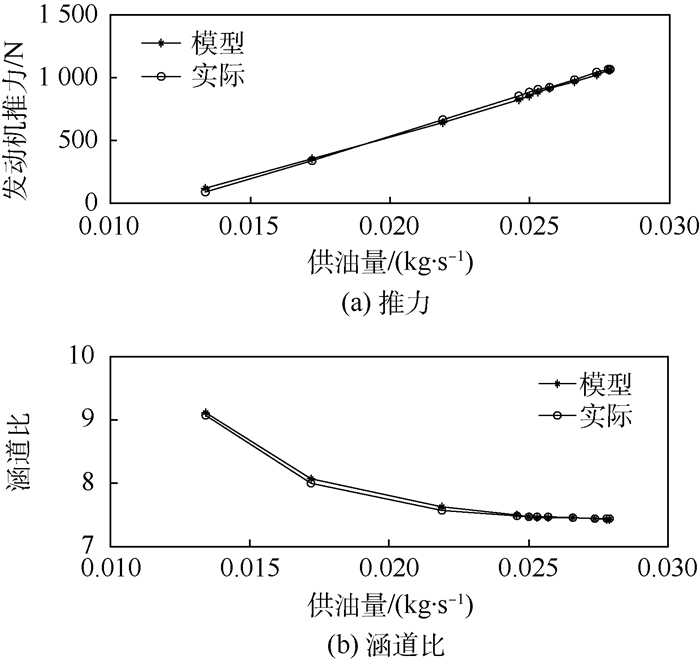 |
| 图 7 推力和涵道比变化对比 Fig. 7 Comparison of thrust and bypass ratio variation |
| 图选项 |
可见,简化模型的仿真结果与实际误差约小于3%,较好地反映了供油量变化时发动机推力及涵道比的变化趋势。
4 动态仿真及验证 将动态过程视为由准稳态平衡点构成的过渡态过程,过程中仍满足部件流量平衡关系,故发动机实际动态工作模型的建立与稳态相似,不同的是动态过程中高、低压转子轴能量不再保持平衡,产生剩余功率[15],其能量平衡方程变为
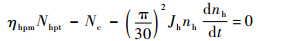 | (10) |
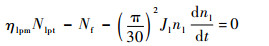 | (11) |
式中:Jh和Jl分别为高压转子和低压转子的转动惯量。本文采用欧拉法计算微分项[16],新方程组求解与稳态类似。
取仿真步长为20 ms,固定飞行条件(高度3 048 m,马赫数0.338)下按给定的加速供油规律进行动态仿真计算。图 8为该过程加速线在旋转部件特性图上的显示(圈内曲线),以风扇和低压涡轮为例,由此可以直观地显示工作点在发动机模型特性图上的变化趋势。
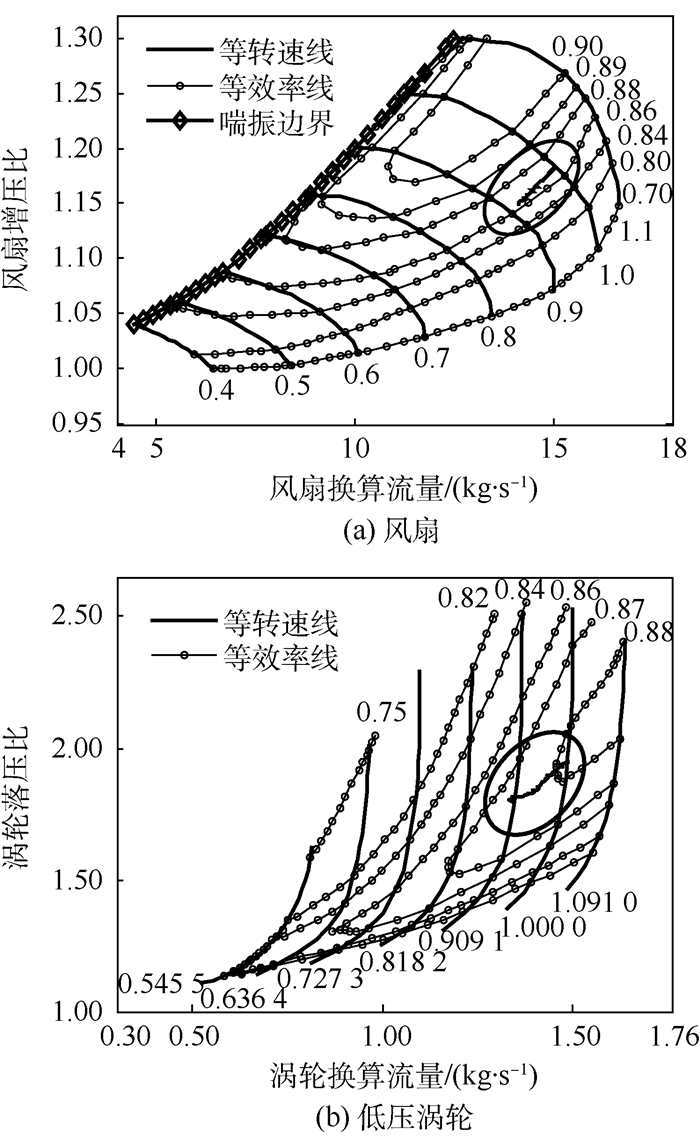 |
| 图 8 风扇和低压涡轮特性图上的加速线 Fig. 8 Acceleration lines on fan and low pressure turbine characteristic maps |
| 图选项 |
图 9为该加速过程给定的供油规律曲线,以及模型性能参数变化与实际的对比,以推力为例。可见, 动态模型仿真结果较好地反映了该加速过程推力变化趋势,对比误差小于3%。
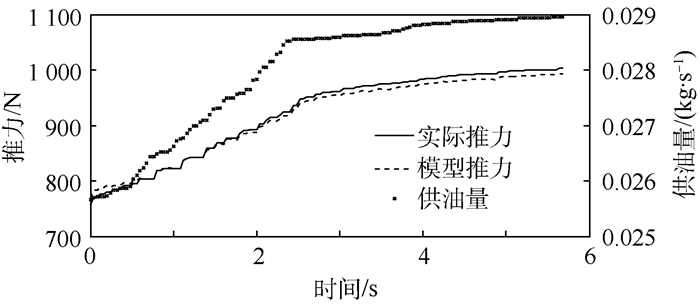 |
| 图 9 推力、供油量变化 Fig. 9 Changes of thrust and fuel supply |
| 图选项 |
5 燃油控制规律 因DGEN380发动机是典型的几何不可调发动机,故采用以供油量为控制量的单变量控制方案。当油门杆(PLA)位置一定而飞行条件发生变化时,发动机控制系统通过调节供油量qmf来保持被控参数不变,并且为了保证不同飞行阶段发动机的潜力能得到较大发挥,随着进口总温T2*变化所选择的被控参数也不同[17];当快速推动PLA加速时,FADEC系统给定加速控油规律使被控转子转速按期望变化。图 10为控制系统示意图。图中:EGT为排气温度。
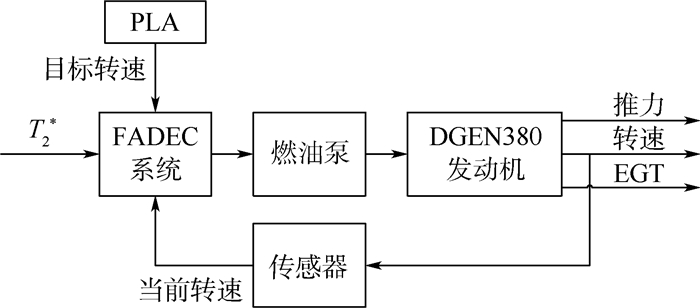 |
| 图 10 DGEN380发动机控制系统 Fig. 10 Control system of DGEN380 engine |
| 图选项 |
以发动机高度特性为例,当飞行高度增加时,发动机进口总温T2*降低,风扇负荷降低,所需低压涡轮功率也降低,若要保持低压转子转速nl不变,则需要减少供油量以降低涡轮进口燃气温度,而此时燃烧室出口的燃气温度也会因此降低,高压转子转速也随之下降,推力则因空气流量减小而持续下降。
基于建立的发动机模型,本文对变飞行高度时发动机燃油控制规律进行模拟计算,即在飞行高度增加过程中保持低压转子转速不变,计算供油量、高压转子转速和推力等参数并观察其变化趋势。计算方法为:将目标转子转速作为已知量,供油量作为未知量,利用发动机临时运行模型进行求解。已知H、Ma和nl 3个输入量时,利用发动机临时运行模型可将平衡方程组中的变量用参数qmf、nh、πf、πc、πhpt和πlpt表示,借此获取一个新的6维平衡方程组,求解方法与之前稳态仿真类似。图 11为飞行高度增加时保持PLA位置及马赫数0.34不变,选取低压转子转速为被控参数,基于发动机模型计算所得的供油量、推力以及高、低压转子转速的变化曲线。
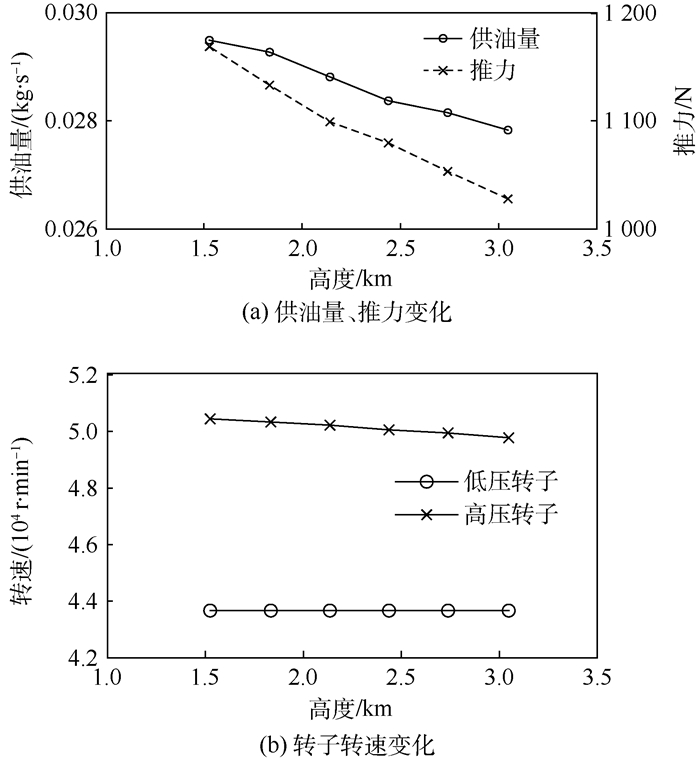 |
| 图 11 供油量、推力和转子转速变化 Fig. 11 Change of fuel supply, thrust and rotating speed |
| 图选项 |
从图 11中可见, 该过程中发动机供油量、高压转子转速和推力均随高度增加而降低,模型仿真结果与理论趋势相符合。
同理,可以通过制定过渡态过程目标转子加速/减速线来计算该过程中供油量变化规律[18],其数值计算方法与第4节的动态仿真类似,此处不再赘述。
6 结论 本文以DGEN380小型涡扇发动机为研究对象,建立其部件级非实时气动热力学模型并进行仿真计算,针对遗传算法在求解发动机模型时的局限性对基础运行模型加以优化改进,并基于模型分析DGEN380发动机的燃油控制规律,试验结果表明:
1) Newton-Raphson法在模型方程组求解时具有更好的精度和收敛速度,而改进模型后遗传算法在搜索最优解时打破了原有的局限性,背离工作点的解被迅速排除,表现出更好的适应性和流畅性。
2)稳态、动态模型仿真结果与实际试验数据十分接近,验证了建模方法的有效性,模型即时显示的部件特性图能够更加直观地展现工作点的变化趋势。
3)当发动机进口总温发生变化时,控制系统通过调节供油量使被控参数保持不变,以变飞行高度时发动机燃油控制规律为例进行仿真计算的结果与理论预期完全符合。
参考文献
| [1] | KONG X X, WANG X, TIAN D L, et al. An extrapolation approach for aeroengine's transient control law design[J].Chinese Journal of Aeronautics, 2013, 26(5): 1106–1113.DOI:10.1016/j.cja.2013.04.027 |
| [2] | 冯海峰.航空涡轴发动机数学建模方法与控制规律研究[D].西安:西北工业大学, 2007:1-3.FENG H F.Study of aero turbine engine mathematic model and control law[D].Xi'an:Northwestern Polytechnical University, 2007:1-3(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10699-2007057945.htm |
| [3] | DUYAR A, GU Z, LITT J. A simplified dynamic model of the T700 turboshaft engine[J].Journal of the American Helicopter Society, 1995, 40(4): 62–70.DOI:10.4050/JAHS.40.62 |
| [4] | JAW L C, MATTINGLY J D. Aircraft engine control design, system analysis, and health monitoring[M].Reston: AIAA, 2009: 187-201. |
| [5] | 钱得峰.大涵道比民用涡扇发动机部件级建模技术研究[D].南京:南京航空航天大学, 2010:17-18.QIAN D F.Research on component-level modeling technology for high bypass ratio civil turbofan engine[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:17-18(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1011291913.htm |
| [6] | 蔡开龙, 谢寿生, 胡金海, 等. 涡扇发动机燃油综合控制半实物仿真试验系统[J].推进技术, 2007, 28(4): 422–427.CAI K L, XIE S S, HU J H, et al. Semi-physical simulation experiment system of fuel integration control system for turbofan engine[J].Journal of Propulsion Technology, 2007, 28(4): 422–427.(in Chinese) |
| [7] | 夏飞.基于MATLAB/Simulink的航空发动机建模与仿真研究[D].南京:南京航空航天大学, 2010:19-31.XIA F.Modeling and simulation of aeroengines based on MATLAB/Simulink[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2010:19-31(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-2007194355.htm |
| [8] | GAUDET S R.Development of a dynamic modeling and control system design methodology for gas turbine[D].Ottawa:Carleton University, 2007:52-58. |
| [9] | 骆广琦. 航空燃气涡轮发动机数值仿真[M].北京: 国防工业出版社, 2007: 70-90.LUO G Q. Numerical simulation of aero gas turbine engine[M].Beijng: National Defence Industry Press, 2007: 70-90.(in Chinese) |
| [10] | 梁宁宁.航空涡轴发动机建模与控制规律研究[D].南京:南京航空航天大学, 2011:14-15.LIANG N N.Research on turboshaft engine modeling and control law[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2011:14-15(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1012041300.htm |
| [11] | 苟学中, 周文祥, 黄金泉. 变循环发动机部件级建模技术[J].航空动力学报, 2013, 28(1): 104–111.GOU X Z, ZHOU W X, HUANG J Q. Component-level modeling technology for variable cycle engine[J].Journal of Aerospace Power, 2013, 28(1): 104–111.(in Chinese) |
| [12] | 葛海.大涵道比涡轮风扇发动机建模技术研究[D].南京:南京航空航天大学, 2013:33-35.GE H.Research on modeling technology for high bypass ratio turbofan engine[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2013:33-35(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1014060689.htm |
| [13] | JOSHI G, KRISHNA M B.Solving system of nonlinear equations using genetic algorithm[C]//International Conference on Advances in Computing, Communications and Informatics.Piscataway, NJ:IEEE Press, 2014:1302-1308. |
| [14] | 陈磊, 霍永亮. 利用改进的遗传算法求解非线性方程组[J].西南师范大学学报(自然科学版), 2015, 40(1): 23–27.CHEN L, HUO Y L. On solution to nonlinear equation group by means of improved genetic algorithm[J].Journal of Southwest China Normal University (Natural Science Edition), 2015, 40(1): 23–27.(in Chinese) |
| [15] | ZHANG S Y, YU X, HU Y.Study of fuzzy control with Smith forecast and compensation for aeroengine[C]//International Conference on Information and Automation.Piscataway, NJ:IEEE Press, 2010:594-598. |
| [16] | 田金虎, 乔渭阳, 彭生红. 小涵道比涡扇发动机动态特性数值计算[J].航空动力学报, 2013, 28(9): 1988–1996.TIAN J H, QIAO W Y, PENG S H. Numerical calculation of dynamic performance of low-bypass ratio turbofan engine[J].Journal of Aerospace Power, 2013, 28(9): 1988–1996.(in Chinese) |
| [17] | 王鑫.航空发动机数学模型与控制规律研究[D].西安:西北工业大学, 2007:13-14.WANG X.Study of aeroengine mathematic model and control law[D].Xi'an:Northwestern Polytechnical University, 2007:13-14(in Chinese).http://www.cnki.com.cn/Article/CJFDTOTAL-DKDX200504030.htm |
| [18] | 樊思齐. 航空发动机控制(下册)[M].西安: 西北工业大学出版社, 2008: 50-61.FAN S Q. Aeroengine control (Ⅱ)[M].Xi'an: Northwestern Polytechnical University Press, 2008: 50-61.(in Chinese) |
