目前,常见的电流环控制策略主要以三角载波电压脉宽调制(PWM)为基础,配合PID或其他控制算法(如模糊控制算法、自适应控制算法、预估预测控制算法等)调整脉宽,共同实现电流闭环控制[2]。在这种控制策略下,通过提高电流采样频率和PWM载波频率可以有效提高电流控制的动态响应[3]。然而,EHA用无刷直流电机功率高(通常超过10 kW),绕组电感和电阻极小(分别在0.1 mH和10 mΩ数量级)[4],这些使得基于PWM的电流控制策略的使用受到限制。具体而言,电机驱动使用的功率器件受开关速度和散热能力限制导致开关频率很难超过20 kHz,PWM载波频率提升因此受到限制。与此同时,由于电机绕组电感和电阻极小,绕组电流最大上升速度超过2 000 A/ms,PWM控制策略中,相邻控制周期间的更新延迟加之控制周期限制(>50 μs)会导致绕组电流超过功率元件阈值电流,进而造成功率元件的损坏。这个问题极大地影响了基于PWM的电流控制策略的频率响应性能以及控制可靠性。为了解决PWM电流环控制策略存在的限制,文献[5]分析了PWM周期中不同电流采样和占空比更新时间造成的延时,并提出了单个载波周期2次电流采样更新占空比的策略,而文献[6]提出了一种即时更新PWM占空比的方式。这些方法将PWM的更新延时降低为原来的一半,电流环的动态响应性能和稳定性相应提高。但即便如此,基于PWM的电流控制策略存在的缺陷仍未得到解决。
滞环电流控制策略是实现高性能电流控制的另一种方法。滞环电流控制将直流母线的电压源变为响应快速的电流源,解决了PWM控制的固有缺点。其结构简单,易于通过模拟电路实现,响应速度快,具有天然的过流保护能力和稳定性,并且不依赖系统模型,对负载参数变化不敏感。当电流环使用滞环电流控制时,速度环取很大的增益也能保持系统稳定,适合对动态响应要求高的场合使用。然而,滞环电流控制中不确定的功率元件开关频率一方面使得功率元件面临过热风险,另一方面使得电流谐波频率分布广泛,难以通过滤波器滤除,这给系统的电磁兼容设计带来困难[7-8],这个主要缺点也使得滞环电流控制的应用局限于小功率和实验室研究领域,解决开关频率不确定的问题成为滞环电流控制研究的主要内容。
学界关于定频滞环电流控制做了大量研究。由于开关频率影响因素中的电流斜率在母线电压不变时无法改变,文献[9-16]等均通过变环宽的方式来实现开关频率的基本恒定。在这种方法中,通过微处理器定期采样电机电流、直流母线电压、转子位置,通过转子位置计算反电动势等参数,再根据不同算法计算环宽,通过DAC和运放输出电流值来调整电流控制的滞环环宽,需要的数据多,计算量大,结构复杂。滞环电流控制的一种数字定频实现是按照开关频率进行电流ADC采样,由微处理器对比期望电流值并直接给出开关信号[17-19]。若这种方式的滞环环宽取为零[20],形成一种类似bang-bang控制的电流控制模式,则实现简单,但是由于存在与PWM控制相同的采样间隔延时以及运算量大的问题,并不适合本文研究的EHA无刷直流电机控制。
针对基于PWM的电流控制策略以及滞环电流控制在对具有宽调速范围、大负载变化、高动态响应特点的EHA用无刷直流电机进行控制时存在的问题,本文开展定频数字滞环电流控制策略研究,以实现对EHA用无刷直流电机电流环的高效控制。首先以某EHA原理样机为基础,建立无刷直流电机绕组的电学数学模型;然后通过分析已有定频滞环电流控制方法的原理,设计一种低延时、定频、高响应的定频数字滞环电流控制策略;最后通过仿真和实验验证所提出控制策略的可行性。
1 无刷直流电机数学模型构建 本文针对的EHA用无刷直流电机为表贴式永磁无刷直流电机,Y形集中整距绕组,工作于120°两两导通状态,功率管开关信号采用PWM_ON调制模式。为便于分析,假设电机三相绕组完全对称,反电动势为120°理想梯形波,铁心不饱和,忽略非导通相电流,忽略电枢反应、涡流、磁滞损耗和齿槽效应。无刷直流电机系统(包括无刷直流电机及驱动控制器)等效电路如图 1所示。
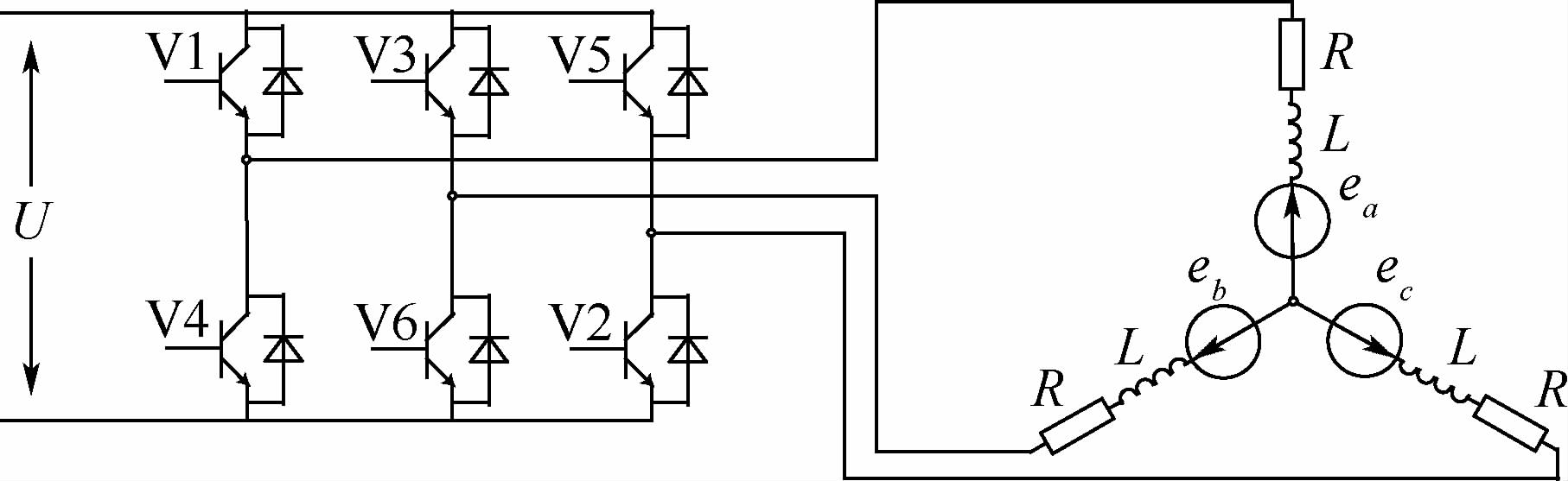 |
| 图 1 无刷直流电机系统等效电路 Fig. 1 Equivalent circuit of a brushless DC motor system |
| 图选项 |
a、b、c三相绕组的端电压方程可表述为
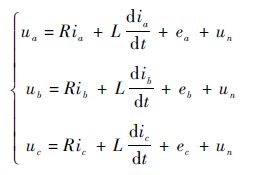 | (1) |
式中:ua、ub和uc为相绕组端电压;ia、ib和ic为相绕组电流;ea、eb和ec为相反电动势;R为相绕组等效电阻,包括绕组电阻和功率元件的等效电阻;L为相绕组等效电感,等于相绕组自感减相绕组互感,即相绕组漏电感,通常包括槽部漏感、齿顶漏感和端部漏感;un为绕组中心点电压。
不考虑换向过程,在所假设的理想状态,且电机处于两相导通状态时,等效电路可简化为图 2所示。
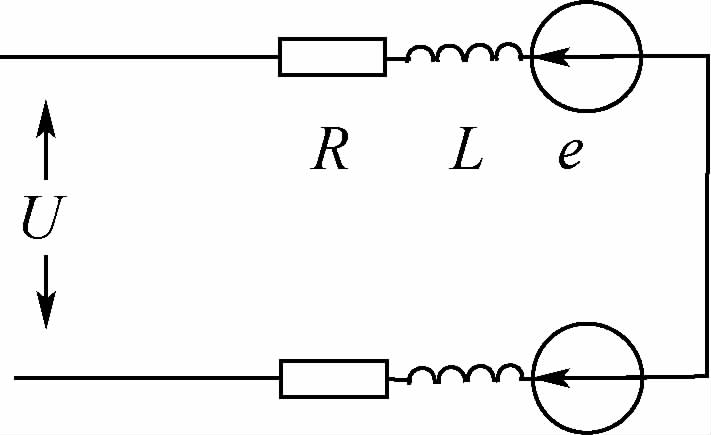 |
| 图 2 无刷直流电机系统在两相导通模式下的简化等效电路 Fig. 2 Simplified equivalent circuit of a brushless DC motorsystem in two-phase conduction mode |
| 图选项 |
进而,方程式(1)可简化为
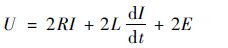 | (2) |
式中:E为120°理想梯形波反电动势e在当前转速的幅值。
解微分方程式(2),可得导通相电流为
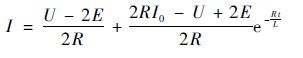 | (3) |
式中:I0为初始电流值。
同理,可以获得当电机处于PWM_ON调制模式,单斩输出关闭信号,即处于单相导通状态时的相电流表达式为
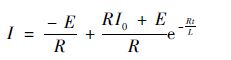 | (4) |
对式(3)和式(4)求导,可以获得电机相电流上升、下降速率分别为
 | (5) |
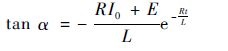 | (6) |
式中:θ为两相导通时相电流上升角;α为PWM_ON调制模式单相导通时相电流下降角。
由于EHA用无刷直流电机正常工作的电流远小于电流曲线最大值U/2R且连续导通时间短,因此I0R的值约等于0,e-Rt/L约等于1,在分析额定电流范围以内的电流上升、下降角时均可忽略。由此得到近似的上升、下降角表达式为
 | (7) |
2 改进的定频数字滞环电流控制策略设计 2.1 滞环电流控制策略 滞环电流控制的工作原理可以描述为:当电机电流大于正环宽时关断开关管,使电流下降;当电机电流小于负环宽时开通开关管,使电流上升,如图 3所示。
 |
| 图 3 滞环电流控制的工作原理示意图 Fig. 3 Schematic diagram of working principle ofhysteresis current control |
| 图选项 |
由滞环电流控制的工作原理分析可知,其功率管开关频率并非常数。当环宽ΔI较小或电流斜率tan θ、tan α较大时,开关频率较高;当环宽ΔI较大或电流斜率较小时,开关频率较低。过高的开关频率会增加开关损耗,甚至超过功率器件的上限。同时,不确定的开关频率也会产生大量的电流谐波,进而对控制性能产生不利影响。滞环电流控制策略的定频化显得尤为重要。
2.2 混合滞环电流控制策略 我们知道,PWM电流控制方式通过三角载波与给定阈值的比较来获得恒定的开关频率,那么将三角载波和滞环电流控制相结合,构造出一种基于三角载波比较的滞环电流控制策略,也能实现开关频率的基本固定,弥补滞环电流控制开关频率不固定的缺陷[21-22],如图 4所示。
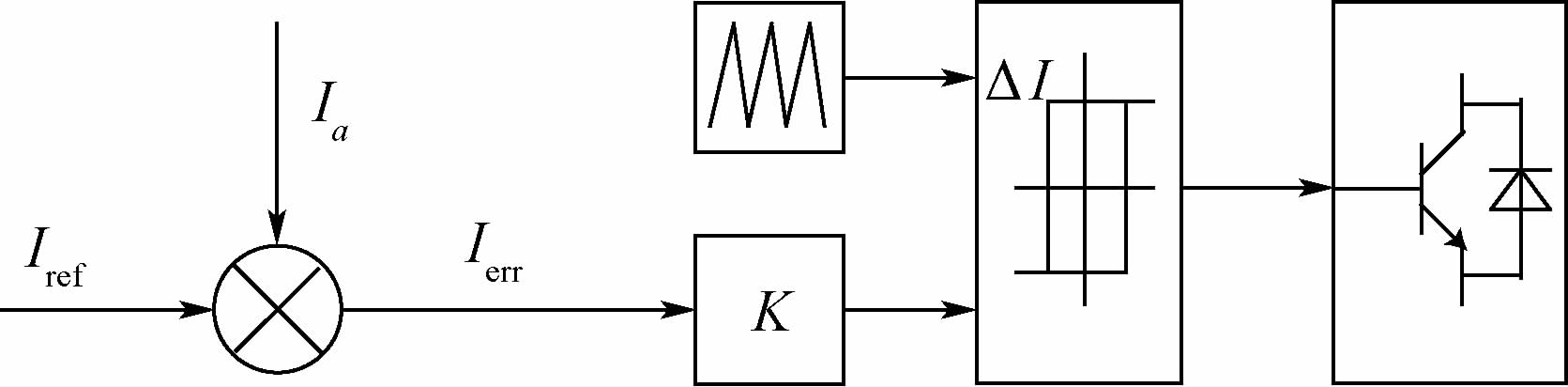 |
| 图 4 三角载波滞环电流控制的工作原理示意图 Fig. 4 Schematic diagram of working principle of triangularcarrier hysteresis current control |
| 图选项 |
为了工程实现简单,将图 4中的增益K取为1,并将三角载波位置前移,获得图 5所示的混合滞环电流控制原理图。
算法可描述为:在目标电流值上叠加一个定频三角波,此三角波的频率即为预设的功率元件开关频率,即
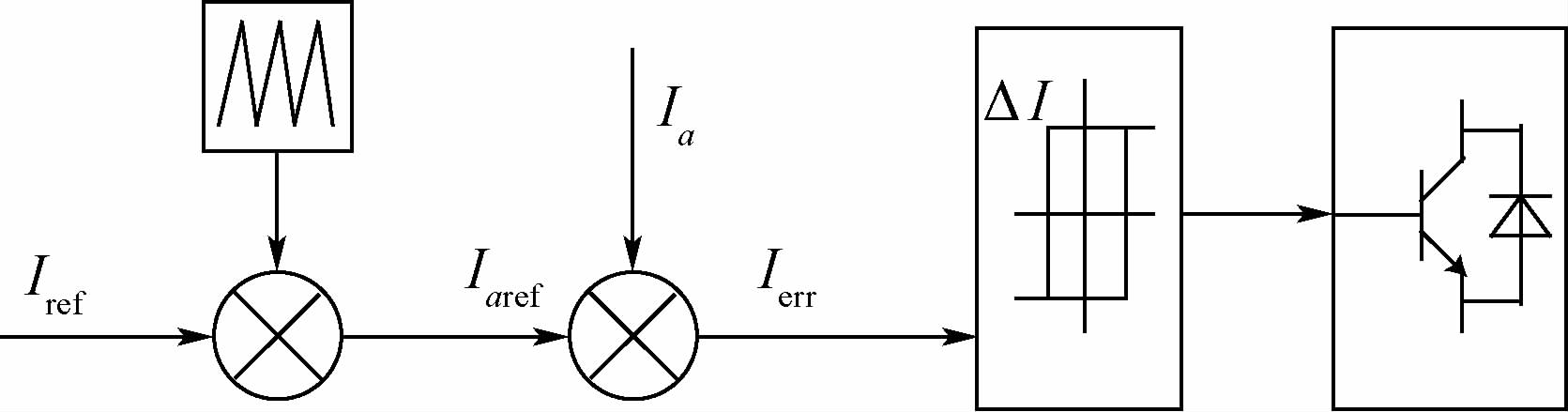 |
| 图 5 混合滞环电流控制的工作原理示意图 Fig. 5 Schematic diagram of working principle of hybrid hysteresis current control |
| 图选项 |
 | (8) |
式中:Iaref为叠加后的目标电流;Iref为参考电流;Itri为叠加的三角波电流。
叠加三角波后的目标电流值Iaref与电流反馈信号Ia相减获得电流误差值Ierr,即
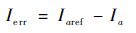 | (9) |
误差值经过以0为阈值的滞回比较器后获得功率管开关信号。
算法亦可表述为:由叠加三角波之后的电流目标值,加减环宽ΔI获得电流上下限,即
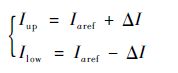 | (10) |
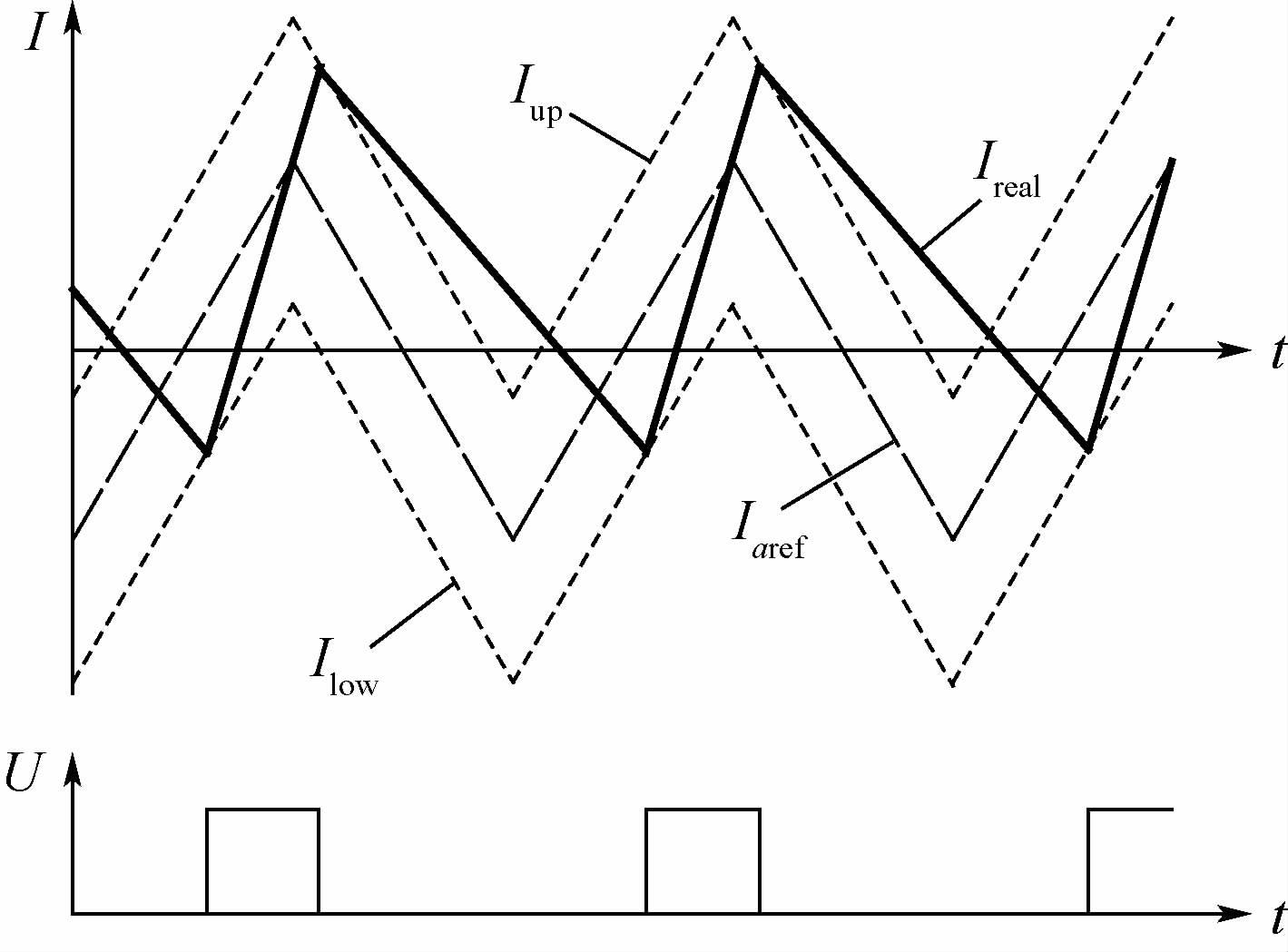
当实际电流Ireal大于电流上限Iup时,关断开关管,当实际电流Ireal小于电流下限Ilow时,开通开关管,如图 6所示。
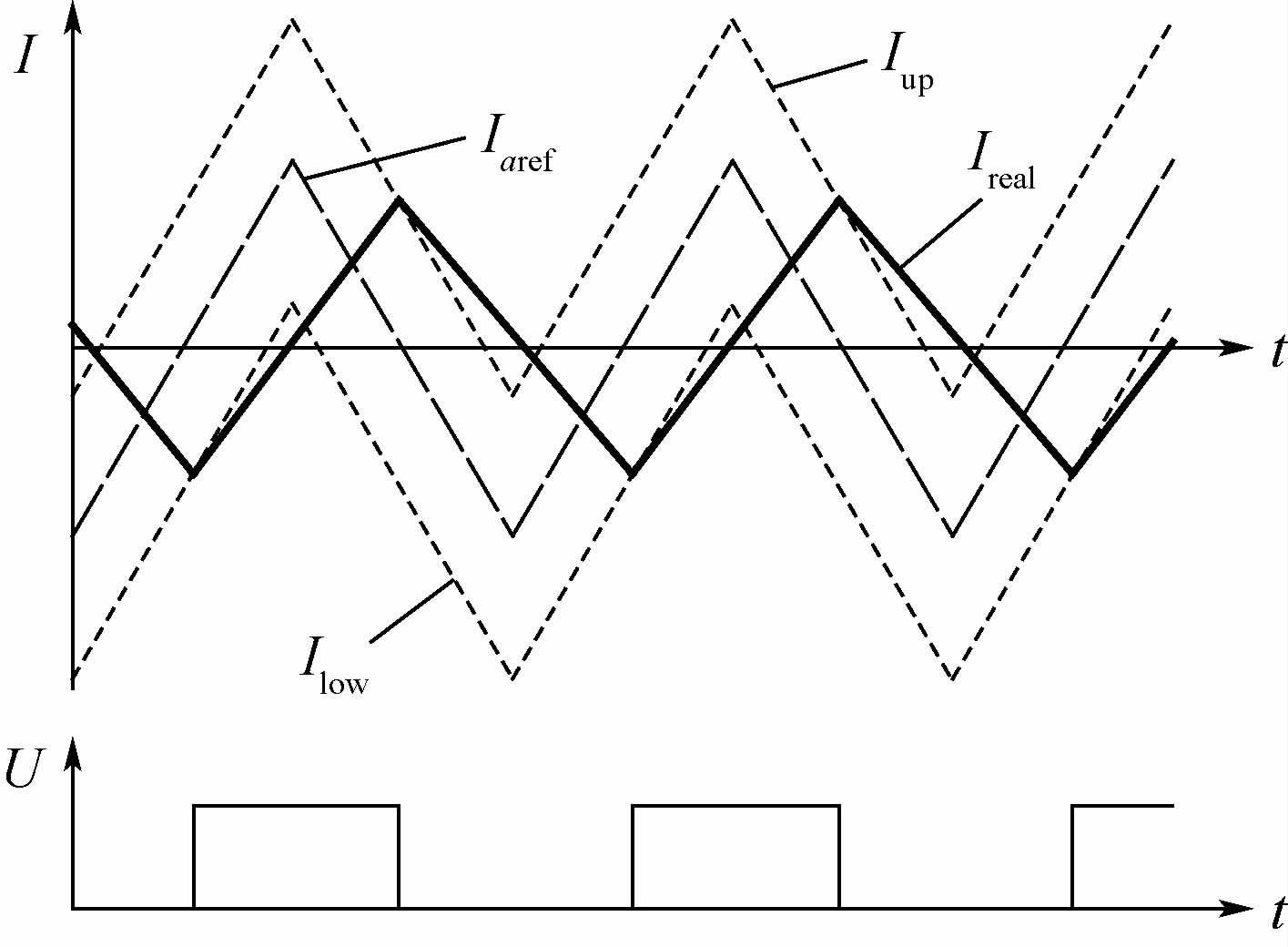 |
| 图 6 混合滞环电流控制电流轨迹及开关信号时序图 Fig. 6 Curves of current track and sequence chart ofswitch signal in hybrid hysteresis current control |
| 图选项 |
2.3 改进的准定频滞环电流控制策略 混合滞环电流控制实现定频控制存在约束条件,本节将通过分析混合滞环电流控制的定频约束条件,对混合滞环电流控制进行改进以扩展其定频实现范围,对于新的控制策略,本文称为改进的准定频滞环电流控制策略,并在以下章节中对此控制策略的数字化实现和器件延时影响进行探究。
如图 7所示,当电流上升速率大于tan θmax时,可能出现一个三角波周期内发生多次开关的情况,这会超出设定的开关频率。而当电流斜率小于tan θmin时,开关信号将跳过一个或多个三角波周期,导致实际开关频率低于给定的开关频率。同理,电流下降率也存在限制条件tan αmax和tan αmax。
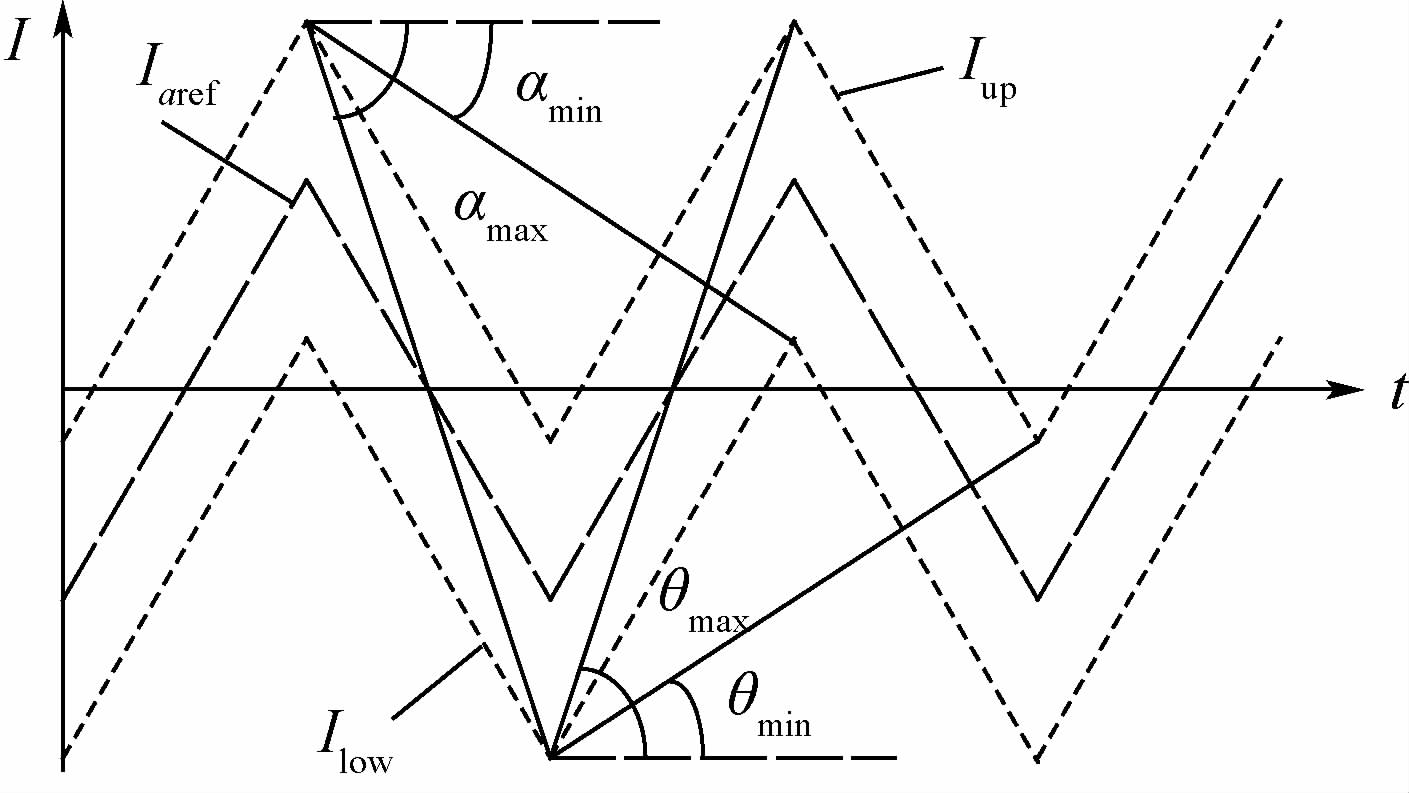 |
| 图 7 混合滞环电流控制实现定频的约束条件示意图 Fig. 7 Schematic diagram of constraint conditions for constant-frequency in hybrid hysteresis current control |
| 图选项 |
显然,这个范围与叠加的三角波幅值Atr、三角波周期Ttr、滞环环宽ΔI相关,可求得数值如下:
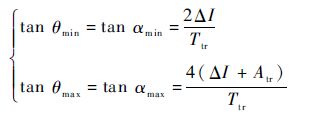 | (11) |
结合式(7),则对于运行于一、三象限的PWM_ON调制模式,实现定频控制需满足:
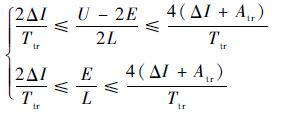 | (12) |
进一步分析,若仅要求稳态时实现定频,而不要求电流给定大幅变化过程中保持定频,超出式(11)限制的电流斜率数值组合也能符合要求,典型示例如图 8所示。稳态时实现定频同样需要约束条件。设此时电流上升速率为tan θ,由功率元件处于定频开关状态可知,稳定时实际电流曲线与Ilow曲线交点的电流值保持恒定,即如图 9中BC和EF均平行于t轴,且电流上升轨迹局限在AB和DE之间(即极限情况下,开关状态在A点或B点发生切换)。分析轨迹可得出如下定频条件:当电流上升速率大于tan θmax时,如果电流下降速率处于tan αmax2和tan αmin2之间,功率器件仍可工作在定频状态。
 |
| 图 8 仅要求稳态定频的滞环电流控制电流轨迹及开关信号时序图(仅为典型示例) Fig. 8 Curves of current track and sequence chart ofswitch signal in hysteresis current control when constant-frequency is only required in stable state (just a typical example presented) |
| 图选项 |
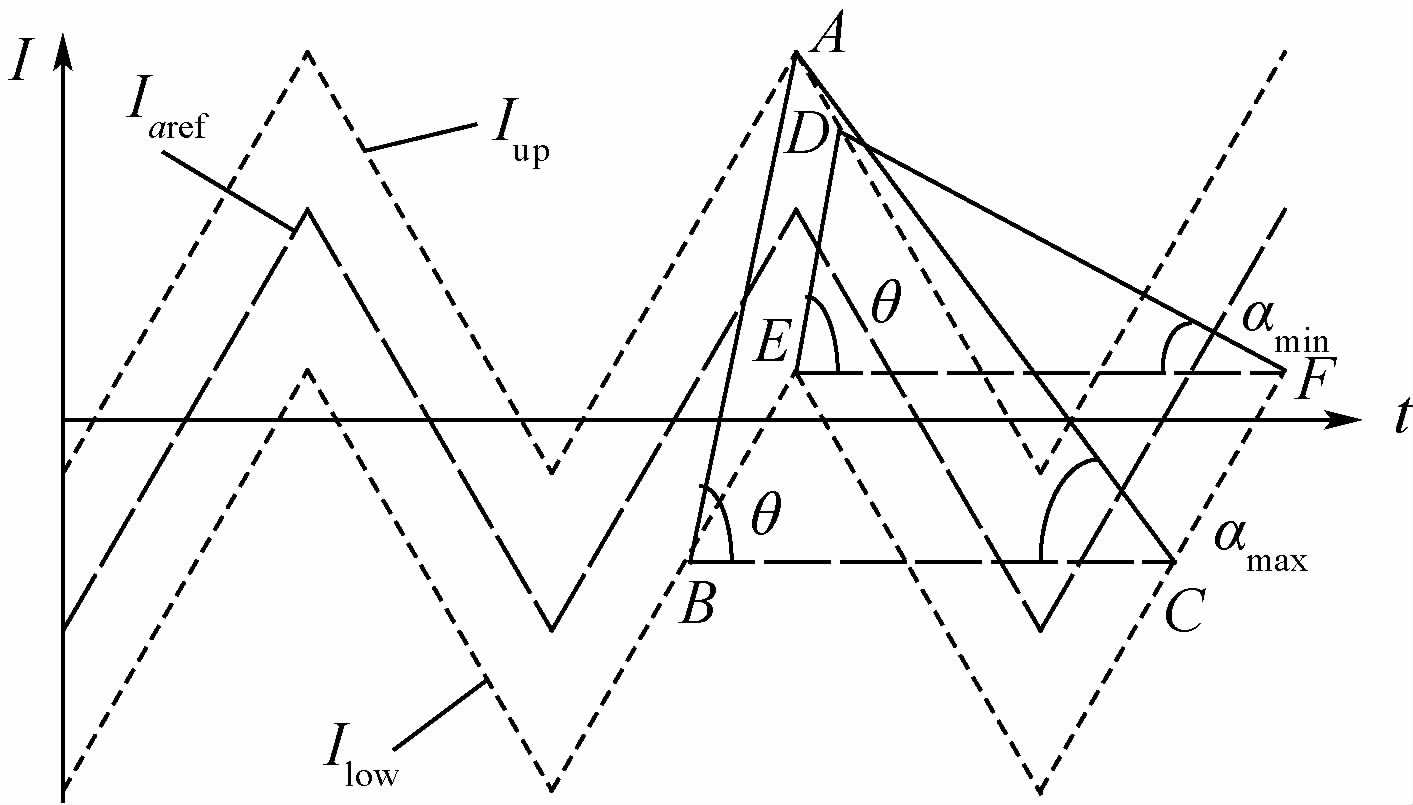 |
| 图 9 滞环电流控制中电流上升率过高时的定频约束条件示意图 Fig. 9 Schematic diagram of constraint conditions forconstant-frequency in hysteresis current control when current rising rate exceeds its upper limit |
| 图选项 |
分别解图 9中△ABC和△DEF可以获得tan αmax2和tan αmin2的表达式为
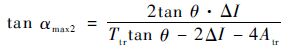 | (13) |
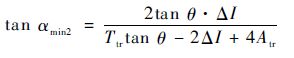 | (14) |
当电机运行于一、三象限,功率管开关信号为PWM_ON调制模式时,电机电流上升、下降速率满足式(5)和式(6),为便于几何分析,不考虑斜率正负号,有
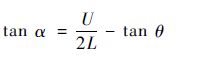 | (15) |
可推出当电流上升速率大于tan θmax时,实现定频的条件为
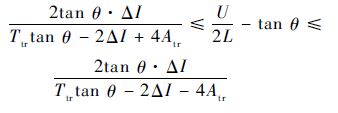 | (16) |
进而实现稳态定频需取合适的三角波幅值Atr、三角波周期Ttr、滞环环宽ΔI使其满足式(16)。由于过大的三角波幅值和滞环环宽会使电流控制静差变大,因此尽量取符合要求且较小的数值。
电流上升速率超过tan θmax时,通过一定的约束条件仍能实现稳态定频控制,但电流上升速率也需要限制在一定的范围内。图 10为当母线电压为270 V,自感为0.2 mH,互感为0.1 mH,三角波频率为20 kHz,幅值为6 A,滞环环宽为±4 A时,以tanθ为横坐标,tan θ>tan θmax时的tan α、tan αmax2、tan αmin2与tanθ的关系曲线。可见,当电流上升速率tan θ≤1.22时,均能实现定频控制。当tan θ>1.22时,反电动势数值较小,电机处于低转速段,电流上升速率大而下降速率小,一次开通并关断之后会跳过一个或多个三角波周期,造成开关频率变化,此时的电流轨迹如图 11所示。
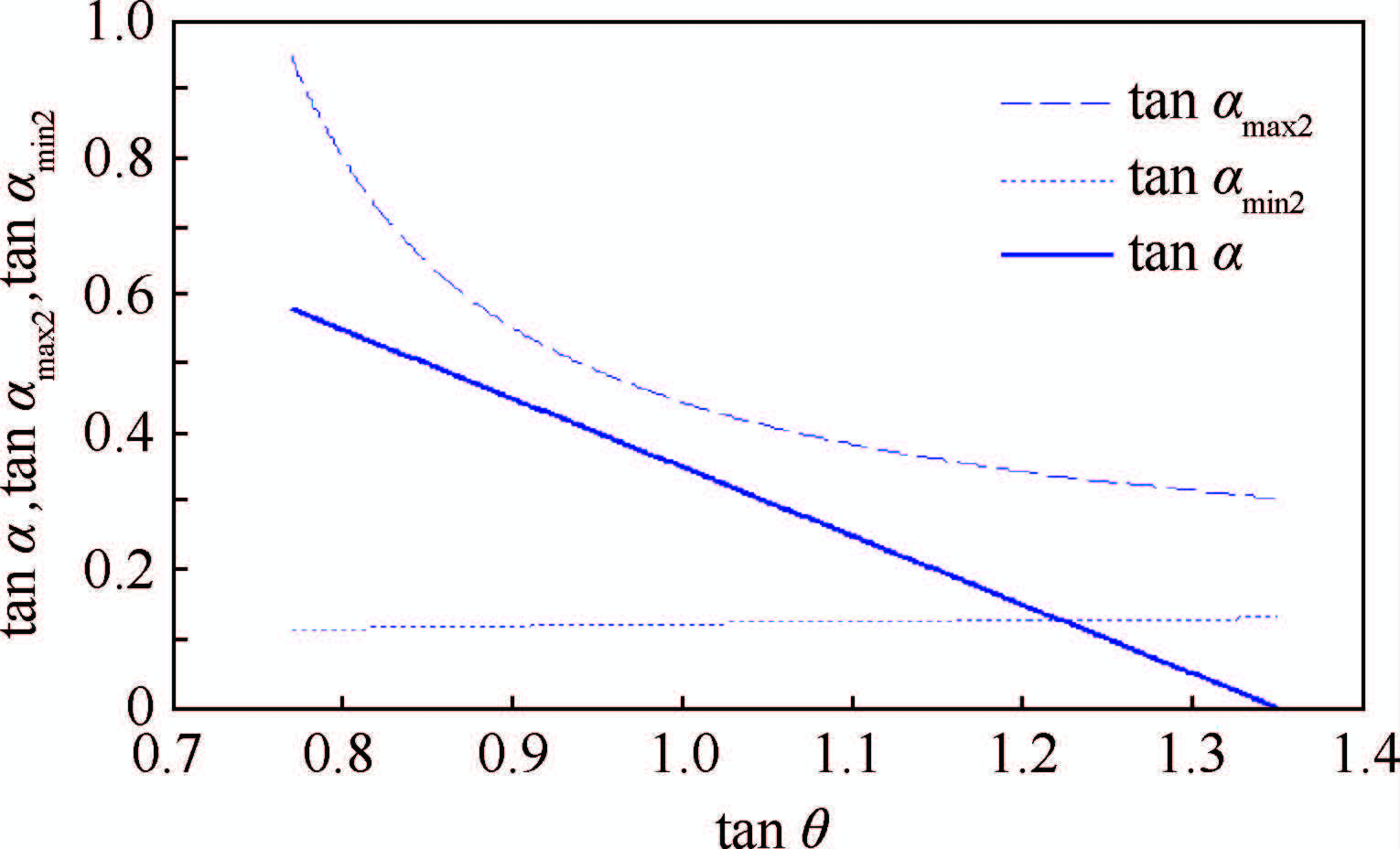 |
| 图 10 给定参数下稳态时定频约束关系曲线 Fig. 10 Constraint relation curves for constant-frequency only required in stable state with given parameters |
| 图选项 |
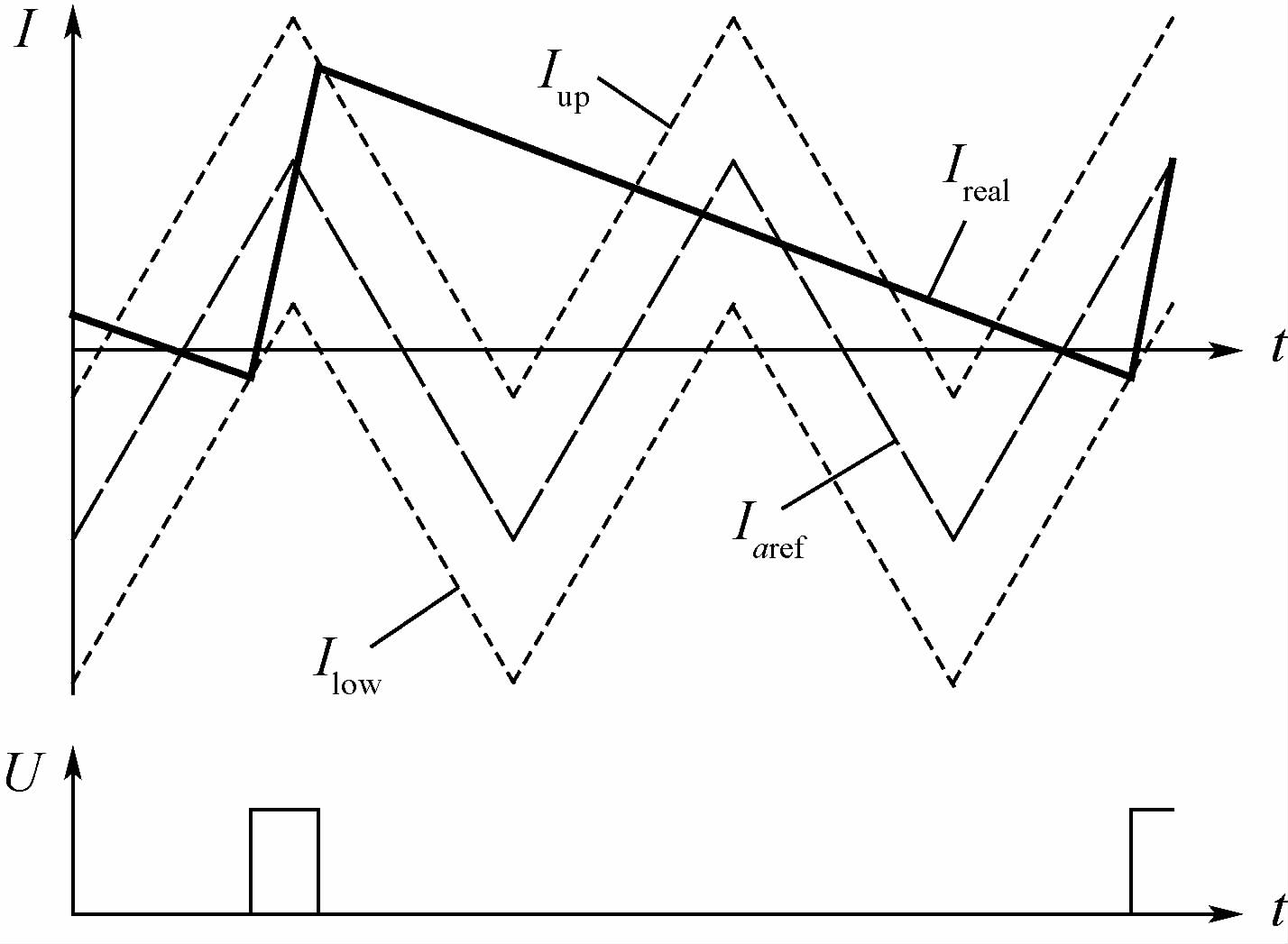 |
| 图 11 滞环电流控制中因反电动势过小导致开关频率变化时的电流轨迹及开关信号时序图 Fig. 11 Curves of current track and sequence chart ofswitch signal in hysteresis current control whenswitch frequency varies due to over-low back EMF |
| 图选项 |
同样地,当电机转速较高,反电动势数值较大,上升速率极低时,也会出现类似的现象。
以上分析基于PWM_ON调制模式,若采用双斩调制模式,20 kHz的开关频率下定频条件将难以满足,需要使用开关频率更高的功率器件,如新型的SiC基大功率功率元件,其开关频率可达到100 kHz或更高。可见,PWM_ON调制模式的应用不仅降低了功率元件的开关损耗,还使得在混合滞环电流控制方法下的定频范围得到扩展。
2.4 改进的定频数字滞环电流控制策略 根据第2.3节分析,虽然通过参数取值使得控制器在稳态时可以实现开关频率基本恒定,但在动态过程中仍可能发生单周期内多次开通关断的现象,以致超出功率器件的频率范围;另外,反电动势较低或较高时,也会出现开关频率变化的现象。当滞环电流控制策略数字化之后,在时序上对这些问题进行处理变得非常容易。为了解决这些问题,在改进的准定频滞环电流控制策略中增加数字化规则以实现完全的定频控制,进而形成改进的定频数字滞环电流控制策略。在改进的定频数字滞环电流控制策略中设计如下数字化规则:
1) 规则1:在一个三角波周期内,只允许开关信号开通一次。
2) 规则2:在三角载波处于最大值时,如果电流值小于滞环上限,转为开关信号开通状态。
3) 规则3:在三角载波处于最小值时,如果电流值大于滞环下限,转为开关信号关断状态。
4) 规则4:当一个周期内开关信号均为关闭状态且电流值始终大于滞环上限或电机处于二、四象限运行时,转为HPWM_LPWM双斩调制的功率管同时关断状态。
如图 12所示,前3个规则可举例为:在t0~t2时刻之间,只允许开关信号开通一次;在t1时刻,如果电流值小于滞环上限,转为开关信号开通状态;在t0或t2时刻,如果电流值大于滞环下限,转为开关信号关断状态。
 |
| 图 12 规则2示例的电流轨迹 Fig. 12 Curves of current track in example for rule 2 |
| 图选项 |
规则1使得在任何情况下,功率管开关频率不会超过20 kHz,确保了器件安全;规则2使得图 11所示的频率变化状态转变为图 12所示的定频状态;规则3则使得当反电动势较大时,也能保持定频状态,如图 13所示;规则4则解决了电流给定值大幅下降时电流下降速率不足无法跟随给定,以及电机处于第二、四象限运行时,负负载造成PWM_ON调制模式的滞环不稳定的情况。
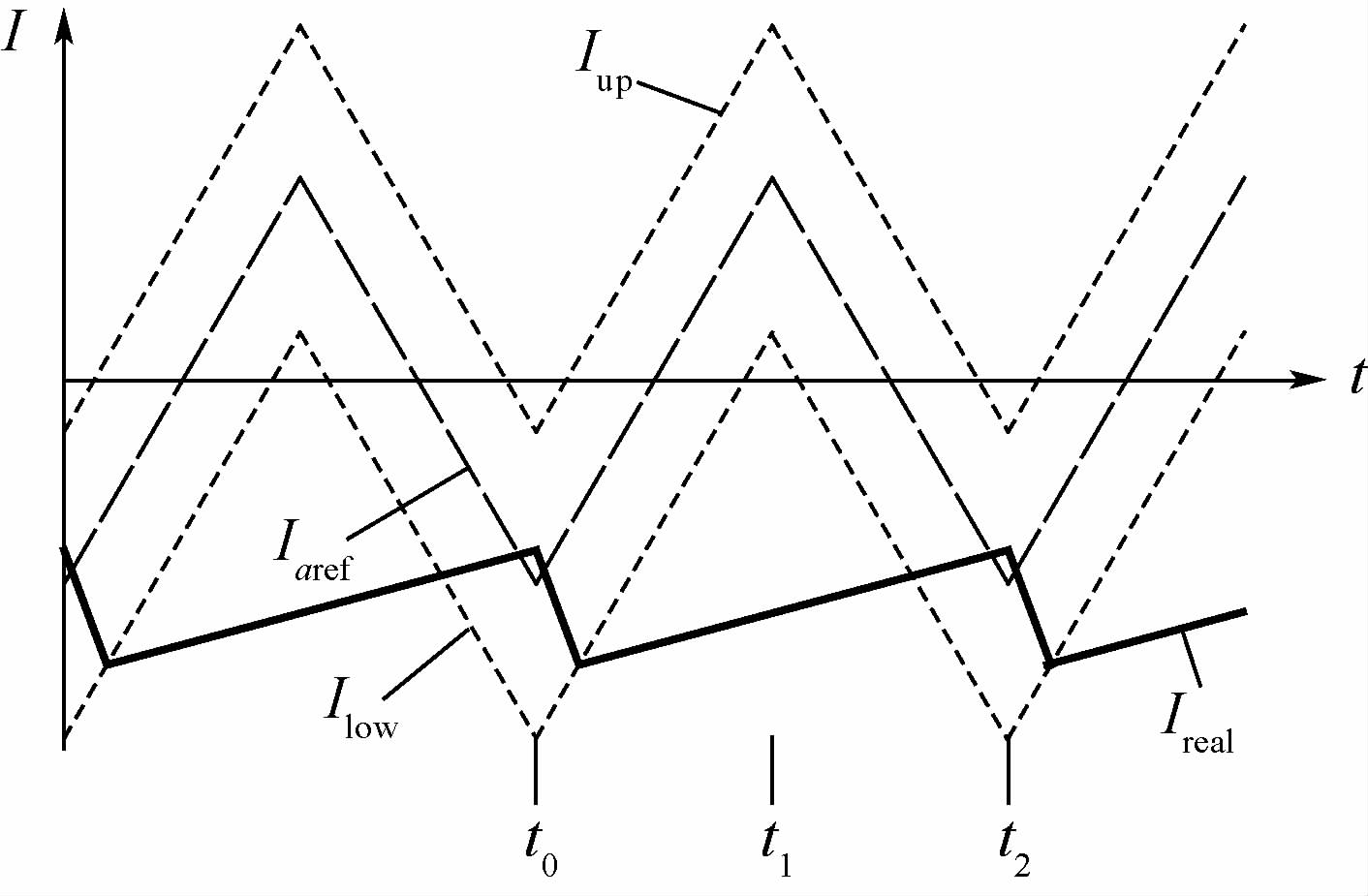 |
| 图 13 规则3示例的电流轨迹 Fig. 13 Curves of current track in example for rule 3 |
| 图选项 |
此外,通过对符合式(12)和式(16)条件的电流轨迹进行分析,可以发现规则1、规则2和规则3并不会对正常情况的电流轨迹造成影响。由此,可以实现PWM_ON调制模式任意转速的定频滞环电流控制。
2.5 系统器件延时环节带来的影响 在控制器实际实现中,电流采样、数字电路逻辑判断、功率器件开关都存在延时,这使得实际情况与理想状态存在差异。虽然开关频率达到20 kHz,但因绕组电感和电阻极小,电流上升速率极高,即便使用高频率响应的电流传感器,选用很高的电流采样频率,器件延时造成的不良影响仍不可忽略。表 1列出了本文所采用器件的大致平均延时。
表 1 滞环电流控制器各器件的典型平均延时 Table 1 Typical averaged delay of parts inhysteresis current controller
| 器件或过程 | 平均延时/μs |
| 霍尔电流传感器 | 0.50 |
| 信号调理电路 | 0.10 |
| ADC采样 | 0.50 |
| CPLD逻辑处理 | 0.01 |
| 光耦隔离器件 | 0.50 |
| IGBT器件开通关断 | 1.00 |
表选项
由表 1中列出的延时信息可知,系统总延时Td可达2.5 μs左右。当延时时间大于理想状态时的电流上升时间或下降时间时,会导致系统出现次谐波振荡或开关频率变化,如图 14所示。
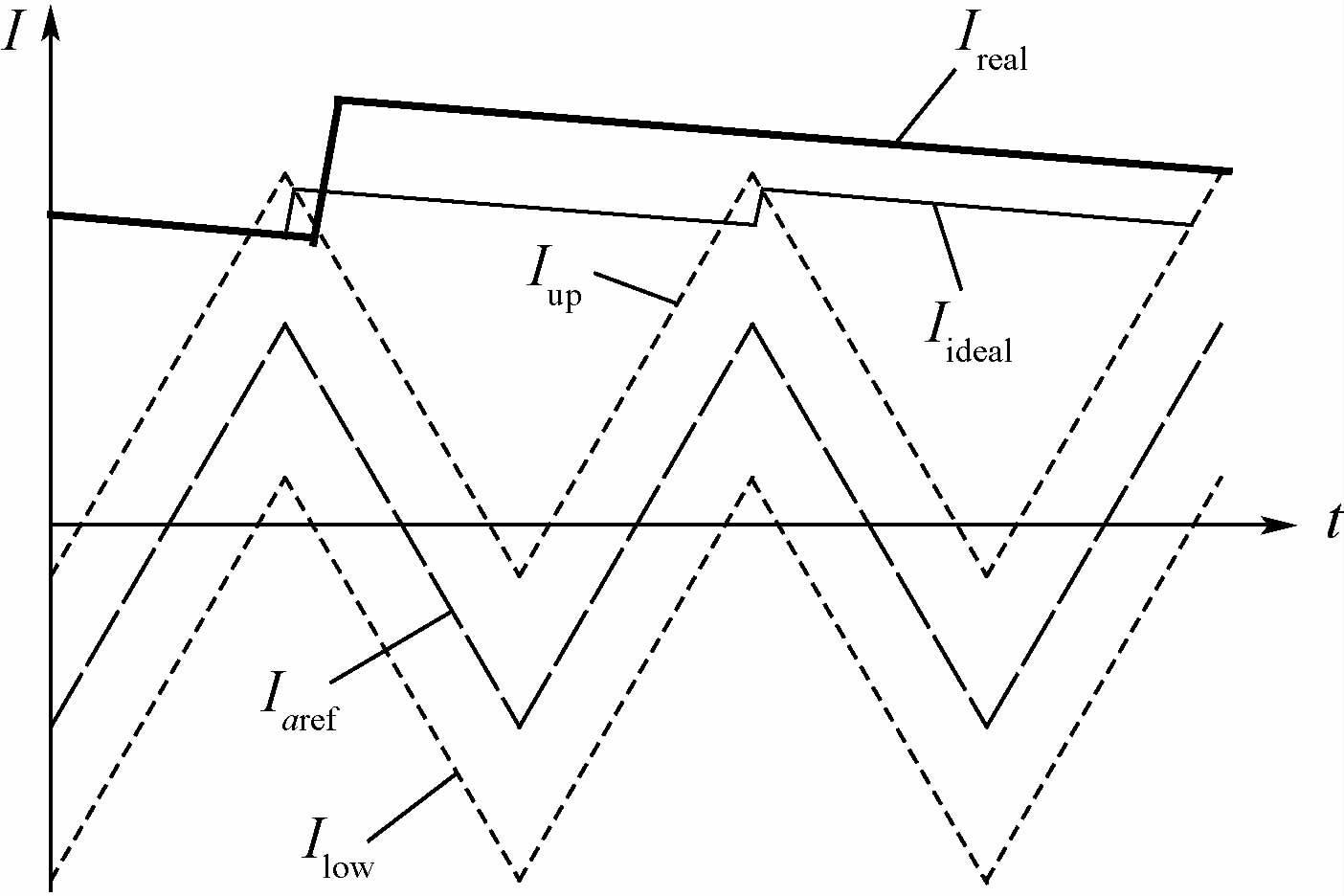 |
| 图 14 器件延时影响开关频率示意图 Fig. 14 Schematic diagram of effect of devicedelay on switch frequency |
| 图选项 |
Iideal为不考虑延时的理想电流轨迹,Ireal为延时大于理想状态电流上升时间时的电流轨迹。由于延时的存在,部分抵消了改进的定频数字滞环电流控制规则2和规则3带来的定频效果。当反电动势值较小或较大时,计入延时Td,要保证系统开关频率恒定,电流上升速率应满足:
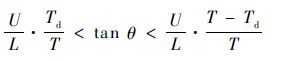 | (17) |
对于本文所研究的无刷直流电机,当Td=2.5 μs时,由式(17)和反电动势参数等可知,当转速超过800 r/min时,开关频率才能达到恒定。可见系统延时对定频效果有较大影响,应尽可能降低系统各个环节的延时。
3 MATLAB/Simulink仿真 为验证本文提出的改进的定频数字滞环电流控制算法的有效性,在MATLAB/Simulink中搭建了电机电流环控制模型。电机模型参数为:母线电压为270 V,电机自感为0.2 mH,互感为0.1 mH,反电动势系数为0.056 V/(rad/s),绕组相电阻为25 mΩ,各个延时环节按照表 1设置。仿真结果如图 15~图 17所示。
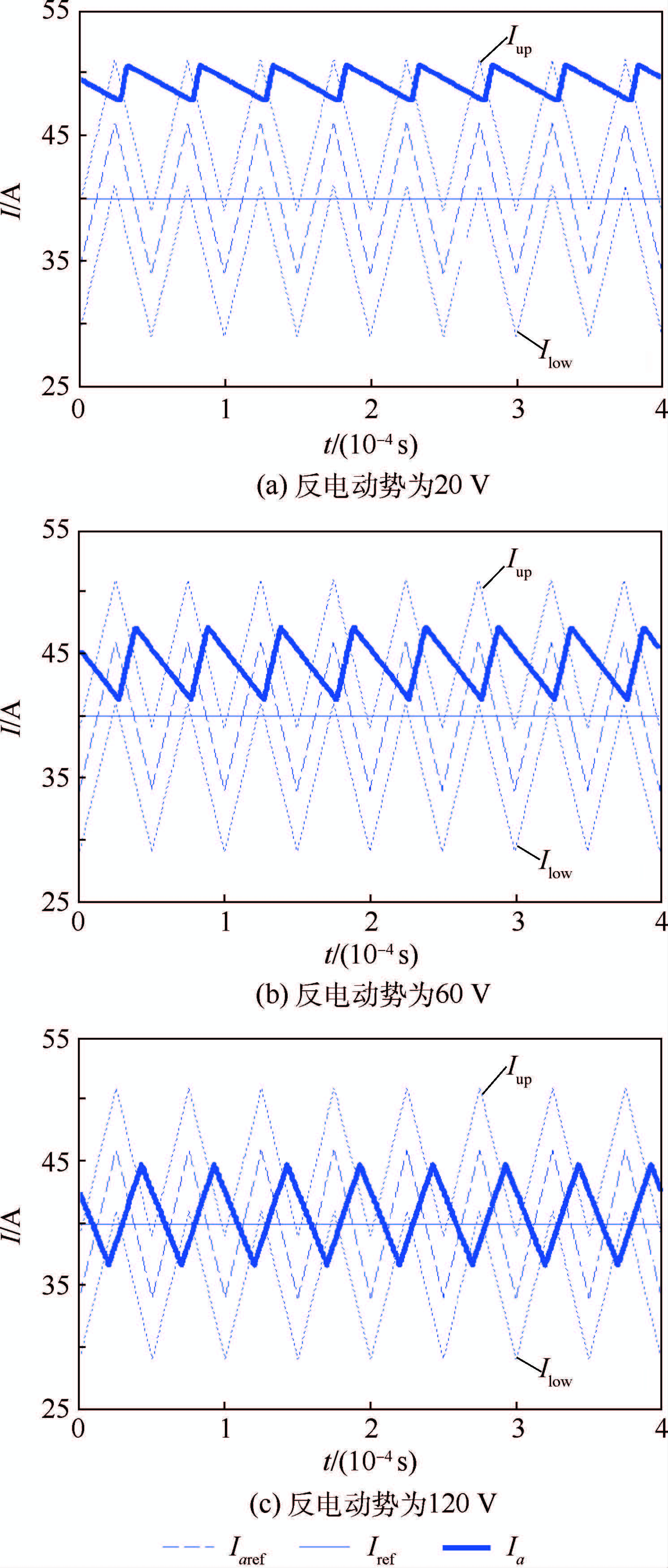 |
| 图 15 反电动势取值不同时的恒值电流仿真响应 Fig. 15 Simulated response of constant targetcurrent when different back EMFs are applied |
| 图选项 |
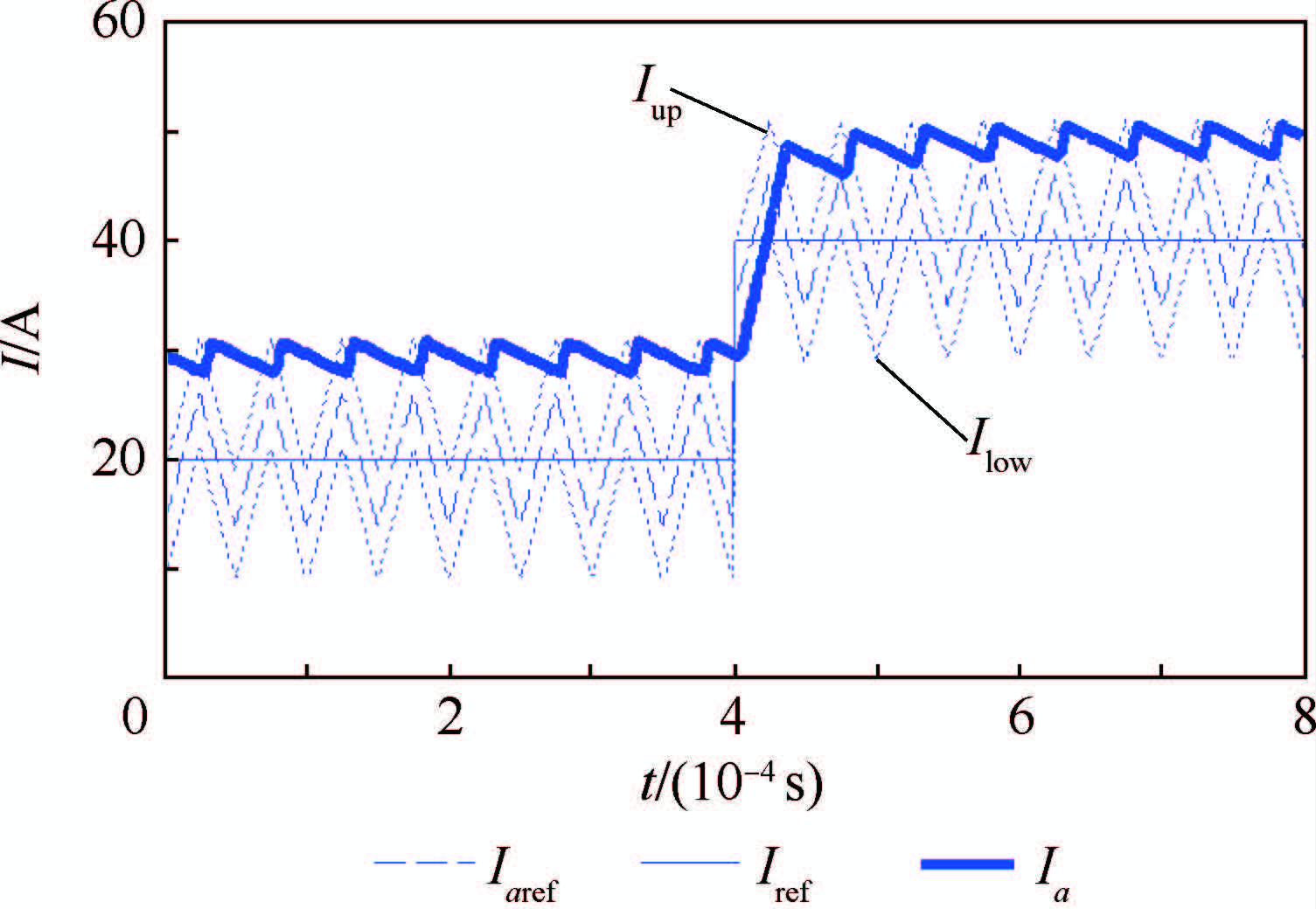 |
| 图 16 反电动势为20 V时的20 A阶跃电流仿真响应 Fig. 16 Simulated response of 20 A steptarget current when back EMF is 20 V |
| 图选项 |
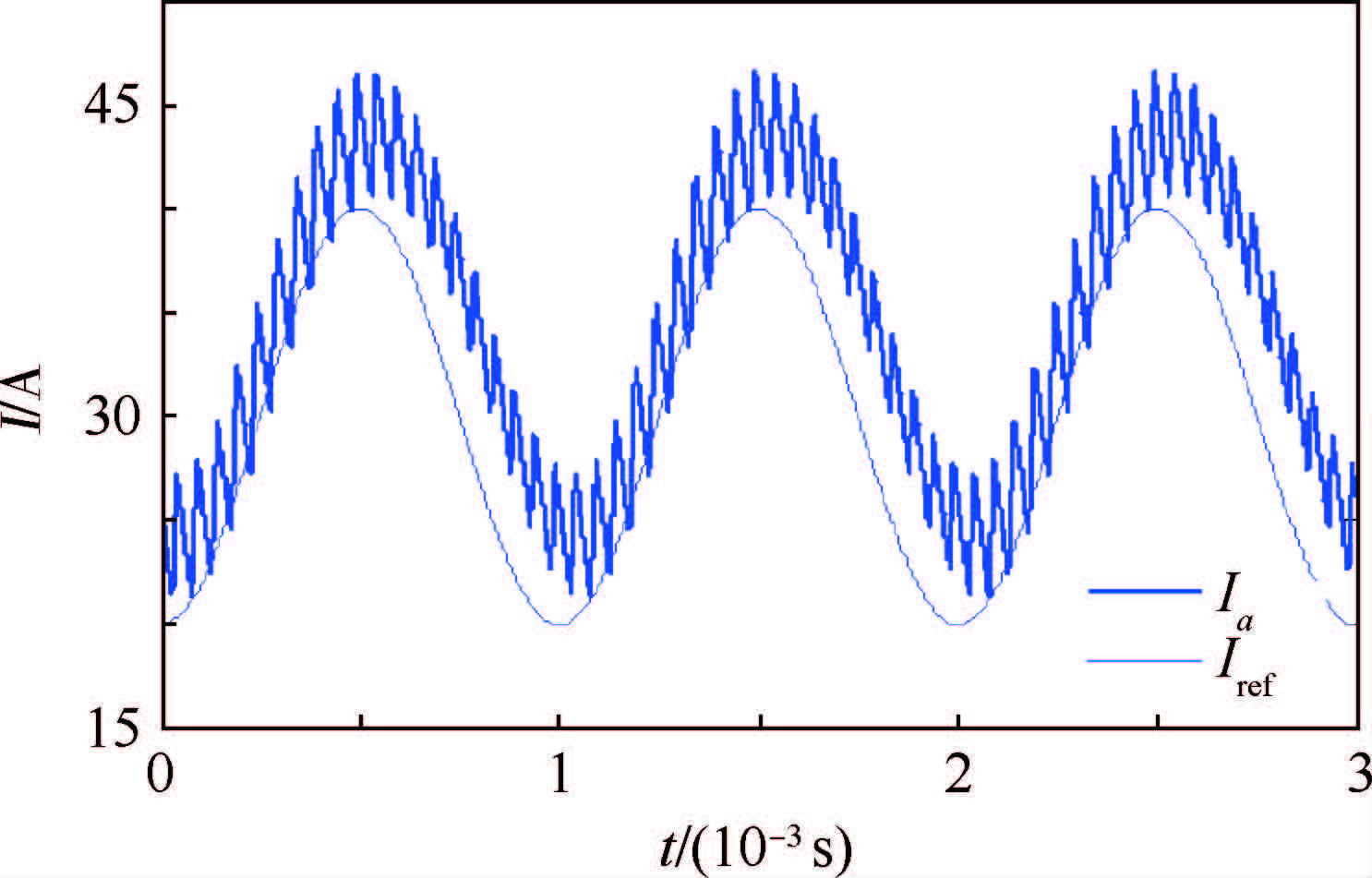 |
| 图 17 反电动势为60 V时的1 kHz、20 A正弦电流仿真响应 Fig. 17 Simulated response of 1 kHz,20 A sinusoidal current when back EMF is 60 V |
| 图选项 |
仿真结果表明,电流环带宽可以达到1 kHz,定频效果良好,同时电流峰值仅略高于给定电流值,开关频率和峰值电流均不会超出功率器件工作范围。
4 实验验证 为进一步验证算法,采用TI TMS320F28335 DSP和ALTERA EPM1270 CPLD作为核心搭建了高响应EHA无刷直流电机控制系统实验平台,系统结构如图 18所示。
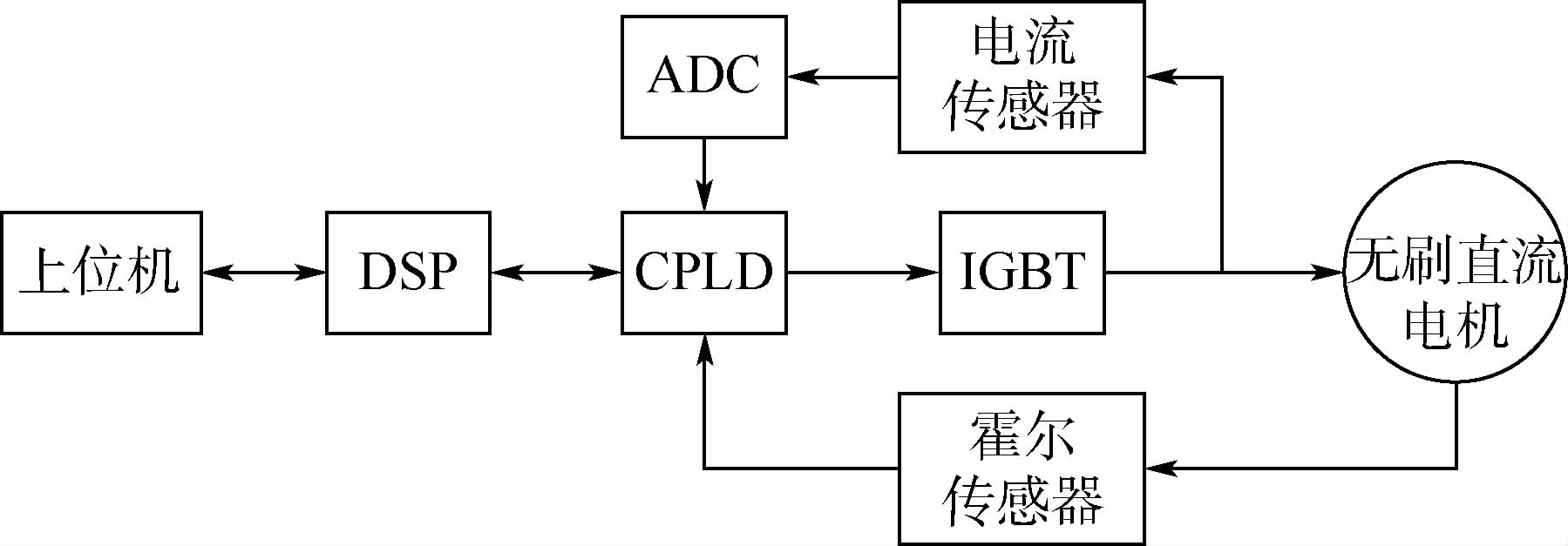 |
| 图 18 无刷直流电机控制系统实验平台结构 Fig. 18 Structure of experimental platform forbrushless DC motor controller system |
| 图选项 |
数字三角载波电流环控制器由电流传感器、信号调理滤波电路、高速14位ADC和CPLD实现,由CPLD完成电流传感器信号ADC的读取、三角载波生成和开关信号输出,并完成故障信号检测保护和输出死区保护。ADC电流信号采样频率为1 MSPS(SPS为采样频率单位,samples per second),电流阈值判断频率为1MHz,设定的功率管开关频率即三角波频率为20 kHz。速度环控制基于DSP实现,与CPLD通过DSP的XINTF接口进行通信,速度环输出,即电流值给定频率,为2~100 kHz可调。
实验结果如图 19~图 21所示。由图 20可见,对于20 A的阶跃输入,电流响应的上升时间小于50 μs,即小于一个开关周期,且开关频率保持恒定。由图 21可见,对于峰峰值20 A、频率1 kHz的正弦波电流输入,跟踪效果良好,开关频率保持恒定。综上,所设计的改进的定频数字滞环电流控制策略跟踪速度快,跟踪全过程定频效果良好。
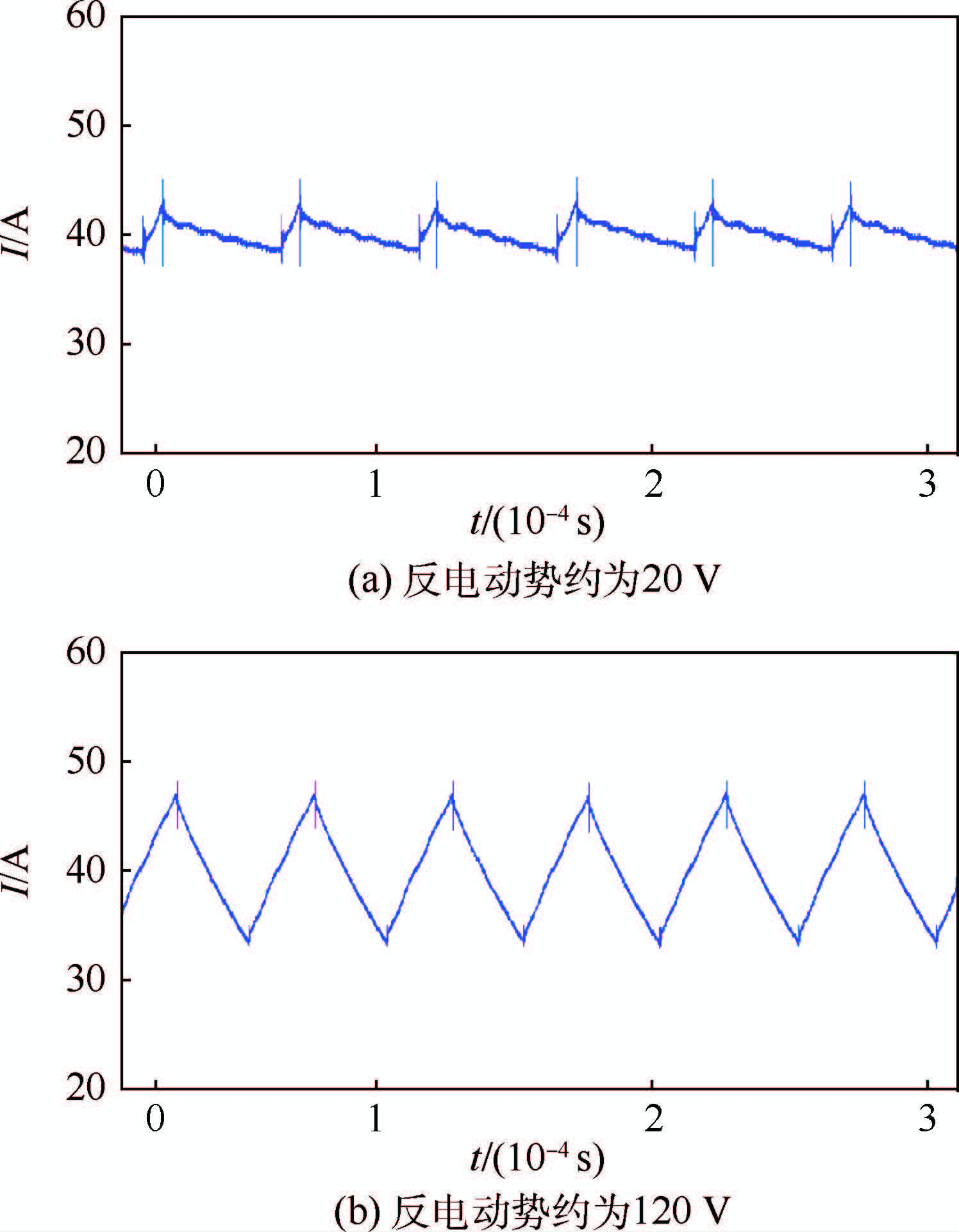 |
| 图 19 反电动势取值不同时的恒值电流实验响应 Fig. 19 Experimental response of constant targetcurrent when different back EMFs are applied |
| 图选项 |
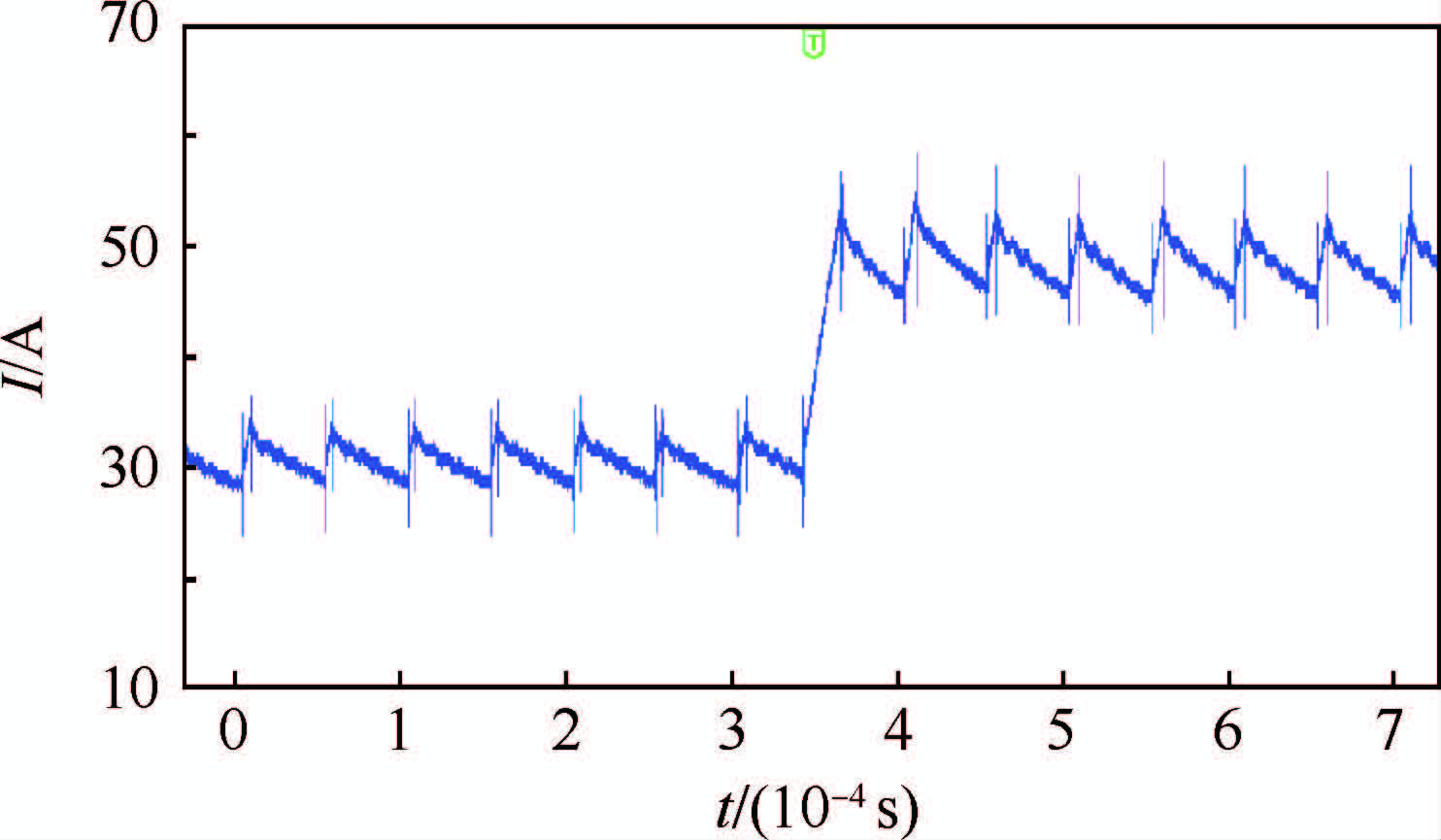 |
| 图 20 反电动势约为20 V时的20 A阶跃电流实验响应 Fig. 20 Experimental response of 20 A steptarget current when back EMF is about 20 V |
| 图选项 |
 |
| 图 21 反电动势约60 V时的1 kHz、20 A正弦电流响应 Fig. 21 Experimental response of 1 kHz,20 Asinusoidal current when back EMF is about 60 V |
| 图选项 |
5 结 论 本文针对EHA用20 kW级大功率无刷直流电机,开展高响应的定频数字滞环电流控制策略研究。
1) 通过对PWM_ON调制模式下相电流数学模型的构建以及相应电流环控制模式的分析,对混合滞环电流控制策略进行改进,进而设计了改进的准定频滞环电流控制策略,使混合滞环电流控制策略的定频范围得到扩展。
2) 针对所设计的改进的准定频滞环电流控制策略在电流控制非稳态区间的非定频控制缺陷,设计数字化规则,形成改进的定频数字滞环电流控制策略,实现了电流控制的全区间定频控制。
3) 分析了器件延时对电流定频控制的不良影响,并确定了计入器件延时时实现定频控制对电流上升速率的约束条件。
4) 构建仿真和实验平台,对所设计的改进的定频数字滞环电流控制策略的控制效果进行分析验证,结果表明,所提出控制策略在定频控制条件下的频响不低于1 kHz,跟踪速度快。
本文所提出的改进的定频数字滞环电流控制策略继承了滞环电流控制策略实现简单、控制稳定、具有天然过流保护功能的特点,同时能实现完全的定频控制,这对降低功率元件损耗、提升电流控制频响和稳定性、提高系统的控制性能具有的积极作用。
参考文献
| [1] | 马纪明, 付永领, 李军, 等. 一体化电动静液作动器(EHA)的设计与仿真分析[J].航空学报, 2005, 26(1): 79–83.MA J M, FU Y L, LI J, et al. Design,simulation and analysis of integrated electrical hydrostatic actuator[J].Acta Aeronautica et Astronautica Sinica, 2005, 26(1): 79–83.(in Chinese) |
| [2] | 夏长亮, 方红伟. 永磁无刷直流电机及其控制[J].电工技术学报, 2012, 27(3): 25–34.XIA C L, FANG H W. Permanent-magnet brushless DC motor and its control[J].Transactions of China Electrotechnical Society, 2012, 27(3): 25–34.(in Chinese) |
| [3] | 董玮. 电流环采样时间对伺服系统快速性影响的研究[J].电气传动, 2004(1): 15–16.DONG W. Study on the sample time of current loop influence to the servo system[J].Electric Drive, 2004(1): 15–16.(in Chinese) |
| [4] | 朱耀忠, 王自强. 飞行控制用无刷直流电动机的电磁设计[J].北京航空航天大学学报, 2000, 26(3): 307–310.ZHU Y Z, WANG Z Q. Consideration in the electromagnetic design of brushless DC motor for flight control[J].Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(3): 307–310.(in Chinese) |
| [5] | WANG H J, YANG M,NIU L,et al.Current-loop bandwidth expansion strategy for permanent magnet synchronous motor drives[C]//Proceedings of the 20105th IEEE Conference on Industrial Electronics and Applications.Piscataway,NJ:IEEE Press,2010:183-188. |
| [6] | 唐小琦, 苏玲宏, 周向东, 等. 基于FPGA的交流伺服系统电流环带宽扩展[J].华中科技大学学报(自然科学版), 2014, 42(2): 1–5.TANG X Q, SU L H, ZHOU X D, et al. Bandwidth expansion of current loop for AC servo system based on FPGA[J].Journal of Huazhong University of Science and Technology(Natural Science Edition), 2014, 42(2): 1–5.(in Chinese) |
| [7] | 卢晓焱, 周元钧. 飞机电源系统恒功率电子负载的EMI滤波器设计[J].电力电子, 2007(4): 29–32.LU X Y, ZHOU Y J. The design of EMI filter for electrical constant power loads of aircraft power system[J].Power Electronics, 2007(4): 29–32.(in Chinese) |
| [8] | 肖春燕, 高帅. 多电飞机电气负载引起的电磁干扰[J].北京航空航天大学学报, 2015, 41(5): 793–801.XIAO C Y, GAO S. Electromagnetic interference caused by electric load of more electric aircraft[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 793–801.(in Chinese) |
| [9] | MALESANI L, TENTI P. A novel hysteresis control method for current-controlled voltage-source PWM inverters with constant modulation frequency[J].IEEE Transactions on Industry Applications, 1990, 26(1): 88–92.DOI:10.1109/28.52678 |
| [10] | BOSE B K. An adaptive hysteresis-band current control technique of a voltage-fed PWM inverter for machine drive system[J].IEEE Transactions on Industry Electronics, 1990, 37(5): 402–408.DOI:10.1109/41.103436 |
| [11] | 洪峰, 单任仲, 王慧贞, 等. 一种变环宽准恒频电流滞环控制方法[J].电工技术学报, 2009, 24(1): 115–119.HONG F, SHAN R Z, WANG H Z, et al. A varied hysteresis-band current controller with fixed switching frequency[J].Transactions of China Electrotechnical Society, 2009, 24(1): 115–119.(in Chinese) |
| [12] | 杨旭, 王兆安. 一种新的准固定频率滞环PWM电流控制方法[J].电工技术学报, 2003, 18(3): 24–28.YANG X, WANG Z A. A novel quasi-constant hysteretic PWM current mode control approach[J].Transactions of China Electrotechnical Society, 2003, 18(3): 24–28.(in Chinese) |
| [13] | 廖金国, 花为, 程明, 等. 一种永磁同步电机变占空比电流滞环控制策略[J].中国电机工程学报, 2015, 35(18): 4762–4770.LIAO J G, HUA W, CHENG M, et al. A variable-duty-cycle current-hysteresis control strategy for permanent magnet synchronous motors[J].Proceedings of the CSEE, 2015, 35(18): 4762–4770.(in Chinese) |
| [14] | 朱思国, 欧阳红林, 刘鼎, 等. 基于电流滞环控制的H桥级联型逆变器新型调制方法[J].电工技术学报, 2013, 28(2): 212–218.ZHU S G, OUYANG H L, LIU D, et al. A new modulation method based on current hysteresis control for cascaded H-bridge inverter[J].Transactions of China Electrotechnical Society, 2013, 28(2): 212–218.(in Chinese) |
| [15] | 徐永海, 刘晓博. 考虑指令电流的变环宽准恒频电流滞环控制方法[J].电工技术学报, 2012, 27(6): 90–95.XU Y H, LIU X B. A variable hysteresis-band and quasi-constant current controller with reference current[J].Transactions of China Electrotechnical Society, 2012, 27(6): 90–95.(in Chinese) |
| [16] | PEREIRA R R,DA SILVA C H,CAVALCANTI L E M,et al.A simple full digital adaptive current hysteresis control with constant modulation frequency for active power filters[C]//42nd IAS Annual Industry Applications Conference.Piscataway,NJ:IEEE Press,2007:1644-1648. |
| [17] | 刘全伟, 邓焰, 胡义华, 等. 基于电流预测和虚拟过采样的数字滞环控制[J].电工技术学报, 2014, 29(10): 127–133.LIU Q W, DENG Y, HU Y H, et al. Current prediction and virtual over-sampling based digital hysteresis control[J].Transactions of China Electrotechnical Society, 2014, 29(10): 127–133.(in Chinese) |
| [18] | 余文涛, 胡育文, 郝振洋, 等. 一种改进型永磁电机数字电流滞环控制方法[J].电气传动, 2010, 40(2): 29–32.YU W T, HU Y W, HAO Z Y, et al. Improved digital current hysteresis control method of fault tolerant permanent magnet machine[J].Electric Drive, 2010, 40(2): 29–32.(in Chinese) |
| [19] | MATTAVELLI P, STEFANUTTI W. Fully digital hysteresis modulation with switching time prediction[J].IEEE Transactions on Industry Applications, 2006, 42(3): 763–769.DOI:10.1109/TIA.2006.873665 |
| [20] | WU F J, FENG F, LUO L S, et al. Sampling period online adjusting-based hysteresis current control without band with constant switching frequency[J].IEEE Transactions on Industrial Electronics, 2015, 62(1): 270–277.DOI:10.1109/TIE.2014.2326992 |
| [21] | RAHMAN M A, RADWAN T S, OSHEIBA A M, et al. Analysis of current controllers for voltage-source inverter[J].IEEE Transactions on Industry Electronics, 1997, 44(4): 477–485.DOI:10.1109/41.605621 |
| [22] | KADJOUDJ M,BENBOUZID M E H,ABDESSEMED R,et al.A robust hybrid current control for permanennt magnet synchronous motor drive[C]//27th Annual Conference of the IEEE Industrial Electronics Society.Piscataway,NJ:IEEE Press,2001:2068-2073. |
